Development of Soft Composite Based Anisotropic Synthetic Skin for Biomechanical Testing
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Matrix and Fiber Materials
2.2. Anisotropic Synthetic Skin Fabrication
2.2.1. Development of Single-Layer Synthetic Skin
2.2.2. Development of Multi-Layer Synthetic Skin
2.3. Method Parameters and Testing Setup
2.4. Anisotropic Material Characterization
3. Results and Discussion
3.1. Stress Analysis of Single-Layer Synthetic Skin
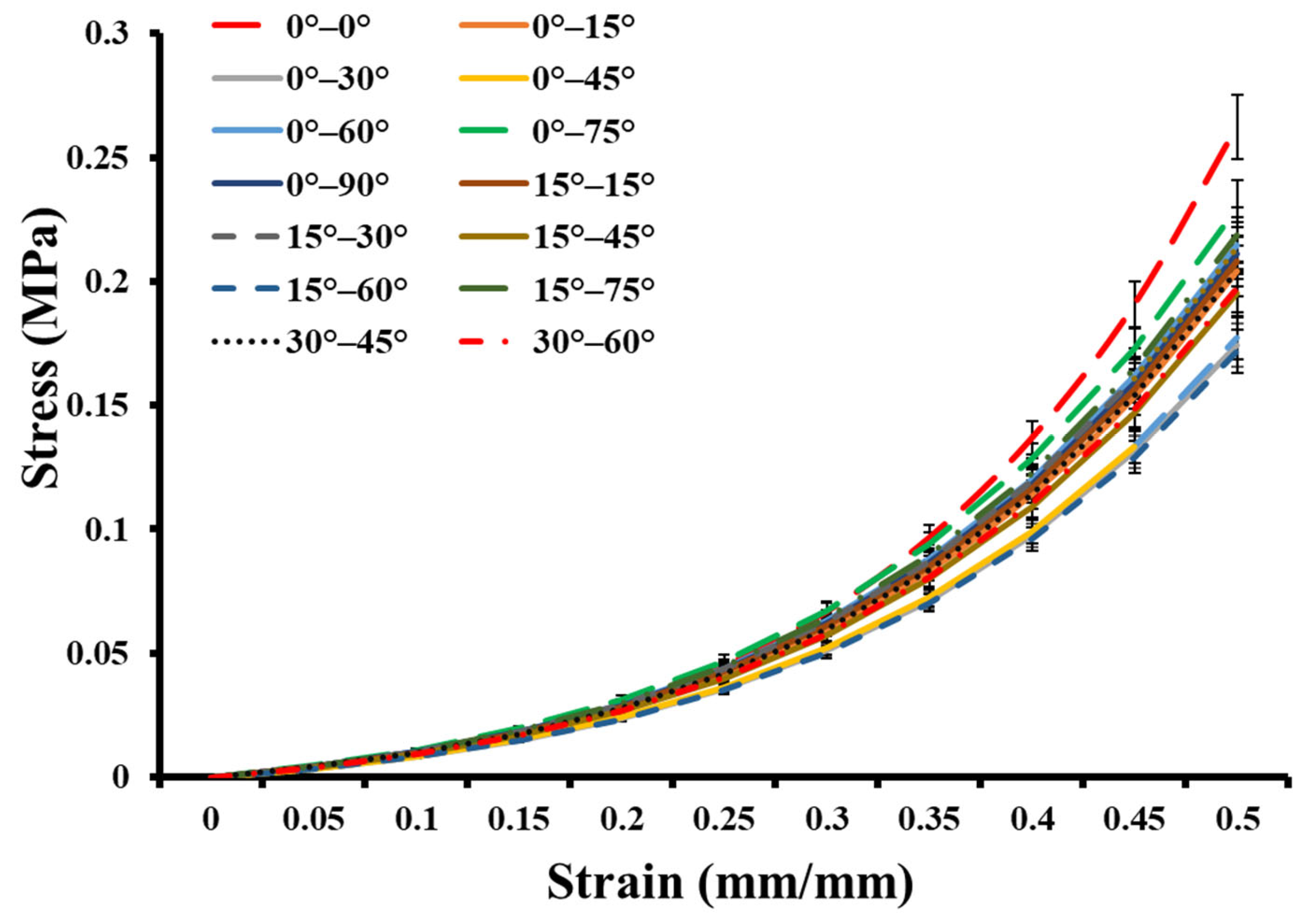
3.2. Stress Analysis of Two-Layer Synthetic Skin
3.3. Hyperelastic Modelling of Synthetic Skin
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yi, D.; Choe, Y.M.; Byun, M.S.; Sohn, B.K.; Seo, E.H.; Han, J.; Park, J.; Woo, J.I.; Lee, D.Y. Differences in functional brain connectivity alterations associated with cerebral amyloid deposition in amnestic mild cognitive impairment. Front. Aging Neurosci. 2015, 7, 15. [Google Scholar] [CrossRef] [PubMed]
- Picinbono, G.; Delingette, H.; Ayache, N. Non-linear and anisotropic elastic soft tissue models for medical simulation. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Republic of Korea, 21–26 May 2001; Volume 2, pp. 1370–1375. [Google Scholar] [CrossRef]
- Singh, G.; Chanda, A. Mechanical properties of whole-body soft human tissues: A review. Biomed. Mater. 2021, 16, 062004. [Google Scholar] [CrossRef] [PubMed]
- Serebrakian, A.T.; Pickrell, B.B.; Varon, D.E.; Mohamadi, A.; Grinstaff, M.W.; Rodriguez, E.K.; Nazarian, A.; Halvorson, E.G.; Sinha, I. Meta-analysis and Systematic Review of Skin Graft Donor-site Dressings with Future Guidelines. Plast. Reconstr. Surg. Glob. Open 2018, 6, e1928. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.L.E.; Joyce, T.J.; Goh, K.L. Resolving the viscoelasticity and anisotropy dependence of the mechanical properties of skin from a porcine model. Biomech. Model. Mechanobiol. 2016, 15, 433–446. [Google Scholar] [CrossRef]
- Flynn, C.; Taberner, A.; Nielsen, P. Mechanical characterisation of in vivo human skin using a 3D force-sensitive micro-robot and finite element analysis. Biomech. Model. Mechanobiol. 2011, 10, 27–38. [Google Scholar] [CrossRef]
- Groves, R.B.; Coulman, S.A.; Birchall, J.C.; Evans, S.L. An anisotropic, hyperelastic model for skin: Experimental measurements, finite element modelling and identification of parameters for human and murine skin. J. Mech. Behav. Biomed. Mater. 2013, 18, 167–180. [Google Scholar] [CrossRef]
- Roberts, D.E.; Scher, A.M. Effect of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ. Res. 1982, 50, 342–351. [Google Scholar] [CrossRef]
- Aslanidi, O.V.; Boyett, M.R.; Dobrzynski, H.; Li, J.; Zhang, H. Mechanisms of transition from normal to reentrant electrical activity in a model of rabbit atrial tissue: Interaction of tissue heterogeneity and anisotropy. Biophys. J. 2009, 96, 798–817. [Google Scholar] [CrossRef]
- Liu, M.; Wang, L.; Peng, X. Testing, characterizing, and forming of glass twill fabric/polypropylene prepregs. J. Compos. Mater. 2019, 53, 3939–3950. [Google Scholar] [CrossRef]
- Mandal, B.B.; Kundu, S.C. Cell proliferation and migration in silk fibroin 3D scaffolds. Biomaterials 2009, 30, 2956–2965. [Google Scholar] [CrossRef]
- Singh, G.; Gupta, V.; Chanda, A. Artificial skin with varying biomechanical properties. Mater. Today Proc. 2022, 62, 3162–3166. [Google Scholar] [CrossRef]
- Carotenuto, F.; Politi, S.; Ul Haq, A.; De Matteis, F.; Tamburri, E.; Terranova, M.L.; Teodori, L.; Pasquo, A.; Di Nardo, P. From Soft to Hard Biomimetic Materials: Tuning Micro/Nano-Architecture of Scaffolds for Tissue Regeneration. Micromachines 2022, 13, 780. [Google Scholar] [CrossRef]
- Patel, S.; Caldwell, J.M.; Doty, S.B.; Levine, W.N.; Rodeo, S.; Soslowsky, L.J.; Thomopoulos, S.; Lu, H.H. Integrating soft and hard tissues via interface tissue engineering. J. Orthop. Res. 2018, 36, 1069–1077. [Google Scholar] [CrossRef]
- Michels, J.; Appel, E.; Gorb, S.N. Functional diversity of resilin in Arthropoda. Beilstein J. Nanotechnol. 2016, 7, 1241–1259. [Google Scholar] [CrossRef]
- Carlsen, R.W.; Daphalapurkar, N.P. The importance of structural anisotropy in computational models of traumatic brain injury. Front. Neurol. 2015, 6, 28. [Google Scholar] [CrossRef]
- Fang, Y.; Yang, X.; Lin, Y.; Shi, J.; Prominski, A.; Clayton, C.; Ostroff, E.; Tian, B. Dissecting Biological and Synthetic Soft-Hard Interfaces for Tissue-Like Systems. Chem. Rev. 2022, 122, 5233–5276. [Google Scholar] [CrossRef]
- Liu, Z.; Liao, Z.; Wang, D.; Wang, C.; Song, C.; Li, H.; Liu, Y. Recent Advances in Soft Biological Tissue Manipulating Technologies. Chin. J. Mech. Eng. 2022, 35, 89. [Google Scholar] [CrossRef]
- Famaey, N.; Sloten, J.V. Soft tissue modelling for applications in virtual surgery and surgical robotics. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 351–366. [Google Scholar] [CrossRef]
- Martins, P.; Peña, E.; Calvo, B.; Doblaré, M.; Mascarenhas, T.; Jorge, R.N.; Ferreira, A. Prediction of nonlinear elastic behaviour of vaginal tissue: Experimental results and model formulation. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 327–337. [Google Scholar] [CrossRef]
- Natali, A.N.; Pavan, P.G.; Carniel, E.L.; Dorow, C. A transversally isotropic elasto-damage constitutive model for the periodontal ligament. Comput. Methods Biomech. Biomed. Eng. 2003, 6, 329–336. [Google Scholar] [CrossRef]
- Ranamukhaarachchi, S.A.; Lehnert, S.; Ranamukhaarachchi, S.L.; Sprenger, L.; Schneider, T.; Mansoor, I.; Rai, K.; Häfeli, U.O.; Stoeber, B. A micromechanical comparison of human and porcine skin before and after preservation by freezing for medical device development. Sci. Rep. 2016, 6, 32074. [Google Scholar] [CrossRef] [PubMed]
- Blair, M.J.; Jones, J.D.; Woessner, A.E.; Quinn, K.P. Skin Structure-Function Relationships and the Wound Healing Response to Intrinsic Aging. Adv. Wound Care 2020, 9, 127–143. [Google Scholar] [CrossRef] [PubMed]
- Belkoff, S.M.; Haut, R.C. A structural model used to evaluate the changing microstructure of maturing rat skin. J. Biomech. 1991, 24, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, C.T.; Birch, H.L.; Clegg, P.D.; Screen, H.R.C. The role of the non-collagenous matrix in tendon function. Int. J. Exp. Pathol. 2013, 94, 248–259. [Google Scholar] [CrossRef]
- Li, Y.; Fessel, G.; Georgiadis, M.; Snedeker, J.G. Advanced glycation end-products diminish tendon collagen fiber sliding. Matrix Biol. 2013, 32, 169–177. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Biomechanics of skin grafts: Effect of pattern size, spacing and orientation. Eng. Res. Express 2022, 4, 015006. [Google Scholar] [CrossRef]
- Payne, T.; Mitchell, S.; Bibb, R.; Waters, M. Initial validation of a relaxed human soft tissue simulant for sports impact surrogates. Procedia Eng. 2014, 72, 533–538. [Google Scholar] [CrossRef]
- Shergold, O.A.; Fleck, N.A.; Radford, D. The uniaxial stress versus strain response of pig skin and silicone rubber at low and high strain rates. Int. J. Impact Eng. 2006, 32, 1384–1402. [Google Scholar] [CrossRef]
- Arm, R.; Shahidi, A.; Dias, T. Mechanical behaviour of silicone membranes saturated with short strand, loose polyester fibres for prosthetic and rehabilitative surrogate skin applications. Materials 2019, 12, 3647. [Google Scholar] [CrossRef]
- Hossain, M.; Liao, Z. An additively manufactured silicone polymer: Thermo-viscoelastic experimental study and computational modelling. Addit. Manuf. 2020, 35, 101395. [Google Scholar] [CrossRef]
- Zhang, J.; Keith, A.N.; Sheiko, S.S.; Wang, X.; Wang, Z. To mimic mechanical properties of the skin by inducing oriented nanofiber microstructures in bottlebrush cellulose-graft-diblock copolymer elastomers. ACS Appl. Mater. Interfaces 2021, 13, 3278–3286. [Google Scholar] [CrossRef]
- MacNeil, S. Progress and opportunities for tissue-engineered skin. Nature 2007, 445, 874–880. [Google Scholar] [CrossRef]
- Chanda, A.; Callaway, C. Tissue anisotropy modeling using soft composite materials. Appl. Bionics Biomech. 2018, 2018, 4838157. [Google Scholar] [CrossRef]
- Ojogbo, E.; Tzoganakis, C.; Mekonnen, T.H. Effect of extrusion, batch-mixing, and co-coagulation on the dispersion of CNCs in natural rubber-CNC nanocomposites. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106580. [Google Scholar] [CrossRef]
- Mongkolsuttirat, K.; Sanponpute, T. Prototype of Depth Standard for Elastomer Hardness Tester. J. Phys. Conf. Ser. 2018, 1065, 062012. [Google Scholar] [CrossRef]
- Durban, M.M.; Lenhardt, J.M.; Wu, A.S.; Small, W.; Bryson, T.M.; Perez-Perez, L.; Nguyen, D.T.; Gammon, S.; Smay, J.E.; Duoss, E.B.; et al. Custom 3D Printable Silicones with Tunable Stiffness. Macromol. Rapid Commun. 2018, 39, 1700563. [Google Scholar] [CrossRef]
- Herzberger, J.; Sirrine, J.M.; Williams, C.B.; Long, T.E. Polymer Design for 3D Printing Elastomers: Recent Advances in Structure, Properties, and Printing. Prog. Polym. Sci. 2019, 97, 101144. [Google Scholar] [CrossRef]
- Webster, T.; Yao, C.; Hedrick, M.; Pareek, G.; Haleblian, G.; Renzulli, J. Nanostructured polyurethane-poly-lactic- co-glycolic acid scaffolds increase bladder tissue regeneration: An in vivo study. Int. J. Nanomed. 2013, 8, 3285. [Google Scholar] [CrossRef]
- Parikh, D.V.; Calamari, T.A.; Sawhney, A.P.S.; Blanchard, E.J.; Screen, F.J.; Myatt, J.C.; Muller, D.H.; Stryjewski, D.D. Thermoformable Automotive Composites Containing Kenaf and Other Cellulosic Fibers. Text. Res. J. 2002, 72, 668–672. [Google Scholar] [CrossRef]
- Singh, G.; Gupta, V.; Chanda, A. Mechanical Characterization of Rotating Triangle Shaped Auxetic Skin Graft Simulants. Facta Univ. Ser. Mech. Eng. 2022, 1–16. [Google Scholar] [CrossRef]
- Chanda, A.; Upchurch, W. Biomechanical Modeling of Wounded Skin. J. Compos. Sci. 2018, 2, 69. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z.; Lackey, K. Experimental study on tissue phantoms to understand the effect of injury and suturing on human skin mechanical properties. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Ní Annaidh, A.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef] [PubMed]




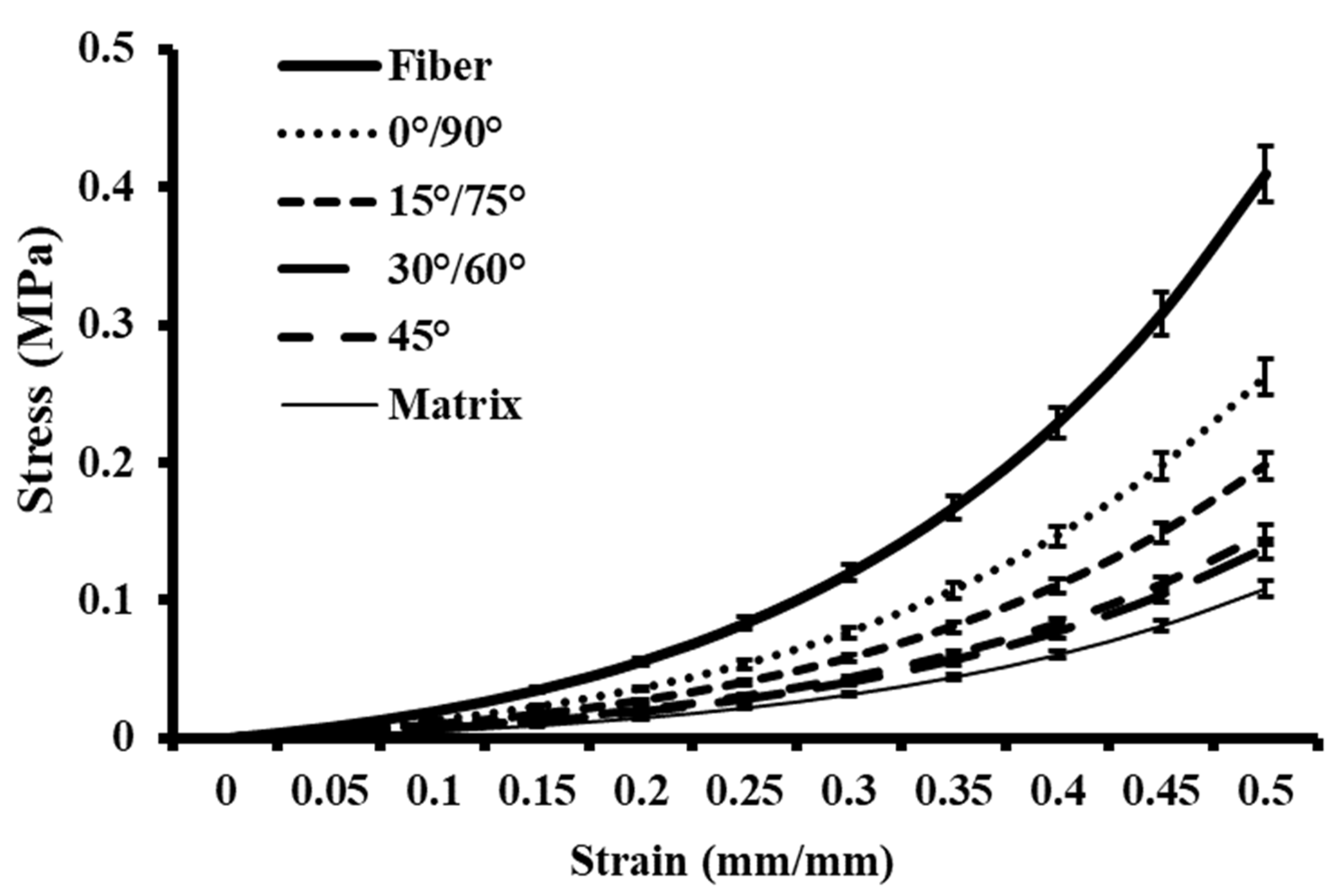
| Design | Matrix Volume (mm3) | Fiber Volume (mm3) | Fiber Volume Fraction | Matrix Volume Fraction |
|---|---|---|---|---|
| 0/90° | 15,180 | 4820 | 0.243 | 0.757 |
| 15/75° | 14,776 | 5224 | 0.261 | 0.739 |
| 30/60° | 15,392 | 4608 | 0.234 | 0.766 |
| 45° | 15,392 | 4608 | 0.234 | 0.766 |
| Composition | Stress Values in MPa | ||||
|---|---|---|---|---|---|
| At 0.1 mm/mm Strain | At 0.2 mm/mm Strain | At 0.3 mm/mm Strain | At 0.4 mm/mm Strain | At 0.5 mm/mm Strain | |
| 0–0° | 0.009 | 0.029 | 0.067 | 0.137 | 0.262 |
| 0–15° | 0.010 | 0.028 | 0.060 | 0.114 | 0.204 |
| 0–30° | 0.008 | 0.024 | 0.051 | 0.098 | 0.174 |
| 0–45° | 0.008 | 0.024 | 0.052 | 0.099 | 0.177 |
| 0–60° | 0.010 | 0.029 | 0.063 | 0.120 | 0.215 |
| 0–75° | 0.011 | 0.031 | 0.067 | 0.128 | 0.229 |
| 0–90° | 0.010 | 0.029 | 0.062 | 0.118 | 0.211 |
| 15–15° | 0.010 | 0.028 | 0.061 | 0.116 | 0.208 |
| 15–30° | 0.010 | 0.029 | 0.063 | 0.119 | 0.213 |
| 15–45° | 0.009 | 0.027 | 0.057 | 0.109 | 0.195 |
| 15–60° | 0.008 | 0.023 | 0.050 | 0.096 | 0.172 |
| 15–75° | 0.010 | 0.030 | 0.064 | 0.122 | 0.219 |
| 30–45° | 0.010 | 0.028 | 0.060 | 0.114 | 0.204 |
| 30–60° | 0.009 | 0.027 | 0.058 | 0.110 | 0.197 |
| Synthetic Skin | Mooney-Rivlin Model | Yeoh | |||
|---|---|---|---|---|---|
| c1 (MPa) | c2 (MPa) | c1 (MPa) | c2 (MPa) | c3 (MPa) | |
| Matrix | 0.02525 | 0.00010 | 0.00806 | 0.01825 | 0.00474 |
| Fiber | 0.09531 | 0.00010 | 0.03044 | 0.06891 | 0.01788 |
| 0° | 0.06106 | 0.00010 | 0.0195 | 0.04415 | 0.01145 |
| 15° | 0.04603 | 0.00010 | 0.0147 | 0.03328 | 0.00863 |
| 30° | 0.03199 | 0.00010 | 0.01022 | 0.02313 | 0.00600 |
| 45° | 0.03447 | 0.00010 | 0.01101 | 0.02492 | 0.00647 |
| 0–0° | 0.06971 | 0.00010 | 0.01612 | 0.06174 | 0.00586 |
| 0–15° | 0.03343 | 0.05307 | 0.01518 | 0.03436 | 0.00891 |
| 0–30° | 0.0665 | 0.00010 | 0.01518 | 0.03436 | 0.00892 |
| 0–45° | 0.05841 | 0.01731 | 0.01587 | 0.03592 | 0.00932 |
| 0–60° | 0.0527 | 0.00561 | 0.01297 | 0.02936 | 0.00762 |
| 0–75° | 0.02476 | 0.04198 | 0.01277 | 0.0289 | 0.0075 |
| 0–90° | 0.06186 | 0.01427 | 0.01571 | 0.03557 | 0.00923 |
| 15–15° | 0.00010 | 0.11194 | 0.01598 | 0.03617 | 0.00938 |
| 15–30° | 0.06663 | 0.00133 | 0.01548 | 0.03503 | 0.00909 |
| 15–45° | 4.2 × 10−6 | 0.10614 | 0.01627 | 0.03683 | 0.00956 |
| 15–60° | 0.00010 | 0.12614 | 0.01706 | 0.03862 | 0.01002 |
| 15–75° | 0.00010 | 0.09844 | 0.01468 | 0.03322 | 0.00862 |
| 30–45° | 0.05667 | 0.00010 | 0.01318 | 0.02983 | 0.00774 |
| 30–60° | 0.08760 | 0.00713 | 0.02104 | 0.04761 | 0.01235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, V.; Singla, R.; Singh, G.; Chanda, A. Development of Soft Composite Based Anisotropic Synthetic Skin for Biomechanical Testing. Fibers 2023, 11, 55. https://doi.org/10.3390/fib11060055
Gupta V, Singla R, Singh G, Chanda A. Development of Soft Composite Based Anisotropic Synthetic Skin for Biomechanical Testing. Fibers. 2023; 11(6):55. https://doi.org/10.3390/fib11060055
Chicago/Turabian StyleGupta, Vivek, Rohan Singla, Gurpreet Singh, and Arnab Chanda. 2023. "Development of Soft Composite Based Anisotropic Synthetic Skin for Biomechanical Testing" Fibers 11, no. 6: 55. https://doi.org/10.3390/fib11060055
APA StyleGupta, V., Singla, R., Singh, G., & Chanda, A. (2023). Development of Soft Composite Based Anisotropic Synthetic Skin for Biomechanical Testing. Fibers, 11(6), 55. https://doi.org/10.3390/fib11060055








