The Mechanical Response of Epoxy–Sisal Composites Considering Fiber Anisotropy: A Computational and Experimental Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. SFRC Fabrication Process
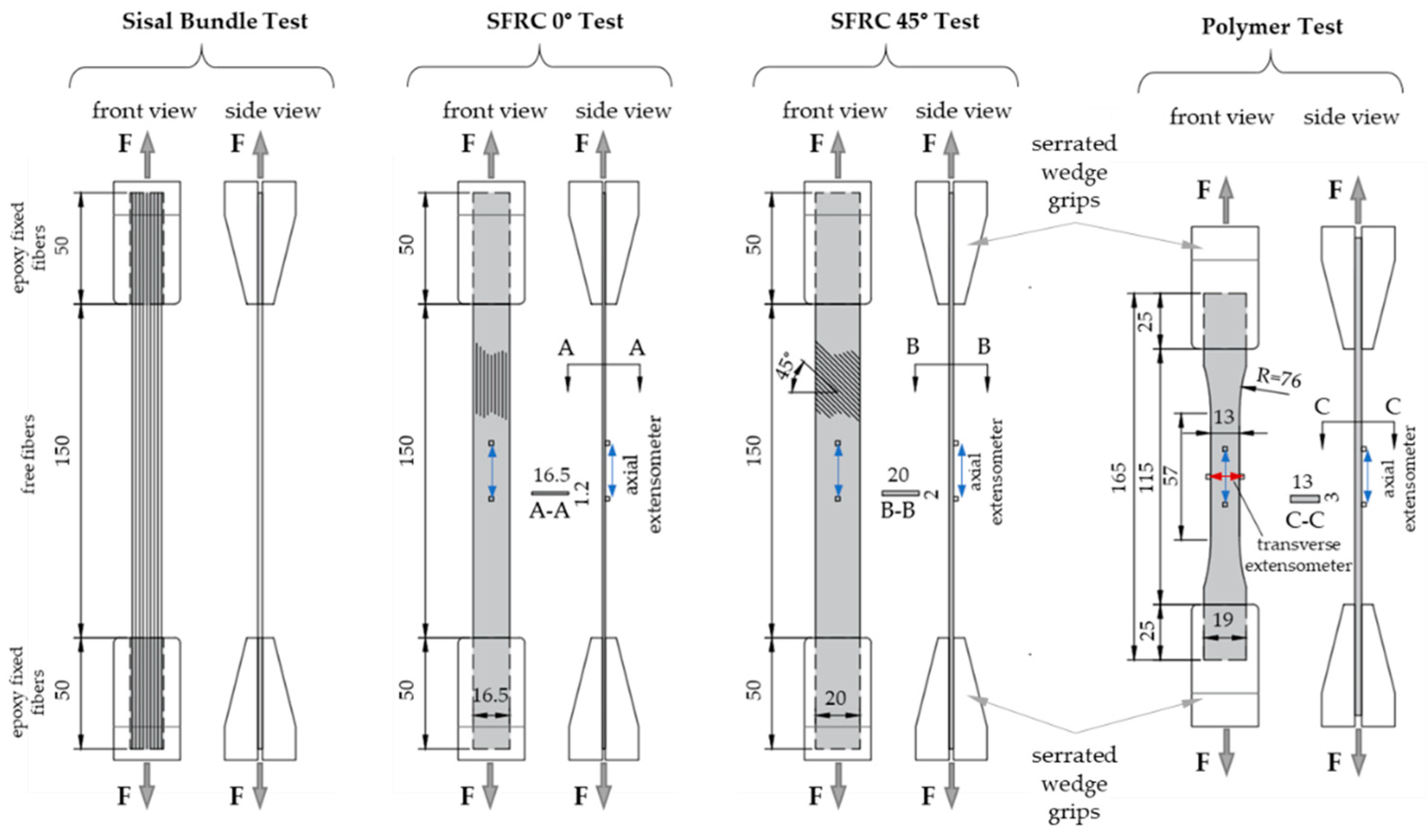
2.2. Mechanical Loading Experiments
2.3. Analytical and Numerical Determination of SFRC Effective Properties
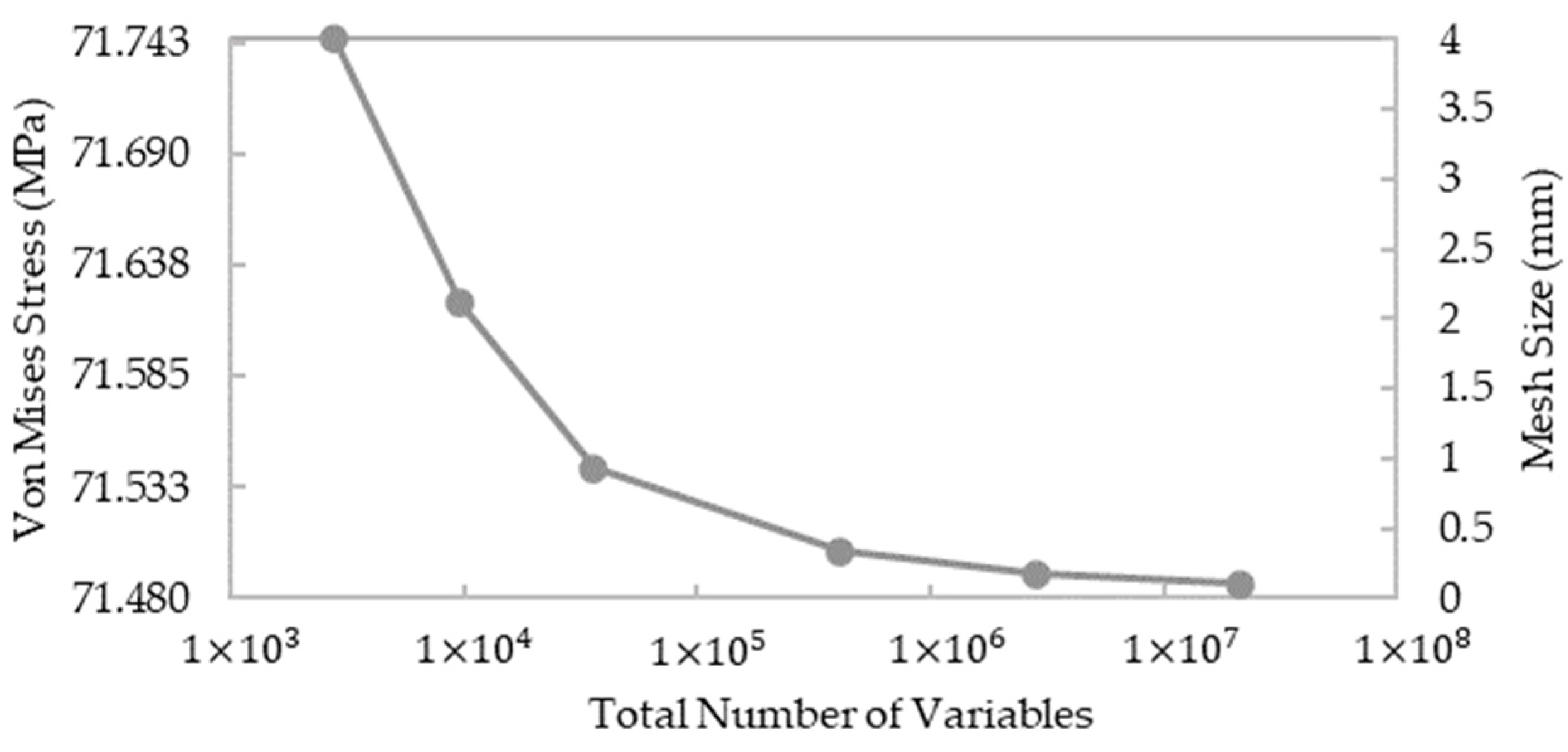
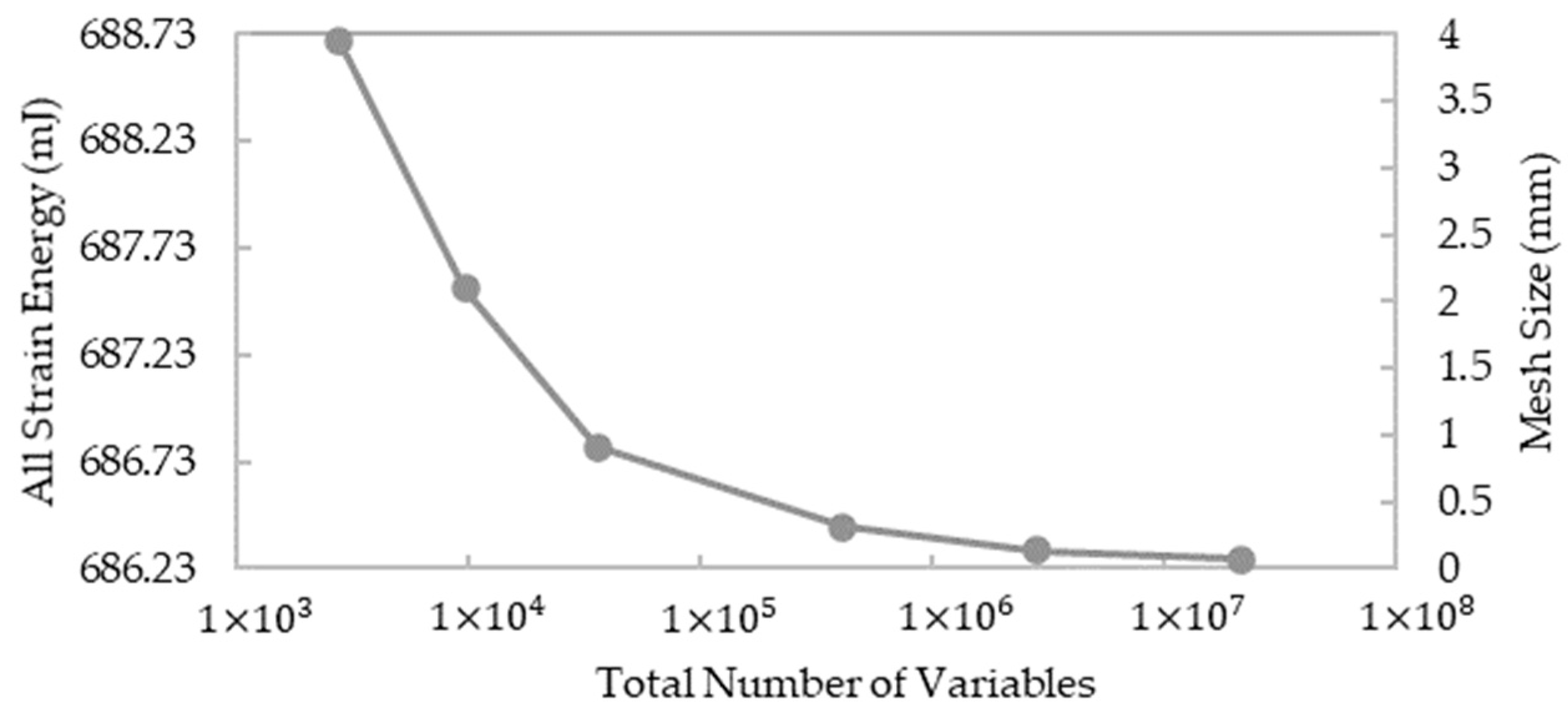
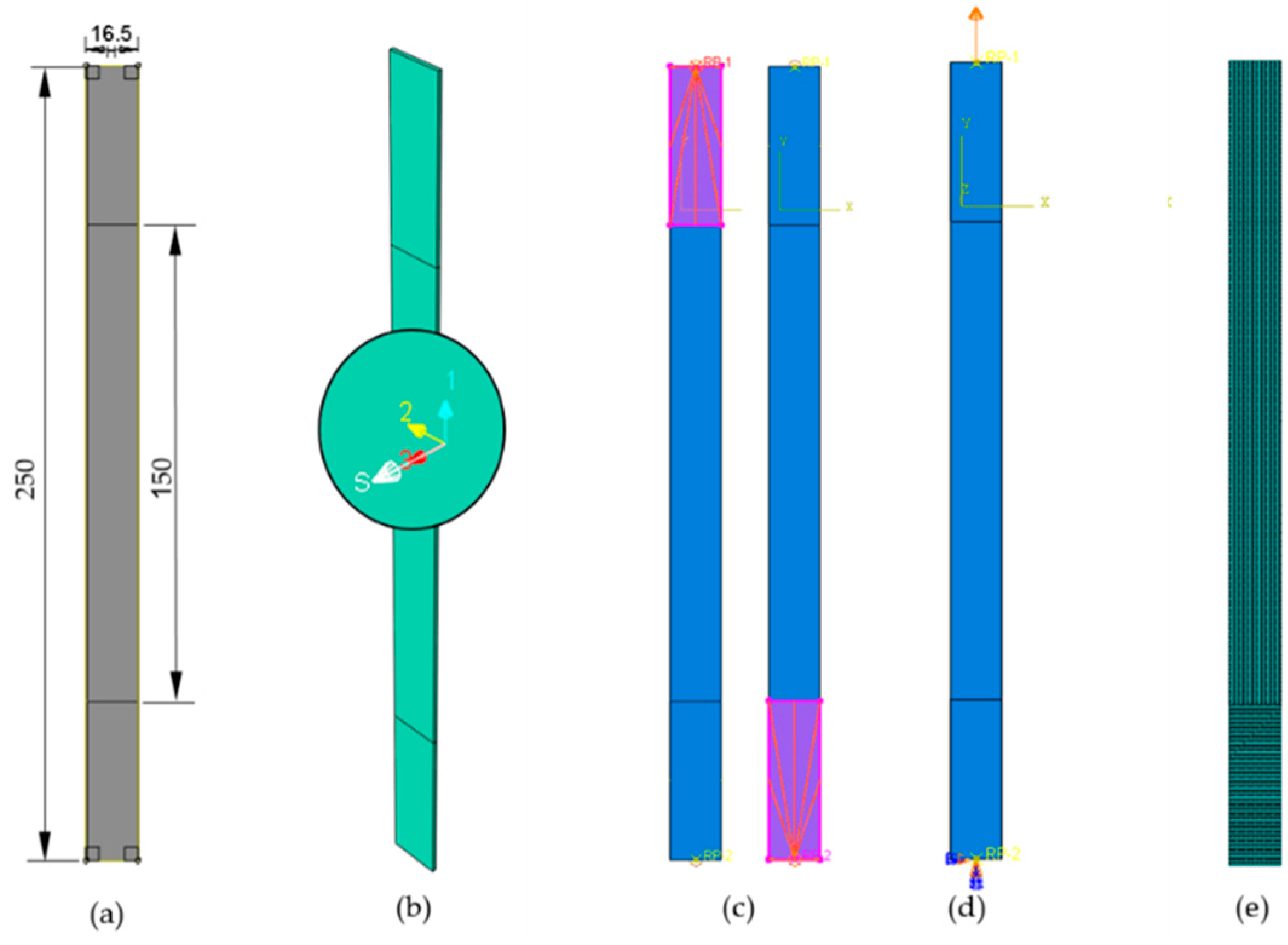
2.4. Finite Element Modeling of SFRC Mechanical Response
3. Results
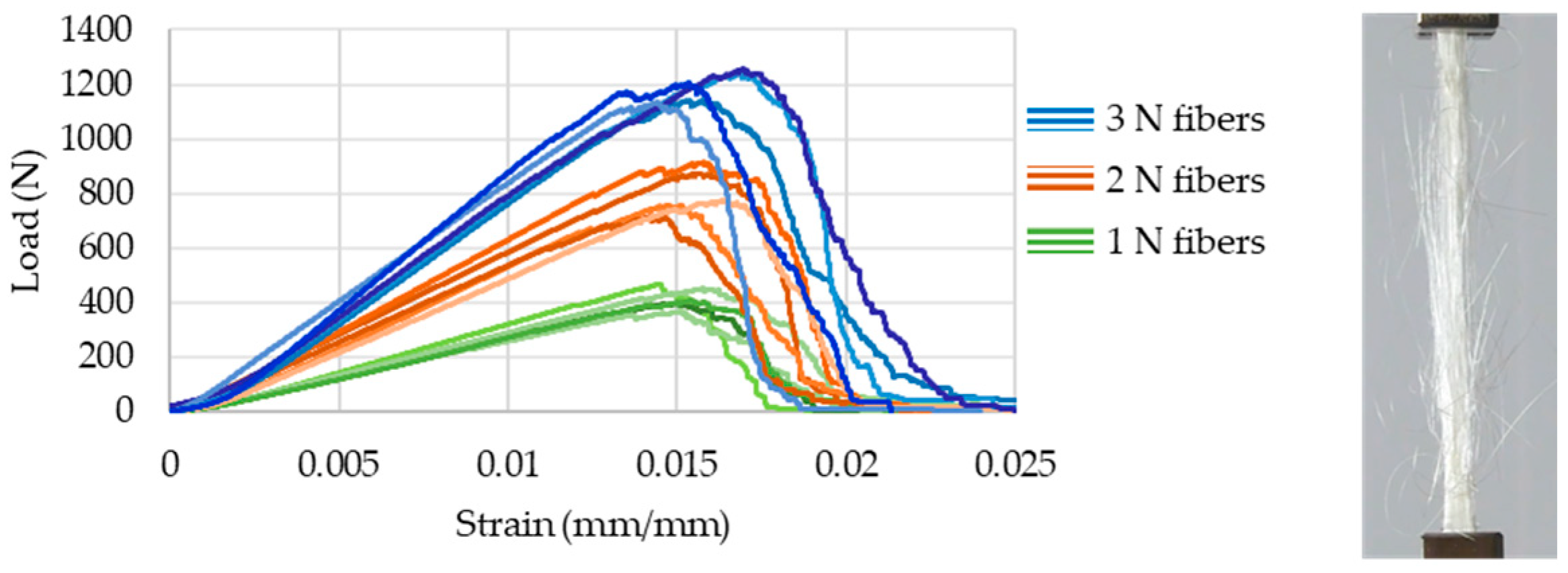
3.1. Sisal-Fiber Mechanical Properties
3.2. Matrix Mechanical Properties
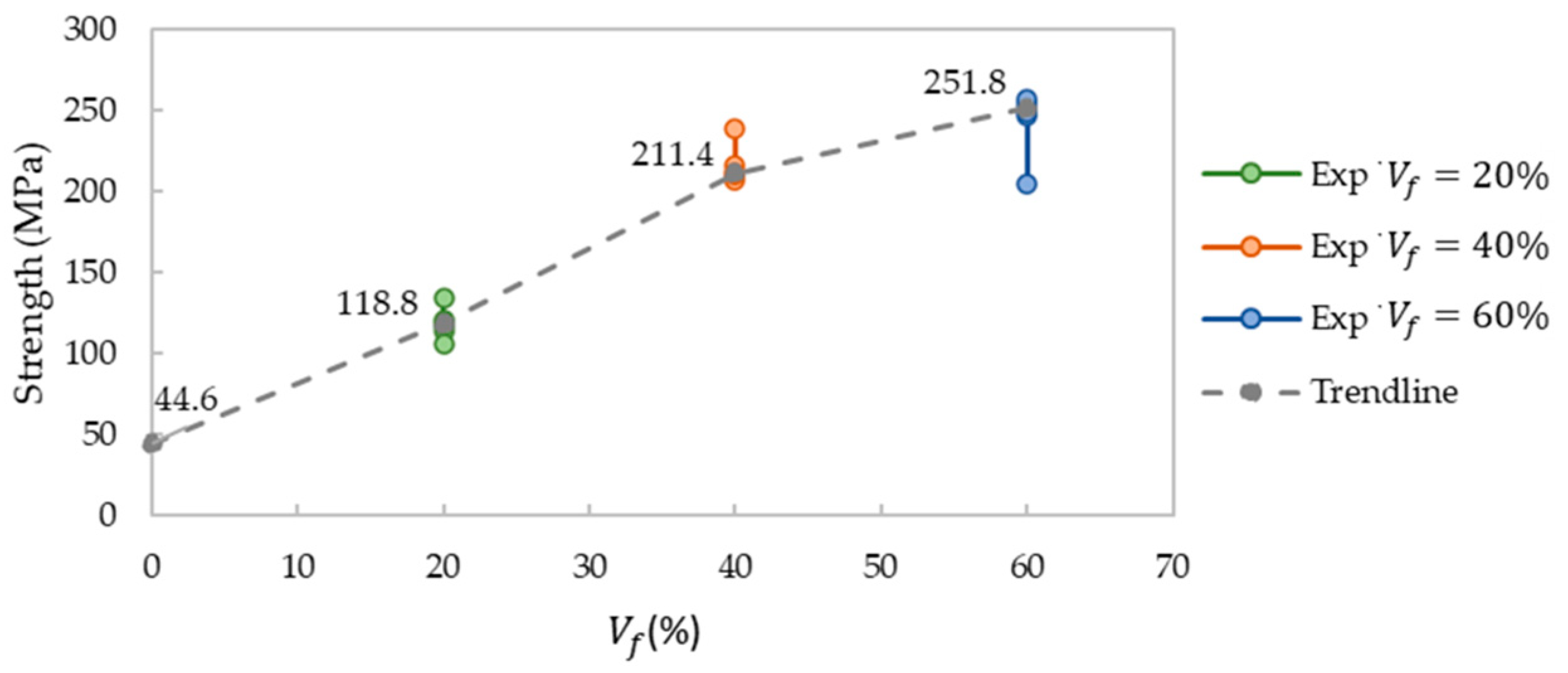
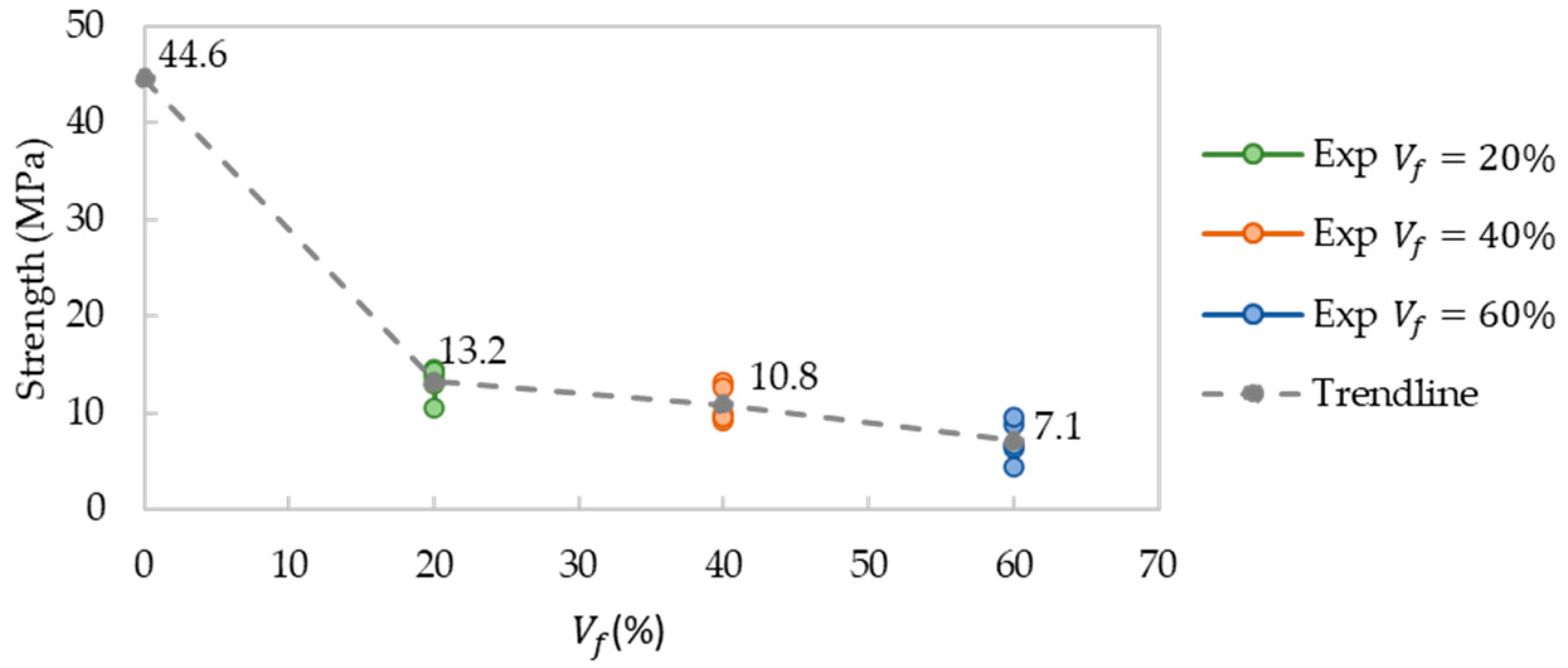
3.3. SFRC Mechanical Properties
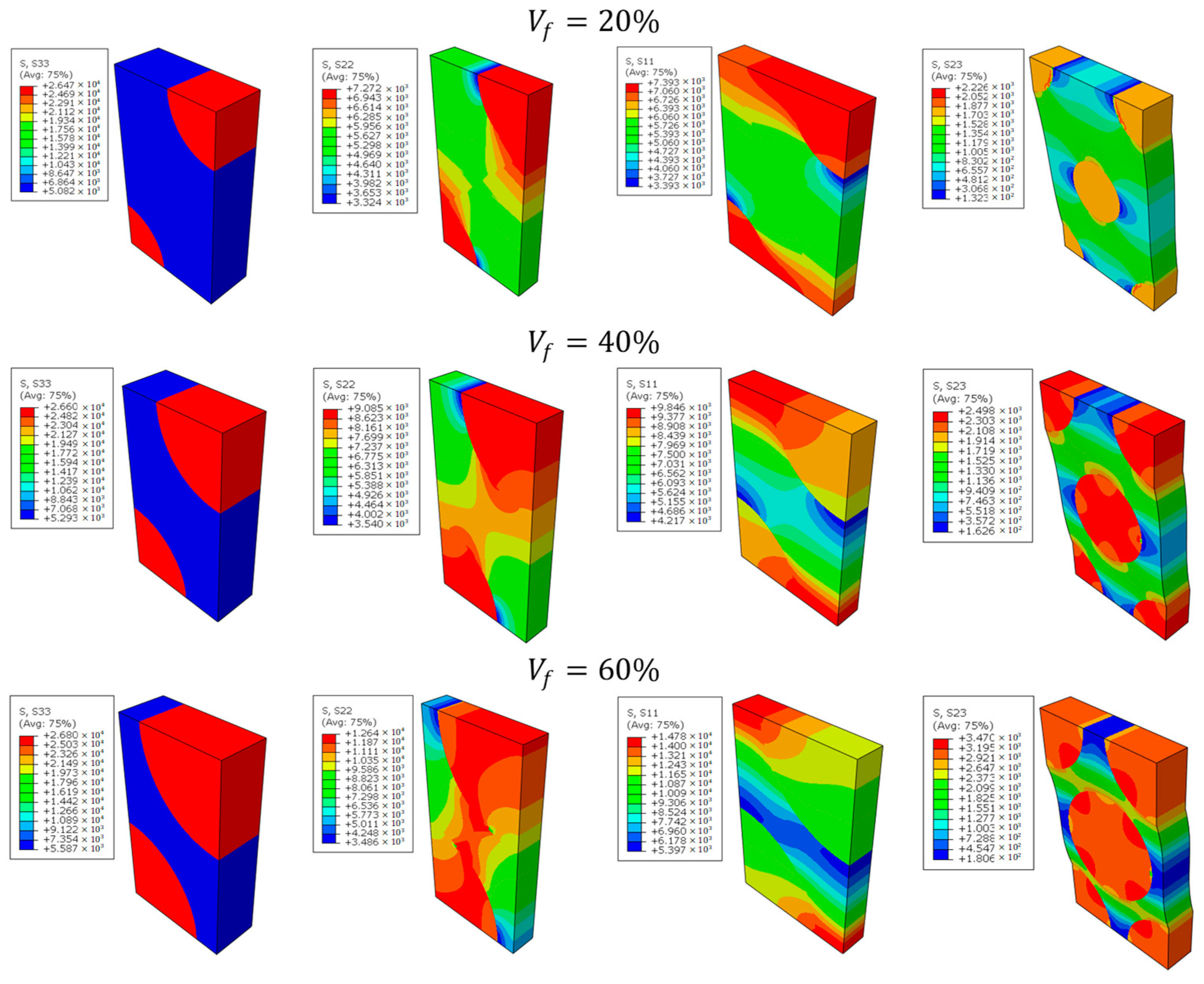
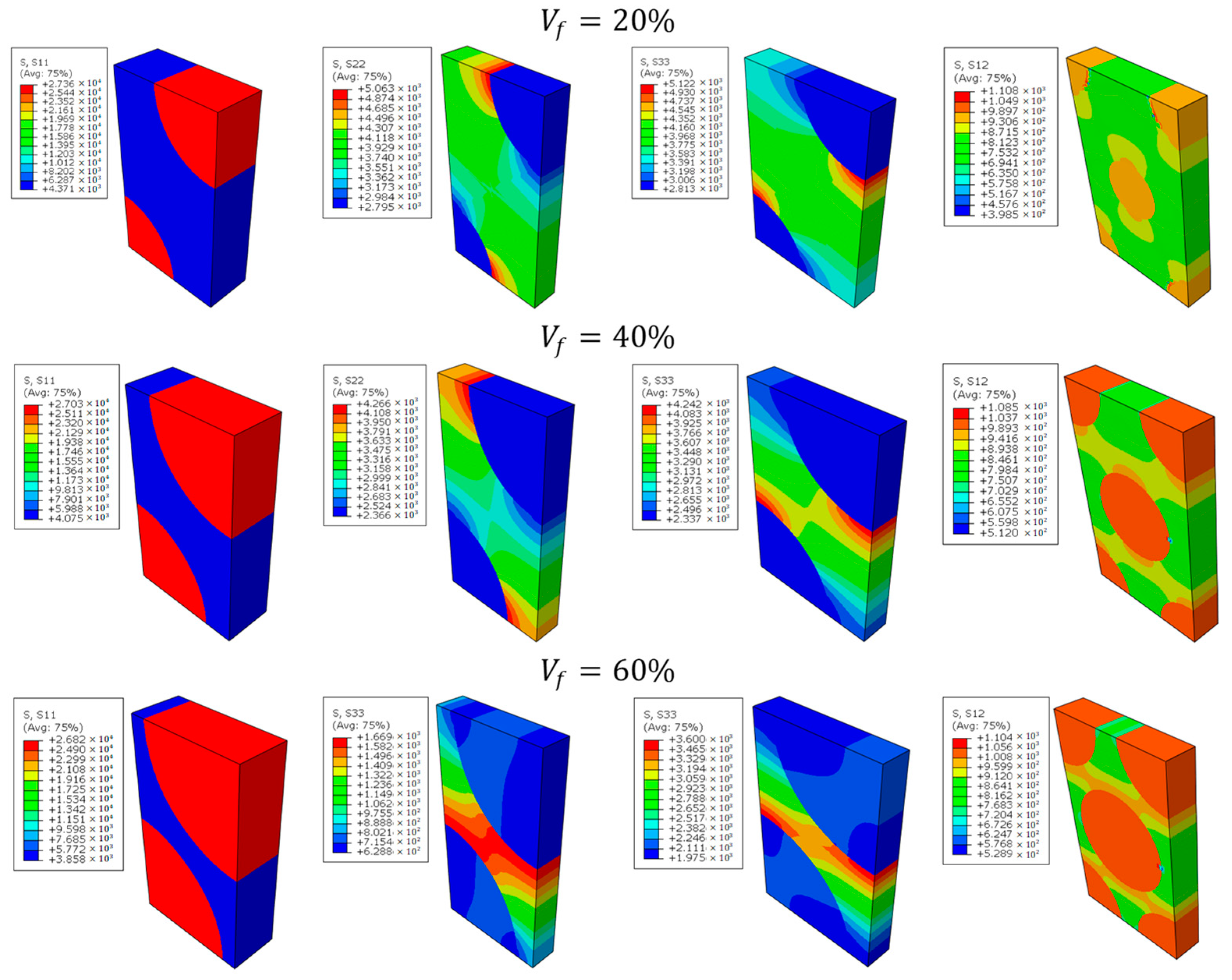
3.4. Estimation of Effective SFRC Mechanical Properties from RVE Computations
- fibers are uniformly distributed throughout the matrix,
- the fibers and the matrix are perfectly bonded,
- the matrix is free of voids.
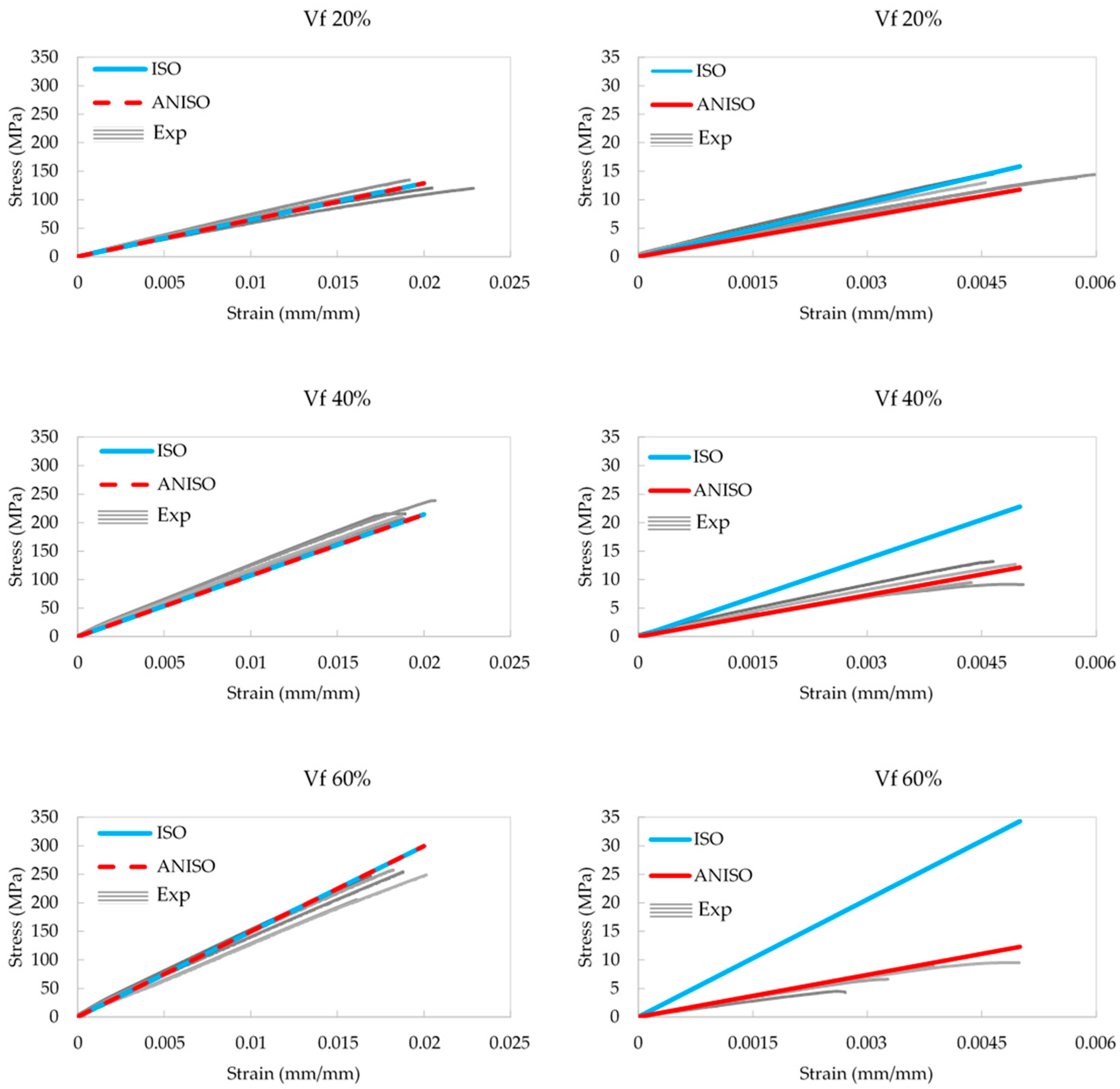
3.5. Measured and Simulate Effective Mechanical Response of SFRC
4. Discussion
4.1. The Influence of Fiber Anisotropy on the Mechanical Response
4.2. The Influence of Fiber-Volume Fraction on the Mechanical Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Pickering, K.L.; Aruan Efendy, M.G.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace glass in fibre reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Holbery, J.; Houston, D. Natural-fiber-reinforced polymer composites in automotive applications. JOM 2006, 58, 80–86. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials and the Environment, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2012; pp. 336–338. [Google Scholar] [CrossRef]
- Silva, F.D.A.; Mobasher, B.; Filho, R.T. Cracking mechanisms in durable sisal fiber reinforced cement composites. Cem. Concr. Compos. 2009, 31, 721–730. [Google Scholar] [CrossRef]
- Silva, F.A.; Zhu, D.; Mobasher, B.; Toledo Filho, R.D. Impact behavior of sisal fiber cement composites under flexural load. ACI Mater. J. 2011, 108, 168. [Google Scholar]
- Ahmad, H.; Fan, M. Interfacial properties and structural performance of resin-coated natural fibre rebars within cementitious matrices. Cem. Concr. Compos. 2018, 87, 44–52. [Google Scholar] [CrossRef]
- Chand, N.; Hashmi, S.A.R. Mechanical properties of sisal fibre at elevated temperatures. J. Mater. Sci. 1993, 28, 6724–6728. [Google Scholar] [CrossRef]
- Inacio, W.; Lopes, F.; Monteiro, S. Diameter dependence of tensile strength by Weibull analysis: Part III. Rev. Mater. 2010, 15, 124–130. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, P.S.; Satyanarayana, K.G. Structure and properties of some vegetable fibres. J. Mater. Sci. 1984, 19, 3925–3934. [Google Scholar] [CrossRef]
- Oksman, K.; Wallström, L.; Berglund, L.A.; Filho, R.D.T. Morphology and mechanical properties of unidirectional sisal-epoxy composites. J. Appl. Polym. Sci. 2002, 84, 2358–2365. [Google Scholar] [CrossRef]
- Silva, F.D.A.; Chawla, N.; Filho, R.D.T. Tensile behavior of high performance natural (sisal) fibers. Compos. Sci. Technol. 2008, 68, 3438–3443. [Google Scholar] [CrossRef]
- Fidelis, M.E.A.; Pereira, T.V.C.; Gomes, O.F.M.; Silva, F.A.; Filho, R.D.T. The effect of fiber morphology on the tensile strength of natural fibers. J. Mater. Res. Technol. 2013, 2, 149–157. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Ma, H.; Shen, Y.; Li, Q.; Zheng, Z. Effects of resin inside fiber lumen on the mechanical properties of sisal fiber reinforced composites. Compos. Sci. Technol. 2015, 108, 32–40. [Google Scholar] [CrossRef]
- Zuccarello, B.; Militello, C.; Bongiorno, F. Influence of the anisotropy of sisal fibers on the mechanical properties of high performance unidirectional biocomposite lamina and micromechanical models. Compos. Part A Appl. Sci. Manuf. 2021, 143, 106320. [Google Scholar] [CrossRef]
- Ntenga, R.; Béakou, A.; Atéba, J.A.; Ohandja, L.A. Estimation of the elastic anisotropy of sisal fibres by an inverse method. J. Mater. Sci. 2008, 43, 6206–6213. [Google Scholar] [CrossRef]
- Thomason, J.; Yang, L.; Gentles, F. Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement. Fibers 2017, 5, 36. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Murillo, C.; Ansell, M. Co-cured in-line joints for natural fibre composites. Compos. Sci. Technol. 2010, 70, 442–449. [Google Scholar] [CrossRef]
- Bisanda, E.; Ansell, M. The effect of silane treatment on the mechanical and physical properties of sisal-epoxy composites. Compos. Sci. Technol. 1991, 41, 165–178. [Google Scholar] [CrossRef]
- Chand, N.; Verma, S.; Khazanchi, A.C. SEM and strength characteristics of acetylated sisal fibre. J. Mater. Sci. Lett. 1989, 8, 1307–1309. [Google Scholar] [CrossRef]
- Bisanda, E.T.N. The Effect of Alkali Treatment on the Adhesion Characteristics of Sisal Fibres. Appl. Compos. Mater. 2000, 7, 331–339. [Google Scholar] [CrossRef]
- Mwaikambo, L.Y.; Ansell, M.P. Mechanical properties of alkali treated plant fibres and their potential as reinforcement materials II. Sisal fibres. J. Mater. Sci. 2006, 41, 2497–2508. [Google Scholar] [CrossRef]
- Pimenta, M.T.B.; Carvalho, A.J.F.; Vilaseca, F.; Gironès, J.; López, J.P.; Mutjé, P.; Curvelo, A.A.S.; Pujol, P.M. Soda-Treated Sisal/Polypropylene Composites. J. Polym. Environ. 2008, 16, 35–39. [Google Scholar] [CrossRef]
- Khan, N.; Bisoyi, D.K.; Shuckla, J.; Sahoo, R. Structural aspects of alkali treated sisal fiber—A SAXS investigation. Fibers Polym. 2011, 12, 765–770. [Google Scholar] [CrossRef]
- Kalia, S.; Vashistha, S. Surface Modification of Sisal Fibers (Agave sisalana) Using Bacterial Cellulase and Methyl Methacrylate. J. Polym. Environ. 2011, 20, 142–151. [Google Scholar] [CrossRef]
- De Castro, B.D.; Silva, K.M.M.N.; Maziero, R.; De Faria, P.E.; Silva-Caldeira, P.P.; Rubio, J.C.C. Influence of Gamma Radiation Treatment on the Mechanical Properties of Sisal Fibers to Use into Composite Materials. Fibers Polym. 2020, 21, 1816–1823. [Google Scholar] [CrossRef]
- Verma, A.; Gaur, A.; Singh, V.K. Mechanical Properties and Microstructure of Starch and Sisal Fiber Biocomposite Modified with Epoxy Resin. Mater. Perform. Charact. 2017, 6, 500–520. [Google Scholar] [CrossRef]
- Verma, A.; Singh, C.; Singh, V.; Jain, N. Fabrication and characterization of chitosan-coated sisal fiber—Phytagel modified soy protein-based green composite. J. Compos. Mater. 2019, 53, 2481–2504. [Google Scholar] [CrossRef]
- Verma, A.; Singh, V.K. Mechanical, Microstructural and Thermal Characterization of Epoxy-Based Human Hair–Reinforced Composites. J. Test. Eval. 2018, 47, 1193–1215. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Halpin, J.C.; Kardos, J.L. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified Composite Micromechanics for Predicting Microstresses. J. Reinf. Plast. Compos. 1987, 6, 268–289. [Google Scholar] [CrossRef]
- Hashin, Z.; Rosen, B.W. The Elastic Moduli of Fiber-Reinforced Materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Rangaraj, S.S.; Bhaduri, S.B. A modified rule-of-mixtures for prediction of tensile strengths of unidirectional fibre-reinforced composite materials. J. Mater. Sci. 1994, 29, 2795–2800. [Google Scholar] [CrossRef]
- Sun, C.; Vaidya, R. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Potluri, R.; Diwakar, V.; Venkatesh, K.; Reddy, B.S. Analytical Model Application for Prediction of Mechanical Properties of Natural Fiber Reinforced Composites. Mater. Today Proc. 2018, 5, 5809–5818. [Google Scholar] [CrossRef]
- Rao, S.; Jayaraman, K.; Bhattacharyya, D. Micro and macro analysis of sisal fibre composites hollow core sandwich panels. Compos. B. Eng. 2012, 43, 2738–2745. [Google Scholar] [CrossRef]
- Pantano, A.; Zuccarello, B. Numerical model for the characterization of biocomposites reinforced by sisal fibres. Procedia Struct. Integr. 2018, 8, 517–525. [Google Scholar] [CrossRef]
- Glouia, Y.; Chaabouni, Y.; El Oudiani, A.; Maatoug, I.; Msahli, S. Finite element analysis of mechanical response of cellulosic fiber-reinforced composites. Int. J. Adv. Manuf. 2019, 103, 4671–4680. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Rajeswari, N.; Vaidheeswaran, K. Analysis of mechanical properties of natural fibre composites by experimental with FEA. Mater. Today Proc. 2020, 28, 1149–1153. [Google Scholar] [CrossRef]
- Bernard, S.S.; Suresh, G.; Srinivasan, T.; Srinivasan, S.; Kaarmugilan, N.; Naveed, L.M.; Kiranmouli, N.; Mahalakshmi, C. Analyzing the mechanical behaviour of sisal fiber reinforced IPN matrix. Mater. Today Proc. 2020, 45, 569–572. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Zhang, Z.; Zhou, L. Multi-layer interfacial fatigue and interlaminar fracture behaviors for sisal fiber reinforced composites with nano- and macro-scale analysis. Compos. Part A Appl. Sci. Manuf. 2020, 135, 105911. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Zhang, Z.; Zhang, Z.; Zhou, L. Quantitative investigations on multi-layer interface debonding behaviors for sisal fiber reinforced composites using acoustic emission and finite element method. Compos. Part B Eng. 2020, 196, 108128. [Google Scholar] [CrossRef]
- Potluri, R. Natural Fiber-Based Hybrid Bio-composites: Processing, Characterization, and Applications. In Green Composites: Processing, Characterisation and Applications; Muthu, S.S., Ed.; Springer Nature Singapore Pte Ltd.: Singapore, 2019; pp. 1–45. [Google Scholar] [CrossRef]
- Resin Research. Technical Data Sheet Kwik Kick Epoxy 2:1 System. Available online: https://resinresearch.net/wp-content/uploads/2022/02/Kwik-Kick-TDS_V2.1.pdf (accessed on 1 May 2022).
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]
- ASTM D3039/D3039M; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
- Autograph AGS-X Series, Shimadzu. Available online: https://www.shimadzu.com/an/products/materials-testing/uni-ttm/autograph-ags-x-series/index.html (accessed on 23 September 2021).
- Epsilon Technology Product Line, Epsilon Technology Corp. WY USA. Available online: https://www.epsilontech.com/extensometers-overview/ (accessed on 23 September 2021).
- ABAQUS/CAE 2021, © Dassault Systems Simulia Corp.: Johnston, RI, USA, 2020.
- Abaqus Documentation, Simulia. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAEEXCRefMap/simaexc-c-docproc.htm (accessed on 1 May 2022).
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Abaqus; CRC Press: Boca Raton, FL, USA, 2013; pp. 215–246. [Google Scholar]
- Szabó, B.; Babuška, I. Introduction to Finite Element Analysis: Formulation, Verification and Validation; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1–14. [Google Scholar]
- Luciano, R.; Barbero, E. Formulas for the stiffness of composites with periodic microstructure. Int. J. Solids Struct. 1994, 31, 2933–2944. [Google Scholar] [CrossRef]
- Barbero, E.; Luciano, R. Micromechanical formulas for the relaxation tensor of linear viscoelastic composites with transversely isotropic fibers. Int. J. Solids Struct. 1995, 32, 1859–1872. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Met. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Abaimov, S.G.; Khudyakova, A.A.; Lomov, S.V. On the closed form expression of the Mori–Tanaka theory prediction for the engineering constants of a unidirectional fiber-reinforced ply. Compos. Struct. 2016, 142, 1–6. [Google Scholar] [CrossRef]
- Betelie, A.A.; Megera, Y.T.; Redda, D.T.; Sinclair, A. Experimental investigation of fracture toughness for treated sisal epoxy composite. AIMS Mater. Sci. 2018, 5, 93–104. [Google Scholar] [CrossRef]




| 1.2 | 25 | 1.6 | 0.6 | 0.2 | 1.1 | 1.1 | 2.3 | 0.4 |
| Approach | |||||||
|---|---|---|---|---|---|---|---|
| 20% | ISO (PMM) | 6.861 | 3.452 | 0.355 | 0.525 | 1.162 | 1.132 |
| ANISO (MTT) | 6.853 | 2.323 | 0.429 | 0.475 | 0.871 | 0.788 | |
| ISO (RVE) | 6.858 | 3.433 | 0.355 | 0.526 | 1.159 | 1.125 | |
| ANISO (RVE) | 6.851 | 2.322 | 0.428 | 0.475 | 0.870 | 0.787 | |
| 40% | ISO (PMM) | 11.411 | 5.024 | 0.313 | 0.506 | 1.679 | 1.668 |
| ANISO (MTT) | 11.400 | 2.152 | 0.462 | 0.424 | 0.923 | 0.755 | |
| ISO (RVE) | 11.407 | 4.888 | 0.313 | 0.517 | 1.673 | 1.616 | |
| ANISO (RVE) | 11.399 | 2.151 | 0.462 | 0.424 | 0.922 | 0.755 | |
| 60% | ISO (PMM) | 15.950 | 7.575 | 0.273 | 0.454 | 2.566 | 2.605 |
| ANISO (MTT) | 15.942 | 1.962 | 0.501 | 0.354 | 0.978 | 0.724 | |
| ISO (RVE) | 15.944 | 7.562 | 0.273 | 0.452 | 2.554 | 2.602 | |
| ANISO (RVE) | 15.938 | 1.961 | 0.500 | 0.354 | 0.977 | 0.724 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinitsky, O.; Trabelsi, N.; Priel, E. The Mechanical Response of Epoxy–Sisal Composites Considering Fiber Anisotropy: A Computational and Experimental Study. Fibers 2022, 10, 43. https://doi.org/10.3390/fib10050043
Sinitsky O, Trabelsi N, Priel E. The Mechanical Response of Epoxy–Sisal Composites Considering Fiber Anisotropy: A Computational and Experimental Study. Fibers. 2022; 10(5):43. https://doi.org/10.3390/fib10050043
Chicago/Turabian StyleSinitsky, Olga, Nir Trabelsi, and Elad Priel. 2022. "The Mechanical Response of Epoxy–Sisal Composites Considering Fiber Anisotropy: A Computational and Experimental Study" Fibers 10, no. 5: 43. https://doi.org/10.3390/fib10050043
APA StyleSinitsky, O., Trabelsi, N., & Priel, E. (2022). The Mechanical Response of Epoxy–Sisal Composites Considering Fiber Anisotropy: A Computational and Experimental Study. Fibers, 10(5), 43. https://doi.org/10.3390/fib10050043








