Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method
Abstract
1. Introduction
2. The PD Formulation for FGMs
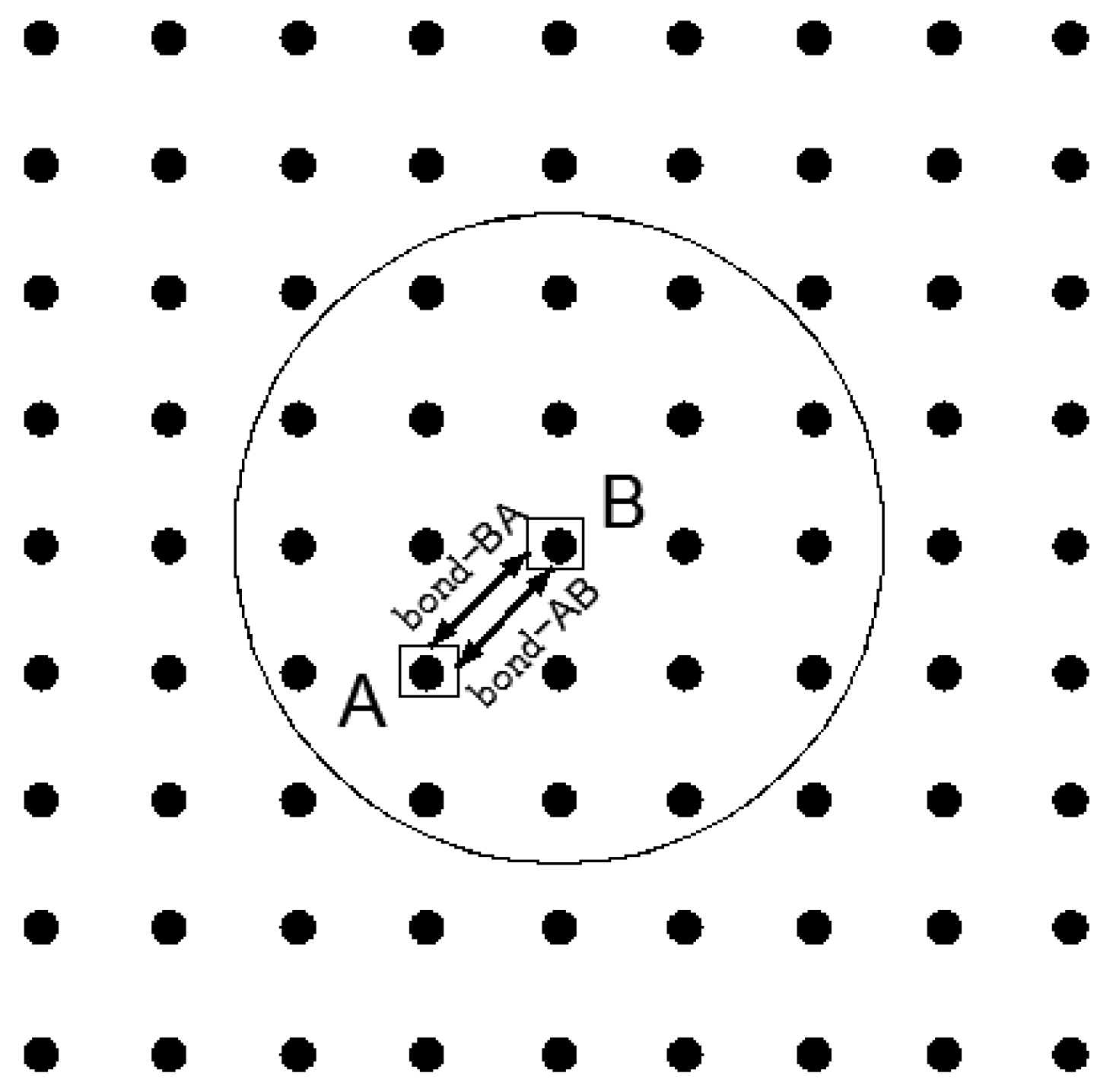
2.1. Basic Review of PD Theory for Elastic Brittle Materials
2.2. PD Model for FGM
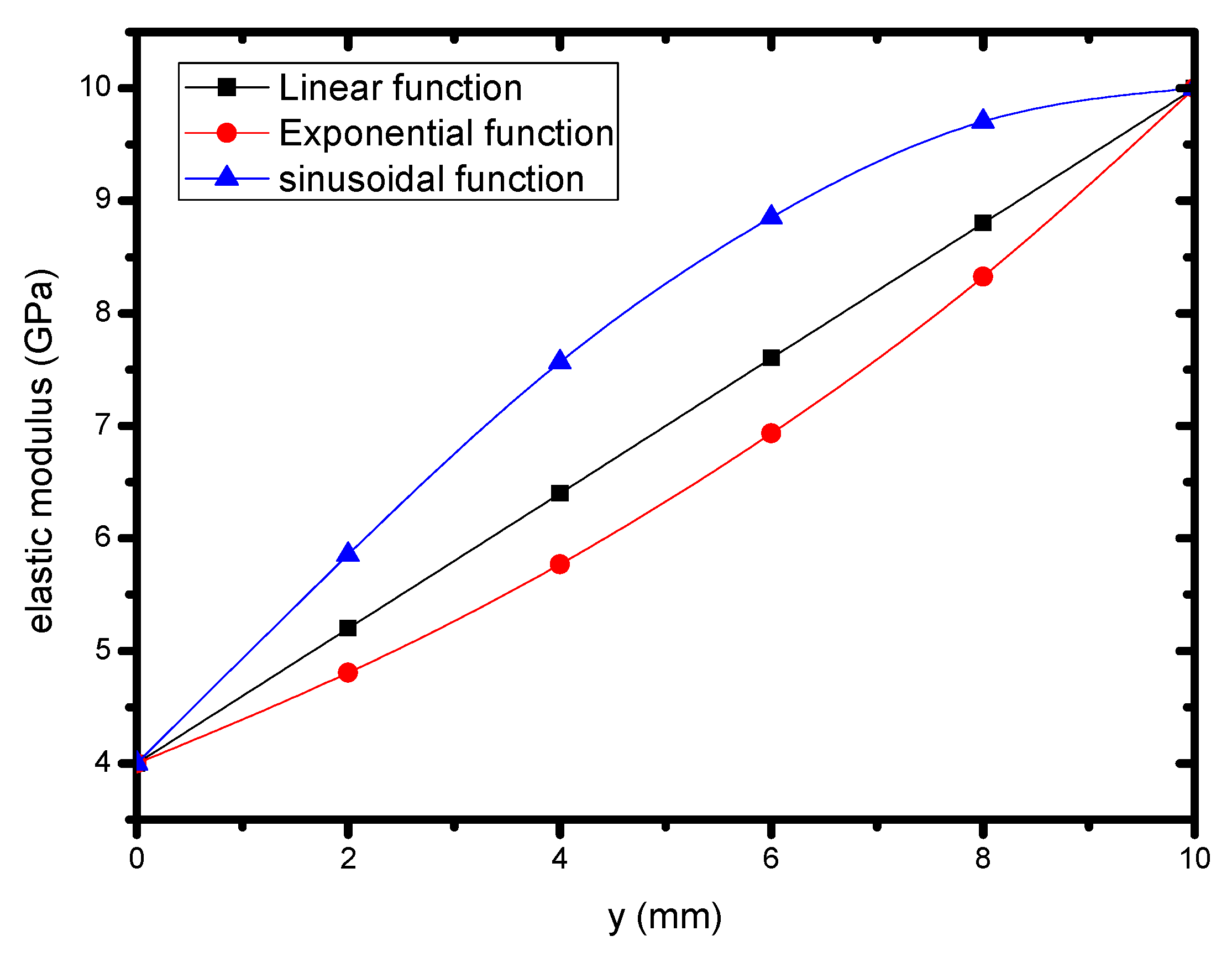
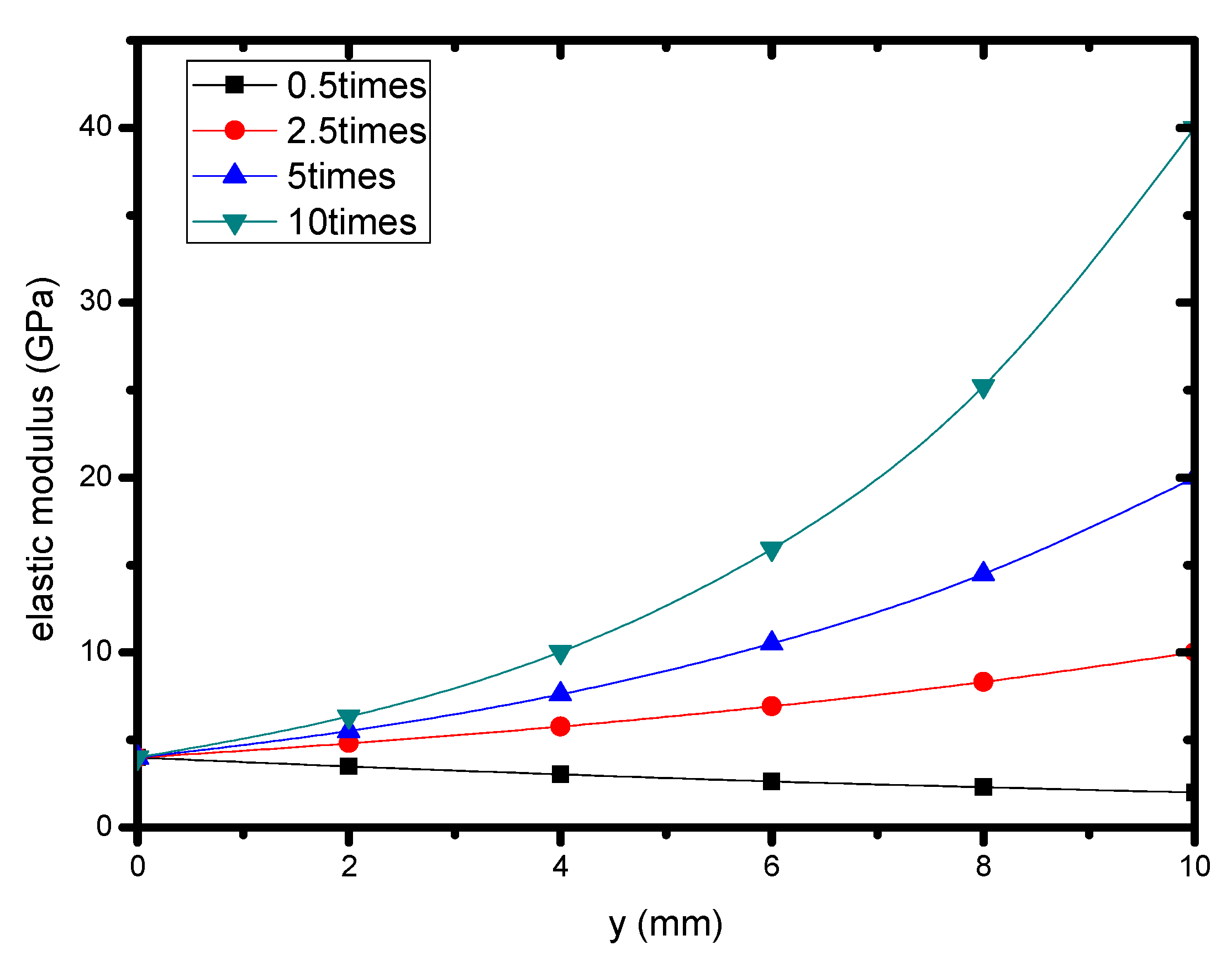
2.2.1. Determination of Micro-Modulus Function c
2.2.2. Determination of the Interaction Function f
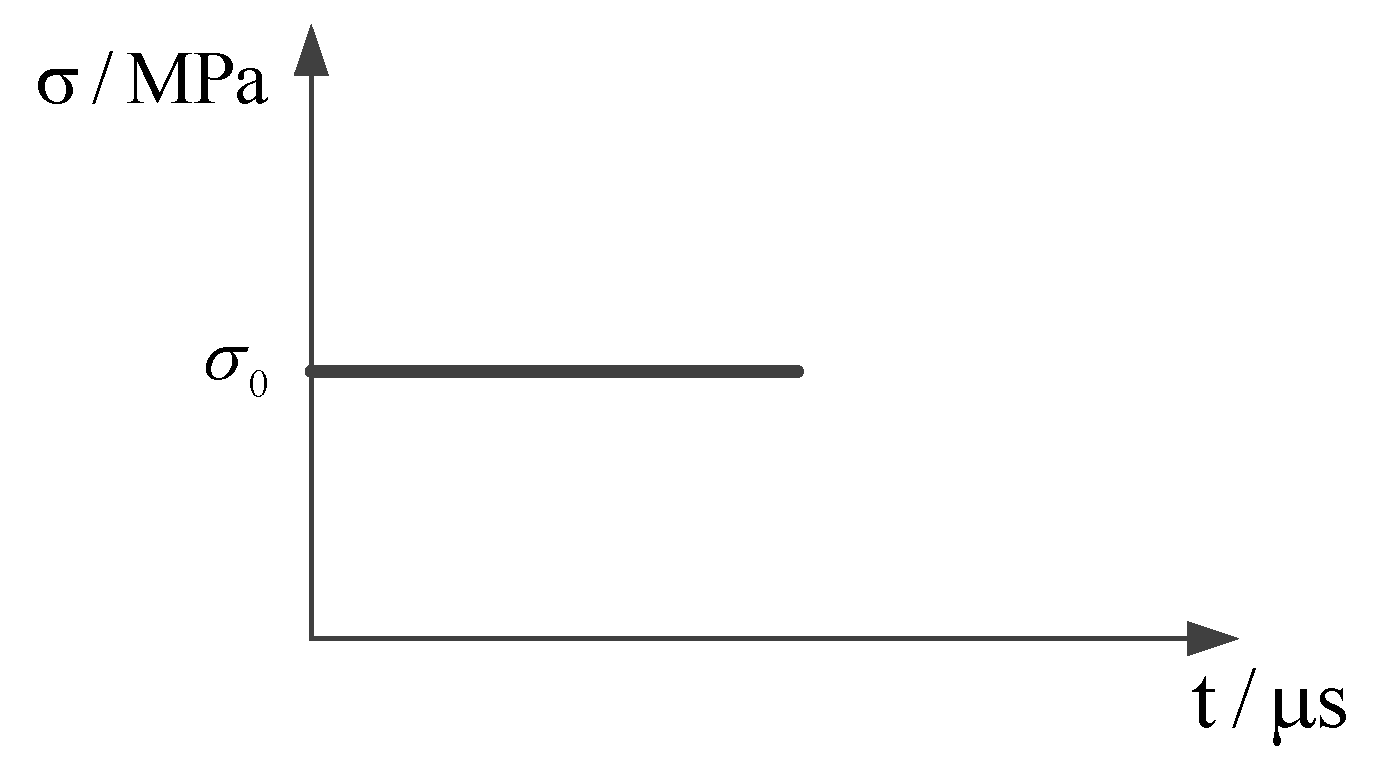
2.2.3. Critical Relative Elongation s0
3. Convergence Studies in Dynamic Crack Branching of FGMs
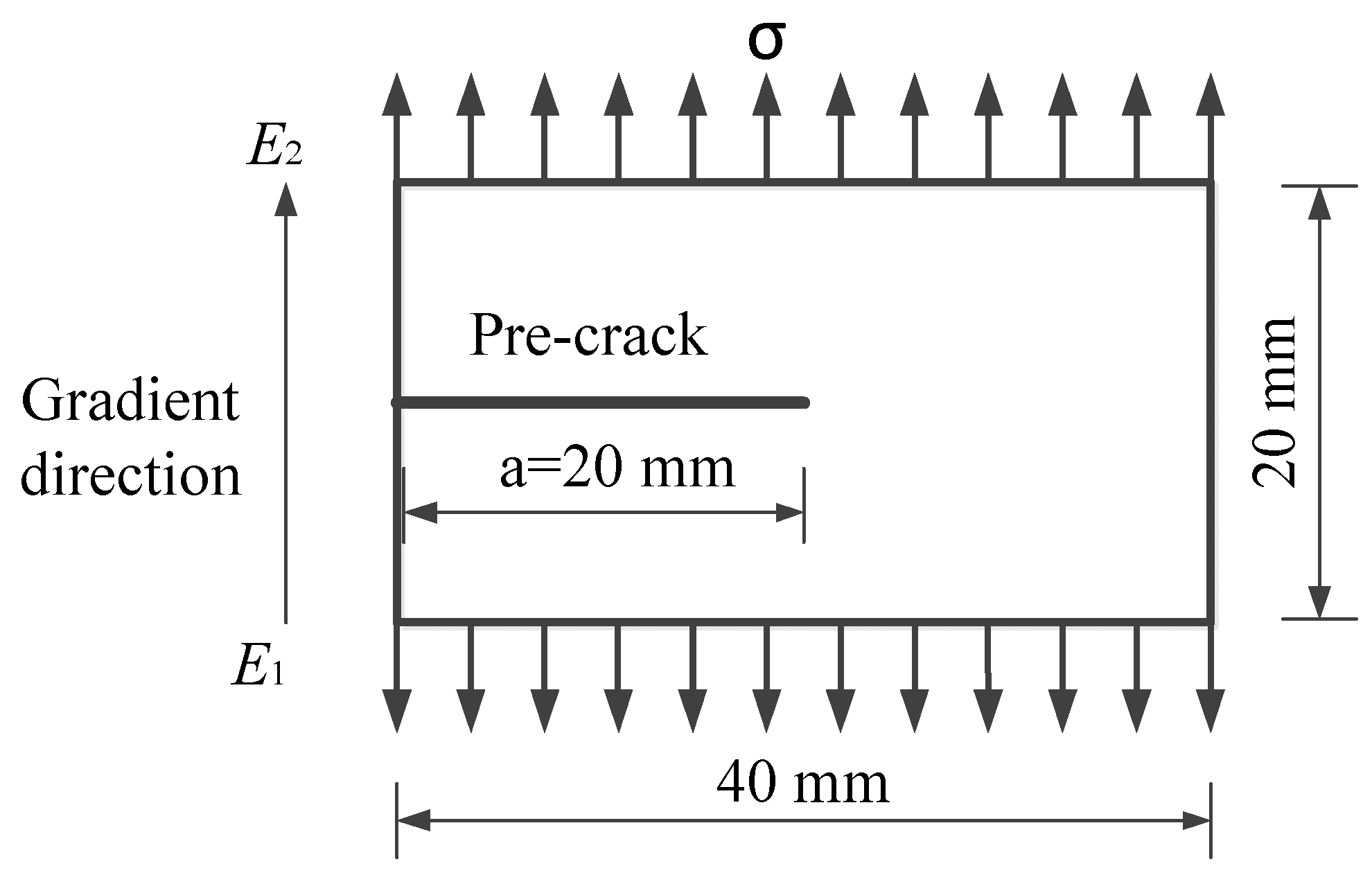
3.1. Problem Setting
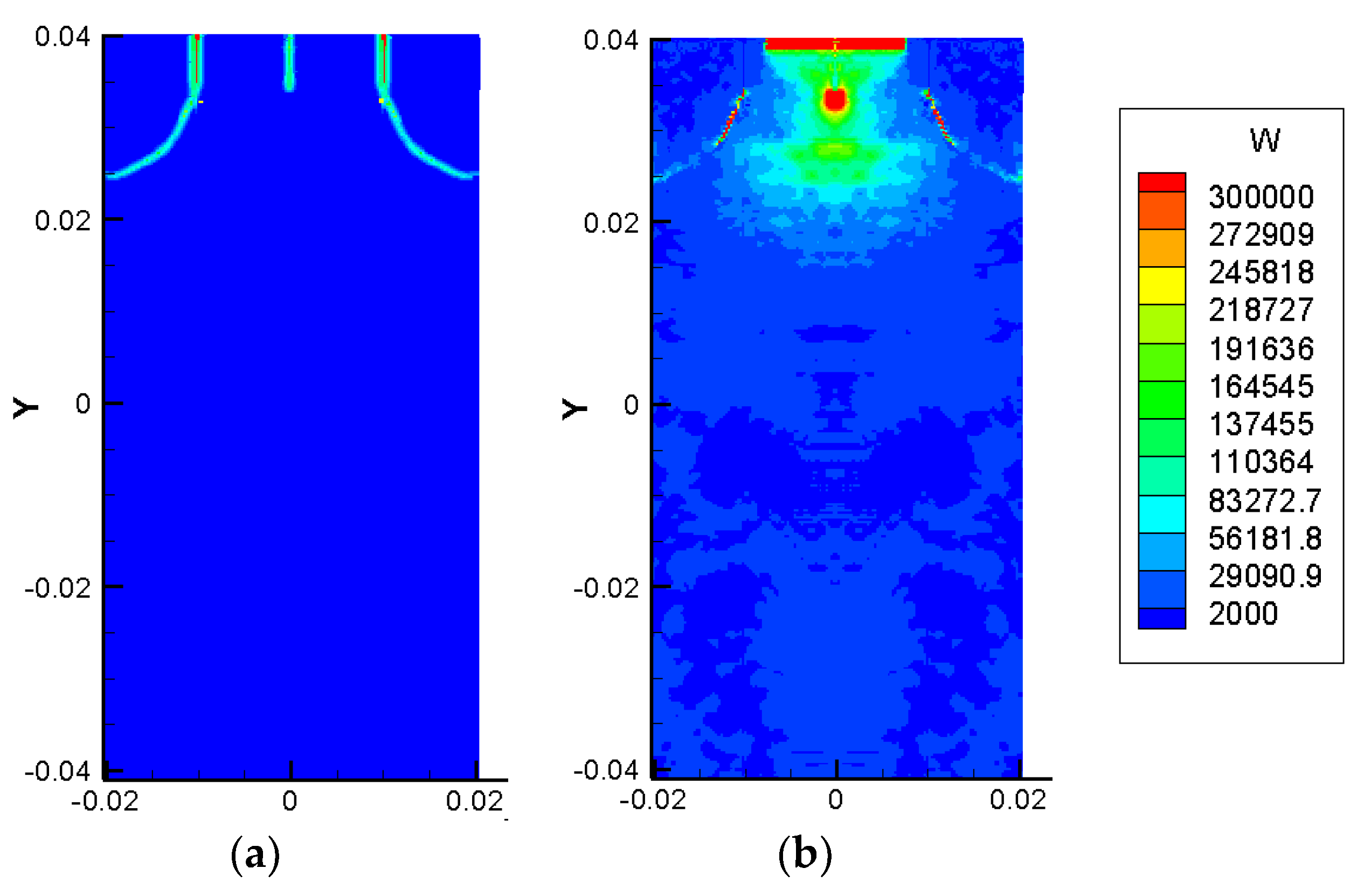
3.2. δ-Convergence of FGM Samples
3.3. m-Convergence of FGM Samples
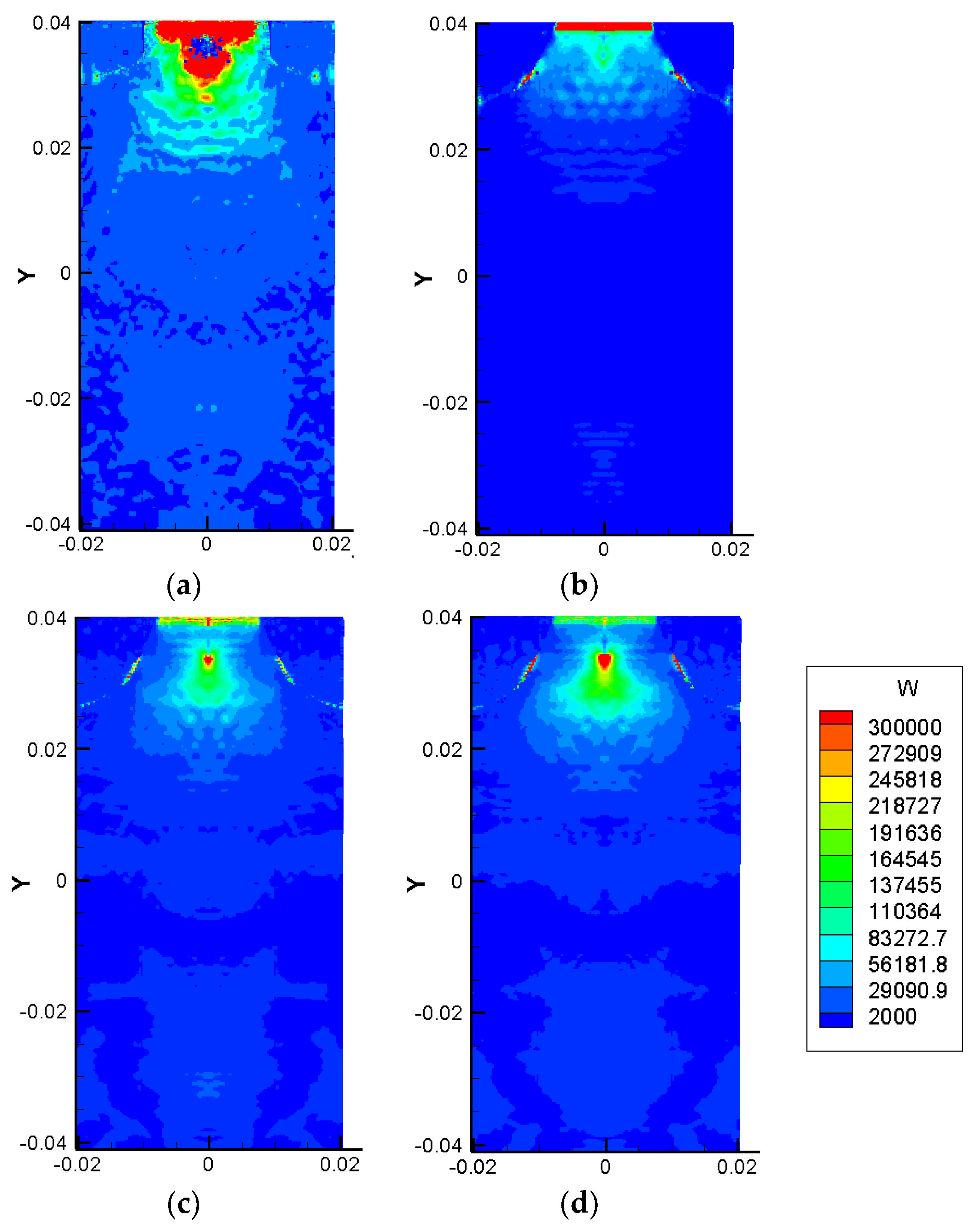
3.4. Δt-Convergence of FGM Samples
4. Simulation of FGM Coating—Substrate
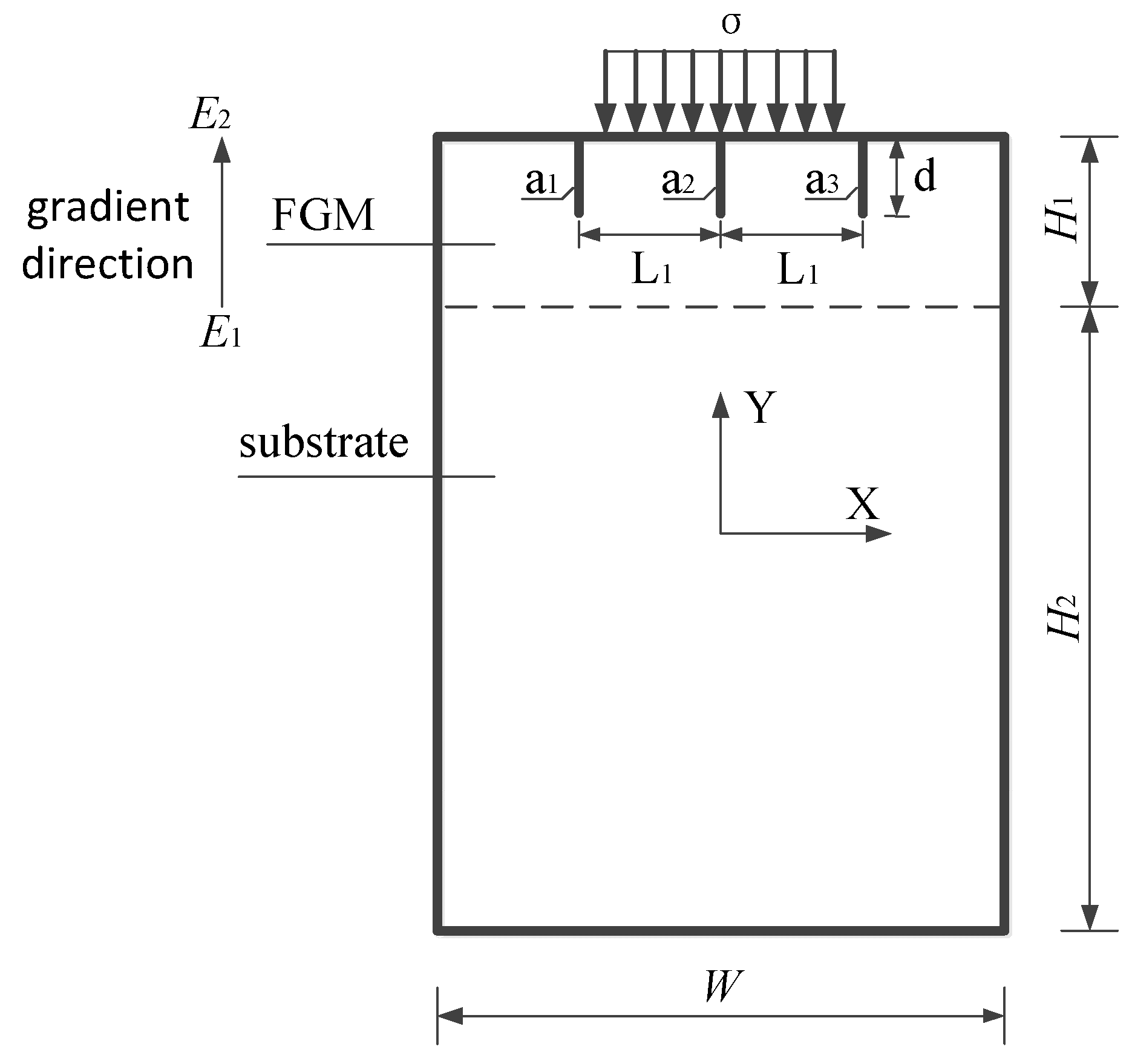
4.1. Problem Setting
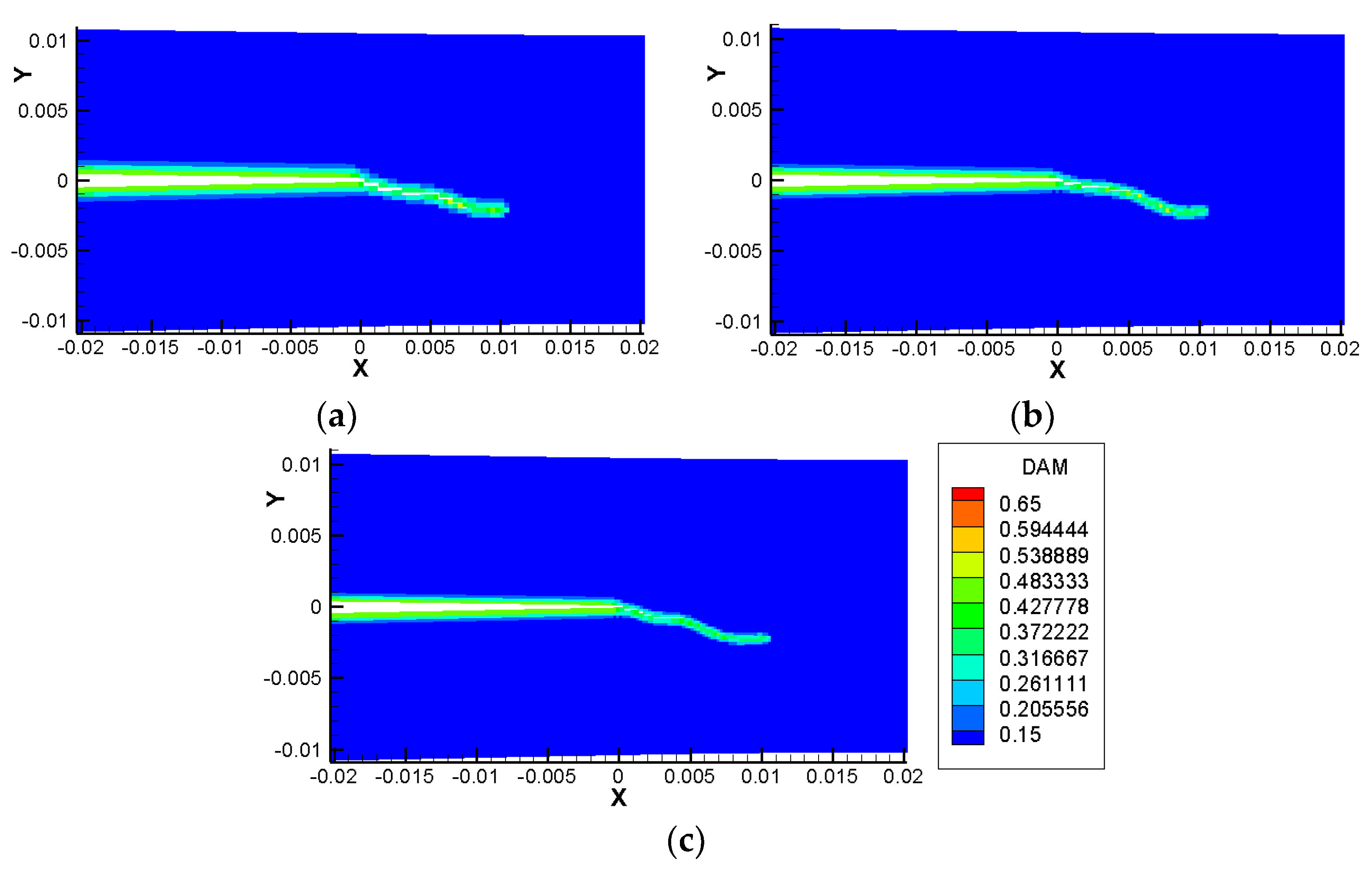
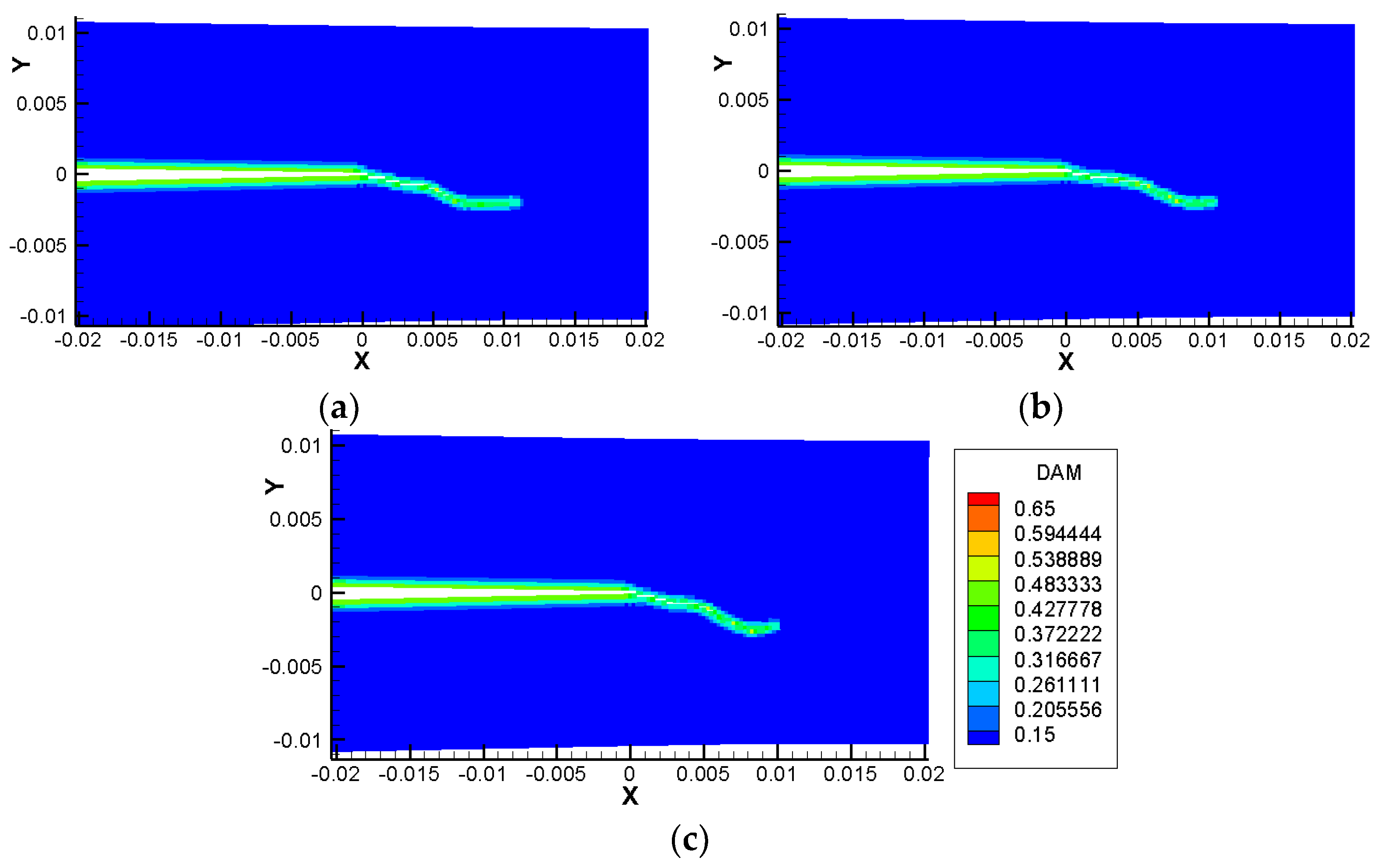
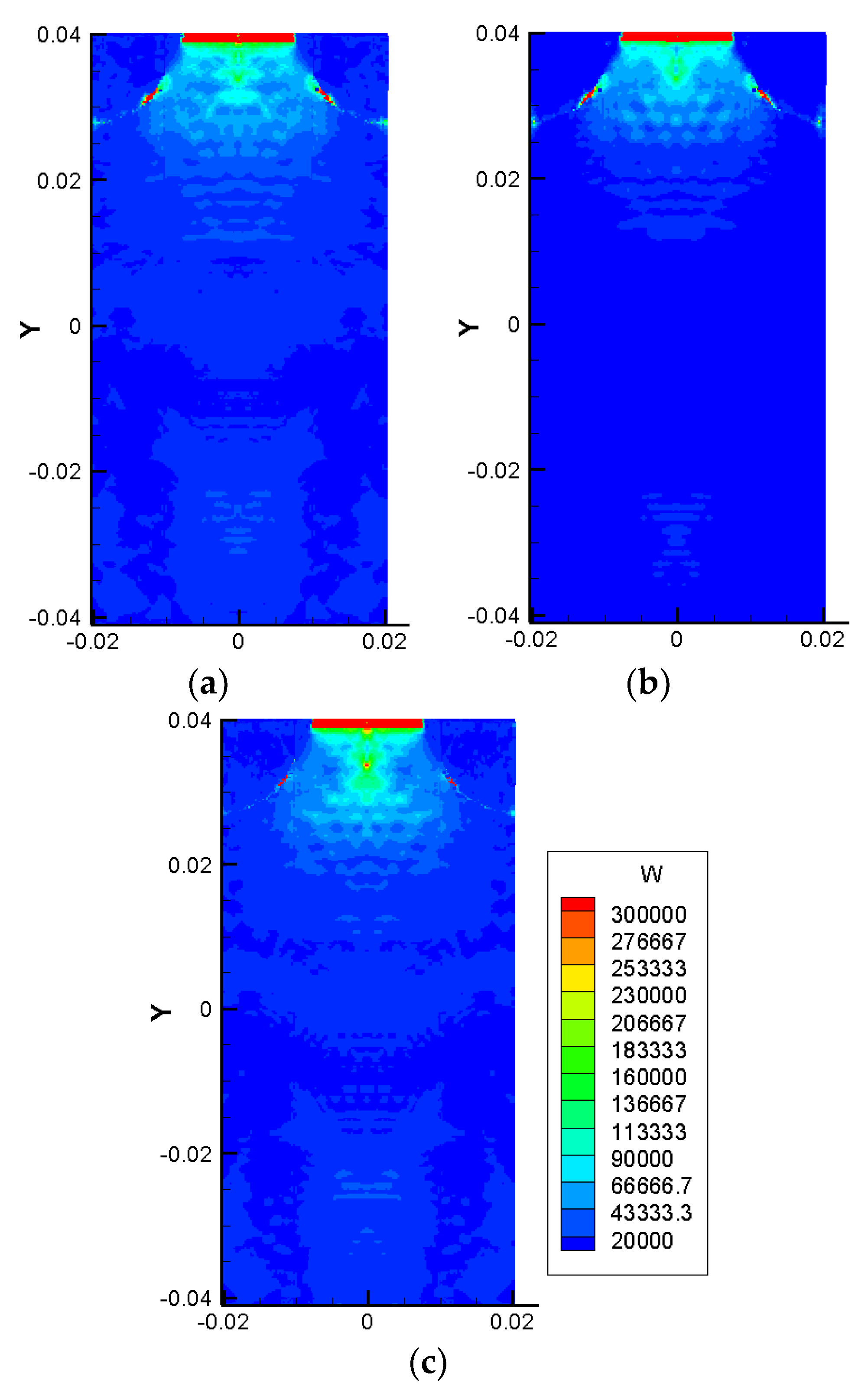
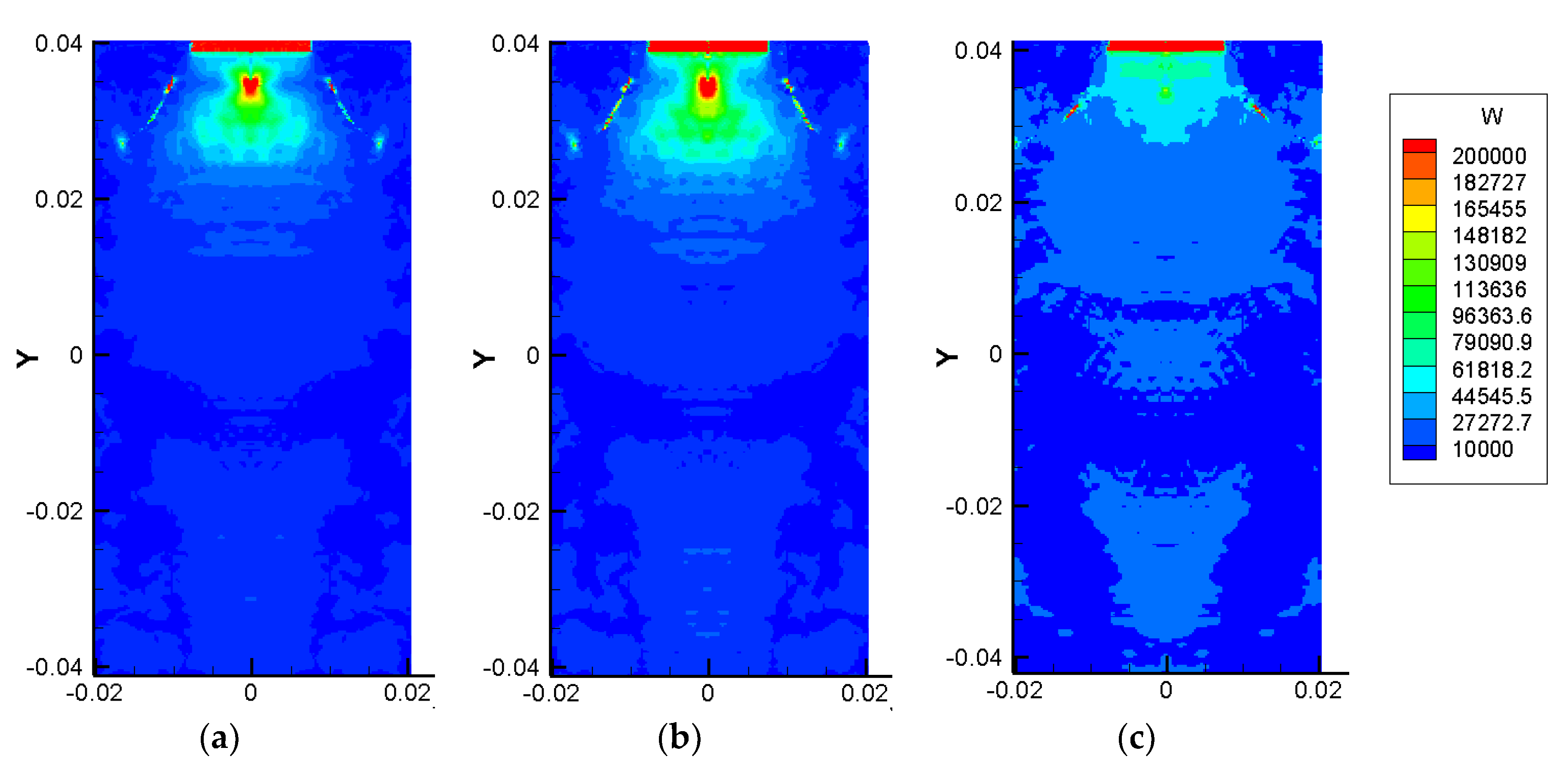
4.2. Crack Propagation and Deflection of the FGM Coating Corresponding to Different Gradient Forms
4.3. Crack Propagation and Deflection of FGMs Corresponding to Different Coating Thicknesses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gu, P.; Asaro, R.J. Cracks in functionally graded materials. Int. J. Solids Struct. 1997, 34, 1–17. [Google Scholar] [CrossRef]
- Zuiker, J.R. Functionally graded materials: Choice of micromechanics model and limitations in property variation. Compos. Eng. 1995, 5, 807–819. [Google Scholar] [CrossRef]
- Pompe, W.; Worch, H.; Epple, M.; Friess, W.; Gelinsky, M.; Greil, P.; Hempel, U.; Scharnweber, D.; Schulte, K. Functionally graded materials for biomedical applications. Mater. Sci. Eng. A 2003, 362, 40–60. [Google Scholar] [CrossRef]
- Zhang, Z.; Paulino, G.H. Wave propagation and dynamic analysis of smoothly graded heterogeneous continua using graded finite elements. Int. J. Solids. Struct. 2007, 44, 3601–3626. [Google Scholar] [CrossRef]
- Li, H.; Lambros, J.; Cheeseman, B.A.; Santare, M.H. Experimental investigation of the quasi-static fracture of functionally graded materials. Int. J. Solids Struct. 2000, 37, 3715–3732. [Google Scholar] [CrossRef]
- Zhang, Z.; Paulino, G.H. Cohesive zone modeling of dynamic failure in homogeneous and functionally graded materials. Int. J. Plast. 2005, 21, 1195–1254. [Google Scholar] [CrossRef]
- Kirugulige, M.; Tippur, H.V. Mixed-mode dynamic crack growth in a functionally graded particulate composite: Experimental measurements and finite element simulations. J. Appl. Mech. 2008, 75, 883–890. [Google Scholar] [CrossRef]
- Jamia, N.; El-Borgi, S.; Fernandes, R.; Vegamoor, V. Analysis of an arbitrarily oriented crack in a functionally graded plane using a non-local approach. Theor. Appl. Fract. Mech. 2016, 85, 387–397. [Google Scholar] [CrossRef]
- Jin, Z.H.; Batra, R.C. Interface cracking between functionally graded coatings and a substrate under antiplane shear. Int. J. Eng. Sci. 1996, 34, 1705–1716. [Google Scholar] [CrossRef]
- Cai, H.; Bao, G. Crack bridging in functionally graded coatings. Int. J. Solids Struct. 1998, 35, 701–717. [Google Scholar] [CrossRef]
- Guler, M.A.; Erdogan, F. Contact mechanics of graded coatings. Int. J. Solids Struct. 2004, 41, 3865–3889. [Google Scholar] [CrossRef]
- Almeida, C.A.; Albino, J.C.R.; Menezes, I.F.M.; Paulino, G.H. Geometric nonlinear analyses of functionally graded beams using a tailored Lagrangian formulation. Mech. Res. Com. 2011, 38, 553–559. [Google Scholar] [CrossRef]
- Kim, J.H.; Paulino, G.H. Mixed-mode fracture of orthotropic functionally graded materials using finite elements and the modified crack closure method. Eng. Fract. Mech. 2002, 69, 1557–1586. [Google Scholar] [CrossRef]
- Kim, J.H.; Paulino, G.H. Simulation of crack propagation in functionally graded materials under mixed-mode and non-proportional loading. Mech. Mater. Des. 2004, 1, 63–94. [Google Scholar] [CrossRef]
- Erdogan, F. Fracture mechanics of functionally graded materials. Compos. Eng. 1995, 5, 753–770. [Google Scholar] [CrossRef]
- Guo, L.C.; Wu, L.Z.; Zeng, T.; Ma, L. The dynamic fracture behavior of a functionally graded coating-substrate system. Compos. Struct. 2004, 64, 433–441. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. Reduction in stress concentration around a pair of circular holes with functionally graded material layer. Acta Mech. 2018, 229, 1045–1060. [Google Scholar] [CrossRef]
- Rezaei, S.; Wulfinghoff, S.; Reese, S. Prediction of fracture and damage in micro/nano coating systems using cohesive zone elements. Int. J. Solids Struct. 2017, 121, 62–74. [Google Scholar] [CrossRef]
- Rousseau, C.E.; Tippur, H.V. Compositionally graded materials with cracks normal to the elastic gradient. Acta Mater. 2000, 48, 4021–4033. [Google Scholar] [CrossRef]
- Marur, P.R.; Tippur, H.V. Numerical analysis of crack-tip fields in functionally graded materials with a crack normal to the elastic gradient. Int. J. Solids Struct. 2000, 37, 5353–5370. [Google Scholar] [CrossRef]
- Abanto-Bueno, J.; Lambros, J. An experimental study of mixed mode crack initiation and growth in functionally graded materials. Exp. Mech. 2006, 6, 179–196. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 8, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 3, 1526–1535. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Studies of dynamic crack propagation and crack branching with peridynamics. Int. J. Fract. 2010, 162, 229–244. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Characteristics of dynamic brittle fracture captured with peridynamics. Eng. Fract. Mech. 2011, 78, 1156–1168. [Google Scholar] [CrossRef]
- Hu, W.; Ha, Y.D.; Bobaru, F. Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 247–261. [Google Scholar] [CrossRef]
- Hu, Y.L.; Carvalho, N.V.D.; Madenci, E. Peridynamic modeling of delamination growth in composite laminates. Compos. Struct. 2015, 132, 610–620. [Google Scholar] [CrossRef]
- Ha, Y.D.; Lee, J.; Hong, J.W. Fracturing patterns of rock-like materials in compression captured with peridynamics. Eng. Fract. Mech. 2015, 144, 176–193. [Google Scholar] [CrossRef]
- Qiao, P.Z.; Huang, D.; Zhang, Q. Damage and progressive failure of concrete structures using non-local peridynamic modeling. Sci. China Tech. Sci. 2011, 54, 591–596. [Google Scholar]
- Gu, X.; Zhang, Q.; Huang, D.; Yv, Y. Wave dispersion analysis and simulation method for concrete SHPB test in peridynamics. Eng. Fract. Mech. 2016, 160, 124–137. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, G.; Wang, Y.; Bobaru, F. A peridynamic model for dynamic fracture in functionally graded materials. Compos. Struct. 2015, 133, 529–546. [Google Scholar] [CrossRef]
- Delale, F.; Erdogan, F. The crack problem for a nonhomogeneous plane. J. Appl. Mech. 1983, 50, 609–614. [Google Scholar] [CrossRef]
- Bobaru, F.; Yang, M.; Alves, L.F.; Silling, S.A.; Askari, E.; Xu, F. Convergence, adaptive refinement, and scaling in 1D peridynamics. Int. J. Num. Methods Eng. 2010, 77, 852–877. [Google Scholar] [CrossRef]
- Cheng, Z.; Liu, Y.; Zhao, J.; Feng, H.; Wu, Y. Numerical simulation of crack propagation and branching in functionally graded materials using peridynamic modeling. Eng. Fract. Mech. 2018, 191, 13–32. [Google Scholar] [CrossRef]
- Tilbrook, M.T.; Rutgers, L.; Moon, R.J.; Hoffman, M. Fatigue crack propagation resistance in homogeneous and graded alumina-epoxy composites. Int. J. Fatigue 2007, 29, 158–167. [Google Scholar] [CrossRef]
- Guo, L.; Huang, S.; Zhang, L.; Jia, L. The interface crack problem for a functionally graded coating-substrate structure with general coating properties. Int. J. Solids Struct. 2018, 146, 136–153. [Google Scholar] [CrossRef]






| Material | Elastic Modulus E (GPa) | Density ρ (kg m−3) | Poisson Ratio ν | Fracture Toughness KIC (MPa·m1/2) |
|---|---|---|---|---|
| Lower FGM l | 4 | 1175 | 0.33 | 1.4 |
| Upper FGM | 10 | 1750 | 0.33 | 2.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cheng, Z.; Feng, H. Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method. Coatings 2019, 9, 62. https://doi.org/10.3390/coatings9010062
Zhang Y, Cheng Z, Feng H. Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method. Coatings. 2019; 9(1):62. https://doi.org/10.3390/coatings9010062
Chicago/Turabian StyleZhang, Yu, Zhanqi Cheng, and Hu Feng. 2019. "Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method" Coatings 9, no. 1: 62. https://doi.org/10.3390/coatings9010062
APA StyleZhang, Y., Cheng, Z., & Feng, H. (2019). Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method. Coatings, 9(1), 62. https://doi.org/10.3390/coatings9010062






