Interdiffusion at Room Temperature in Cu-Ni(Fe) Nanolaminates
Abstract
1. Introduction
2. Materials and Methods
2.1. Nanolaminate Synthesis and X-ray Characterization
2.2. Analytic Interfdiffusion Model
3. Results
4. Discussion
4.1. Bimodal Interdiffusion Behavior
4.2. Anomalous Diffusivity
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

References
- Cahn, J.W.; Hilliard, J.E. Free energy of a non-uniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W. On spinodal decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Cahn, J.W. On spinodal decomposition in cubic crystals. Acta Metall. 1962, 10, 179–183. [Google Scholar] [CrossRef]
- Cahn, J.W. Coherent fluctuations and nucleation in isotropic solids. Acta Metall. 1962, 10, 907–913. [Google Scholar] [CrossRef]
- Hillert, M.A. A solid-solution model for inhomogeneous systems. Acta Metall. 1961, 9, 525–535. [Google Scholar] [CrossRef]
- Khachaturyan, A.G. On the theory of modulated structures in binary solid solutions. Sov. Phys. Crystallogr. 1965, 10, 248–255. [Google Scholar]
- Khachaturyan, A.G. Microscopic theory of diffusion in crystalline solid solutions and the time evolution of the diffuse scattering of X-rays and thermal neutrons. Sov. Phys. Solid State 1968, 9, 2040–2046. [Google Scholar]
- Fraerman, A.A.; Mel’nikov, A.S.; Nefedov, I.M.; Shereshevskii, I.A.; Shpiro, A.V. Nonlinear relaxation dynamics in decomposing alloys: One-dimensional cahn-hilliard model. Phys. Rev. B 1997, 55, 6316–6323. [Google Scholar] [CrossRef]
- Koyama, M.; Zhang, Z.; Wang, M.; Ponge, D.; Raae, D.; Tsuzaki, K.; Noguchi, H.; Tasan, C. Bone-like crack resistance in hierarchical metastable nanolaminate steels. Science 2017, 355, 1055–1057. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.; Li, Y.; Zuo, Z.; Liu, H.; Huang, C.; Li, Y. Synthesis and properties of 2D carbon—Graphdiyne. Acc. Chem. Res. 2017, 50, 2470–2478. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.H.; Ghosh, S.; Pradhan, B.; Dalui, A.; Shrestha, L.K.; Acharya, S.; Ariga, K. Two-dimensional (2D) nanomaterials towards electrochemical nanoarchitectonics in energy-related applications. Bull. Chem. Soc. Jpn. 2017, 90, 627–648. [Google Scholar] [CrossRef]
- Hida, R.; Falub, C.V.; Perraudeau, S.; Morin, C.; Favier, S.; Mazel, Y.; Saghi, Z.; Michel, J.-P. Nanolamnated FeCoB/FeCo and FeCoB/NiFe soft magnetic thin films with tailored magnetic properties deposited by magnetron sputtering. J. Magn. Mater. 2018, 453, 211–219. [Google Scholar] [CrossRef]
- Khachaturyan, A.G.; Pokrovskii, B.I. Concentration wave approach in structural and thermodynamic characterization of ceramic crystals. Prog. Mater. Sci. 1985, 29, 1–138. [Google Scholar] [CrossRef]
- Tsakalakos, T. Composition-modulated films: New materials for studying stability and critical phenomena in solid solutions. Thin Solid Films 1981, 86, 79–90. [Google Scholar] [CrossRef]
- Tsakalakos, T. Nonlinear diffusion. Scripta Metal. 1986, 20, 471–478. [Google Scholar] [CrossRef]
- Tsakalakos, T.; Hilliard, J.E. Effect of long-range interaction on diffusion in copper-nickel composition modulated alloys. J. Appl. Phys. 1984, 55, 2885–2894. [Google Scholar] [CrossRef]
- Cook, H.E.; De Fontaine, D.; Hilliard, J.E. A model for diffusion on cubic lattices and its applications to the early stages of ordering. Acta Metall. 1969, 17, 765–773. [Google Scholar] [CrossRef]
- Cook, H.E.; De Fontaine, D. On the elastic free energy of solid solutions—I. Microscopic theory. Acta Metall. 1969, 17, 915–924. [Google Scholar] [CrossRef]
- Jankowski, A.F.; Tsakalakos, T. Phase stability by the artificial concentration wave method. Metall. Trans. A 1989, 20, 357–362. [Google Scholar] [CrossRef]
- Ditchek, B.; Schwartz, L.B. Applications of spinodal alloys. Annual Rev. Mater. Sci. 1979, 9, 219–253. [Google Scholar] [CrossRef]
- Pyataev, A.V.; Manapov, R.A. Mössbauer study of the process of the room-temperature aging of the alloy Cu79Ni14Fe7. Phys. Met. Metall. 2011, 111, 38–44. [Google Scholar] [CrossRef]
- Jankowski, A.F. Strain energy effects in the spinodal decomposition of Cu-Ni(Fe) nanolaminate coatings. Coatings 2015, 5, 246–262. [Google Scholar] [CrossRef]
- Butler, E.P.; Thomas, G. Structure and properties of spinodally decomposed Cu-Ni-Fe alloys. Acta Metall. 1970, 18, 347–365. [Google Scholar] [CrossRef]
- Hilliard, J.E. Spinodal Decomposition. In Phase Transformations; Aaronson, H.I., Ed.; ASM International: Metals Park, OH, USA, 1970; pp. 497–559. [Google Scholar]
- Guinier, A. X-ray Diffraction in Crystals, Imperfect Crystals and Amorphous Bodies; W.H. Freeman & Company: San Francisco, CA, USA, 1963; pp. 253–348. [Google Scholar]
- Paulson, W.M.; Hilliard, J.E. Interdiffusion in composition-modulated gold-copper thin films. J. Appl. Phys. 1977, 48, 2117–2123. [Google Scholar] [CrossRef]
- Erdélyi, Z.; Girardeaux, C.; Tôkei, Z.; Beke, D.L.; Cserháti, C.; Rolland, A. Investigation of the interplay of nickel dissolution and copper segregation in Ni/Cu(111) system. Surface Sci. 2002, 496, 129–140. [Google Scholar] [CrossRef]
- Erdélyi, Z.; Beke, D.L. Nanoscale volume diffusion. J. Mater. Sci. 2011, 46, 6465–6483. [Google Scholar] [CrossRef]
- Monma, K.; Sato, H.; Oikawa, H. Diffusion of Ni63 and Cr51 in nickel-chromium alloys (On the relation between high-temperature creep and diffusion in nickel base solid solutions. I). J. Jpn Inst. Met. 1964, 28, 188–192. [Google Scholar] [CrossRef]
- Gust, W.; Wachtel, E.; Frühauf, B.; Predel, B. Coarsening of extremely small particles in the Cu-Ni-Fe system. MRS Proc. 1983, 21, 461–466. [Google Scholar] [CrossRef]
- Poerschke, R.; Wagner, W.; Wollenberger, H. Alloy decomposition in Cu-Ni-Fe. I. Equilibrium states and kinetics of homophase fluctuations. J. Phys. F Met. Phys. 1986, 16, 421–434. [Google Scholar] [CrossRef]
- Wagner, W.; Poerschke, R.; Wollenberger, H. Alloy decomposition in Cu-Ni-Fe. III. Influence of electron irradiation on decomposition kinetics and morphology. J. Phys. F Met. Phys. 1987, 17, 2017–2029. [Google Scholar] [CrossRef]
- Jankowski, A.F.; Saw, C.K.; Hayes, J.P. The thermal stability of nanocrystalline Au-Cu alloys. Thin Solid Films 2006, 515, 1152–1156. [Google Scholar] [CrossRef]
- Gjostein, N.A. Surface Self Diffsion in FCC and BCC Metals: A Comparison of Theory and Experiment. In Surfaces and Interfaces. I. Chemical and Physical Characteristics; Burke, J.J., Reed, N.L., Weiss, W., Eds.; Syracuse University Press: Syracuse, NY, USA, 1967; pp. 271–304. [Google Scholar]
- Gjostein, N.A. Short Circuit Diffusion. In Diffusion; Aaronson, H.I., Ed.; Transactions of American Society for Metals: Metals Park, OH, USA, 1973; pp. 241–274. [Google Scholar]
- Balluffi, R.W. On measurements of self-diffusion rates along dislocations in f.c.c. metals. Phys. Status Solidi 1970, 42, 11–34. [Google Scholar] [CrossRef]
- Wang, Z.; Jeurgens, L.P.H.; Sigle, W.; Mittemeijer, E.J. Observation and origin of extraordinary atomic mobility at metal-semiconductor interfaces at low temperatures. Phys. Rev. Lett. 2015, 115, 016102. [Google Scholar] [CrossRef] [PubMed]
- Garbrecht, M.; Saha, B.; Schroeder, J.L.; Hultman, L.; Sands, T.D. Dislocation-pipe diffusion in nitride superlattices observed in direct atomic resolution. Sci. Rep. 2017, 7, 46092. [Google Scholar] [CrossRef] [PubMed]
- Kaptay, G.; Janczak-Rusch, J.; Jeurgens, L.P.H. Melting point depression and fast diffusion in nanostructured brazing fillers confined between barrier nanolayers. J. Mater. Eng. Perform. 2016, 25, 3275–3284. [Google Scholar] [CrossRef]
- Legros, M.; Dehm, G.; Arzt, E.; Balk, T.J. Observation of giant diffusivity along dislocation cores. Science 2008, 319, 1646–1649. [Google Scholar] [CrossRef] [PubMed]
- Harrison, L.G. Influence of dislocations on diffusion kinetics in solids with particular reference to the alkali halides. Trans. Faraday Soc. 1961, 57, 1191–1197. [Google Scholar] [CrossRef]
- Divinski, S.; Ribbe, J.; Schmitz, G.; Herzig, C. Grain boundary diffusion and segregation of Ni in Cu. Acta Mater. 2007, 55, 3337–3346. [Google Scholar] [CrossRef]
- Wegner, M.; Leuthold, J.; Peterlechner, M.; Song, X.; Divinski, S.V.; Wilde, G. Grain boundary and triple junction diffusion in nanocrystalline copper. J. Appl. Phys. 2014, 116, 093514. [Google Scholar] [CrossRef]
- Wang, Z.B.; Lu, K.; Wilde, G.; Divinski, S.V. Interfacials diffusion in Cu with a gradient nanostructured surface layer. Acta Mater. 2010, 58, 2376–2386. [Google Scholar] [CrossRef]
- Ribbe, J.; Schmitz, G.; Divinski, S.V. Grain boundary diffusion of Fe in high-purity copper. Defect Diffus. Forum 2009, 289–292, 211–217. [Google Scholar] [CrossRef]
- Prokoshkina, D.; Esin, V.A.; Divinski, S.V. Experimental evidences for anomalous grain boundary diffusion of Fe in Cu and Cu-Fe alloys. Acta Mater. 2017, 133, 240–246. [Google Scholar] [CrossRef]
- Prokoshkina, D.; Esin, V.A.; Wilde, G.; Divinski, S.V. Grain boundary width, energy and self-diffusion in nickel: Effect of material purity. Acta Mater. 2013, 61, 5188–5197. [Google Scholar] [CrossRef]
- den Broeder, F.J.A.; Nakahara, S. Diffusion induced grain boundary migration and recrystallization in the Cu-Ni system. Scripta Metall. 1983, 17, 399–404. [Google Scholar] [CrossRef]
- Jankowski, A.F.; Shewbridge, J.F. Grain size dependence on layer thickness in composition modulated thin films. Mater. Lett. 1987, 4, 313–315. [Google Scholar] [CrossRef]



 Jankowski [22];
Jankowski [22];  Gust, et al. [30];
Gust, et al. [30];  Poerschke, et al. [31,32];
Poerschke, et al. [31,32];  Tsakalakos and Hilliard [16];
Tsakalakos and Hilliard [16];  Garbrecht, et al. [38];
Garbrecht, et al. [38];  Legros, et al. [40];
Legros, et al. [40];  Divinski, et al. [42];
Divinski, et al. [42];  Wegner, et al. [43];
Wegner, et al. [43];  Ribbe, et al. [45];
Ribbe, et al. [45];  Prokoshkina, et al. [47];
Prokoshkina, et al. [47];  Wang, et al. [44];
Wang, et al. [44];  present).
present).
 Jankowski [22];
Jankowski [22];  Gust, et al. [30];
Gust, et al. [30];  Poerschke, et al. [31,32];
Poerschke, et al. [31,32];  Tsakalakos and Hilliard [16];
Tsakalakos and Hilliard [16];  Garbrecht, et al. [38];
Garbrecht, et al. [38];  Legros, et al. [40];
Legros, et al. [40];  Divinski, et al. [42];
Divinski, et al. [42];  Wegner, et al. [43];
Wegner, et al. [43];  Ribbe, et al. [45];
Ribbe, et al. [45];  Prokoshkina, et al. [47];
Prokoshkina, et al. [47];  Wang, et al. [44];
Wang, et al. [44];  present).
present).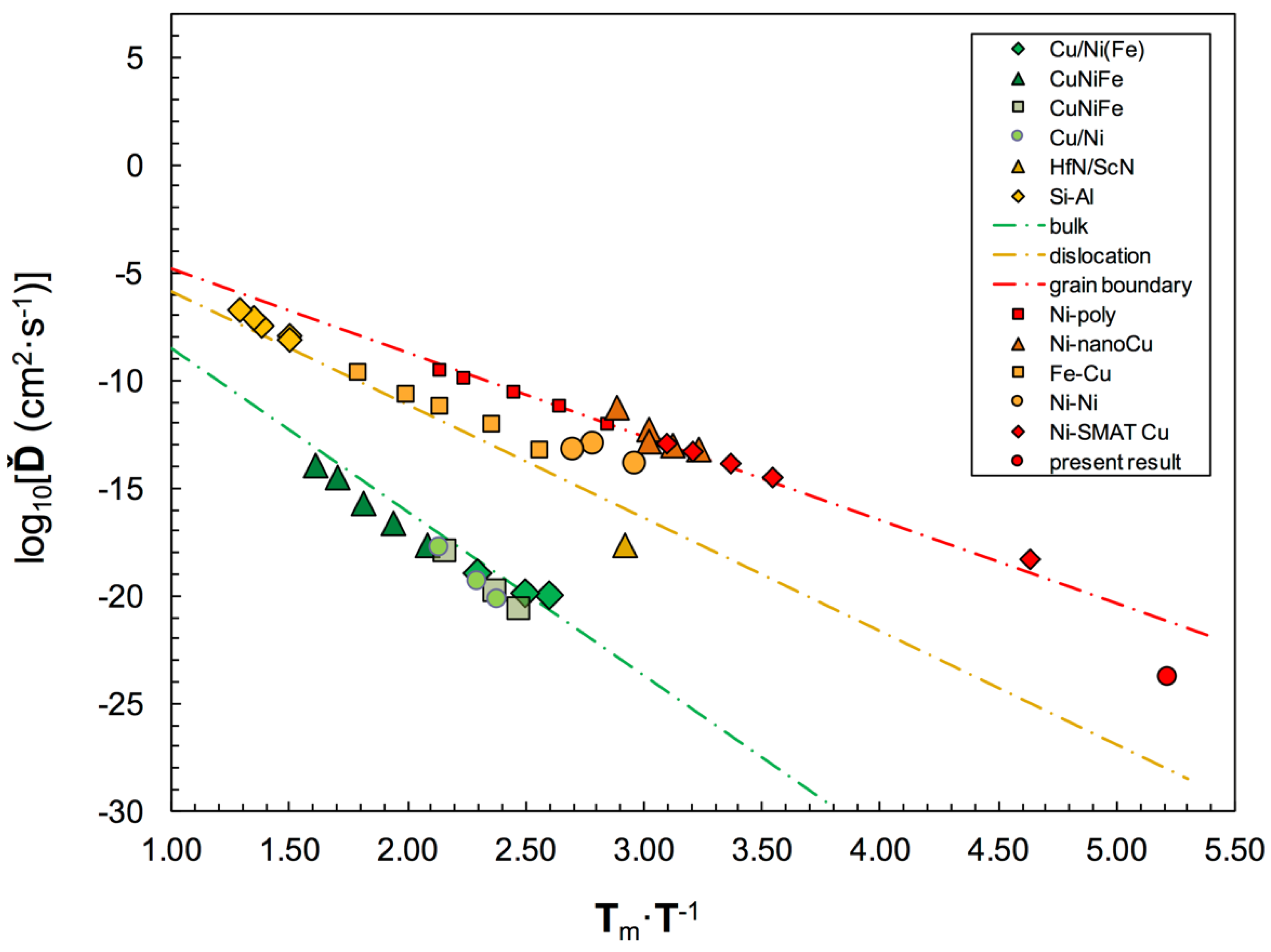
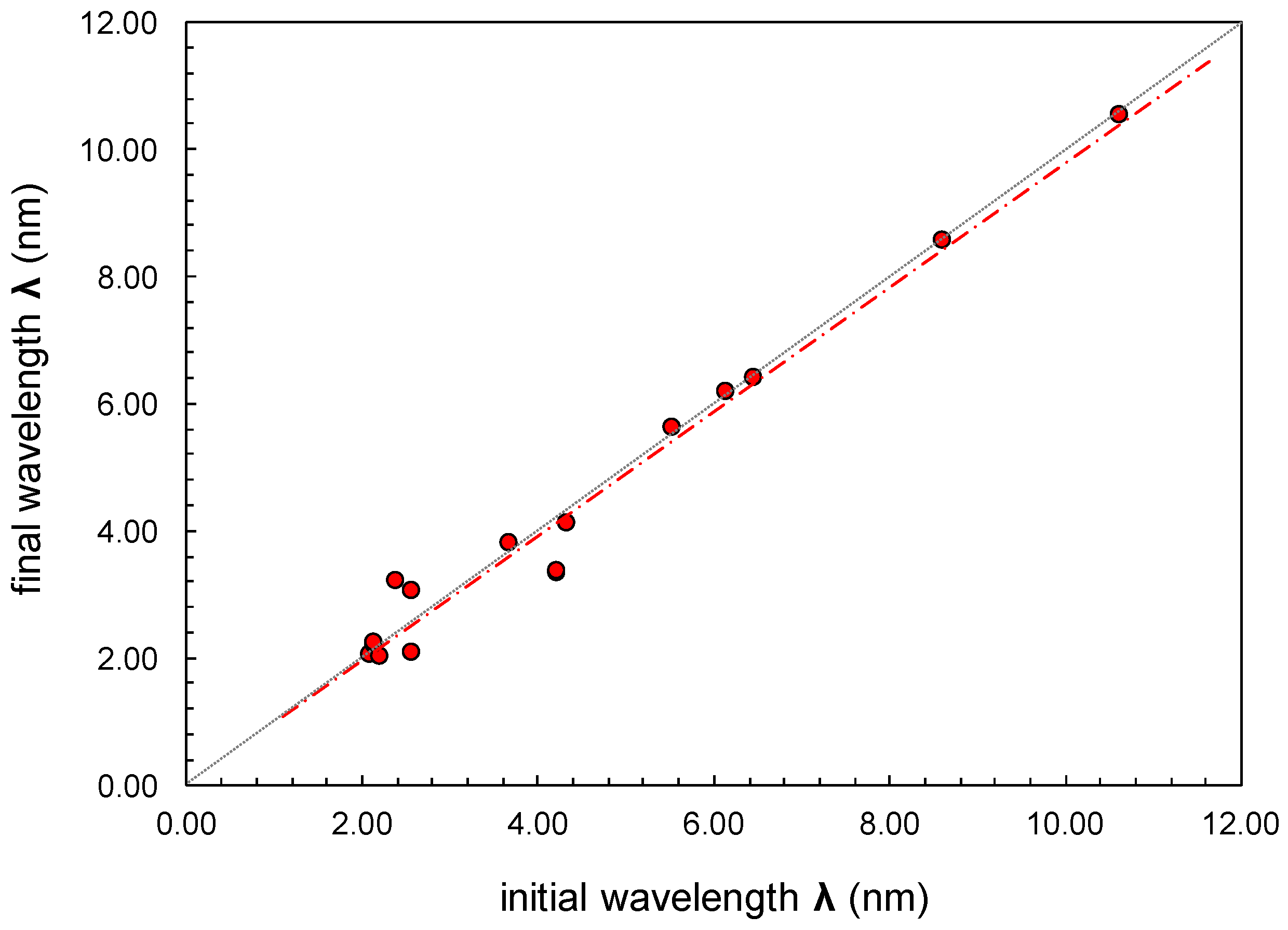
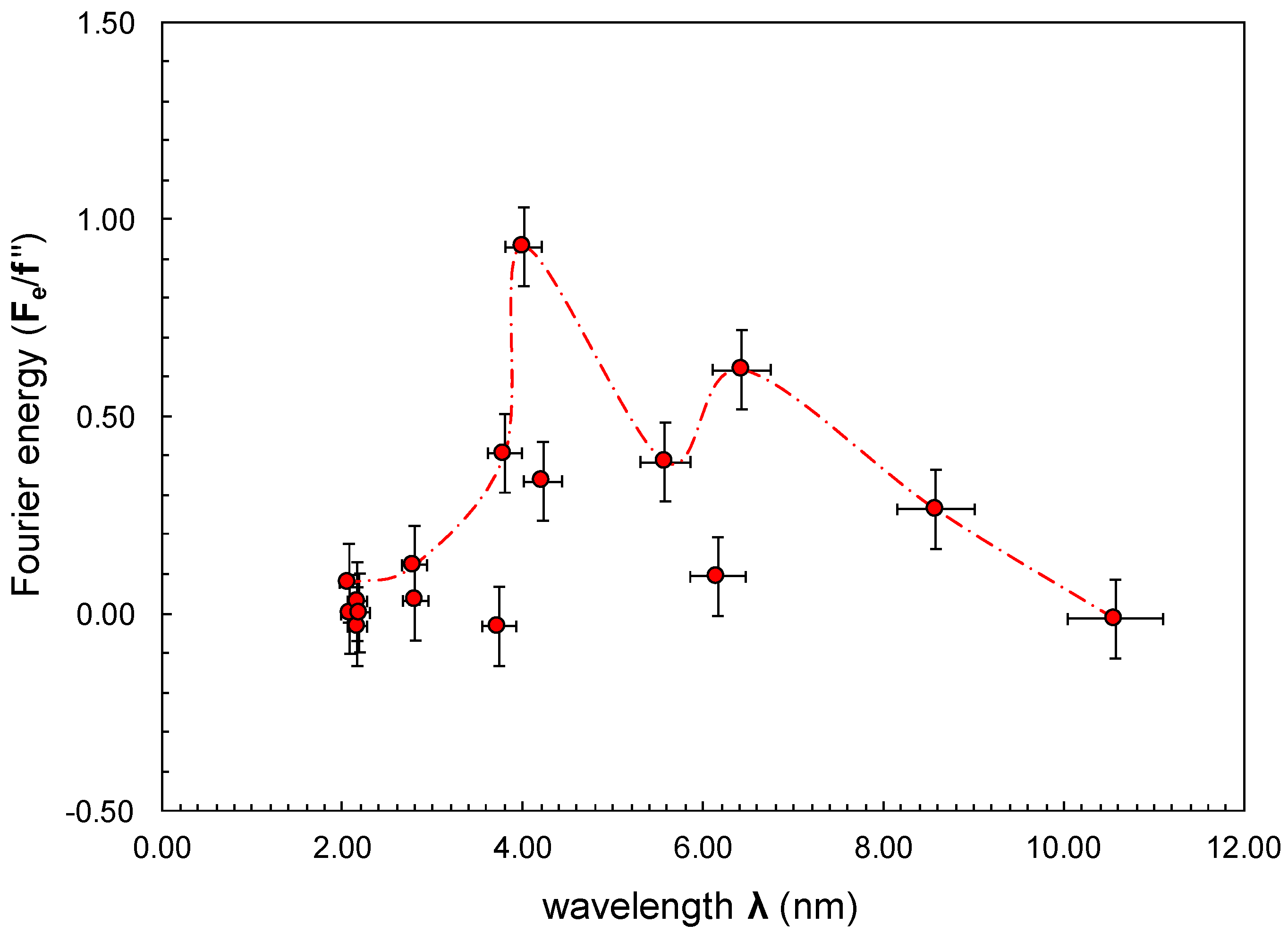
| Wavelength λ (nm) | B2 | (I−1/IB)corrected | R(B) | Ď(B) | ||
|---|---|---|---|---|---|---|
| Initial | Final | (nm−2) | Initial | Final | (10−10 s−1) | (10−24 cm2·s−1) |
| 10.63 | 10.51 | 0.35 | 0.17590 | 0.18879 | 0.37 | −1.037 |
| 8.61 | 8.54 | 0.54 | 0.11493 | 0.13803 | 0.94 | −1.746 |
| 6.46 | 6.40 | 0.95 | 0.06798 | 0.10785 | 2.44 | −2.563 |
| 6.16 | 6.17 | 1.04 | 0.03480 | 0.07060 | 3.74 | −3.612 |
| 5.55 | 5.61 | 1.26 | 0.03427 | 0.07445 | 4.10 | −3.248 |
| 4.34 | 4.11 | 2.20 | 0.01351 | 0.04003 | 5.82 | −2.648 |
| 4.24 | 3.32 | 2.43 | 0.00344 | 0.00627 | 3.20 | −1.314 |
| 4.24 | 3.37 | 2.70 | 0.00959 | 0.02561 | 5.19 | −1.919 |
| 3.68 | 3.80 | 2.80 | 0.00286 | 0.01136 | 7.24 | −2.588 |
| 2.58 | 3.05 | 4.91 | 0.00539 | 0.01349 | 4.86 | −0.991 |
| 2.41 | 3.19 | 4.95 | 0.00413 | 0.00890 | 4.05 | −0.818 |
| 2.22 | 2.01 | 8.16 | 0.00331 | 0.00955 | 5.65 | −0.692 |
| 2.16 | 2.23 | 7.97 | 0.00302 | 0.00851 | 5.54 | −0.695 |
| 2.14 | 2.19 | 8.17 | 0.00156 | 0.00383 | 4.71 | −0.576 |
| 2.10 | 2.05 | 8.77 | 0.00126 | 0.00221 | 2.99 | −0.341 |
| 2.07 | 2.07 | 8.90 | 0.00539 | 0.00654 | 1.00 | −0.112 |
| Curve Fit | 1 | 2 | 2a | 2b | 3 |
|---|---|---|---|---|---|
| Ď (10−10 nm2·s−1) | −4.108 | −1.767 | 0.7208 | −0.9222 | −1.00 × 10−16 |
| M (1010 nm2·J−1·s−1) | 2.383 | 1.025 | −41.82 | 53.51 | 5.80 × 10−17 |
| f″ (10−18 J·nm−3) | −1.484 | −1.484 | −1.484 | −1.484 | −1.484 |
| K1 (10−20 J·nm−1) | 8.683 | −140.2 | 244.2 | −204.1 | −1.93 × 10−10 |
| K2 (10−21 J·nm) | −2.438 | 711.3 | −1166 | 866.9 | 1.30 × 10−11 |
| K3 (10−22 J·nm3) | 1.264 | −1106 | 1945 | −1142 | −2.35 × 10−12 |
| K4 (10−23 J·nm5) | – | 554.3 | – | 506.8 | 1.36 × 10−11 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankowski, A.F. Interdiffusion at Room Temperature in Cu-Ni(Fe) Nanolaminates. Coatings 2018, 8, 225. https://doi.org/10.3390/coatings8060225
Jankowski AF. Interdiffusion at Room Temperature in Cu-Ni(Fe) Nanolaminates. Coatings. 2018; 8(6):225. https://doi.org/10.3390/coatings8060225
Chicago/Turabian StyleJankowski, Alan F. 2018. "Interdiffusion at Room Temperature in Cu-Ni(Fe) Nanolaminates" Coatings 8, no. 6: 225. https://doi.org/10.3390/coatings8060225
APA StyleJankowski, A. F. (2018). Interdiffusion at Room Temperature in Cu-Ni(Fe) Nanolaminates. Coatings, 8(6), 225. https://doi.org/10.3390/coatings8060225




