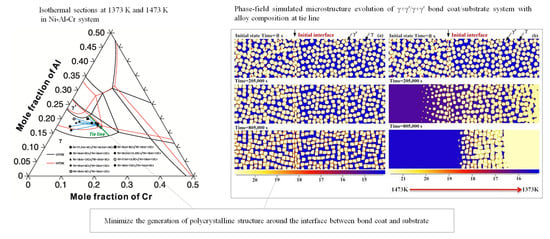
A Trial to Design γ/γ′ Bond Coat in Ni–Al–Cr Mode TBCs Aided by Phase-Field Simulation
Abstract
1. Introduction
2. Multi-Phase-Field Model
3. CALPHAD Coupling and Materials Parameters
4. Results and Discussion
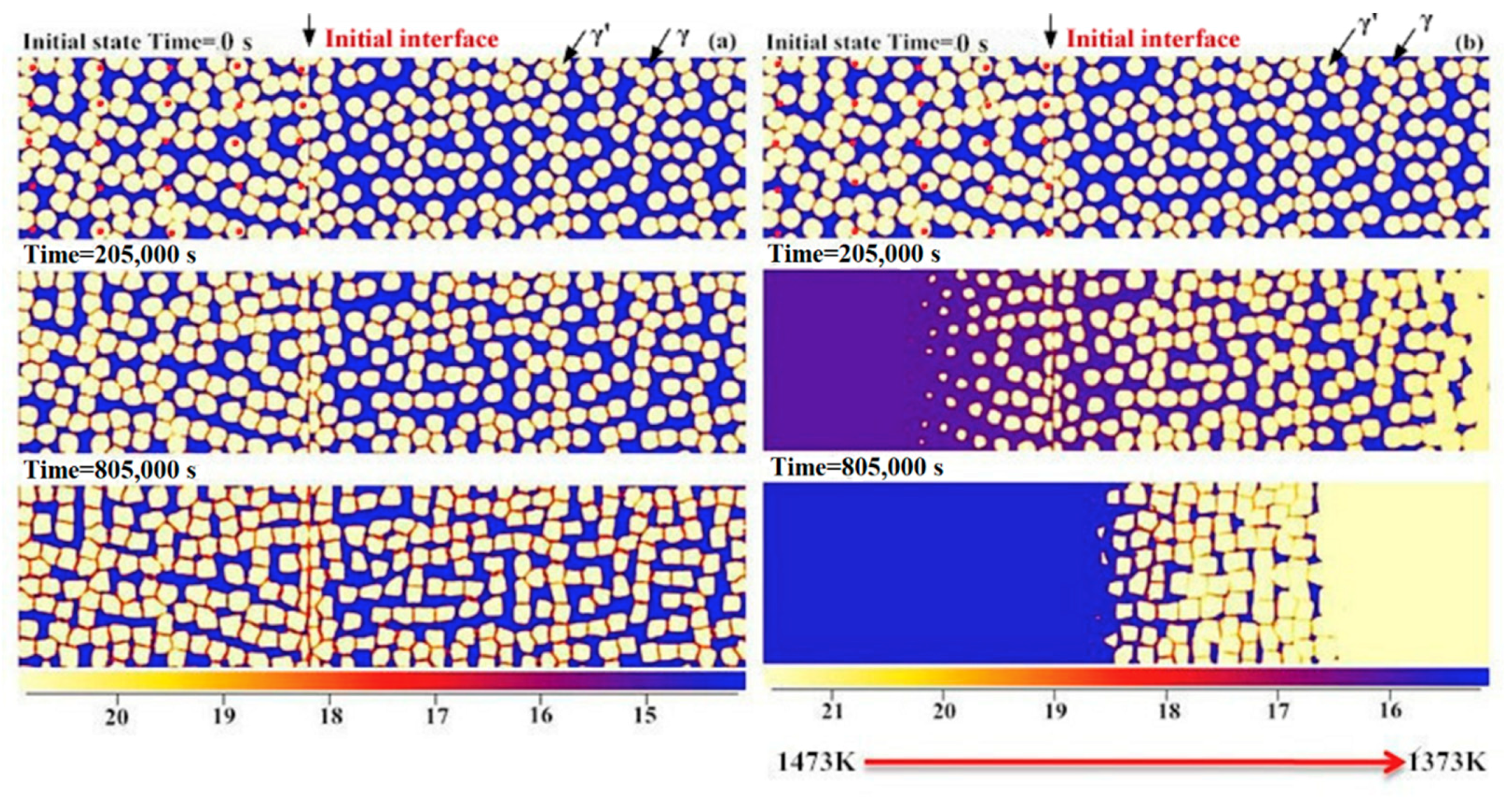
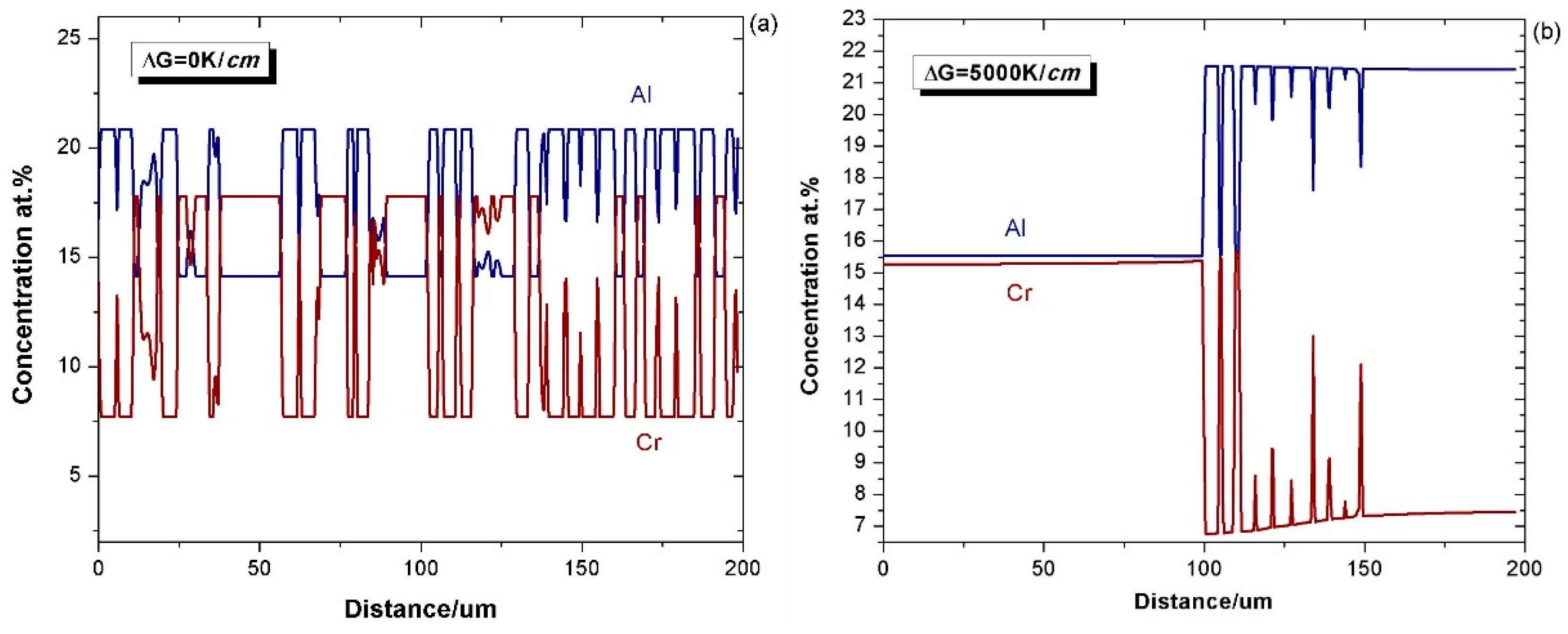
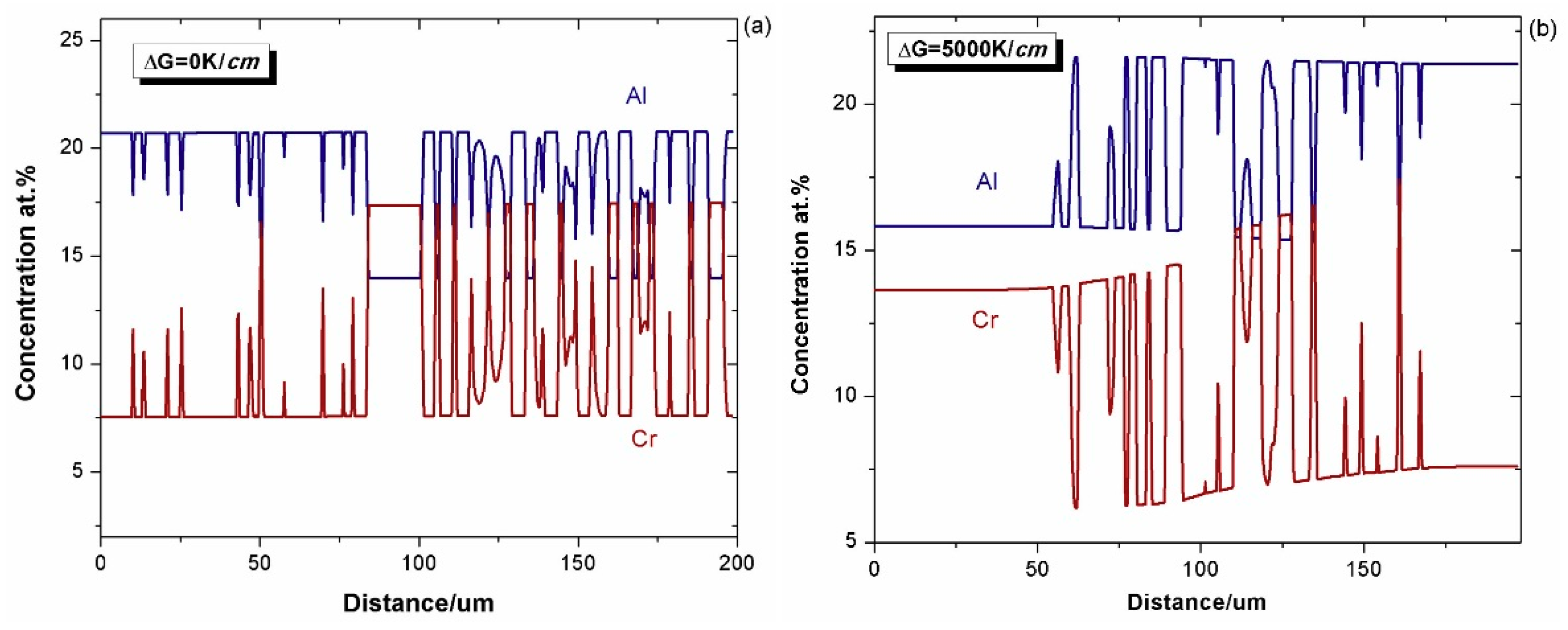
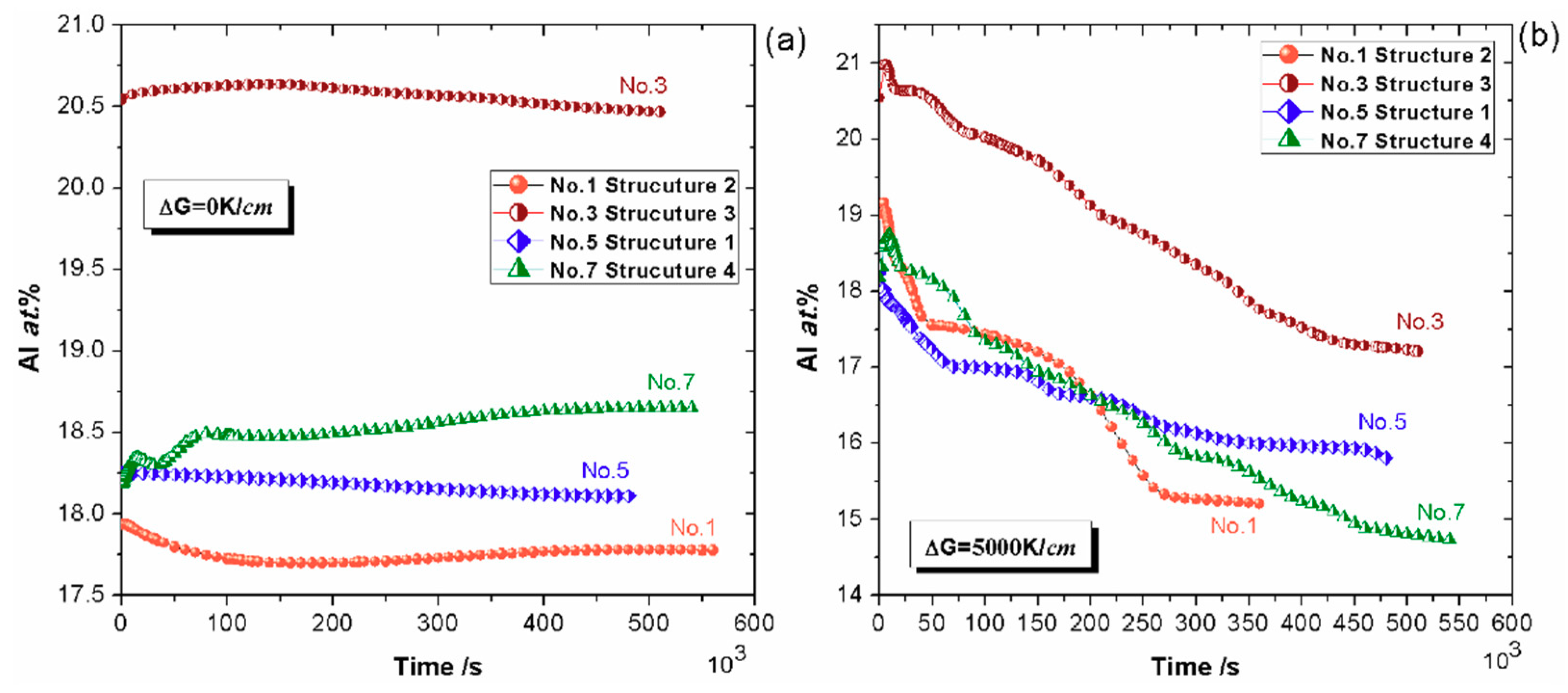
4.1. Effect of Alloy Composition
4.1.1. Cohesiveness Property
4.1.2. Preserved Property of Al
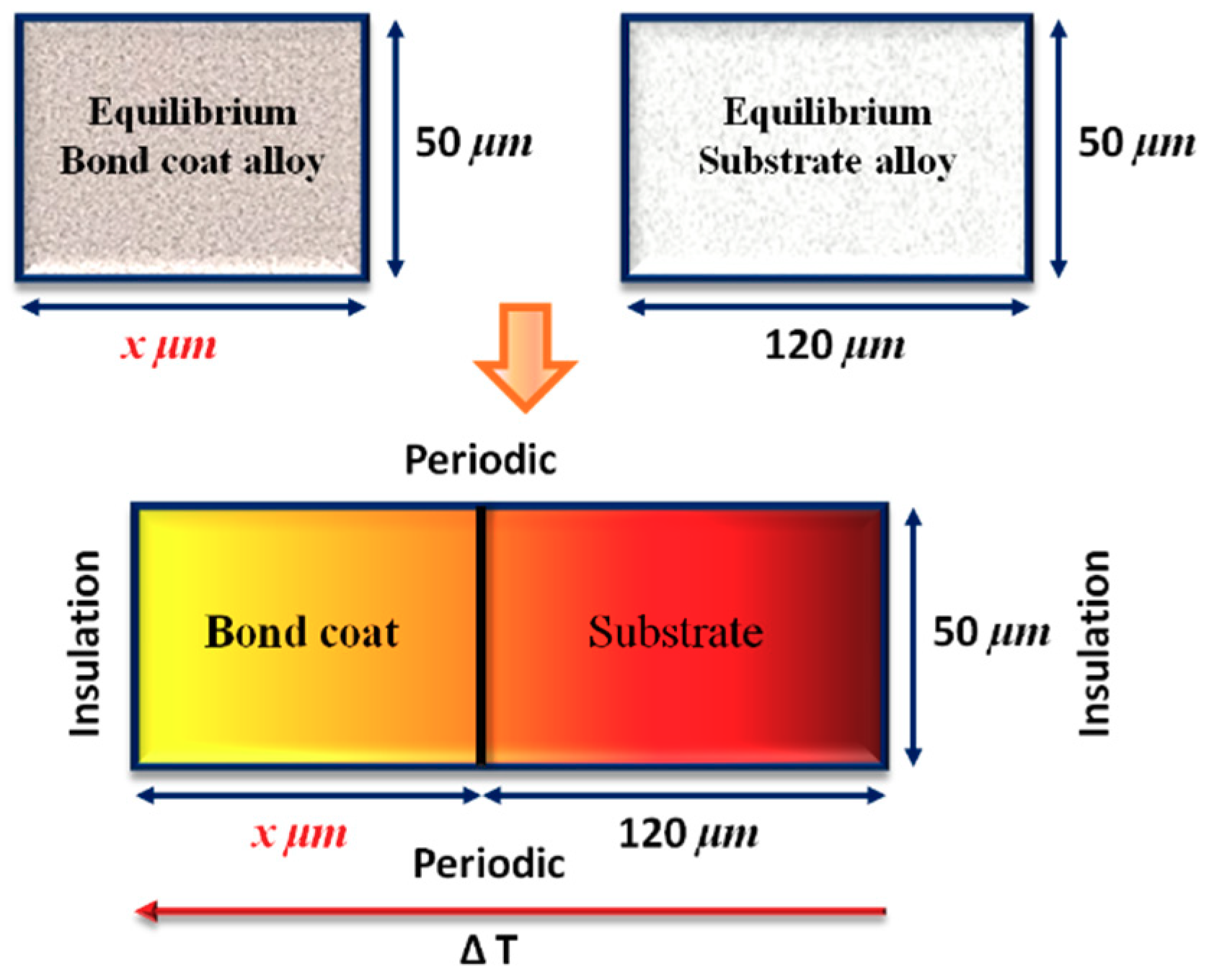
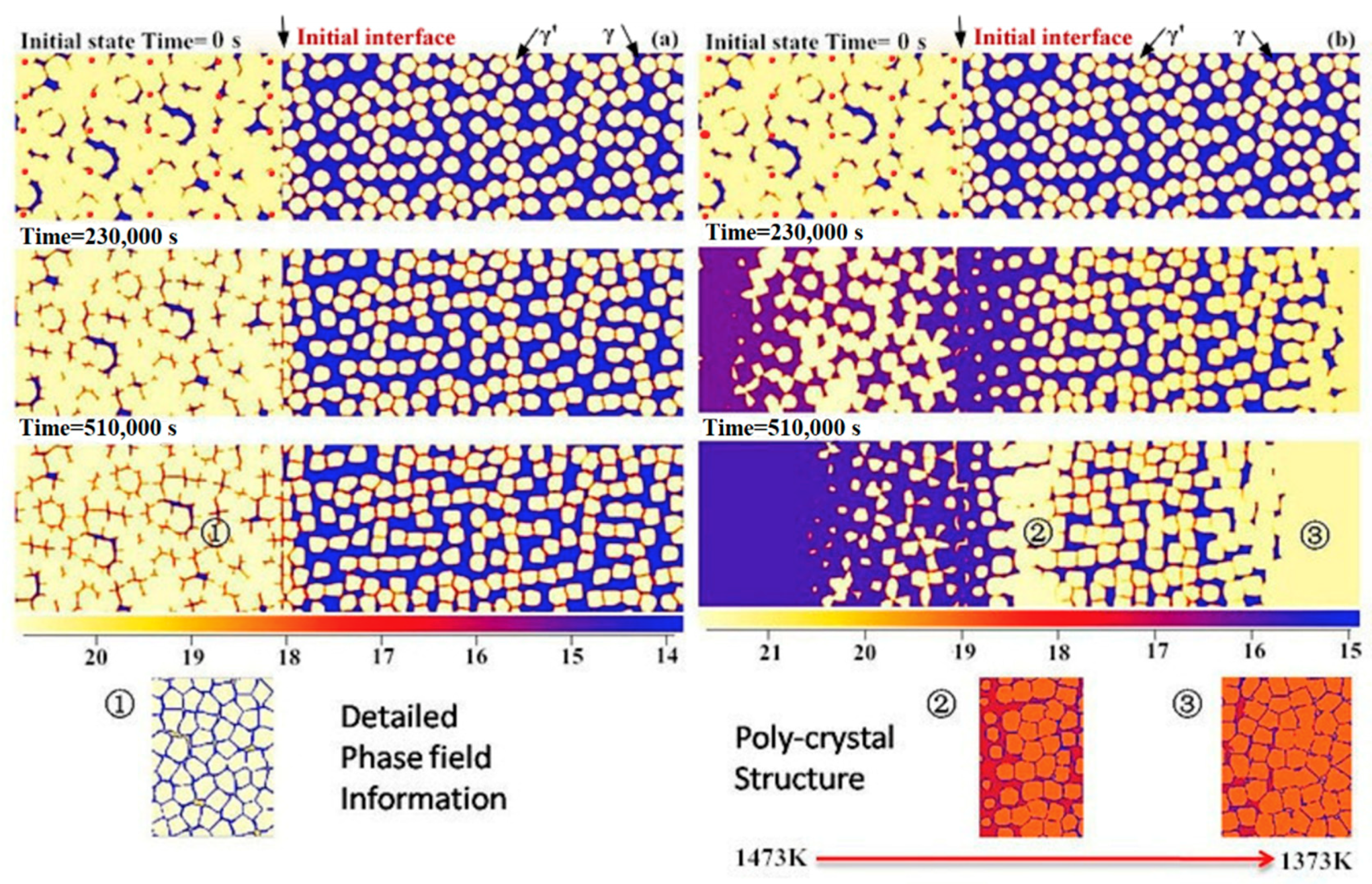
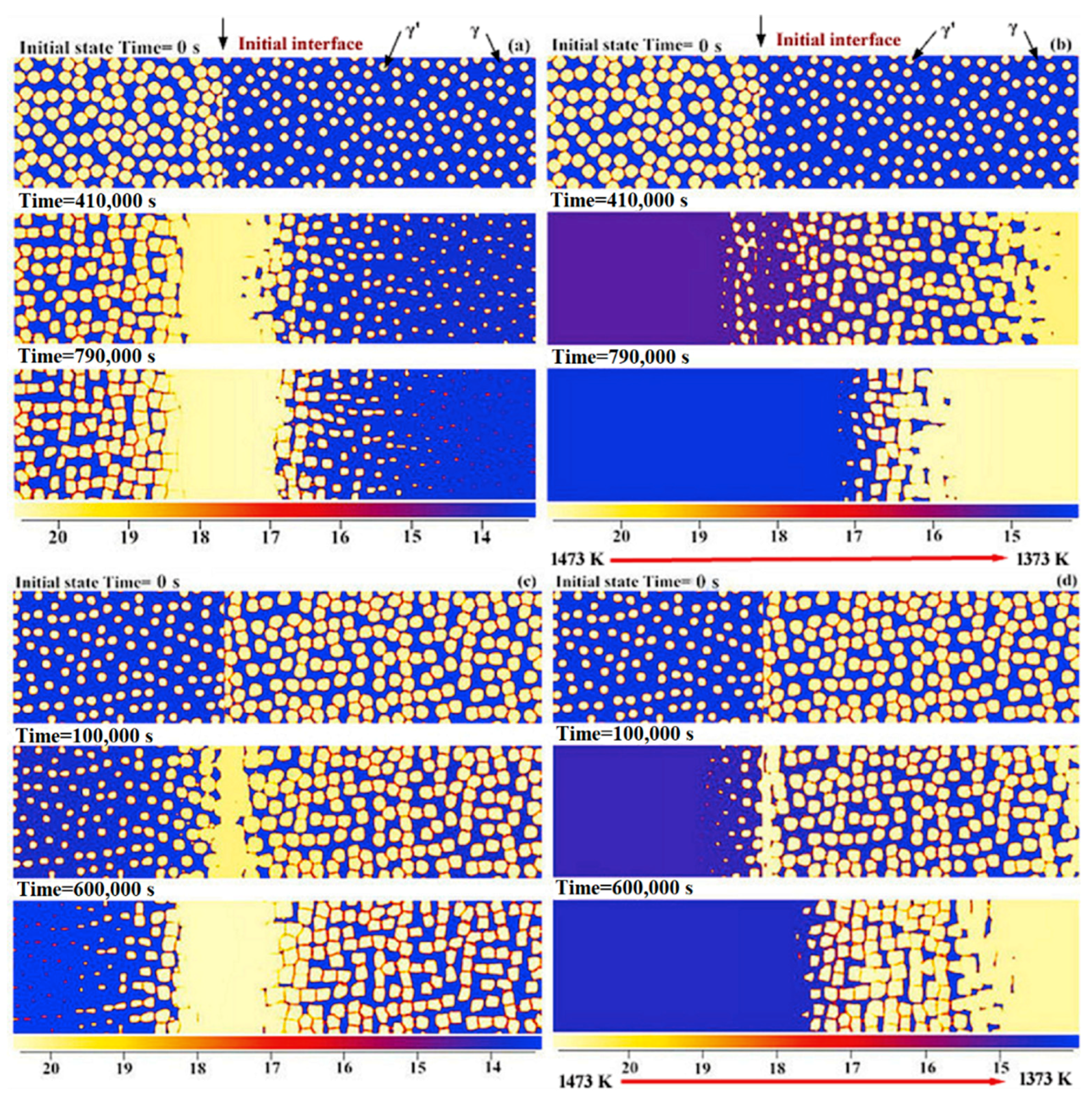
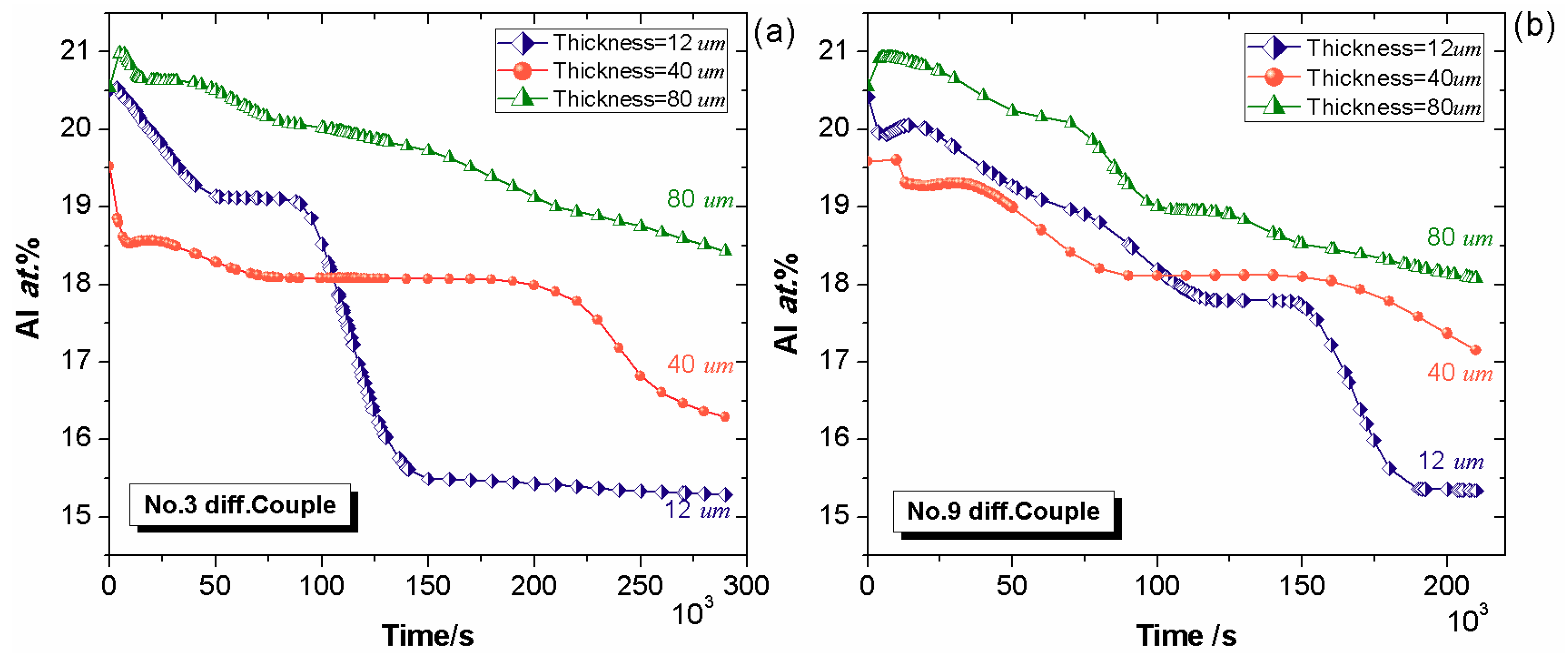
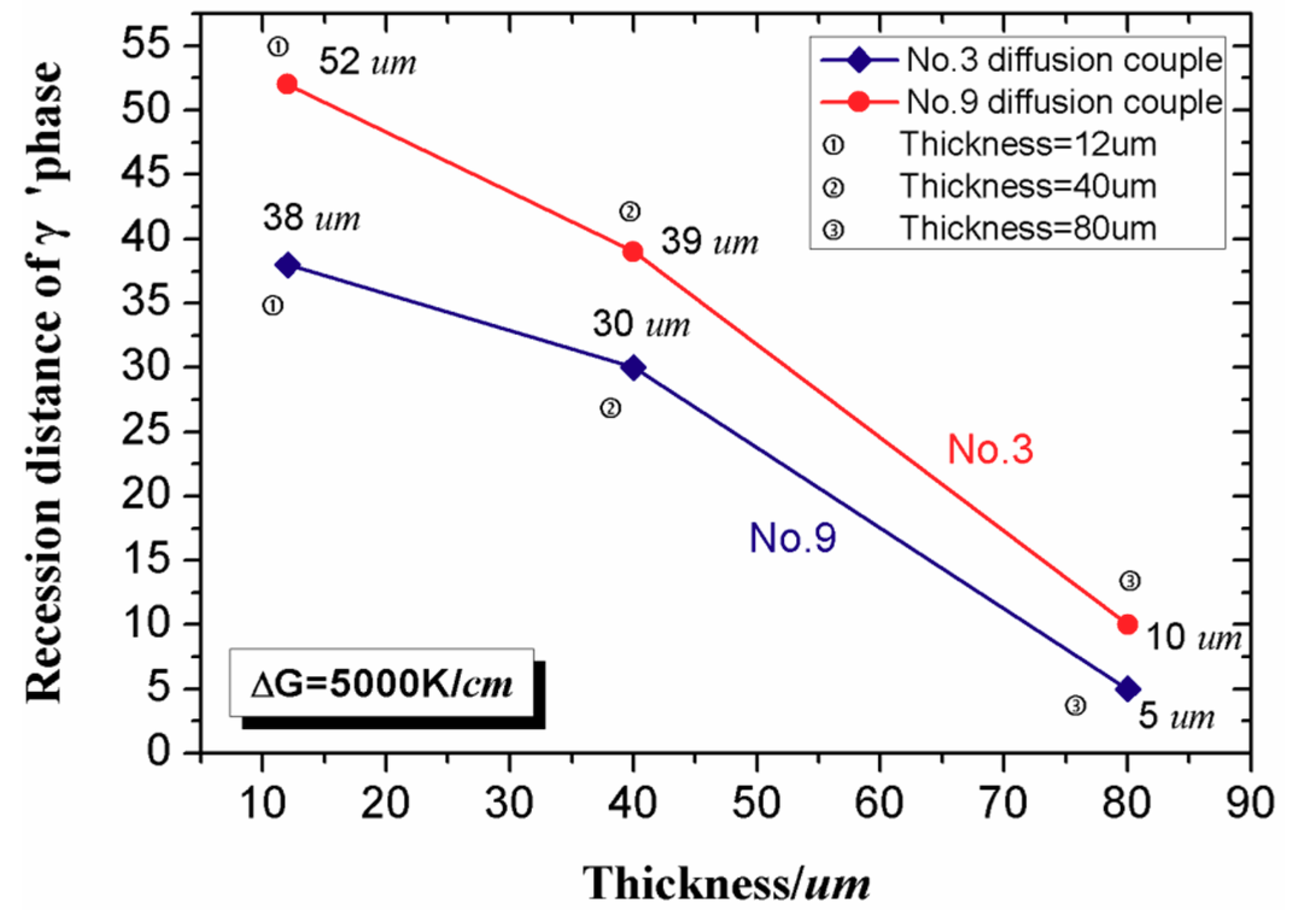
4.2. Effect of Bond Coat Thickness
4.3. Design of γ/γ′ Bond Coat Based on a Semi-Quantitative Structure–Property Relationship
- The optimal alloy composition of the bond coat can be chosen by means of a semi-quantitative design for the bond coat/substrate system with the identical elements.
- For the second case, the elements in the bond coat are less than those in the substrate alloys, the above tie line method is not applicable, but the γ′ phase fraction in the bond coat should be higher than that in the substrate.
- Besides considering the weight of turbine blades and stress conditions, the thickness of the bond coat should be thick enough to lower destruction from the temperature gradient.
5. Conclusions
- A group of 2-D phase field simulations coupled with CALPHAD-type databases were performed to investigate the γ + γ′ Ni–Al–Cr mode bond coat/substrate systems, aiming to investigate the influence of the alloy composition, bond coat thickness and temperature gradient on the cohesiveness and aluminum preserved properties of the bond coat during the interdiffusion process at high temperatures.
- A semi-quantitative tie-line selection criteria for alloy composition of the bond coat/substrate system is proposed, i.e., equilibrium Al concentrations of γ′ and γ phases in the bond coat should be similar to that in the substrate, and the phase fraction of γ′ in the bond coat tends to be higher than that in the substrate, so as to reduce the formation of polycrystal structures and thermal shock from the temperature gradient.
- The present methods for studying the interdiffusion phenomenon in the Ni–Al–Cr bond coat-substrate system can be easily extended to the multicomponent industrial alloy system.
Author Contributions
Funding
Conflicts of Interest
References
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Smialek, J.L.; Lowell, C.E. Effects of diffusion on aluminum depletion and degradation of NiAl Coatings. J. Electrochem. Soc. 1974, 121, 800–805. [Google Scholar] [CrossRef]
- Le Vine, S.R. Reaction diffusion in the NiCrA1 and CoCrA1 system. Metall. Trans. A 1978, 9, 1237–1250. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Rickerby, D.S.; Jones, R.J.; Xiao, P. Evolution of the interfacial toughness of thermal barrier system with a Pt-diffused γ + γ′ bond coat. Acta Mater. 2011, 59, 6401–6411. [Google Scholar] [CrossRef]
- Hayashi, S.; Wang, W.; Sordelet, D.J.; Gleeson, B. Interdiffusion behavior of Pt-modified γ-Ni + γ′-Ni3Al alloys coupled to Ni-Al-based alloys. Metall. Mater. Trans. A 2005, 36, 1769–1775. [Google Scholar] [CrossRef]
- Terock, M.; Fleischmann, E.; Hochmuth, C.; Völkl, R.; Glatzel, U. Synthesis and characterization of a Pt–Al–Cr–Ni γ/γ′-coating on the Ni-based superalloy CMSX-4. Surf. Coat. Technol. 2013, 236, 347–352. [Google Scholar] [CrossRef]
- Gleeson, B.; Wang, W.; Hayashi, S.; Sordelet, D.J. Effects of platinum on the interdiffusion and oxidation behavior of Ni-Al-based alloys. Mater. Sci. Forum 2004, 461, 213–222. [Google Scholar] [CrossRef]
- Nicholls, J.R. Advances in coating design for high-performance gas turbines. MRS Bull. 2003, 28, 659–670. [Google Scholar] [CrossRef]
- Kim, H.J.; Walter, M.E. Characterization of the degraded microstructures of a platinum aluminide coating. Mater. Sci. Eng. A 2003, 360, 7–17. [Google Scholar] [CrossRef]
- Xu, T.; Faulhaber, S.; Mercer, C.; Maloney, M.; Evans, A. Observations and analyses of failure mechanisms in thermal barrier systems with two phase bond coats based on NiCoCrAlY. Acta Mater. 2004, 52, 1439–1450. [Google Scholar] [CrossRef]
- Rangaraj, S.; Kokini, K. Fracture in single-layer zirconia (YSZ)-bond coat alloy (NiCoCrAlY) composite coatings under thermal shock. Acta Mater. 2004, 52, 455–465. [Google Scholar] [CrossRef]
- Alam, M.Z.; Parlikar, C.; Chatterjee, D.; Das, D.K. Comparative tensile behavior of freestanding γ-γ′ and β-(Ni,Pt)Al bond coats and effect on tensile properties of coated superalloy. Mater. Des. 2017, 114, 505–514. [Google Scholar] [CrossRef]
- Wang, B.; Gong, J.; Sun, C.; Huang, R.F.; Wen, L.S. The behavior of MCrAlY coatings on Ni3Al-base superalloy. Mater. Sci. Eng. A 2003, 357, 39–44. [Google Scholar] [CrossRef]
- Achar, D.R.G.; Munoz-Arroyo, R.; Singheiser, L.; Quadakkers, W.J. Modelling of phase equilibria in MCrAlY coating systems. Surf. Coat. Technol. 2004, 187, 272–283. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Hu, X.B.; Zheng, S.J.; Zhu, Y.L.; Wei, H.; Ma, X.L. Microstructural evolution of the interface between NiCrAlY coating and superalloy during isothermal oxidation. Mater. Des. 2015, 80, 63–69. [Google Scholar] [CrossRef]
- Li, M.H.; Sun, X.F.; Hu, W.Y.; Guan, H.R. Thermal shock behavior of EB-PVD thermal barrier coatings. Surf. Coat. Technol. 2007, 201, 7387–7391. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J. Phase field modeling of defects and deformation. Acta Mater. 2010, 58, 1212–1235. [Google Scholar] [CrossRef]
- Karma, A.; Tourret, D. Atomistic to continuum modeling of solidification microstructures. Curr. Opin. Solid State Mater. Sci. 2016, 20, 25–36. [Google Scholar] [CrossRef]
- Bellemans, I.; Moelans, N.; Verbeken, K. Phase-field modelling in extractive metallurgy. Crit. Rev. Solid State Mater. Sci. 2017, 1–38. [Google Scholar] [CrossRef]
- Steinbach, I.; Zhang, L.; Plapp, M. Phase-field model with finite interface dissipation. Acta Mater. 2012, 60, 2689–2701. [Google Scholar] [CrossRef]
- Zhang, L.; Steinbach, I. Phase-field model with finite interface dissipation: Extension to multi-component multi-phase alloys. Acta Mater. 2012, 60, 2702–2710. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, L.; Yang, M.; Li, K.; Liu, S.; Zhao, P.; Du, Y. Phase-field simulation of the solidified microstructure in a new commercial 6××× aluminum alloy ingot supported by experimental measurements. Int. J. Mater. Res. 2018, 109, 91–98. [Google Scholar] [CrossRef]
- Chang, K.; Chen, L.Q.; Krill, C.E.; Moelans, N. Effect of strong nonuniformity in grain boundary energy on 3-D grain growth behavior: A phase-field simulation study. Comput. Mater. Sci. 2017, 127, 67–77. [Google Scholar] [CrossRef]
- Britson, J.; Gao, P.; Pan, X.; Chen, L.Q. Phase field simulation of charged interface formation during ferroelectric switching. Acta Mater. 2016, 112, 285–294. [Google Scholar] [CrossRef]
- Zheng, Y.; Williams, R.E.A.; Wang, D.; Shi, R.; Nag, S.; Kami, P.; Sosa, J.M.; Banerjee, R.; Wang, Y.; Fraser, H.L. Role of ω phase in the formation of extremely refined intragranular α precipitates in metastable β-titanium alloys. Acta Mater. 2016, 103, 850–858. [Google Scholar] [CrossRef]
- Wang, Y.; Khachaturyan, A.G. Shape instability during precipitate growth in coherent solids. Acta Metall. Mater. 1995, 43, 1837–1857. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Wang, T.; Ardell, A.J.; Zhou, S.H.; Liu, Z.K.; Chen, L.Q. Three-dimensional phase-field simulations of coarsening kinetics of γ′ particles in binary Ni-Al alloys. Acta Mater. 2004, 52, 2837–2845. [Google Scholar] [CrossRef]
- Wen, Y.H.; Wang, B.; Simmons, J.P.; Wang, Y. A phase-field model for heat treatment applications in Ni-based alloys. Acta Mater. 2006, 54, 2087–2099. [Google Scholar] [CrossRef]
- Warnken, N.; Ma, D.; Drevermann, A.; Reed, R.C.; Fries, S.G. Steinbach I. Phase-field modeling of as-cast microstructure evolution in nickel-based superalloys. Acta Mater. 2009, 57, 5862–5875. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.J.; Wang, Y. Contributions from elastic inhomogeneity and from plasticity to γ′ rafting in single-crystal Ni-Al. Acta Mater. 2008, 56, 6156–6173. [Google Scholar] [CrossRef]
- Ta, N.; Zhang, L.; Du, Y. Design of the precipitation process for Ni-Al alloys with optimal mechanical properties: A phase-field study. Metall. Mater. Trans. A 2014, 45, 1787–1802. [Google Scholar] [CrossRef]
- Cao, D.; Ta, N.; Zhang, L. Unit-cell design for two-dimensional phase-field simulation of microstructure evolution in single-crystal Ni-based superalloys during solidification. Prog. Nat. Sci. Mater. Sci. 2017, 27, 678–686. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Yang, Y.; Yang, G.; Zhou, Y. Phase field simulation of the effect of interaction among ordered domains on interdiffusion in Ni–Al–Cr alloys. Chin. Phys. B 2009, 18, 4407–4412. [Google Scholar]
- Wu, K.; Chen, S.; Zhang, F.; Chang, Y.A. Integrating CALPHAD into phase field simulations for practical applications. J. Phase Equilib. Diff. 2009, 30, 571–576. [Google Scholar] [CrossRef]
- Pan, X.; Zhou, N.; Morral, J.E.; Wang, Y. Microstructural stability in multi-alloy systems: Nanostructured two-phase, dual alloy multilayers. Acta Mater. 2010, 58, 4149–4159. [Google Scholar] [CrossRef]
- Wu, K.; Zhou, N.; Pan, X.; Morral, J.E.; Wang, Y. Multiphase Ni–Cr–Al diffusion couples: A comparison of phase field simulations with experimental data. Acta Mater. 2008, 56, 3854–3861. [Google Scholar] [CrossRef]
- Wu, K.; Chang, Y.A.; Wang, Y. Simulating interdiffusion microstructures in Ni–Cr–Al diffusion couples: A phase field approach coupled with calphad database. Scr. Mater. 2004, 50, 1145–1150. [Google Scholar] [CrossRef]
- Mohanty, R.R.; Sohn, Y.H. Phase-field investigation of multicomponent diffusion in single-phase and two-phase diffusion couples. J. Phase Equilib. Diff. 2006, 27, 676–683. [Google Scholar] [CrossRef]
- Mohanty, R.R.; Sohn, Y.H. Microstructural stability of fcc-γ + B2-β coatings on γ substrate in Ni–Cr–Al system—A phase field model study. Surf. Coat. Technol. 2008, 203, 407–412. [Google Scholar] [CrossRef]
- Qiao, X. Interdiffusion Microstructure in γ + β/γ + γ′ Diffusion Couples. Master Thesis, University of Connecticut, Storrs, CT, USA, 1998. [Google Scholar]
- Ta, N.; Zhang, L.; Tang, Y.; Chen, W.; Du, Y. Effect of temperature gradient on microstructure evolution in Ni-Al-Cr bond coat/substrate systems: A phase-field study. Surf. Coat. Technol. 2015, 261, 364–374. [Google Scholar] [CrossRef]
- Eiken, J.; Böttger, B.; Steinbach, I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 2006, 73, 066122. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Borgenstam, A.; Engström, A.; Höglund, L. DICTRA, a tool for simulation of diffusional transformations in alloys. J. Phase Equilib. 2000, 21, 269. [Google Scholar] [CrossRef]
- Welcome to Micress®. Available online: http://web.micress.de (accessed on 19 November 2018).
- Thermodynamic Calculation Interface TQ-Interface V8.0; Thermo-Calc Software AB: Stockholm, Sweden, 2013; Available online: https://www.thermocalc.com/media/6030/tq8_usersguide.pdf.
- Huang, W.; Chang, Y.A. Thermodynamic properties of the Ni–Al–Cr system. Intermetallics 1999, 7, 863–874. [Google Scholar] [CrossRef]
- Engström, A.; Ågren, J. Assessment of diffusional mobilities in face-centered cubic Ni–Cr–Al alloys. Z. Metallkd 1996, 87, 2. [Google Scholar]
- Campbell, C.E. Assessment of the diffusion mobilites in the γ′ and B2 phases in the Ni–Al–Cr system. Acta Mater. 2008, 56, 4277–4290. [Google Scholar] [CrossRef]
- Kaptay, G. On the interfacial energy of coherent interfaces. Acta Mater. 2012, 60, 6804–6813. [Google Scholar] [CrossRef]
- Zhou, J.; Zhong, J.; Chen, L.; Zhang, L.; Du, Y.; Liu, Z.K.; Mayrhofer, P.H. Phase equilibria, thermodynamics and microstructure simulation of metastable spinodal decomposition in c–Ti1−xAlxN coatings. Calphad 2017, 56, 92–101. [Google Scholar] [CrossRef]
- Ul-Haq, I.; Booth, J.G. Magnetic and structural properties of Ni3Al based alloys. J. Magn. Magn. Mater. 1986, 62, 256–268. [Google Scholar] [CrossRef]
- Hornbogen, E.; Roth, M. Die verteilung kohärenter teilchen in nickellegierungen. Z. Metallkd 1967, 58, 842–855. [Google Scholar]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook; The MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Kim, D.E.; Shang, S.L.; Liu, Z.K. Effects of alloying elements on elastic properties of Ni3Al by first-principles calculations. Intermetallics 2010, 18, 1163–1171. [Google Scholar] [CrossRef]
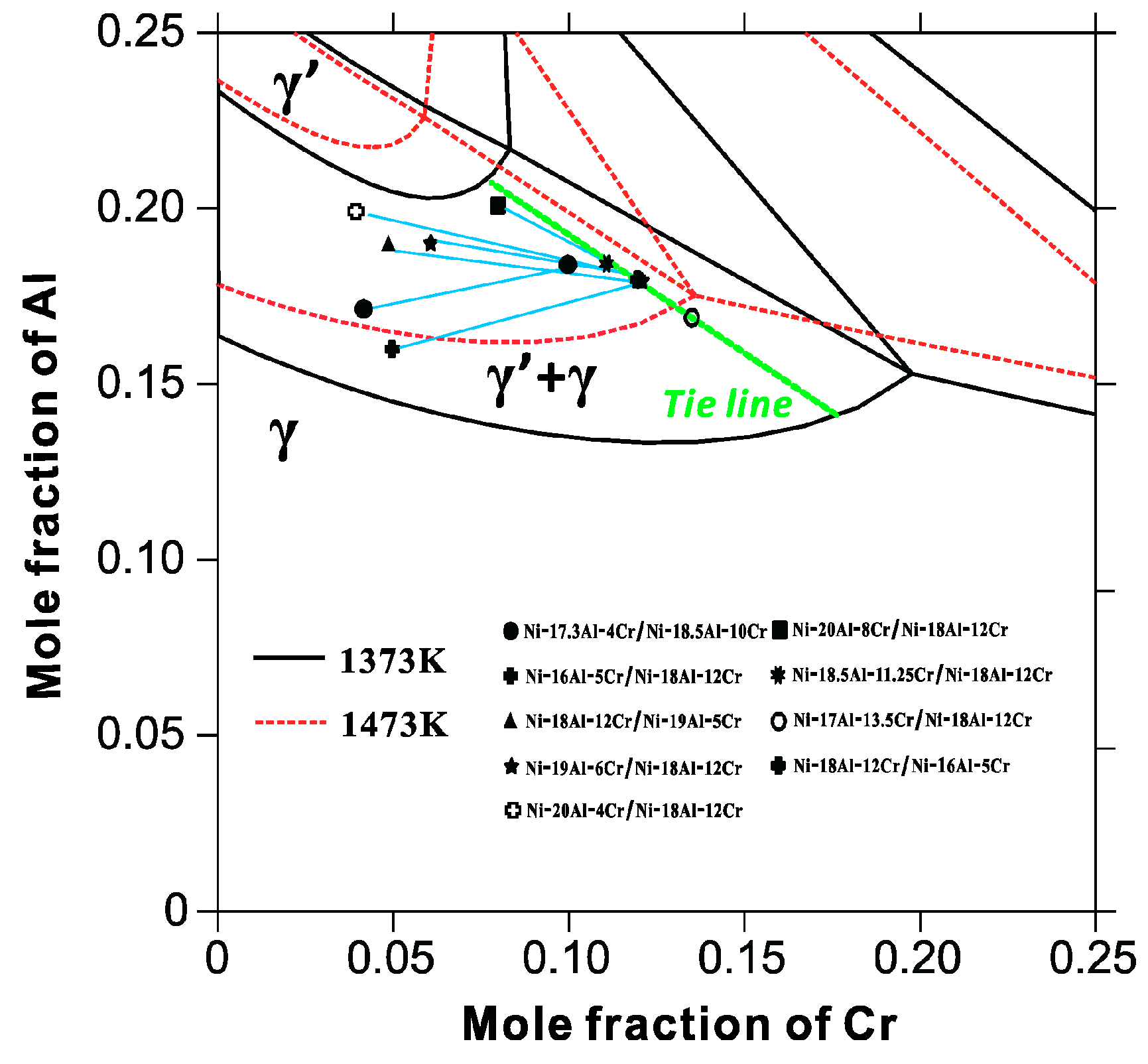






| No. | Composition of Bond Coat (at.%) | Composition of Substrate (at.%) |
|---|---|---|
| 1 | Ni–18Al–12Cr | Ni–19Al–5Cr |
| 2 | Ni–17.3Al–4Cr | Ni–18.5Al–10Cr |
| 3 | Ni–20Al–8Cr | Ni–18Al–12Cr |
| 4 | Ni–19Al–6Cr | Ni–18Al–12Cr |
| 5 | Ni–18.5Al–11.25Cr | Ni–18Al–12Cr |
| 6 | Ni–17Al–13.5Cr | Ni–18Al–12Cr |
| 7 | Ni–18Al–12Cr | Ni–16Al–5Cr |
| 8 | Ni–16Al–5Cr | Ni–18Al–12Cr |
| 9 | Ni–20Al–4Cr | Ni–18Al–12Cr |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ta, N.; Zhang, L.; Du, Y. A Trial to Design γ/γ′ Bond Coat in Ni–Al–Cr Mode TBCs Aided by Phase-Field Simulation. Coatings 2018, 8, 421. https://doi.org/10.3390/coatings8120421
Ta N, Zhang L, Du Y. A Trial to Design γ/γ′ Bond Coat in Ni–Al–Cr Mode TBCs Aided by Phase-Field Simulation. Coatings. 2018; 8(12):421. https://doi.org/10.3390/coatings8120421
Chicago/Turabian StyleTa, Na, Lijun Zhang, and Yong Du. 2018. "A Trial to Design γ/γ′ Bond Coat in Ni–Al–Cr Mode TBCs Aided by Phase-Field Simulation" Coatings 8, no. 12: 421. https://doi.org/10.3390/coatings8120421
APA StyleTa, N., Zhang, L., & Du, Y. (2018). A Trial to Design γ/γ′ Bond Coat in Ni–Al–Cr Mode TBCs Aided by Phase-Field Simulation. Coatings, 8(12), 421. https://doi.org/10.3390/coatings8120421