Non-Local Buckling Analysis of Functionally Graded Nanoporous Metal Foam Nanoplates
Abstract
1. Introduction
2. Theory and Formulation
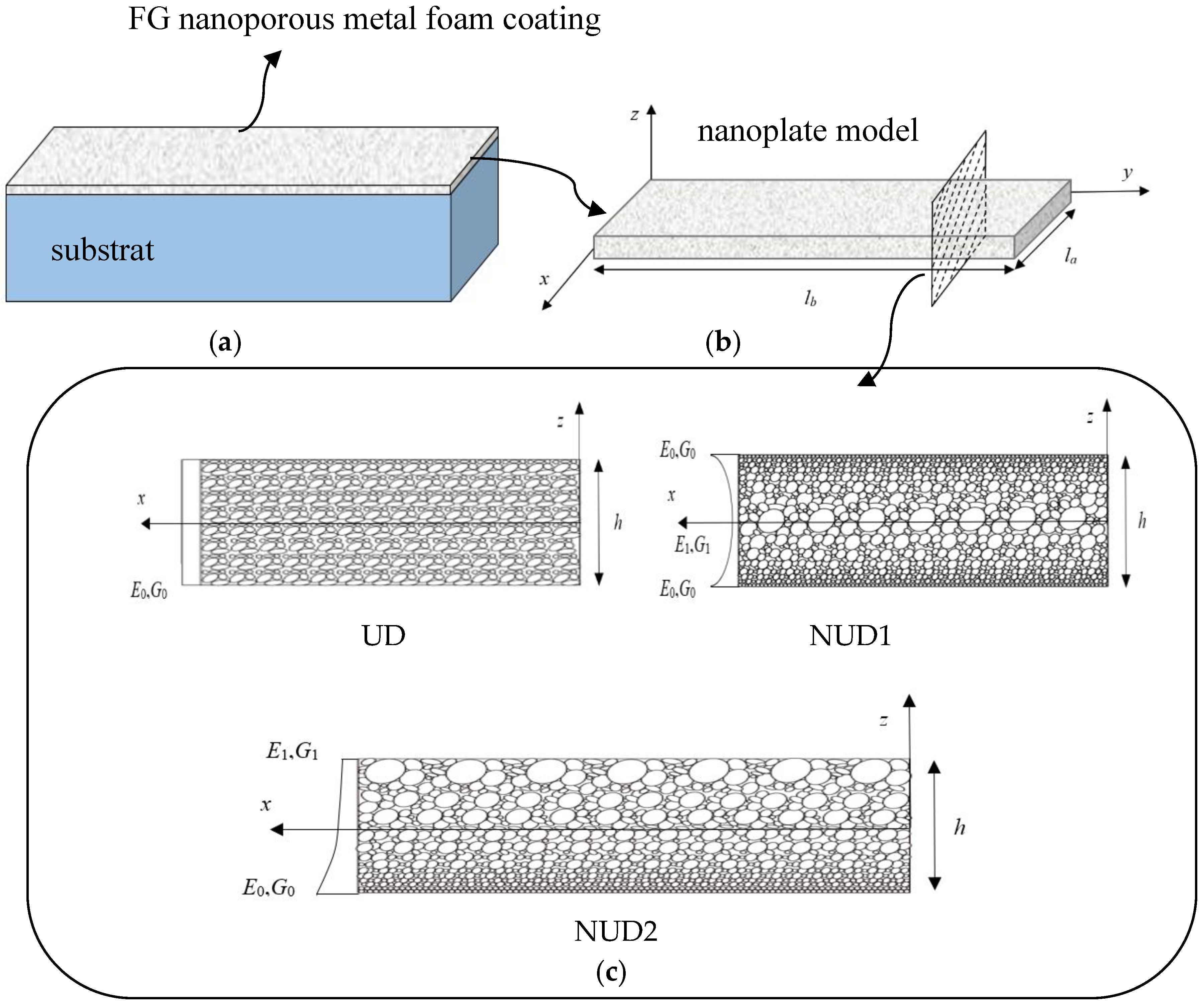
2.1. FG Nanoporous Metal Foam Nanoplate
2.2. The Non-Local Elasticity Theory
2.3. Governing Equations of Motion
- The displacements u (in the x direction), v (in the y direction) and w (in the z direction) are small compared to the thickness h of the nanoplate. Hence, the strains involved are infinitesimal. By considering the strain-displacement relations, the shear strains γxy, γzx, γyz and normal strains εxx, εyy, εzz can be written as:
- Compared with in-plane stresses σxx and σyy, the transverse normal stress σzz can be negligible.
- The displacement components u and v include extension, bending and shear components:
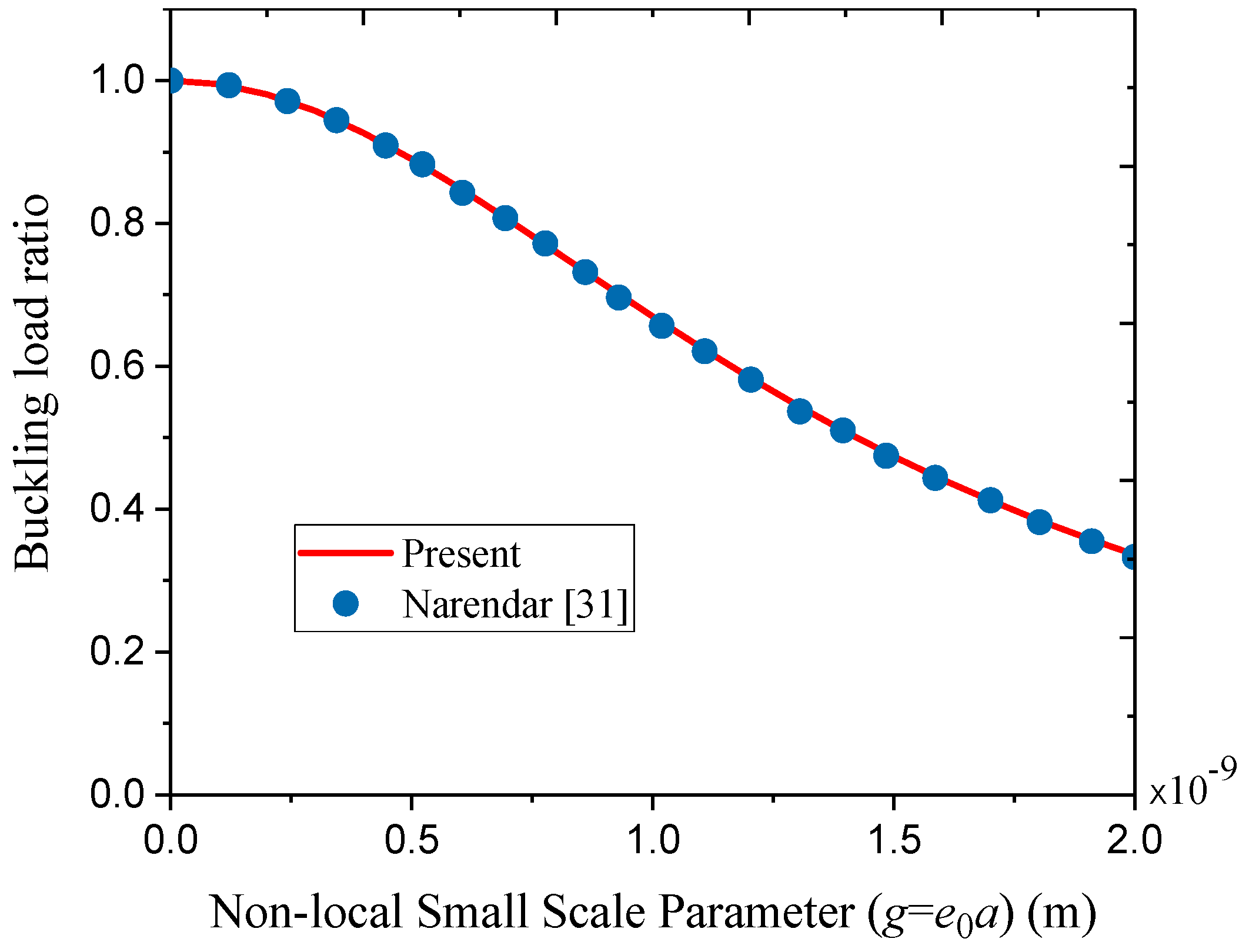
3. Results and Discussion
4. Conclusions
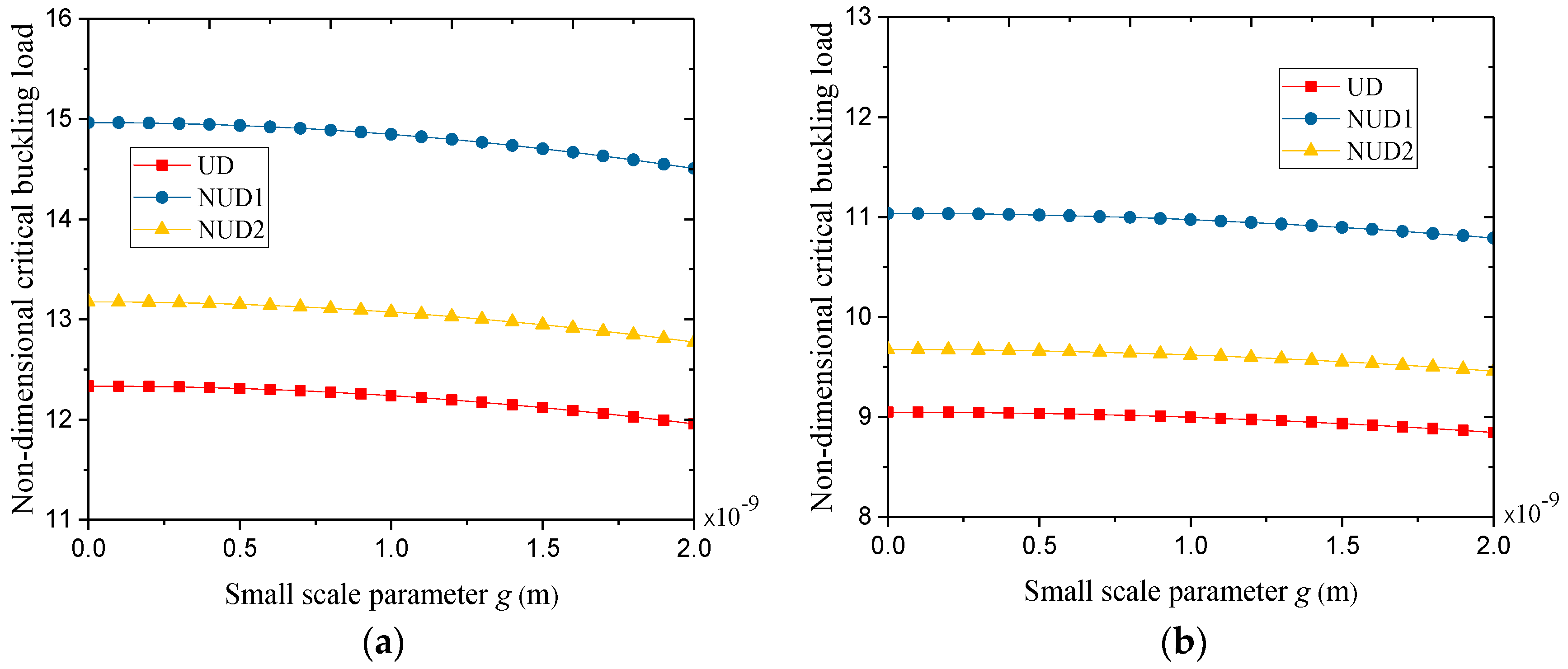
- An FG nanoporous metal foam nanoplate had a smaller critical buckling load than its solid counterpart. Among the three types of porosity distribution, the NUD1 nanoplate had the largest buckling load and the ND nanoplate had the smallest buckling load.
- The critical buckling load of FG nanoporous metal foam nanoplates decreased with the rise of the porosity coefficient and the small-scale parameter.
- The critical buckling load decreased as the aspect ratio increased. Additionally, the FG nanoporous metal foam nanoplate was more stable when the surface area got smaller.
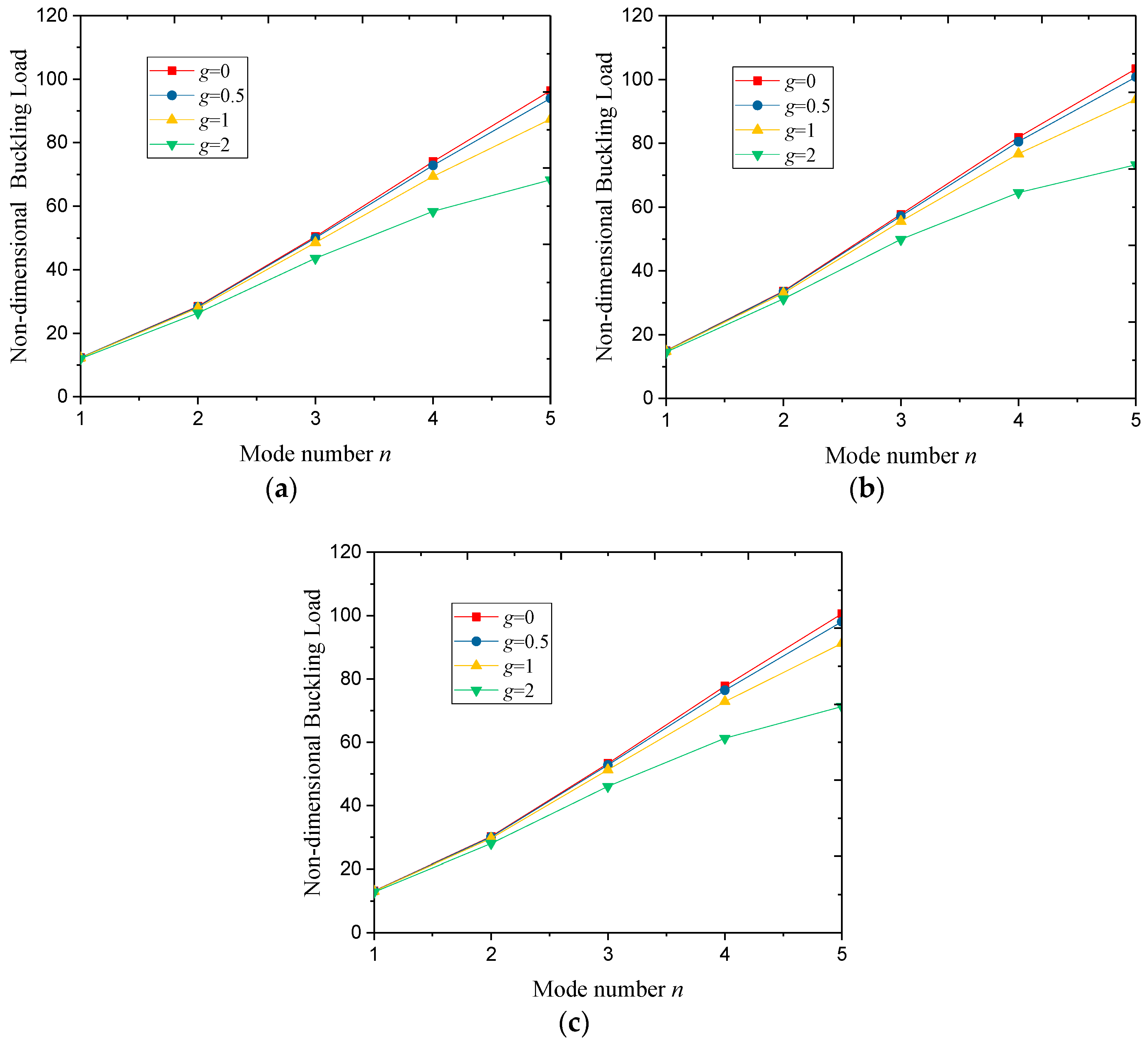
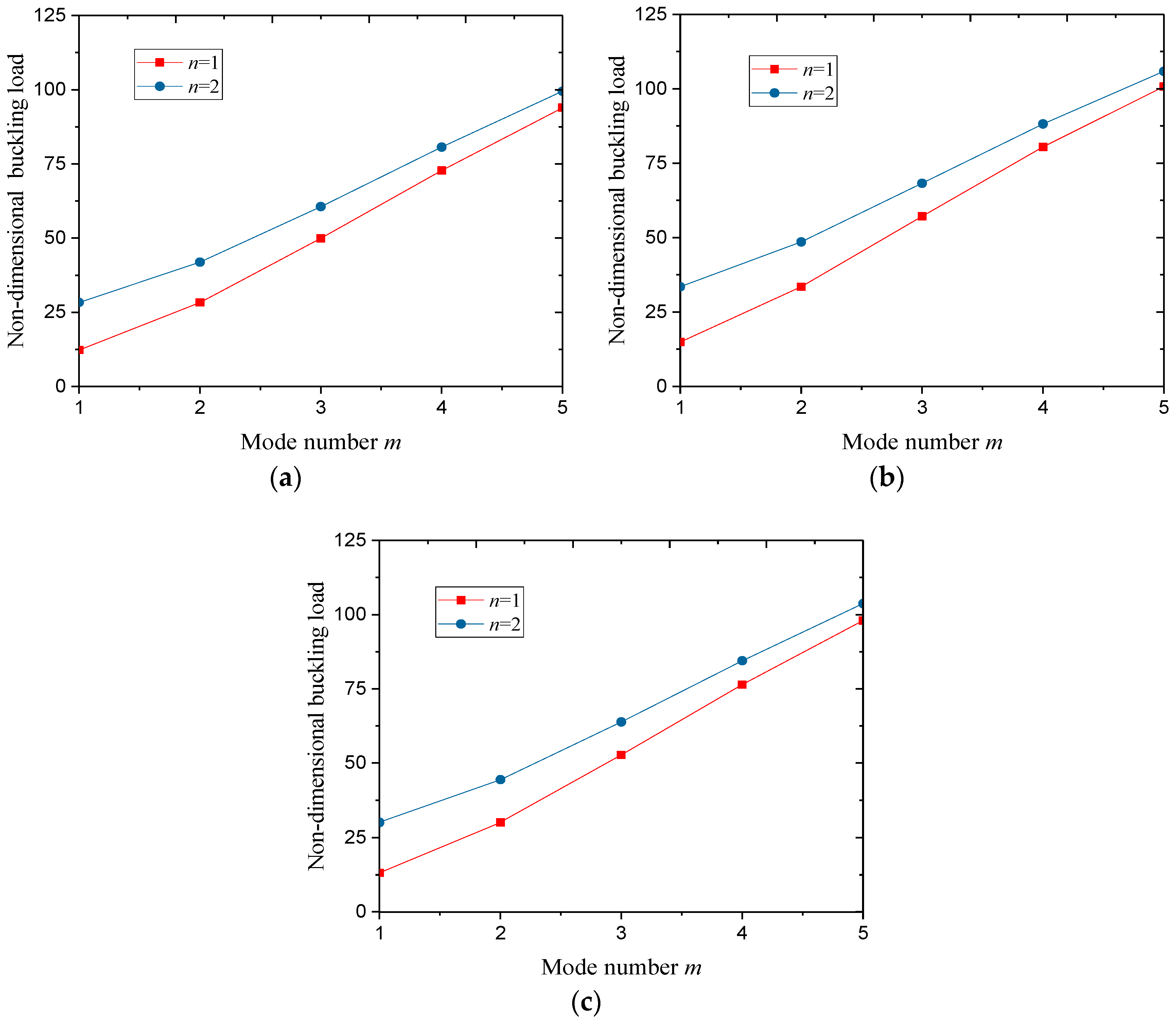
- The buckling load increased as the mode numbers rose; in addition, the scale effect was quite significant on the buckling load at large mode number n.
Author Contributions
Funding
Conflicts of Interest
References
- Biener, J.; Wittstock, A.; Zepeda-Ruiz, L.A.; Biener, M.M.; Zielasek, V.; Kramer, D.; Viswanath, R.N.; Weissmüller, J.; Bäumer, M.; Hamza, A.V. Surface-chemistry-driven actuation in nanoporous gold. Nat. Mater. 2009, 8, 47–51. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Ahn, C.; Jo, H.; Choi, M.; Kim, D.S.; Kim, D.K.; Jeon, S.; Choe, H. Large-area metal foams with highly ordered sub-micrometer-scale pores for potential applications in energy areas. Mater. Lett. 2014, 129, 174–177. [Google Scholar] [CrossRef]
- Freund, L.B.; Suresh, S. Thin Film Materials: Stress, Defect Formation and Surface Evolution, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rongong, J.A.; Goruppa, A.A.; Buravalla, V.R.; Tomlinson, G.R.; Jones, F.R. Plasma deposition of constrained layer damping coatings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 669–680. [Google Scholar] [CrossRef]
- Yu, L.; Ma, Y.; Zhou, C.; Xu, H. Damping efficiency of the coating structure. Int. J. Solids Struct. 2005, 42, 3045–3058. [Google Scholar] [CrossRef]
- Catania, G.; Strozzi, M. Damping oriented design of thin-walled mechanical components by means of multi-layer coating technology. Coatings 2018, 8, 73. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H.J. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Lambin, P. Elastic properties and stability of physisorbed graphene. Appl. Sci. 2014, 4, 282–304. [Google Scholar] [CrossRef]
- Farajpour, A.; Shahidi, A.R.; Mohammadi, M.; Mahzoon, M. Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Compos. Struct. 2012, 94, 1605–1615. [Google Scholar] [CrossRef]
- Aksencer, T.; Aydogdu, M. Levy type solution method for vibration and buckling of nanoplates using nonlocal elasticity theory. Physica E 2011, 43, 954–959. [Google Scholar] [CrossRef]
- Belkorissat, I.; Houari, M.S.A.; Tounsi, A.; Bedia, E.A.A.; Mahmoud, S.R. On vibration properties of functionally graded nano-plate using a new nonlocal refined four variable model. Steel Compos. Struct. 2015, 18, 1063–1081. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech. Sin. 2014, 30, 516–525. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Wang, Z.D. Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory. Compos. Struct. 2012, 94, 2038–2047. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. A two variable refined plate theory for orthotropic plate analysis. Int. J. Solids Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. Free vibrations of plate using two variable refined plate theory. J. Sound Vib. 2006, 296, 979–999. [Google Scholar] [CrossRef]
- Evoy, S.; Carr, D.W.; Sekaric, L.; Olkhovets, A.; Parpia, J.M.; Craighead, H.G. Nanofabrication and electrostatic operation of single-crystal silicon paddle oscillators. J. Appl. Phys. 1999, 86, 6072–6077. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van Der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Zhang, P.Q.; Lee, H.P.; Wang, C.M.; Reddy, J.N. Non-local elastic plate theories. Proc. R. Soc. Lond. Ser. A 2007, 463, 3225–3240. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. Combining effects of surface energy and non-local elasticity on the buckling of nanoplates. Micro Nano Lett. 2011, 6, 941–943. [Google Scholar] [CrossRef]
- Karimi, M.; Haddad, H.A.; Shahidi, A.R. Combining surface effects and non-local two variable refined plate theories on the shear/biaxial buckling and vibration of silver nanoplates. Micro Nano Lett. 2015, 10, 276–281. [Google Scholar] [CrossRef]
- Daneshmehr, A.; Rajabpoor, A.; Hadi, A. Size dependent free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory with high order theories. Int. J. Eng. Sci. 2015, 95, 23–35. [Google Scholar] [CrossRef]
- Karličić, D.; Adhikari, S.; Murmu, T.; Cajić, M. Exact closed-form solution for non-local vibration and biaxial buckling of bonded multi-nanoplate system. Compos. Part B Eng. 2014, 66, 328–339. [Google Scholar] [CrossRef]
- Bounouara, F.; Benrahou, K.H.; Belkorissat, I.; Tounsi, A. A nonlocal zeroth-order shear deformation theory for free vibration of functionally graded nanoscale plates resting on elastic foundation. Steel Compos. Struct. 2016, 20, 227–249. [Google Scholar] [CrossRef]
- Liu, S.; Yu, T.; Bui, T.Q. Size effects of functionally graded moderately thick microplates: A novel non-classical simple-FSDT isogeometric analysis. Eur. J. Mech. A. Solids 2017, 66, 446–458. [Google Scholar] [CrossRef]
- Liu, S.; Yu, T.; Bui, T.Q.; Xia, S. Size-dependent analysis of homogeneous and functionally graded microplates using IGA and a non-classical Kirchhoff plate theory. Compos. Struct. 2017, 172, 34–44. [Google Scholar] [CrossRef]
- Liu, S.; Yu, T.; Van Lich, L.; Yin, S.; Bui, T.Q. Size effect on cracked functional composite micro-plates by an XIGA-based effective approach. Meccanica 2018, 53, 2637–2658. [Google Scholar] [CrossRef]
- Narendar, S. Buckling analysis of micro-/nano-scale plates based on two-variable refined plate theory incorporating nonlocal scale effects. Compos. Struct. 2011, 93, 3093–3103. [Google Scholar] [CrossRef]
- Mechab, I.; Mechab, B.; Benaissa, S.; Serier, B.; Bouiadjra, B.B. Free vibration analysis of FGM nanoplate with porosities resting on Winkler Pasternak elastic foundations based on two-variable refined plate theories. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2193–2211. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M. Free vibration analysis of rectangular nanoplates based on two-variable refined plate theory using a new strain gradient elasticity theory. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 313–324. [Google Scholar] [CrossRef]
- Karimi, M.; Shahidi, A.R. Thermo-mechanical vibration, buckling, and bending of orthotropic graphene sheets based on nonlocal two-variable refined plate theory using finite difference method considering surface energy effects. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2017, 231, 111–130. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Investigating post-buckling of geometrically imperfect metal foam nanobeams with symmetric and asymmetric porosity distributions. Compos. Struct. 2017, 182, 91–98. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhao, H.L.; Ye, C.; Zu, J.W. A porous microbeam model for bending and vibration analysis based on the sinusoidal beam theory and modified strain gradient theory. Int. J. Appl. Mech. 2018, 10, 1850059. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear dynamics of a translational FGM plate with strong mode interaction. Int. J. Struct. Stab. Dyn. 2018, 18, 1850031. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear steady-state responses of longitudinally traveling functionally graded material plates in contact with liquid. Compos. Struct. 2017, 164, 130–144. [Google Scholar] [CrossRef]
- Wang, Y.Q. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Identifying the temperature effect on the vibrations of functionally graded cylindrical shells with porosities. Appl. Math. Mech. 2018, 1–18. [Google Scholar] [CrossRef]
- Chen, D.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of shear deformable sandwich beam with a functionally graded porous core. Thin-Walled Struct. 2016, 107, 39–48. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
- Narendar, S.; Gopalakrishnan, S. Scale effects on buckling analysis of orthotropic nanoplates based on nonlocal two-variable refined plate theory. Acta Mech. 2012, 223, 395–413. [Google Scholar] [CrossRef]

| Mode | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| m = 1, n = 1 | 18.636 | 18.600 | 12.334 | 12.310 | 14.965 | 14.936 | 13.176 | 13.150 |
| m = 2, n = 2 | 63.870 | 63.370 | 42.272 | 41.941 | 48.965 | 48.582 | 44.777 | 44.426 |
| m = 3, n = 3 | 116.14 | 114.12 | 76.869 | 75.527 | 84.672 | 83.194 | 80.648 | 79.241 |
| m = 4, n = 4 | 163.06 | 158.07 | 107.92 | 104.61 | 113.99 | 110.50 | 112.29 | 108.85 |
| m = 5, n = 5 | 201.03 | 191.57 | 133.05 | 126.79 | 136.20 | 129.79 | 137.56 | 131.09 |
| Mode | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| m = 1, n = 1 | 13.672 | 13.652 | 9.0485 | 9.0357 | 11.036 | 11.020 | 9.6751 | 9.6613 |
| m = 2, n = 2 | 48.709 | 48.432 | 32.238 | 32.055 | 37.915 | 37.700 | 34.244 | 34.050 |
| m = 3, n = 3 | 92.762 | 91.587 | 61.394 | 60.616 | 69.135 | 68.259 | 64.687 | 63.867 |
| m = 4, n = 4 | 135.87 | 132.84 | 89.926 | 87.921 | 97.284 | 95.114 | 94.015 | 91.919 |
| m = 5, n = 5 | 173.37 | 167.40 | 114.74 | 110.79 | 120.14 | 116.00 | 119.18 | 115.08 |
| Surface Area | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| la = lb =30 nm | 16.956 | 16.863 | 11.222 | 11.161 | 13.220 | 13.148 | 11.924 | 11.859 |
| la = lb =40 nm | 18.069 | 18.014 | 11.959 | 11.922 | 14.364 | 14.320 | 12.752 | 12.713 |
| la = lb =50 nm | 18.636 | 18.600 | 12.334 | 12.310 | 14.965 | 14.936 | 13.176 | 13.150 |
| la = lb =60 nm | 18.960 | 18.934 | 12.549 | 12.531 | 15.313 | 15.292 | 13.419 | 13.400 |
| la = lb =70 nm | 19.161 | 19.141 | 12.681 | 12.669 | 15.531 | 15.515 | 13.569 | 13.556 |
| h | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| h = 5 nm | 18.636 | 18.600 | 12.334 | 12.310 | 14.965 | 14.936 | 13.176 | 13.150 |
| h = 6 nm | 18.190 | 18.154 | 12.039 | 12.015 | 14.491 | 14.463 | 12.842 | 12.817 |
| h = 7 nm | 17.689 | 17.654 | 11.707 | 11.684 | 13.969 | 13.941 | 12.469 | 12.444 |
| h = 8 nm | 17.145 | 17.111 | 11.347 | 11.325 | 13.411 | 13.385 | 12.064 | 12.040 |
| h = 9 nm | 16.568 | 16.535 | 10.965 | 10.944 | 12.832 | 12.806 | 11.637 | 11.614 |
| h | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| h = 5 nm | 13.672 | 13.652 | 9.0485 | 9.0357 | 11.036 | 11.020 | 9.6751 | 9.6613 |
| h = 6 nm | 13.430 | 13.411 | 8.8883 | 8.8757 | 10.776 | 10.761 | 9.4936 | 9.4801 |
| h = 7 nm | 13.155 | 13.136 | 8.7062 | 8.6939 | 10.484 | 10.469 | 9.2879 | 9.2747 |
| h = 8 nm | 12.851 | 12.833 | 8.5053 | 8.4932 | 10.167 | 10.152 | 9.0614 | 9.0485 |
| h = 9 nm | 12.524 | 12.506 | 8.2887 | 8.2769 | 9.8297 | 9.8157 | 8.8179 | 8.8053 |
| lb/la | Solid Metal | UD | NUD1 | NUD2 | ||||
|---|---|---|---|---|---|---|---|---|
| g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | g = 0 | g = 0.5 | |
| 0.5 | 42.994 | 42.783 | 28.456 | 28.316 | 33.662 | 33.497 | 30.259 | 30.110 |
| 1 | 18.6364 | 18.600 | 12.334 | 12.310 | 14.965 | 14.936 | 13.176 | 13.150 |
| 1.5 | 13.672 | 13.652 | 9.0485 | 9.0357 | 11.036 | 11.020 | 9.6751 | 9.6613 |
| 2 | 11.897 | 11.882 | 7.8739 | 7.8642 | 9.6215 | 9.6097 | 8.4219 | 8.4116 |
| 2.5 | 11.069 | 11.056 | 7.3258 | 7.3174 | 8.9597 | 8.9494 | 7.8369 | 7.8280 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Z. Non-Local Buckling Analysis of Functionally Graded Nanoporous Metal Foam Nanoplates. Coatings 2018, 8, 389. https://doi.org/10.3390/coatings8110389
Wang Y, Zhang Z. Non-Local Buckling Analysis of Functionally Graded Nanoporous Metal Foam Nanoplates. Coatings. 2018; 8(11):389. https://doi.org/10.3390/coatings8110389
Chicago/Turabian StyleWang, Yanqing, and Zhiyuan Zhang. 2018. "Non-Local Buckling Analysis of Functionally Graded Nanoporous Metal Foam Nanoplates" Coatings 8, no. 11: 389. https://doi.org/10.3390/coatings8110389
APA StyleWang, Y., & Zhang, Z. (2018). Non-Local Buckling Analysis of Functionally Graded Nanoporous Metal Foam Nanoplates. Coatings, 8(11), 389. https://doi.org/10.3390/coatings8110389





