Nitrogen Trapping Ability of Hydrogen-Induced Vacancy and the Effect on the Formation of AlN in Aluminum
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. The Formation of H–N Bond Near Al Vacancy
3.2. The Ability of Vacancies to Trap Nitrogen Atoms
4. Discussion and Conclusions
- N–vacancy interaction is repulsive;
- hydrogen reduces the vacancy formation energy and makes the N–vacancy interaction attractive.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zheng, X.; Ren, Z.; Li, X.; Wang, Y. Microstructural characterization and mechanical properties of nitrided layers on aluminum substrate prepared by nitrogen arc. Appl. Surf. Sci. 2012, 259, 508–514. [Google Scholar] [CrossRef]
- Figueroa, U.; Salas, O.; Oseguera, J. Deposition of AlN on Al substrates by reactive magnetron sputtering. Surf. Coat. Technol. 2005, 200, 1768–1776. [Google Scholar] [CrossRef]
- Sheppard, L.M. Aluminum nitride: A versatile but challenging material. Bull. Am. Ceram. Soc. 1990, 69, 1801–1812. [Google Scholar]
- Kuramoto, N.; Taniguchi, H. Transparent AIN ceramics. J. Mater. Sci. Lett. 1984, 3, 471–474. [Google Scholar] [CrossRef]
- Shu, L.; Peng, B.; Cui, Y.; Gong, D.; Yang, Z.; Liu, X.; Zhang, W. Effects of AlN Coating Layer on High Temperature Characteristics of Langasite SAW Sensors. Sensors 2016, 16, 1436. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; You, Z. Modeling and Experimental Analysis on the Temperature Response of AlN-Film Based SAWRs. Sensors 2016, 16, 1205. [Google Scholar] [CrossRef] [PubMed]
- Zamora, R.J.; Nair, A.K.; Hennig, R.G.; Warner, D.H. Ab initio prediction of environmental embrittlement at a crack tip in aluminum. Phys. Rev. B 2012, 86, 60101. [Google Scholar] [CrossRef]
- Aoki, Y.; Fujii, H.; Nogi, K. Effect of atomic oxygen exposure on bubble formation in aluminum alloy. J. Mater. Sci. 2004, 39, 1779–1783. [Google Scholar] [CrossRef]
- Turner, D.E.; Zhu, Z.Z.; Chan, C.T.; Ho, K.M. Energetics of vacancy and substitutional impurities in aluminum bulk and clusters. Phys. Rev. B 1997, 55, 13842–13852. [Google Scholar] [CrossRef]
- Chung, J.P.; Lee, J.S.; Kim, K.R.; Choi, B.H. The change of atomic distribution and hardness by nitrogen implantation into aluminum alloy. Rev. Sci. Instrum. 2008, 79, 02C509. [Google Scholar] [CrossRef] [PubMed]
- Ghoranneviss, M.; Sari, A.H.; Dorranian, D.; Khorshid, P.; Hajihosseini, G.H.S.; Shokouhy, A.; Hesabi, M. Nitrogen Ion Implantation in Pure Aluminium; Japan Society of Plasma Science and Nuclear Fusion Research: Nagoya, Japan, 2006. [Google Scholar]
- Hogg, B.G.; Paulin, R.; Troev, T.D. Detection of nitrogen impurities in aluminum by positron annihilation. Phys. Lett. 1979, 71, 240–242. [Google Scholar] [CrossRef]
- Andrey, I.K.; Dat Duy, V.; Lipnitskii, A.G. The interaction between light impurities and vacancies in titanium and aluminum metals: A DFT study. St. Petersburg Polytech. Univ. J. Phys. Math. 2016, 2, 96–102. [Google Scholar]
- Hehenkamp, T. Absolute vacancy concentrations in noble metals and some of their alloys. J. Phys. Chem. Solids 1994, 55, 907–915. [Google Scholar] [CrossRef]
- Lynn, K.G.; Schultz, P. Vacancy formation energy measurements in single crystal aluminum using a variable-energy positron beam. Appl. Phys. A 1985, 37, 31–36. [Google Scholar] [CrossRef]
- Fluss, M.J.; Smedskjaer, L.C.; Chason, M.K.; Legnini, D.G.; Siegel, R.W. Measurements of the vacancy formation enthalpy in aluminum using positron annihilation spectroscopy. Phys. Rev. B 1978, 17, 3444–3455. [Google Scholar] [CrossRef]
- Carling, K.M.; Wahnström, G.; Mattsson, T.R.; Sandberg, N.; Grimvall, G. Vacancy concentration in Al from combined first-principles and model potential calculations. Phys. Rev. B 2003, 67, 054101. [Google Scholar] [CrossRef]
- Poletaev, D.O.; Aksyonov, D.A.; Dat Duy, V.; Lipnitskii, A.G. Hydrogen solubility in hcp titanium with the account of vacancy complexes and hydrides: A DFT study. Comput. Mater. Sci. 2016, 114, 199–208. [Google Scholar] [CrossRef]
- Peter, E.B.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar]
- Perdew, J.P.; Kieron, B.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Jacobs, P.W.M.; Zhukovskii, Y.F.; Mastrikov, Y.; Shunin, Y.N. Bulk and surface properties of metallic aluminium: DFT simulations. Comput. Model. New Technol. 2002, 6, 7–28. [Google Scholar]
- Evans, D.J.; Holian, B.L. The Nose–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Edwards, R.A.H.; Eichenauer, W. Reversible hydrogen trapping at grain boundaries in superpure aluminium. Scr. Metall. 1980, 14, 971–973. [Google Scholar] [CrossRef]
- Eichenauer, W.; Hattenbach, K.; Pebler, Z. The Solubility of Hydrogen in Solid and Liquid Aluminum. Z. Metallkunde 1961, 52, 682–684. [Google Scholar]
- Sugimoto, H.; Fukai, Y. Solubility of hydrogen in metals under high hydrogen pressures: Thermodynamical calculations. Acta Metall. Mater. 1992, 40, 2327–2336. [Google Scholar] [CrossRef]
- Ichimura, M.; Katsuta, H.; Sasajima, Y.; Imabayashi, M. Hydrogen and deuterium solubility in aluminum with voids. J. Phys. Chem. Solids 1988, 49, 1259–1267. [Google Scholar] [CrossRef]
- Wolverton, C.; Ozoliņš, V.; Asta, M. Hydrogen in aluminum: First-principles calculations of structure and thermodynamics. Phys. Rev. B 2004, 69, 144109. [Google Scholar] [CrossRef]
- Linderoth, S. Hydrogen diffusivity in aluminium. Philos. Mag. Lett. 1988, 57, 229–234. [Google Scholar] [CrossRef]
- Linderoth, S.; Rajainmäki, H.; Nieminen, R.M. Defect recovery in aluminum irradiated with protons at 20 K. Phys. Rev. B 1987, 35, 5524–5528. [Google Scholar] [CrossRef]
- Myers, S.M.; Besenbacher, F.; Norskov, J.K. Immobilization mechanisms for ion-implanted deuterium in aluminum. J. Appl. Phys. 1985, 58. [Google Scholar] [CrossRef]
- Demaison, J.; Margulès, L.; Boggs, J.E. The equilibrium N–H bond length. Chem. Phys. 2000, 260, 65–81. [Google Scholar] [CrossRef]
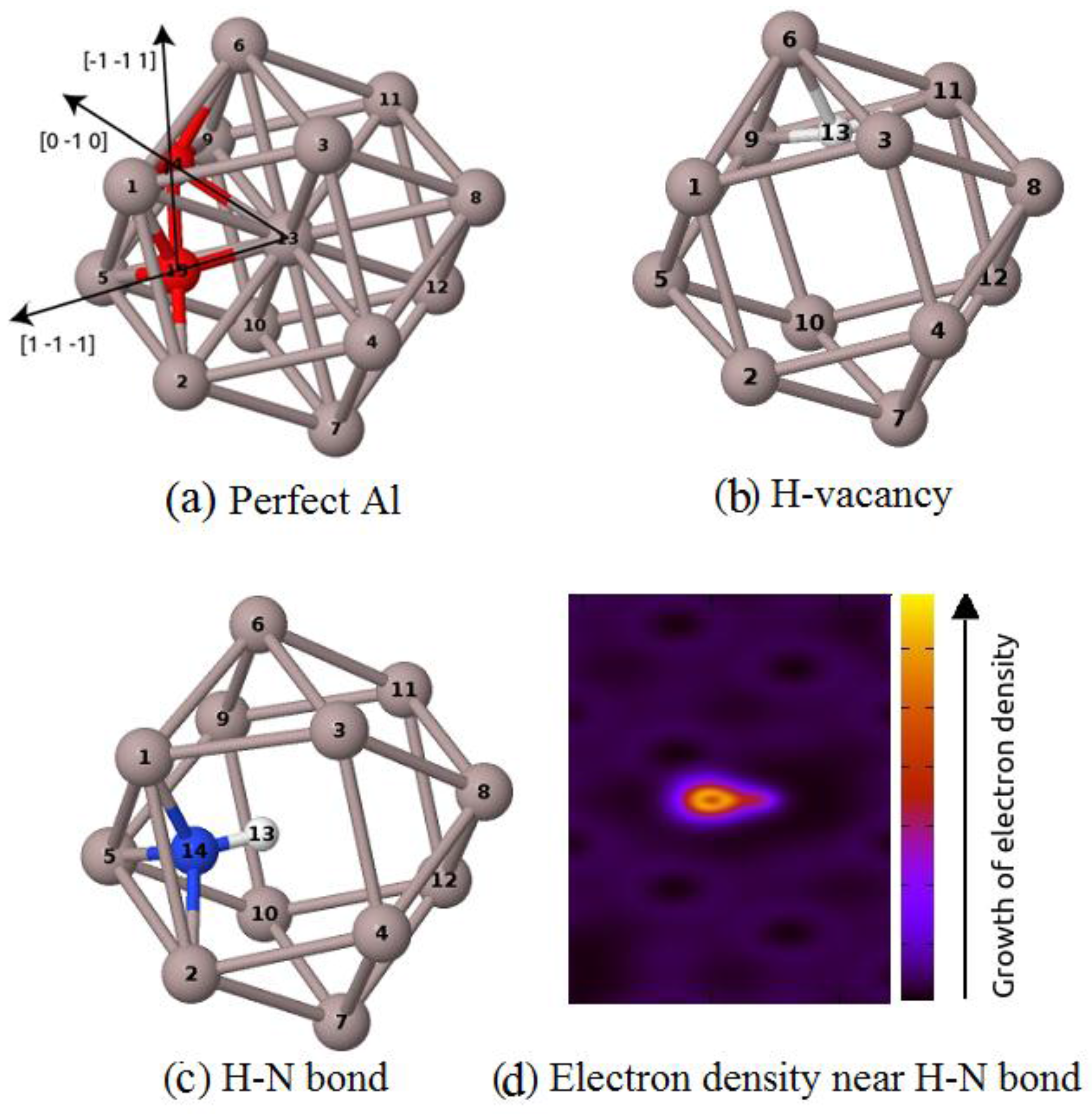
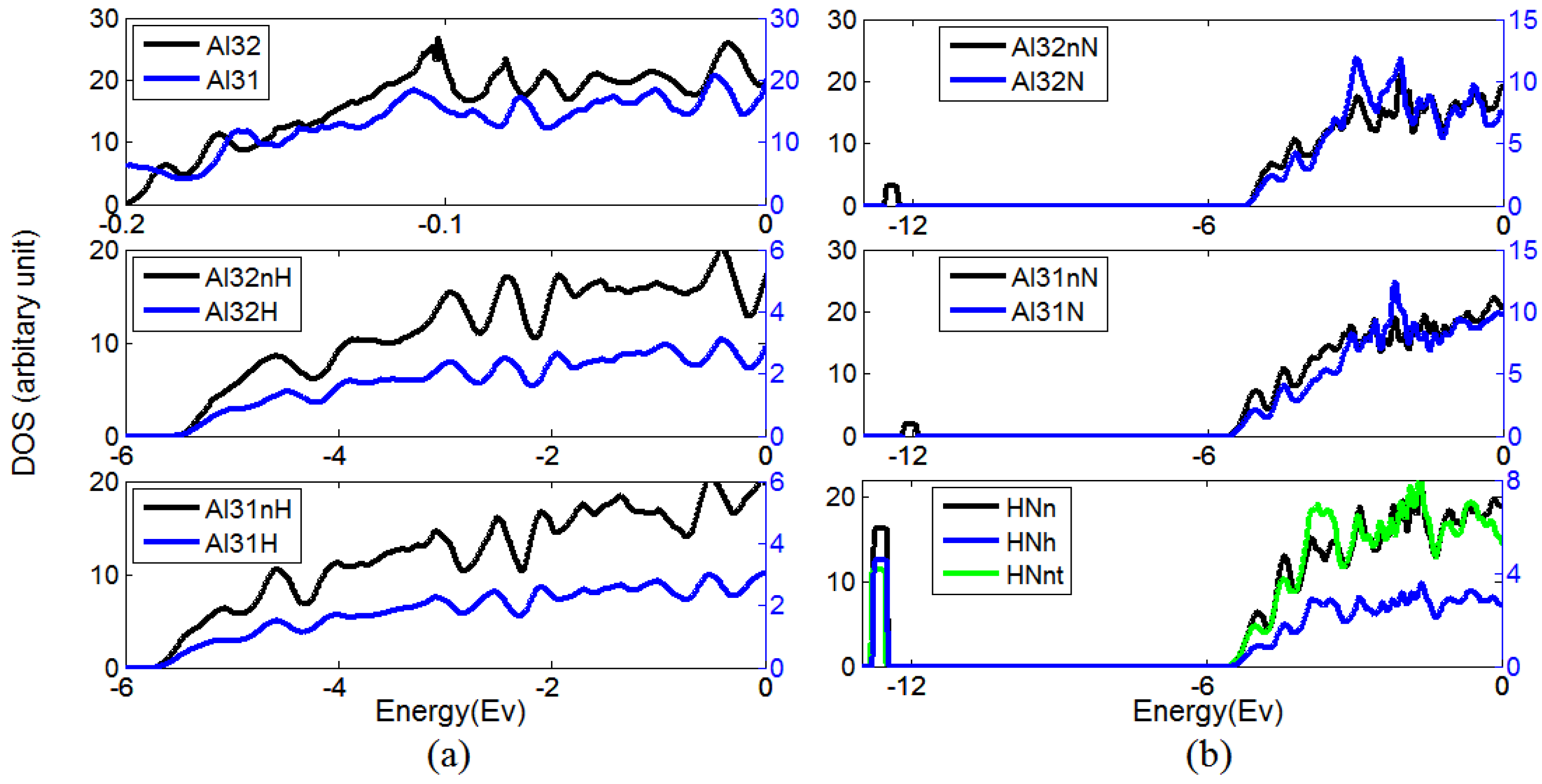
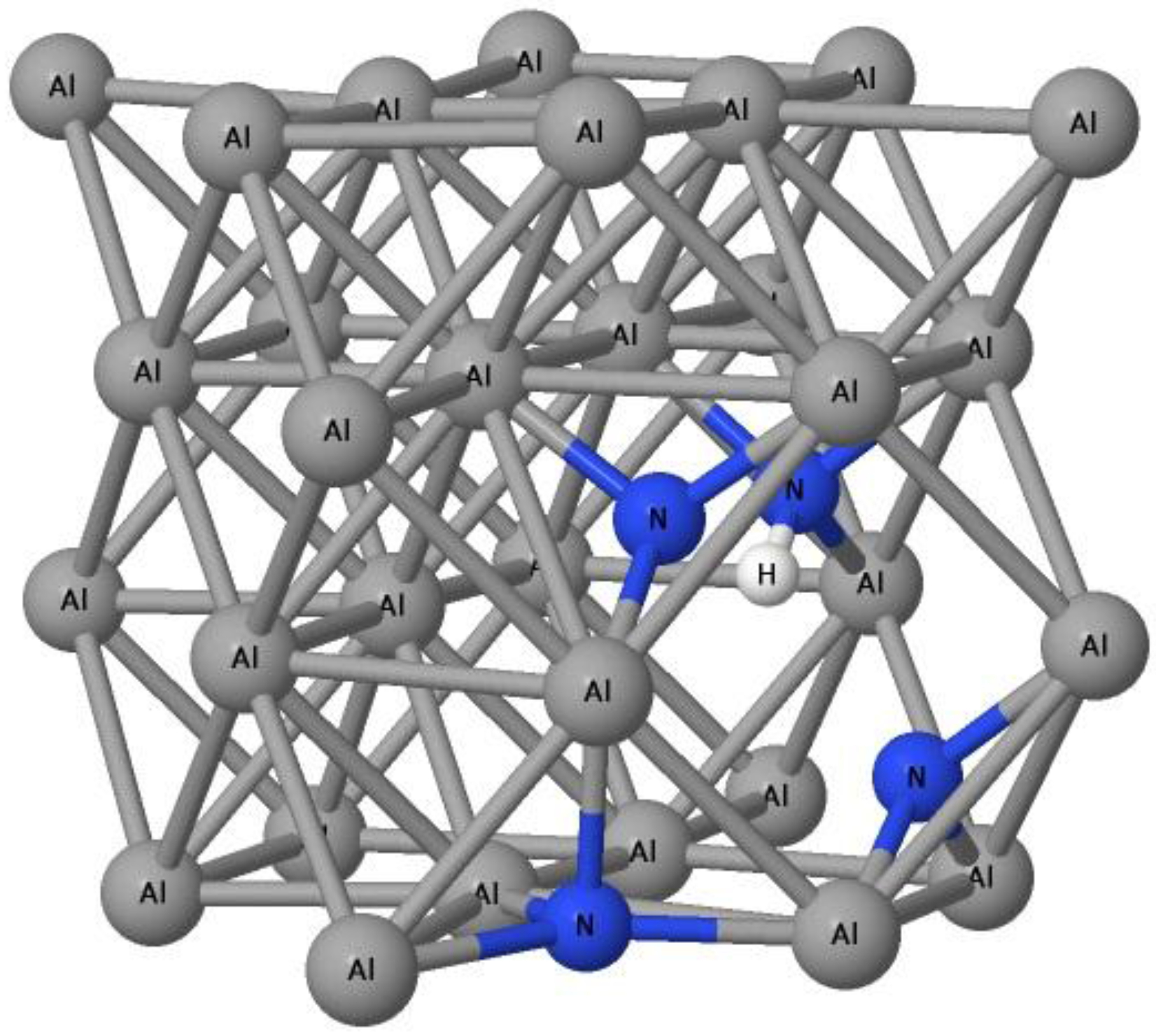
| DFT package | ECH–vacancy | ECN–vacancy | ECN–(H–vacancy) |
|---|---|---|---|
| Abinit | 0.39 | −0.69 | 0.56 |
| VASP | 0.50 | −0.51 | 0.59 |
| DFT package | Evacancyf | Evacancyf[H] | Evacancyf[H + N] |
|---|---|---|---|
| Abinit | 0.55 | 0.16 | −0.38 |
| VASP | 0.65 | 0.15 | −0.44 |
| m | Efvacancy−H+mN | Etrap(m) | ΔV | Δa | Δaver |
|---|---|---|---|---|---|
| 1 | −0.59 | 0.00 | |||
| 2 | −0.54 | −0.16 | 5.69 | 0.04 | 0.02 |
| 3 | −0.69 | −0.35 | 6.12 | 0.07 | 0.17 |
| 4 | −0.49 | −0.01 | 7.47 | 0.05 | 0.11 |
| 5 | 1.57 | 1.90 | 1.43 | 0.15 | 0.38 |
| 6 | −0.08 | −1.90 | 4.92 | 0.10 | 0.47 |
| 7 | −2.62 | −2.74 | 10.91 | 0.24 | 0.80 |
| 8 | −0.62 | 1.80 | 16.37 | -0.30 | 0.30 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, D.D.; Lipnitskii, A.G.; Nguyen, T.K.; Nguyen, T.T. Nitrogen Trapping Ability of Hydrogen-Induced Vacancy and the Effect on the Formation of AlN in Aluminum. Coatings 2017, 7, 79. https://doi.org/10.3390/coatings7060079
Vo DD, Lipnitskii AG, Nguyen TK, Nguyen TT. Nitrogen Trapping Ability of Hydrogen-Induced Vacancy and the Effect on the Formation of AlN in Aluminum. Coatings. 2017; 7(6):79. https://doi.org/10.3390/coatings7060079
Chicago/Turabian StyleVo, Duy Dat, Aleksey G. Lipnitskii, Truong Khang Nguyen, and Thoi Trung Nguyen. 2017. "Nitrogen Trapping Ability of Hydrogen-Induced Vacancy and the Effect on the Formation of AlN in Aluminum" Coatings 7, no. 6: 79. https://doi.org/10.3390/coatings7060079
APA StyleVo, D. D., Lipnitskii, A. G., Nguyen, T. K., & Nguyen, T. T. (2017). Nitrogen Trapping Ability of Hydrogen-Induced Vacancy and the Effect on the Formation of AlN in Aluminum. Coatings, 7(6), 79. https://doi.org/10.3390/coatings7060079






