Multiscale Modeling and Data-Driven Life Prediction of Kinematic Interface Behaviors in Mechanical Drive Systems
Abstract
1. Introduction
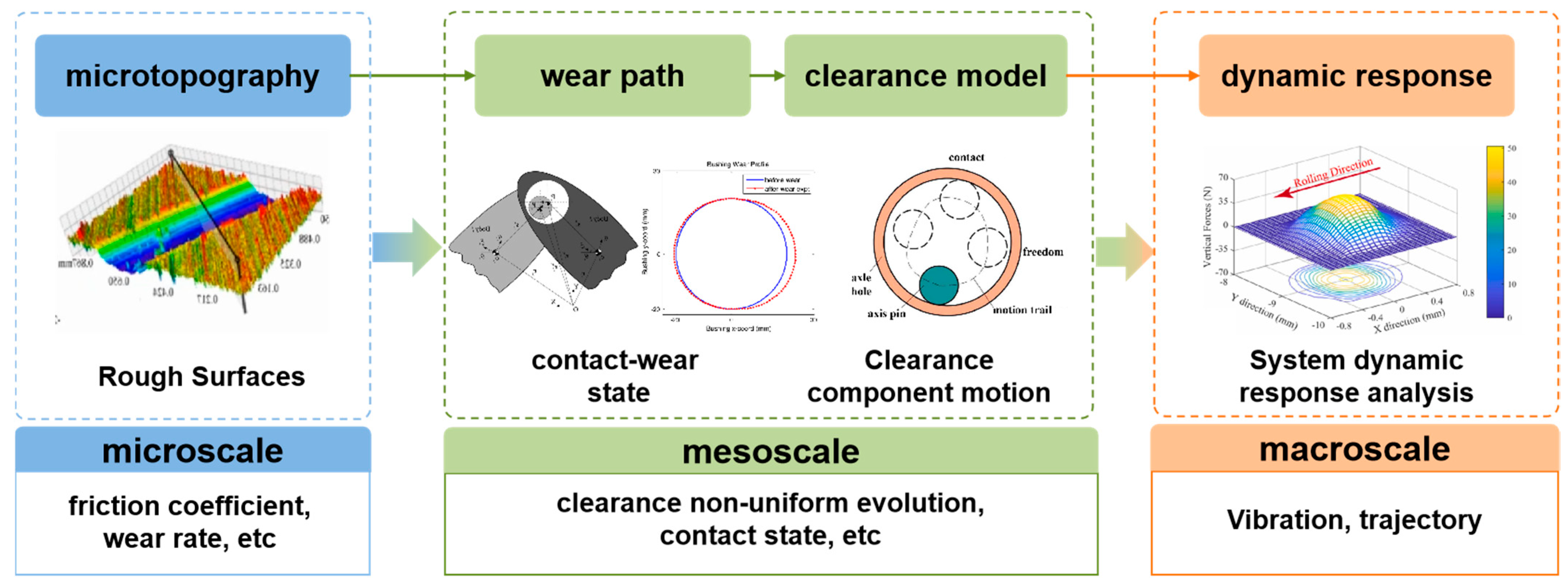
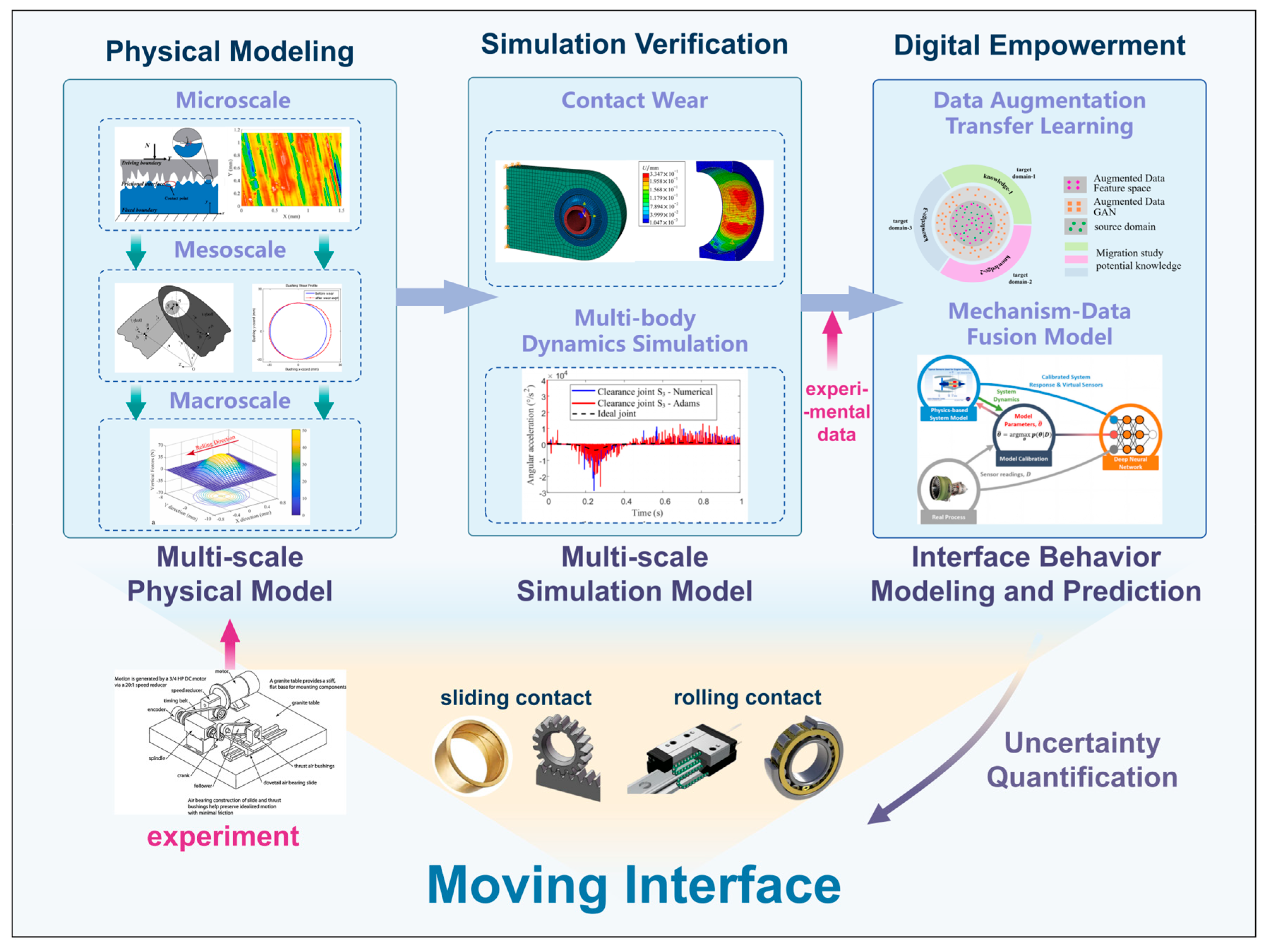
2. Physical Model of Multiscale Interface Behavior
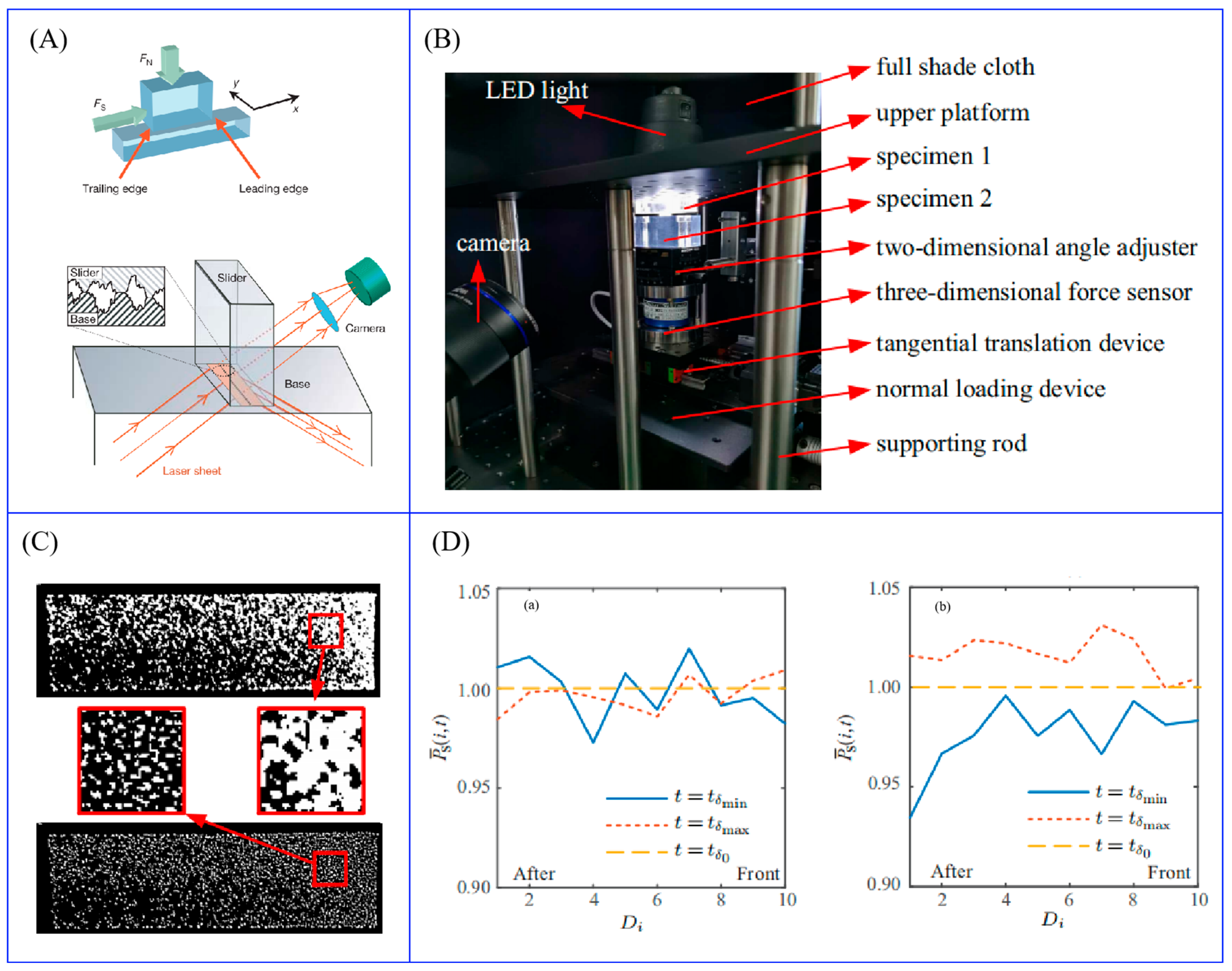
2.1. Contact Properties and Frictional Wear Modulation by Surface Microforms
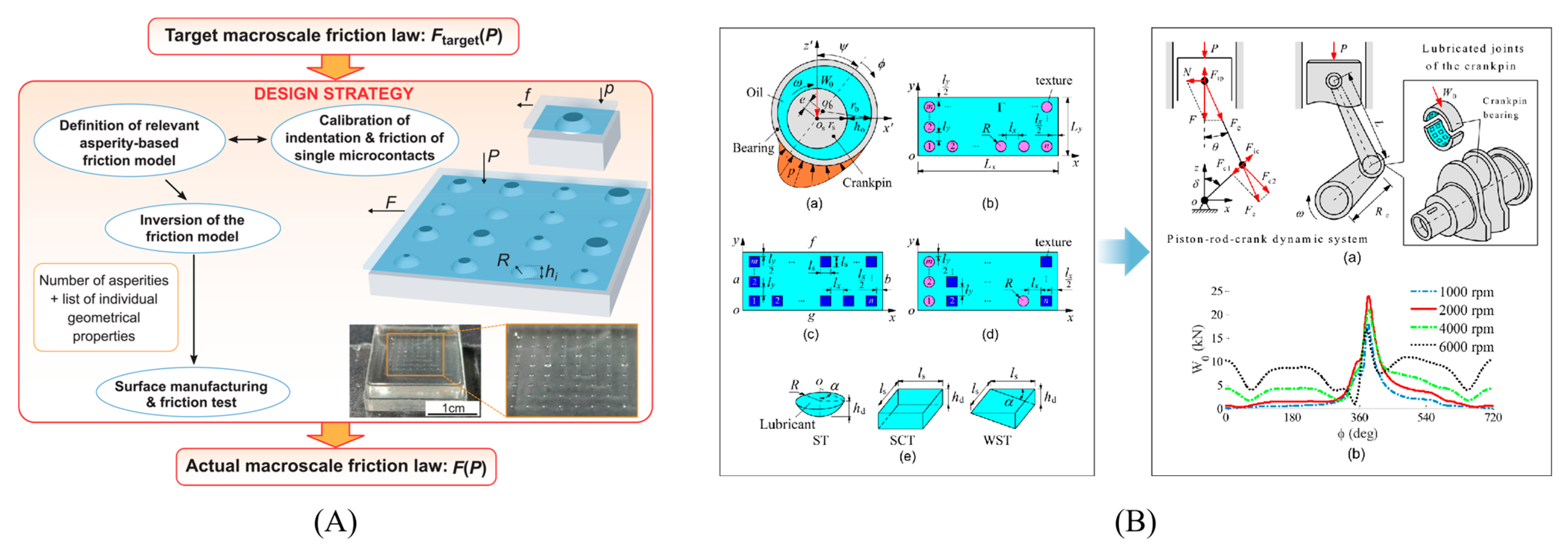
2.1.1. Quantitative Characterization of Surface Morphology and Active Design
2.1.2. Coating Material Modification Co-Optimization
2.2. Interface Wear–Joint Clearance Coevolution
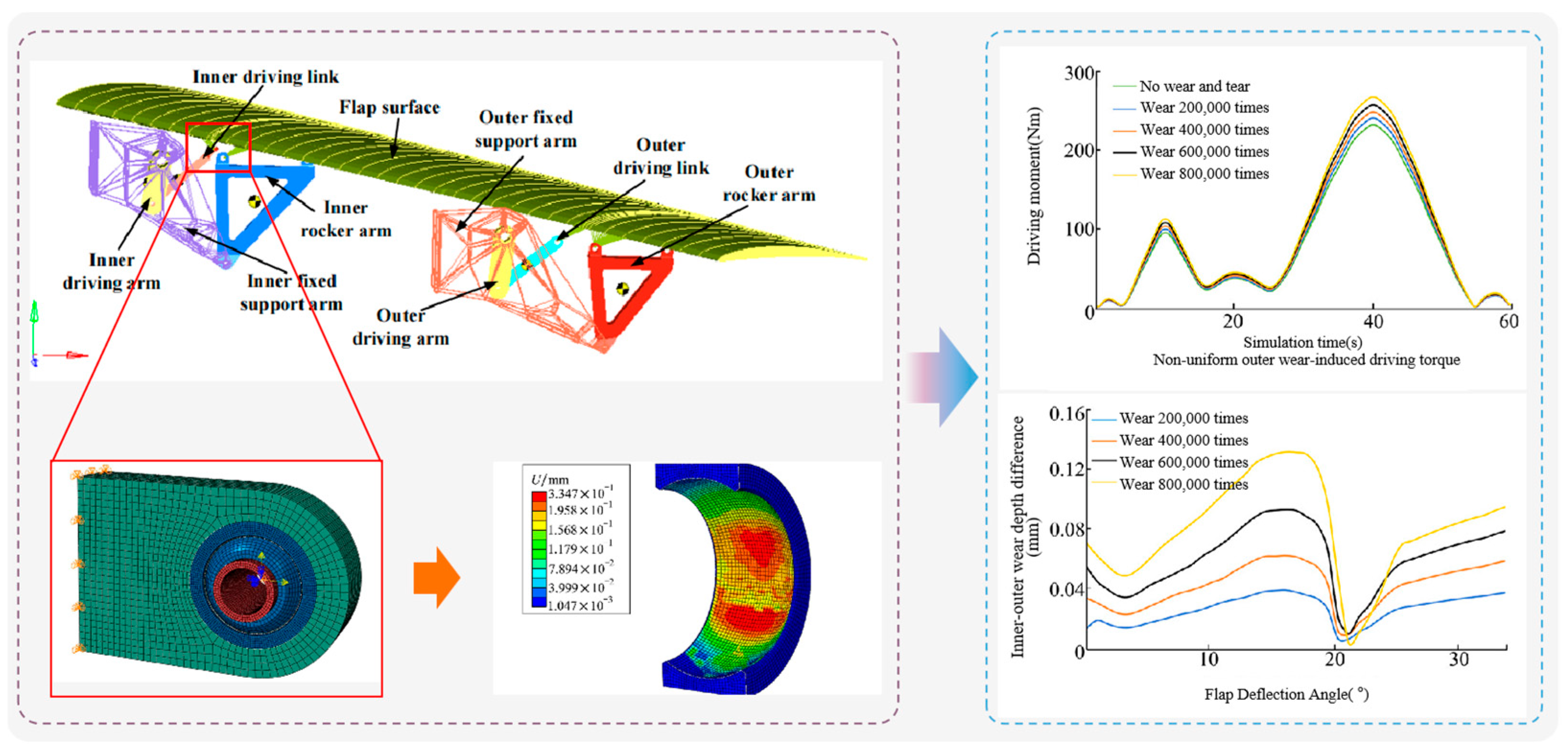
2.2.1. Non-Uniform Evolution of Interfacial Distributions
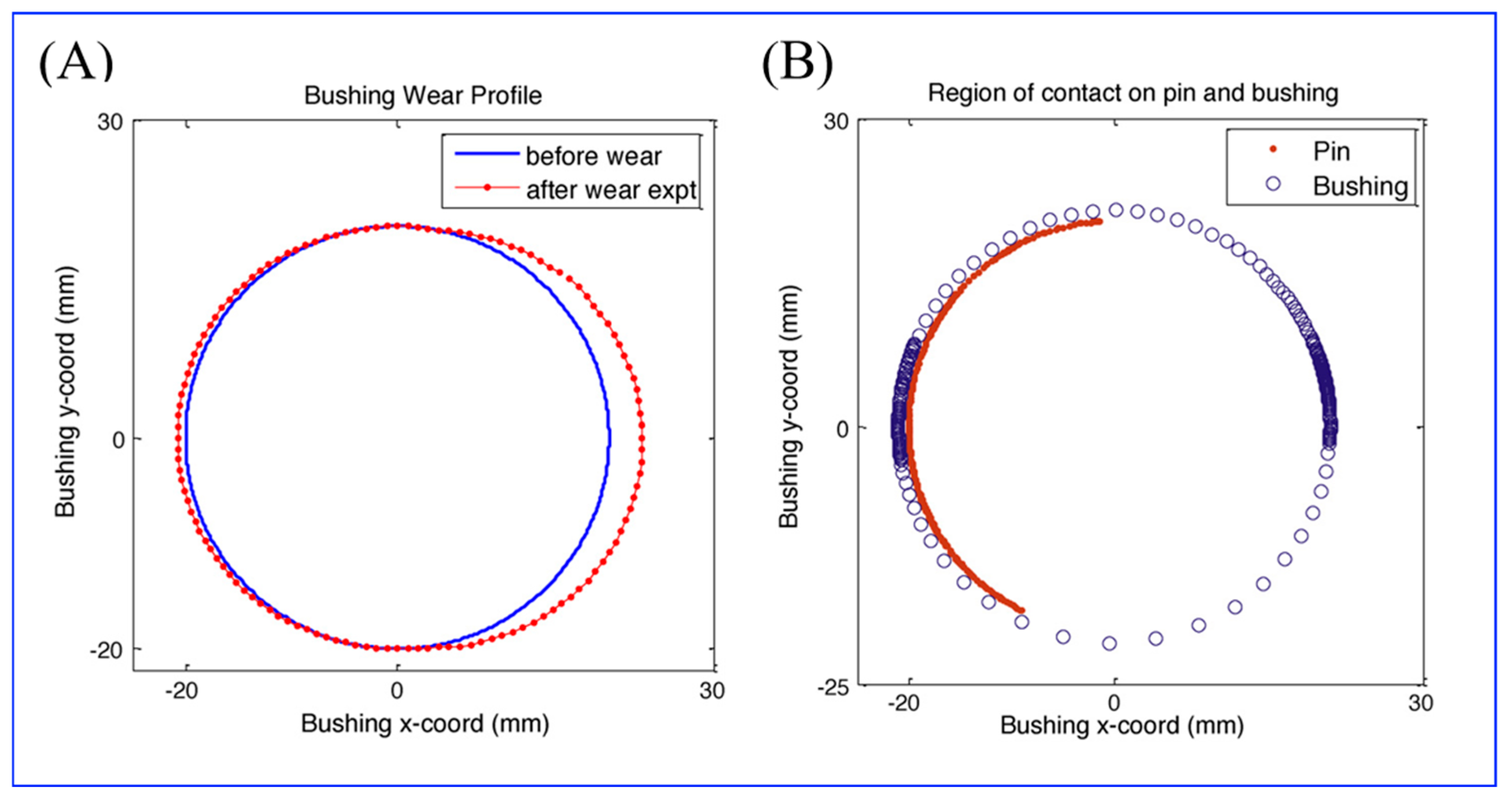
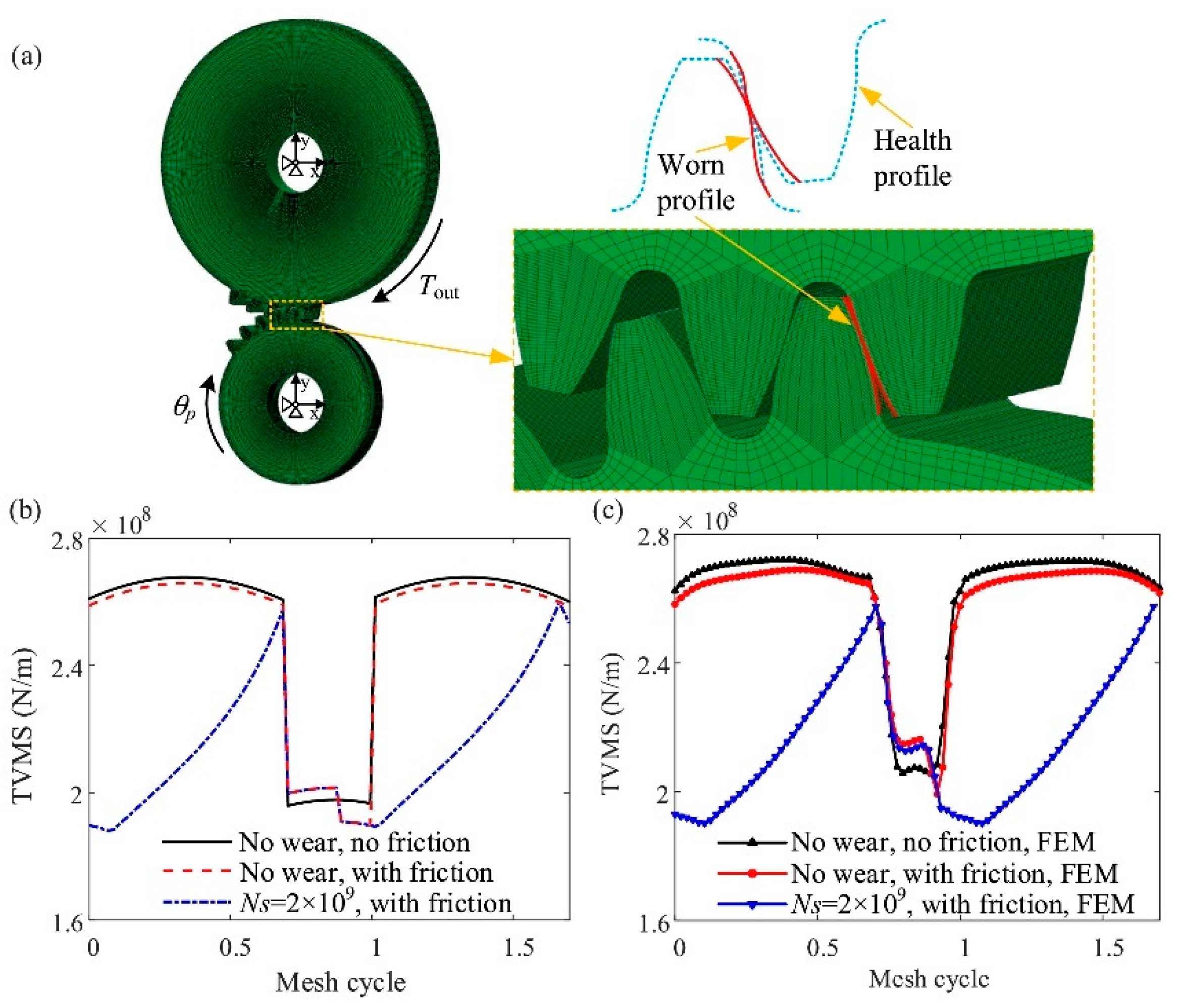
2.2.2. Coating Technology Enhances Wear Resistance
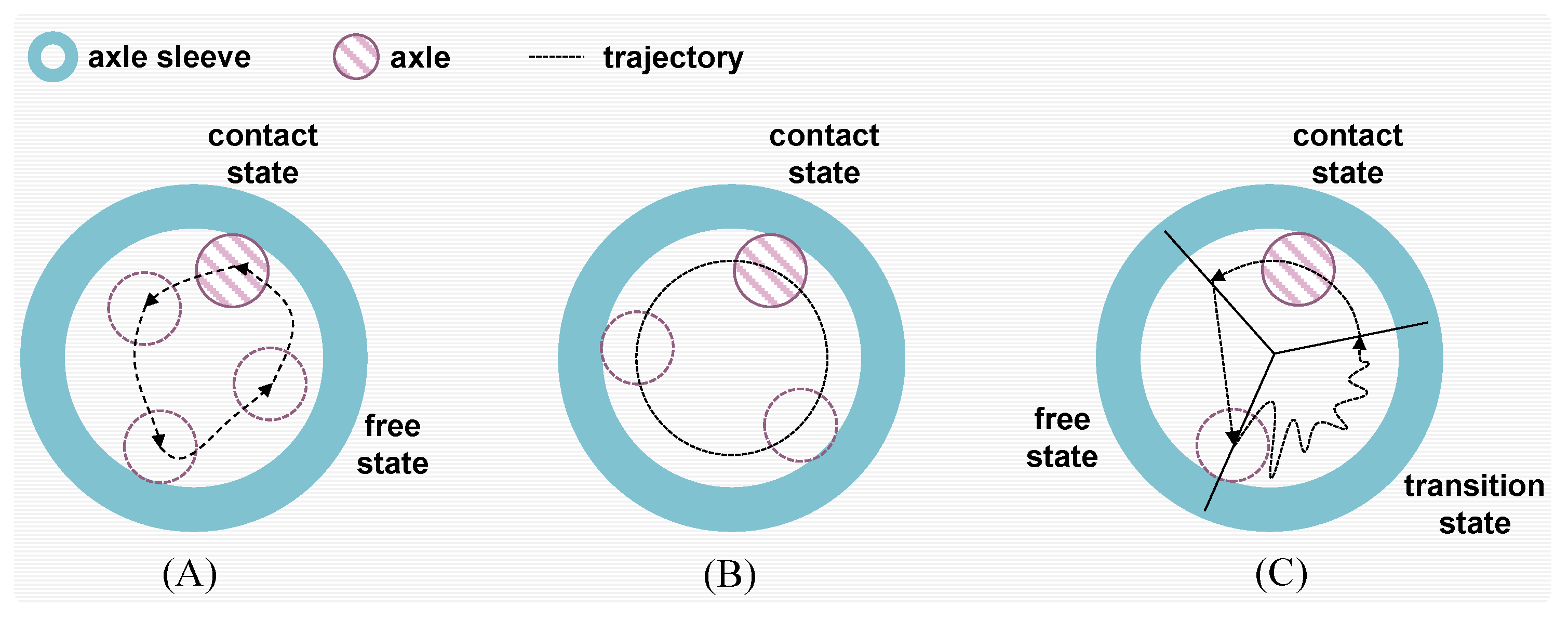
2.3. Clearance Dynamic Contact State Modeling Method
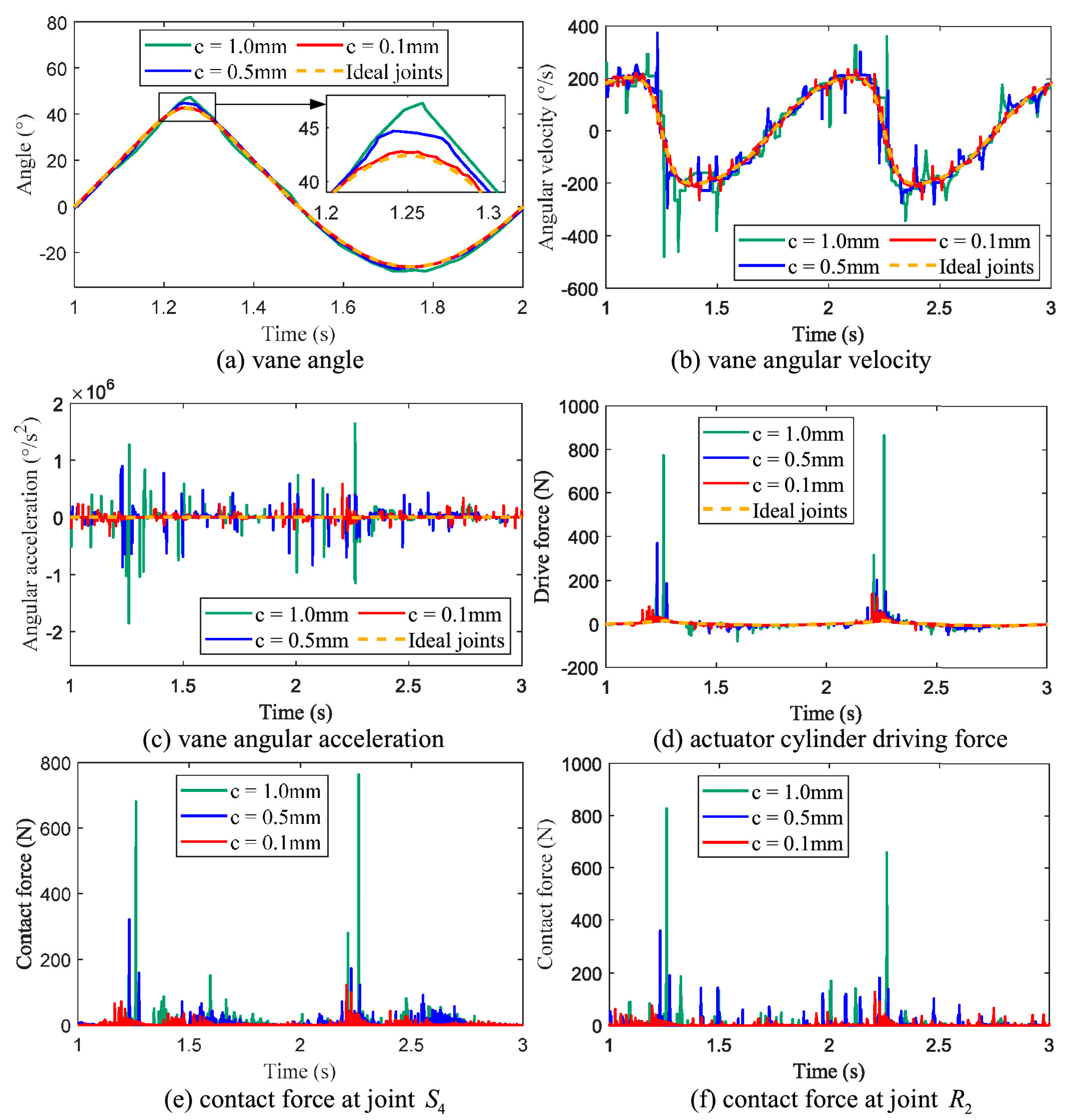
2.4. Dynamic Modeling of Clearance-Containing Mechanisms
3. Multiscale Interface Behavior Simulation Models
3.1. Interface Contact–Wear Joint Simulation
3.2. System Dynamics Simulation
4. Data Empowerment Interface Behavior Analysis and Life Prediction
4.1. Enhanced Strategies for Data Scarcity Scenarios
4.1.1. Data Enhancement Techniques: From Interpolation to Physical Constraint Generation
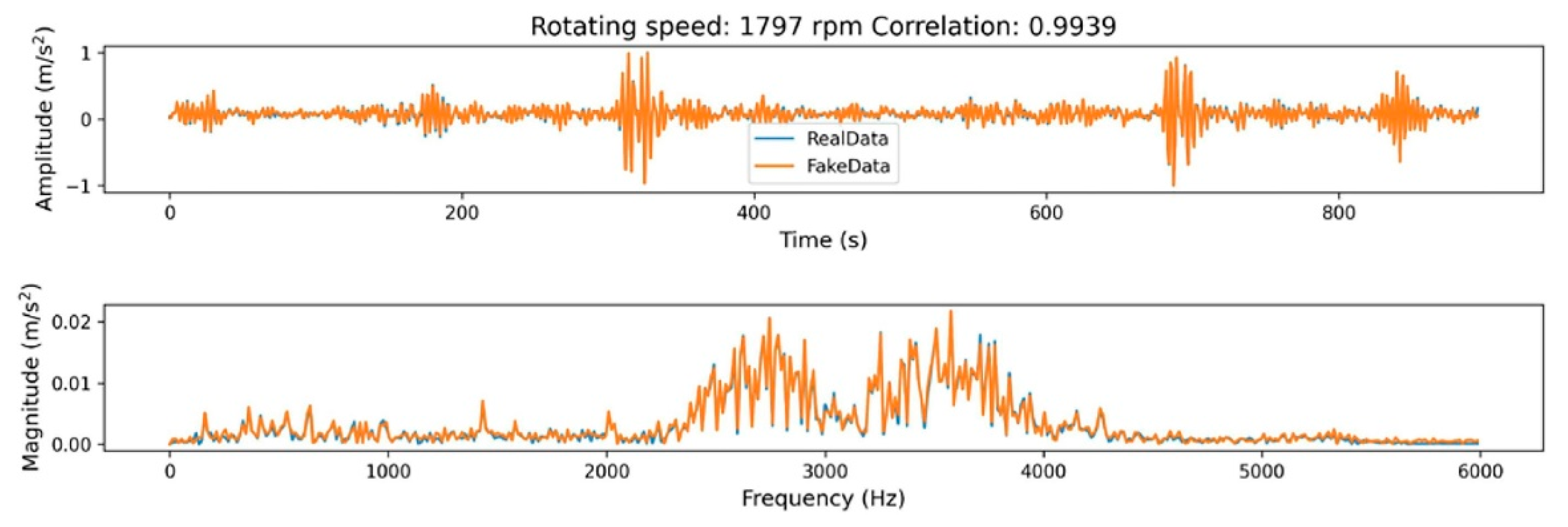
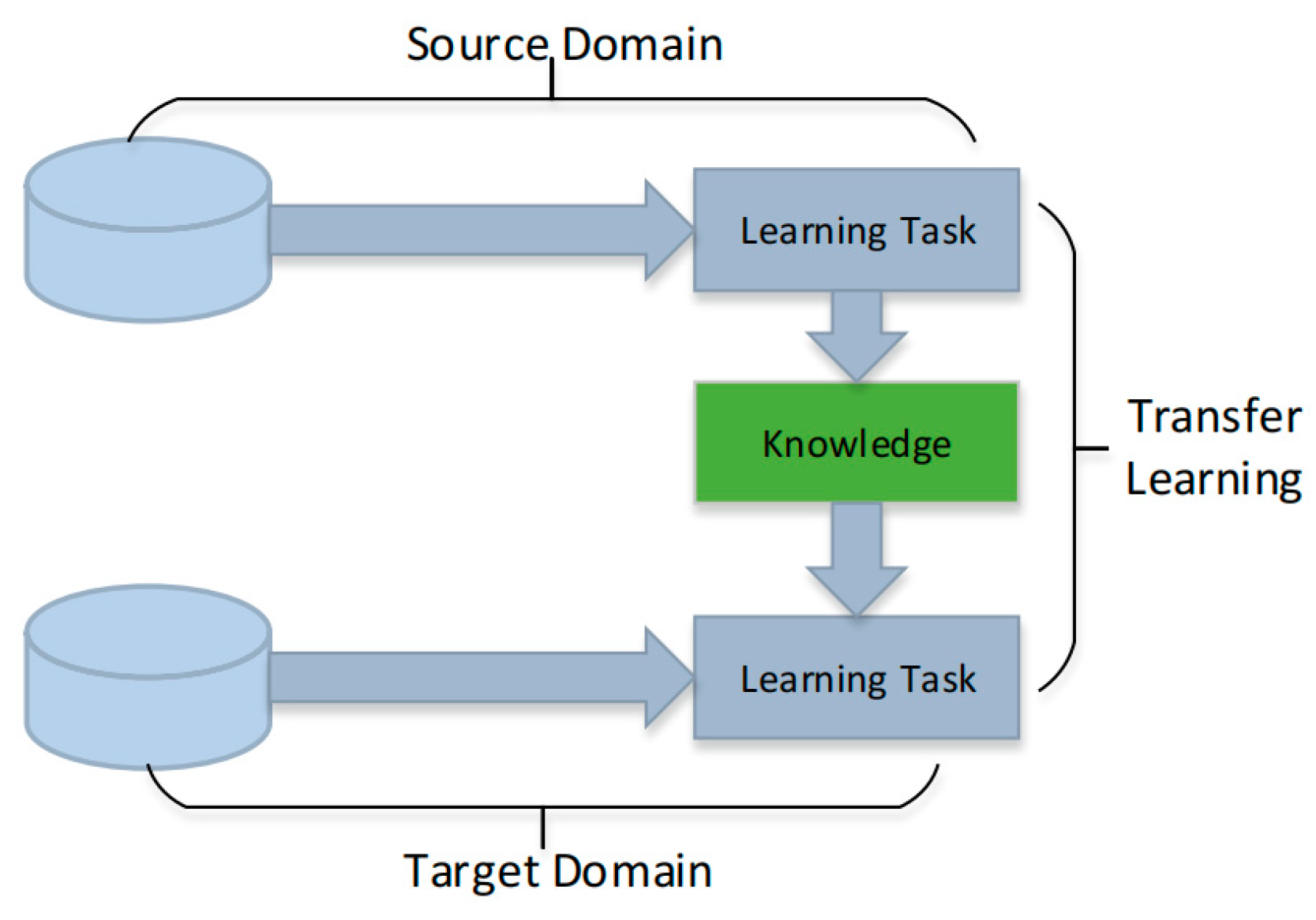
4.1.2. Cross-Domain Transfer Learning
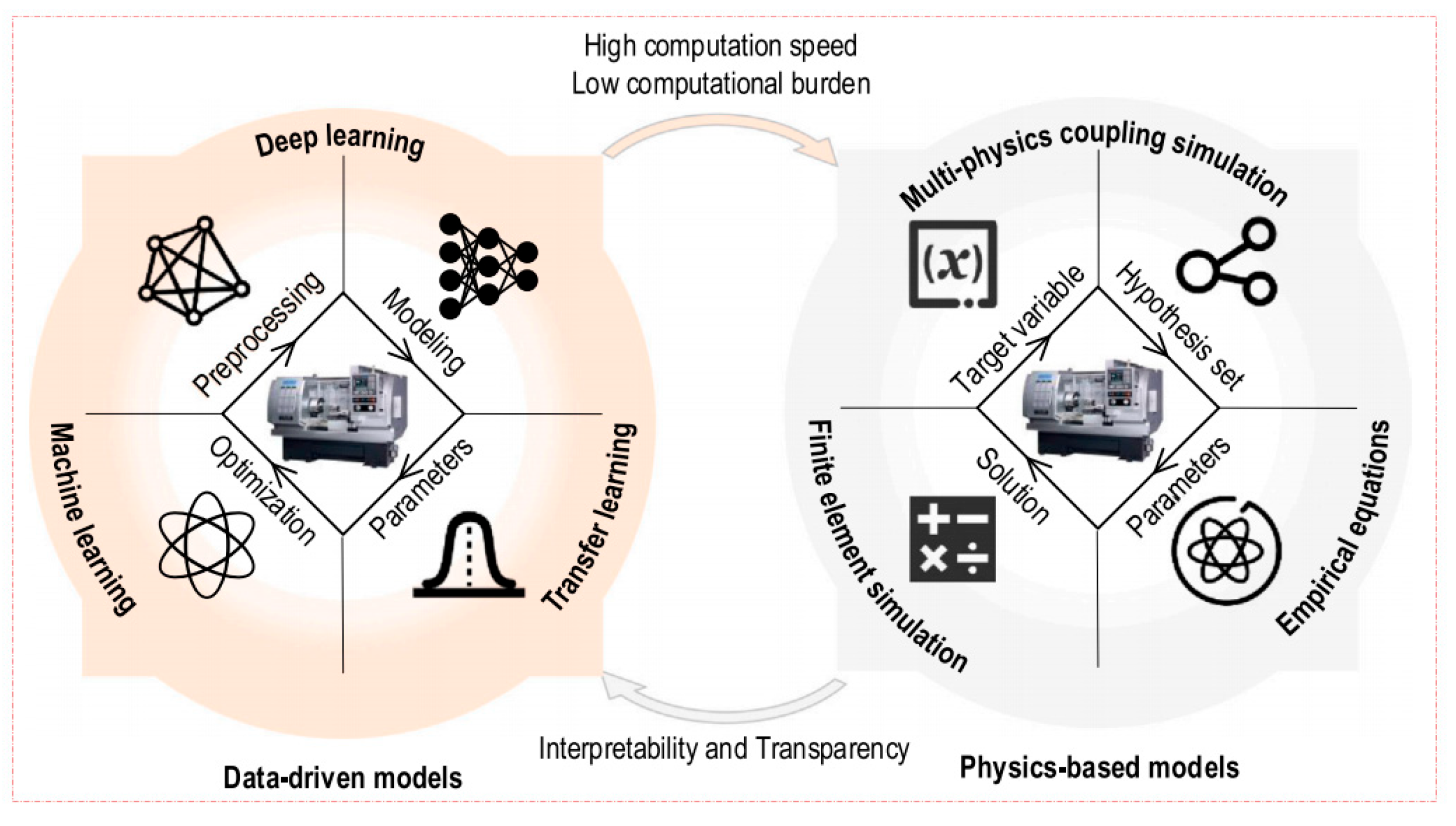
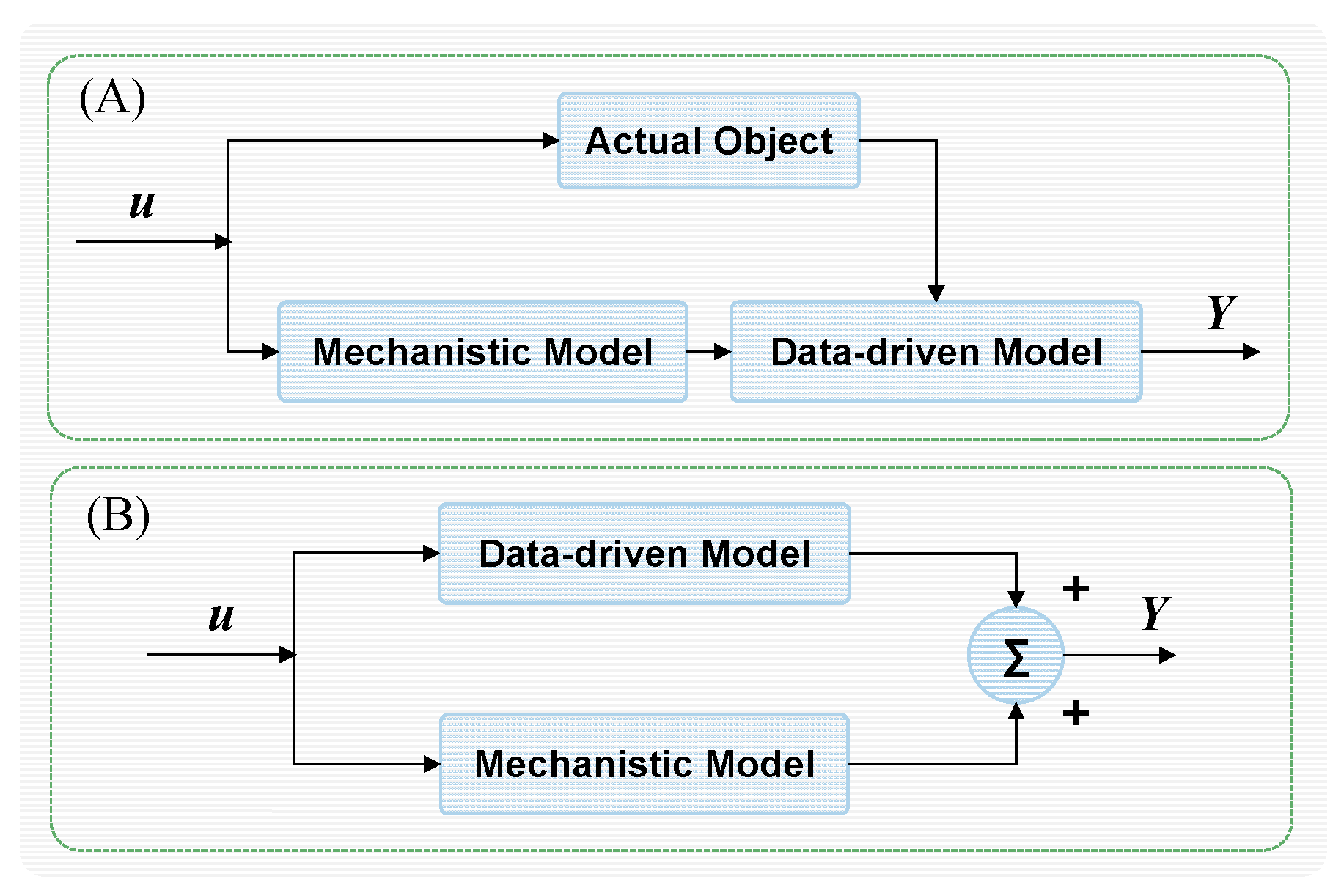
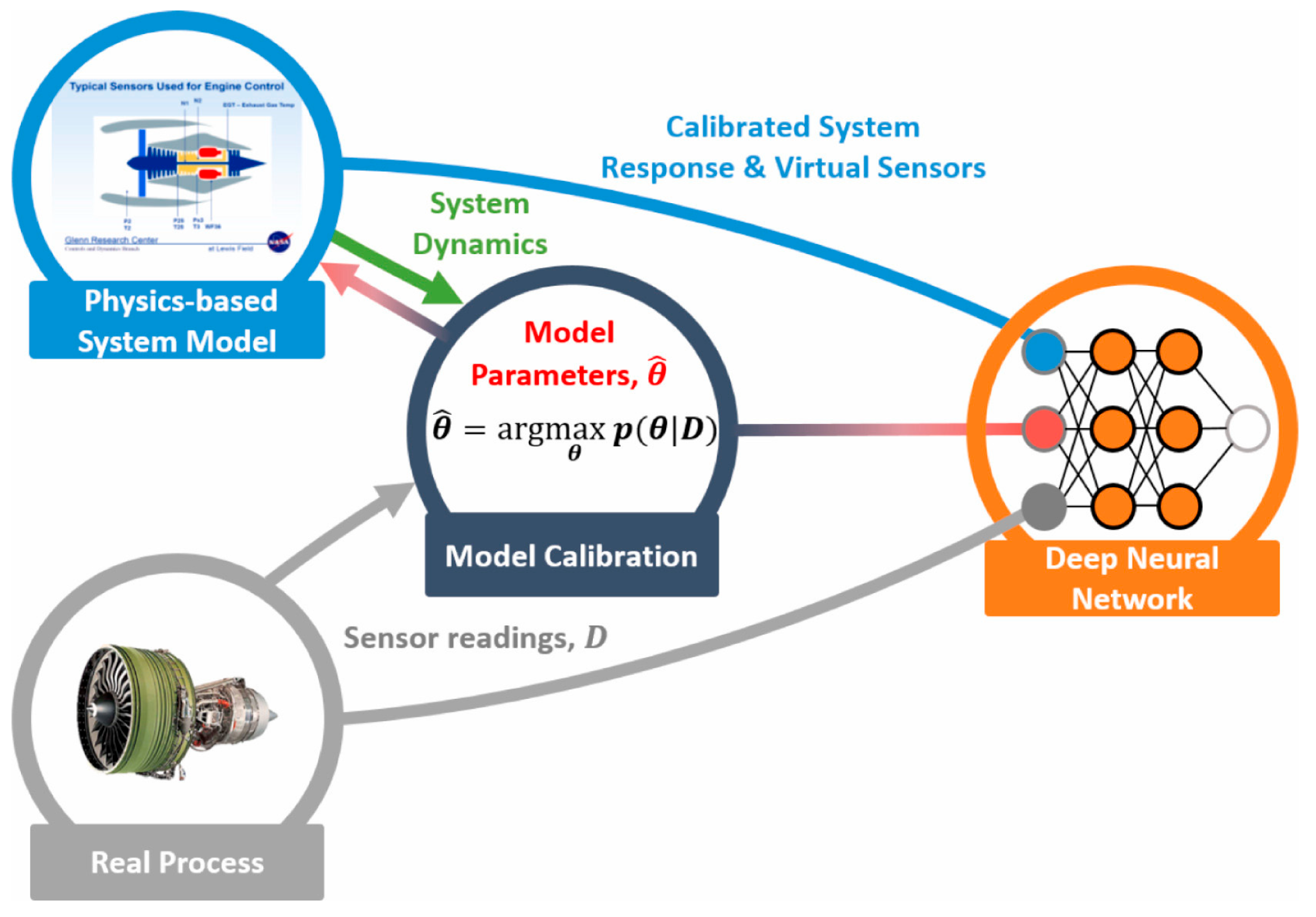
4.2. Mechanism-Data Fusion Approach to Life Prediction
4.2.1. Data-Driven Model
4.2.2. Fusion Enhanced Robust Prediction
4.2.3. Mechanism–Data-Driven Fusion
5. Conclusions
- Multiscale Parameter Transfer Mechanism: To realize the correlation between different scales by modeling the behavior of multiscale physical interfaces and to realize the mapping and transfer of microscale parameters to macroscale dynamics models.
- Dynamic Two-Way Coupling Technique: To establish a positive link of “contact stress–wear depth clearance expansion–dynamics response” in the simulation link, and at the same time, to identify the distribution of wear hotspots through the inversion of vibration signals, so as to form the closed-loop feedback of wear and vibration.
- Uncertainty Quantification System: This system aims to establish a statistical mapping between vibration signals and component lifespan using a data-driven approach to address uncertainties arising from random interface parameters and environmental disturbances.
- Combination of Mechanism–Life Systems: This system is designed to quantify uncertainties related to interface parameters and environmental disturbances by integrating physical constraints into a neural network using a mechanism–data fusion approach, enabling an interpretable analysis of wear damage mechanisms.
6. Prospects and Challenges
- In terms of multiscale modeling, there are theoretical bottlenecks in the dynamic transfer mechanism of parameters at different scales, the nonlinear mapping relationship between microscopic fractal features and macroscopic kinetic response has not yet been established, and the dynamic evolution of the surface gradient structure and the interaction mechanism between system vibration and energy in the process of wear has not yet been quantitatively characterized. In the future, we need to develop multiscale coupling algorithms based on adaptive weights to achieve real-time simulation of extreme working conditions.
- There is also room for improvement in the data-driven approach. Although Generative Adversarial Network (GAN) has potential, the physical credibility of synthetic data are insufficient, and the correlation between the time–frequency characteristics of vibration signals and the real wear mechanism is insufficient, which leads to a large generalization error of the life prediction model, so we can try to break through the adversarial generation framework based on physical constraints. Migration learning also faces the problem of feature drift and needs to build a multidimensional migration mapping network.
- Gradient coating design, due to the complexity of the process and high-cost limitations of the application, can be developed based on a machine learning coating composition–performance reverse design platform to achieve intelligent mapping. At the same time, the stability of the coating interface in extreme environments under the lack of research needs to establish an assessment system.
- The current interface data are severely restricted by the confidentiality agreement, and it is urgent to build a big data platform to break through the limitations; for high-precision machine tools, aerospace hinges, and other extreme scenarios, a large amount of measured data accumulation is needed to test the applicability of the framework under different working conditions, quantify the model robustness through multi-field coupling experiments, and promote the in-depth integration of theory and engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woo, S. Reliability Design of Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2020; p. 20. [Google Scholar]
- Lynwander, P. Gear Drive Systems: Design and Application; CRC Press: Boca Raton, FL, USA, 2019; pp. 5–20. [Google Scholar]
- Mabie, H.H.; Reinholtz, C.F. Mechanisms and Dynamics of Machinery; John Wiley & Sons: New York, NY, USA, 1991; pp. 10–20. [Google Scholar]
- Qu, C.; Wu, L.; Ma, J.; Xia, Q.; Ma, S. A fractal model of normal dynamic parameters for fixed oily porous media joint interface in machine tools. Int. J. Adv. Manuf. Technol. 2013, 68, 2159–2167. [Google Scholar] [CrossRef]
- Wang, W.; Shen, G.; Zhang, Y.M.; Zhu, Z.; Li, C.; Lu, H. Dynamic reliability analysis of mechanical system with wear and vibration failure modes. Mech. Mach. Theory 2021, 163, 104385. [Google Scholar] [CrossRef]
- Budak, E.; Matsubara, A.; Donmez, A.; Munoa, J. Mechanical interfaces in machine tools. CIRP Ann. 2022, 71, 647–670. [Google Scholar] [CrossRef]
- Stoyanov, P.; Chromik, R.R. Scaling Effects on Materials Tribology: From Macro to Micro Scale. Materials 2017, 10, 550. [Google Scholar] [CrossRef]
- Wen, S.Z.; Huang, P.; Liu, Y. Interface Science and Technology; Tsinghua University Press: Beijing, China, 2011; pp. 5–10. [Google Scholar]
- Chang, Y.; Ding, J.; He, Z.; Shehzad, A.; Ding, Y.; Lu, H.; Zhuang, H.; Chen, P.; Zhang, Y.; Zhang, X.; et al. Effect of joint interfacial contact stiffness on structural dynamics of ultra-precision machine tool. Int. J. Mach. Tools Manuf. 2020, 158, 103609. [Google Scholar] [CrossRef]
- Lai, V.V.; Chiello, O.; Brunel, J.F.; Dufrénoy, P. Full finite element models and reduction strategies for the simulation of friction-induced vibrations of rolling contact systems. J. Sound. Vib. 2019, 444, 197–215. [Google Scholar] [CrossRef]
- Pohrt, R. Friction Influenced by Vibrations: A Refined Contact-Mechanics View on Lateral and Rotational Oscillations. Front. Mech. Eng. 2020, 6, 566440. [Google Scholar] [CrossRef]
- Schwede, L.N.; Greve, E.; Krause, D.; Otto, K.; Moon, S.K.; Albers, A.; Kirchner, E.; Lachmayer, R.; Bursac, N.; Inkermann, D.; et al. How to Use the Levers of Modularity Properly-Linking Modularization to Economic Targets. J. Mech. Des. 2022, 144, 071401. [Google Scholar] [CrossRef]
- Li, Y.; Ni, Y.; Zhang, N.; Liu, Z. Modularization for the complex product considering the design change requirements. Res. Eng. Des. 2021, 32, 507–522. [Google Scholar] [CrossRef]
- Fu, M.W.; Wang, J.L. Size effects in multi-scale materials processing and manufacturing. Int. J. Mach. Tools Manuf. 2021, 167, 103755. [Google Scholar] [CrossRef]
- Liu, Q.H.; Ma, J.D.; Xin, C. Research progress on multiscale modelling of interface based on continuum mechanics. Acta Mater. Compos. Sin. 2024, 41, 6414–6424. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, F.; Huang, Z.F.; Jia, M.; Chen, G.; Ye, Y.; Lin, Y.; Liu, W.; Chen, B.; Shen, Q.; et al. Additive manufacturing of functionally graded materials: A review. Mater. Sci. Eng. A 2019, 764, 0921–5093. [Google Scholar] [CrossRef]
- Li, N.; Xiong, Y.; Xiong, H.P.; Shi, G.; Blackburn, J.; Liu, W.; Qin, R. Microstructure, formation mechanism and property characterization of Ti + SiC laser cladded coatings on Ti6Al4V alloy. Mater. Charact. 2019, 148, 43–51. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, Z.; Zhou, Z.; Wang, H.; Li, J.; Cai, Z.; Xing, Z.; Ding, C.; Piao, Z. Effect of surface roughness on friction and wear behavior of GCr15 bearing steel under different loads. Surf. Sci. Technol. 2024, 2, 28. [Google Scholar] [CrossRef]
- Li, W.; El Hoseny, M.; Ma, J. Dynamic responses of steady-state transition structures under impact loading. Thin-Walled Struct. 2024, 198, 111761. [Google Scholar] [CrossRef]
- Wang, K.; Lai, J.; Xu, J.; Liao, T.; Wang, P.; Chen, R.; Qian, Y.; Li, L.; Ma, X. Multiscale analysis of wheel-rail rolling contact wear and damage mechanisms using molecular dynamics and explicit finite elements. Tribol. Int. 2023, 185, 108574. [Google Scholar] [CrossRef]
- Li, Y.F.; Wang, H.; Sun, M. ChatGPT-like large-scale foundation models for prognostics and health management: A survey and roadmaps. Reliab. Eng. Syst. Safe 2024, 243, 109850. [Google Scholar] [CrossRef]
- Xin, G.U.; Zhang, Q.; Erdogan, M. Review of peridynamics for multi-physics coupling modeling. Adv. Mech. 2019, 49, 201910. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, K.; Qiu, H.; Wang, M.; Tian, W.; Su, G. Preliminary Implementation of High-Resolution Multi-Scale coupling calculations for the entire pressure vessel based on OpenFOAM. Appl. Therm. Eng. 2025, 259, 124911. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Gao, R.X.; Zhang, F. Hybrid physics-based and data-driven models for smart manufacturing: Modelling, simulation, and explainability. J. Manuf. Syst. 2022, 63, 381–391. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Zhao, R.; Gao, R.X. Physics guided neural network for machining tool wear prediction. J. Manuf. Syst. 2020, 57, 298–310. [Google Scholar] [CrossRef]
- Hou, J.; Hu, J.; Cao, X.; Peng, X.; Li, Q.; Wang, C. The implementation of M-integral in cross-scale correlation analysis of porous materials. Mech. Res. Commun. 2024, 142, 104337. [Google Scholar] [CrossRef]
- Huang, Q. Study on the Operating Mechanics Mechanism of Sleeve on Macro-micro Cross-scale. J. Mech. Eng. 2016, 52, 213–220. [Google Scholar] [CrossRef]
- Kim, N.H.; Won, D.; Burris, D.; Holtkamp, B.; Gessel, G.R.; Swanson, P.; Sawyer, W.G. Finite element analysis and experiments of metal/metal wear in oscillatory contacts. Wear 2005, 258, 1787–1793. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, B.; Li, Y.; Huang, Y.; Shao, X.; Deng, J. Numerical simulation of tip vortex cavitation using a multiscale method. Int. J. Multiph. Flow 2025, 188, 105183. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Mumuni, A.; Mumuni, F. Data augmentation: A comprehensive survey of modern approaches. Array 2022, 16, 100258. [Google Scholar] [CrossRef]
- Bayer, M.; Kaufhold, M.A.; Reuter, C. A Survey on Data Augmentation for Text Classification. ACM Comput. Surv. 2022, 55, 1–39. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1345–1459. [Google Scholar] [CrossRef]
- Arias Chao, M.; Kulkarni, C.; Goebel, K.; Fink, O. Fusing physics-based and deep learning models for prognostics. Reliab. Eng. Syst. Saf. 2022, 217, 107961. [Google Scholar] [CrossRef]
- Kalliorinne, K.; Larsson, R.; Pérez-Ràfols, F.; Liwicki, M.; Almqvist, A. Artificial Neural Network Architecture for Prediction of Contact Mechanical Response. Front. Mech. Eng. 2021, 6, 579825. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, D.; Ta, W.; Zhou, Y. Reconstruction and prediction of opaque rough surface morphology based on friction force evolution. Tribol. Int. 2025, 206, 110599. [Google Scholar] [CrossRef]
- Mukras, S.; Kim, N.H.; Mauntler, N.A.; Schmitz, T.L.; Sawyer, W.G. Analysis of planar multibody systems with revolute joint wear. Wear 2010, 268, 643–652. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, M.; Liu, Y.; Huang, Y. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Process. 2022, 162, 108059. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Yang, Z.; Chen, R.; Yang, H. The influence of tooth surface wear on dynamic characteristics of gear-bearing system based on fractal theory. J. Comput. Nonlinear Dyn. 2020, 15, 041004. [Google Scholar] [CrossRef]
- Zhou, G.; Leu, M.C.; Blackmore, D. Fractal geometry model for wear prediction. Wear 1993, 170, 1–14. [Google Scholar] [CrossRef]
- Yuan, C.; Li, J.; Yan, X.; Peng, Z. The use of the fractal description to characterize engineering surfaces and wear particles. Wear 2003, 255, 315–326. [Google Scholar] [CrossRef]
- He, W.T.; Wang, S.P.; Zhang, C.; Wang, X.; Liu, D. Lubrication and Wear Characteristics of Mechanical Face Seals under Random Vibration Loading. Materials 2020, 13, 1285. [Google Scholar] [CrossRef]
- Wang, Y.; Gang, L.; Liu, S.; Cui, Y. Coupling Fractal Model for Fretting Wear on Rough Contact Surfaces. J. Tribol. 2021, 143, 091701. [Google Scholar] [CrossRef]
- Ni, X.; Sun, J.; Ma, C.; Zhang, Y. Wear Model of a Mechanical Seal Based on Piecewise Fractal Theory. Fractal Fract. 2023, 7, 251. [Google Scholar] [CrossRef]
- Dong, Y. Research on Modeling and Simulation of Surface Topography Obtained by Trochoidal Milling Mode with Ball End Milling Cutter. J. Mech. Eng. 2018, 54, 212–223. [Google Scholar] [CrossRef]
- Yang, H.J. Friction and Wear with Wear Resistant Materials; Chongqing University Press: Chongqing, China, 2023; pp. 30–35. [Google Scholar]
- Xiong, W. Review on Key Technology of Hydrodynamic and Hydrostatic High-frequency Motor Spindles. J. Mech. Eng. 2009, 45, 1–18. [Google Scholar] [CrossRef]
- He, D.Q.; He, C.; Li, W.S.; Shang, L.; Wang, L.; Zhang, G. Tribological behaviors of in-situ textured DLC films under dry and lubricated conditions. Appl. Surf. Sci. 2020, 525, 146581. [Google Scholar] [CrossRef]
- Wang, P.; Liang, H.; Jiang, L.; Qian, L. Effect of nanoscale surface roughness on sliding friction and wear in mixed lubrication. Wear 2023, 530–531, 204995. [Google Scholar] [CrossRef]
- Lee, C.M.; Park, H.; Yoo, J.; Lee, C.; Woo, W.; Park, S. Residual stress and crack initiation in laser clad composite layer with Co-based alloy and WC+NiCr. Appl. Surf. Sci. 2015, 345, 286–294. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Liu, M.; Wu, S. Analytical description of the wear process using a multi-stage contact fractal approach. Wear 2024, 548–549, 205364. [Google Scholar] [CrossRef]
- Mo, S.; Wang, L.; Hu, Q.; Cen, G.; Huang, Y. Coupling failure dynamics of tooth surface morphology and wear based on fractal theory. Nonlinear Dyn. 2024, 112, 175–195. [Google Scholar] [CrossRef]
- Borodich, F.M.; Jin, X.; Pepelyshev, A. Probabilistic, Fractal, and Related Techniques for Analysis of Engineering Surfaces. Front. Mech. Eng. 2020, 6, 64. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q. Application study of fractal theory in mechanical transmission. Chin. J. Mech. Eng. 2016, 29, 871–879. [Google Scholar] [CrossRef]
- Ghosh, S.; Sarkar, B.; Saha, J. Wear characterization by fractal mathematics for quality improvement of machine. J. Qual. Maint. Eng. 2005, 11, 318–332. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhu, W. Prediction of surface wear of involute gears based on a modified fractal method. J. Tribol. 2019, 141, 031603. [Google Scholar] [CrossRef]
- Bigerelle, M.; Najjar, D.; Iost, A. Multiscale functional analysis of wear: A fractal model of the grinding process. Wear 2005, 258, 232–239. [Google Scholar] [CrossRef][Green Version]
- Narayanan, V.; Singh, R.; Marla, D. A computational model to predict surface roughness in laser surface processing of mild steel using nanosecond pulses. J. Manuf. Process 2021, 68, 1880–1889. [Google Scholar] [CrossRef]
- Zhao, S.; Yu, M.; Yan, R.; Zhai, Q.; Liu, J.; Dai, X.; Lei, C.; Wang, D. Surface roughness and microhardness improvement of laser cladding stainless-steel 316 by laser polishing based on multiple remelting. Opt. Laser Technol. 2024, 176, 110903. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Le, K.; Niu, Y.; Gao, X.; Che, Q.; Xu, S.; Liu, Y.; Liu, W. Effect of Substrate Roughness and Contact Scale on the Tribological Performance of MoS2 Coatings. Lubricants 2023, 11, 191. [Google Scholar] [CrossRef]
- Aymard, A.; Delplanque, E.; Dalmas, D.; Scheibert, J. Designing metainterfaces with specified friction laws. Science 2024, 383, 200–204. [Google Scholar] [CrossRef]
- Artur, K.; Norbert, R.; Łukasz, O.; Jacek, P.; Marcin, S.; Jozef, B. Laser Surface Texturing: Characteristics and Applications. Syst. Saf. Hum.-Tech. Facil.-Environ. 2023, 5, 240–248. [Google Scholar] [CrossRef]
- Woźniak, A.; Bialas, O.; Adamiak, M.; Hadzima, B.; Szewczenko, J. The influence of laser texturing on the tribological behavior of titanium alloy Ti6Al4V in medical applications. Arch. Civ. Mech. Eng. 2024, 24, 146. [Google Scholar] [CrossRef]
- Cai, F.; Gao, Y.; Zhang, S.H.; Zhang, L.; Wang, Q. Gradient architecture of Si containing layer and improved cutting performance of AlCrSiN coated tools. Wear 2019, 424, 193–202. [Google Scholar] [CrossRef]
- Shan, X.H. Preparation and Performance Study of Nb2O5/NB2O5-Ti/Ti Gradient Coating on the Surface of Medical Titanium Alloys. Master’s Thesis, Hunan University of Technology, Zhuzhou, China, 2022. [Google Scholar]
- Tao, Y. The Influence of Magnetron Sputtering Process Parameters on the Performance of SnO2 and FTO Thin Films. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Liem, N.V.; Wu, Z.; Jiao, R. Effect of shape/size and distribution of microgeometries of textures on tribo-performance of crankpin bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 236, 421–433. [Google Scholar] [CrossRef]
- Maier, M.; Pusterhofer, M.; Grün, F. Multiscale Wear Simulation in Textured, Lubricated Contacts. Coatings 2023, 13, 697. [Google Scholar] [CrossRef]
- Mróz, Z.; Kucharski, S.; Páczelt, I. Anisotropic friction and wear rules with account for contact state evolution. Wear 2018, 396–397, 1–11. [Google Scholar] [CrossRef]
- Zeng, L.; Deng, X.; Li, F.; Dong, C.; Wang, S.; Yang, H.; Tang, C.; Li, Y. Study on dynamic wear evolution of modified gear rack considering the real-time variation of contact characteristics. Wear 2025, 205845. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, R.; Hu, Z.; Tang, J.; Sun, Z.; Ning, A.; Yang, S. Dynamic modeling and analysis considering friction-wear coupling of gear system. Int. J. Mech. Sci. 2024, 275, 109343. [Google Scholar] [CrossRef]
- Argatov, I.; Chai, Y.S. Contact Geometry Adaptation in Fretting Wear: A Constructive Review. Front. Mech. Eng. 2020, 6, 51. [Google Scholar] [CrossRef]
- Mukras, S.; Kim, N.H.; Sawyer, W.G.; Jackson, D.B.; Bergquist, L.W. Numerical integration schemes and parallel computation for wear prediction using finite element method. Wear 2009, 266, 822–831. [Google Scholar] [CrossRef]
- Rubinstein, S.; Cohen, G.; Fineberg, J. Detachment fronts and the onset of dynamic friction. Nature 2004, 430, 4. [Google Scholar] [CrossRef]
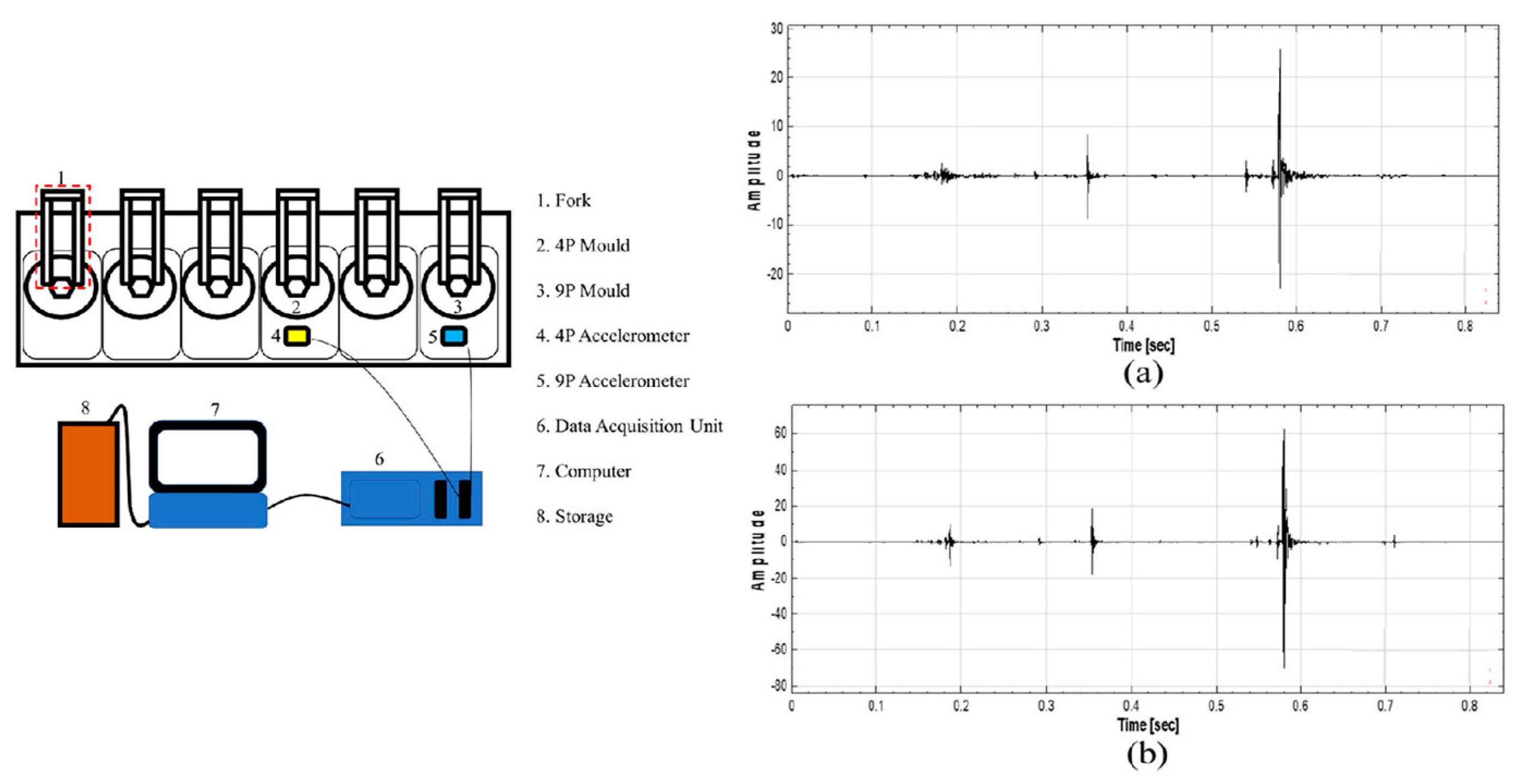
- Han, J.; Luo, Z.; Zhang, Y.; Yan, S. Experimental analysis of interface contact behavior using a novel image processing method*. Chin. Phys. B 2021, 30, 054601. [Google Scholar] [CrossRef]
- Lu, S.H.; Han, J.Y.; Yan, S.Z. Micro sliding friction model considering periodic variation stress distribution of contact surface and experimental verification. Chin. Phys. B 2023, 32, 044602. [Google Scholar] [CrossRef]
- Calabrese, L.; Proverbio, E. A Review on the Applications of Acoustic Emission Technique in the Study of Stress Corrosion Cracking. Corros. Mater. Degrad. 2021, 2, 1–30. [Google Scholar] [CrossRef]
- Weiffenbach, F.A.L.; Romero, F. Experimental analysis of acoustic emissions in rolling and sliding friction: Implications to gear transmissions. Preprint 2024. [CrossRef]
- Towsyfyan, H.; Gu, F.; Ball, A.D.; Liang, B. Modelling acoustic emissions generated by tribological behaviour of mechanical seals for condition monitoring and fault detection. Tribol. Int. 2018, 125, 46–58. [Google Scholar] [CrossRef]
- Tu, R.; Jiao, J.; Jiang, M. Effect of Gradient Multilayer Design on Tribological Performance of TiN/TiSiN Coatings Prepared by Cathodic Arc Ion Plating. Coatings 2023, 13, 836. [Google Scholar] [CrossRef]
- Akbarpour, M.R.; Hosseini, S.F.; Kim, H.S. Microstructure, hardness, and tribological properties of Ni-Co/SiO2 nanocomposite coating produced through pulsed current electrodeposition. Ceram. Int. 2024, 22, 50. [Google Scholar] [CrossRef]
- Huda, A.; Hadia, K.J. Effect of Al2O3 reinforcement nanoparticles on the tribological behaviour and mechanical properties of Al6061 alloy. AIMS Mater. Sci. 2020, 4, 486–498. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Zhou, F. The Improvement of CrN Coatings Wear Resistance by Adjusting the Cycle Number of Electrochemical. Lubricants 2024, 12, 295. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Weng, Z.; Wang, C.; Yin, H.; Zhou, F.; Zhou, Z. Sealing Effect of Electrochemical Polarization and Its Influence on the Tribological Properties of CrN Coatings. Tribology 2026, 46, 1–13. [Google Scholar]
- Feng, T.; Duan, H.T.; Pan, L.; Xu, X.; Qin, J.; Wei, Q.; Luo, G. Microstructural, frictional, and wear properties of CrN/TiAlN multilayer coatings. China Surf. Eng. 2024, 37, 232–241. [Google Scholar]
- Fan, Y.; Gu, F.; Ball, A. Modelling acoustic emissions generated by sliding friction. Wear 2010, 268, 811–815. [Google Scholar] [CrossRef]
- Geng, Z.; Puhan, D.; Reddyhoff, T. Using acoustic emission to characterize friction and wear in dry sliding steel contacts. Tribol. Int. 2019, 134, 394–407. [Google Scholar] [CrossRef]
- Pau, M.; Leban, B.; Baldi, A. Simultaneous subsurface defect detection and contact parameter assessment in a wheel–rail system. Wear 2008, 265, 1837–1847. [Google Scholar] [CrossRef]
- Quinn, A.M.; Drinkwater, B.W.; Dwyer-Joyce, R.S. The measurement of contact pressure in machine elements using ultrasound. Ultrasonics 2002, 39, 495–502. [Google Scholar] [CrossRef]
- Guo, M.; Jiang, Y.; Spielberg, A.E.; Wu, J.; Liu, K. Benchmarking Rigid Body Contact Models. In Proceedings of the 5th Annual Learning for Dynamics and Control Conference, Philadelphia, PA, USA, 15–16 June 2023; pp. 1480–1492. [Google Scholar]
- Flores, P. Contact mechanics for dynamical systems: A comprehensive review. Multibody Syst. Dyn. 2022, 54, 127–177. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, X.; Zhang, Z.; Feng, G.; Zhao, Q.; Zhao, L.; He, G. A continuous contact force model for impact analysis. Mech. Syst. Signal Process. 2022, 168, 108739. [Google Scholar] [CrossRef]
- Wang, B.; Li, M.Q.; Yu, H.; Li, J. Research Progress of System Dynamics with Clearance. Mach. Tool Hydraul. 2015, 43, 163–166. [Google Scholar]
- Zhang, J.; Li, W.; Zhao, L.; He, G. A continuous contact force model for impact analysis in multibody dynamics. Mech. Mach. Theory 2020, 153, 103946. [Google Scholar] [CrossRef]
- Saura, M.; Segado, P.; Dopico, D. Computational kinematics of multibody systems: Two formulations for a modular approach based on natural coordinates. Mech. Mach. Theory 2019, 142, 103602. [Google Scholar] [CrossRef]
- Rhee, J.; Akay, A. Dynamic response of a revolute joint with clearance. Mech. Mach. Theory 1996, 31, 121–134. [Google Scholar] [CrossRef]
- Xia, T.; Qu, J.; Liu, Y. A Joint Surface Contact Stiffness Model Considering Micro-Asperity Interaction. Aerospace 2024, 11, 472. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, M.; Lu, X.; Wang, S.; Li, Z. A Review of Cross-Scale Theoretical Contact Models for Bolted Joints Interfaces. Coatings 2024, 14, 539. [Google Scholar] [CrossRef]
- Xu, L.X.; Han, Y.C.; Dong, Q.B.; Jia, H.L. An approach for modelling a clearance revolute joint with a constantly updating wear profile in a multibody system: Simulation and experiment. Multibody Syst. Dyn. 2019, 45, 457–478. [Google Scholar] [CrossRef]
- López-Lombardero, M.; Cuadrado, J.; Cabello, M.; Martinez, F.; Dopico, D.; López-Varela, A. A multibody-dynamics based method for the estimation of wear evolution in the revolute joints of mechanisms that considers link flexibility. Mech. Mach. Theory 2024, 194, 105583. [Google Scholar] [CrossRef]
- Zhou, J.S. Dynamic and Experimental Study of Flexible Mechanism Considering Wear Clearance of Moving Pair. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Popov, M. The Influence of Vibration on Friction: A Contact-Mechanical Perspective. Front. Mech. Eng. 2020, 6, 69. [Google Scholar] [CrossRef]
- Ahmedalbashir, M.; Romdhane, L.; Lee, J. Dynamics of a four-bar mechanism with clearance and springs—Modeling and experimental analysis. J. Mech. Sci. Technol. 2017, 31, 1023–1033. [Google Scholar] [CrossRef]
- Jing, Q.; Liu, H. Dynamics and Wear Prediction of Mechanisms Considering Multiple Clearances and Coatings. Lubricants 2023, 11, 310. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, Z.; Yao, S.; Xu, C.; Ji, H.; Li, L. Dynamic response and chaos analysis of a spatial multi-body system with multiple clearance joints and a flexible component. Commun. Nonlinear Sci. 2025, 145, 108699. [Google Scholar] [CrossRef]
- McClenny, L.D.; Braga-Neto, U.M. Self-adaptive physics-informed neural networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Tang, Y.; Orzechowski, G.; Prokop, A.; Mikkola, A. Monte Carlo tree search control scheme for multibody dynamics applications. Nonlinear Dyn. 2024, 112, 8363–8391. [Google Scholar] [CrossRef]
- Sandu, A.; Sandu, C.; Ahmadian, M. Modeling Multibody Systems with Uncertainties. Part I Theor. Comput. Aspects. Multibody Syst. Dyn. 2006, 15, 369–391. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Y.; Wu, J. Interval analysis method based on Legendre polynomial approximation for uncertain multibody systems. Adv. Eng. Softw. 2018, 121, 223–234. [Google Scholar] [CrossRef]
- Bai, Z.F.; Zhao, J.J.; Chen, J.; Zhao, Y. Design optimization of dual-axis driving mechanism for satellite antenna with two planar revolute clearance joints. Acta Astronaut. 2018, 144, 80–89. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, K.; Wu, X.; Sun, Y.; Zhong, T. Kinematic accuracy and nonlinear dynamics of a flexible slider-crank mechanism with multiple clearance joints. Eur. J. Mech.—A/Solids 2021, 88, 104277. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Qian, M.; Qin, Z.; Yan, S.; Zhang, L. A comprehensive method for the contact detection of a translational clearance joint and dynamic response after its application in a crank-slider mechanism. Mech. Mach. Theory 2020, 145, 103717. [Google Scholar] [CrossRef]
- He, Y.; Liang, Z.H. Research on the Influence of Rotating Pair Clearance on the Dynamic Performance of the Main Mechanism of Gear Shaping Machine. J. Mech. Transm. 2021, 45, 33–38. [Google Scholar] [CrossRef]
- Pappalardo, C.M. Dynamic Analysis of Multibody Mechanical Systems. Machines 2024, 12, 626. [Google Scholar] [CrossRef]
- Moravič, M.; Hroncová, D.; Ostertag, O. Vibration of Mechanical System Using MSC Adams Software. Am. J. Mech. Eng. 2015, 3, 244–247. [Google Scholar] [CrossRef]
- Hroncová, D.; Delyová, I.; Frankovský, P. Kinematic Analysis of Mechanisms Using MSC Adams. AMM 2014, 611, 83–89. [Google Scholar] [CrossRef]
- Awwad, K.Y.E.; Fallahnezhad, K.; Yousif, B.F.; Mostafa, A.; Alajarmeh, O.; Shalwan, A.; Zeng, X. Finite element analysis and experimental validation of polymer–metal contacts in block-on-ring configuration. Friction 2023, 12, 554–568. [Google Scholar] [CrossRef]
- Li, W.; Tan, Y.; Tao, Y.; Bai, D. Wear analysis of rolling bearing contact surfaces based on finite element method. Phys. Scr. 2023, 99, 015916. [Google Scholar] [CrossRef]
- Feng, Y.; He, Z.; Xue, X.; Dong, M. Dynamic simulation of complex multi-hinge space flap mechanism. J. Phys. Conf. Ser. 2022, 2235, 012072. [Google Scholar] [CrossRef]
- Feng, Y.W.; Tang, J.Q.; Xue, X.F.; Li, S.; Chen, X. Study on dynamic simulation of hinged flap mechanism considering wear evolution. J. Northwestern Polytech. Univ. 2024, 42, 222–231. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Huang, W. Dynamics analysis of planar rigid-flexible coupling deployable solar array system with multiple revolute clearance joints. Mech. Syst. Signal Process. 2019, 117, 188–209. [Google Scholar] [CrossRef]
- Pereira, K.; Vanegas-Useche, L.V.; Wahab, M.A. Aspects of Fretting Fatigue Finite Element Modelling. Comput. Mater. Contin. 2020, 64, 97–144. [Google Scholar] [CrossRef]
- Wang, Q.J.; Sun, L.; Zhang, X.; Liu, S.; Zhu, D. FFT-Based Methods for Computational Contact Mechanics. Front. Mech. Eng. 2020, 6, 61. [Google Scholar] [CrossRef]
- Arnaud, P.; Fouvry, S.; Garcin, S. A numerical simulation of fretting wear profile taking account of the evolution of third body layer. Wear 2017, 376–377, 1475–1488. [Google Scholar] [CrossRef]
- Cai, M.; Zhang, P.; Xiong, Q.; Cai, Z.; Luo, S.; Gu, L.; Zeng, L. Finite element simulation of fretting wear behaviors under the ball-on-flat contact configuration. Tribol. Int. 2023, 177, 107930. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Ye, W.-L.; Correia, J.A.; Jesus, A.M.; Wang, Q. Stress gradient effect in metal fatigue: Review and solutions. Theor. Appl. Fract. Mech. 2022, 121, 103513. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Simulating sliding wear with finite element method. Tribol. Int. 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Yan, L.; Guan, L.; Wang, D.; Xiang, D. Application and Prospect of Wear Simulation Based on ABAQUS: A Review. Lubricants 2024, 12, 57. [Google Scholar] [CrossRef]
- Choudhry, J.; Almqvist, A.; Larsson, R. Improving Archard’s Wear Model: An Energy-Based Approach. Tribol. Lett. 2024, 72, 93. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, Y.; Gorbachev, S.; Kuzin, V.; Du, J.; Yao, H. Research on numerical simulation and prediction of tool wear in cutting ultra-high-strength aluminum alloys. J. Braz. Soc. Mech. Sci. 2024, 46, 686. [Google Scholar] [CrossRef]
- Zhao, J.J.; Yin, D.; Tang, L.C.; Qian, H.; Huo, Y.Z. Numerical calculation and analysis of the effect of frictional contact conditions on the wear rate of zirconium alloys. Eng. Mech. 2016, 33, 275–282. [Google Scholar] [CrossRef]
- Patil, A.P.; Mishra, B.K.; Harsha, S.P. Analytical model of rolling element bearing for studying its wear modelled as change in its clearance. Mater. Today Proc. 2021, 46, 10741–10746. [Google Scholar] [CrossRef]
- Liu, L.Q.; Li, X.; Yang, J.W.; Tian, S.; Zhang, Y. Finite element analysis of fretting contact state of cylindrical-plane fretting wear. J. Mech. Electr. Eng. 2023, 40, 896–902. [Google Scholar] [CrossRef]
- Springis, G.; Boiko, I. Comparative Analysis of Wear Models for Accurate Wear Predictions. Lubricants 2025, 13, 100. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, G.; Yuan, Y.; Zhang, H.; Wu, Y. Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure. Lubricants 2023, 11, 421. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.; Lankarani, H.; Koshy, C. A study on dynamics of mechanical systems including joints with clearance and lubrication. Mech. Mach. Theory 2006, 41, 247–261. [Google Scholar] [CrossRef]
- Wang, J.H. Dynamic Modeling and Simulation of RSSR Space Mechanism with Spherical RSSR Space Mechanism with Spherical Clearance Joints Clearance Joints. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Askari, E.; Flores, P.; Dabirrahmani, D.; Appleyard, R. A Computational Analysis of Squeaking Hip Prostheses. J. Comput. Nonlinear Dyn. 2015, 10, 024502. [Google Scholar] [CrossRef]
- Erkaya, S. Experimental investigation of flexible connection and clearance joint effects on the vibration responses of mechanisms. Mech. Mach. Theory 2018, 121, 515–529. [Google Scholar] [CrossRef]
- Erkaya, S.; Doğan, S.; Şefkatlıoğlu, E. Analysis of the joint clearance effects on a compliant spatial mechanism. Mech. Mach. Theory 2016, 104, 255–273. [Google Scholar] [CrossRef]
- Zhang, L.X.; Bai, Z.F.; Zhao, Y.; Bin Cao, X. Dynamic response of solar panel deployment on spacecraft system considering joint clearance. Acta Astronaut. 2012, 81, 174–185. [Google Scholar] [CrossRef]
- David, B. Linear-time dynamics using Lagrange multipliers. Assoc. Comput. Mach. 1996, 1, 137–146. [Google Scholar] [CrossRef]
- Zhang, J.C.; Qian, F.; Li, X.Y.; Yao, W.; Gao, Y. Dynamic Modeling and Analysis of Multi-link Mechanism with Clearance. Mech. Electr. Eng. Technol. 2015, 51, 42–45. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A.; Ratner, A.; Smith, V.; De Sa, C.; Ré, C. A Kernel Theory of Modern Data Augmentation. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 1528–1537. [Google Scholar]
- Müller, S.G.; Hutter, F. Trivialaugment: Tuning-free yet state-of-the-art data augmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 774–782. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Ellis, J.L.; Jacobs, M.; Dijkstra, J.; van Laar, H.; Cant, J.; Tulpan, D.; Ferguson, N. Review: Synergy between mechanistic modelling and data-driven models for modern animal production systems in the era of big data. Animal 2020, 14, s223–s237. [Google Scholar] [CrossRef]
- Li, N.; Wang, X.; Wang, W.; Xin, M.; Yuan, D.; Zhang, M. A multi-feature dataset of coated end milling cutter tool wear whole life cycle. Sci. Data 2025, 12, 16. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, G.; Xiao, S.; Wang, F.; Zhao, G.; Ma, S. Mechanism- and data-driven based dynamic hybrid modeling for multi-condition processes. Chemom. Intell. Lab. Syst. 2025, 260, 105353. [Google Scholar] [CrossRef]
- Ruzova, T.A.; Haddadi, B. Surface Roughness and Its Measurement Methods—Analytical Review. Results Surf. Interfaces 2025, 19, 100441. [Google Scholar] [CrossRef]
- Su, J.; Yu, X.; Wang, X.; Wang, Z.; Chao, G. Enhanced transfer learning with data augmentation. Eng. Appl. Artif. Intell. 2024, 129, 107602. [Google Scholar] [CrossRef]
- Yu, K.; Lin, T.R.; Ma, H.; Li, X.; Li, X. A multi-stage semi-supervised learning approach for intelligent fault diagnosis of rolling bearing using data augmentation and metric learning. Mech. Syst. Signal Process. 2021, 146, 107043. [Google Scholar] [CrossRef]
- Khan, A.; Hwang, H.; Kim, H.S. Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines. Mathematics 2021, 9, 2336. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Zhu, F.; Sun, Z. Domain Disentanglement with Interpolative Data Augmentation for Dual-Target Cross-Domain Recommendation. In Proceedings of the 17th ACM Conference on Recommender Systems, Singapore, 18–22 September 2023; pp. 515–527. [Google Scholar]
- Kim, Y.; Kim, Y.; Yang, C.; Park, K.; Gu, G.X.; Ryu, S. Deep learning framework for material design space exploration using active transfer learning and data augmentation. Npj Comput. Mater. 2021, 7, 140. [Google Scholar] [CrossRef]
- Antoniou, A.; Storkey, A.J.; Edwards, H. Data Augmentation Generative Adversarial Networks. arXiv 2017, arXiv:1711.04340. [Google Scholar]
- Krichen, M. Generative Adversarial Networks. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023; pp. 1–7. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, DC, USA, 14–19 June 2020; pp. 702–703. [Google Scholar]
- Zhang, L.; Suganthan, P.N. Random Forests with ensemble of feature spaces. Pattern Recogn. 2014, 47, 3429–3437. [Google Scholar] [CrossRef]
- Yi, X.; Xu, Y.; Hu, Q.; Krishnamoorthy, S.; Li, W.; Tang, Z. ASN-SMOTE: A synthetic minority oversampling method with adaptive qualified synthesizer selection. Complex Intell. Syst. 2022, 8, 2247–2272. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F.; Kamalov, F. A theoretical distribution analysis of synthetic minority oversampling technique (SMOTE) for imbalanced learning. Mach. Learn. 2024, 113, 4903–4923. [Google Scholar] [CrossRef]
- Li, Q.; Tang, Y.; Chu, L. Generative adversarial networks for prognostic and health management of industrial systems: A review. Expert Syst. Appl. 2024, 253, 124341. [Google Scholar] [CrossRef]
- Brophy, E.; Wang, Z.; She, Q.; Ward, T. Generative Adversarial Networks in Time Series: A Systematic Literature Review. ACM Comput. Surv. 2023, 55, 199. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, S.; Liu, S.; Liu, W.; Ding, A. A bearing fault diagnosis method for high-noise and unbalanced dataset. Smart Resilient Transp. 2022, 5, 28–45. [Google Scholar] [CrossRef]
- Ahang, M.; Jalayer, M.; Shojaeinasab, A.; Ogunfowora, O.; Charter, T.; Najjaran, H. Synthesizing Rolling Bearing Fault Samples in New Conditions: A Framework Based on a Modified CGAN. Sensors 2022, 22, 5413. [Google Scholar] [CrossRef]
- Tang, P.; Li, Z.; Wang, X.; Liu, X.; Mou, P. Time Series Data Augmentation for Energy Consumption Data Based on Improved TimeGAN. Sensors 2025, 25, 493. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Ong, Z.C.; Khoo, S.Y.; Siow, P.Y.; Zhang, J.; Wang, T. SeqInfo-SAWGAN-GP: Adaptive feature extraction from vibration time data under variable operating conditions for imbalanced bearing fault diagnosis. Measurement 2025, 243, 116344. [Google Scholar] [CrossRef]
- Wu, J.D.; Luo, W.J.; Yao, K.C. Electric Motor Vibration Signal Classification Using Wigner–Ville Distribution for Fault Diagnosis. Sensors 2025, 25, 1196. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2018, Rhodes, Greece, 4–7 October 2018; pp. 270–279. [Google Scholar]
- Yao, Q.; Qin, Y.; Wang, X.; Qian, Q. Multiscale domain adaption models and their application in fault transfer diagnosis of planetary gearboxes. Eng. Appl. Artif. Intell. 2021, 104, 104383. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. In Domain Adaptation in Computer Vision Applications; Csurka, G., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 189–209. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1180–1189. [Google Scholar]
- Shao, S.; Wang, P.; Yan, R. Generative adversarial networks for data augmentation in machine fault diagnosis. Comput. Ind. 2019, 106, 85–93. [Google Scholar] [CrossRef]
- Zheng, T.; Song, L.; Wang, J.; Teng, W.; Xu, X.; Ma, C. Data synthesis using dual discriminator conditional generative adversarial networks for imbalanced fault diagnosis of rolling bearings. Measurement 2020, 158, 107741. [Google Scholar] [CrossRef]
- Ye, R.; Dai, Q. A novel transfer learning framework for time series forecasting. Knowl.-Based Syst. 2018, 156, 74–99. [Google Scholar] [CrossRef]
- Yu, Z.; Shen, D.; Jin, Z.; Huang, J.; Cai, D.; Hua, X.-S. Progressive Transfer Learning. IEEE Trans. Image Process 2022, 31, 1340–1348. [Google Scholar] [CrossRef]
- Hao, L.; Pagani, R.; Beschi, M.; Legnani, G. Dynamic and Friction Parameters of an Industrial Robot: Identification, Comparison and Repetitiveness Analysis. Robotics 2021, 10, 49. [Google Scholar] [CrossRef]
- Zou, J.; Tang, L.; Liu, Y.; Yang, S.; Wang, S. A two-stage direction-guided evolutionary algorithm for large-scale multiobjective optimization. Inform. Sci. 2024, 674, 120719. [Google Scholar] [CrossRef]
- Pérez-Villar, J.I.B.; García-Martín, Á.; Bescós, J. Spacecraft Pose Estimation Based on Unsupervised Domain Adaptation and on a 3D-Guided Loss Combination. In Proceedings of the Computer Vision—ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; pp. 37–52. [Google Scholar]
- Sun, B.; Li, H.; Wang, C.; Ma, Z.; Guan, X. Optimized weights Time-Frequency Analysis: A novel method for fault diagnosis in rotating Machinery under Time-Varying speeds. Mech. Syst. Signal Process. 2025, 226, 112345. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Jiang, D.; He, C.; Chen, Z.; Zhao, J. Are Novel Deep Learning Methods Effective for Fault Diagnosis? IEEE Trans. Reliab. 2024, 1–15. [Google Scholar] [CrossRef]
- Meng, W.; Zhao, P.; Shi, Y.; Li, L.; Meng, Z. Intelligent fault diagnosis of mechanical engineering using NLF-LSTM optimized deep learning model. Optim. Eng. 2024, 26, 891–912. [Google Scholar] [CrossRef]
- Neupane, D.; Bouadjenek, M.R.; Dazeley, R.; Aryal, S. Data-driven machinery fault diagnosis: A comprehensive review. Neurocomputing 2025, 627, 129588. [Google Scholar] [CrossRef]
- Bai, Y.; Cheng, W.; Wen, W.; Liu, Y. Application of Time-Frequency Analysis in Rotating Machinery Fault Diagnosis. Shock. Vib. 2023, 2023, 9878228. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Wang, J.; Wang, J. Time–frequency analysis for bearing fault diagnosis using multiple Q-factor Gabor wavelets. ISA Trans. 2019, 87, 225–234. [Google Scholar] [CrossRef]
- He, Q.; Ding, X. Time-Frequency Manifold for Machinery Fault Diagnosis. In Structural Health Monitoring: An Advanced Signal Processing Perspective; Yan, R., Chen, X., Mukhopadhyay, S.C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 131–154. [Google Scholar]
- Varanis, M.; Silva, A.L.; Balthazar, J.M.; Pederiva, R. A Tutorial Review on Time-Frequency Analysis of Non-Stationary Vibration Signals with Nonlinear Dynamics Applications. Braz. J. Phys. 2021, 51, 859–877. [Google Scholar] [CrossRef]
- Li, C.; Liang, M. Time–frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mech. Syst. Signal Process. 2012, 26, 205–217. [Google Scholar] [CrossRef]
- Novelo, X.E.A.; Chu, H.Y. Application of vibration analysis using time-frequency analysis to detect and predict mechanical failure during the nut manufacturing process. Adv. Mech. Eng. 2022, 14. [Google Scholar] [CrossRef]
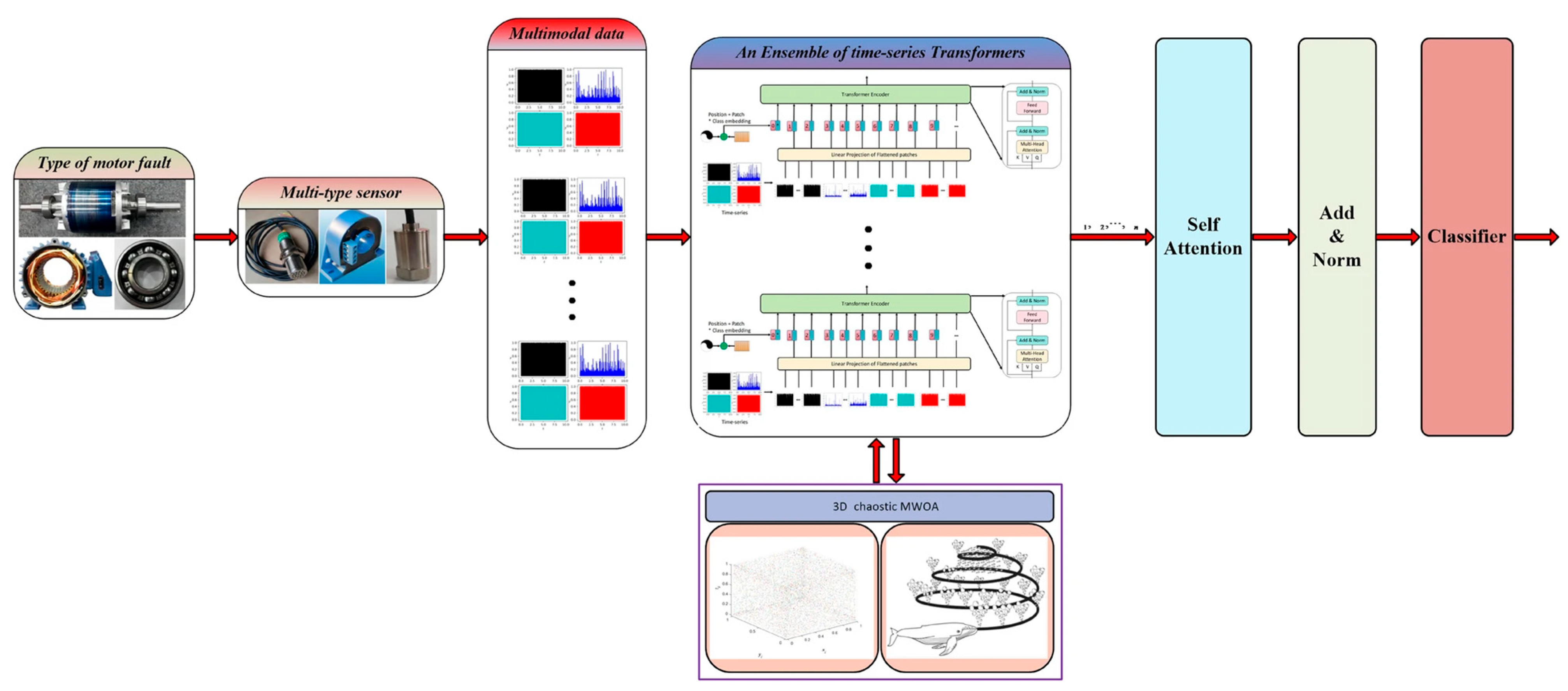
- Xu, B.; Li, H.; Ding, R.; Zhou, F. Fault diagnosis in electric motors using multi-mode time series and ensemble transformers network. Sci. Rep. 2025, 15, 7834. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.U.; Hua, C.; Li, L.; Zhang, L.; Yang, F.; Liu, W. Remaining useful life prediction for a cracked rotor system via moving feature fusion based deep learning approach. Measurement 2025, 239, 115433. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Bebis, G.; Stathaki, T. Recent Developments in Deep Learning for Engineering Applications. Intell. Neurosci. 2018, 2018, 2. [Google Scholar] [CrossRef]
- Yang, Z.; Li, G.; He, B. Multisensor-Driven Intelligent Mechanical Fault Diagnosis Based on Convolutional Neural Network and Transformer. IEEE Sens. J. 2025, 25, 5087–5101. [Google Scholar] [CrossRef]
- Luo, Z.; Pan, S.; Dong, X.; Zhang, X. Interpretable quadratic convolutional residual neural network for bearing fault diagnosis. J. Braz. Soc. Mech. Sci. 2025, 47, 158. [Google Scholar] [CrossRef]
- Yang, T.; Wu, D.; Qiu, S.; Guo, S.; Li, X.; Han, Q. The STAP-Net: A new health perception and prediction framework for bearing-rotor systems under special working conditions. Reliab. Eng. Syst. Saf. 2025, 254, 110633. [Google Scholar] [CrossRef]
- An, Q.; Tao, Z.; Xu, X.; El Mansori, M.; Chen, M. A data-driven model for milling tool remaining useful life prediction with convolutional and stacked LSTM network. Measurement 2020, 154, 107461. [Google Scholar] [CrossRef]
- Zhou, K.; Lu, N.; Jiang, B.; Ye, Z. FEV-Swin: Multi-source heterogeneous information fusion under a variant swin transformer framework for intelligent cross-domain fault diagnosis. Knowl.-Based Syst. 2025, 310, 112982. [Google Scholar] [CrossRef]
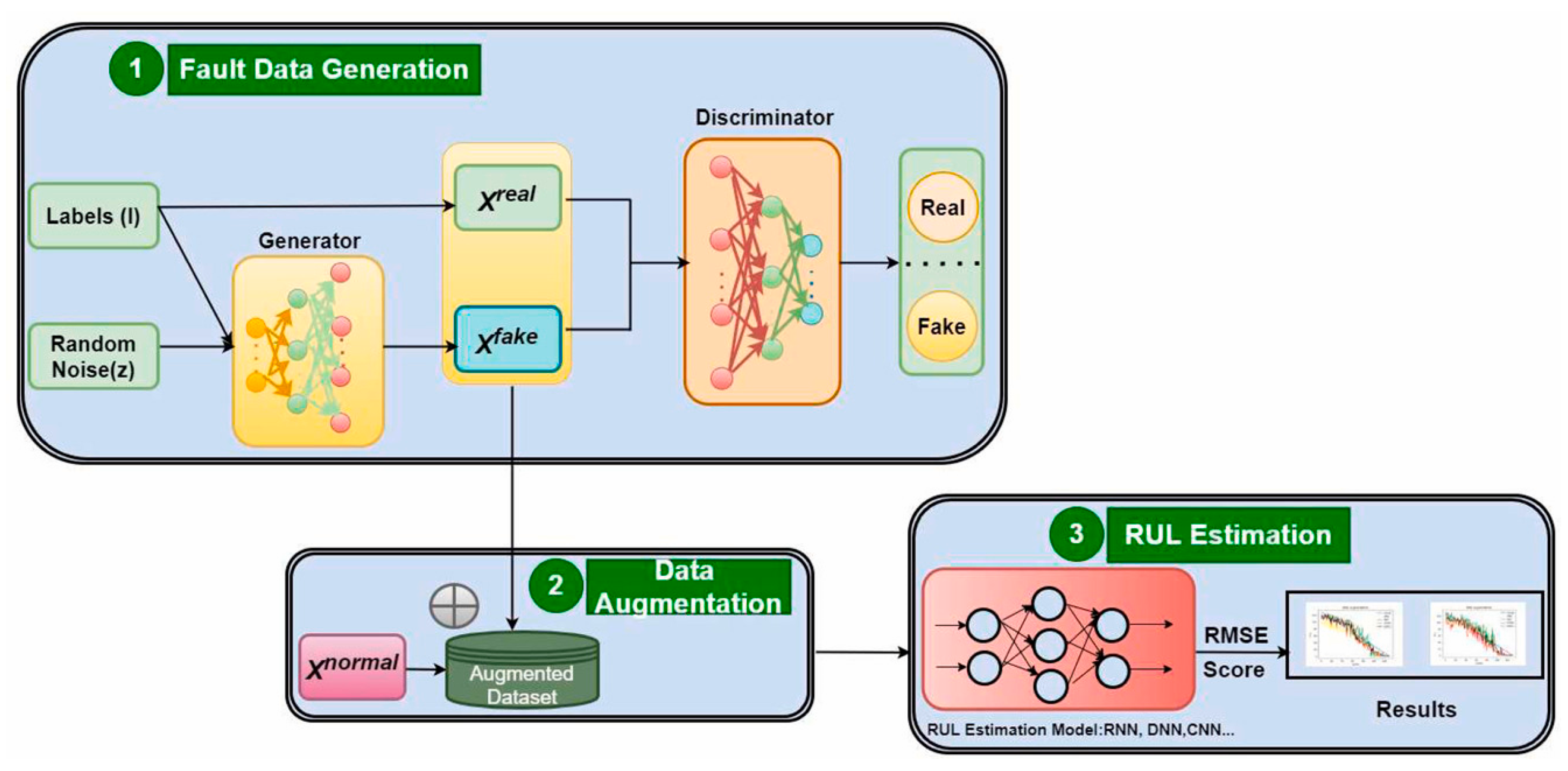
- Behera, S.; Misra, R. Generative adversarial networks based remaining useful life estimation for IIoT. Comput. Electr. Eng. 2021, 92, 107195. [Google Scholar] [CrossRef]
- Fan, Y.; Nowaczyk, S.; Rögnvaldsson, T. Transfer learning for remaining useful life prediction based on consensus self-organizing models. Reliab. Eng. Syst. Saf. 2020, 203, 107098. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, R.; He, M.; Du, L.; Bao, S.; Yuan, J.; Wan, W. Dynamic modeling and analysis for a differential modular robot joint with the friction model. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; pp. 1545–1550. [Google Scholar]
- Xu, Z.; Zhao, K.; Wang, J.; Bashir, M. Physics-informed probabilistic deep network with interpretable mechanism for trustworthy mechanical fault diagnosis. Adv. Eng. Inform. 2024, 62, 102806. [Google Scholar] [CrossRef]
- Sinha, U.; Dindoruk, B. Review of Physics-Informed Machine Learning (PIML) Methods Applications in Reservoir Engineering. Geoenergy Sci. Eng. 2025, 250, 213713. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, S.; Gao, D.; Sun, Y.; Bai, W. A Review of Physics-Based, Data-Driven, and Hybrid Models for Tool Wear Monitoring. Machines 2024, 12, 833. [Google Scholar] [CrossRef]
- Li, J.X.; Zhou, D.J.; Xiao, W.; Zhang, H. Hybrid Modeling of Gas Turbine based on Neural Network. J. Eng. Therm. Energy Power 2019, 34, 33–39. [Google Scholar] [CrossRef]
- Ni, C.; Yang, J.; Ding, H. Mechanism and data hybrid-driven cutting forces prediction model for end milling. J. Intell. Manuf. 2025. [Google Scholar] [CrossRef]
- Meng, Y.; Dong, S.-M.; Sun, X.-S.; Wei, S.-L.; Liu, X.-L. A mechanism-data hybrid-driven modeling method for predicting machine tool-cutting energy consumption. Adv. Manuf. 2025, 13, 167–195. [Google Scholar] [CrossRef]
- Sadoughi, M.; Hu, C. A Physics-Based Deep Learning Approach for Fault Diagnosis of Rotating Machinery. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5919–5923. [Google Scholar]
- Fan, Z.; Li, W.; Chang, K.C. A Two-Stage Attention-Based Hierarchical Transformer for Turbofan Engine Remaining Useful Life Prediction. Sensors 2024, 24, 824. [Google Scholar] [CrossRef]
- Cao, H.; Xiao, W.; Sun, J.; Gan, M.-G.; Wang, G. A hybrid data- and model-driven learning framework for remaining useful life prognostics. Eng. Appl. Artif. Intell. 2024, 135, 108557. [Google Scholar] [CrossRef]
- Zaman, W.; Siddique, M.F.; Ullah, S.; Saleem, F.; Kim, J.-M. Hybrid Deep Learning Model for Fault Diagnosis in Centrifugal Pumps: A Comparative Study of VGG16, ResNet50, and Wavelet Coherence Analysis. Machines 2024, 12, 905. [Google Scholar] [CrossRef]
- Hu, J.X.; Tang, Y.; Li, F.; Wang, Q.; Zhao, X. Performance Analysis on Parallel Mode of Data-Physical Fusion Model in Power System. Autom. Electr. Power Syst. 2022, 46, 15–24. [Google Scholar] [CrossRef]
- Hanachi, H.; Yu, W.; Kim, I.Y.; Liu, J.; Mechefske, C.K. Hybrid data-driven physics-based model fusion framework for tool wear prediction. Int. J. Adv. Manuf. Technol. 2018, 101, 2861–2872. [Google Scholar] [CrossRef]




| Symbol | Definition | Description |
|---|---|---|
| k | Wear coefficient | Material-dependent factor in Archard’s law |
| H | Material hardness | abrasion resistance |
| Ra | Arithmetic roughness | Average vertical deviation of surface profile |
| Friction coefficient | Ratio of frictional force to normal load | |
| Rq | Root mean square value of surface roughness | The spatial distribution dispersion degree of morphology |
| D | Fractal dimension | Multiscale roughness descriptor |
| Fn | Normal contact force | |
| s | Sliding distance |
| Coating Type | Hardness | Applicable Working Conditions |
|---|---|---|
| CrN | 20–25 | High load gears and bearings |
| DLC | 15–20 | Vacuum and dry friction |
| MoS2 | 0.5–1.0 | Aerospace lubrication and cryogenic environments |
| Clearance Modeling Methods | Advantages | Drawbacks | Applicable Occasions |
|---|---|---|---|
| Two-state model | Closer to reality and more accurate modeling | Computationally complex and difficult to use for multiple clearance systems | Single-clearance systems |
| Continuous contact modeling | simple calculation | Unable to reflect crash impacts | Small clearance and multiple clearance systems |
| Three-state modeling | Consistent with the actual situation | Complex modeling and computational instability | Fewer applications |
| Method | Core Problem-Solving | Technical Advantages |
|---|---|---|
| Feature space expansion | Sparse data in a single domain; for example, the Random Forest model has a 20% increase in generalization ability in sparse data scenarios | Highly interpretable and computationally efficient |
| Generative Adversarial Networks | Complex/extreme conditions data generation; for example, CGAN generates bearing failure data with 92% classification accuracy | Generate high-dimensional and complex data to break through distribution boundaries |
| Dimensionality | Theoretical Foundation | Feature Extraction Method | Interpretability |
|---|---|---|---|
| Time–frequency characteristic drive | Signal Processing and Statistics | Artificial design features (time-domain statistics, frequency-domain energy, etc.) | Characteristics and physical phenomena can be directly correlated |
| Deep learning | Neural Networks and Pattern Recognition | Automatic learning of features (convolutional kernels, attention weights, etc.) | Black box model and reliance on visualization tools |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wei, Q.; Wang, W.; Zhao, L.; Hu, N. Multiscale Modeling and Data-Driven Life Prediction of Kinematic Interface Behaviors in Mechanical Drive Systems. Coatings 2025, 15, 660. https://doi.org/10.3390/coatings15060660
Liu Y, Wei Q, Wang W, Zhao L, Hu N. Multiscale Modeling and Data-Driven Life Prediction of Kinematic Interface Behaviors in Mechanical Drive Systems. Coatings. 2025; 15(6):660. https://doi.org/10.3390/coatings15060660
Chicago/Turabian StyleLiu, Yue, Qiang Wei, Wenkui Wang, Libin Zhao, and Ning Hu. 2025. "Multiscale Modeling and Data-Driven Life Prediction of Kinematic Interface Behaviors in Mechanical Drive Systems" Coatings 15, no. 6: 660. https://doi.org/10.3390/coatings15060660
APA StyleLiu, Y., Wei, Q., Wang, W., Zhao, L., & Hu, N. (2025). Multiscale Modeling and Data-Driven Life Prediction of Kinematic Interface Behaviors in Mechanical Drive Systems. Coatings, 15(6), 660. https://doi.org/10.3390/coatings15060660