Investigating the Microstructural Behavior and Energy Absorption of Pure Copper Lattice Structures Fabricated by Selective Electron Beam Melting
Abstract
1. Introduction
2. Experiment
2.1. Lattice Structure Design and Relative Density
2.2. Sample Preparation
2.3. Sample Performance Testing Methodology
3. Results and Discussion
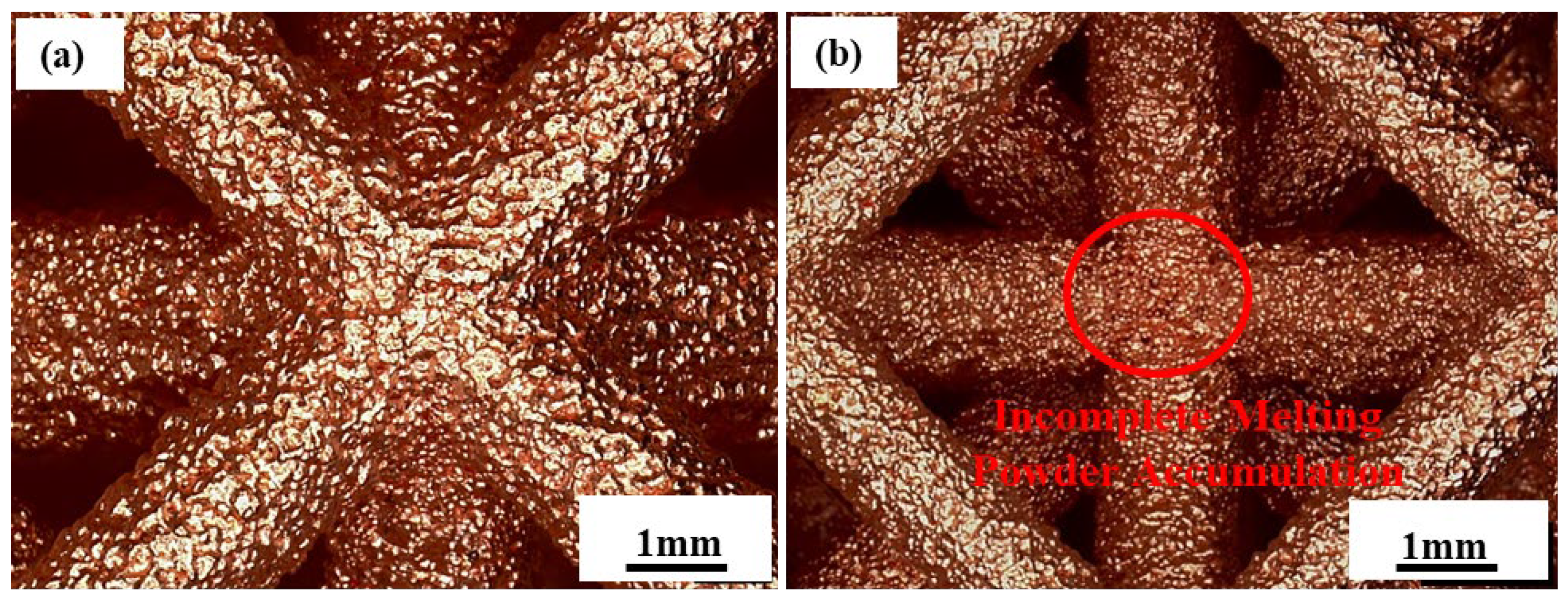
3.1. Overall Quality Analysis of Samples
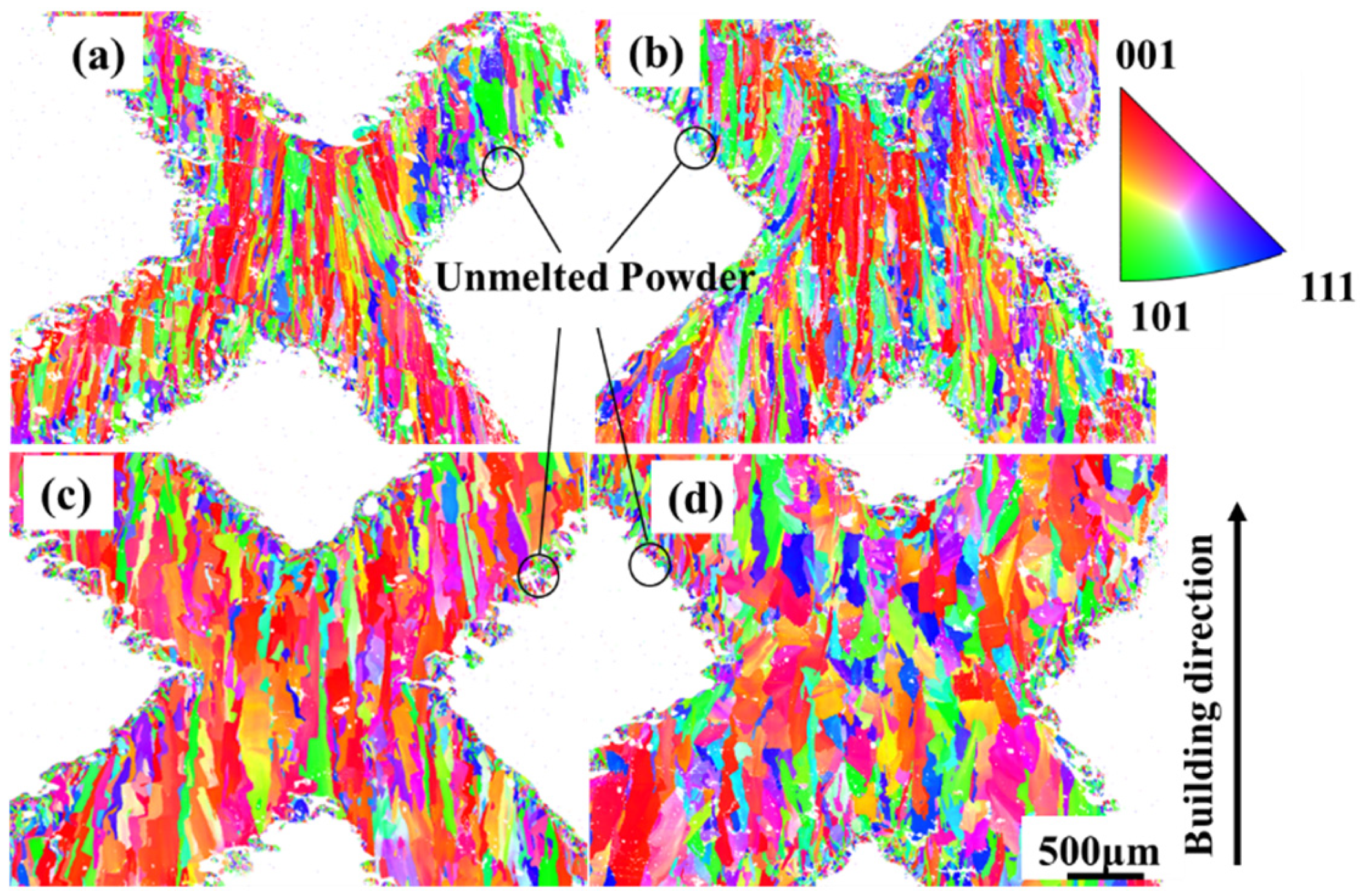
3.2. Microstructure Analysis
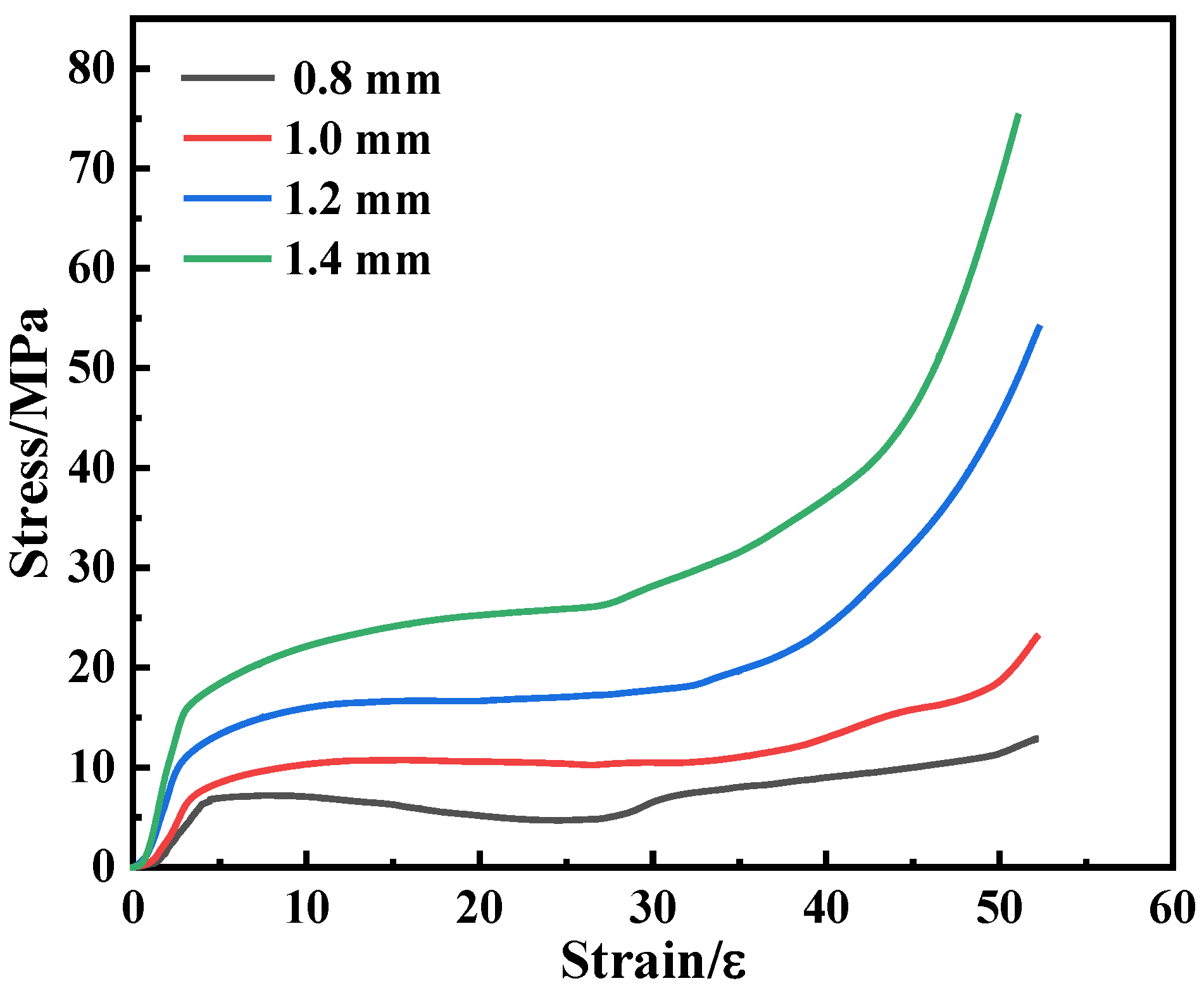
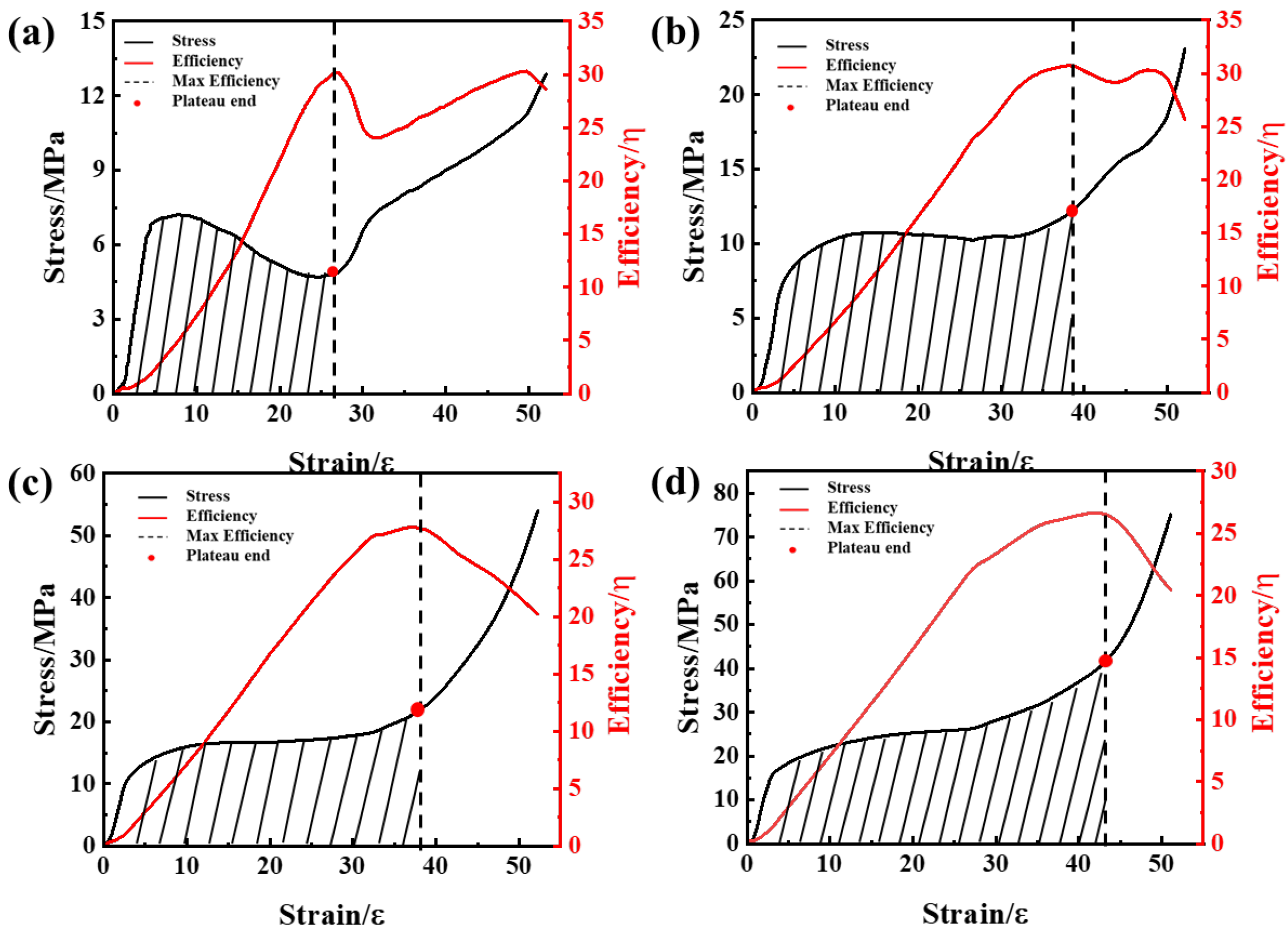
3.3. Compression Properties
3.3.1. Numerical Study
3.3.2. Experimental Study
3.3.3. Effect of the Strut Diameter on the Compression Failure Mode
3.4. Surface Morphology and Compression Properties After Surface Treatment
3.4.1. Surface Morphology
3.4.2. Compression Properties
4. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomas, A.; Fribourg, G.; Blandin, J.-J.; Lhuissier, P.; Dendievel, R.; Martin, G. Effect of the build orientation on mechanical and electrical properties of pure Cu fabricated by E-PBF. Addit. Manuf. 2021, 48, 102393. [Google Scholar] [CrossRef]
- Guschlbauer, R.; Momeni, S.; Osmanlic, F.; Körner, C. Process development of 99.95% pure copper processed via selective electron beam melting and its mechanical and physical properties. Mater. Charact. 2018, 143, 163–170. [Google Scholar] [CrossRef]
- Ledford, C.; Rock, C.; Carriere, P.; Frigola, P.; Gamzina, D.; Horn, T. Characteristics and Processing of Hydrogen-Treated Copper Powders for EB-PBF Additive Manufacturing. Appl. Sci. 2019, 9, 3993. [Google Scholar] [CrossRef]
- Selivanov, V.V.; Silnikov, M.V.; Markov, V.A.; Popov, Y.V.; Pusev, V.I. Using highly porous aluminum alloys and honeycomb structures in spacecraft landing gear. Acta Astronaut. 2021, 180, 105–109. [Google Scholar] [CrossRef]
- Nanda, S.; Gupta, A.; Manthiram, A. Anode-Free Full Cells: A Pathway to High-Energy Density Lithium-Metal Batteries. Adv. Energy Mater. 2021, 11, 2000804. [Google Scholar] [CrossRef]
- Zhang, G.; Li, L.; Zhao, Z.-J.; Wang, T.; Gong, J. Electrochemical Approaches to CO2 Conversion on Copper-Based Catalysts. Acc. Mater. Res. 2023, 4, 212–222. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Design for additive manufacturing. In Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021; pp. 555–607. [Google Scholar]
- Manyika, J.; Chui, M.; Bughin, J.; Dobbs, R.; Bisson, P.; Marrs, A. Disruptive Technologies: Advances That Will Transform Life, Business, and the Global Economy; McKinsey Global Institute: San Francisco, CA, USA, 2013. [Google Scholar]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Development of additive manufacturing technology. In Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021; pp. 23–51. [Google Scholar]
- Liu, G.; Zhang, X.; Chen, X.; He, Y.; Cheng, L.; Huo, M.; Yin, J.; Hao, F.; Chen, S.; Wang, P.; et al. Additive manufacturing of structural materials. Mater. Sci. Eng. R Rep. 2021, 145, 100596. [Google Scholar] [CrossRef]
- Körner, C. Additive manufacturing of metallic components by selective electron beam melting—A review. Int. Mater. Rev. 2016, 61, 361–377. [Google Scholar] [CrossRef]
- Eiji, H.; Yuji, S.; Tomoki, S.; Koji, T.; Masahiro, T. Development of SLM process using 200 W blue diode laser for pure copper additive manufacturing of high density structure. J. Laser Appl. 2021, 33, 12008. [Google Scholar]
- Surajdinkar, J.; Loucaraphaël, G.; Yannis, K.; Brecht, V.H.; Kim, V. Laser-based powder bed fusion additive manufacturing of pure copper. Addit. Manuf. 2021, 42, 101990. [Google Scholar]
- Colopi, M.; Caprio, L.; Demir, A.; Previtali, B. Selective laser melting of pure Cu with a 1 kW single mode fiber laser. Procedia Cirp 2018, 74, 59–63. [Google Scholar] [CrossRef]
- Shinichiro, M.; Masahiro, T.; Koji, T.; Asano, K.; Asuka, K.; Funada, Y.; Sakon, Y. Metal powder bed fusion additive manufacturing with 100W blue diode laser. In International Congress on Applications of Lasers & Electro-Optics; Laser Institute of America: Orlando, FL, USA, 2017; p. 130. [Google Scholar]
- Singh, A.; Caprio, L.; Previtali, B.; Demir, A.G. Processability of pure Cu by LPBF using a ns-pulsed green fiber laser. Opt. Laser Technol. 2022, 154, 108310. [Google Scholar] [CrossRef]
- Lodes, M.A.; Guschlbauer, R.; Koerner, C. Process development for the manufacturing of 99.94% pure copper via selective electron beam melting. Mater. Lett. 2015, 143, 298–301. [Google Scholar] [CrossRef]
- Megahed, S.; Fischer, F.; Nell, M.; Forsmark, J.; Leonardi, F.; Zhu, L.; Hameyer, K.; Schleifenbaum, J.H. Manufacturing of Pure Copper with Electron Beam Melting and the Effect of Thermal and Abrasive Post-Processing on Microstructure and Electric Conductivity. Materials 2022, 16, 73. [Google Scholar] [CrossRef]
- Frigola, P.; Harrysson, O.L.; Horn, T.; West, H.; Aman, R.; Rigsbee, J.; Ramirez, D.; Murr, L.; Medina, F.; Wicker, R.; et al. Fabricating copper components. Adv. Mater. Process 2014, 172, 20–24. [Google Scholar]
- Ramirez, D.A.; Murr, L.E.; Li, S.; Tian, Y.; Martinez, E.; Martinez, J.; Machado, B.; Gaytan, S.; Medina, F.; Wicker, R. Open-cellular copper structures fabricated by additive manufacturing using electron beam melting. Mater. Sci. Eng. A 2011, 528, 5379–5386. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Design and Characterization of Orthotropic Re-Entrant Auxetic Structures Made via EBM Using Ti6Al4V and Pure Copper. In Proceedings of the 2011 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2011. [Google Scholar]
- Xueyan, C.; Huifeng, T. An effective length model for octet lattice. Int. J. Mech. Sci. 2018, 140, 279–287. [Google Scholar]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Peng, Z.; Deqing, H.; Yongfu, Z.; Zhang, H.; Chen, W. Microstructure and Properties of Hollow Octet Nickel Lattice Materials. Materials 2022, 15, 8417. [Google Scholar] [CrossRef]
- O’Masta, M.R.; Dong, L.; St-Pierre, L.; Wadley, H.; Deshpande, V.S. The fracture toughness of octet-truss lattices. J. Mech. Phys. Solids 2017, 98, 271–289. [Google Scholar] [CrossRef]
- Wang, N.; Meenashisundaram, G.K.; Chang, S.; Fuh, J.Y.H.; Dheen, S.T.; Kumar, A.S. A comparative investigation on the mechanical properties and cytotoxicity of Cubic, Octet, and TPMS gyroid structures fabricated by selective laser melting of stainless steel 316L. J. Mech. Behav. Biomed. Mater. 2022, 129, 105151. [Google Scholar] [CrossRef] [PubMed]
- ASTM B170-99(2020); Standard Specification for Oxygen-Free Electrolytic Copper—Refinery Shapes. ASTM International: West Conshohocken, PA, USA, 2020.
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Manuela, G.; Luca, I. A literature review of powder-based electron beam melting focusing on numerical simulations. Addit. Manuf. 2018, 19, 1–20. [Google Scholar]
- Wendy, G.; Julia, G. Ultra-strong architected Cu meso-lattices. Extrem. Mech. Lett. 2015, 2, 7–14. [Google Scholar] [CrossRef]
- Shoudao, Q.; Zesheng, Y.; Ruicong, G.; Yao, J.; Jing Tao, W. Fracture toughness anisotropy of ultrafine-grained pure copper processed by equal channel angular pressing. Mater. Sci. Eng. A 2020, 782, 139260. [Google Scholar]
- ISO 13314:2011; Mechanical testing of metals-Ductility testing-Compression test for porous and cellular metals. ISO International Organization for Standardization: Geneva, Switzerland, 2011.
- Sharma, D.; Hiremath, S.S. Bio-inspired repeatable lattice structures for energy absorption: Experimental and finite element study. Compos. Struct. 2022, 283, 115102. [Google Scholar] [CrossRef]
- Jianhu, S.; Guoxing, L.; Dong, R. Compressive behaviour of closed-cell aluminium foams at high strain rates. Compos. Part B Eng. 2010, 41, 678–685. [Google Scholar]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical response of Ti–6Al–4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
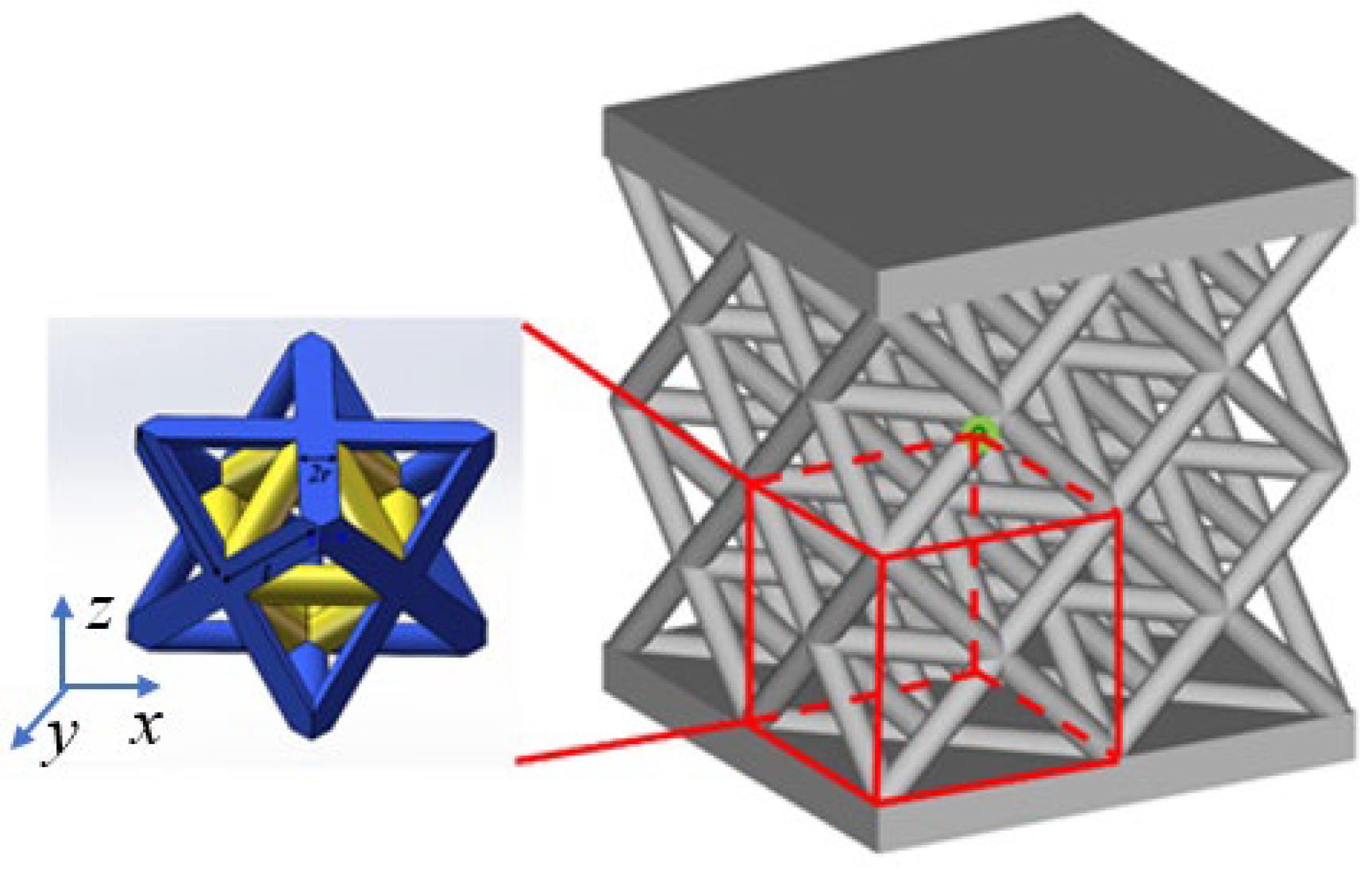



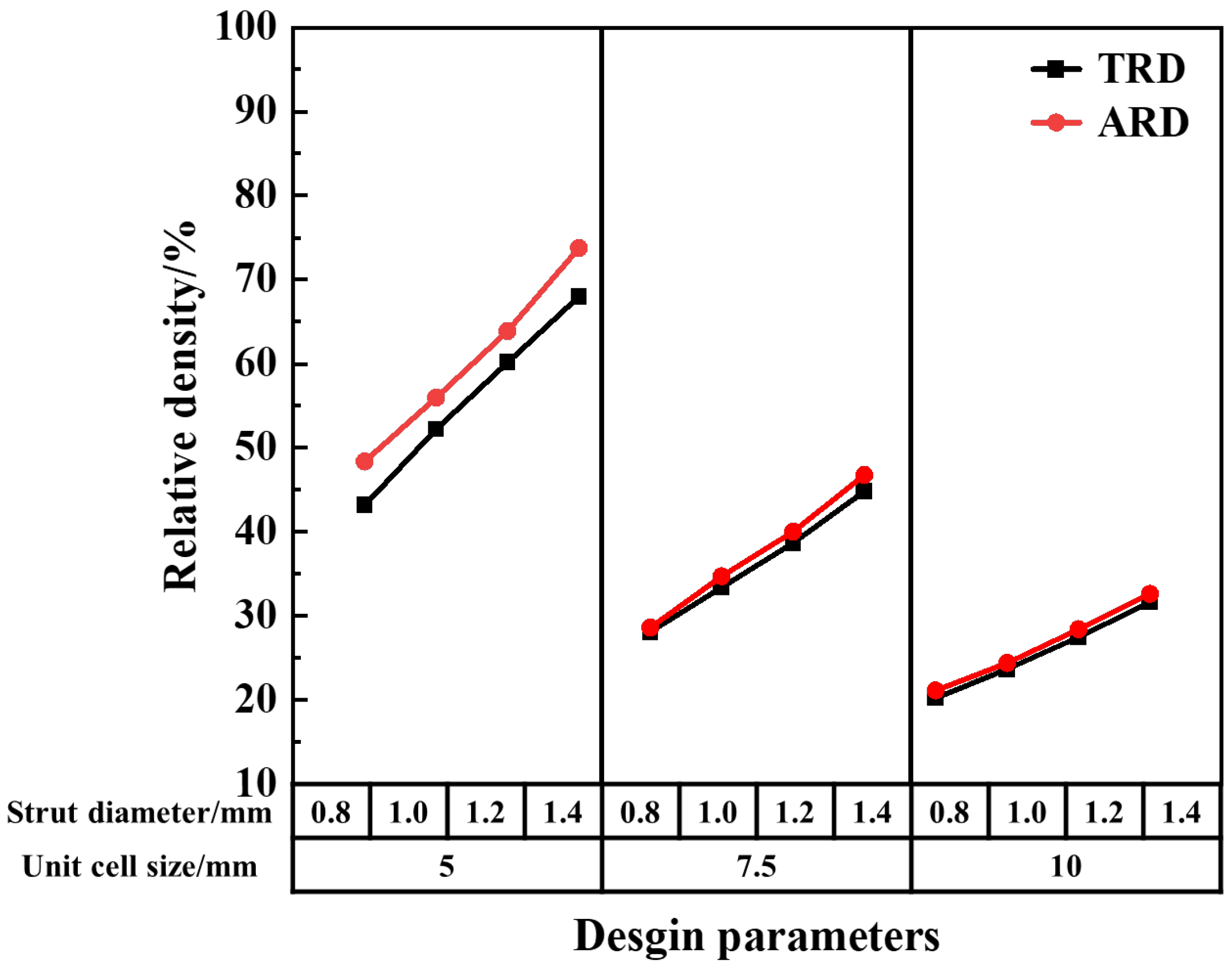
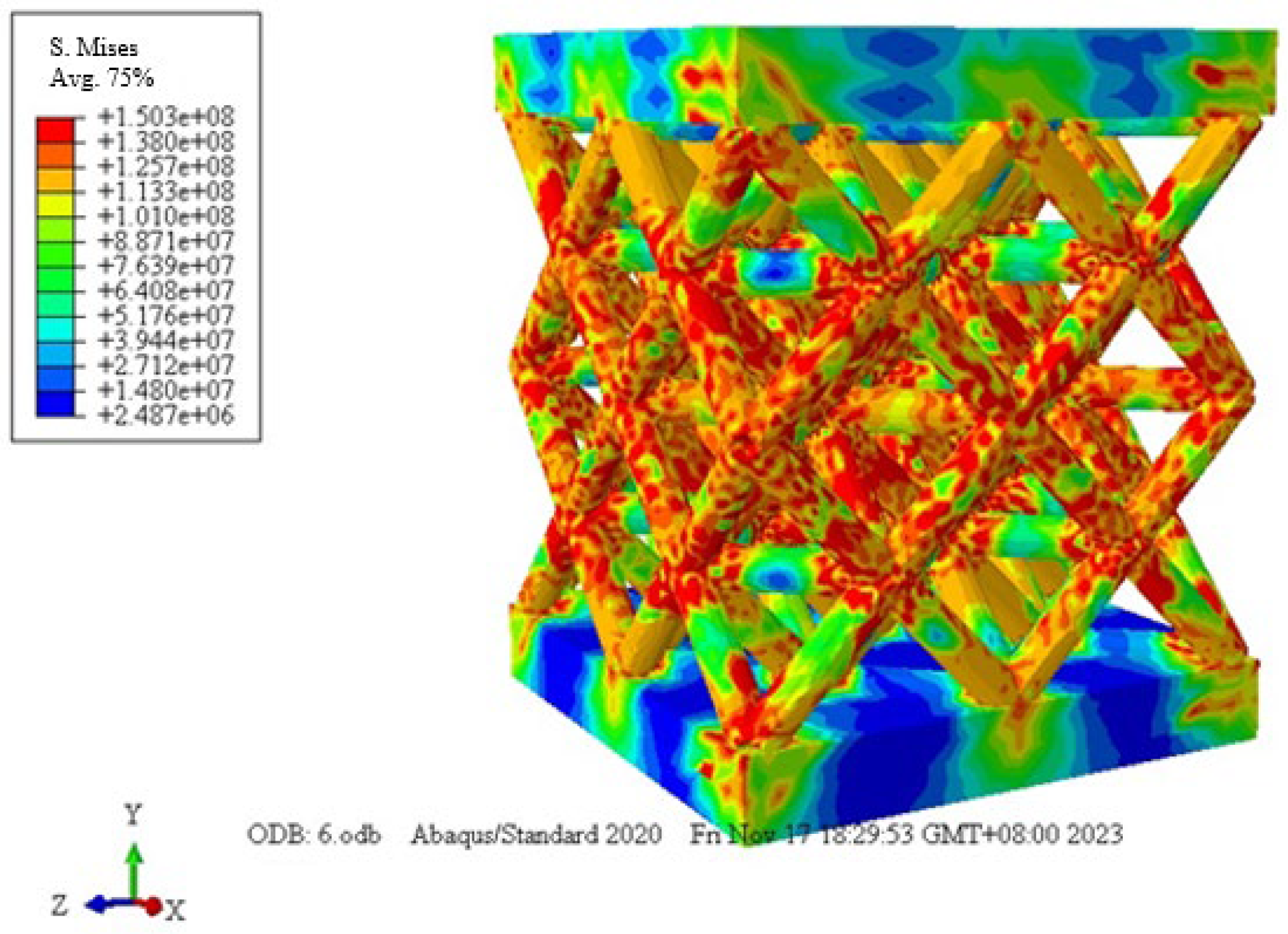
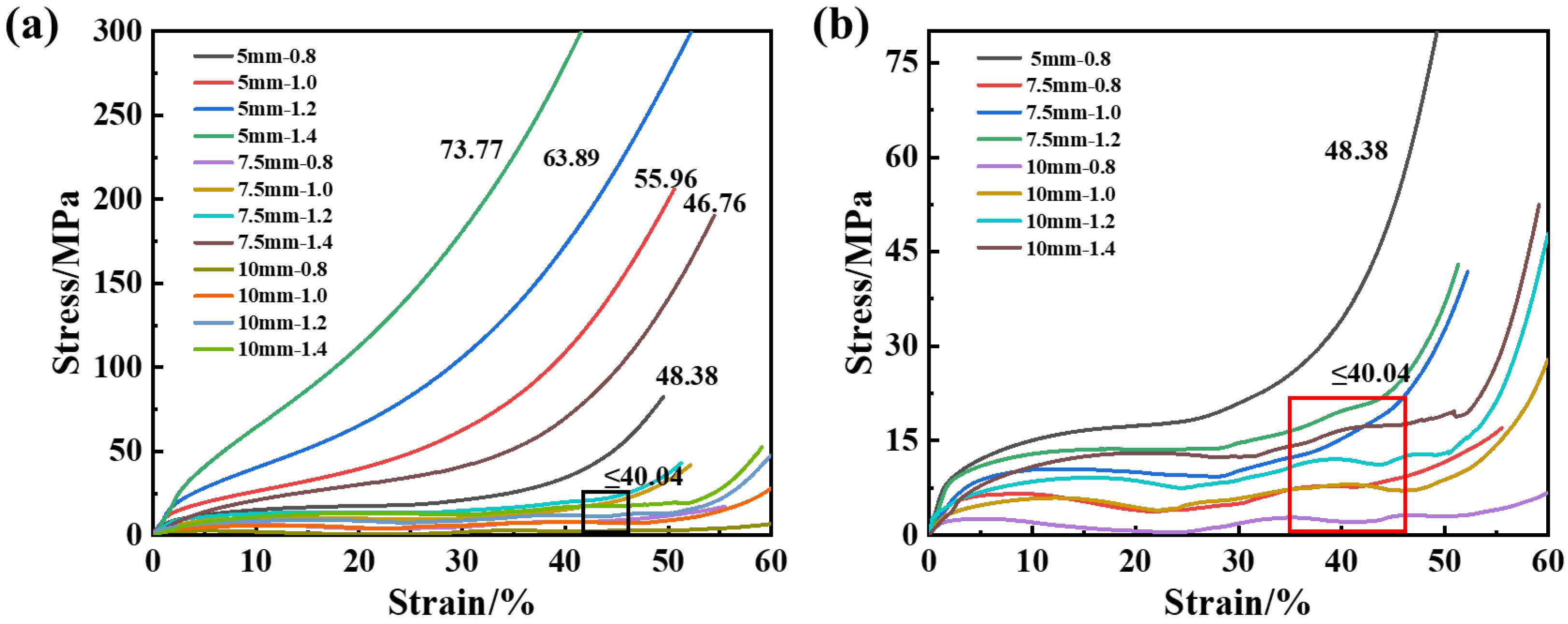
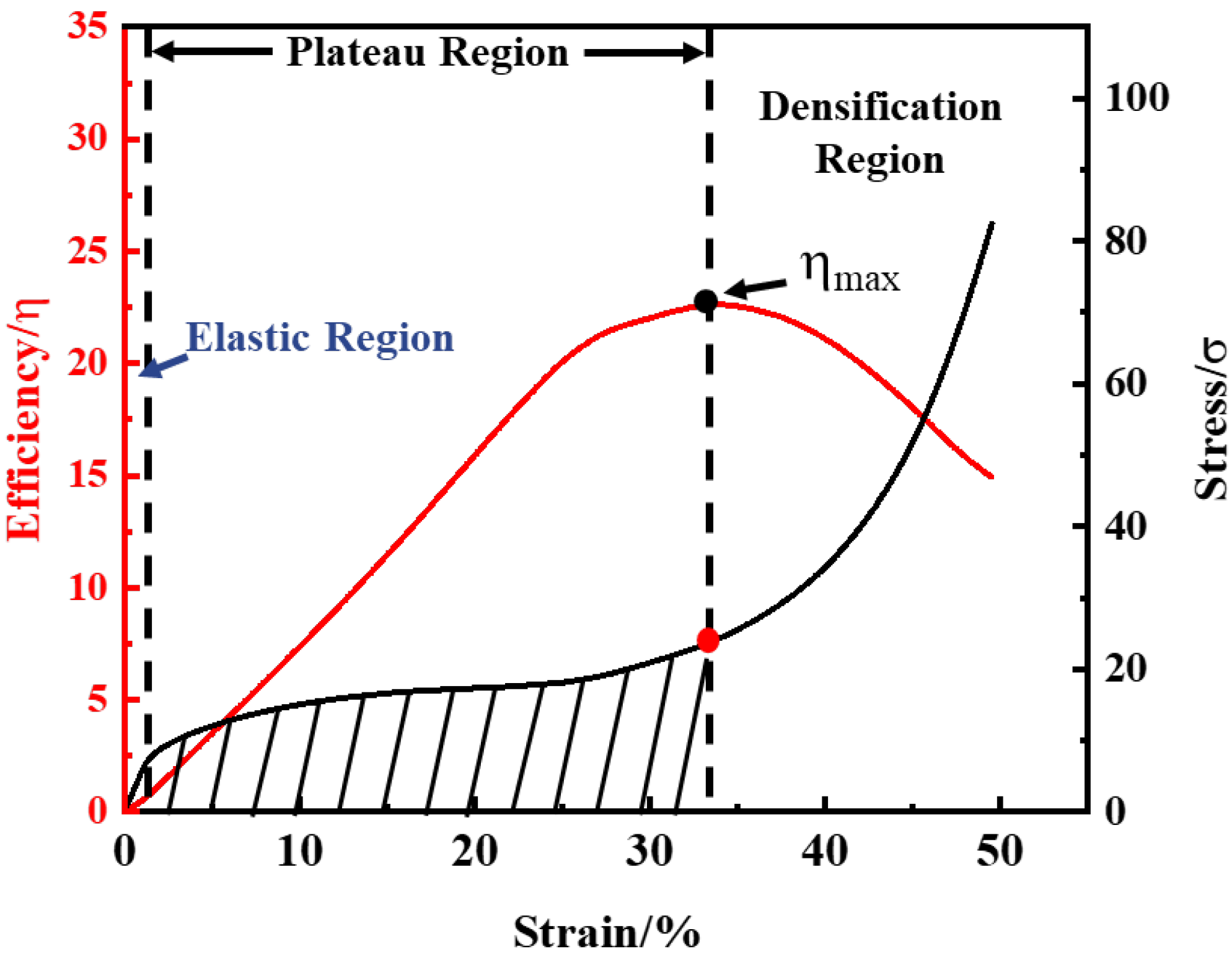

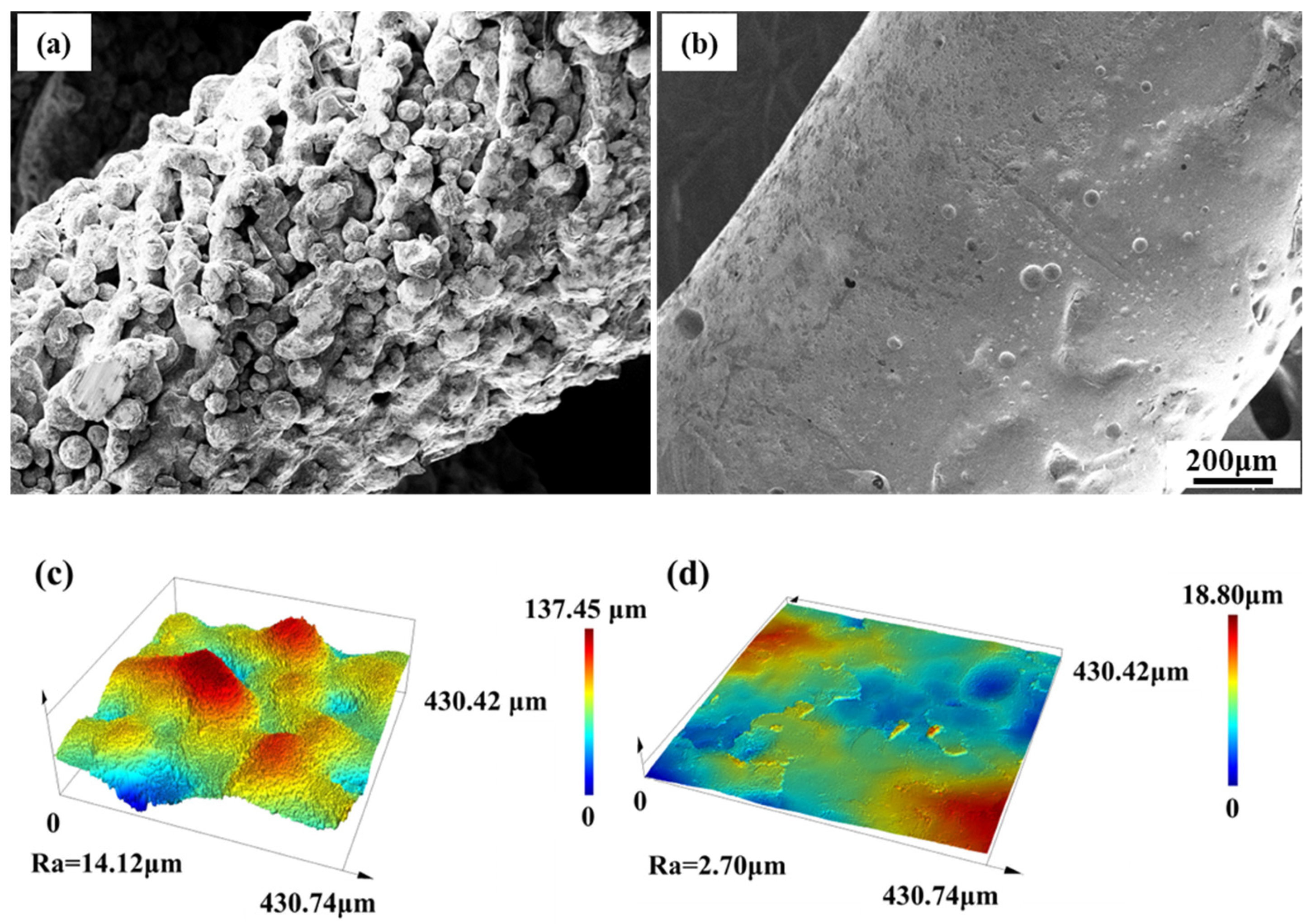

| Samples a–b | Cell Size, mm | Strut Length, mm | Strut Diameter, mm | Length–Diameter Ratio, % | Designed Relative Density, % |
|---|---|---|---|---|---|
| 5–0.8 | 5 | 3.54 | 0.8 | 4.42 | 43.19 |
| 5–1.0 | 1.0 | 3.54 | 52.23 | ||
| 5–1.2 | 1.2 | 2.95 | 60.25 | ||
| 5–1.4 | 1.4 | 2.53 | 68.21 | ||
| 7.5–0.8 | 7.5 | 5.30 | 0.8 | 6.63 | 28.13 |
| 7.5–1.0 | 1.0 | 5.30 | 33.40 | ||
| 7.5–1.2 | 1.2 | 4.42 | 38.69 | ||
| 7.5–1.4 | 1.4 | 3.79 | 44.84 | ||
| 10–0.8 | 10 | 7.07 | 0.8 | 8.84 | 20.25 |
| 10–1.0 | 1.0 | 7.07 | 23.70 | ||
| 10–1.2 | 1.2 | 5.89 | 27.50 | ||
| 10–1.4 | 1.4 | 5.05 | 31.65 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Accelerating voltage | 60 kV | Hatch distance | 100 μm |
| Scanning strategy | Rotate 90° between layers | Layer thickness | 50 μm |
| Atmosphere | He | Substrate temperature | 300 °C |
| Electric current | 12.5 mA | Spot diameter | 200 μm |
| Samples | Test Strut Length, mm | Test Strut Diameter, mm | Designed Length–Diameter Ratio | Test Length–Diameter Ratio | Error |
|---|---|---|---|---|---|
| 5–0.8 | 3.56 ± 0.09 | 0.94 ± 0.01 | 4.42 | 3.79 ± 0.02 | 0.63 |
| 5–1.0 | 3.57 ± 0.03 | 1.16 ± 0.02 | 3.54 | 3.08 ± 0.06 | 0.46 |
| 5–1.2 | 3.59 ± 0.03 | 1.43 ± 0.03 | 2.95 | 2.51 ± 0.05 | 0.44 |
| 5–1.4 | 3.61 ± 0.02 | 1.63 ± 0.03 | 2.53 | 2.21 ± 0.04 | 0.32 |
| 7.5–0.8 | 5.43 ± 0.04 | 0.89 ± 0.08 | 6.63 | 6.10 ± 0.35 | 0.53 |
| 7.5–1.0 | 5.42 ± 0.01 | 1.13 ± 0.01 | 5.30 | 4.80 ± 0.03 | 0.50 |
| 7.5–1.2 | 5.44 ± 0.02 | 1.36 ± 0.01 | 4.42 | 4.00 ± 0.03 | 0.42 |
| 7.5–1.4 | 5.50 ± 0.01 | 1.57 ± 0.02 | 3.79 | 3.50 ± 0.03 | 0.29 |
| 10–0.8 | 7.20 ± 0.01 | 0.87 ± 0.03 | 8.84 | 8.28 ± 0.18 | 0.56 |
| 10–1.0 | 7.24 ± 0.01 | 1.10 ± 0.02 | 7.07 | 6.58 ± 0.09 | 0.49 |
| 10–1.2 | 7.26 ± 0.01 | 1.32 ± 0.01 | 5.89 | 5.50 ± 0.03 | 0.39 |
| 10–1.4 | 7.27 ± 0.03 | 1.52 ± 0.02 | 5.05 | 4.78 ± 0.03 | 0.27 |
| Samples | Relative Density, % | Compressive Strength, MPa | Densification | |||
|---|---|---|---|---|---|---|
| Strain, % | Stress, MPa | EA, MJ/m3 | η, % | |||
| 5–0.8 | 48.38 ± 0.16 | 16.90 ± 0.09 | 33.75 ± 0.12 | 25.83 ± 0.12 | 5.71 ± 0.16 | 22.64 ± 0.10 |
| 5–1.0 | 55.96 ± 0.08 | 40.59 ± 0.17 | 36.74 ± 0.25 | 96.71 ± 0.06 | 15.00 ± 0.28 | 16.89 ± 0.47 |
| 7.5–0.8 | 28.61 ± 0.27 | 5.54 ± 0.25 | 24.82 ± 0.15 | 4.46 ± 0.04 | 1.27 ± 0.07 | 31.30 ± 0.13 |
| 7.5–1.0 | 34.72 ± 0.20 | 9.93 ± 0.06 | 28.34 ± 0.09 | 9.65 ± 0.14 | 2.64 ± 0.23 | 27.67 ± 0.22 |
| 7.5–1.2 | 40.04 ± 0.10 | 14.59 ± 0.13 | 43.47 ± 0.14 | 21.54 ± 0.32 | 6.18 ± 0.22 | 28.41 ± 0.15 |
| 7.5–1.4 | 46.76 ± 0.08 | 29.68 ± 0.43 | 35.16 ± 0.16 | 53.36 ± 0.13 | 9.72 ± 0.14 | 18.75 ± 0.13 |
| 10–0.8 | 21.16 ± 0.02 | 2.65 ± 0.34 | 23.96 ± 0.19 | 0.53 ± 0.25 | 0.37 ± 0.11 | 75.61 ± 0.12 |
| 10–1.0 | 24.43 ± 0.07 | 5.94 ± 0.11 | 47.03 ± 0.10 | 7.64 ± 0.13 | 2.71 ± 0.11 | 37.42 ± 0.08 |
| 10–1.2 | 28.44 ± 0.11 | 9.36 ± 0.19 | 50.33 ± 0.16 | 13.99 ± 0.23 | 4.69 ± 0.07 | 35.47 ± 0.09 |
| 10–1.4 | 32.65 ± 0.10 | 13.67 ± 0.10 | 51.68 ± 0.11 | 19.15 ± 0.21 | 6.72 ± 0.01 | 35.10 ± 0.10 |
| Samples | Relative density, % | Yield strength, MPa | Modulus, GPa |
|---|---|---|---|
| 7.5–0.8 | 23.21 ± 0.06 | 6.35 ± 0.02 | 0.23 ± 0.01 |
| 7.5–1.0 | 29.15 ± 0.16 | 7.36 ± 0.04 | 0.31 ± 0.01 |
| 7.5–1.2 | 36.11 ± 0.06 | 11.55 ± 0.05 | 0.54 ± 0.01 |
| 7.5–1.4 | 45.23 ± 0.08 | 17.34 ± 0.09 | 0.71 ± 0.03 |
| Samples | Compressive Strength, MPa | Densification | |||
|---|---|---|---|---|---|
| Strain, % | Stress, MPa | EA, MJ/m3 | η, % | ||
| 7.5–0.8 | 5.98 ± 0.22 | 26.87 ± 0.21 | 4.84 ± 0.01 | 1.47 ± 0.04 | 30.11 ± 0.13 |
| 7.5–1.0 | 10.41 ± 0.05 | 38.07 ± 0.12 | 12.03 ± 0.10 | 3.69 ± 0.05 | 30.76 ± 0.12 |
| 7.5–1.2 | 18.99 ± 0.09 | 37.26 ± 0.1 | 21.58 ± 0.11 | 5.91 ± 0.14 | 27.73 ± 0.09 |
| 7.5–1.4 | 25.71 ± 0.15 | 42.04 ± 0.02 | 39.75 ± 0.04 | 10.60 ± 0.09 | 26.63 ± 0.11 |
| Samples | Relative Density, % | Compressive Strength, MPa | Theoretical Compressive Strength, MPa |
|---|---|---|---|
| 7.5–0.8 | 23.21 ± 0.06 | 5.98 ± 0.02 | 10.29 ± 0.05 |
| 7.5–1.0 | 29.15 ± 0.16 | 10.41 ± 0.05 | 12.93 ± 0.04 |
| 7.5–1.2 | 36.11 ± 0.06 | 18.99 ± 0.10 | 16.01 ± 0.11 |
| 7.5–1.4 | 45.23 ± 0.08 | 25.71 ± 0.08 | 20.05 ± 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, Z.; Song, F.; Xie, X.; Qi, H.; Ding, C. Investigating the Microstructural Behavior and Energy Absorption of Pure Copper Lattice Structures Fabricated by Selective Electron Beam Melting. Coatings 2025, 15, 348. https://doi.org/10.3390/coatings15030348
Yang X, Zhang Z, Song F, Xie X, Qi H, Ding C. Investigating the Microstructural Behavior and Energy Absorption of Pure Copper Lattice Structures Fabricated by Selective Electron Beam Melting. Coatings. 2025; 15(3):348. https://doi.org/10.3390/coatings15030348
Chicago/Turabian StyleYang, Xin, Zhaoyang Zhang, Fan Song, Xiaodong Xie, Huan Qi, and Chao Ding. 2025. "Investigating the Microstructural Behavior and Energy Absorption of Pure Copper Lattice Structures Fabricated by Selective Electron Beam Melting" Coatings 15, no. 3: 348. https://doi.org/10.3390/coatings15030348
APA StyleYang, X., Zhang, Z., Song, F., Xie, X., Qi, H., & Ding, C. (2025). Investigating the Microstructural Behavior and Energy Absorption of Pure Copper Lattice Structures Fabricated by Selective Electron Beam Melting. Coatings, 15(3), 348. https://doi.org/10.3390/coatings15030348







