Abstract
Engineering equipment is an important material foundation for supporting national defense security and promoting the development of the national economy. Large and complex mechanical equipment has a complex structural composition and a large number of components, with a great deal of connection structures such as bolts and flanges inside. Affected by long-term loading conditions, phenomena like the degradation of contact stiffness will occur at the connection interfaces between components. This, in turn, will affect the dynamic characteristics of the entire system and seriously impact the reliability and performance of the equipment. By combining the microscopic contact mechanism with the cross-scale modeling method, the proposed contact framework can study the contact behavior of the connection interfaces more comprehensively. This paper classifies and summarizes the research status of the asperity contact model from the perspective of geometric modeling, classifies and summarizes the research status of the statistical contact model of rough surfaces according to different height distributions of asperities, and looks ahead to the research directions of the cross-scale model of connection structures in the future.
1. Introduction
Against the backdrop of the continuously accelerating global industrialization process, engineering equipment serves as the core material foundation that underpins the national defense security system and drives the steady development of the national economy, and its significance is self-evident. Various complex engineering equipment is assembled from numerous components, and the connection structure plays a crucial key role in it, enabling the effective combination of components through various different connection forms. As the key area for load and energy transfer, the connection interface continuously bears the effects of dynamic loads, such as vibration and impact, throughout the entire product life cycle. Under the influence of these complex loads, phenomena such as friction, wear, sliding, collision, and separation inevitably occur at the contact parts of the connection interface. These phenomena may lead to a gradual decrease in the pre-tightening force of the interface, which in turn may trigger structural damage or even failure [1,2,3]. Take aerospace engines as an example. In their extreme operating environments with high temperature, high pressure, and high rotational speed, the connected components are constantly under complex dynamic load conditions for a long time, and the problem of connection interface failure occurs frequently, posing a serious threat to the reliability and safety of the engines. Therefore, constructing an accurate contact model of the connection interface and conducting in-depth research on its mechanical behavior is of great theoretical and practical significance for improving the overall performance of engineering equipment and extending its service life.
With the continuous development and in-depth integration of related disciplines such as contact mechanics, tribology, and plasticity mechanics, the nonlinear dynamic order reduction modeling methods for constructing the contact model of the connection interface can be mainly categorized into two types: the top-down modeling approach driven by data and the bottom-up modeling approach based on physical mechanisms [4].
The top-down modeling method is essentially a data-driven modeling strategy based on the framework of the phenomenological mathematical model. This method is based on the dynamic response data of the connection structure at the macroscopic scale, and with the help of nonlinear system identification algorithms, it realizes the construction of the contact model of the connection interface. In engineering scenarios with high requirements for the prediction accuracy of the dynamic behavior of macroscopic structures, such as large bridge structures in the field of civil engineering and offshore platforms in the field of ocean engineering, this method has been widely applied [5].
The bottom-up modeling method, on the other hand, takes the mesoscopic and microscopic scale morphological features of rough surfaces and the contact mechanics mechanism as its theoretical foundation. Starting from the stick-slip friction contact behavior of individual asperities at the mesoscopic and microscopic scales, it uses the cross-scale analysis method based on mathematical statistics theory or fractal theory to accurately describe the nonlinear dynamic characteristics of the connection interface. Compared with the top-down modeling method, the bottom-up method can more realistically reflect the microscopic contact mechanism of the contact interface and more accurately depict the influence of surface roughness on the stick-slip behavior, and most of the parameters in the model have clear physical meanings [6]. In the field of micro-electromechanical systems (MEMS), the research group led by Zheng [7] from the University of Science and Technology of China innovatively proposed the fully self-consistent model (FSCM) by establishing self-consistent equations for the deformation and interaction of rough surfaces. This successfully revealed the influence mechanism of surface roughness on the strength and adsorption mode of the contact interface, providing important theoretical basis and model reference for the study of the mechanical properties of the contact interface in MEMS devices.
Under the bottom-up modeling method system, it mainly includes the fractal contact model and the statistical contact model. The microscopic morphology of the rough contact interface of the connection structure exhibits typical fractal characteristics, such as cross-scale, disorder, irregular randomness, and self-similarity. When the connection interface is observed with infinite magnification, its distribution characteristics at various magnitude levels have significant similarities, and these distribution characteristics are usually manifested as mathematical features such as multi-scale, discontinuity, non-differentiability, and statistical self-affinity [8], providing a solid theoretical basis and data support for constructing the contact model of rough surfaces based on fractal theory. Since the fractal theory was proposed, it has been widely applied and deeply studied in fields such as the analysis of material surface morphology and tribology.
The fractal contact model, based on the fractal geometry theory, has the ability of multi-scale analysis and can effectively conduct cross-scale research on the microscopic morphology of rough surfaces. This model accurately characterizes the features of rough surfaces by introducing fractal parameters, getting rid of the dependence on the sampling length and the resolution of the instrument, and thus ensuring the accuracy and reliability of the model. However, since not all engineering surfaces have typical fractal features, the fractal contact model has certain limitations in practical applications [9], and its universality is relatively poor. At present, the research on the hysteresis behavior of this model under tangential cyclic loads is still in the exploratory stage, and its applicability remains to be further verified.
The statistical contact model is constructed based on geometric and physical parameters, and it has strong universality and wide applicability. This model can deeply explain the stiffness characteristics of the contact interface and the damping energy dissipation mechanism from a microscopic perspective, and it has developed relatively maturely in the research of the field of contact mechanics. The construction process of the statistical contact model of a rough surface usually involves first establishing the asperity contact model and then using the statistical summation theory to expand the asperity contact model to the entire rough surface, thus forming a complete statistical contact model of the rough surface.
Most of the summary literature on the research status of the asperity contact model at the microscopic level only focuses on the contact state of asperities [10,11]. They classify and summarize the models according to the different contact states studied by these models (e.g., the elastic asperity contact model, the plastic asperity contact model, and the elastoplastic contact model), ignoring the fact that the geometric shape and contact form of the model are equally significant in the model establishment. This paper classifies the asperity contact models based on the geometric contact types of the asperity models and different assumptions about the geometric shapes of asperities so as to summarize and discuss the research status and development trends in geometric modeling methods.
Regarding the summary work on the research status of the statistical contact model of rough surfaces at the macroscopic level, this paper classifies and summarizes it according to the different assumptions of the asperity height distribution in the models rather than classifying and summarizing it according to the contact stages like most related review literature.
This paper provides a new perspective for understanding the rough surface contact model, which is helpful for discovering new research directions and problems. It offers researchers an innovative classification framework, which can be combined with other classification methods (e.g., those based on theoretical approaches, application fields, etc.) for comprehensive research. This classification method is intuitive and easy to understand, with a wide coverage, and it is beneficial for identifying new research directions and issues. By implementing this classification method, we can better understand the characteristics and application scope of the rough surface contact model and promote innovation and development in related fields.
2. Research on Asperity Contact Model
On the microscopic level, asperities are randomly distributed on rough surfaces. Therefore, the actual contact between two rough surfaces is actually the mutual contact of asperities on a microscopic scale, which results in the fact that the actual contact area is always smaller than the nominal contact area [12,13]. Hence, the fundamental issue in studying the contact model of rough surfaces is to study the contact problem of asperities on rough surfaces under the action of tangential or normal loads. Establishing an appropriate asperity contact model has become a major research approach.
2.1. Contact Theory and Classification of Asperity Contact Models
2.1.1. Hertz Contact Theory
The deformation law of asperities on a rough surface is known as point—contact or Hertz contact [10]—which is the most important problem in contact mechanics and has attracted the attention of scholars for more than a century. Hertz contact theory is the basis of the classical contact model and analyzes and solves the contact stress of various common elastic bodies theoretically. According to Hertz theory, when two spheres with radii and are in elastic contact, the contact area , contact load , maximum contact pressure , and average contact pressure can be expressed as functions of the deformation amount .
In Equations (1)–(4), the relation is satisfied, where is the relative curvature; satisfies the relation (, , , and are the elastic moduli and Poisson’s ratios of the two contacting bodies, respectively), and is the equivalent elastic modulus.
Hertz contact theory contains some assumptions:
- (1)
- The material of asperities is uniformly distributed and isotropic.
- (2)
- Asperities only undergo small, completely elastic deformations.
- (3)
- Only the stress condition of a single asperity is considered without taking into account the interaction between asperities.
- (4)
- Asperities are only subjected to normal contact loads without considering tangential loads.
Hertz contact theory is a classic theory in elastic contact mechanics. It is aimed at the contact of ideal elastic bodies. Through rigorous elastic mechanics analysis and mathematical derivations, it provides a precise mathematical analysis and physical model description. When the asperities in the asperity contact model are in the elastic contact stage, Hertz contact theory offers theoretical support for analyzing the contact behavior of a single pair of asperities. Subsequently, the contact theory in elastic mechanics has also evolved into contact theories that consider friction (e.g., the Cartwright–Lund theory), contact theories that take into account adhesion and friction (e.g., JKR theory [14], DMT theory, etc.), contact theories for multi-layered media, and dynamic contact theories.
2.1.2. Persson Contact Theory
Persson contact theory studies the contact mechanics problems of randomly rough surfaces, providing theories and methods for the establishment of contact models of randomly rough surfaces. Persson believes that most actual rough surfaces possess statistical self-affine characteristics, that is, the surfaces exhibit similarity at different scales. Even at the atomic scale, the surface topography shows multi-scale, self-affine, and non-stationary fractal features. The Hertz contact theory is applicable to the elastic stage, where the interactions between asperities are not considered, and to the research scale with a relatively small magnification under low load conditions.
At a low magnification, it appears that there is complete contact between many macroscopic rough regions. However, when the magnification increases, roughness at a smaller scale can be detected, and it is observed that only partial contact occurs on these rough peaks. As the magnification increases further, it will be found that the contact between two nominally flat planes occurs on smaller pairs of asperities. This leads to the local load being greater than the yield force of the material, and the asperities will undergo plastic deformation (even though it appears to be in the elastic contact stage macroscopically). Interactions will occur between the contacting asperities, and the contact regions will gradually merge to form larger contact regions. In this situation of high magnification, that is, at a more microscopic scale, the Hertz contact theory may no longer be applicable [15].
The magnification refers to some (arbitrary) chosen reference length scale. This could be, for example, the lateral size of the nominal contact area, in which case
where λ is the shortest wavelength roughness, which can be resolved at magnification ζ. In this case, the stress distribution of the magnified part is defined as
Here, is the stress at the interface calculated when only the surface roughness components with wavevector is included. The angular brackets in (6) stand for ensemble average or, what is in most cases equivalent, average over the surface area,
where A is the area of contact.
From the perspective of elastic contact, in his research, he took into account issues such as the elastic deformation of rough surfaces. His theory is capable of analyzing the influence of factors, such as the surface roughness of contacting objects on the contact mechanical behavior during the elastic stage. In subsequent studies, he also extended the Persson theory to the case of plastic bodies [16]. By comparing the Persson theory with the discrete dislocation plasticity theory, the status and role of the Persson theory in dealing with the plastic contact problems of self-affine surfaces were further clarified. The Persson contact theory is applicable to various fields involving the contact of rough surfaces. Whether at the macroscopic or microscopic scale, as long as it is necessary to analyze the mechanical behavior and characteristics of the contact interface, this theory can play an important role.
2.1.3. Classification of Asperity Contact Models
Figure 1 shows the classification and research content of the asperity contact models in this chapter. It is mainly divided into two major categories according to two different contact forms, namely the flat plate–asperity contact model and the asperity–asperity contact model.
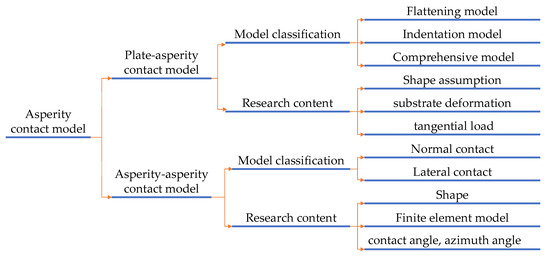
Figure 1.
Classification and research content of asperity contact models.
The flat plate–asperity contact model is extended based on the assumptions in the GW model. This model simplifies the contact form and reduces the computational amount. It is widely applied in specific research contexts. For example, under low load conditions, using this type of model can conveniently study the contact characteristics of asperities.
The asperity–asperity contact model is based on the actual contact situation of rough surfaces. It regards both contact surfaces as rough surfaces. Therefore, at the microscopic level, it studies the contact issue between asperities rather than the contact between asperities and a flat plate. This type of model has a higher complexity and larger computational amount. However, due to its contact form being more in line with the actual contact situation, it has the advantage of more accurate prediction and calculation results.
In the flat–asperity contact model, the contact surface is regarded as the contact between a rough surface and a smooth flat plate. The deformation and contact mechanical characteristics of the asperities under load are analyzed, as shown in Figure 2.
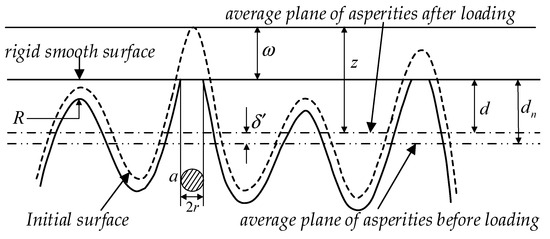
Figure 2.
Flat plate–asperity contact model.
Many models adopt this method to simplify the models and apply the finite element method or a combination of the elastic contact theory and approximate solutions to simulate this kind of contact. This research idea was first put forward by Sinclair and Follansbee [17,18]. Such contact models can be divided into three major categories [10], as shown in Figure 3, namely, the flattening model, the indentation model, and the comprehensive model. In the flattening model, the smooth flat plate is regarded as a rigid plane, and only the asperities undergo deformation. In the indentation model, the asperities are considered to be rigid, and only the smooth flat plate undergoes deformation. In the comprehensive model, both the asperities and the smooth flat plate are considered to be deformable.
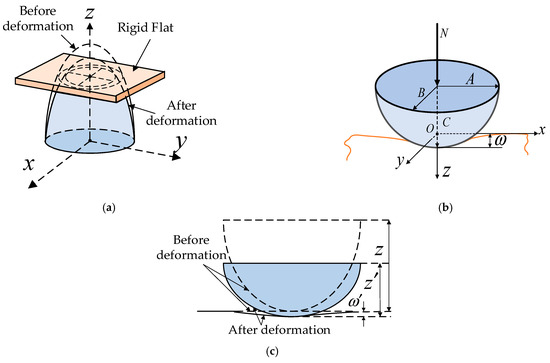
Figure 3.
Three types of elastic flat–asperity contact models: (a) flattening model; (b) indentation model; (c) comprehensive model.
The three types of flat–asperity contact models each have their own applicable scenarios and limitations. The flattening model enables a more detailed analysis of the geometric shape changes and stress distribution patterns of asperities during the contact process. In particular, it provides an intuitive means for studying the influence of geometric parameters such as asperity height and shape on the contact behavior. In situations where the accuracy requirements are not extremely high and the focus is mainly on factors related to the deformation of asperities themselves, a simplified model that only considers the deformation of asperities can quickly conduct theoretical derivations and preliminary estimations. However, in engineering applications that require precise analysis of the interaction between the two contacting surfaces and demand a high level of accuracy for the overall contact performance, the applicability of this model is limited. In some practical situations, for example, when the hardness of asperities is much higher than that of the flat plate material or when the flat plate is relatively thin and more prone to deformation, the indentation model can better reflect the dominant role of the flat plate’s deformation during the contact process, thus being more suitable for such specific actual contact scenarios. However, in most conventional cases of rough surface contact, the deformation of asperities and the flat plate are often interrelated and jointly affect the contact effect. The integrated model can more comprehensively reflect the essence of contact and has a wide range of applicability. It is suitable for contact problems under various combinations of different materials, different surface roughness, and different load conditions. However, this model has a relatively high level of complexity, and it is rather difficult to obtain and calibrate the parameters.
The flat–asperity contact model constitutes a significant part of the research on asperity contact models. It includes aspects such as the study of asperity shapes, the research on contact mechanics considering substrate deformation, and the research on contact mechanics considering tangential loads.
The second research method is to regard both contacting surfaces as rough surfaces. The asperities on the upper and lower surfaces come into contact with each other under the action of force, and both undergo deformation. The contact forms are mainly divided into normal contact and lateral contact, where normal contact can be regarded as a special case of lateral contact, as shown in Figure 4.
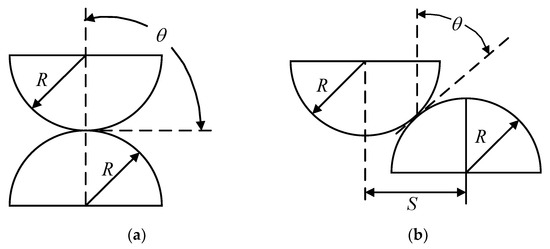
Figure 4.
Contact form of asperity–asperity. (a) normal contact; (b) lateral contact. Reprinted from Ref. [6].
The asperity–asperity contact model focuses on the contact behavior between asperities. It can describe the interaction between rough surfaces in more detail, reflecting the microscopic characteristics during the contact process. This is helpful for a deep understanding of the microscopic physical mechanisms in the contact process, such as the formation and development of contact points. Compared with the flat–asperity contact model, the asperity–asperity contact model can more realistically simulate the contact phenomena of rough surfaces in actual engineering, improving the accuracy and reliability of the model. Its drawback is that since it is necessary to consider multiple factors, such as the geometric shapes, distribution laws, and material properties of asperities, the process of establishing and solving the model is relatively complex, and the calculation cost is also relatively high. With the development of computer technology, the use of finite element analysis methods can effectively solve a series of problems, such as high complexity and large computational amount.
The research content of the asperity–asperity contact model mainly includes aspects such as the study of asperity shapes, the research on the probability distribution functions of contact angles and contact azimuth angles, and the research on finite element models.
2.2. Flat Plate–Asperity Contact Model
During the establishment of the statistical contact model, it is necessary to first establish the asperity contact model. The Hertz theory is the foundation of classical contact mechanics. Hertz established the asperity contact model based on the flat plate–asperity contact assumption and was the first to derive the analytical solution for the elastic contact of curved surfaces. The research on the contact model of asperities under normal and tangential loads aims to describe the contact state between rough contact surfaces more comprehensively and accurately. As such models are widely used in the study of the contact characteristics of rough surfaces, it is of great significance to optimize the models reasonably.
In the research on the flat–asperity contact model, scholars carry out innovative research in different directions according to various requirements and research focuses. This involves optimizing assumptions regarding aspects such as the shape of asperities, whether the substrate undergoes deformation, and whether tangential loads are taken into account.
2.2.1. Innovation in the Shape of Asperities
In practical engineering, rough surfaces are generally highly anisotropic, that is, the surfaces under consideration have obvious textures in certain directions. For such surfaces, the major axis direction of asperities needs to be consistent with the texture direction. Therefore, scholars have begun to assume that the shape of asperities is a non-single-curvature shape for modeling, such as an ellipsoidal shape. Bush et al. [19] chose highly eccentric ellipsoids with the major axis along the texture direction to represent asperities and established the BGT model. They analyzed the conditions for the transition from the elastic contact stage to the plastic contact stage. However, the deformation state of asperities was only limited to the elastic contact stage in their research. So and Liu [20] combined the maximum principal stress yield criterion to analyze the elastoplastic contact between rough surfaces and planes and extended the ellipsoidal asperity model to the elastoplastic and plastic deformation stages. Greenwood [21] verified that most of the asperity peaks were only slightly elliptical by extending Nayak’s theory. By using the approximate solution of elliptical Hertz contact based on the geometric mean value of the peak curvature, a new ellipsoidal contact model on rough surfaces was established. This model can reproduce the results of the BGT model in a simpler and more accurate manner.
Horng et al. [22] introduced the concept of the ratio of the radius in the principal direction to that in the secondary direction of asperities, extended the CEB model [23] to ellipsoidal asperities, and established the Horng–Jeng Haur (JH) model. Similar to the CEB model, this model fails to take into account the elastoplastic transition stage. The Jeng–Wang (JW) contact model of elastoplastic ellipsoidal asperities established by Jeng and Wang [24] has improved the deficiencies of the JH model and the ZMC model [25] established by Zhao, Maietta, and Chang. Buczkowski et al. [26] combined the BGT model, the CEB model, and the ZMC model to establish a new statistical model for rough surfaces.
Chung [27] assumed that asperities were in the shape of ellipsoids and established a finite element model. This model successfully simulated the contact pressure distribution and the evolution of the plastic region of ellipsoids with different ellipticities under different deformation amounts. For the first time, it conducted a detailed analysis of the elastic–plastic deformation behavior between ellipsoids with different ellipticities and a rigid flat plate, filling the gap in this field. Jackson et al. [28] studied the variation of the friction coefficient of a contact surface with elliptical asperities under different parameters. It was found that the friction coefficient increased with the increase of the plastic index but decreased with the increase of the effective radius ratio.
Some scholars believe it is more in line with the actual situation to assume the asperities shape as the sinusoidal shape. It seems logical to use the sinusoidal contact model instead of the spherical contact model [24,29]. Their measurement and research on rough surfaces found that sinusoidal contact can simulate the asperity contact better than hemispherical contact. Jackson et al. [30] found through research that for light-load contact, the behavior of sinusoidal contact may be very similar to that of a sphere. However, as the load increases and the contact approaches completion, the behavior of the sinusoidal curved surface is quite different from that of the spherical surface.
By assuming the shape of asperities to be a half-period cosine curve of revolution, Qi et al. [31] established a contact model that can effectively simulate the asperities on ground surfaces. Shang et al. [32] proposed a method of using a parabolic body of revolution to equivalent asperities and derived the calculation equation for the normal contact stiffness of rough surfaces in the elastic contact stage. Ling et al. [33], based on the rough surface topography measurement experiments, put forward a method of using a parabolic body of revolution to equivalent asperities, established the analytical relationship between the contact radius of asperities and the contact deformation amount, and, according to the geometric model, rederived the contact expressions of a single asperity in the three deformation stages of elasticity, elastoplasticity, and full plasticity.
Tiwari et al. [34] assumed the shape of asperities to be cylinders and mainly explored the influence of surface roughness on the nominal contact pressure when a rigid cylinder is in contact with an elastic half-space. A new parameter was defined to characterize the influence of surface roughness on the contact pressure distribution. Through this parameter, it is possible to clearly distinguish the types of contact pressure distributions under different roughness conditions, further subdivide the types of contact pressure distributions, deepen the understanding of the contact problem between a rigid cylinder and an elastic half-space, and also provide important theoretical basis and technical support for relevant engineering applications.
Chen et al. [35] improved the assumption of a smooth sphere to that of a rough sphere based on the assumptions of the GW model and established an elastoplastic rough sphere contact model for modeling. Through finite element simulation, they derived an explicit expression for the contact pressure in a smooth elastoplastic sphere. According to this expression, they estimated the calculation formula for the local load of a rough sphere and derived the total contact area through integration. They also studied issues, such as the influencing factors of the load-contact area in the elastoplastic rough sphere contact model. This model breaks through the limitation in the assumptions of traditional contact models, which design asperities as smooth, and is more in line with the actual situation. It provides new ideas and research directions for the study of rough surface contact models.
Table 1 comprehensively presents the diverse research achievements in the field of asperity contact models, covering a variety of asperity shape assumptions, demonstrating the efforts of scholars to improve the contact models from different perspectives. In the future, with the development of materials science and engineering technology, there will be more innovations in the shape assumptions of asperity contact models. In addition to continuing to explore the combination or deformation of existing shapes, such as the composite elliptical–parabolic shape, to more accurately simulate the microstructures of complex surfaces; it may also combine advanced surface characterization techniques to construct highly specific asperity shape models based on the actually measured surface profile data, breaking the limitations of traditional regular shapes. At the same time, the models will develop in the direction of greater refinement and multi-scale coupling, comprehensively considering the influence of various factors on contact behavior. With the progress of computer technology, the combination of numerical simulation and theoretical models will also be closer to verify and optimize the models, improve their prediction accuracy under complex working conditions, and further expand their applications in emerging fields.

Table 1.
Information sheet of asperity contact model.
2.2.2. Substrate Deformation
Traditional contact models often neglect the substrate deformation or the interaction among asperities, resulting in a relatively low prediction accuracy for contact characteristics [36]. Since asperities are located on a continuous substrate, the deformation of one asperity will change the height of adjacent asperities through the deformation of the substrate, thus affecting the contact situation of the entire joint interface, as shown in Figure 5. When the ratio of the actual contact area to the nominal contact area of two rough surfaces is small, the influence of asperity interaction can be neglected. For example, the Greenwood–Williamson [37] (GW) model provides relatively good prediction results for contacts under low-load conditions [38,39]. However, when the contact load is relatively large, the distance between asperities will gradually decrease, and adjacent asperities will interact with each other and thus affect the contact characteristics of the contact interface. Therefore, the study of the contact characteristics of the contact interface should also take into account the asperity interaction and the deformation of the substrate.
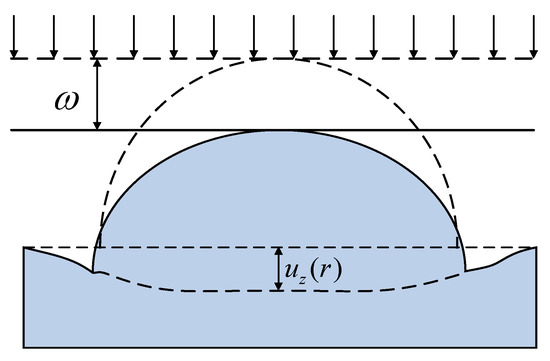
Figure 5.
Substrate deformation of a single asperity.
Ling et al. [40] assumed the asperity contact model to be the contact between a smooth flat plate and a rough flat plate. Under the condition of considering the interactions between asperities, they improved the interpolation interval of the Hermite polynomial function, enabling the contact stiffness curve of the rough peaks to smoothly transition among the elastic, elastoplastic, and fully plastic stages. After extending the microscopic contact model to the entire contact surface using statistical principles, the simulation results showed that surface roughness is the main factor affecting contact stiffness, and the influence of the interactions between rough peaks cannot be ignored.
Zhao and Chang [41], based on the ZMC model, combined the Saint–Venant’s principle and Love’s formula with the deformation amount of asperities for the first time. They assumed that the area at the bottom of each asperity was proportional to the load it bore and established a substrate deformation model, namely the ZC model. Jeng and Peng [42], also based on the Saint–Venant’s principle and Love’s formula, analyzed the influence of asperity interaction on the average spacing and contact area between rough surfaces, where the asperity height had a non-Gaussian distribution. Ciavarella et al. [43] improved the GW theory. They regarded the contact pressure as being uniformly distributed on the nominal contact area. This modification was equivalent to adding a parameter proportional to the nominal pressure to the effective separation distance of the average plane, resulting in the reduction of the true contact area and the total load at a given separation distance. The improved GW theory was able to predict the numerical contact response at intermediate load levels.
Vakis [44] combined the total substrate deformation generated by the interaction with the KE model and proposed a new substrate deformation model. Tang et al. [45] introduced the substrate deformation of asperities themselves and the interaction among adjacent asperities to predict the closure behavior of rock joints under compressive loads. Song et al. [46] utilized the deformation response of three-dimensional single asperities, took into account the interaction effect of asperities through substrate deformation, and conducted statistical calculations on the contact characteristics of rough surfaces. Zhang Lihua [47] explored the relationship between the total substrate deformation, with and without considering the interaction among asperities, and introduced the surface asperity area density function to establish a rough surface contact model that takes into account the interaction among asperities. Li et al. [48] considered the elastic deformation of surface asperities and the nonlinear deformation effect of the substrate and proposed a modified elastic contact stiffness model. They mainly studied the influence of substrate deformation on contact stiffness in rough surface contact. This model shows higher adaptability than the traditional Hertz model in dealing with high-stress conditions and can provide more accurate predictions of contact stiffness. Its main drawback lies in its high sensitivity to material parameters, requiring precise parameter measurements during the experiment.
Wen et al. [49] reconstructed the asperities into ellipsoids and segmented the rough surface based on the watershed algorithm. By introducing the local contact pressure and the iterative correction method and taking into account the substrate deformation and the interactions between asperities, they established a contact model that can more accurately describe the complex morphological features. This model shows that whether to consider the interactions between asperities has a significant impact on contact stiffness. When studying the contact stiffness of rough surfaces, the interactions between asperities should be taken into account.
Therefore, under higher load conditions, the deformation of the substrate should be given more consideration. With the in-depth development of research and the advancement of computing power, in order to make the calculation and prediction results of the model more accurate, there is also a growing trend of taking into account the substrate deformation condition, which is gradually extending toward the direction of lower loads.
2.2.3. Research on Contact Mechanics Under Tangential Loads
During the normal operation of the equipment, the joint interface will be simultaneously subjected to the combined action of normal and tangential loads. As a result, complex behaviors, such as friction, slip, and sliding, will occur at the joint interface, and energy dissipation will be generated at the contact interface, which also has an impact on contact stiffness and contact damping. Therefore, when studying the contact behavior of joint interfaces, the tangential load is also an influencing factor that cannot be ignored. Among them, the exploration of the tangential load-displacement relationship of joint interfaces has always been regarded as one of the rather challenging problems [50,51,52,53].
Figure 6a shows the contact between a single asperity and a rigid smooth flat plate without tangential force. Figure 6b shows contact that considers tangential force. Many experimental results indicate [54] that the tangential force will cause the contact area to become larger compared to the contact area without tangential force.
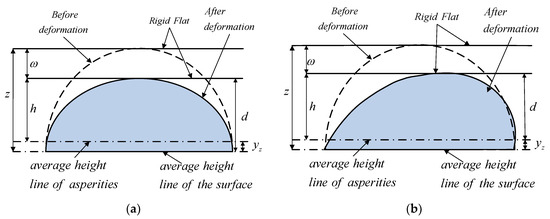
Figure 6.
Deformation of asperities under loads in different directions. (a) Deformation of asperities under normal load; (b) deformation of asperities under tangential load.
Mindlin [55] was the first to theoretically explore the slip-sliding behavior of two asperities under the combined action of normal and tangential loads. Mindlin assumed that asperities only underwent elastic deformation, the contact satisfied Coulomb’s friction law, and the friction coefficient was a constant value. He then derived the nonlinear relationship between the interfacial tangential load and the tangential displacement. According to Mindlin’s theory, when the tangential load borne by the contact interface is less than the critical force for macroscopic sliding, there is no sliding in the central area of the contact, and only microscopic slip occurs at the edge of the contact area. When the tangential load increases, the area of the slip zone also increases until the tangential load reaches the critical value for macroscopic sliding, at which point the entire contact interface will experience macroscopic sliding.
As shown in Figure 7, Mindlin’s theory presents the distribution laws of normal and tangential forces on the elastic contact interface, as well as the relationship between the tangential load and the relative displacement as follows:
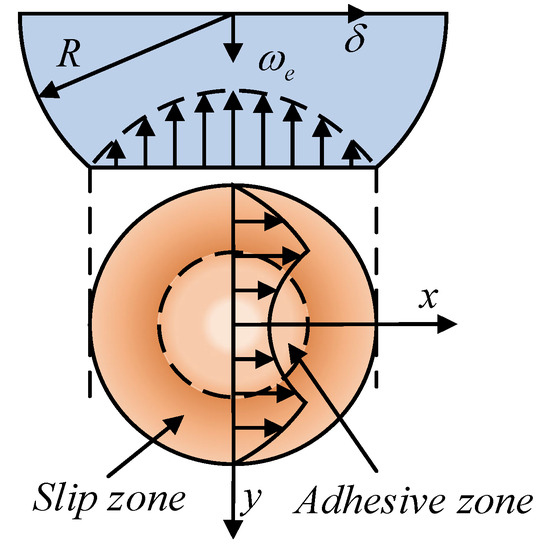
Figure 7.
Contact force in the fully elastic stage.
In the formula, is the friction coefficient; is the tangential relative displacement; is the tangential load acting on the elastic asperity; is the normal load acting on the elastic asperity; is the tangential relative displacement when the elastic asperity undergoes macroscopic sliding; is the radius of the actual contact area of the asperity; is the equivalent shear modulus, where , is the shear modulus of the asperity material, and is the Poisson’s ratio of the asperity material.
Johnson’s experimental results [56] show that under large loads, the asperities undergo plastic deformation, which leads to the final fatigue and fretting of the surface in the high-stress annulus region. The energy consumed is quantitatively consistent with the results calculated by Mindlin, providing considerable support for Mindlin’s theoretical analysis.
Kogut [57] analyzed a sphere that underwent completely elastic and completely plastic deformations under the load of a rigid plane by using the finite element analysis method. He defined the “internal static friction coefficient” and gave simple analytical expressions for both elastic and plastic cases. Dong et al. [58] introduced a new load-displacement relationship for plastically contacted asperities and drew on the probabilistic and statistical analysis method of the GW model to derive the relationship between the tangential load and displacement of the entire rough surface. Gang et al. [59] combined the two modeling methods of rough surface contact models, namely the constitutive model and the phenomenological model, and proposed a rough surface tangential contact model based on the KE normal contact theory and the Iwan model. By considering the constitutive equation for tangential motion occurring between rough surfaces and comparing it with the Iwan model, they derived a probability distribution function of the critical slip force of friction plates based on measurable physical parameters.
Under the action of tangential loads, due to the factor of tangential friction, the contact shape is different from that under a single normal load, and the contact area also changes at the same time. In practical engineering applications, joint interfaces usually transmit both normal and tangential loads simultaneously. Therefore, when establishing a joint interface contact model that is more in line with the actual situation according to the actual working conditions of the joint interface, the coupling effect of normal and tangential loads should be taken into account.
2.3. Asperity–Asperity Contact Model
Adopting the flat plate–asperity contact assumption method in the Hertz contact theory greatly simplifies the complexity of the model and reduces the amount of calculation. However, some important parameters are also ignored in this way, and there are deviations between the established model and the actual contact situation [60]. In order to be more in line with the real contact behavior of rough surfaces, some scholars have chosen to use the asperity–asperity contact assumption to conduct research on the asperity contact model, as shown in Figure 4.
2.3.1. Improvements in the Shape of Asperities
The contact behavior of asperity–asperity can be classified into normal contact and lateral contact. Normal contact means that the tops of two asperities are in contact with each other. Lateral contact is the form of contact among the vast majority of asperities, and normal contact can also be regarded as a special case of lateral contact. In the flat plate–asperity model, scholars have made innovations and improvements in the shape of asperities. In the asperity–asperity model, scholars have also explored the contact behaviors of asperities with different shapes.
Jager [61] studied the lateral contact behavior between two spheres and proposed a calculation method for estimating the energy consumption due to friction. However, this model only considered the elastic deformation stage of asperities and ignored the elastoplastic and plastic stages. Faulkner and Arnell [62] assumed the shapes of asperities to be cylinders and spheres, respectively, and established finite element models to explore the influence of roughness on the overall friction coefficient. It was found that the friction coefficient of a rough surface with spherical asperities was smaller than that with cylindrical asperities.
Kogut and Etsion [57,63] modified the deformation stage of asperities based on the ZMC model by using the finite element method. They removed the limitation of volume conservation in the asperity deformation stage and divided the elastoplastic stage of asperities into the first elastoplastic and the second elastoplastic, enabling all the deformation stages to be connected more smoothly into a whole. Thus, they obtained contact models for elastic, elastoplastic, and fully plastic deformations and established the KE model.
Sepehri et al. [64] established the Sepehri–Farhang (SF) contact model. Based on the asperity constitutive relationship derived from the KE model, they deduced the governing equations for asperity contact and developed approximate equations in closed form for contact force components and contact area. Li et al. [65] combined the KE model and the SF model to establish an oblique impact contact model for ellipsoidal asperities on double rough surfaces. They discussed the contact behavior during the elastoplastic deformation stage of a single asperity and applied it to the research on predicting the contact resistance of electrical components.
Jamshidi et al. [66] established an oblique contact model for spherical asperities on double rough surfaces. They studied the frictional contact hysteresis behavior between two planes. By analyzing the partial slip and total slip on rough surfaces, they modified Mindlin’s spherical elastic contact solution and developed an improved contact model using the double rough surface contact theory. However, this model only took the elastic deformation stage into consideration.
2.3.2. Contact Angle and Contact Azimuth Angle
In the process of expanding the asperity–asperity contact model to the rough surface contact model by using statistical methods, the research on key parameters, such as the contact angle between asperities, the contact azimuth angle, and the height distribution function of asperities, is of great significance. When two rough surfaces are in contact, lateral contact is mainly affected by the contact angle, and the uniformity of the contact azimuth angle determines the degree of interfacial anisotropy, while the height distribution of asperities determines the roughness of the surface. Therefore, in the process of establishing the rough surface contact model, how to select the distribution functions of the contact angle, the contact azimuth angle, and the height of asperities among asperities has become one of the research directions that scholars pay attention to.
Gorbatikh [60], based on the lateral contact of asperities, assumed the distribution function of the contact angle and studied the characteristics of the lateral contact between asperities by using statistical methods. A new statistical contact model for the contact interface was established, but the theoretical basis for this angle distribution function was not provided. Gao Zhiqiang [67] studied the contact characteristics of asperities in the three deformation stages of elasticity, elastoplasticity, and plasticity based on the lateral contact and interaction of asperities. By adopting the contact angle distribution function assumed by Gorbatikh [60], a contact interface contact model (GZQ model) that reflects the normal and tangential contact energy consumption of asperities was established. However, the contact angle distribution function cited in this model has no exact theoretical or experimental basis. Misra and Huang [68,69] creatively introduced the joint probability density function of the contact angle and azimuth angle during the lateral contact of asperities. Combining the calculation schemes of asperity contact sliding and stress-displacement increment and coupling the tangential and normal contact stiffnesses, they studied the sliding behavior of asperities in lateral contact.
Shi et al. [70] established a three-dimensional lateral contact model using two elastoplastic spherical asperities. They described the initial offset state of the lateral contact by using two parameters, namely the contact azimuth angle and the contact angle, and found that the load ratio of asperities is mainly determined by Young’s modulus of the material and interfacial shear strength, while the maximum force on asperities during the unloading stage is mainly related to the contact angle of asperities. However, this model only conducted the force analysis and modeling research on asperities and was not extended to the study of the contact characteristics of rough surfaces. Gao and Fu [71], based on the joint distribution function of the contact angle and the contact azimuth angle proposed by Misra and Huang [68,69], combined with the KE model, the ZC model, and the adhesion-slip theory, established an anisotropic rough surface contact model (GF model) considering the lateral contact and interaction of asperities. They analyzed the adhesion and slip conditions of the contact surface under the action of tangential force and the influence of the standard deviation of asperity height and asperity contact angle on the contact surface. Jamshidi et al. [66] defined the contact state according to the relative positional relationship when asperities are in contact and, at the same time, modified Misra’s contact angle function. Thus, they established the HJ model with the coupling of the normal load and the shear force on the contact interface.
Lingsong et al. [72,73] studied the horizontal distance distribution of adjacent asperities on rough surfaces and found that the horizontal distance follows the Gaussian distribution law. For the first time, they replaced the assumed contact angle distribution function with the distribution law of the horizontal distance of asperities. According to the statistical theory, they established the FLS model containing the normal and tangential contact characteristics, breaking through the theoretical bottleneck that the contact angle distribution function still needs to be assumed when building the lateral contact model.
2.3.3. Numerical Contact Models of Asperities
The more closely the contact model conforms to the actual situation, the greater its complexity will be. For complex rough surface contact problems, it is necessary to conduct research and calculations with the help of the finite element method and experiments. The finite element model can accurately simulate and calculate contact parameters, such as pressure distribution, deformation amount, or load when a single asperity or multiple asperities are under pressure and deformed. Experiments can verify the correctness of previous models, and the proposed new calculation results and calculation-fitting formulas intuitively and accurately analyze these contact problems. Finite element simulation is an important means of simulating and testing the effect of the model, and it is also an important method for studying contact characteristics.
The elastoplastic hemispherical finite element contact model established by Jackson and Green [74], namely the Jackson–Green (JG) model, verified the correctness of the Hertz contact theory under the extremely small deformation amounts. It was also pointed out that when the contact deformation amount is too large, the final result is not the same as the fully plastic contact of the Abbott–Firestone (AF) model [75]. In the elastoplastic contact deformation stage, the JG model is closer to the simulation results than the KE model and the ZMC model. It can effectively study the contact behavior of asperities and also has a certain degree of adaptability to macroscopic contact.
Jackson et al. [76], based on the initial state of asperities on rough surfaces being lateral contact, derived empirical formulas for the average tangential force and the average normal force of spherical asperities in the sliding state through semi-analytical methods and finite element simulation analysis, respectively.
Mulvhill et al. [77], based on the condition of asperity lateral contact, established an elastoplastic interaction finite element model for the contact between cylindrical asperities and spherical asperities. The difference between this model and the models established by predecessors lies in that it allows a greater overlap of asperities in the height, has a higher interfacial viscous shear strength, and allows the occurrence of material failure.
Chandrasekar et al. [78] improved the analytical model of asperity interaction based on the finite element method and proposed that the surface roughness density is an important parameter for determining the influence of asperity interaction on the contact interface.
Zhu L B [79] added the elastoplastic deformation stage of asperity lateral contact on the basis of predecessors who only considered the elastic deformation stage and the plastic deformation stage and established the Zhu Lingbo (ZLB) model. Compared with the original elastic–plastic contact models of the contact interface, this model is closer to the finite element results. Zhao et al. [80] established an analytical contact model for the interaction of multiple asperities applying power-law hardening materials by considering the position, height, and radius of curvature of asperities on rough surfaces and studied the influence of the material properties of power-law hardening materials on the interaction of asperities.
Finite element analysis (FEA) is a numerical simulation technique used to predict how materials will perform under given conditions and has a very wide range of application scenarios. It solves complex engineering problems by decomposing complex structures into many small and simple parts. By increasing the number of elements in the model, the accuracy of the calculation results can be improved. This enables engineers to conduct extremely detailed analyses of designs, thereby ensuring the safety and reliability of products. Compared with traditional test methods, virtual testing using FEA can significantly reduce the number of physical prototypes, thus cutting down time and cost. The application of FEA in micromechanical analysis is gradually becoming an important analytical method in the fields of materials science and engineering, especially in the fields of multi-scale modeling and nonlinear analysis. Although numerical simulation provides a powerful prediction tool, this method involves a large number of ideal conditions compared to experiments, and experimental verification remains the key to ensuring the reliability of the model. Therefore, the future development trend of finite element model verification methods will be to strengthen the combination of experiments and simulations, form a closed-loop feedback mechanism, and continuously improve and refine the finite element model.
In the asperity–asperity contact models, the shapes of asperities are mostly assumed to be ellipsoids, cylinders, and other shapes at present. In the future, they may be expanded in the directions of paraboloids, revolving bodies of trigonometric functions, and other shapes so as to establish contact models that are more in line with the actual situation. With the progress of the finite element algorithm, it will also be applicable to the fitting calculations of more complex contact models. The combination of finite element analysis and experimental verification has gradually become an important method for studying the complex contact behaviors of rough surfaces. Besides using the two parameters of contact angle distribution and contact azimuth angle to characterize the anisotropy of asperities, using the horizontal distance distribution of asperities for characterization is also a new approach.
3. Statistical Contact Model of Rough Surfaces
The GW model [37] is the earliest rough surface contact model established by the method based on statistical analysis. The GW model has obtained the relationships among the contact pressure, contact area, and deformation amount of rough surfaces by studying the heights of asperities and their characteristics of distribution. The GW model is shown in Figure 8.
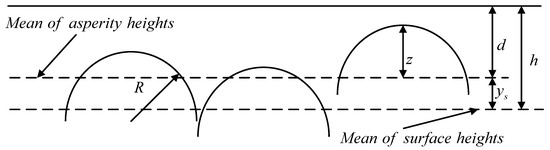
Figure 8.
GW model.
This model equivalent the contact behavior of two rough surfaces to the contact between a smooth rigid plane and a rough surface and assumes that the radius of curvature of each asperity is R. As shown in Figure 8, is the height of the asperity, is the separation distance between the average height of the asperities and the rigid plane (the deformation of the asperity is ), is the distance between the average height of the rough surface and the rigid plane, and is the distance between the average height of the asperities and the average height of the rough surface. is the height distribution function of the asperities, which follows a Gaussian distribution. Thus, according to the Hertz contact theory, the total number of asperities is
In the above formula, is the areal density function of the asperities; is the nominal contact area. When the deformation amount of a single asperity, that is, , the asperity will come into contact, and the number of asperities in contact is
The total contact area and the total contact load are, respectively,
In order to facilitate model establishment and derivation calculations, the GW model makes the following assumptions: (1) the shape of asperities is spherical, with a radius of an average value, and their heights are randomly distributed; (2) asperities are evenly distributed on the rough surface and have no directionality; (3) during the contact process, only asperities undergo deformation, the substrate does not deform, and the deformations among asperities do not affect each other; and (4) the upper and lower asperities are in tip-to-tip contact, and lateral contact behaviors are not considered.
As a typical representative of statistical contact analysis, the GW model has laid a milestone foundation for the contact theory between rough surfaces. Up to now, this model is still accepted and used by researchers.
As a seminal contribution, the GW model established fundamental principles for subsequent surface contact research. Based on this, scholars have continuously conducted in-depth research on the statistical contact model and established models that can describe the actual contact behaviors of rough surfaces more accurately.
In the process of expanding the asperity contact model to the rough surface contact model by means of the statistical summation method, one of the core steps is to determine the height distribution function of the asperities on the rough surface. The GW model regards the height distribution of asperities on the rough surface as a random function that obeys the Gaussian distribution. Therefore, most models also adopt the Gaussian distribution. In the gradual development of contact models, there have also been some attempts to use non-Gaussian distributions for height. This chapter will classify and discuss the development and research status of contact models according to different height distributions.
3.1. Surface Contact Model Based on Gaussian Distribution
Since Greenwood and Williamson established the classic GW model, Chang et al. [23] studied the deformation situations of asperities on rough surfaces beyond the elastic contact stage based on the GW model. They took into account the volume conservation law of asperities in the plastic deformation stage and extended the GW model to plastic deformation, thus establishing the CEB model. Horng et al. [22] extended the CEB model to ellipsoidal asperities and established the JH model. However, just like the CEB model, its shortcoming is that it did not study the elastoplastic transition stage. Jeng and Wang [24] established the JW contact model for elastoplastic ellipsoidal asperities in order to make up for the defect that the plastic transition stage was not considered in the JH model. They took into account the assumed mutation in the transition process from elastic deformation to fully plastic deformation and improved the deficiencies of the JH model and the ZMC model.
The research on the elastoplastic contact stage is to study the contact state of the joint interface of engineering equipment when the load changes from low to high during actual assembly and operation, which has important engineering significance. Under high load conditions, the fully plastic flow of asperities has a significant impact on the contact stiffness, and the stress distribution within the contact area has a nonlinear relationship with the load. How to achieve a smooth transition of contact parameters from the elastic contact stage to the plastic contact stage in the model is a major difficulty.
The team led by Zhao Yongwu and other scholars has conducted in-depth research on the transition stage to the elastoplastic state for rough surface contact models based on the Gaussian distribution. In 2000, Zhao et al. [25] studied the discontinuity problem at the critical point from elastic to plastic deformation by using the function interpolation and fitting method, proposed the ZMC model, and established a complete deformation model for asperities on rough surfaces. However, the ZMC model has some shortcomings due to the limitations of the interpolation function properties. For example, the fitted average contact pressure is not smooth at the critical points of elastic, elastoplastic, and plastic deformations, and the critical point of fully plastic deformation has not been determined. In 2001, Zhao et al. [41], based on the ZMC model, assumed that the area at the bottom of each asperity is proportional to the load it bears, combined the Saint–Venant’s principle and the Love formula with the deformation amount of asperities, derived the interaction formula, and established the substrate deformation model, namely the ZC model. In 2007, Yongwu et al. [81] aimed at the problem that the ZMC model is not smooth at the critical points and the critical point of fully plastic deformation has not been determined. They used the function interpolation and fitting method to establish a new model with continuous and smooth critical points. This model solved the problem that the critical point of plastic deformation has not been determined and achieved a smooth transition from elasticity to elastoplasticity. In 2019, Wang et al. [82], aiming at the problem of discontinuous elastoplastic deformation of asperities, adopted the improved Hermite interpolation method, combined with the GW model and the AF model on the basis of other assumptions, and established an improved ZMC model.
ZHAO et al. [83] divided the elastoplastic deformation stage into three stages, namely the pre-elastic-plastic deformation stage, the mid-elastic-plastic deformation stage, and the post-elastic-plastic deformation stage. Through this method, they established an elastoplastic contact model that is continuous at the critical point. The present model fits well with ZMC and KE models on contact characteristics and also overcomes the shortcoming of discontinuity at critical point (KE model) and non-monotonicity of average contact pressure (ZMC model).
Ling et al. [84] established a new polynomial function to describe the relationship between the contact deformation amount and the contact area according to the fact that both the real contact area of asperities and the transformation of contact load satisfy the continuous and smooth conditions at the critical point of the deformation state transformation. This has solved the problem that the contact mechanism in the elastoplastic region of the contact interface is difficult to determine.
Nayak [85] put forward a new method, that is, using three important parameters related to the power spectral moments, namely the root mean square of asperity height, the root mean square of surface gradient, and the root mean square of asperity radius of curvature, to characterize a random and isotropic Gaussian surface. And he pointed out three simple methods for obtaining these parameters from the rough surface profile, as well as the method for expanding this theory to non-isotropic Gaussian surfaces.
Li [40] proposed a contact stiffness model combining continuous smooth characteristics and asperity interaction by introducing a surface smoothness parameter, which makes the prediction of contact stiffness more accurate. The drawback of this model is its relatively high complexity and large amount of calculation, so it is applicable to small-scale, high-precision engineering designs. Xu Gang [59] derived a probability distribution function of the critical slip force of friction plates based on measurable physical parameters by comparing the constitutive equation of tangential motion occurring between rough surfaces with the Iwan model and proposed a tangential contact model for rough surfaces based on the KE normal contact theory and the Iwan model. Wei et al. [86], based on the GW statistical contact model, derived expressions for the normal contact load and stiffness of the contact interface when considering the substrate deformation or interaction of asperities separately. They took into account the substrate deformation and the interaction of adjacent asperities but ignored the elastoplastic deformation stage and the plastic deformation stage of asperities.
Li Ling [33] put forward a method of using revolving bodies of quadratic functions to equivalent asperities. She rederived the contact equations of a single asperity in the three deformation stages of elasticity, elastoplasticity, and full plasticity and established a microscopic contact model for rough surfaces. This model provided new ideas for establishing the contact model of the joint interface. Yakovenko and Goryacheva [87] established a model considering the mutual influence of asperities by using the localization method. The constructed contact model can study the dependence of contact characteristics on the applied pressure, and within a wide range of nominal pressures, it can display the experimentally observed real contact area and the saturation effect of the additional compliance caused by roughness.
All of the above models assume that the height distribution of asperities follows a Gaussian distribution. During the statistical summation process, their forms are simple. Therefore, currently, the Gaussian distribution assumed by the GW model is still adopted for the asperity height distribution in most statistical contact models. However, it is not easy to obtain analytical solutions for contact models under the Gaussian distribution. Through the exploration of some scholars, it has been found that similar analytical results can be obtained by adopting other non-Gaussian distribution assumptions [88,89,90], and it is easier to obtain analytical solutions. In subsequent research, it has also been discovered that, at a more microscopic level, the height of asperities does not always follow a Gaussian distribution [91,92]. Thus, scholars have launched research on rough surface contact models under the assumption that the asperity height distribution is other non-Gaussian distributions.
3.2. Surface Contact Model Based on Non-Gaussian Distribution
The experiments of GW show that the height distribution of asperities on engineering surfaces mostly follows a Gaussian distribution. However, adopting the Gaussian distribution is not conducive to obtaining the analytical solutions of the contact parameters of the contact interface. On the basis of GW’s pioneering work, researchers selected the exponential distribution as the height distribution of asperities when obtaining simplified closed-form solutions. Hess and Soom [88,89], as well as Hess and Wagh, utilized the exponential distribution of asperity heights in their dynamic friction modeling work. Etsion and Front [90] also adopted the exponential distribution in their static seal structure modeling work. Polycarpou and Etsion [91] modified the exponential distribution and used a modified exponential distribution with two additional constants to approximate the Gaussian distribution, obtaining simple analytical expressions with acceptable accuracy. You and Chen [93] established a new contact model to analyze the influence of different height distributions on the calculation results of contact parameters under three different random distributions of asperity heights, namely the Gaussian distribution, the simple exponential distribution, and the modified exponential distribution. The results indicate that the modified exponential distribution has a relatively good approximation to the Gaussian distribution, while the error between the simple exponential distribution and the Gaussian distribution is relatively large. Goryacheva and Yakovenko [94] assumed the asperity height distribution to be the exponential distribution and the single-stage distribution to study the influence of the interaction of asperity parameters on the macroscopic contact characteristics and pointed out that ignoring the interaction among the asperities on the contact surface in the discrete contact model will lead to significant errors when determining the contact characteristics on both the macroscopic and microscopic scales.
Borodich and Pepelyshev [92] found that on the nanometer and micrometer scales, the height distributions of the studied surfaces were not Gaussian distributions. This once again proved that the normal distribution is not applicable to the description of the topography of all rough surface asperities. When studying rough surfaces on a more microscopic scale, they also pointed out that the Markov surface proposed by Whitehouse [95] is more suitable for the description of rough surfaces.
Li Ling [39] pointed out that since the Gaussian distribution function and the exponential distribution function have no upper limit and do not conform to the actual variation range of asperity height, adopting a new distribution with the same standard deviation as that of the Gaussian distribution can solve the drawback that the asperity height in the Gaussian distribution and the exponential distribution has no upper limit, which is more in line with the actual situation. Li Ling introduced the triangular distribution function to characterize the height distribution of surface asperities. On the basis of improving the GW model, a new elastic contact stiffness model was established, revealing the influence laws of the distribution function, substrate deformation, and surface roughness on the contact characteristics of the contact interface. The results showed that the triangular distribution function can effectively characterize the height distribution of surface asperities. However, there is currently no more literature to support the universality of the triangular distribution. Therefore, it is still not mature enough to use the triangular distribution to study rough surface contact models.
Some scholars assume that the height distribution of asperities follows a Weibull distribution. This distribution has high flexibility. By adjusting the shape parameter and the scale parameter, various distribution curves with different shapes can be obtained, which can well fit different distribution patterns in many actual data. Sabino et al. [96] adopted the Weibull distribution for modeling to analyze the influence of the non-Gaussian distribution on the statistical geometry of isotropic randomly rough surfaces. It was observed that the average curvature of the negatively skewed surface decreases as the height increases, which contradicts the trend in the Gaussian case.
McCool [97,98] suggested using the Weibull probability density function to simulate the distribution of asperity height. The two-parameter Weibull distribution is different from the commonly assumed symmetric Gaussian model. It can explain the skewness in the roughness height distribution, whether it is positive or negative. In addition, the contact between two Weibull surfaces can be approximated as the contact between an equivalent single Weibull surface and a smooth flat plate. Yu et al. [99] considered extending the GW model with a two-parameter Weibull distribution to make it applicable to different types of roughness height distributions. Sabion et al. [100] studied the influence of the Weibull height distribution on the evolution of the real contact area in elastic, frictionless, and non-adhesive contacts.
Besides assuming that the height distribution of asperities is a certain known typical distribution function, it is also possible to directly generate rough surfaces with different height distributions through algorithms. In 1996, Kotwal [101] proposed a statistical analysis method for non-Gaussian surfaces by using the Pearson frequency curve system based on the method of moments to provide a group of curves to generate a distribution equation with the first four moments known so as to obtain the probability density function of a distribution with known average, standard deviation, skewness, and kurtosis. For example, non-Gaussian sequences can be obtained from Gaussian sequences by using transformation systems of the Johnson type or Pearson type. Tomota et al. [102] utilized the mapping relationship between the height and curvature of asperities in the Johnson distribution and the Gaussian distribution to carry out corresponding conversions on rough surfaces with non-Gaussian distributions and applied the mapping relationship between Gaussian and non-Gaussian roughness height distributions to the asperity height distribution. A contact model of a rough distribution model that can predict the distribution of surface asperities only through basic roughness parameters was established.
Gao et al. [103] selected a non-Gaussian distribution to develop a normal contact model under mixed lubrication conditions. They took into account the relative motion between two planes and derived the calculation results of the contact stiffness. The research results show that several key factors, such as the normal load, viscosity, relative motion speed, and non-Gaussian roughness parameters, have a significant impact on the normal contact stiffness of the non-Gaussian rough surface in the mixed lubrication mating surface. This model provides valuable insights for understanding the performance of the mating surface under mixed lubrication.
The algorithms adopted in Chilamakuri et al. [104,105,106,107,108,109,110] can essentially be regarded as improvements on the same concept mentioned above. The algorithms used to generate surfaces with non-Gaussian height distributions are still not as versatile, robust, or widely applied as those for Gaussian distributions. As Francisco and Brunetière [111] pointed out, this method has some limitations, including issues regarding stability and accuracy. Nevertheless, after a series of improvements, today’s algorithms allow the specification of skewness and kurtosis, thus being able to offer a considerable degree of flexibility [112].
To sum up, the Gaussian distribution has a simple form, but it is difficult to obtain analytical solutions during the calculation process. In the case of slight contact on rough surfaces, the exponential distribution can be adopted for the height distribution of asperities. The exponential distribution can make it easier to obtain analytical solutions. However, the error between the simple exponential distribution and the Gaussian distribution is relatively large, and it needs to be modified before it can be used as an approximation of the Gaussian distribution. Moreover, in the case of high loads, the exponential distribution will no longer be applicable. Since the traditional Gaussian model is symmetric about its average, this means that the traditional Gaussian model cannot accurately describe the skewness characteristics of surface roughness. The two-parameter Weibull distribution can solve this problem well. It can explain the skewness in the roughness height distribution, whether it is positive or negative. The Weibull distribution can reflect asymmetry well, and its parameters can be calculated based on the given root mean square value and the dimensionless skewness value of the asperity height distribution. In addition, the contact between two Weibull surfaces can be equivalent to the contact between a single Weibull surface and a smooth plane, which simplifies the calculation process. However, the parameter estimation of the Weibull distribution is complex, and since the Weibull distribution does not have the additivity property, this increases the computational burden in practical applications. Using algorithms to generate non-Gaussian distributions allows for more freedom when generating non-Gaussian surfaces. This method performs well in specifying commonly used height probability distributions and power spectra and can handle particularly difficult height probability distributions, having quite high versatility. However, as the requirement for calculation accuracy increases, the computational complexity of the algorithms also increases correspondingly, requiring more computational costs. With the development and optimization of relevant algorithms, using algorithms to generate height distributions of asperities on rough surfaces that are more in line with the real situation is also a trend.
4. Discussion
The statistical contact model has had an extremely profound and extensive impact in multiple industrial fields, and at the same time, it also demonstrates a highly promising future development trend, continuously injecting strong impetus into the development of these industries.
In the mechanical manufacturing industry, the statistical contact model is a key tool for the design and performance optimization of mechanical components. By accurately simulating the contact state of the surfaces of components under different working conditions, it can effectively predict wear, fatigue life, and distribution of contact stress, thereby guiding engineers to optimize the design and improve the reliability and durability of products. For example, in the design of automotive engines, using the statistical contact model to analyze the contact between the piston and the cylinder wall can precisely control the fit clearance, reduce frictional losses, improve fuel efficiency, and reduce energy consumption and exhaust emissions, which is of great significance for promoting energy conservation and emission reduction in the automotive industry.
The field of materials science also cannot do without the statistical contact model. In terms of the performance evaluation of new materials, the statistical contact model helps to deeply understand the relationship between the microstructure of materials and their macroscopic contact performance, providing an important basis for the innovative research and development of materials and promoting the widespread application of high-performance materials in high-end fields such as aerospace and electronics.
In the electronics manufacturing industry, with the development of electronic products toward miniaturization and high performance, the contact reliability between chips and packaging materials, as well as between electronic components, has become a key issue. The statistical contact model can help engineers optimize the design of the packaging structure, ensure the stable connection of electronic components in complex environments, reduce the risk of failures, and improve the overall performance and stability of electronic products, providing strong support for the rapid development of the electronic information industry.
In the field of biomedical engineering, in the design of medical devices such as artificial joints and dental implants, by simulating the contact mechanical behavior between the implants and human tissues, the shape and surface characteristics of products can be optimized, biocompatibility can be improved, and postoperative complications can be reduced, providing patients with higher-quality medical services and promoting technological progress in the field of biomedical engineering.
This review mainly focuses on the current research status of the multi-scale contact models of connection interfaces from the microscopic to the macroscopic scale. Based on the rough surface contact model, the multi-scale model of two rough contact surfaces in the connection structure is introduced. The phenomenological contact models of rough surfaces have been developed and applied quite maturely, but there is still much room for development in the constitutive models based on the microscopic contact mechanism.
Asperities are the basic components of rough surfaces. There are still many assumptions in the establishment of asperity contact models. For example, relatively regular geometric shapes are selected for asperities, while the asperities on real rough surfaces have non-unique and irregular shapes. Currently, most asperity contact models are built based on the assumption of asperity shapes. Integrating surface topography measurement technology into the research of asperity contact models and conducting modeling based on the microscopic topography measurement of rough surfaces is one of the trends in the research of asperity contact models. With the in-depth research of asperity contact models, considering the substrate deformation and the combined action of normal and tangential loads simultaneously is also a trend.
The asperity height distribution is crucial for the research of statistical contact models. Compared with the traditional Gaussian distribution, obtaining a more realistic height distribution through the analysis and fitting of topography measurement data is an important trend. As a new technology, generating general rough surfaces using algorithms will also be better integrated into the research of rough surface contact models with the development of computer algorithms.
In addition, in the field of cross-scale research on contact models of connection interfaces, the contact theory based on surface energy spectral density proposed by Professor Persson has successfully integrated fractal geometry with statistical mechanics. This theory provides a brand-new theoretical framework for the study of the contact behavior of multi-scale rough surfaces. Professor Persson’s work has not only deepened our understanding of the mechanisms of friction, adhesion, and contact but has also been widely applied in various fields such as rubber friction, tire dynamics, and sealing technology. His research achievements possess a high degree of theoretical depth and practical application value and have significantly promoted the development of related disciplines. Therefore, conducting cross-scale research on connection interfaces by combining fractal geometry with statistical mechanics is also an important research direction for the future.
5. Conclusions
There are a large number of complex large-scale mechanical equipment in industries such as aerospace, mechanical processing, and transportation. The components of these equipment are mainly assembled through different forms of connection structures, such as bolts, flanges, wedge rings, and so on. Due to the strong nonlinearity of the contact stiffness and contact damping of their joint interfaces, in order to improve the overall performance of the equipment and extend its service life, it is necessary to establish joint interface contact models to accurately predict their contact characteristics. This paper mainly focuses on the current research status of statistical contact models and summarizes and elaborates on two aspects: asperity contact models and rough surface contact models, respectively. It summarizes the current research status of asperity contact models under the two modeling methods of flat plate–asperity and asperity–asperity, as well as the current research status of rough surface contact models under different height distribution assumptions. It also summarizes the previous work and points out some research trends. Based on the previous research, it is found that there are still some problems that need to be solved urgently in the research field of joint interface contact models.
Problems urgently to be solved:
- Utilize more precise surface detection methods and signal processing methods to detect real surfaces so as to explore the assumption methods for the shape of asperities and the height distribution of asperities that are universally applicable to different materials under different processing techniques.
- The mainstream method for characterizing the anisotropy of the contact interface is to characterize it by assuming the distribution of contact angles and the distribution of contact azimuth angles, which lacks a practical basis. It is necessary to explore characterization methods with a practical basis to make the research results more convincing and realistic.
- Establish contact models that take into account the normal load and tangential load with inclined angles and coupled dynamic changes so as to establish contact models that are more in line with the actual working conditions of the equipment and conduct theoretical analysis on the contact mechanism of the joint interface more clearly.
Author Contributions
Z.L. and M.G. summarized the current state of development and frontiers of the various efforts. Y.L. and S.W. organized and classified the relevant literature. X.L. and Z.X. reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing does not apply to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, X. Research on the Dynamic Characteristics of the Rocket Body Structure Based on the Simplified Modeling of Bolted Flange Connections. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Luan, Y. Research on the Dynamic Modeling Method of Bolted Flange Connections in Spacecraft Structures. Dalian University of Technology. Ph.D. Thesis, Dalian University of Technology, Dalian, China,, 2012. [Google Scholar]
- Cao, J.; Liu, Q.; Hong, J. A Review of the Research from Microscopic Friction to Macroscopic Dynamics of Bolted Connections. China Mech. Eng. 2021, 32, 1261–1273. [Google Scholar]
- Wang, D.; Xu, C.; Hu, J.; Wan, Q.; Chen, H. Research on Nonlinear Mechanical Modeling of Contact Interfaces of Connection Structures. Acta Mech. Sin. 2018, 50, 44–57. [Google Scholar]
- Liu, K.; Liu, J.; Wang, L.; Zhao, Y.; Li, F. A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces. Appl. Sci. 2023, 13, 11680. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, M.; Lu, X.; Wang, S.; Li, Z. A Review of Cross-Scale Theoretical Contact Models for Bolted Joints Interfaces. Coatings 2024, 14, 539. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, Z.; Zhang, Y.; Wu, H.; Yu, J. Adhesion of elastic wavy surfaces: Interface strengthening/weakening and mode transition mechanisms. J. Mech. Phys. Solids 2021, 151, 104402. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Thomas, T. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Xie, S.; Ai, Y.; Zhao, D.; Tian, J.; Liu, Y.; Guan, P.; Liu, J. Research on the Contact Stiffness of Three-Dimensional Rough Surfaces Based on Stochastic Processes. Surf. Technol. 2022, 51, 326–334. [Google Scholar]
- Ghaednia, H.; Wang, X.; Saha, S.; Xu, Y.; Sharma, A.; Jackson, R.L. A review of elastic–plastic contact mechanics. Appl. Mech. Rev. 2017, 69, 60804. [Google Scholar] [CrossRef]
- Bhushan, B. Contact mechanics of rough surfaces in tribology: Single asperity contact. Appl. Mech. Rev. 1996, 49, 275–298. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Liu, Y.; Zhou, P. A Novel Method to Identify the Scaling Region of Rough Surface Profile. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2019, 27, 1950011. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, K.; Wang, W.; Liu, X. Research Status and Prospect of Rough Surface Contact Model. Cryog. Supercond. 2011, 39, 71–74. [Google Scholar]
- Linford, R. Surface energy of solids. Chem. Soc. Rev. 1972, 1, 445–464. [Google Scholar] [CrossRef]
- Persson, B.N. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Venugopalan, S.P.; Irani, N.; Nicola, L. Plastic contact of self-affine surfaces: Persson’s theory versus discrete dislocation plasticity. J. Mech. Phys. Solids 2019, 132, 103676. [Google Scholar] [CrossRef]
- Follansbee, P.; Sinclair, G. Quasi-static normal indentation of an elasto-plastic half-space by a rigid sphere—I: Analysis. Int. J. Solids Struct. 1984, 20, 81–91. [Google Scholar] [CrossRef]
- Sinclair, G.; Follansbee, P.; Johnson, K. Quasi-static normal indentation of an elasto-plastic half-space by a rigid sphere—II. Results. Int. J. Solids Struct. 1985, 21, 865–888. [Google Scholar] [CrossRef]
- Bush, A.W.; Gibson, R.D.; Keogh, G.P. Strongly Anisotropic Rough Surfaces. J. Lubr. Technol. 1979, 101, 15–20. [Google Scholar] [CrossRef]
- So, H.; Liu, D.C. An elastic-plastic model for the contact of anisotropic rough surfaces. Wear 1991, 146, 201–218. [Google Scholar] [CrossRef]
- Greenwood, J.A. A simplified elliptic model of rough surface contact. Wear 2006, 261, 191–200. [Google Scholar] [CrossRef]
- Horng, J.H. An Elliptic Elastic-Plastic Asperity Microcontact Model for Rough Surfaces. J. Tribol. 1998, 120, 82–88. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Wang, P.-Y. An Elliptical Microcontact Model Considering Elastic, Elastoplastic, and Plastic Deformation. J. Tribol. 2003, 125, 232–240. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow. J. Tribol. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Buczkowski, R.; Kleiber, M. Statistical Models of Rough Surfaces for Finite Element 3D-Contact Analysis. Arch. Comput. Methods Eng. 2009, 16, 399–424. [Google Scholar] [CrossRef]
- Chung, J.C. Elastic–plastic contact analysis of an ellipsoid and a rigid flat. Tribol. Int. 2010, 43, 491–502. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Peng, S.-R. Static Friction Model of Elastic-Plastic Contact Behavior of Surface With Elliptical Asperities. J. Tribol. 2009, 131, 21403. [Google Scholar] [CrossRef]
- Shah, S.; Krithivasan, V.; Jackson, R.L. An electro-mechanical contact analysis of a three-dimensional sinusoidal surface against a rigid flat. Wear 2011, 270, 914–921. [Google Scholar] [CrossRef]
- Jackson, R.L.; Krithivasan, V.; Wilson, W.E. The pressure to cause complete contact between elastic—Plastic sinusoidal surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 857–863. [Google Scholar] [CrossRef]
- An, Q.; Suo, S.; Lin, F.; Bai, Y.; Di, H.; Shi, J. Microscopic Contact Model of Rough Surfaces Ground by Plane Grinding. J. Mech. Eng. 2020, 56, 240–248. [Google Scholar]
- Shang, S.; Cao, X.; Liu, Z.; Shi, J. Analysis of Normal Elastic Contact Stiffness of Rough Surfaces Based on Ubiquitiform Theory. J. Tribol. 2019, 141, 111401. [Google Scholar] [CrossRef]
- Li, L.; He, B.; Wang, J.; Zhang, J.; Cai, A. Construction of Asperity Model for Rough Surface and Analysis of Contact Characteristics. J. Vib. Shock. 2023, 42, 43–50. [Google Scholar]
- Tiwari, A.; Persson, B.N.J. Cylinder-Flat Contact Mechanics with Surface Roughness. Tribol. Lett. 2020, 69, 4. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, G.-F. A contact model for elastic-plastic rough spheres. Tribol. Int. 2025, 206, 110578. [Google Scholar] [CrossRef]
- Nassar, S.A.; Abboud, A. An improved stiffness model for bolted joints. J. Mech. Des. 2009, 131, 121001. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Wang, G.F.; Long, J.M.; Feng, X.Q. A self-consistent model for the elastic contact of rough surfaces. Acta Mech. 2015, 226, 285–293. [Google Scholar] [CrossRef]
- Ling, L.; Jingjing, W.; Xiyong, P.; Wei, C. A New Method for Modeling the Contact Stiffness of Mechanical Joint Surfaces. J. Mech. Eng. 2020, 56, 162–169. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Shi, X.; Ma, S.; Cai, A. Contact stiffness model of joint surface considering continuous smooth characteristics and asperity interaction. Tribol. Lett. 2021, 69, 43. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L. A model of asperity interactions in elastic-plastic contact of rough surfaces. J. Tribol. 2001, 123, 857–864. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Peng, S.-R. Elastic-Plastic Contact Behavior Considering Asperity Interactions for Surfaces With Various Height Distributions. J. Tribol. 2005, 128, 245–251. [Google Scholar] [CrossRef]
- Ciavarella, M.; Greenwood, J.A.; Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 2008, 265, 729–734. [Google Scholar] [CrossRef]
- Vakis, A.I. Asperity Interaction and Substrate Deformation in Statistical Summation Models of Contact Between Rough Surfaces. J. Appl. Mech. 2013, 81, 41012. [Google Scholar] [CrossRef]
- Tang, Z.C.; Jiao, Y.Y.; Wong, L.N.Y. Theoretical model with multi-asperity interaction for the closure behavior of rock joint. Int. J. Rock Mech. Min. Sci. 2017, 97, 15–23. [Google Scholar] [CrossRef]
- Song, H.; Vakis, A.I.; Liu, X.; Van der Giessen, E. Statistical model of rough surface contact accounting for size-dependent plasticity and asperity interaction. J. Mech. Phys. Solids 2017, 106, 1–14. [Google Scholar] [CrossRef]
- Lihua, Z. Research on the Contact Characteristics of Anisotropic Rough Surfaces Considering the Interaction of Asperities. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Li, L.; Wang, J.; Pei, X.; Chu, W.; Cai, A. A modified elastic contact stiffness model considering the deformation of bulk substrate. J. Mech. Sci. Technol. 2020, 34, 777–790. [Google Scholar] [CrossRef]
- Wen, Y.; Tang, J.; Zhou, W.; Li, L.; Zhu, C. New analytical model of elastic-plastic contact for three-dimensional rough surfaces considering interaction of asperities. Friction 2021, 10, 217–231. [Google Scholar] [CrossRef]
- Cai, L.; Wang, F.; Li, L.; Guo, T.; Zhao, Y.; Liu, Z. Research Progress on the Dynamic Characteristics of Bolted Joints. J. Mech. Eng. 2013, 49, 158–168. [Google Scholar] [CrossRef]
- Gaul, L.; Lenz, J. Nonlinear dynamics of structures assembled by bolted joints. Acta Mech. 1997, 125, 169–181. [Google Scholar] [CrossRef]
- Farhang, K.; Segalman, D.; Starr, M. Approximate Constitutive Relation for Lap Joints Using a Tribo-Mechanical Approach. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007. [Google Scholar]
- Argatov, I.I.; Butcher, E.A. On the Iwan models for lap-type bolted joints. Int. J. Non-Linear Mech. 2011, 46, 347–356. [Google Scholar] [CrossRef]
- Tabor, D.; Bowden, F.P. Junction growth in metallic friction: The role of combined stresses and surface contamination. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 251, 378–393. [Google Scholar]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Johnson, K.L.; Bowden, F.P. Surface interaction between elastically loaded bodies under tangential forces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 230, 531–548. [Google Scholar]
- Kogut, L.; Etsion, I. A finite element based elastic-plastic model for the contact of rough surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Dong, W.; Chao, X.; Qiang, W. Tangential Load-Displacement Model of Elastoplastic Contact Rough Surfaces. J. Xi’an Jiaotong Univ. 2015, 49, 122–127. [Google Scholar]
- Gang, X.; Wei, L.; Ping, H.; Wanglong, Z. Numerical Analysis and Experimental Study of the Tangential Contact Model for Rough Surfaces. J. Xi’an Jiaotong Univ. 2022, 56, 110–117. [Google Scholar]
- Gorbatikh, L.; Popova, M. Modeling of a locking mechanism between two rough surfaces under cyclic loading. Int. J. Mech. Sci. 2006, 48, 1014–1020. [Google Scholar] [CrossRef]
- Jager, J. Uniaxial deformation of a random packing of particles. Arch. Appl. Mech. 1999, 69, 181–203. [Google Scholar] [CrossRef]
- Faulkner, A.; Arnell, R.D. The development of a finite element model to simulate the sliding interaction between two, three-dimensional, elastoplastic, hemispherical asperities. Wear 2000, 242, 114–122. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Sepehri, A.; Farhang, K. A Finite Element-Based Elastic-Plastic Model for the Contact of Rough Surfaces. Model. Simul. Eng. 2011, 2011, 561828. [Google Scholar] [CrossRef]
- Li, B.T.; Hong, J.; Shao, G.Q.; Du, F. An Integrated Mechanical-Electrical Predictive Model of Electrical Contact Resistance between Two Rough Surfaces. Tribol. Trans. 2015, 58, 537–548. [Google Scholar] [CrossRef]
- Jamshidi, H.; Ahmadian, H. A modified rough interface model considering shear and normal elastic deformation couplings. Int. J. Solids Struct. 2020, 203, 57–72. [Google Scholar] [CrossRef]
- Gao, Z. Research on the Theoretical Models of Contact Stiffness and Damping of Mechanical Joint Surfaces. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2018. [Google Scholar]
- Misra, A.; Huang, S. Effect of loading induced anisotropy on the shear behavior of rough interfaces. Tribol. Int. 2011, 44, 627–634. [Google Scholar] [CrossRef]
- Misra, A.; Huang, S. Micromechanical stress–displacement model for rough interfaces: Effect of asperity contact orientation on closure and shear behavior. Int. J. Solids Struct. 2012, 49, 111–120. [Google Scholar] [CrossRef]
- Shi, X.; Zou, Y.; Fang, H. Numerical Investigation of the Three-Dimensional Elastic–Plastic Sloped Contact Between Two Hemispheric Asperities. J. Appl. Mech. 2016, 83, 101004. [Google Scholar] [CrossRef]
- Gao, Z.; Fu, W.; Wang, W.; Kang, W.; Liu, Y. The study of anisotropic rough surfaces contact considering lateral contact and interaction between asperities. Tribol. Int. 2018, 126, 270–282. [Google Scholar] [CrossRef]
- Wang, S.J.; Fan, L.S.; Wu, J.W.; Li, P.Y. A Side Contact Model of Joint Considering the Horizontal Distance Distribution Between Asperities. J. Tribol.-Trans. ASME 2022, 144, 101501. [Google Scholar] [CrossRef]
- Lingsong, F.; Shijun, W.; Jingwei, W.; Pengyang, L. Modeling of the Normal Contact Stiffness of Joint Surfaces Considering the Horizontal Distance Distribution and Interaction of Asperities. J. Mech. Eng. 2022, 58, 201–214. [Google Scholar]
- Jackson, R.L.; Green, I. A finite element study of elasto-plastic hemispherical contact against a rigid flat. J. Tribol. 2005, 127, 343–354. [Google Scholar] [CrossRef]
- Abbott, E. Specifying surface quality a method based on accurate measurement and comparison. Mech. Eng. 1933, 55, 569–572. [Google Scholar]
- Jackson, R.L.; Duvvuru, R.S.; Meghani, H.; Mahajan, M. An analysis of elasto-plastic sliding spherical asperity interaction. Wear 2007, 262, 210–219. [Google Scholar] [CrossRef]
- Mulvihill, D.M.; Kartal, M.E.; Nowell, D.; Hills, D.A. An elastic–plastic asperity interaction model for sliding friction. Tribol. Int. 2011, 44, 1679–1694. [Google Scholar] [CrossRef]
- Chandrasekar, S.; Eriten, M.; Polycarpou, A.A. An Improved Model of Asperity Interaction in Normal Contact of Rough Surfaces. J. Appl. Mech. 2012, 80, 11025. [Google Scholar] [CrossRef]
- Linbo, Z.; Yan, Z.; Jun, H.; Guoqing, Y. An Elastoplastic Contact Mechanics Model of Asperities Considering Side Contact. J. Xi’an Jiaotong Univ. 2013, 47, 48–52+104. [Google Scholar]
- Zhao, B.; Zhang, S.; Qiu, Z. Analytical asperity interaction model and numerical model of multi-asperity contact for power hardening materials. Tribol. Int. 2015, 92, 57–66. [Google Scholar] [CrossRef]
- Yongwu, Z.; Yanming, L.; Jianzhong, J. A New Elastoplastic Contact Model of Rough Surfaces. J. Mech. Eng. 2007, 43, 95–101. [Google Scholar]
- Wang, D.; Zhang, Z.S.; Jin, F.; Fan, X.H. Normal Contact Model for Elastic and Plastic Mechanics of Rough Surfaces. Acta Mech. Solida Sin. 2019, 32, 148–159. [Google Scholar] [CrossRef]
- Zhao, G.; Li, S.-X.; Xiong, Z.-L.; Gao, W.D.; Han, Q.K. A statistical model of elastic-plastic contact between rough surfaces. Trans. Can. Soc. Mech. Eng. 2018, 43, 38–46. [Google Scholar] [CrossRef]
- Ling, L.; Anjiang, C.; Ligang, C.; Xiaoguang, R. Micro-contact Model of Bolted-joint Interface. J. Mech. Eng. 2016, 52, 205–212. [Google Scholar]
- Nayak, P.R. Random Process Model of Rough Surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, X.; Wen, S.; Wang, Y.; Yin, D.; Chen, Y. A Normal Contact Stiffness Model of Joint Surfaces Considering the Substrate Deformation and Interaction of Asperities. J. Xi’an Jiaotong Univ. 2020, 54, 115–121. [Google Scholar]
- Yakovenko, A.A.; Goryacheva, I.G. Analysis of the discrete contact characteristics based on the Greenwood-Williamson model and the localization principle. Friction 2024, 12, 1042–1056. [Google Scholar] [CrossRef]
- Hess, D.P.; Soom, A. Normal and Angular Motions at Rough Planar Contacts During Sliding With Friction. J. Tribol. 1992, 114, 567–578. [Google Scholar] [CrossRef]
- Hess, D.P.; Soom, A. The Effects of Relative Angular Motions on Friction at Rough Planar Contacts. J. Tribol. 1993, 115, 96–101. [Google Scholar] [CrossRef]
- Etsion, I.; Front, I. A Model for Static Sealing Performance of End Face Seals. Tribol. Trans. 1994, 37, 111–119. [Google Scholar] [CrossRef]
- Polycarpou, A.A.; Etsion, I. Analytical Approximations in Modeling Contacting Rough Surfaces. J. Tribol. 1999, 121, 234–249. [Google Scholar] [CrossRef]
- Borodich, F.M.; Pepelyshev, A.; Savencu, O. Statistical approaches to description of rough engineering surfaces at nano and microscales. Tribol. Int. 2016, 103, 197–207. [Google Scholar] [CrossRef]
- Jinmin, Y.; Tianning, C. Research on the Statistical Model of Static Contact Parameters of Joint Surfaces. J. Vib. Shock. 2010, 29, 47–50. [Google Scholar]
- Goryacheva, I.G.; Yakovenko, A.A. The Asperities Density and Height Distribution Combined Effect on Rough Elastic Bodies Contact Characteristics. Lobachevskii J. Math. 2024, 45, 2279–2292. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Fractal or fiction. Wear 2001, 249, 345–353. [Google Scholar] [CrossRef]
- Silva Sabino, T.; Couto Carneiro, A.M.; Pinto Carvalho, R.; Andrade Pires, F.M. The impact of non-Gaussian height distributions on the statistics of isotropic random rough surfaces. Tribol. Int. 2022, 173, 107578. [Google Scholar] [CrossRef]
- Mccool, J.I. Non-Gaussian effects in microcontact. Int. J. Mach. Tools Manuf. 1992, 32, 115–123. [Google Scholar] [CrossRef]
- Mccool, J.I. Extending the Capability of the Greenwood Williamson Microcontact Model. J. Tribol. 2000, 122, 496–502. [Google Scholar] [CrossRef]
- Yu, N.; Polycarpou, A.A. Contact of Rough Surfaces With Asymmetric Distribution of Asperity Heights. J. Tribol. 2001, 124, 367–376. [Google Scholar] [CrossRef]
- Silva Sabino, T.; Couto Carneiro, A.M.; Pinto Carvalho, R.; Andrade Pires, F.M. Evolution of the real contact area of self-affine non-Gaussian surfaces. Int. J. Solids Struct. 2023, 268, 112173. [Google Scholar] [CrossRef]
- Kotwal, C.A.; Bhushan, B. Contact Analysis of Non-Gaussian Surfaces for Minimum Static and Kinetic Friction and Wear. Tribol. Trans. 1996, 39, 890–898. [Google Scholar] [CrossRef]
- Tomota, T.; Kondoh, Y.; Ohmori, T. Modeling Solid Contact between Smooth and Rough Surfaces with Non-Gaussian Distributions. Tribol. Trans. 2019, 62, 580–591. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Wei, X.; Peng, L.; Fu, W.; Wang, W.; Hu, W. Study on normal contact stiffness characteristics in non-Gaussian rough surfaces under mixed lubrication. Acta Mech. 2024, 235, 3535–3555. [Google Scholar] [CrossRef]
- Chilamakuri, S.K.; Bhushan, B. Contact analysis of non-Gaussian random surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1998, 212, 19–32. [Google Scholar] [CrossRef]
- Kim, T.; Bhushan, B.; Cho, Y. The contact behavior of elastic/plastic non-Gaussian rough surfaces. Tribol. Lett. 2006, 22, 1–13. [Google Scholar] [CrossRef]
- Yang, G.; Li, B.; Wang, Y.; Hong, J. Numerical simulation of 3D rough surfaces and analysis of interfacial contact characteristics. CMES-Comput. Model. Eng. Sci. 2014, 103, 251–279. [Google Scholar]
- Wu, J.-J. Simulation of non-Gaussian surfaces with FFT. Tribol. Int. 2004, 37, 339–346. [Google Scholar] [CrossRef]
- Liao, D.; Shao, W.; Tang, J.; Li, J. An improved rough surface modeling method based on linear transformation technique. Tribol. Int. 2018, 119, 786–794. [Google Scholar] [CrossRef]
- Bakolas, V. Numerical generation of arbitrarily oriented non-Gaussian three-dimensional rough surfaces. Wear 2003, 254, 546–554. [Google Scholar] [CrossRef]
- Manesh, K.; Ramamoorthy, B.; Singaperumal, M. Numerical generation of anisotropic 3D non-Gaussian engineering surfaces with specified 3D surface roughness parameters. Wear 2010, 268, 1371–1379. [Google Scholar] [CrossRef]
- Francisco, A.; Brunetière, N. A hybrid method for fast and efficient rough surfacegeneration. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 747–768. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Almqvist, A. Generating randomly rough surfaces with given height probability distribution and power spectrum. Tribol. Int. 2019, 131, 591–604. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).