A Numerical Simulation Study on the Tensile Properties of Welds in Laser-Arc Hybrid Welding of Q355 Medium-Thick Plates

Abstract

Laser-arc hybrid welding was applied to Q355 medium-thick steel plates to improve weld tensile properties, with experimental verification comparing welds to the base material. Numerical simulations identified optimal process parameters, analyzing the effects of heat source distance, welding speed, laser power, and arc power on temperature field distribution and molten pool morphology. Heat source distance had the greatest influence, followed by welding speed, laser power, and arc power. Maintaining a peak welding temperature of 900–1000 K refined the weld grain structure, enhancing the tensile performance. Under optimal parameters (laser power: 800 W, arc power: 1200 W, wire distance: 5 mm, welding speed: 15 mm/s), the weld achieved a 77% elongation rate compared to the base material’s 73% at a loading rate of 0.5 mm/min, demonstrating superior tensile properties. These results comply with the Code for Welding of Steel Structures. SEM analysis showed uniform, deep dimples in both the weld and base material, indicating a dense structure, excellent plasticity, and strong fracture resistance. This study offers theoretical and experimental insights for optimizing laser-arc hybrid welding processes.

1. Introduction

Steel structures are highly regarded for their lightweight design, high strength, seismic resistance, fast construction, durability, and environmental benefits. Medium-thick steel plates, known for their excellent strength, toughness, and corrosion resistance, are essential materials for bridges and high-rise buildings. The primary failure mode of steel structures is often caused by the welds at the joints, where the tensile properties of the welds are lower than those of the base material, leading to a reduction in the service life of the relevant steel structures or equipment. However, traditional high heat input welding methods, such as arc welding, submerged arc welding, and electroslag welding, often result in uneven temperature distribution and excessively high peak temperatures, which negatively impact the mechanical properties of the welds, especially tensile strength. Under conventional welding methods, the tensile properties of the welds are inferior to those of the base material, leading to an overall reduction in the service life of the steel structure that is below its expected lifespan [1,2,3].

Improving weld tensile properties is essential and can be achieved through methods such as using high-quality welding materials, optimizing weld composition, fine-tuning welding parameters, and applying preheating or post-weld heat treatments; however, these approaches increase production costs and complexity [4,5,6]. Laser-arc hybrid welding offers a more efficient alternative by optimizing temperature distribution and peak temperature control, refining grain structure, and enhancing tensile properties [7].

Research on medium-thick plate welding has drawn significant attention due to its broad applications. Manugula et al. [8] demonstrated that increased cross-sectional thickness during full-penetration friction stir welding of ferritic–martensitic steel led to a higher heat input, affecting microstructure and hardness. Xu et al. [9] developed a regression model for optimizing key process variables in BCTW-GIA welding, achieving tensile strengths of 558 MPa, 539 MPa, and 547 MPa for plates of 8 mm, 10 mm, and 12 mm thickness, respectively. Chen et al. [10] explored arc oscillation in arc welding guns, finding that controlled arc motion enhanced the molten metal flow, improving penetration depth and grain refinement.

Although these studies primarily focus on pre- and post-weld treatments, research on laser-arc hybrid welding for medium-thick plates remains limited. Laser-arc hybrid welding combines laser and arc heat sources to enhance welding efficiency, reduce the heat-affected zone, and improve penetration depth and weld quality. Zhao et al. [11] and Zhu et al. [12] investigated the effects of laser power and hybrid welding methods, but their studies focused mainly on thin plates.

Laser-arc hybrid welding (HLAW) technology combines the high-energy density of laser welding with the filling capability of arc welding [13,14]. It has been widely evaluated in fields such as thick plate structures, aerospace, shipbuilding, and nuclear power. Research has demonstrated that HLAW can significantly improve welding quality and efficiency. This technology enables both full-penetration and partial-penetration welding of thick-walled steels, and process parameters can be optimized through numerical modeling. In materials like Q355B steel, HLAW has improved the tensile and impact strengths of duplex stainless steels, and it can effectively control the ratio of ferrite to austenite, enhancing the corrosion resistance. In the welding of 316LN stainless steel, adjusting laser-arc parameters can optimize the δ-ferrite content in the weld, thereby improving mechanical properties. However, corrosion due to element loss during high-strength steel welding remains a key research challenge. Furthermore, HLAW has been shown to have an excellent low-temperature impact strength in low-carbon bainitic steels, with the weld structure primarily consisting of refined bainite [15,16,17,18,19]. Although HLAW technology offers significant advantages, the control of welding defects, optimization of process parameters, and further improvement of the welding performance remain critical areas for future research.

This study established a numerical model for laser-arc hybrid welding using finite element analysis and heat conduction theory. Through orthogonal experimental design and simulation, the effects of laser power, arc power, heat source distance, and welding speed on the tensile properties of the weld were analyzed. The optimal process parameters were determined through numerical simulation to maintain the peak temperature within the ideal range [20]. The reliability of the simulation results was first validated using an infrared thermometer, and further verification was carried out through hardness testing and tensile experiments on the weld, heat-affected zone (HAZ), and base material. The results showed that the material properties of the weld and HAZ were superior to those of the base material, indicating high weld quality. Therefore, laser-arc hybrid welding for medium-thick steel plates can effectively enhance the service life of the welded components.

2. Materials and Methods

2.1. Numerical Simulation

The present study employed COMSOL numerical simulation software (COMSOL Multiphysics 6.1), focusing on a Q355 medium-thick steel plate with a thickness of 10 mm, length of 150 mm, and width of 30 mm. By simplifying the actual steel structure, a three-dimensional finite element model was developed to primarily investigate variations in the temperature field. The finite element model and its mesh structure are shown in Figure 1.

In Figure 1, the mesh division required balancing accuracy and computational efficiency. Overly large elements would compromise accuracy, while excessively fine elements would significantly increase the computational demand. Based on the characteristics of the welding process, the temperature gradient near the weld is steep, whereas it is relatively shallow in regions far from the weld. Therefore, an optimized meshing strategy was adopted, wherein fine mesh elements were applied in areas near the weld, while coarser elements were used in distant regions. This method achieves an optimal balance between computational accuracy and efficiency, ensuring reliable simulation results.

The model dimensions are 150 mm in length, 30 mm in width, and 10 mm in height. The complete mesh comprises 388,875 domain elements, 23,540 boundary elements, and 912 edge elements, all using four-node tetrahedral elements. This approach ensures sufficient detail in critical areas while maintaining computational efficiency.

2.2. Basic Assumptions of the Model

In the process of performing numerical simulations of welding, a series of assumptions and simplifications of the actual welding conditions are usually required in order to make the welding model solvable [21]. These assumptions help to reduce the complexity of the model, making it possible to simulate the welding process while still capturing key features of the welding process. The following simplifications and assumptions are made based on the above:

• The simulation assumes that the initial temperature of the weldment before welding is room temperature, i.e., 295 K. Excluding extreme temperature conditions during welding, a temperature variation of ±5 K around room temperature, does not significantly affect weld quality.
• The temperature effect of the spot-welding stage on the main welding process is not considered in the simulation.
• The heat source in the model is assumed to move forward along the Z-axis with a certain velocity, V. The whole welding process is considered as a steady-state process without considering the unsteady phases, including the weld initiation phase.
• In the simulation, the residual height of the weld generated during the actual welding process is ignored, and the surface of the molten pool obtained from the simulation is assumed to be perfectly horizontal.
• The heat transfer in welding is modeled solely based on thermal conduction, without considering fluid flow and convection within the molten pool. However, to compensate for the absence of fluid flow effects, an equivalent volumetric heat source with a specific shape is applied within the material to generate heat, ensuring that the fusion occurs.
• The material is considered isotropic and homogeneous; however, certain physical properties, such as thermal conductivity and specific heat, are temperature-dependent.
• The mechanisms of laser–material interaction and absorption are not considered.
• The simulation excludes the initial gap between the plates (butt joint seam) and treats the finite element model as a bead-on-plate.

2.3. Heat Conduction Model

The main heat transfer modes involved in the laser-arc hybrid welding process include heat conduction, heat convection, and heat radiation. Heat conduction is primarily used to accurately explain the cooling process at the contact points between the workpiece, fixture, and workbench. Heat convection is used to simulate the cooling process between the workpiece and the surrounding air, while heat radiation is employed to model the heating process of the laser-arc system. The heat conduction process involves the dissipation of heat from the welded workpiece in contact with the fixture.

Temperature propagates in different directions, meaning that temperature changes occur in three-dimensional space and vary with time. This type of heat transfer process is referred to as three-dimensional unsteady heat transfer, and the heat diffusion equation is well-suited to simulate the heat distribution and diffusion within the workpiece [21].

$${\displaystyle \frac{\partial \left(k\frac{\partial T}{\partial x}\right)}{\partial x}}+{\displaystyle \frac{\partial \left(k\frac{\partial T}{\partial y}\right)}{\partial y}}+{\displaystyle \frac{\partial \left(k\frac{\partial T}{\partial z}\right)}{\partial z}}+q=\rho c_p{\displaystyle \frac{\partial T}{\partial t}}$$

(1)

where

• x, y, z is the three-dimensional coordinate system;
• c_p is the constant pressure-specific heat capacity;
• ρ is the density.

Thermal convection mainly involves the convective heat dissipation process between the weldment and the air during the welding process, and the thermal convection transfer rate equation, which is as follows:

$$Q=hA(T_s-T_f)$$

(2)

where Q is the heat flow rate, H is the thermal convection heat transfer coefficient, A is the surface area for heat exchange, $T_s$ is the surface temperature, and $T_f$ is the fluid temperature.

Thermal radiation is mainly concerned with the laser-arc heating process of welds and weldments. In this paper, the Stefan–Boltzmann law equation is used, which is as follows:

$$P=\sigma A{T}^4$$

(3)

where P is the radiant power, $\sigma$ is the Stefan–Boltzmann constant, A is the surface area of an object, and T is the absolute temperature of an object.

The welding process is very complex, and in order to obtain a unique solution through the heat balance equation, reasonable boundary conditions and initial conditions must be given in the modeling. The boundary conditions involved in this paper are mainly of the following three types:

Temperature constrained boundary conditions;

$$\lambda {\displaystyle \frac{\partial T}{\partial x}}{n}_x+\lambda {\displaystyle \frac{\partial T}{\partial y}}{n}_y+\lambda {\displaystyle \frac{\partial T}{\partial z}}{n}_z=T_s(x,y,z,t)$$

(4)

Boundary constraints on heat flow density values;

$$\lambda {\displaystyle \frac{\partial T}{\partial x}}{n}_x+\lambda {\displaystyle \frac{\partial T}{\partial y}}{n}_y+\lambda {\displaystyle \frac{\partial T}{\partial z}}{n}_z=q_s(x,y,z,t)$$

(5)

Boundary constraints on medium temperature and heat transfer coefficient;

$$\lambda {\displaystyle \frac{\partial T}{\partial x}}{n}_x+\lambda {\displaystyle \frac{\partial T}{\partial y}}{n}_y+\lambda {\displaystyle \frac{\partial T}{\partial z}}{n}_z=\alpha \left({T_a-T}_s\right)$$

(6)

where $T_a$ is the medium temperature, $T_s$ is the boundary temperature, $q_s$ is the external energy input per unit area, $\alpha$ is the surface heat transfer coefficient of an object, and $n_x,n_y,n_z$ is the cosine of the boundary along the normal direction.

2.4. Heat Source Modeling

The laser-arc composite weldment is a superposition of two heat sources; thus, to better simulate it numerically, it is necessary to establish simulated heat sources corresponding to the laser and the arc to simulate the composite weldment. A Gaussian surface heat source is used to simulate the thermal effect of the arc, while a rotating Gaussian body heat source is used to simulate the effect of the laser. The simulation method takes into account the front and rear guidance and weight of the heat source, usually half of each, which can truly reflect the phenomenon of laser-arc composite welding and provide theoretical and experimental support for process optimization [22].

2.4.1. Arc Heat Source Modeling

The Gaussian surface heat source model is widely used in arc simulation by virtue of its ability to accurately simulate welding heat distribution. It utilizes the Gaussian distribution principle to make the simulated thermal effects closer resemble reality. Figure 2 illustrates the Gaussian surface heat source model. The model is recognized by researchers, significantly improving the welding simulation effect, helping to optimize welding parameters and processes, in which both theory and practice are very beneficial. The following is the Gaussian surface heat source formula:

$$q\left(x,y\right)=q_m·e^{-K(x^2+y^2)}$$

(7)

$$q_m={\displaystyle \frac{Q·K}{\pi }}$$

(8)

$$K={\displaystyle \frac{3}{R_0^2}}$$

(9)

where $q_m$ is the peak heat flow density and $R_0$ is the radius of the heat source.

2.4.2. Laser Heat Source Modeling

The Gaussian body heat source model uses Gaussian distribution to accurately simulate the laser energy distribution and realize the simulation of laser heat source behavior in high-precision material processing. Figure 3 shows the selected Gaussian body heat source diagram. The rotating Gaussian body heat source formula is as follows:

$$q\left(x,y,z\right)=q(\mathrm{0,0})e^{[{\displaystyle \frac{-3c_s}{\log \left(\frac{H}{z}\right)}}(x^2+y^2)]}$$

(10)

$$q\left(\mathrm{0,0}\right)={\displaystyle \frac{3c_{s}Q}{\pi H(1-e^{-3})}}$$

(11)

$$c_s={\displaystyle \frac{3}{R_1^2}}$$

(12)

where q is the heat flow density, H is the height of heat source, $R_1$ is the heat source opening radius, and $c_s$ is the heat source shape concentration factor.

2.5. Material Model

Thermophysical properties of steel, such as thermal conductivity, heat capacity, and density, have an important influence on the welding simulation results. In this study, thermal conductivity and heat capacity are considered as a function of temperature, taking constant values above the melting point. The solid phase change is approximated by increasing the heat capacity in the interval from 900 K to 1000 K. The thermal conductivity increases at the melting point, promoting heat dissipation from the melt pool and obtaining a realistic peak temperature.

Table 1. Thermophysical performance of Q355 [23].

Temp/K	20	100	300	500	1000	1500
thermal conductivity/[W·(m·K)−1]	0.189	0.187	0.169	0.144	0.100	0.109
densities/(kg·m−3)	7866	7845	7740	7711	7578	7552
specific heat capacity/[J·(kg·K)−1]	1.668	1.810	2.073	2.505	2.853	1.465
coefficient of thermal expansion/×10−8·K−1	2.260	3.044	0.450	5.022	5.919	6.652
modulus of elasticity/GPa	207	203	183	150	63	10
yield strength/MPa	345	326	278	179	11	5
Poisson’s ratio	0.28	0.31	0.33	0.37	0.47	0.49

shows the physical properties of the material during simulation.

2.6. Simulation of Orthogonal Experimental Design

The relationship between the temperature field and grain size is primarily characterized by the effect of temperature on grain growth. Grain growth requires a driving force, and temperature is the primary factor in providing this driving force. After the initial stages of recrystallization are over, continued heating causes the crystal to grow, and higher temperatures increase the diffusion coefficients of the atoms, making it easier for grain boundaries to migrate. Grain boundary migration is an intrinsic process of grain growth, so increasing the temperature accelerates grain growth. In order to obtain a grain of the right size, the temperature field needs to be reasonably controlled. Additionally, coarse grains will lead to a decrease in tensile properties. Experimental investigations into the optimal crystallization temperature for welding Q355 steel plates have demonstrated that achieving a peak temperature between 900 K and 1000 K results in a weld with refined grain structures [24]. In the case of a certain peak temperature, the shorter the holding time, the more the grain refinement.

In the process of laser-arc hybrid welding, key parameters significantly influencing the temperature field include laser power, arc power, welding speed, and heat source spacing. To systematically analyze these factors, we implemented an orthogonal experimental design with four factors and three levels. The experimental matrix, as detailed in

Table 2. Parameter list of orthogonal experimental design.

Serial Number	1	2	3	4
Considerations	Laser Power	Arc Power	Heat Source Spacing	Welding Speed
level 1	800 W	800 W	1 mm	5 mm/s
level 2	1200 W	1200 W	3 mm	10 mm/s
level 3	2400 W	2400 W	5 mm	15 mm/s

, specifies the selected parameters and their corresponding levels for this investigation. This methodological approach enables efficient evaluation of parameter interactions while maintaining experimental feasibility through reduced test combinations.

2.7. Experimental Equipment and Materials

The experimental material used in this study was Q355 steel with dimensions of 100 mm in length, 30 mm in width, and 8 mm in thickness. The welding wire was ER50-6, with a diameter of 1.2 mm. Prior to welding, the oxide layer on the steel plate surface was removed using a steel brush, and the workpiece surface was cleaned with anhydrous ethanol.

Table 3. The chemical composition of Q355.

Ingredient	C	P	Mn	Si	S
quantity contained	0.18	0.0011	1.5	0.41	0.0014

presents the chemical composition of Q355 steel [24].

The welded steel plates were prepared with a 35° bevel at the joint, leaving a 4 mm root face at the bottom. The gap between the two plates was set between 1 mm and 2 mm and secured using a fixture, as shown in Figure 4.

Table 4. The mechanical properties of Q355.

Materials	Tensile Strength/MPa	Yield Strength/MPa	Procrastination Rate (%)	Aku
Q355	450	355	73	35

presents the mechanical properties of Q355 steel plate, as follows:

In this experiment, the laser-arc hybrid welding system used is composed of several key components. The system includes the FC3000S fiber laser, the MFR-280 gas-shielded welding machine, the BRTIRUS1820A Bronte six-axis robot, the TEYU industrial cooling system CW-6260, and the CVD infrared temperature sensor, as shown in Figure 5. When welding on Q355 steel plates, the following process parameters obtained through simulation were used: a laser power of 800 W, arc power of 1200 W, beam offset of 5 mm, and welding speed of 15 mm/s.

In this experiment, the heat source configuration placed the laser ahead of the arc. The welding torch was set at a 60° angle to the horizontal plane, with a wire stick-out length of 10 mm. The distance between the welding wire and the laser beam on the surface of the medium-thick plate was 3 mm. Argon (Ar) was used as the shielding gas at a flow rate of 20 L/min. The spot diameter is 2 mm.

2.8. Tensile Test

After welding, tensile test specimens were prepared in accordance with the ISO 5178 standard, Tensile Testing of Welded Joints. Specimens were selected from areas perpendicular to the weld zone and the base material zone. The sampling method is illustrated in Figure 6.

Figure 7 shows the detailed dimensions and specifications of the tensile specimens prepared for the tensile test. The overall dimensions of the specimens are as follows: a length of 25 mm, width of 7.5 mm, and thickness of 2 mm.

The tensile specimens were processed using specialized wire cutting. Specimen 1 in the diagram represents the weld zone tensile specimen, while 0 represents the base material tensile specimen. The specimens were subsequently polished using sandpaper (rough and fine) and cleaned with anhydrous ethanol. The final tensile specimens are shown in Figure 8.

The tensile test was conducted at a loading rate of 0.5 mm/min. Data were collected and transmitted using a universal testing machine, while the initial specimen length of 25 mm was measured with a ruler.

3. Results and Discussion

3.1. Orthogonal Experiment Polar Analysis

The orthogonal experimental design requires identifying the correspondence between factors and their levels [25], and determining the most influential factor on the results through variance analysis, along with its corresponding optimal level [26,27,28].

Using the orthogonal experimental design method, we concluded that nine simulation experiments are required to comprehensively evaluate the effects of welding parameters on the temperature field distribution and molten pool morphology. This experimental design allows for a systematic analysis of each parameter—such as heat source spacing, welding speed, laser power, and arc power—enabling an independent assessment of their influence on welding quality.

The peak value of the temperature field can be converted into the corresponding stress by the formula to carry out orthogonal experimental analysis [29], and the peak temperature can also be used directly as a criterion. The tensile properties of the metal can be approximated by a quadratic function that is symmetrical around the optimal temperature range [30]. Therefore, in the orthogonal experimental range analysis, segmented temperature values were used as evaluation criteria, with temperatures divided into the following two segments: below 900 K and above 1000 K.

$$\left\{\begin{array}{c}T=1000K-\left(T_A-1000K\right),T_A\gg 1000K\\ T=100K+T_A{ ,T}_A<900K\end{array}\right.$$

(13)

T is the converted temperature value and $T_A$ is the actual temperature value.

Table 5. Simulation results of orthogonal experiments.

Serial Number	1	2	3	4	In the End
Considerations	Laser Power	Arc Power	Heat Source Spacing	Welding Speed	Temperature Size
test 1	800 W	800 W	1 mm	5 mm/s	758 K
test 2	800 W	1200 W	3 mm	10 mm/s	744 K
test 3	800 W	2400 W	5 mm	15 mm/s	985 K
test 4	1200 W	800 W	1 mm	5 mm/s	624 K
test 5	1200 W	1200 W	3 mm	10 mm/s	794 K
test 6	1200 W	2400 W	5 mm	15 mm/s	640 K
test 7	2400 W	800 W	1 mm	5 mm/s	788 K
test 8	2400 W	1200 W	3 mm	10 mm/s	930 K
test 9	2400 W	2400 W	5 mm	15 mm/s	635 K

shows each set of experiments and their corresponding results, as follows:

Table 6. Polar analysis of the data from the orthogonal experiments.

Serial Number	1	2	3	4
Considerations	Laser Power	Arc Power	Heat Source Spacing	Welding Speed
average value 1	829	723	776	729
average value 2	686	823	667	724
average value 3	784	753	856	846
extremely poor	143	99	188	122

shows the data of the orthogonal experiments, which result from analyzing the results of the orthogonal experiments in terms of polarity analysis.

In laser-arc hybrid welding, heat source spacing has the greatest impact on temperature because it directly affects the interaction between the laser and the arc. Laser power ranks second, as the energy from the laser is more concentrated compared to the arc, making its effect on peak temperature more pronounced. Welding speed has a moderate effect, while arc power has the least influence on peak temperature.

The optimal process parameters for achieving the best tensile performance of the weld are presented in

Table 7. Optimal process parameter values.

Considerations	Laser Power	Arc Power	Heat Source Spacing	Welding Speed
Parameter Size	800 W	1200 W	5 mm	15 mm/s

. Using these parameters ensures that the peak temperature remains within the range of 900 K to 1000 K, thereby enhancing weld quality and tensile properties.

Through the aforementioned simulation experiments, we obtained temperature distribution maps and molten pool morphology diagrams for the weld area. A temperature probe was placed at the center of the weld, 10 mm from the welding start point, to observe the relationship between peak temperature and holding time. By comparing the simulation results, we identified the parameter set that achieved a peak temperature within the range of 900 K to 1000 K with the shortest holding time. This parameter set was selected as the optimal experimental condition for the welding test.

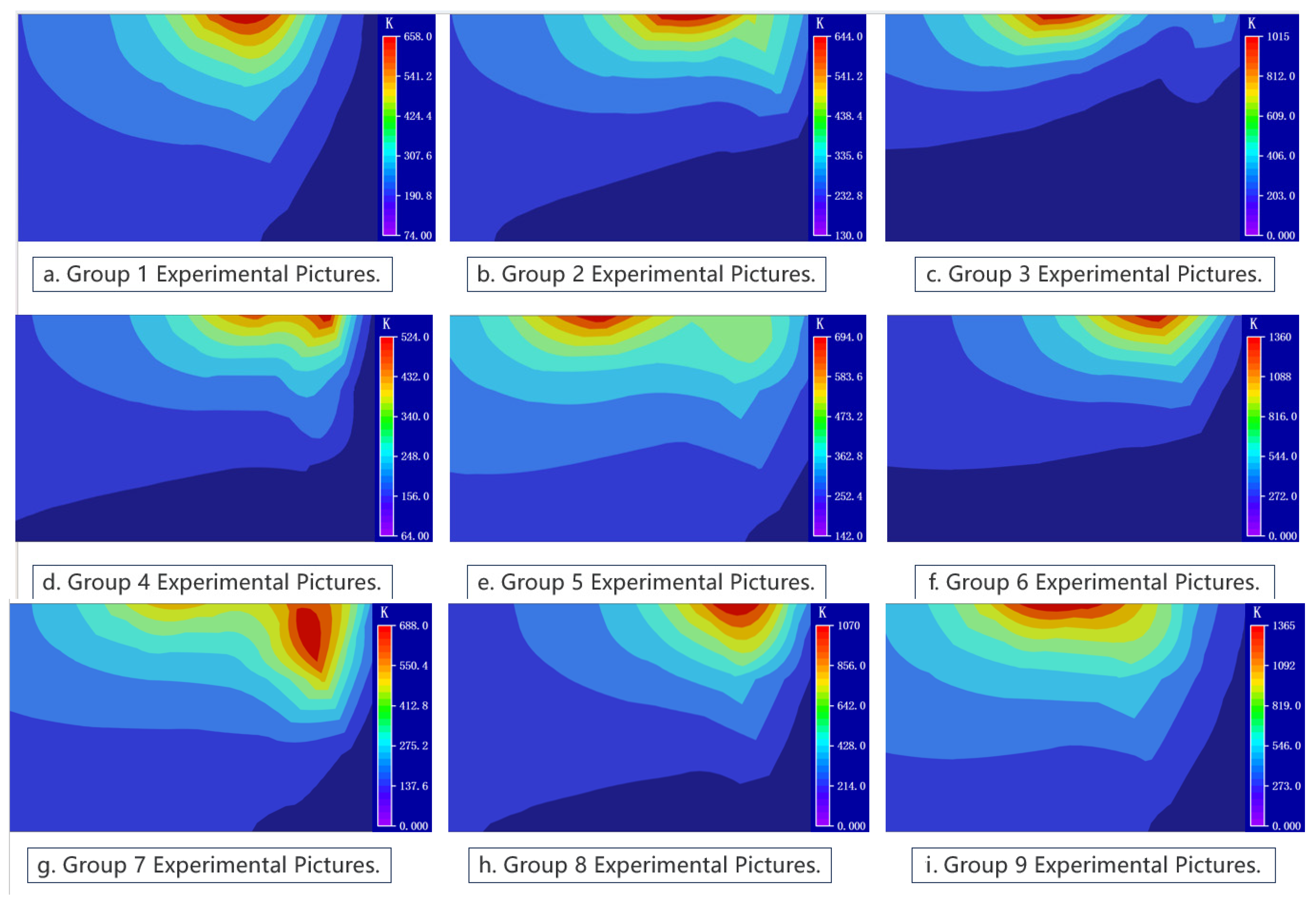
Figure 9 shows the peak temperatures during the simulation of the orthogonal experimental parameters. Figure 9a–i corresponds to experimental groups 1 to 9, respectively. From the simulated temperature field diagrams, the peak temperature of the weld and the corresponding molten pool morphology can be clearly observed.

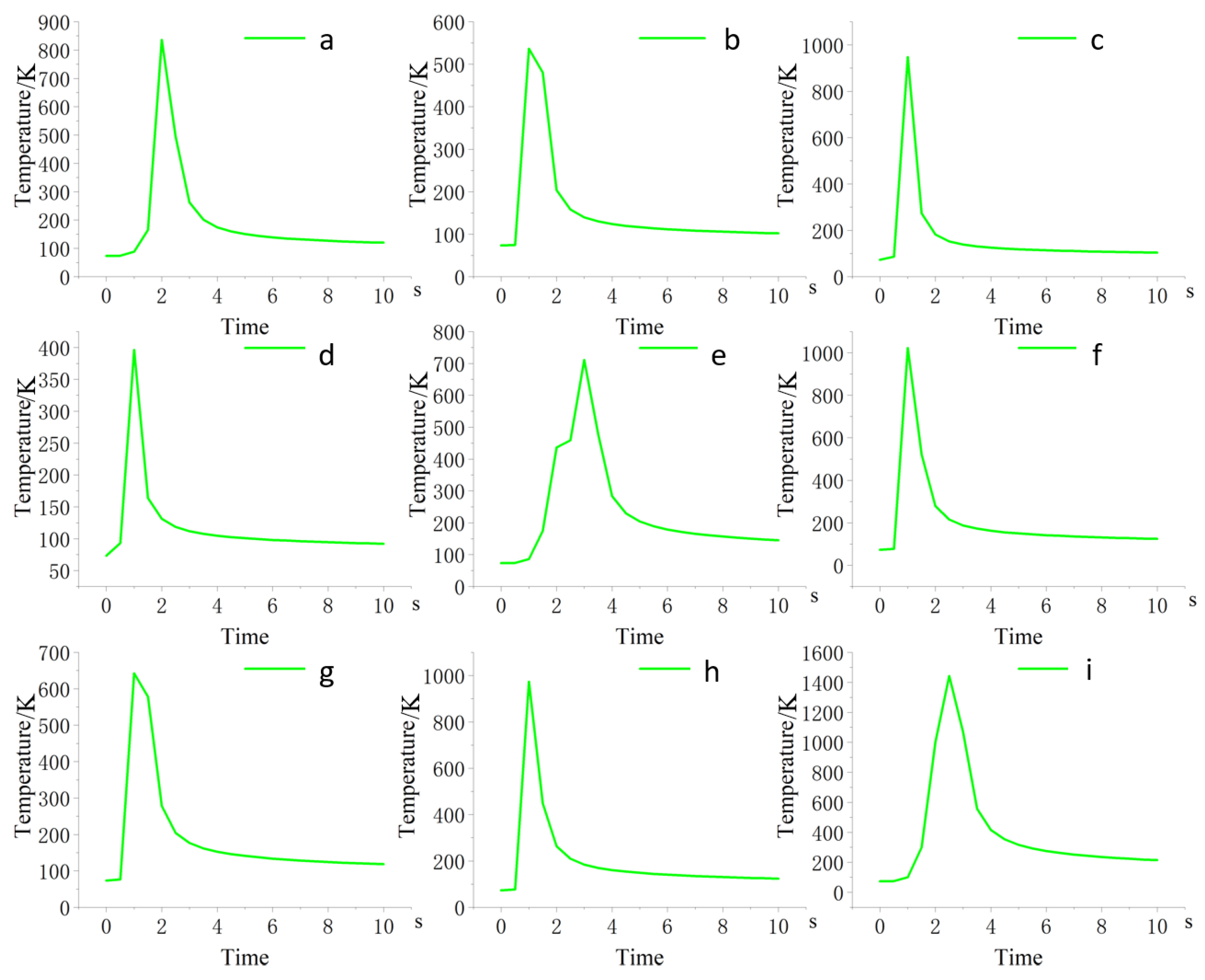
Figure 10 shows the temperature variation over time at the weld center, 10 mm from the welding start point. By comparing the point temperature graphs from Experiments 1 to 9, the following conclusions can be drawn:

Under the condition that the peak temperature falls within the range of 900–1000 K, a higher welding speed results in a shorter holding time. This is beneficial for grain refinement. From the nine graphs (a–i), it is evident that the temperature profile in graph E has the largest area, indicating a relatively long holding time. In contrast, the temperature profiles in graphs C and F have smaller areas, reflecting shorter holding times.

The comparison of experimental groups clearly shows that holding time is most significantly influenced by welding speed. The shorter the heat source dwell time, the shorter the holding time.

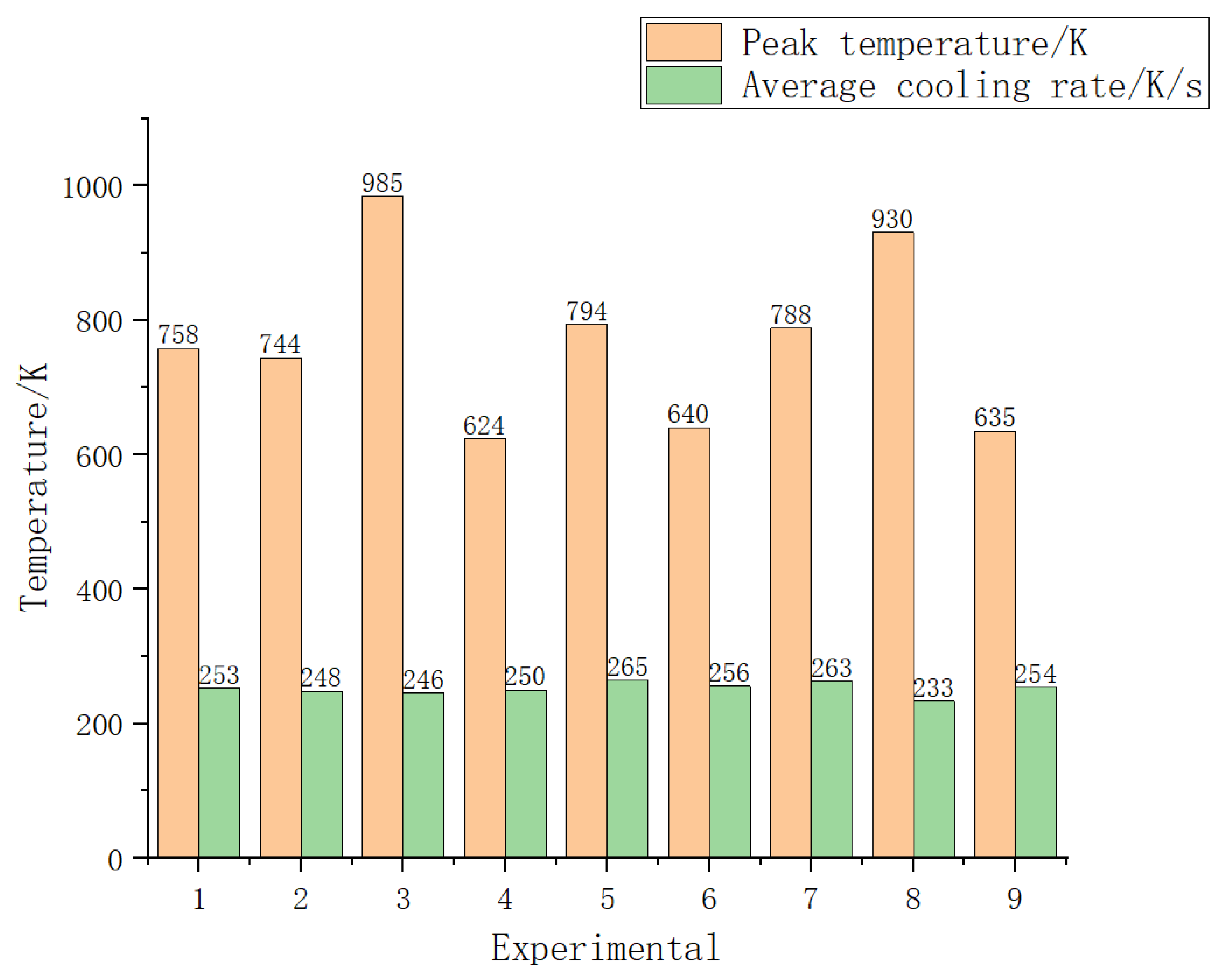
Figure 11 demonstrates the relationship between peak temperature and cooling rate under natural cooling conditions in the simulation. As shown, the magnitude of the peak temperature exhibits a negligible influence on the natural cooling rate of Q355 steel. Specifically, the average cooling rate from peak temperature to 700 K remained approximately 250 K/s under natural cooling conditions without additional insulation. This consistency suggests that process parameters (e.g., laser power, arc current) have a limited impact on cooling rates during laser-arc hybrid welding. Instead, the cooling behavior is determined primarily by the intrinsic thermal properties of the base metal. Furthermore, such cooling rate stability implies that there is no significant correlation with the mechanical performance of the weldments.

3.2. Welding Test Results

Within the optimal temperature range, the simulation of the surface numerical model is reliable. The weld seam is uniform, with a smooth and even surface, and distinct weld ripples. This indicates a stable welding heat source and the absence of significant welding defects, such as undercut, lack of fusion, or porosity.

The heat-affected zone (HAZ) is minimal. The laser-arc hybrid welding technique combines the high-energy density of the laser with the stable heat input of the arc, resulting in a narrow HAZ. This reduces changes to the base material’s properties and minimizes distortion.

The weld exhibits significant penetration. From the weld coloration and heat input distribution, the deep penetration is evident, which is attributed to the synergistic effect of the laser and the arc, which concentrates the heat transfer deep into the molten pool.

The improvement in weld quality can be primarily credited to the laser-arc synergy, which enhances penetration depth, reduces defect rates, and optimizes HAZ distribution. Figure 12 shows the welding experiment results.

During the numerical simulation, ten-point temperature probes were inserted at 10 mm intervals along the weld seam to record the peak temperatures at the corresponding points throughout the welding process. These simulated peak temperatures were then compared to experimental measurements obtained from infrared thermometers positioned at identical probe locations during physical welding trials. The discrepancies between the simulated and experimental results were systematically evaluated through residual analysis to validate the model’s accuracy against actual welding processes. The formula for calculating residuals is as follows:

$$e_i=y_i-\widehat{y_i}$$

(14)

$${\epsilon }_i={\displaystyle \frac{\left|e_i\right|}{y_i}}\times 100\%$$

(15)

where $e_i$ is the residual value, $y_i$ is the observed value, $\widehat{y_i}$ is the model’s predicted value, and ${\epsilon }_i$ is the relative error.

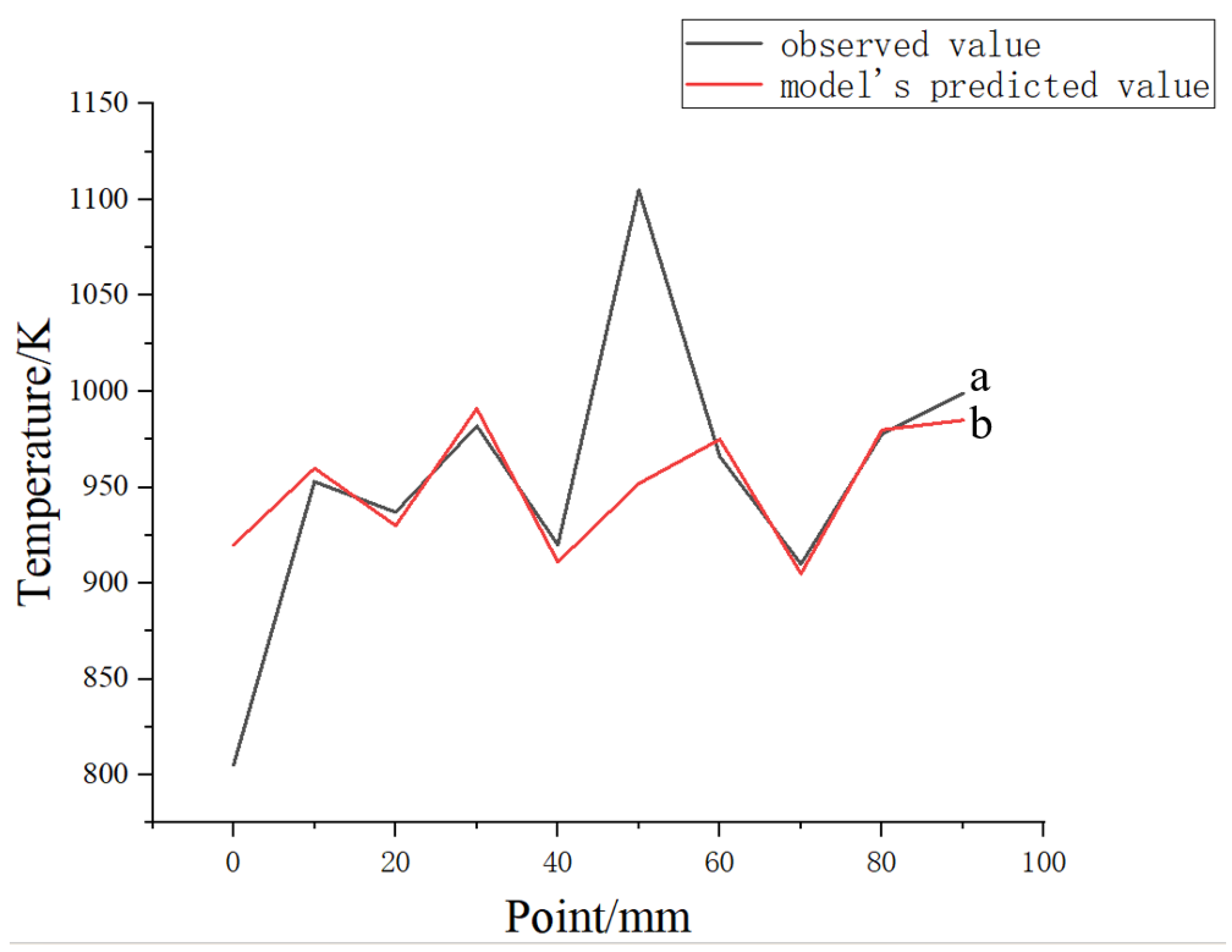
Figure 13 presents the temperature curves, comparing the observed and simulated values. Curve ‘a’ represents the observed values, while curve ‘b’ represents the model’s predicted values. By comparing these curves, we observe that, except for a few points, the temperature trends of the observed and predicted values align well, indicating a good agreement between the simulation and experimental results.

Table 8. Residual and error analysis table.

Point	${\mathit{y}}_{\mathit{i}}$	$\widehat{{\mathit{y}}_{\mathit{i}}}$	${\mathit{e}}_{\mathit{i}}$	${\mathit{\epsilon }}_{\mathit{i}}$
1	805 K	920 K	−115 K	14.29%
2	953 K	960 K	−7 K	0.73%
3	937 K	930 K	7 K	0.75%
4	982 K	991 K	−9 K	0.92%
5	920 K	911 K	9 K	0.98%
6	1105 K	952 K	153 K	13.85%
7	966 K	975 K	−9 K	0.93%
8	910 K	905 K	5 K	0.55%
9	978 K	980 K	−2 K	0.20%
10	999 K	985 K	14 K	1.40%
Average value	956 K	951 K	5 K	0.52%

presents a comparison of error and residual analyses between the actual welding process and the simulation model’s peak temperature differences. By selecting ten points along the weld seam at 10 mm intervals, starting from the center, we observe that, except for the initial point and the sixth point, the predicted and observed values for all other points align within approximately 1%. Overall, the average error is only 5%, indicating that the numerical simulation model is reliable.

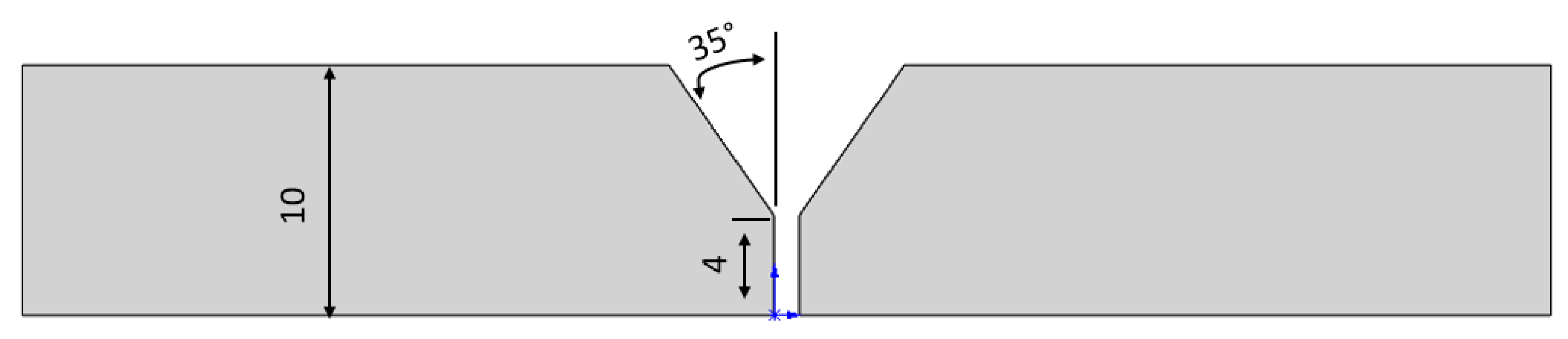
The HV-1000 Vickers hardness tester was used to measure the hardness at the center of the weld, in the heat-affected zone (HAZ), 6 mm away from the weld center, and in the base material zone, 25 mm away from the weld. Figure 14 illustrates the process of selecting the locations for microhardness test points.

The hardness was tested at five points along the weld, with a spacing of 0.5 mm between adjacent points. A load of 1000 N was applied for 10 s.

Table 9. Hardness values in different regions.

Region	Point 1	Point 1	Point 1	Point 1	Point 1	Average Value
weld area	190 HV	188 HV	191 HV	185 HV	192 HV	189.2 HV
heat-affected zone	202 HV	204 HV	208 HV	200 HV	205 HV	203.8 HV
masterbatch	169 HV	173 HV	165 HV	170 HV	172 HV	169.8 HV

shows the hardness measurement results for the weld zone, heat-affected zone, and base material zone. By comparing the hardness values from different regions, it was found that the average hardness in the heat-affected zone was the highest, at 203.8 HV, followed by the weld zone, at 189.2 HV, and the lowest was in the base material zone, at 169.8 HV. The reason for this result is that the base material has finer grains, resulting in lower hardness, while the grain growth during welding increases the hardness in the heat-affected zone and the weld zone, making them harder than the base material.

3.3. Tensile Test Results

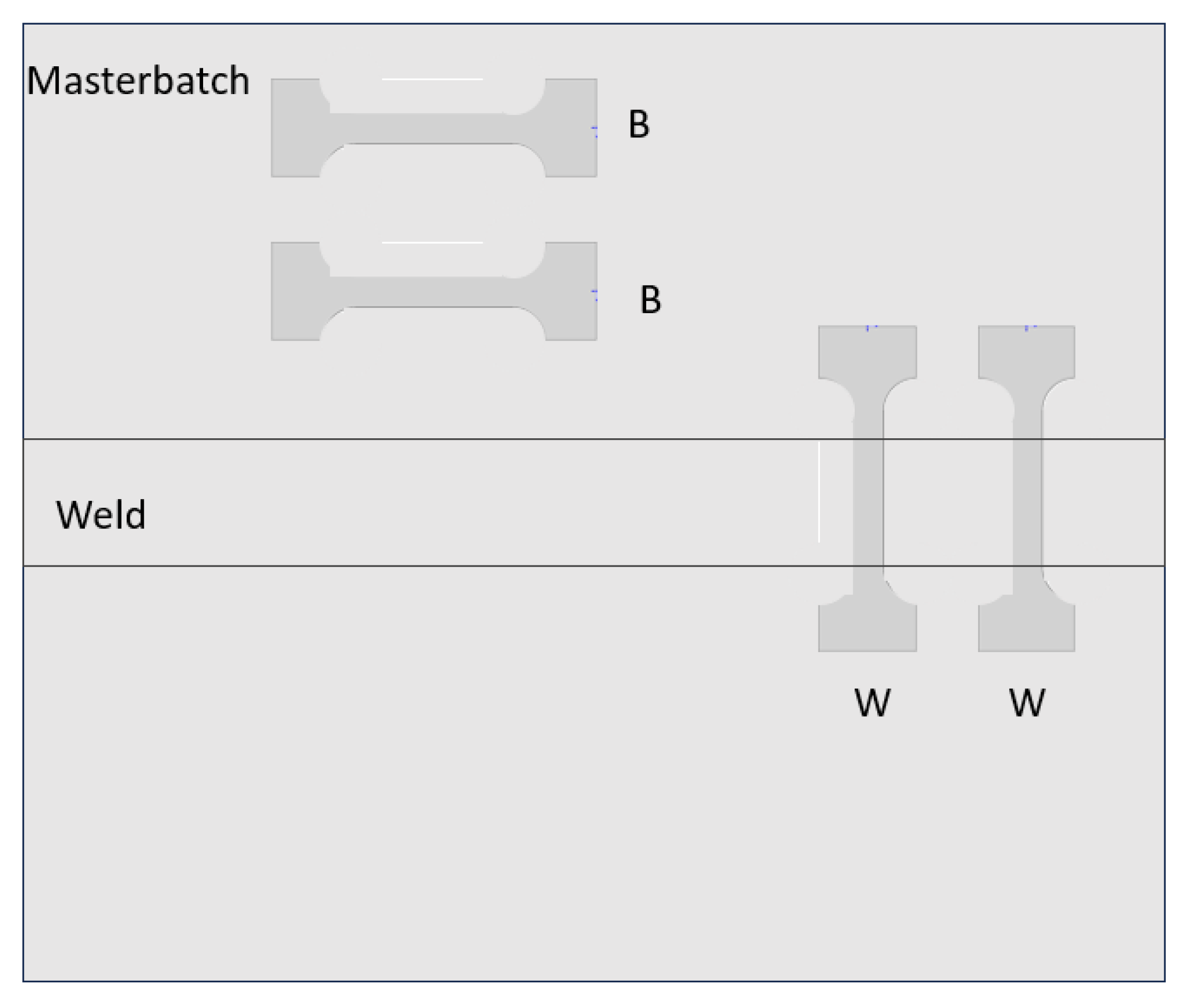
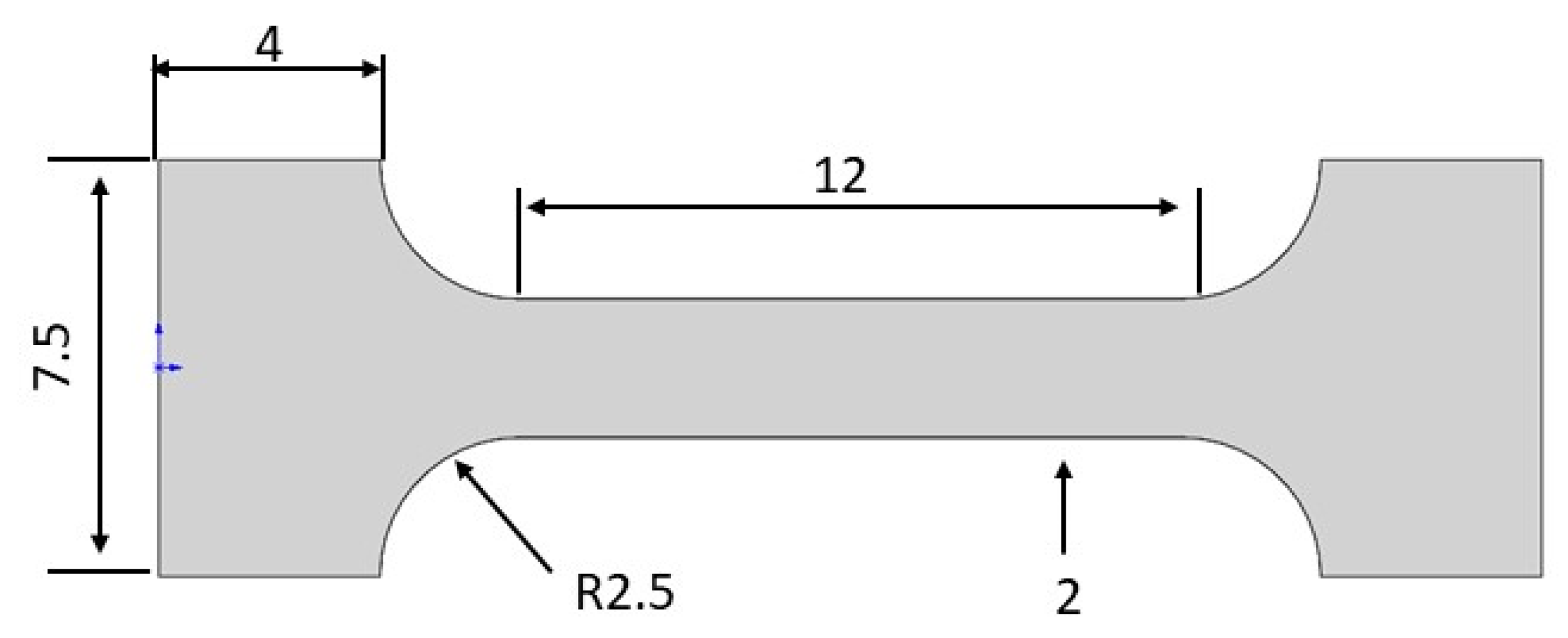
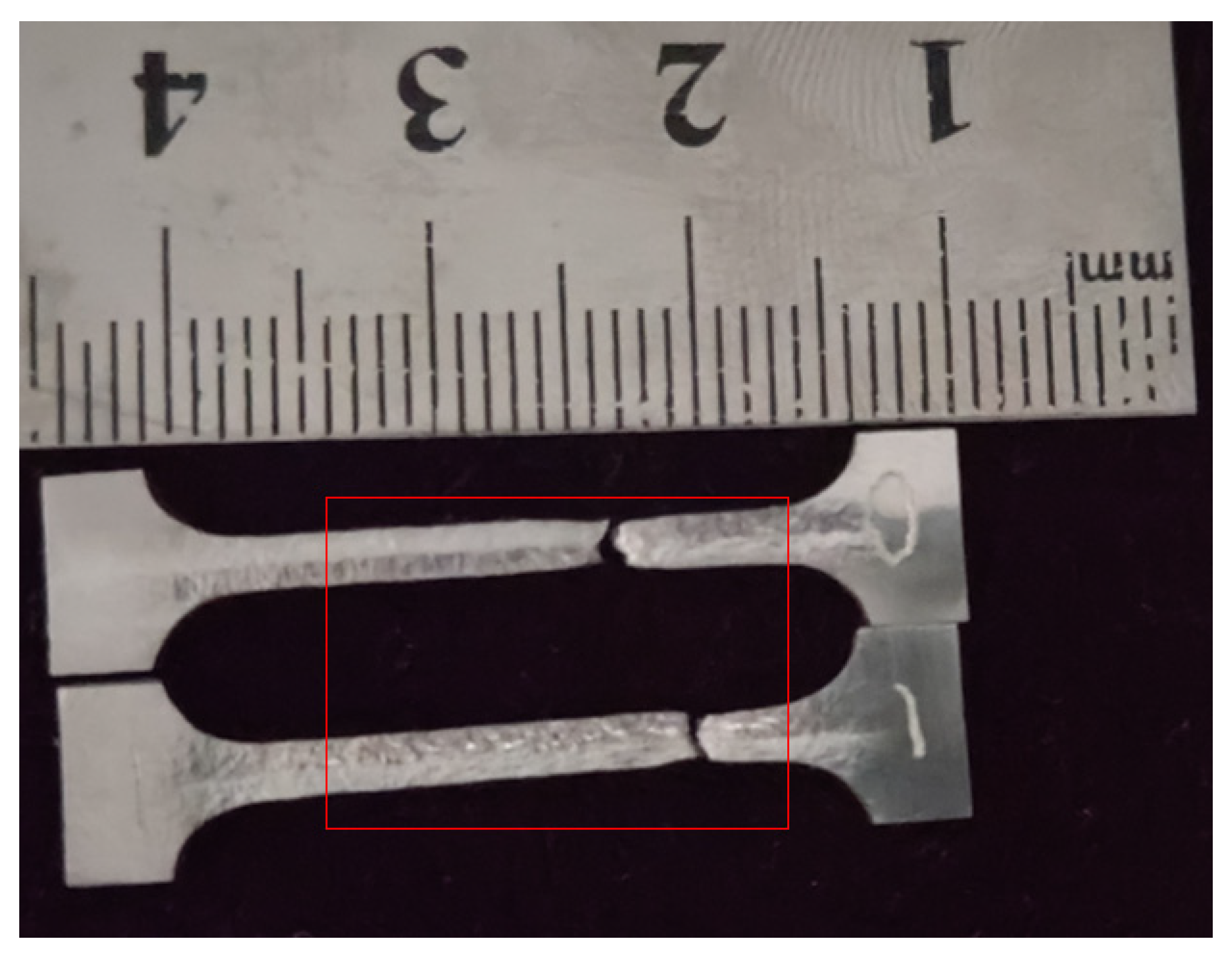
The tensile test results for specimens from the base material and weld zone under a loading rate of 0.5 mm/min are shown in Figure 15. From the post-tensile comparison, it is evident that both the weld and base material specimens fractured in the same location, concentrated in the base material zone, with noticeable elongation compared to their original state. The fracture occurred in the base material rather than in the weld or heat-affected zone, indicating that the weld exhibits excellent tensile performance.

The strain range of the weld (a) is consistent with that of the base material and (b) exhibits a more prolonged plastic deformation phase under high-stress conditions. Notably, at a strain of 55%, the weld curve shows a brief stress spike (indicated by the arrow in Figure 16), which may result from the pinning effect of solute atoms on dislocations during dynamic strain aging. This reflects the dynamic interaction between dislocation movement and microstructure in the fine-grained weld. This indicates that the weld possesses ductility comparable to, or even exceeding, that of the base material. The weld zone elongation reaches 77%, a 4% improvement over the base material’s at 73%, fully demonstrating the weld’s excellent plasticity. This performance indicates that the welding process effectively suppresses grain coarsening or defect formation in the weld zone, ensuring that the weld’s plasticity and toughness indicators align well with those of the base material, in accordance with the technical requirements of the Chinese national standard, “Steel Structure Welding Code” (GB 50661-2011). The fracture locations and stress levels of both are highly consistent, and the weld does not exhibit brittle fracture characteristics, indicating that its plasticity and fracture resistance have reached or surpassed the base material’s level.

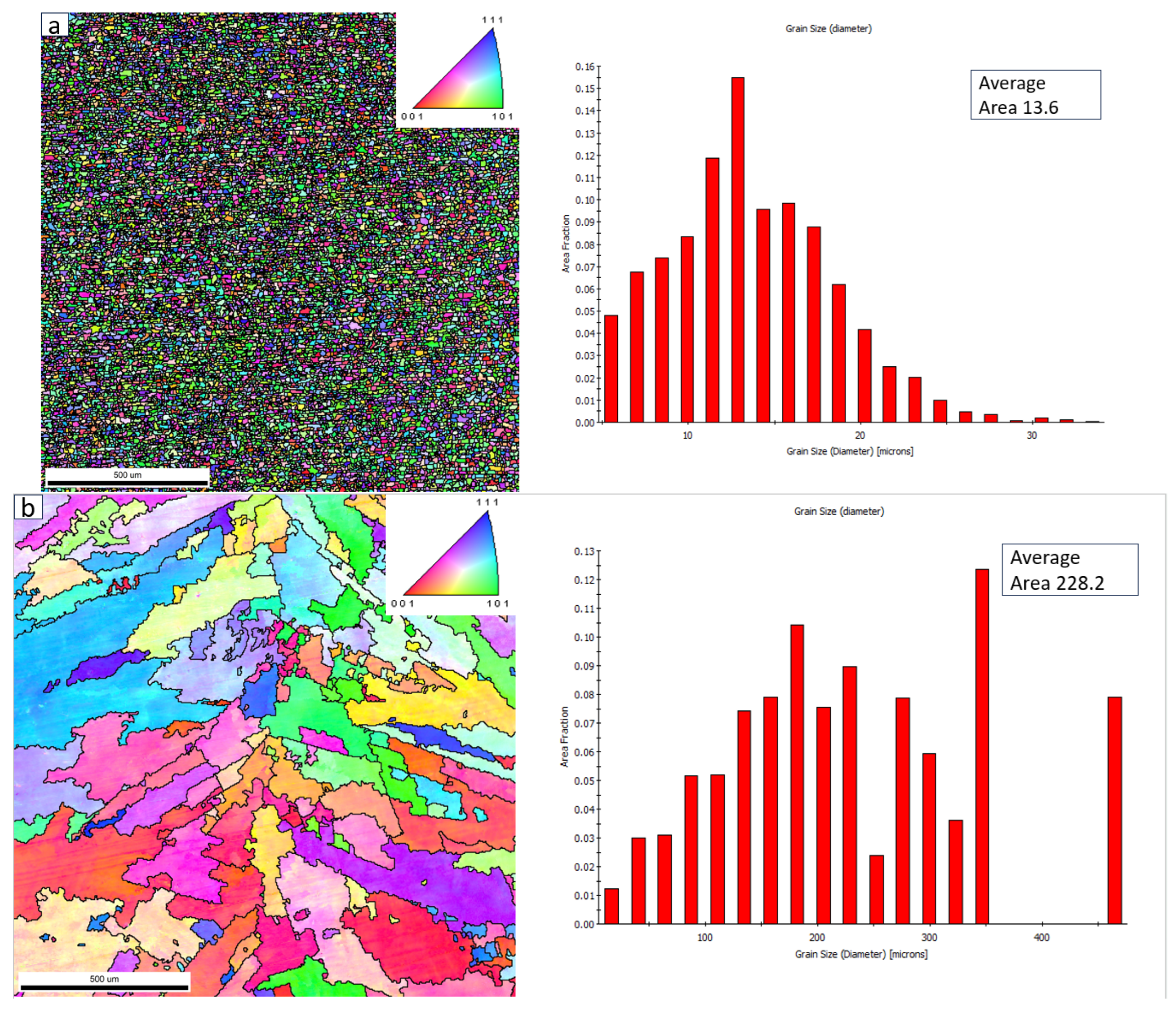
Figure 17 shows the EBSD microstructure maps of the base material and the weld. Subfigure (a) represents the microstructure of the base material, and subfigure (b) represents the microstructure of the weld. By comparison, we observe that the grain structure of the base material is tightly arranged, while the grains in the weld grow in a dendritic pattern from the center and are also closely packed. Both grain arrangements contribute to excellent mechanical properties. The average grain size of the base material is only 13 μm, and such a fine grain structure leads to lower tensile properties and hardness compared to the weld. In contrast, the average grain size of the weld has grown to 228 μm due to the welding process, resulting in improved mechanical properties, as well as particularly better tensile strength and overall performance. Both the weld and the base material are primarily composed of alpha (α) and gamma (γ) phases.

The following are the SEM tensile fracture images of the weld and base metal, at a tensile rate of 0.5 mm/min. The images below show the SEM morphology of the base metal and weld fracture surfaces [31]. As shown in Figure 18, the cross-sectional morphology comparison reveals that the base metal fracture (a) exhibits a relatively uniform and dense distribution of dimples, indicating good toughness and plasticity, with the ductile fracture being dominant. The weld fracture (b) also shows clear dimple features, with the depth and diameter of the dimples being comparable to those of the base metal. In some areas, the dimples are even deeper, suggesting that the weld metal underwent significant plastic deformation during loading. The fracture process was accompanied by the accumulation of numerous microvoids and an increase in toughness. Dimples are features of microvoid accumulation formed during plastic deformation in tensile fracture, and the quantity, depth, and distribution of dimples directly reflect the material’s overall toughness and tensile properties. An analysis of the dimple features reveals that the weld fracture (b) exhibits well-formed and evenly distributed dimples, indicating that the weld metal has good plasticity and fracture resistance. Both the base metal and weld fractures are dominated by ductile fracture, with no brittle fracture features observed. The deep and evenly distributed dimple structure in the weld (b) suggests that the weld metal can effectively absorb energy and delay fracturing, demonstrating tensile properties similar to those of the base metal.

4. Conclusions

Compared to traditional welding methods for steel structures, laser-arc hybrid welding offers superior physical properties in the welds. The experimental results of this study are applicable to the engineering field, as thick plates are widely used. Therefore, the findings can provide valuable references for steel structure construction, bridges, building frameworks, industrial tanks, and other areas. Additionally, these results can help reduce the costs associated with introducing laser-arc hybrid welding technology into these industries.

• Through orthogonal experiments and simulation analysis, the following conclusions were drawn: In laser-arc hybrid welding, the heat source distance has the greatest impact on the temperature field distribution and molten pool morphology, followed by welding speed, laser power, and arc power. Welding speed directly affects the heat retention time; the faster the speed, the shorter the heat retention time, which in turn promotes grain refinement. When the process parameters are set to a laser power of 800 W, arc power of 1200 W, heat source distance of 5 mm, and welding speed of 15 mm/s, the peak temperature remains within the range of 900 K to 1000 K, resulting in optimal welding tensile properties.
• The Gaussian surface heat source was used to simulate the arc, while the rotating Gaussian volume heat source was employed to simulate the laser, accurately reflecting the thermal effects and energy distribution in laser-arc hybrid welding. Through numerical simulation, the optimal process parameters for achieving grain refinement in the weld were determined to be a laser power of 800 W, arc power of 1200 W, heat source distance of 5 mm, and a welding speed of 15 mm/s. Thermal imaging measurements confirmed that, under these process parameters, the peak temperature during welding was 985 K, within the 900–1000 K temperature range, thereby validating the reliability of the numerical simulation model. This provides both theoretical and experimental support for optimizing welding parameters and processes, significantly enhancing the effectiveness of welding simulations.
• Hardness measurements using the HV-1000 Vickers hardness tester were conducted in the weld zone, heat-affected zone (HAZ), and base material zone. The results showed that the average hardness in the heat-affected zone was the highest, at 203.8 HV, followed by the weld zone, at 189.2 HV, and the lowest being in the base material zone, at 169.8 HV. This indicates that the base material has finer grains, leading to lower hardness, while grain growth during welding increases the hardness in the heat-affected zone and weld zone, making them harder than the base material.
• The tensile tests and SEM fracture surface analysis indicate that the weld exhibits an excellent tensile performance under a loading rate of 0.5 mm/min, with an elongation of 77%, which is 4% higher than the base material’s 73% elongation. The weld’s tensile strength is comparable to that of the base material, with slightly better ductility. Fractures in both the weld and base material predominantly display ductile characteristics, with no significant welding defects observed. This demonstrates that the internal structure of the weld is dense and that the laser-arc hybrid welding process effectively enhances grain refinement and plasticity.