Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Measurement of Splitting Tensile Strength of Asphalt Mixtures
3. EDEM Simulation Modeling of Asphalt Mixtures
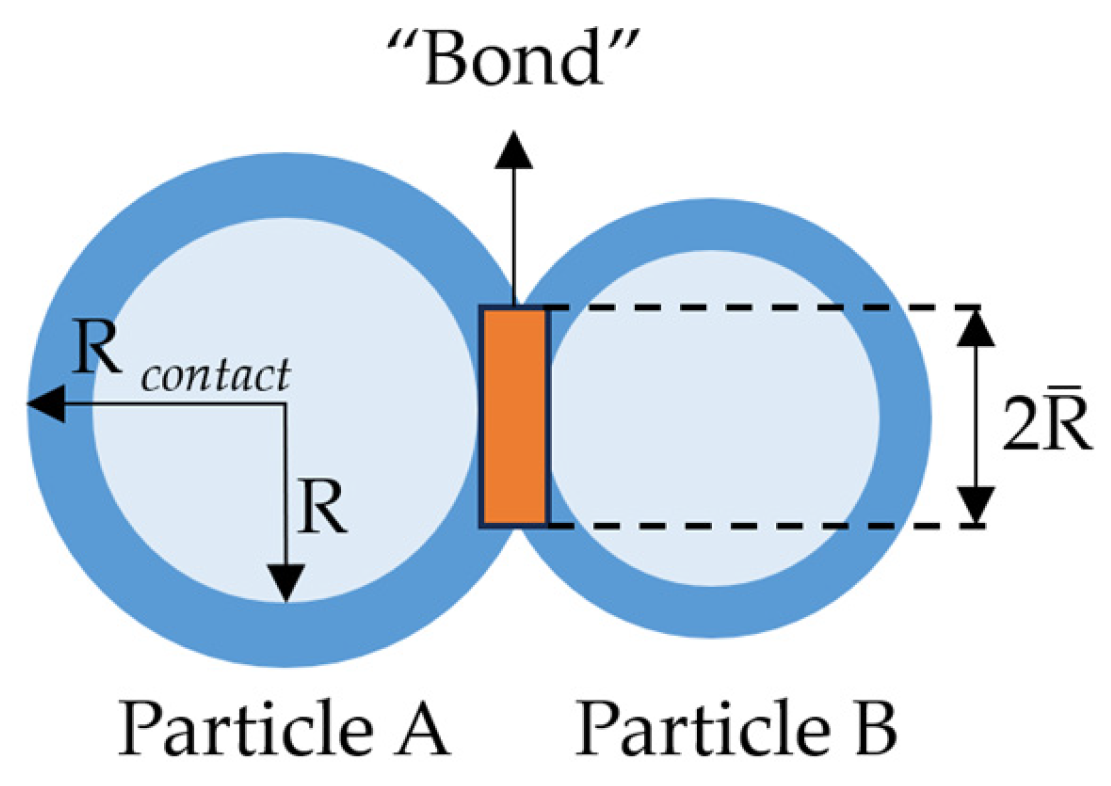
3.1. Selection of Bonded Contact Model
3.2. Simulation Modeling of Asphalt Mixtures
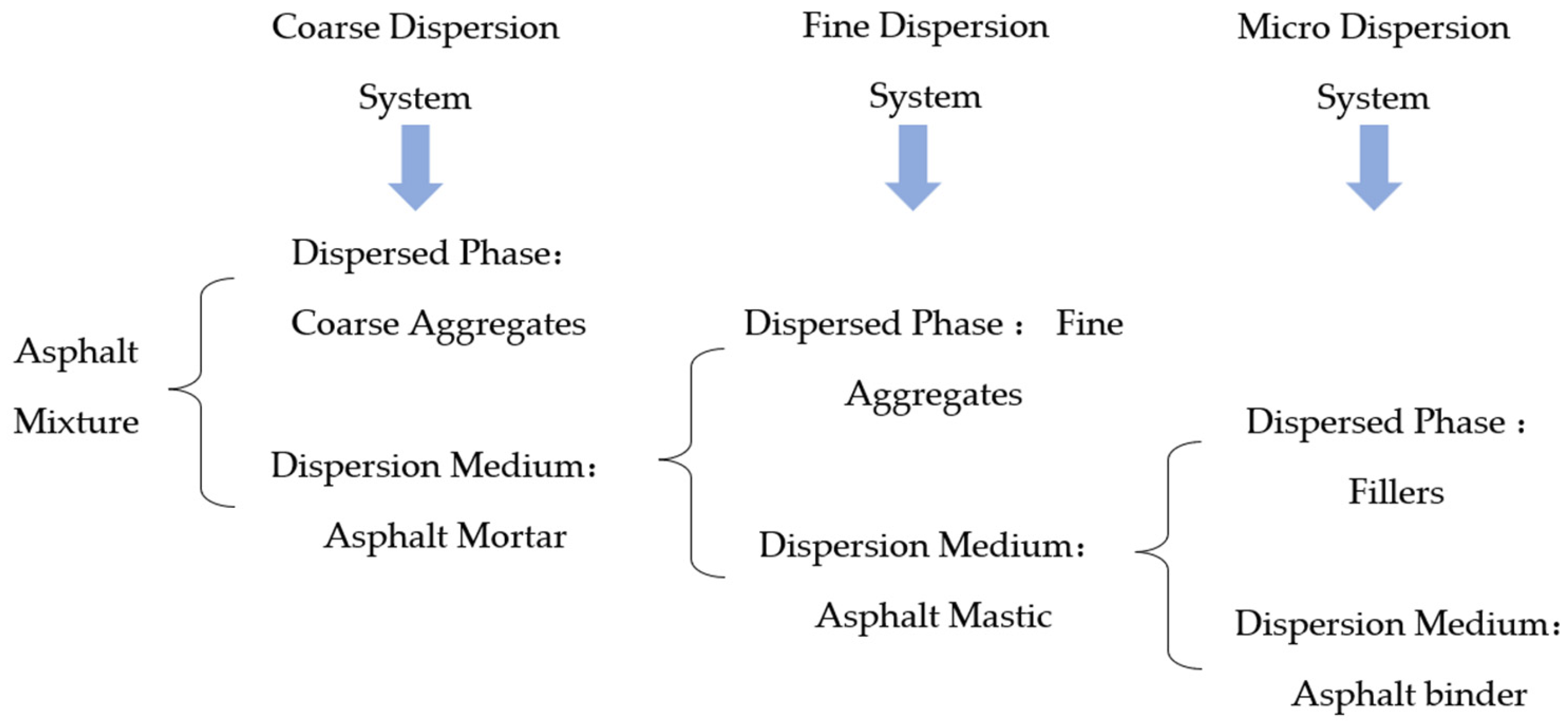
3.2.1. Particle Modeling and Basic Material Parameters
3.2.2. Simulation Model of the Splitting Test
4. Design of Experiments for Calibration Methods of Bonding Parameters
4.1. Response Surface Methodology (RSM) Design and Simulation Results of the Bonded Contact Parameters
4.2. Analysis of Simulation Results
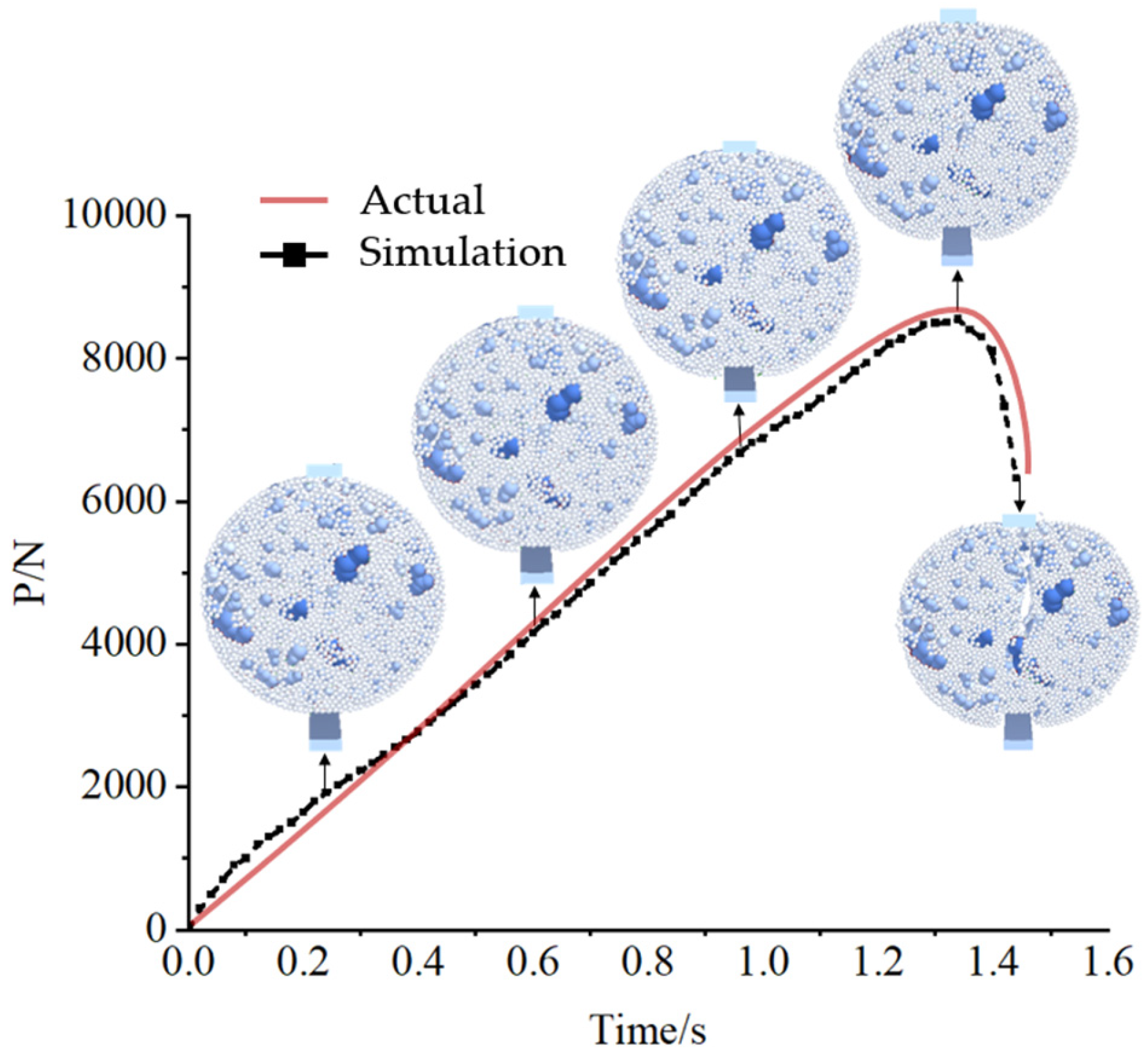
5. Verification of EDEM Simulation Model for Asphalt Mixtures
6. Conclusions
- (1)
- In the discrete element software EDEM’s Hertz–Mindlin with bonding contact modeling, the significance of the influence of the four bonding parameters on the splitting tensile strength of the asphalt mixture simulation model is as follows: critical normal stress () > shear stiffness per unit area () > normal stiffness per unit area () > critical shear stress ().
- (2)
- The regression models between the four bonding parameters and splitting tensile strength were established by the response surface methodology (RSM). The splitting tensile strength of asphalt mixtures in the laboratory tests was calibrated as follows: the normal stiffness per unit area, shear stiffness per unit area, critical normal stress, and critical shear stress were 1.31 × 1010 , 8.24 × 109 , 5.78 × 109 Pa, and 5.28 × 109 Pa, respectively.
- (3)
- The comparative validation results between the discrete element simulation tests and laboratory tests show that the trends of time–load curve changes between the simulation and actual tests are generally consistent. The feasibility and accuracy of the bond parameter calibration method for the EDEM simulation models of asphalt mixtures are proved. The calibration method can provide a basis for accurate studies of asphalt mixtures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Editorial Department of China Journal of Highway and Transport. Review on China’s Pavement Engineering Research: 2024. China J. Highw. Transp. 2024, 37, 1–81. [Google Scholar]
- Sun, Y.; Xue, B.; Sun, Y.; Wang, Z.; Pan, J. Mesoscale simulation of cracking behavior of asphalt mixture considering heterogeneity. J. Jilin Univ. Eng. Technol. Ed. 2024, 54, 1708–1718. [Google Scholar]
- Xie, Y.; Yuan, M.; Zhao, Y. Analysis of mechanism and evaluation of asphalt mixtures segregation based on DEM simulation. Constr. Build. Mater. 2023, 398, 132500. [Google Scholar] [CrossRef]
- Ge, H.; Quezada, J.C.; Houerou, V.L.; Chazallon, C. Multiscale analysis of tire and asphalt pavement interaction via coupling FEM–DEM simulation. Eng. Struct. 2022, 256, 113925. [Google Scholar] [CrossRef]
- Wang, H.; Wu, H.; Xiang, J.; Ye, G. Simulation of Creep Damage of Asphalt Mixture Based on Discrete Element Method. J. Mater. Civ. Eng. 2023, 35, 04023185. [Google Scholar] [CrossRef]
- Pouranian, M.R.; Shishehbor, M.; Haddock, J.E. Impact of the coarse aggregate shape parameters on compaction characteristics of asphalt mixtures. Powder Technol. Int. J. Sci. Technol. Wet Dry Part. Syst. 2020, 363, 369–386. [Google Scholar] [CrossRef]
- Al Khateeb, L.; Anupam, K.; Erkens, S.; Scarpas, T. Micromechanical simulation of porous asphalt mixture compaction using discrete element method (DEM). Constr. Build. Mater. 2021, 301, 124305. [Google Scholar] [CrossRef]
- Ning, Y.; Huang, Q.; Shi, C.; Meng, Q. Numerical Simulation Study on Compression Characteristics of Gravelly Soil Mixture Based on Soft Servo Method. Geofluids 2021, 2021, 9946628. [Google Scholar] [CrossRef]
- Zhu, X.; Qian, G.; Yu, H.; Yao, D.; Shi, C.; Zhang, C. Evaluation of coarse aggregate movement and contact unbalanced force during asphalt mixture compaction process based on discrete element method. Constr. Build. Mater. 2022, 328, 127004. [Google Scholar] [CrossRef]
- Ren, J.; Yin, C. Investigating mechanical characteristics of aggregate structure for road materials. Int. J. Pavement Eng. 2022, 23, 372–386. [Google Scholar] [CrossRef]
- Guo, H.; Dai, X.; Zhang, K.; Pan, Y.; Wu, J. Study on the compaction space of coarse aggregates of asphalt mixtures. Constr. Build. Mater. 2022, 359, 129487. [Google Scholar] [CrossRef]
- Liang, X.; Hu, Z.; Zheng, L.; Wang, Y. Optimization of the discrete element contact model for tidal flat soil and field shoveling experiment. Trans. Chin. Soc. Agric. Eng. 2024, 40, 107–115. [Google Scholar]
- MA, D.; Xu, T.; Gui, X.; Wang, E. Design and simulation analysis of real-time automatic detection system for RAP gradation. J. Harbin Inst. Technol. 2024, 56, 145–152. [Google Scholar]
- Yu, W.; Wang, S.; Gong, Z.; Miao, Y. Effect of compaction degree on the topological characteristics of force chain network (FCN) in aggregate blend. Constr. Build. Mater. 2024, 419, 135554. [Google Scholar] [CrossRef]
- Ai, X.M.; Yi, J.Y.; Pei, Z.S.; Zhou, W.Y.; Feng, D.C. Advances in Discrete Element Modeling of Asphalt Mixture: A Literature Review. Arch. Comput. Methods Eng. 2024, 31, 4003–4029. [Google Scholar] [CrossRef]
- Zhang, H.; Pan, L.Y.; Pan, Q.; Jin, C.J.; Ji, S.S.; Liu, X.Y. Experimental Study on Splitting Tensile Damage Characteristics and Discrete Element Simulation of Concrete Based on Acoustic Emission Technology. J. Mater. Civ. Eng. 2023, 35, 04022385. [Google Scholar] [CrossRef]
- Sun, X.Y.; Wang, H.X.; Gu, X.; He, Z.; Xu, L.D.; Shi, M.F. Effects of Needle Flake Particles on Splitting Experiment of Asphalt Mixture: An Experimental and Numerical Investigation. Nanosci. Nanotechnol. Lett. 2020, 12, 1166–1170. [Google Scholar] [CrossRef]
- Liang, B.; Zhang, K.; Zhang, H. Adhesion Performance of Aminosilane-Montmorillonite/SBS Modified Asphalt and Modified Aggregate. J. Hunan Univ. Nat. Sci. 2023, 50, 195–205. [Google Scholar]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- JTG 3432-2024; Aggregate Testing Procedure for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2024.
- Yao, Y.S.; Li, J.; Ni, J.J.; Liang, C.H.; Zhang, A.S. Effects of gravel content and shape on shear behaviour of soil-rock mixture: Experiment and DEM modelling. Comput. Geotech. 2022, 141, 104476. [Google Scholar] [CrossRef]
- Wang, S.Q.; Ji, S.Y. A unified level set method for simulating mixed granular flows involving multiple non-spherical DEM models in complex structures. Comput. Methods Appl. Mech. Eng. 2022, 393, 114802. [Google Scholar] [CrossRef]
- Wang, H. Bending and Pulling of Asphalt MixturesConsidering Coarse Aggregate Morphology Using Discrete Elements. Master’s Thesis, Harbin Engineering University, Harbin, China, 2022. [Google Scholar]
- Wu, G.; Jiang, Y.; Zhang, W.; Chen, H. Influence of Coarse Aggregate Distribution Morphology on the Fatigue Performance of Asphalt Mixtures. J. Chongqing Jiaotong Univ. Nat. Sci. 2023, 42, 80–86. [Google Scholar]
- Wang, S.D.; Miao, Y.H.; Wang, L.B. Investigation of the force evolution in aggregate blend compaction process and the effect of elongated and flat particles using DEM. Constr. Build. Mater. 2020, 258, 119674. [Google Scholar] [CrossRef]
- Stahl, M.; Konietzky, H. Discrete element simulation of ballast and gravel under special consideration of grain-shape, grain-size and relative density. Granul. Matter 2011, 13, 417–428. [Google Scholar] [CrossRef]
- Lu, M.; McDowell, G.R. The importance of modelling ballast particle shape in the discrete element method. Granul. Matter 2007, 9, 69–80. [Google Scholar] [CrossRef]
- Deng, Z. Study on Numerical Simulation Method of Asphalt Mixture Based on Three Dimensional Discrete Element Method. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. [Google Scholar]
- Luo, M. Analysis of Planetary Mixing Parameters for Regeneration of Used Asphalt Pavement Materials. Master’s Thesis, University of Jinan, Jinan, China, 2022. [Google Scholar]
- Qian, G.; Hu, K.; Li, J.; Bai, X.; Li, N. Compaction process tracking for asphalt mixture using discrete element method. Constr. Build. Mater. 2020, 235, 117478. [Google Scholar] [CrossRef]
- Vatanparast, M.; Sarkar, A.; Sahaf, S.A. Optimization of asphalt mixture design using response surface method for stone matrix warm mix asphalt incorporating crumb rubber modified binder. Constr. Build. Mater. 2023, 369, 130401. [Google Scholar] [CrossRef]
- Wang, J. Numerical Simulation and Structural Improvement of the Milling Process of Asphalt Pavement Milling Machine. Master’s Thesis, Xiangtan University, Xiangtan, China, 2022. [Google Scholar]
- Huang, Y. Study on Agglomeration Rate of Recycled Asphalt Mixture Based on Discrete Element Method. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar]
- Guo, Q.; Xu, H.; Wang, J.; Hang, J.; Wang, K.; Hu, P.; Li, H. Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture. Coatings 2023, 13, 1965. [Google Scholar] [CrossRef]
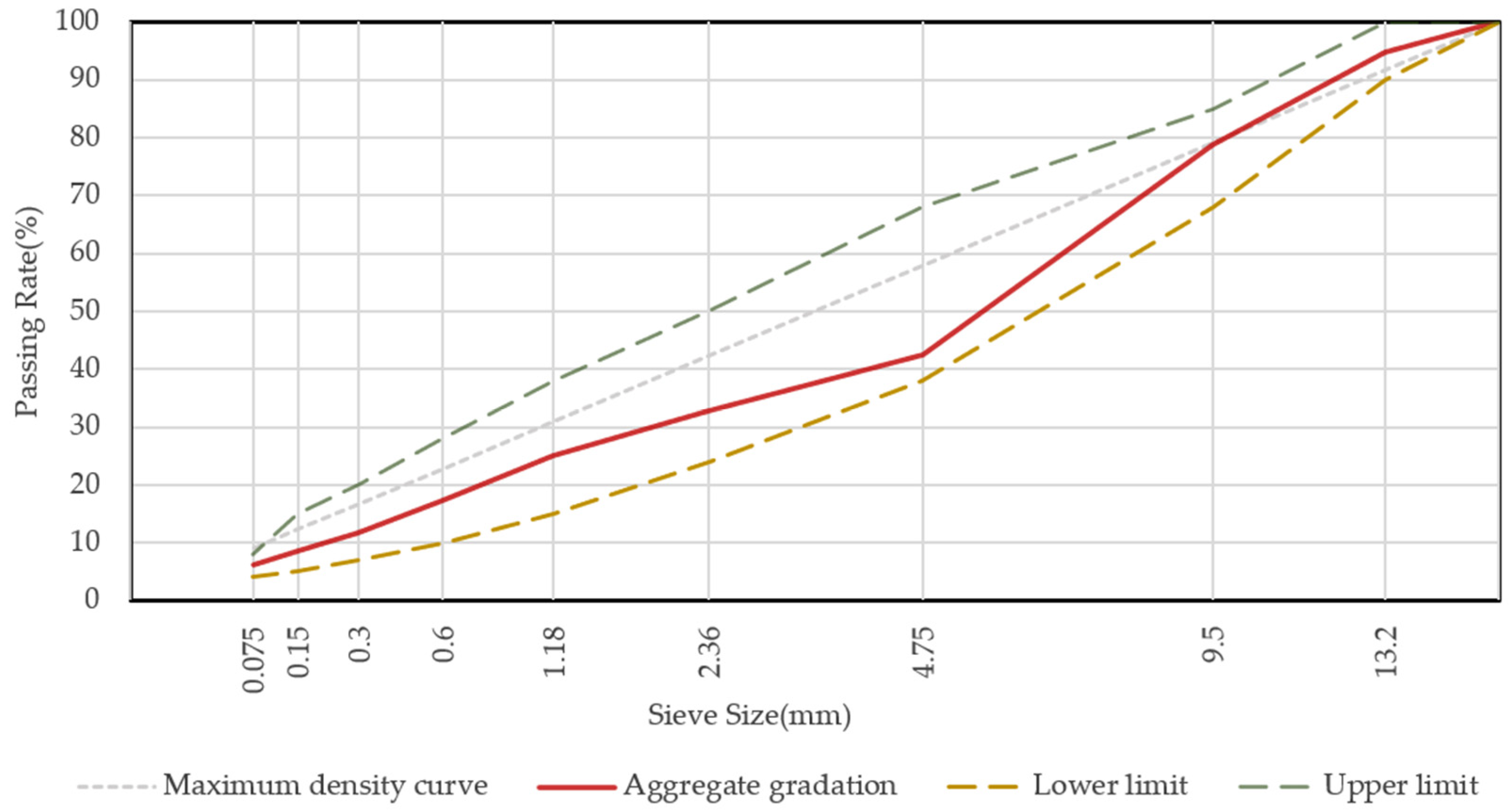
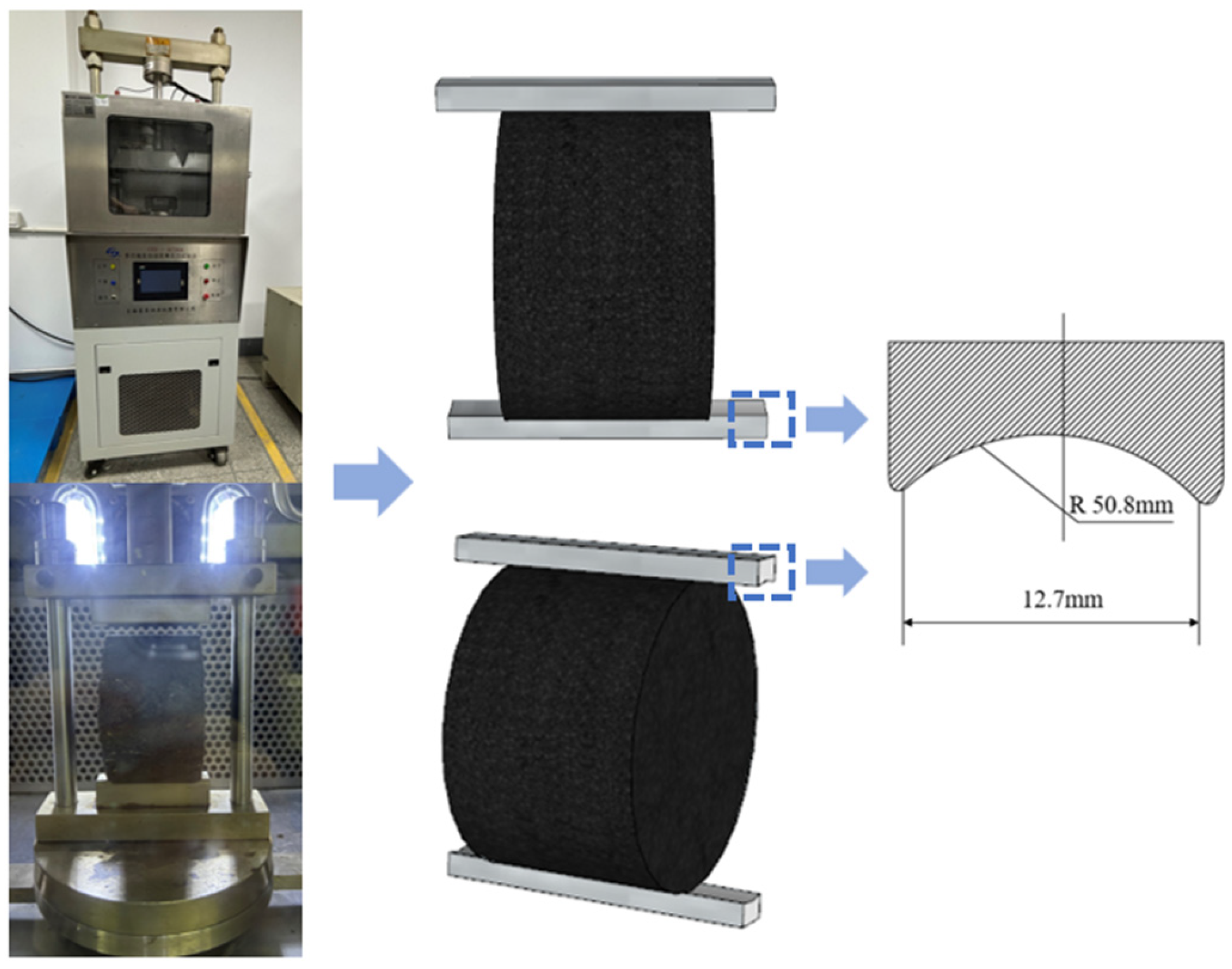
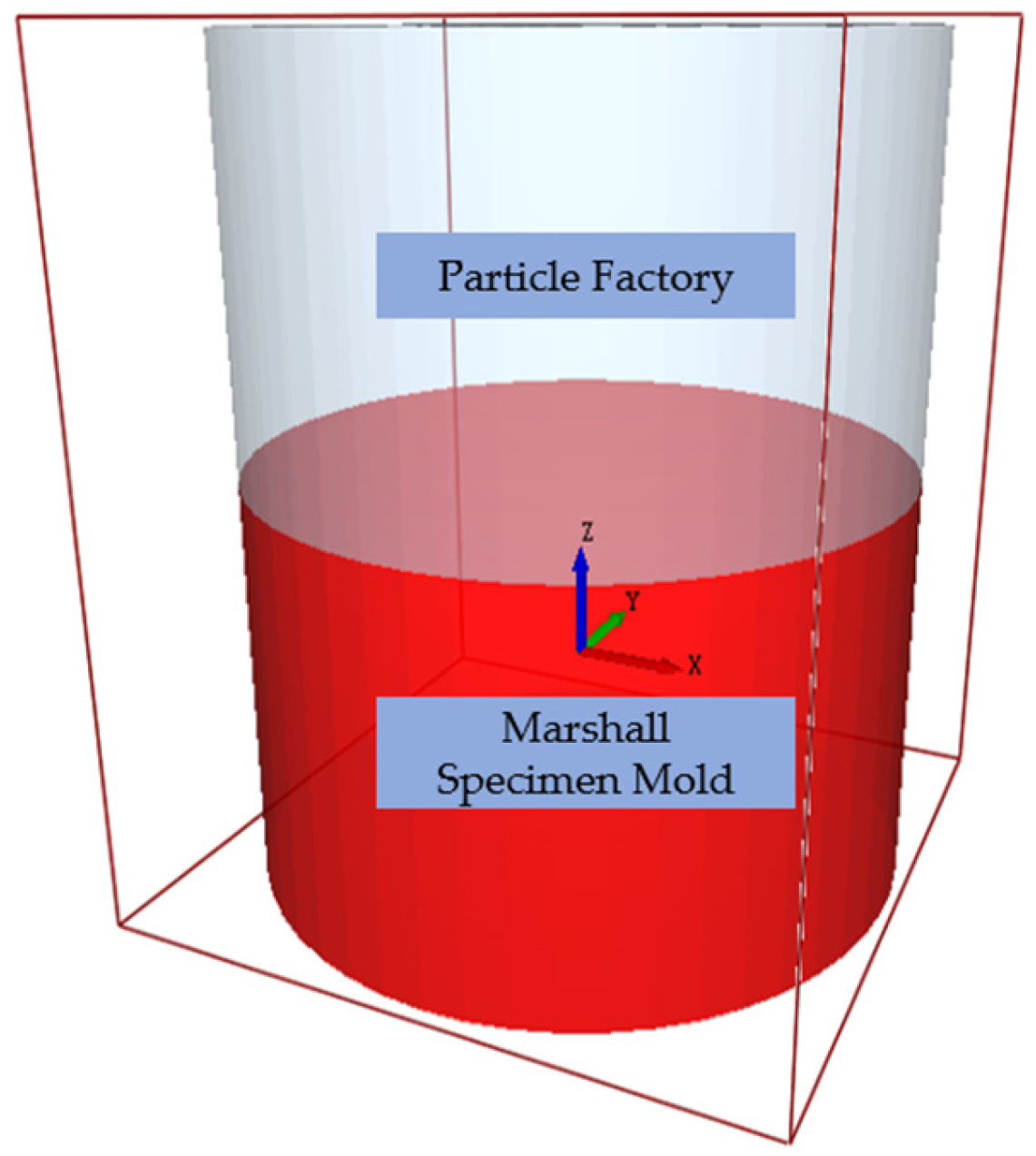
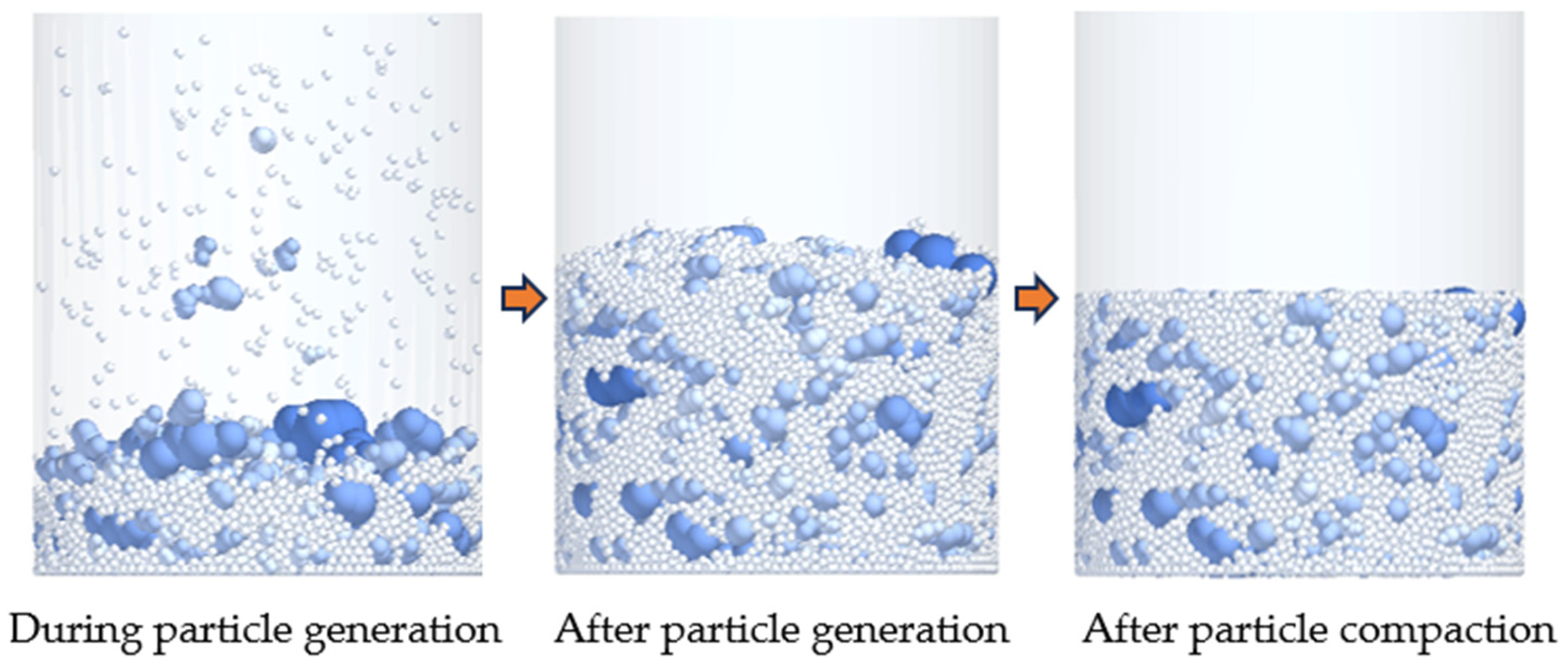

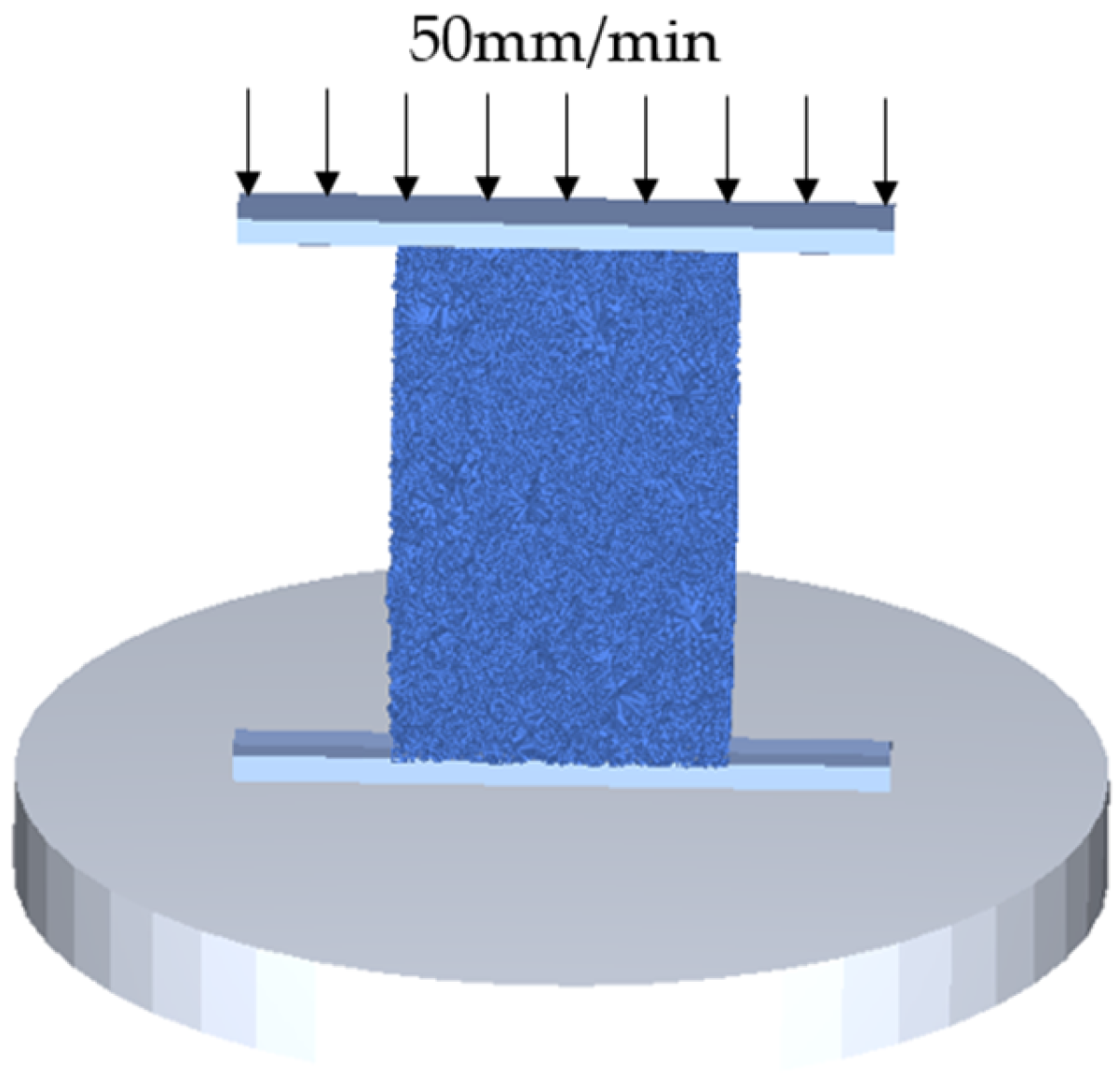
| Item | Unit | Test Value | Specification | Testing Method | |
|---|---|---|---|---|---|
| Penetration (25 °C, 100 g, 5 s) | 0.1 mm | 70.8 | 60~80 | T 0604 | |
| Penetration Index (PI) | —— | 0.2 | ≥−0.4 | T 0604 | |
| Ring and Ball Softening Point | °C | 78.6 | ≥55 | T 0606 | |
| Residual Ductility at 5 °C | cm | 42.1 | ≥30 | T 0605 | |
| Viscosity at 135 °C | Pa·s | 1.532 | ≤3 | T 0625 | |
| Elastic Recovery at 25 °C | % | 95 | ≥65 | T 0662 | |
| Density at 25 °C | g/cm3 | 1.0036 | Measured | T 0603 | |
| RTFOT | Mass Change | % | 0.23 | ≤±1.0 | T 0609 |
| Penetration Ratio | % | 84.8 | ≥60 | T 0604 | |
| Residual Ductility at 5 °C | cm | 24.2 | ≥20 | T 0605 | |
| Test Item | Unit | Standard Requirement | Coarse Aggregate Test Result | Assessment | Testing Method | ||
|---|---|---|---|---|---|---|---|
| 15~25 mm | 5~15 mm | 3~5 mm | |||||
| Apparent Relative Density | g/cm3 | ≥2.60 | 2.867 | 2.718 | 2.825 | Qualified | T 0304 |
| Bulk Relative Density | g/cm3 | Measured | 2.818 | 2.648 | 2.732 | Qualified | T 0304 |
| Water Absorption Rate | % | ≤2.0 | 0.62 | 0.97 | 1.2 | Qualified | T 0304 |
| Adhesion to Asphalt | Stage | ≥5 | 5 | Qualified | T 0616 | ||
| Crushing Value | % | ≤28 | 16.2 | Qualified | T 0316 | ||
| Elongated and Flaky Particle Content | % | ≤18 | 8.6 | Qualified | T 0312 | ||
| Soft Stone Content | % | ≤3 | 2.3 | Qualified | T 0320 | ||
| Sturdiness | % | ≤12 | 7 | Qualified | T 0314 | ||
| Test Item | Unit | Standard Requirement | Test Result | Assessment | Testing Method |
|---|---|---|---|---|---|
| Apparent Density | g/cm3 | Measured | 2.701 | Qualified | T 0328 |
| Apparent Relative Density | — | ≥2.50 | 2.705 | — | T 0328 |
| Robustness (>0.3 mm) | % | ≤12 | 8.8 | Qualified | T 0340 |
| Sand Equivalent | % | ≥60 | 63 | Qualified | T 0334 |
| Test Item | Unit | Standard Requirement | Test Result | Assessment | Testing Method | |
|---|---|---|---|---|---|---|
| Apparent Density | g/cm3 | Measured | 2.698 | Qualified | T 0352 | |
| Water Content | % | ≤1 | 0.33 | Qualified | T 0103 Drying Method | |
| Particle Size Range | <0.6 mm | % | 100 | 100 | Qualified | T 0351 |
| <0.15 mm | % | 90~100 | 96.6 | Qualified | ||
| <0.075 mm | % | 75~100 | 85.8 | Qualified | ||
| Appearance | — | Free from Agglomeration and Caking | Free from Agglomeration and Caking | Qualified | — | |
| Hydrophilic Coefficient | — | <1.0 | 0.8 | Qualified | T 0353 | |
| Specimen Number | ||
|---|---|---|
| 1 | 8610 | 0.853 |
| 2 | 8730 | 0.868 |
| 3 | 8690 | 0.849 |
| 4 | 8490 | 0.841 |
| 5 | 8280 | 0.829 |
| Mean Value | 8560 | 0.848 |
| Aggregate Type | Actual Photo | 3D Model Diagram | Packing Effects |
|---|---|---|---|
| Regular Particle |  |  |  |
| Elongated Particle |  |  |  |
| Flat Particle |  |  |  |
| Material Type | Poisson’s Ratio | Density (kg/m3) | Shear Modulus (Pa) |
|---|---|---|---|
| Coarse Aggregate | 0.33 | 2600 | 1 × 108 |
| Asphalt Mortar | 0.15 | 2400 | 1 × 108 |
| Steel | 0.3 | 7850 | 7 × 1010 |
| Contact Type | Coefficient of Restitution | Static Friction Coefficient | Dynamic Friction Coefficient |
|---|---|---|---|
| Coarse Aggregate–Coarse Aggregate | 0.01 | 0.7 | 0.1 |
| Coarse Aggregate–Asphalt Mortar | 0.005 | 0.75 | 0.15 |
| Coarse Aggregate–Steel | 0.01 | 0.6 | 0.1 |
| Asphalt Mortar–Asphalt Mortar | 0.001 | 0.7 | 0.1 |
| Asphalt Mortar–Steel | 0.005 | 0.5 | 0.05 |
| Range of Particle Size/mm | 16~19 | 13.2~16 | 9.5~13.2 | 4.75~9.5 | 2.36~4.75 | Asphalt Mortar (2.36) |
|---|---|---|---|---|---|---|
| Simulation Ratio/% | 0.0 | 5.0 | 15.1 | 34.7 | 9.0 | 36.1 |
| Bonding Parameters | Upper Limit of Parameters | Lower Limit of Parameters |
|---|---|---|
| ) | 3.05 × 109 | 2.31 × 1010 |
| ) | 3.05 × 109 | 2.31 × 1010 |
| 4.25 × 108 | 6.00 × 109 | |
| 4.25 × 108 | 6.00 × 109 |
| Number | Parameters | /MPa | |||
|---|---|---|---|---|---|
| /(N·m−3) | /(N·m−3) | /Pa | /Pa | ||
| 1 | 3.05 × 109 | 1.31 × 1010 | 3.21 × 109 | 4.25 × 108 | 0.53 |
| 2 | 1.31 × 1010 | 2.31 × 1010 | 4.25 × 108 | 3.21 × 109 | 0.23 |
| 3 | 1.31 × 1010 | 3.05 × 109 | 3.21 × 109 | 6.00 × 109 | 0.32 |
| 4 | 3.05 × 109 | 2.31 × 1010 | 3.21 × 109 | 3.21 × 109 | 0.79 |
| 5 | 1.31 × 1010 | 2.31 × 1010 | 3.21 × 109 | 6.00 × 109 | 0.65 |
| 6 | 3.05 × 109 | 1.31 × 1010 | 4.25 × 108 | 3.21 × 109 | 0.28 |
| 7 | 1.31 × 1010 | 1.31 × 1010 | 4.25 × 108 | 6.00 × 109 | 0.18 |
| 8 | 1.31 × 1010 | 3.05 × 109 | 4.25 × 108 | 3.21 × 109 | 0.12 |
| 9 | 1.31 × 1010 | 3.05 × 109 | 3.21 × 109 | 4.25 × 108 | 0.33 |
| 10 | 2.31 × 1010 | 1.31 × 1010 | 3.21 × 109 | 6.00 × 109 | 0.39 |
| 11 | 1.31 × 1010 | 1.31 × 1010 | 6.00 × 109 | 6.00 × 109 | 1.01 |
| 12 | 2.31 × 1010 | 2.31 × 1010 | 3.21 × 109 | 3.21 × 109 | 0.47 |
| 13 | 1.31 × 1010 | 1.31 × 1010 | 6.00 × 109 | 4.25 × 108 | 0.82 |
| 14 | 1.31 × 1010 | 1.31 × 1010 | 3.21 × 109 | 3.21 × 109 | 0.49 |
| 15 | 1.31 × 1010 | 2.31 × 1010 | 6.00 × 109 | 3.21 × 109 | 1.12 |
| 16 | 1.31 × 1010 | 1.31 × 1010 | 3.21 × 109 | 3.21 × 109 | 0.64 |
| 17 | 3.05 × 109 | 1.31 × 1010 | 6.00 × 109 | 3.21 × 109 | 1.21 |
| 18 | 1.31 × 1010 | 1.31 × 1010 | 3.21 × 109 | 3.21 × 109 | 0.58 |
| 19 | 2.31 × 1010 | 1.31 × 1010 | 3.21 × 109 | 4.25 × 108 | 0.42 |
| 20 | 3.05 × 109 | 1.31 × 1010 | 3.21 × 109 | 6.00 × 109 | 0.79 |
| 21 | 1.31 × 1010 | 3.05 × 109 | 6.00 × 109 | 3.21 × 109 | 0.67 |
| 22 | 2.31 × 1010 | 1.31 × 1010 | 4.25 × 108 | 3.21 × 109 | 0.19 |
| 23 | 2.31 × 1010 | 1.31 × 1010 | 6.00 × 109 | 3.21 × 109 | 0.79 |
| 24 | 3.05 × 109 | 3.05 × 109 | 3.21 × 109 | 3.21 × 109 | 0.41 |
| 25 | 1.31 × 1010 | 2.31 × 1010 | 3.21 × 109 | 4.25 × 108 | 0.56 |
| 26 | 1.31 × 1010 | 1.31 × 1010 | 4.25 × 108 | 4.25 × 108 | 0.18 |
| 27 | 2.31 × 1010 | 3.05 × 109 | 3.21 × 109 | 3.21 × 109 | 0.30 |
| Sources | Quadratic Sum | Degree of Freedom | Mean Square | F-Value | Significance Level p | |
|---|---|---|---|---|---|---|
| Models | 2.23 | 14 | 0.1591 | 103.72 | <0.0001 | Significant |
| 0.1752 | 1 | 0.1752 | 114.21 | <0.0001 | ||
| 0.2324 | 1 | 0.2324 | 151.50 | <0.0001 | ||
| X3 | 1.64 | 1 | 1.64 | 1070.91 | <0.0001 | |
| 0.0208 | 1 | 0.0208 | 13.58 | 0.0031 | ||
| 0.0110 | 1 | 0.0110 | 7.19 | 0.0200 | ||
| 0.0272 | 1 | 0.0272 | 17.75 | 0.0012 | ||
| 0.0210 | 1 | 0.0210 | 13.71 | 0.0030 | ||
| 0.0289 | 1 | 0.0289 | 18.84 | 0.0010 | ||
| 0.0025 | 1 | 0.0025 | 1.63 | 0.2259 | ||
| 0.0090 | 1 | 0.0090 | 5.88 | 0.0320 | ||
| 0.0001 | 1 | 0.0001 | 0.073 | 0.7916 | ||
| 0.0264 | 1 | 0.0264 | 17.24 | 0.0013 | ||
| 0.0059 | 1 | 0.0059 | 3.86 | 0.0729 | ||
| 0.0104 | 1 | 0.0104 | 6.78 | 0.0230 | ||
| Residual | 0.0184 | 12 | 0.0015 | |||
| Loss of Fit | 0.0070 | 10 | 0.0007 | 0.1230 | 0.9920 | Not Significant |
| Error | 0.0114 | 2 | 0.0057 | |||
| Total Deviation | 2.25 | 26 |
| Sources | Quadratic Sum | Degree of Freedom | Mean Square | F-Value | Significance Level p | |
|---|---|---|---|---|---|---|
| Models | 2.22 | 11 | 0.2017 | 111.69 | <0.0001 | Significant |
| 0.1752 | 1 | 0.1752 | 97.01 | <0.0001 | ||
| 0.2324 | 1 | 0.2324 | 128.69 | <0.0001 | ||
| X3 | 1.64 | 1 | 1.64 | 909.64 | <0.0001 | |
| 0.0208 | 1 | 0.0208 | 11.54 | 0.004 | ||
| 0.011 | 1 | 0.011 | 6.1 | 0.026 | ||
| 0.0272 | 1 | 0.0272 | 15.07 | 0.0015 | ||
| 0.021 | 1 | 0.021 | 11.64 | 0.0039 | ||
| 0.0289 | 1 | 0.0289 | 16 | 0.0012 | ||
| 0.009 | 1 | 0.009 | 5 | 0.041 | ||
| 0.0409 | 1 | 0.0409 | 22.62 | 0.0003 | ||
| 0.0184 | 1 | 0.0184 | 10.2 | 0.006 | ||
| Residual | 0.0271 | 15 | 0.0018 | |||
| Loss of Fit | 0.0157 | 13 | 0.0012 | 0.2117 | 0.9713 | Not Significant |
| Pure Error | 0.0114 | 2 | 0.0057 | |||
| Total Deviation | 2.25 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, Z.; Zhao, L.; Zhang, H.; Shi, F. Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures. Coatings 2024, 14, 1553. https://doi.org/10.3390/coatings14121553
Li X, Zhang Z, Zhao L, Zhang H, Shi F. Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures. Coatings. 2024; 14(12):1553. https://doi.org/10.3390/coatings14121553
Chicago/Turabian StyleLi, Xiujun, Zhipeng Zhang, Linhao Zhao, Heng Zhang, and Fangzhi Shi. 2024. "Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures" Coatings 14, no. 12: 1553. https://doi.org/10.3390/coatings14121553
APA StyleLi, X., Zhang, Z., Zhao, L., Zhang, H., & Shi, F. (2024). Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures. Coatings, 14(12), 1553. https://doi.org/10.3390/coatings14121553





