Multi-Scale Thermo-Mechanical Model Simulation of Residual Stress in Atmospheric Plasma Spray Process
Abstract
1. Introduction
2. Numerical Model
2.1. One-Way Coupled Thermo-Mechanical Analysis Based on Submodelling Method
2.2. Plasma Spray Process Parameters
2.3. Thermal Model
2.4. Thermal and Mechanical Material Properties
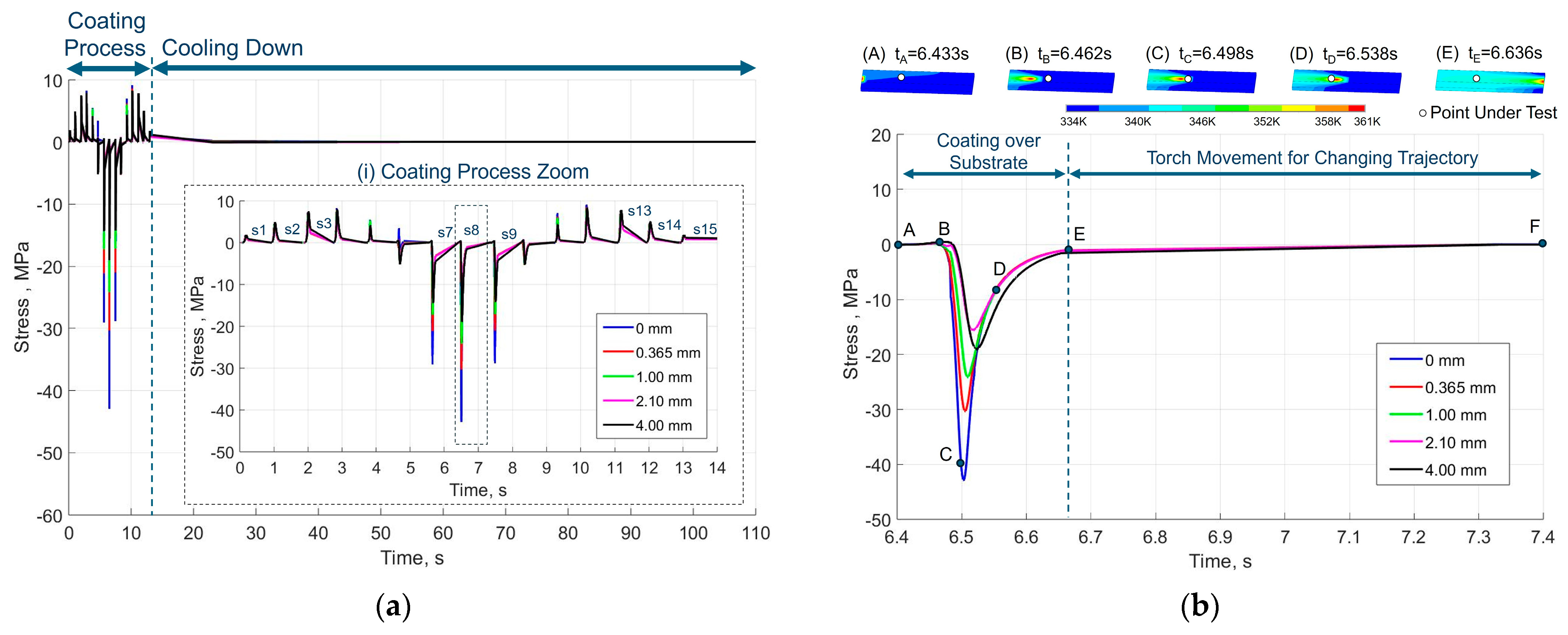
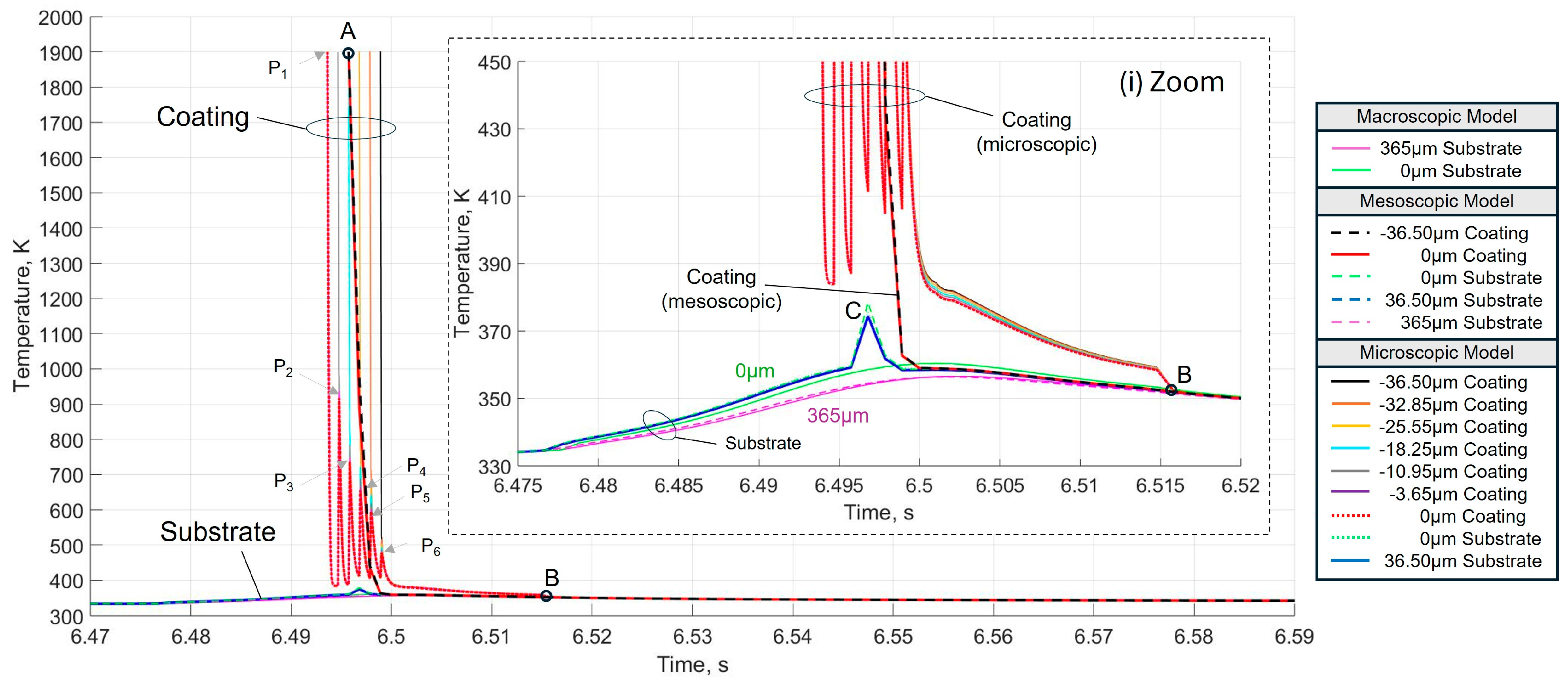
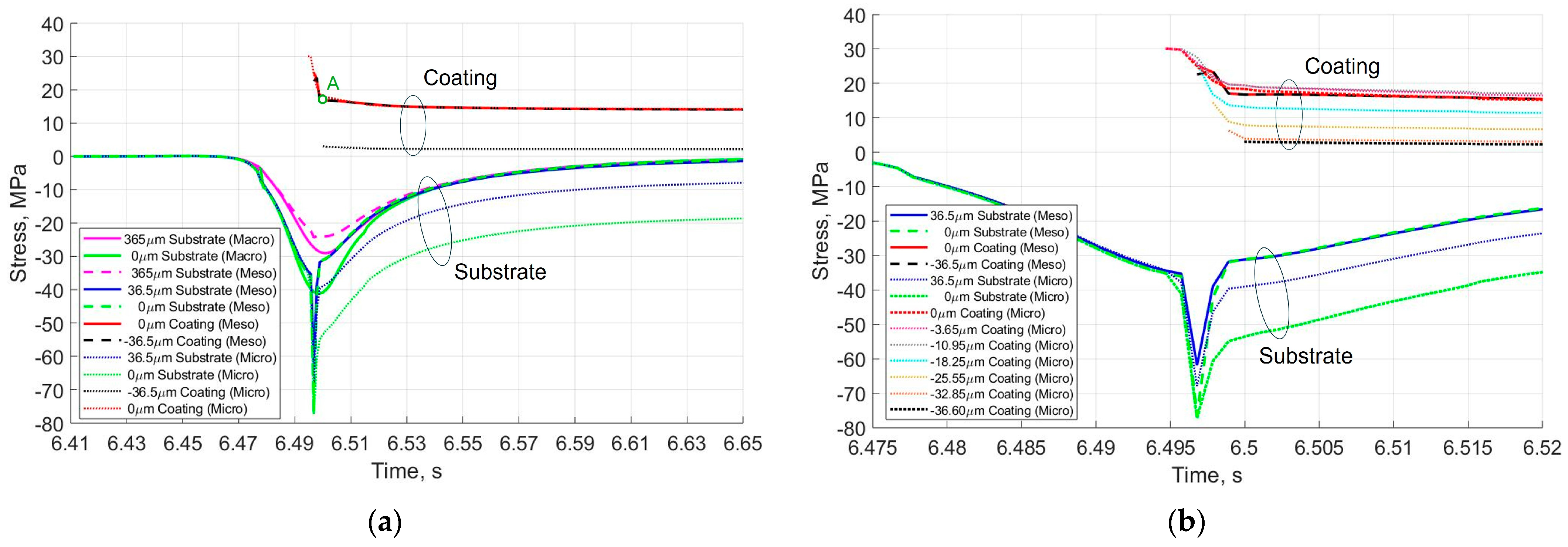
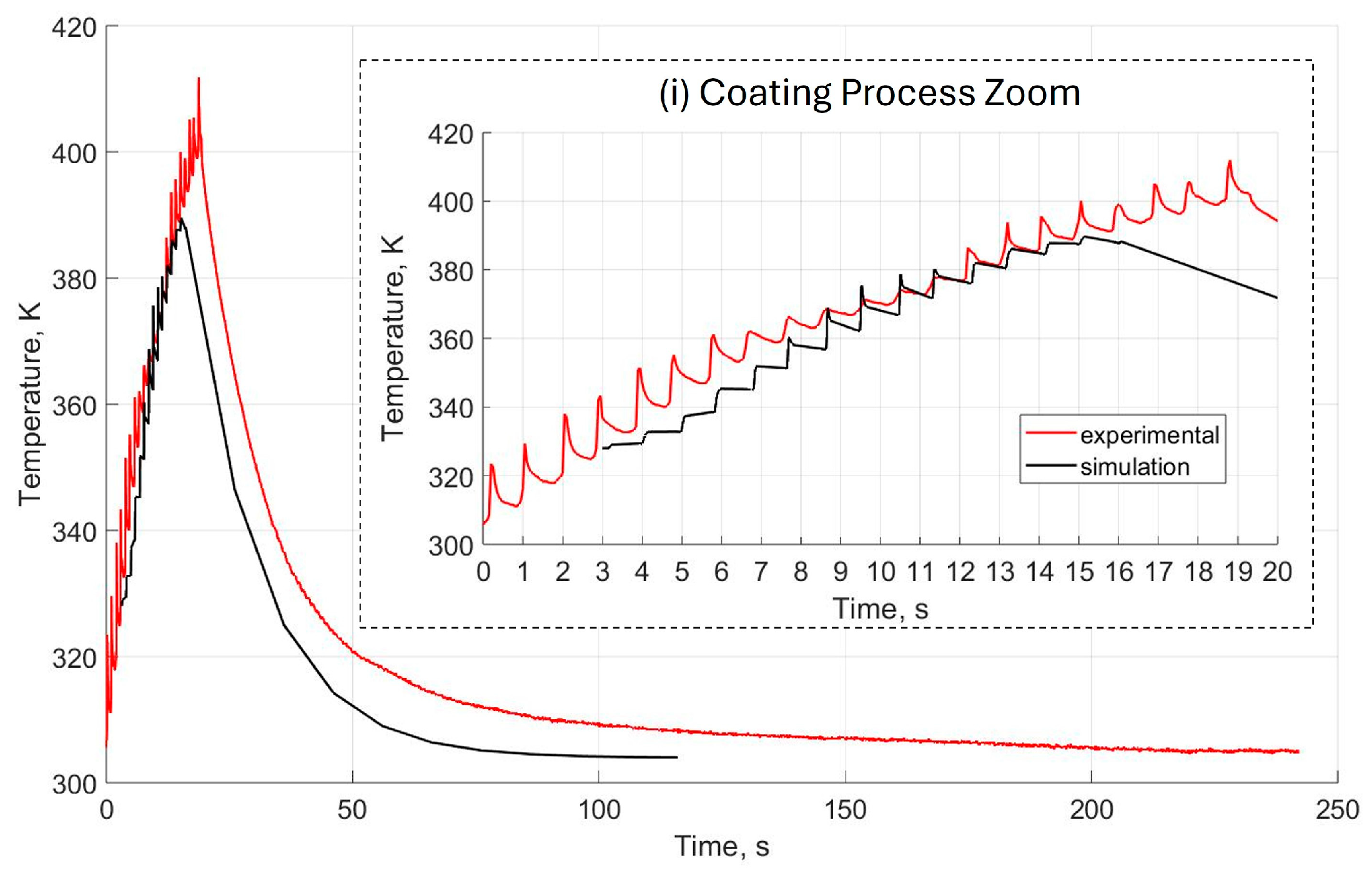
3. Simulation Results
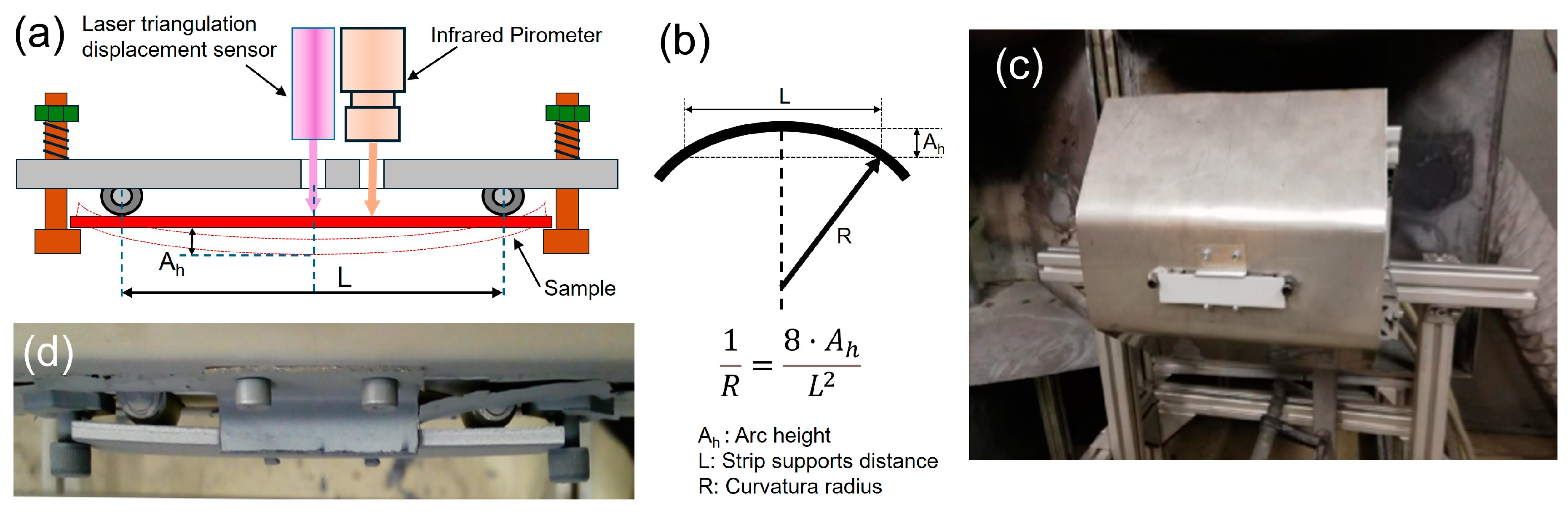
4. Experimental Quenching Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Espallargas, N. Future Development of Thermal Spray Coatings, 1st ed.; Woodhead Publishing: Cambridge, UK, 2015; ISBN 978-0-85709-769-9. [Google Scholar]
- Hogmark, S.; Jacobson, S.; Larsson, M. Design And Evaluation Of Tribological Coatings. Wear 2000, 246, 20–33. [Google Scholar] [CrossRef]
- Li, C.J.; Luo, X.T.; Dong, X.Y.; Zhang, L.; Li, C.X. Recent Research Advances in Plasma Spraying of Bulk-Like Dense Metal Coatings with Metallurgically Bonded Lamellae. J. Therm. Spray Technol. 2022, 31, 5–27. [Google Scholar] [CrossRef]
- Heimann, R.B. Plasma-Spray Coating: Principles and Applications; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1996; ISBN 978-3-527-61484-4. [Google Scholar]
- Pawlowski, L. The Science and Engineering of Thermal Spray Coatings, 2nd ed.; John Wiley & Sons, Ltd.: London, UK, 2008; ISBN 978-0-471-49049-4. [Google Scholar]
- Ang, A.S.M.; Berndt, C.C. A Review of Testing Methods for Thermal Spray Coatings. Int. Mater. Rev. 2014, 59, 179–223. [Google Scholar] [CrossRef]
- Davis, J.R. Handbook of Thermal Spray Technology, 1st ed.; ASM International: Novelty, OH, USA, 2004; ISBN 0-87170-795-0. [Google Scholar]
- Bach, F.; Laarmann, A.; Wenz, T. Modern Surface Technology, 1st ed.; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2006; ISBN 978-3-52731-532-1. [Google Scholar]
- Abubakar, A.A.; Arif, A.F.M.; Al-Athel, K.S.; Akhtar, S.S.; Mostaghimi, J. Modeling Residual Stress Development in Thermal Spray Coatings: Current Status and Way Forward. J. Therm. Spray Technol. 2017, 26, 1115–1145. [Google Scholar] [CrossRef]
- Buchmann, M.; Gadow, R. Estimation of Residual Stresses from the Simulation of the Deposition Process of Ceramic Coatings on Light Metal Cylinder Liners. In Proceedings of the 25th Annual Conference on Composites, Advanced Ceramics, Materials, and Structures, Cocoa Beach, FL, USA, 21–27 January 2001; Singh, B.M., Jessen, T., Eds.; pp. 67–74. [Google Scholar]
- Wenzelburger, M.; Riegert-Escribano, M.J.; Gadow, R. Methods of Residual Stress Analysis in Layer Composites and Their Application, Mech. Prop. Perform. Enginnering Ceram. Compos, Ceram. Eng. Sci. Proc. 2009, 26, 371–379. [Google Scholar]
- Elhoriny, M.; Wenzelburger, M.; Killinger, A.; Gadow, R. Finite Element Simulation of Residual Stress Development in Thermally Sprayed Coatings. J. Therm. Spray Technol. 2017, 26, 735–744. [Google Scholar] [CrossRef]
- Floristán, M.; Montesinos, J.A.; García-Marín, J.A.; Killinger, A.; Gadow, R. Robot Trajectory Planning For High Quality Thermal Spray Coating Processes On Complex Shaped Components. In Proceedings of the ITSC 2012, ASM International, Houston, TX, USA, 21–24 May 2012; pp. 448–453. [Google Scholar] [CrossRef]
- Liu, J.; Bolot, R.; Costil, S. Residual Stresses and Final Deformation of an Alumina Coating: Modeling and Measurement. Surf. Coat. Technol. 2015, 268, 241–246. [Google Scholar] [CrossRef]
- Ng, H.W.; Gan, Z. A Finite Element Analysis Technique For Predicting as-Sprayed Residual Stresses Generated by the Plasma Spray Coating Process. Finite Elem. Anal. Des. 2005, 41, 1235–1254. [Google Scholar] [CrossRef]
- Gan, Z.; Ng, H.W.; Devasenapathi, A. Deposition-Induced Residual Stresses In Plasma-Sprayed Coatings. Surf. Coat. Technol. 2004, 187, 307–319. [Google Scholar] [CrossRef]
- Martínez García, V.; Gadow, R.; Killinger, A.; Moreno Nicolás, J.A. Submodeling of Alumina Coatings by APS. In Proceedings of the ITSC 2017, Dusseldorf, Germany, 7–9 June 2017; pp. 1112–1117. [Google Scholar]
- ANSYS. Advanced Analysis Technique Guide; ANSYS Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Stamenkovic, D.; Vasovic, I. Finite Element Analysis of Residual Stress in Butt Welding Two Similar Plates. Sci. Tech. Rev. 2009, 59, 57–60. [Google Scholar]
- Cormier, N.G.; Smallwood, B.S.; Sinclair, G.B.; Meda, G. Aggressive Submodelling Of Stress Concentrations. Int. J. Numer. Meth. Engng. 1999, 46, 889–909. [Google Scholar] [CrossRef]
- Advanced Analysis Guide—Chapter 9: Submodeling, Release 12.1; ASNYS Inc.: Canonsburg, PA, USA, 2009.
- Soundararajan, B.; Sofia, D.; Barletta, D.; Poletto, M. Review On Modeling Techniques For Powder Bed Fusion Processes Based On Physical Principles. Addit. Manuf. 2021, 47, 102336. [Google Scholar] [CrossRef]
- Mulero, M.A.; Zapata, J.; Vilar, R.; Martínez, V.; Gadow, R. Automated Image Inspection System To Quantify Thermal Spray Splat Morphology. Surf. Coat. Technol. 2015, 278, 1–11. [Google Scholar] [CrossRef]
- Martínez-García, J.; Martínez-García, V.; Killinger, A. Modelling and Experimental Validation of the Flame Temperature Profile in Atmospheric Plasma Coating Processes on the Substrate. Coatings 2024, 14, 1248. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI Heat Atlas, 2nd ed.; Springer: Heidelberg, Germany, 2010; ISBN 978-3-540-77876-9. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 6th ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Faghri, A.; Zhang, Y. Transport Phenomena Iin Multiphase Systems; Elsevier Academic Press: New York, NY, USA, 2006; pp. 1013–1030. [Google Scholar]
- Powell, R.W.; Ho, C.Y.; Liley, P.E. Thermal Conductivity of Selected Materials. United States National Bureau of Standards; United States Department of Commerce: Washington, DC, USA, 1966. [Google Scholar]
- McLellan, R.B.; Ishikawa, T. The Elastic Properties of Aluminum at High Temperatures. J. Phys. Chem. Solids 1987, 48, 603–606. [Google Scholar] [CrossRef]
- Touloukian, Y.S. Thermophysical Properties of High Temperature Solid Materials: Vol. 4. Oxides And Their Solutions And Mixtures—Part I: Simple Oxygen Compounds and Their Mixture; Macmillan: New York, NY, USA, 1967; pp. 3–48. [Google Scholar]
- Touloukian, Y.S. Thermophysical Properties of Matter. Volume 2: Nonferrous alloys—Part I: Nonferrous Binay Alloys; The MacMilan Company: New York, NY, USA, 1967. [Google Scholar]
- Metals, Alloys, Compounds, Ceramics, Polymers, Composites—Catalogue 1993/94; Goodfellow Metals Ltd.: Cambridge, UK, 1993.
- Morrell, J. Handbook of Technical and Engineering Ceramics, Part 1: An Introduction for the Engineer and Designer; Her Majesty’s Stationery Office (HMSO): London, UK, 1985. [Google Scholar]
- Sun, D.; You, E.; Zhang, T.; Xu, J.; Wang, X.; Ren, X.; Tao, W. A review of thermal contact conductance research of conforming contact surfaces, Part B. Int. Commun. Heat Mass Transf. 2024, 159, 108065. [Google Scholar] [CrossRef]
- Kuroda, S.; Clyne, T.W. The Quenching Stress In Thermally Sprayed Coatings. Thin Solid. Films 1991, 200, 49–66. [Google Scholar] [CrossRef]
- Mutter, M.; Mauer, G.; Mücke, R. Investigations on the Initial Stress Evolution During Atmospheric Plasma Spraying of YSZ by In Situ Curvature Measurement. J. Therm. Spray Technol. 2016, 25, 672–683. [Google Scholar] [CrossRef]
- Zhang, X.; Watanabe, M.; Kuroda, S. Effects of Processing Conditions on the Mechanical Properties and Deformation Behaviors of Plasma-Sprayed Thermal Barrier Coatings: Evaluation of Residual Stresses and Mechanical Properties of Thermal Barrier Coatings on the Basis of in Situ Curvature Measurement Under a Wide Range of Spray Parameters. Acta Mater. 2013, 61, 1037–1047. [Google Scholar] [CrossRef]
- Totemeier, T.C.; Wright, J.K. Residual Stress Determination in Thermally Sprayed Coatings—A Comparison of Curvature Models and X-Ray Techniques. Surf. Coat. Technol. 2006, 200, 3955–3962. [Google Scholar] [CrossRef]
- Matejicek, J.; Sampath, S. In Situ Measurement of Residual Stresses and Elastic Moduli in Thermal Sprayed Coatings: Part 1: Apparatus and Analysis. Acta Mater. 2003, 51, 863–872. [Google Scholar] [CrossRef]
- Liao, H.; Vaslin, P.; Yang, Y.; Coddet, C. Determination of Residual Stress Distribution from in Situ Curvature Measurements for Thermally Sprayed WC/Co Coatings. J. Therm. Spray Technol. 1997, 6, 235–241. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films Deposited by Electrolysis. Proc. R. Soc. Lond. A 1909, 82, 172–175. [Google Scholar] [CrossRef]
- Clyne, T.W.; Gill, S.C. Residual Stresses in Thermal Spray Coatings and Their Effect on Interfacial Adhesion: A Review of Recent Work. J. Therm. Spray Technol. 1996, 5, 401–418. [Google Scholar] [CrossRef]
- Tsui, Y.C.; Clyne, T.W. An analytical Model for Predicting Residual Atresses in Progressively Deposited Coatings Part 1: Planar Geometry. Thin Solid Films 1997, 306, 23–33. [Google Scholar] [CrossRef]
- Chu, Y.; Hao, B.; Li, Z.; Zhu, J.; He, X. An Analytical Model for Predicting Residual Stresses in Multiple Layers By Plasma Cladding Process. AIP Adv. 2019, 9, 085103. [Google Scholar] [CrossRef]
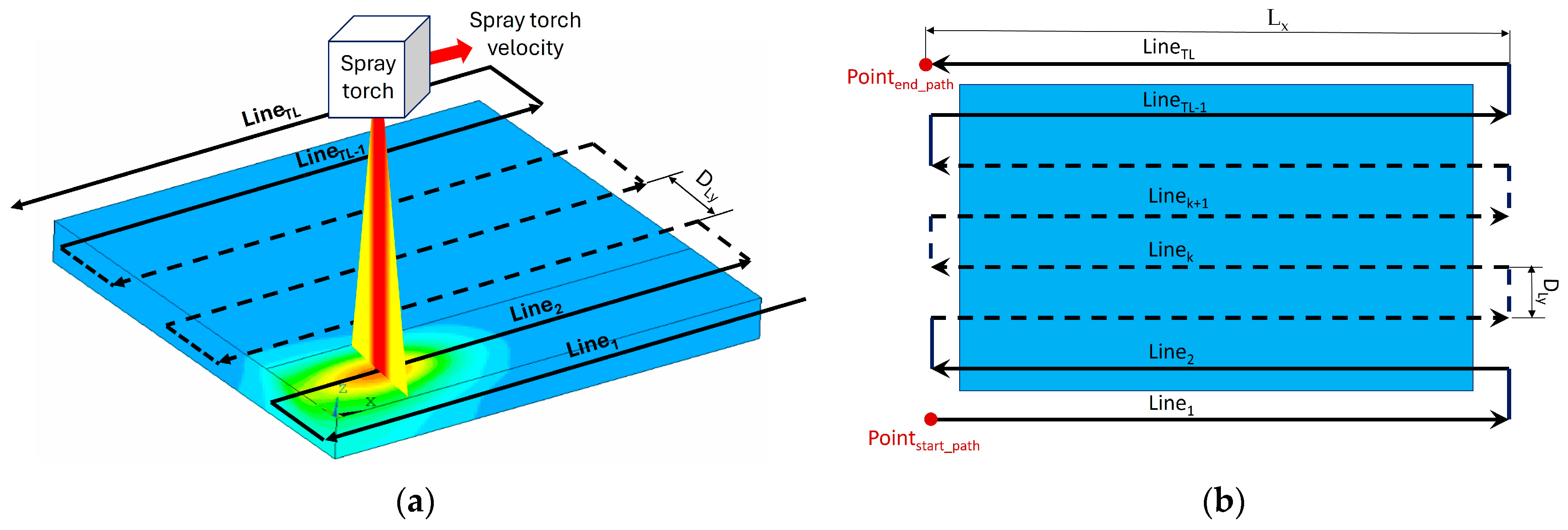
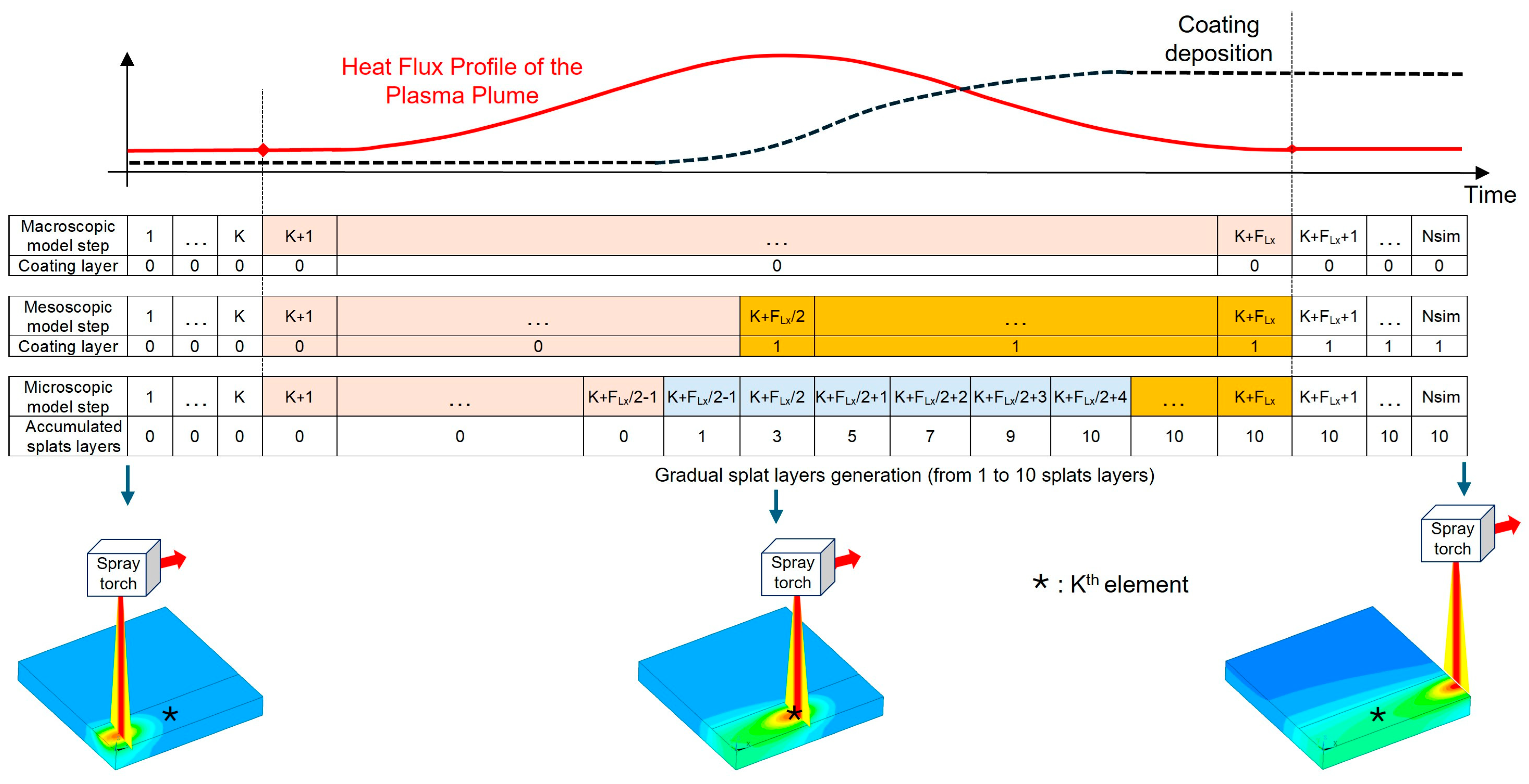
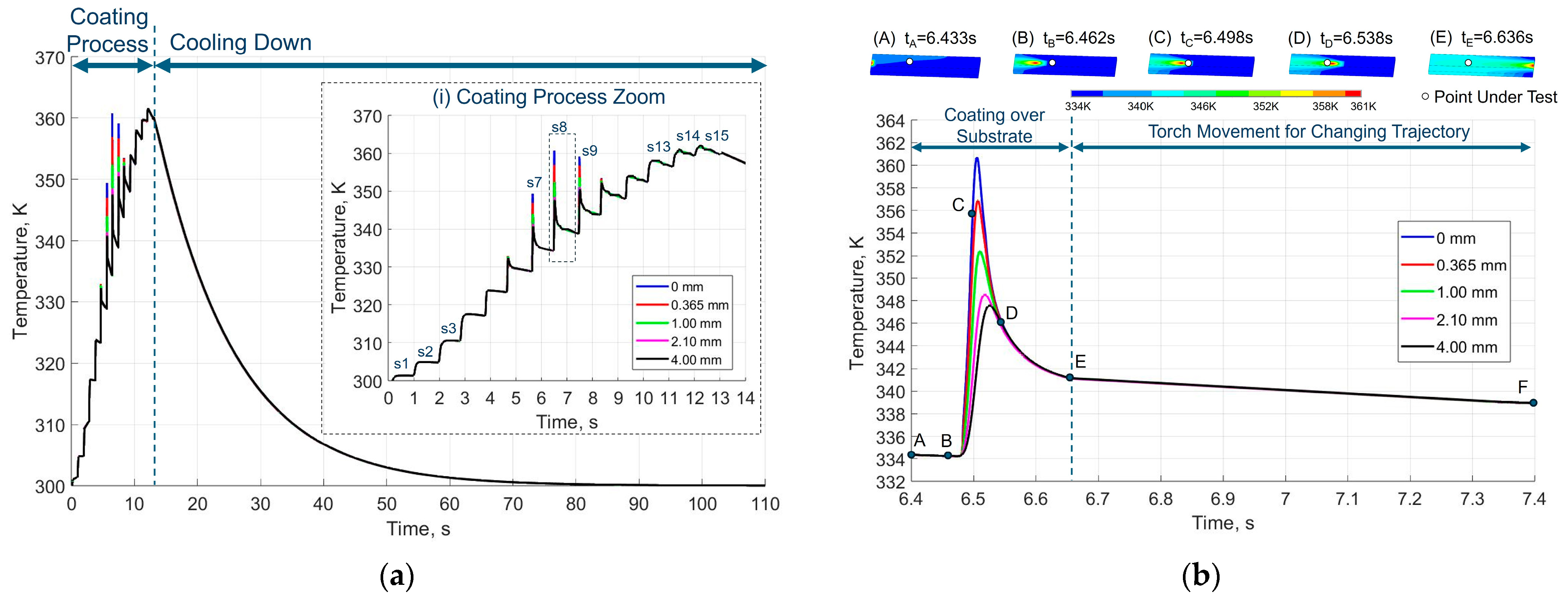



| Parameter | Value |
|---|---|
| Substrate dimensions (DX × DY × DZ), mm3 | 101.6 × 25.4 × 4 |
| Number elements: first layer (MTX × MTY) | 192 × 48 |
| Number of node layers | 5 |
| Surface element dimensions (dx × dy × dz), µm3 | 529.2 × 529.2 × 365 |
| Analyzed elements (Ne) | 21,312 |
| Torch speed (vtorch), mm/s | 500 |
| Torch line change time (timetor), s | 1 |
| Ambient temperature (TAmb), K | 300 |
| Number elements of the line offset (ΔLZ) | 5 |
| Total number of spray lines (TL) | 15 |
| Parameter | Value |
|---|---|
| Plasma gun | GTV F6 |
| Torch distance to the plate, mm | 120 |
| Torch Speed (vtorch), mm/s | 500 |
| Hydrogen, slpm | 10 |
| Argon, slpm | 44 |
| Current, A | 500 |
| Voltage, V | 75 |
| Power, kW | 37.5 |
| Powder carrier gas mass flow rate, slpm | 5 |
| Powder feed rate, g/min | 4.2 |
| Trajectory length (Lx), mm | 200 |
| Line offset (DLy), mm | 2.65 |
| Parameter | Value |
|---|---|
| Number of elements for the X-axis dimension of the plasma area or footprint (FLx) | 36 |
| Number of elements for the Y-axis dimension of the plasma area or footprint (FLy) | 16 |
| Maximum plasma plume temperature (THigh), K | 1476 |
| Minimum plasma plume temperature (TLow), K | 634 |
| X-Axis standard deviation of the Gaussian plasma plume temperature profile, σx2 | 49 |
| Y-Axis standard deviation of the Gaussian plasma plume temperature profile, σy2 | 14.5 |
| Maximum convective coefficient (FilmHigh), W/m2·K | 2500 |
| Minimum convective coefficient (FilmLow), W/m2·K | 2000 |
| Temp (K) | Density (kg/m3) [27] | Thermal Conductivity (W/(m·K)) [28] | Specific Heat (J/(kg·K)) [27] | Emissivity Coefficient [25] | Elastic Modulus (Pa) [29] | Poisson’s Ratio [30] | Thermal Expansion Coefficient (10−6 K−1) [31] |
|---|---|---|---|---|---|---|---|
| 300 | 2700 | 237 | 871 | 0.07 | 83.80 × 109 | 0.334 | 23.0 |
| 600 | 232 | 1072 | 56.16 × 109 | 30.0 | |||
| 900 | 213 | 1190 | 48.00 × 109 | 34.0 | |||
| 1200 | 99 | 1273 | 100 | 36.9 | |||
| 1500 | 102 | 1338 | 100 | 39.1 | |||
| 1800 | 103 | 1391 | 100 | 41.0 | |||
| 2100 | 103 | 1436 | 100 | 42.5 |
| Temp (K) | Density (kg/m3) [32] | Thermal Conductivity (W/(m·K)) [30] | Specific Heat (J/(kg·K)) [30] | Emissivity Coefficient [25] | Elastic Modulus (Pa) [32] | Poisson’s Ratio [30] | Thermal Expansion Coefficient (10−6 K−1) [33] |
|---|---|---|---|---|---|---|---|
| 300 | 3950 | 36.96 | 789 | 0.8 | 3.85 × 1011 | 0.254 | 4.3 |
| 600 | 16.01 | 1114 | 3.63 × 1011 | 7.1 | |||
| 900 | 8.87 | 1220 | 3.41 × 1011 | 8.7 | |||
| 1200 | 6.66 | 1270 | 3.19 × 1011 | 9.9 | |||
| 1500 | 5.78 | 1308 | 2.97 × 1011 | 10.8 | |||
| 1800 | 6.13 | 1304 | 2.75 × 1011 | 11.5 | |||
| 2100 | 6.09 | 1310 | 2.53 × 1011 | 12.1 | |||
| 2400 | 6.05 | 1316 | 100 | 12.6 | |||
| 2700 | 6.01 | 1322 | 100 | 13.1 |
| Parameter | Value |
|---|---|
| Young’s modulus of aluminium, GPa | 69 |
| Young’s modulus of Al2O3, GPa | 306 |
| Poisson’s coefficient for aluminium | 0.334 |
| Poisson’s coefficient for Al2O3 | 0.254 |
| Specimen width, mm | 25.4 |
| Substrate thickness, mm | 4 |
| Coating thickness, µm | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-García, J.; Martínez-García, V.; Killinger, A. Multi-Scale Thermo-Mechanical Model Simulation of Residual Stress in Atmospheric Plasma Spray Process. Coatings 2024, 14, 1547. https://doi.org/10.3390/coatings14121547
Martínez-García J, Martínez-García V, Killinger A. Multi-Scale Thermo-Mechanical Model Simulation of Residual Stress in Atmospheric Plasma Spray Process. Coatings. 2024; 14(12):1547. https://doi.org/10.3390/coatings14121547
Chicago/Turabian StyleMartínez-García, Jose, Venancio Martínez-García, and Andreas Killinger. 2024. "Multi-Scale Thermo-Mechanical Model Simulation of Residual Stress in Atmospheric Plasma Spray Process" Coatings 14, no. 12: 1547. https://doi.org/10.3390/coatings14121547
APA StyleMartínez-García, J., Martínez-García, V., & Killinger, A. (2024). Multi-Scale Thermo-Mechanical Model Simulation of Residual Stress in Atmospheric Plasma Spray Process. Coatings, 14(12), 1547. https://doi.org/10.3390/coatings14121547







