Nonlinear Oxidation Behavior at Interfaces in Coated Steam Dual-Pipe with Initial Waviness and Cooling Temperature
Abstract
1. Introduction
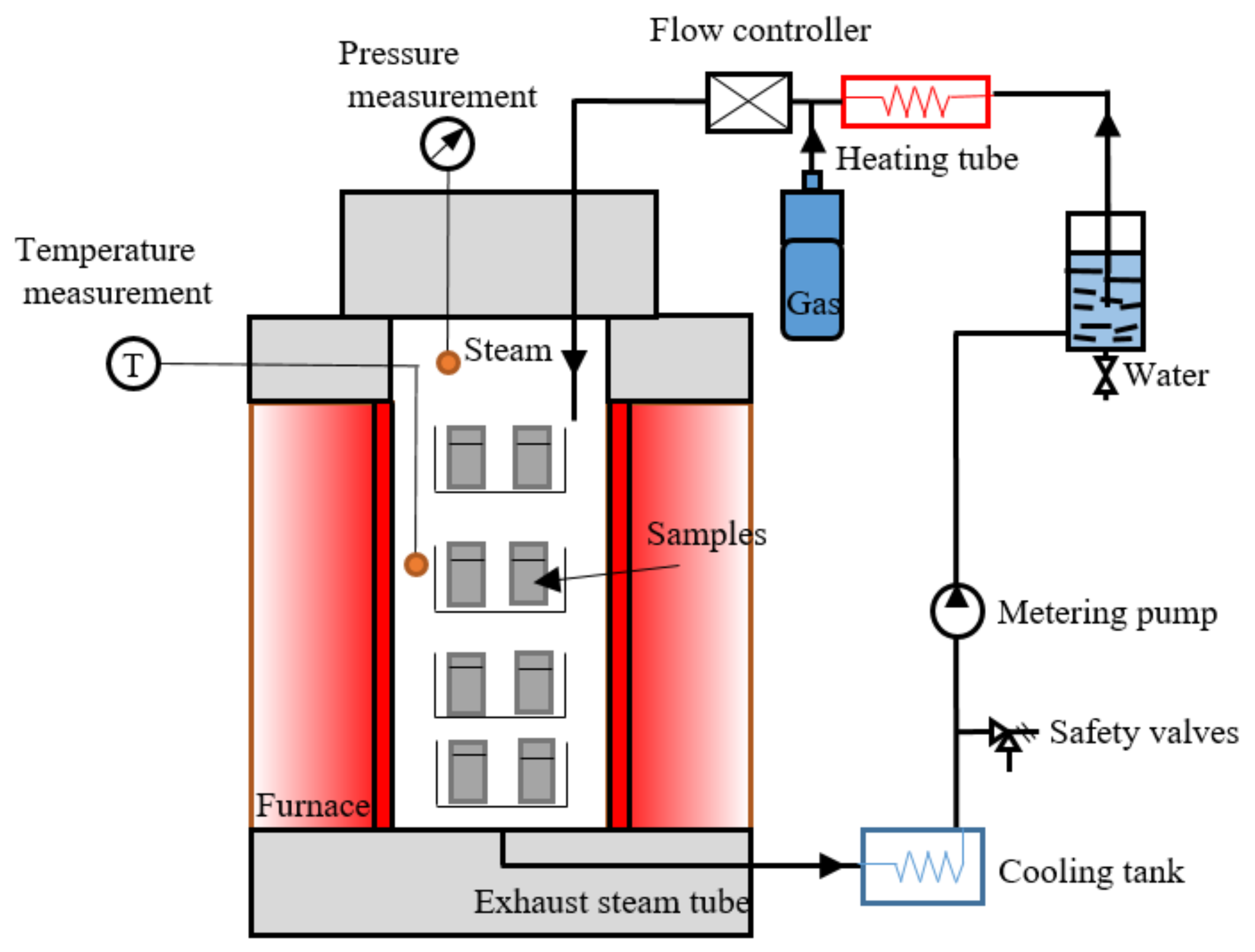
2. TBC High-Temperature Water Vapor Oxidation Experiments
3. Simulation Strategy for the Nonlinear Growth of TGO Layer
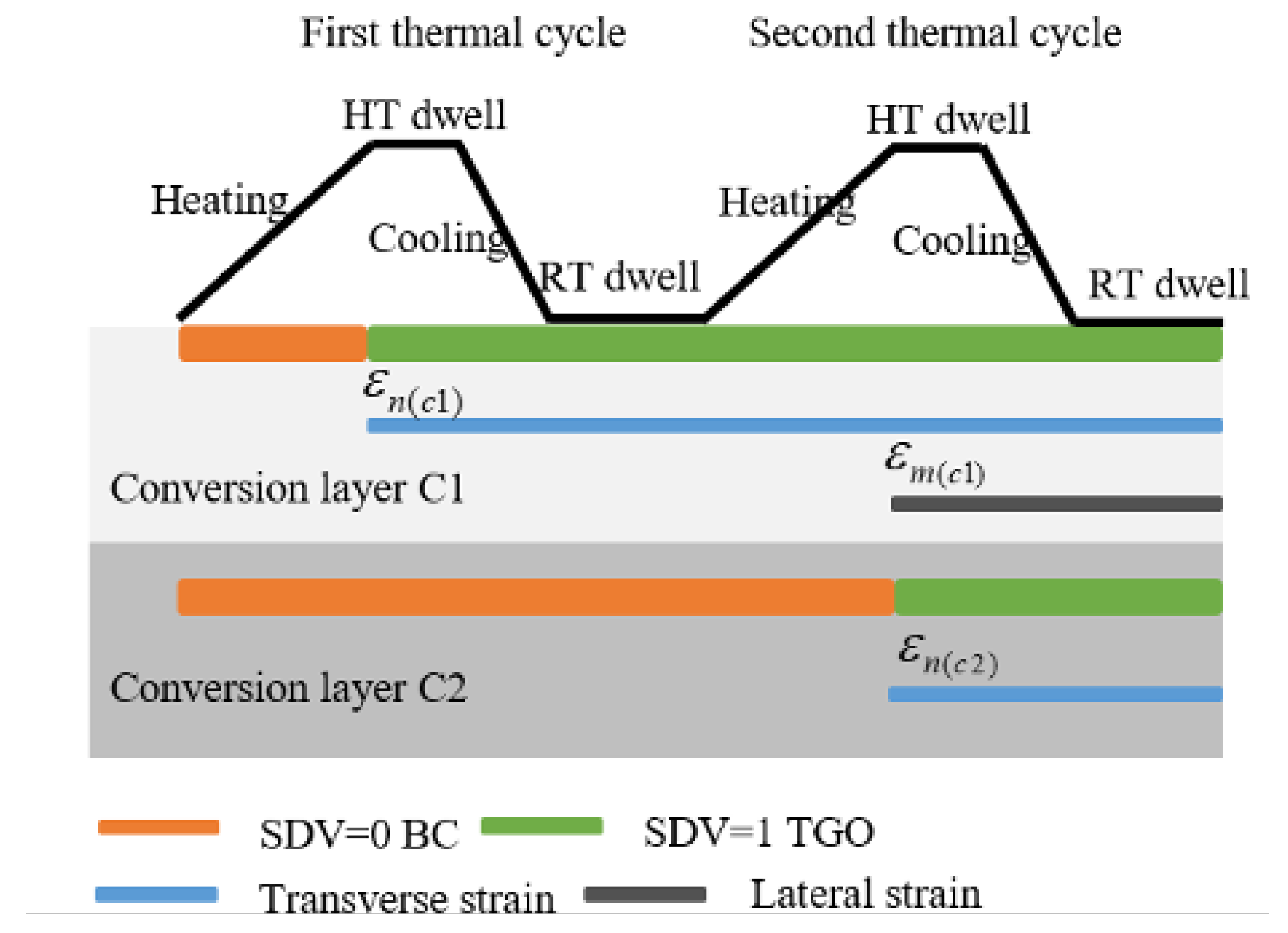
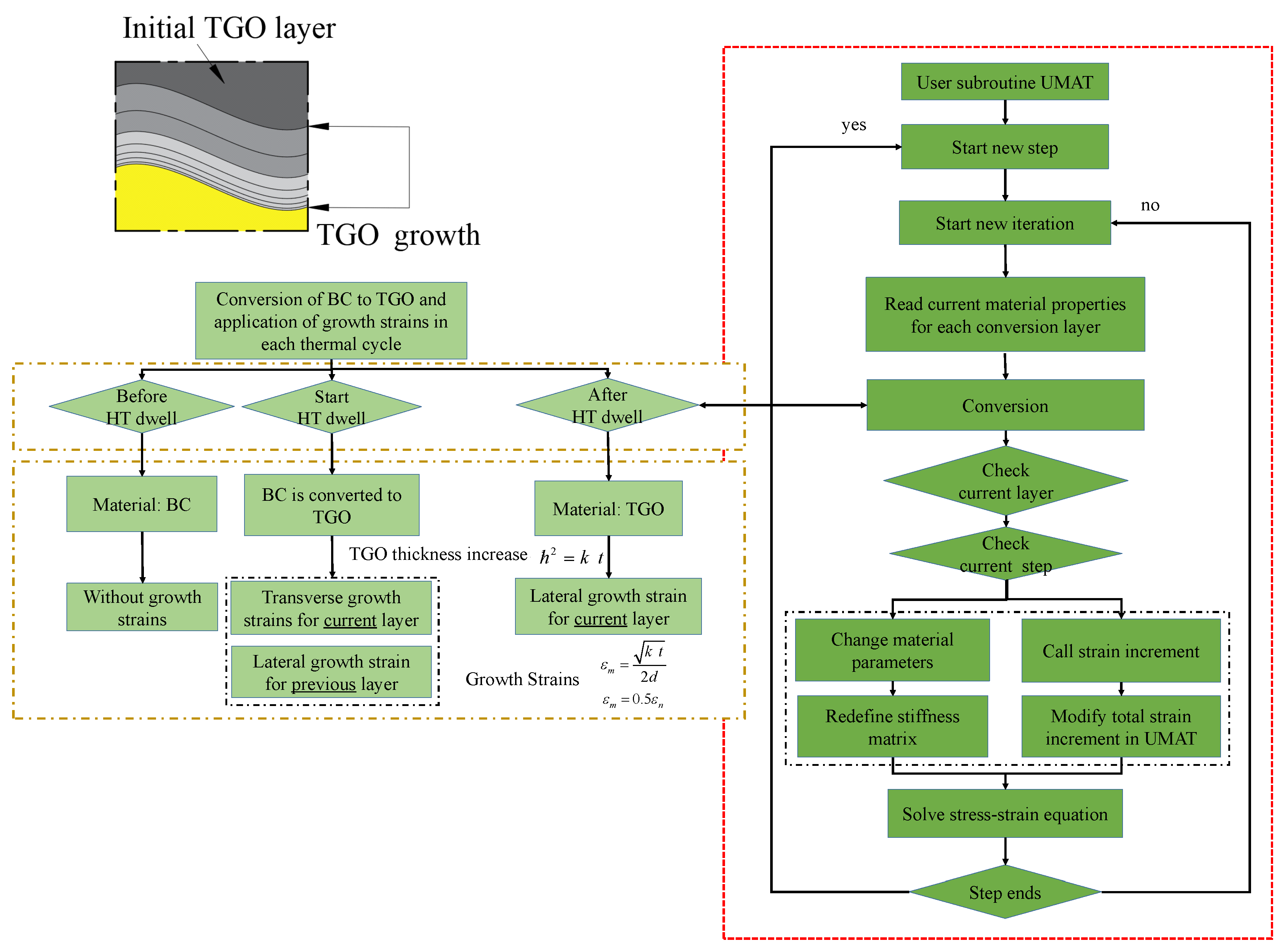
3.1. Material Parameter Transformation Method and Growth Strain Imposition
3.2. UMAT Development in ABAQUS for the Nonlinear Growth of TGO Layer
4. Simulation Details for the Coated Steam Dual-Pipe System
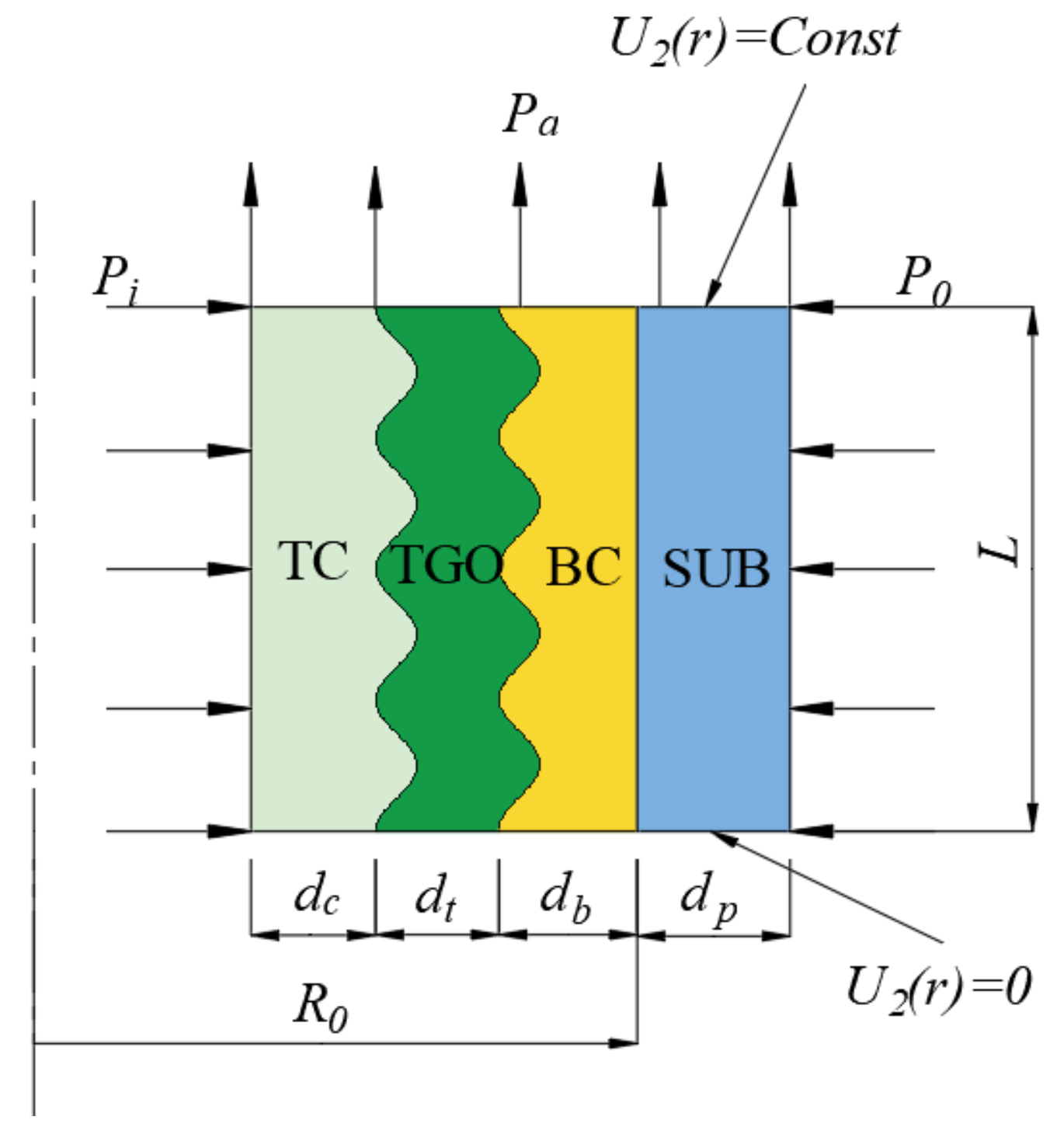
4.1. Geometry and Meshing
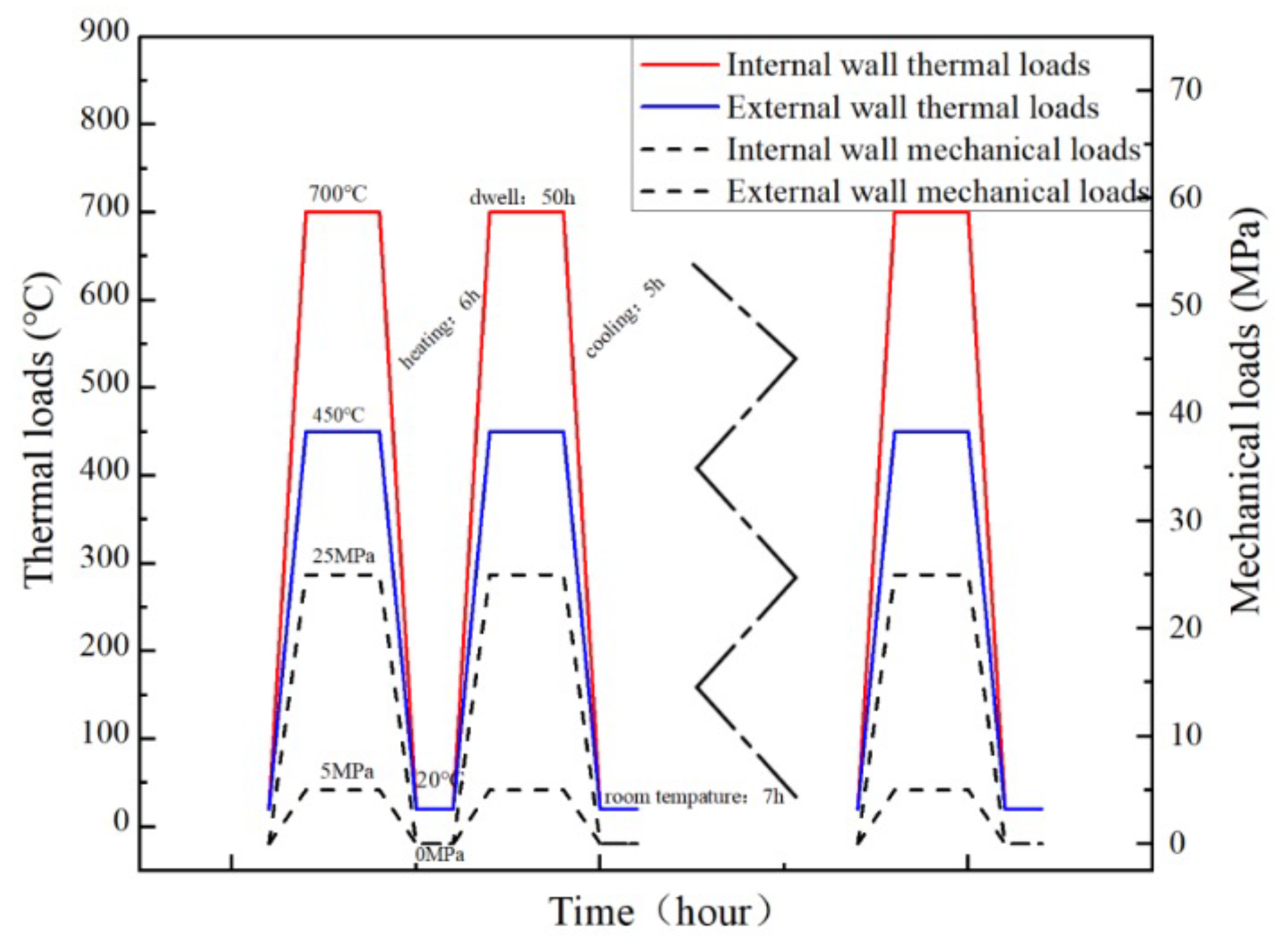
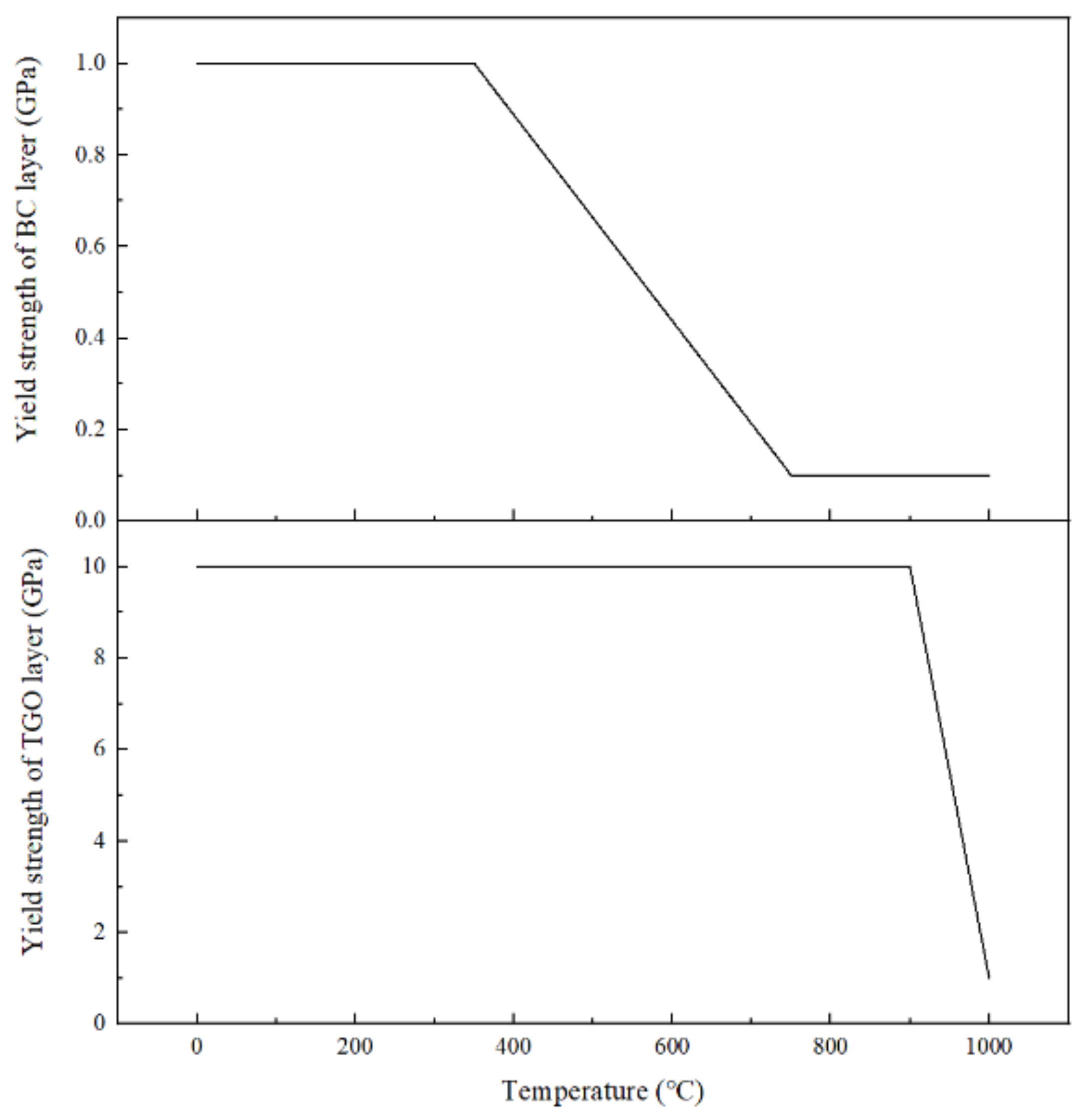
4.2. Boundary Conditions and Materials Parameters
5. Results and Discussion
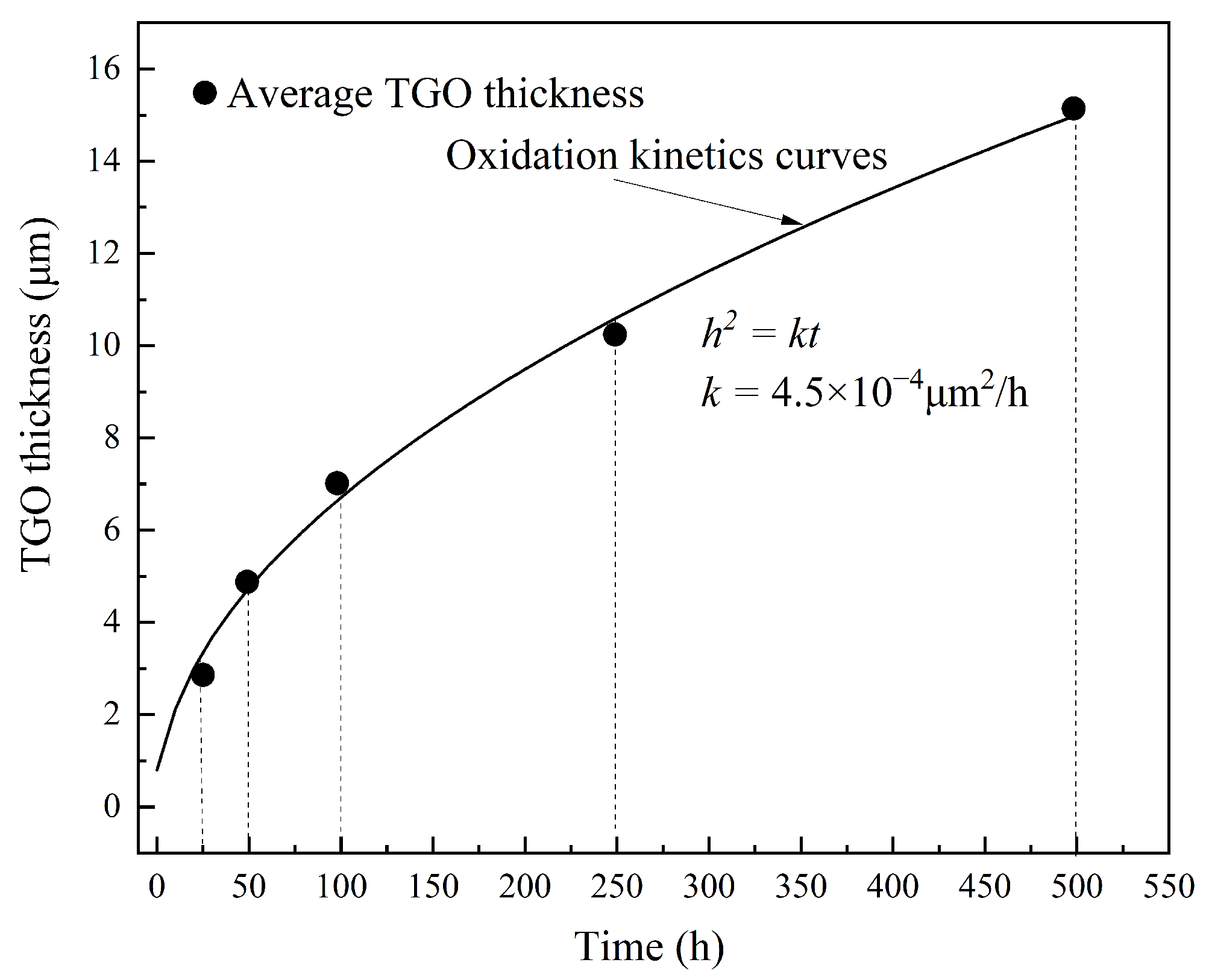
5.1. TGO Growth Kinetics Curve
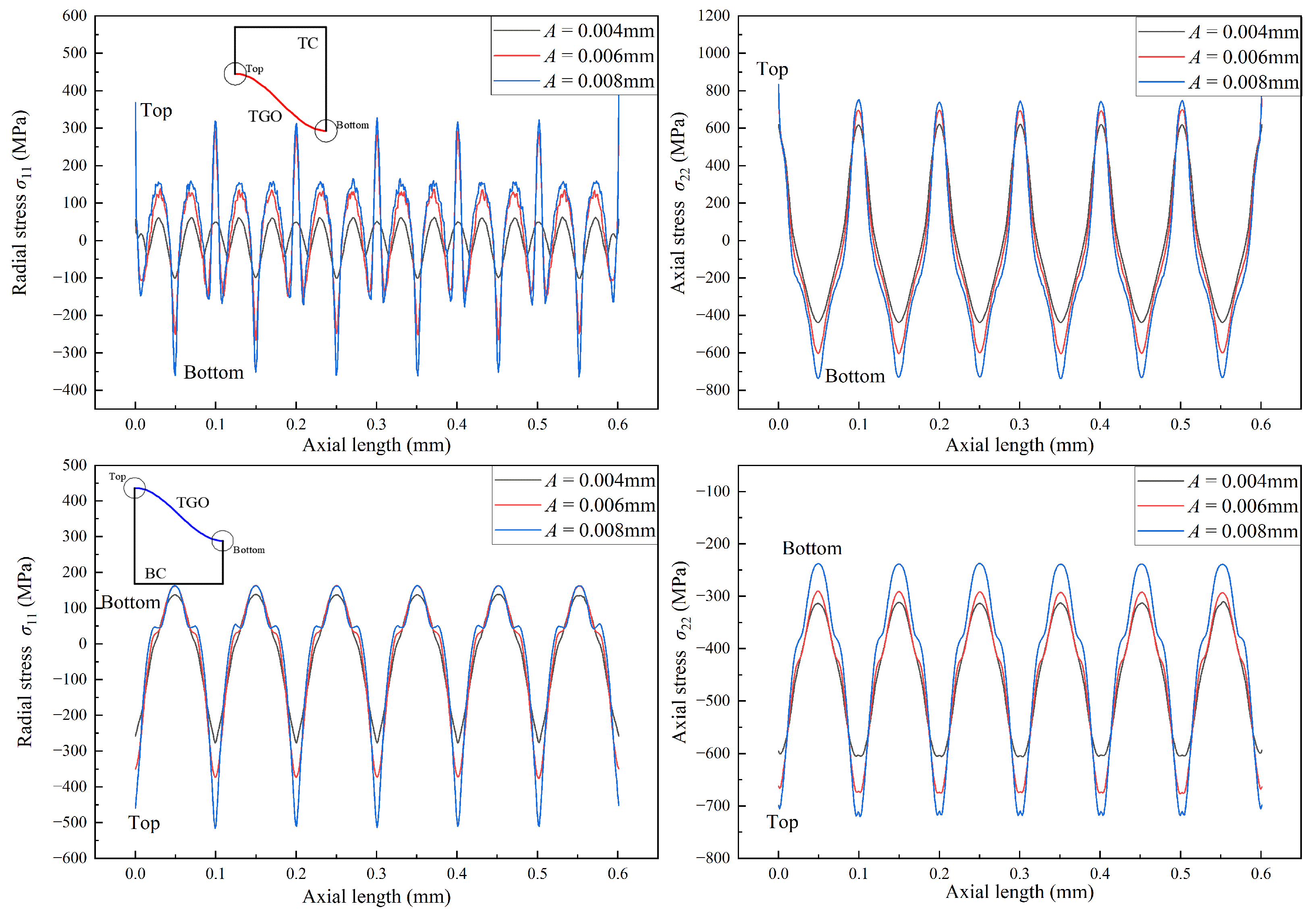
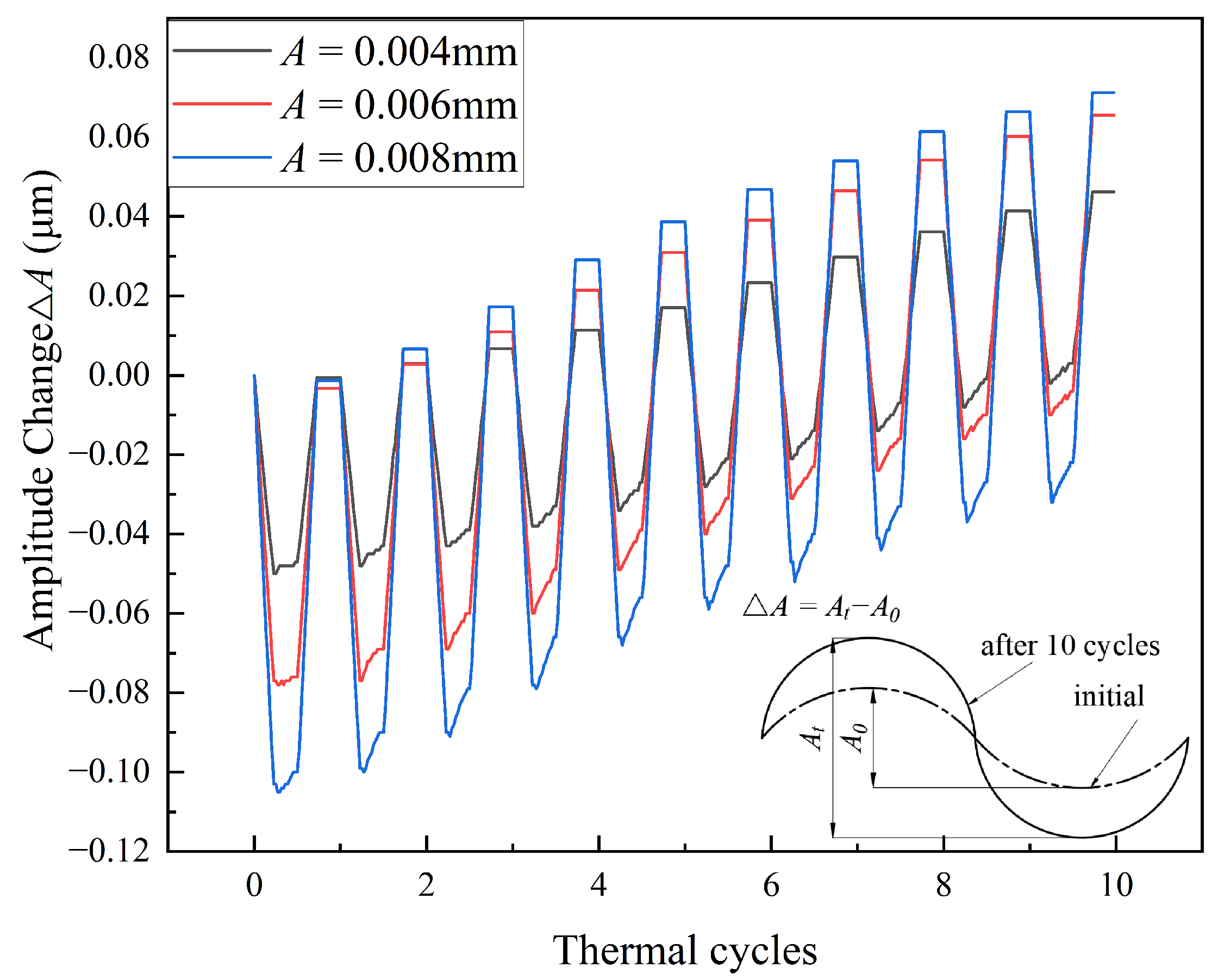
5.2. Stress and Morphology Evolution with Initial Waviness at TGO Interfaces
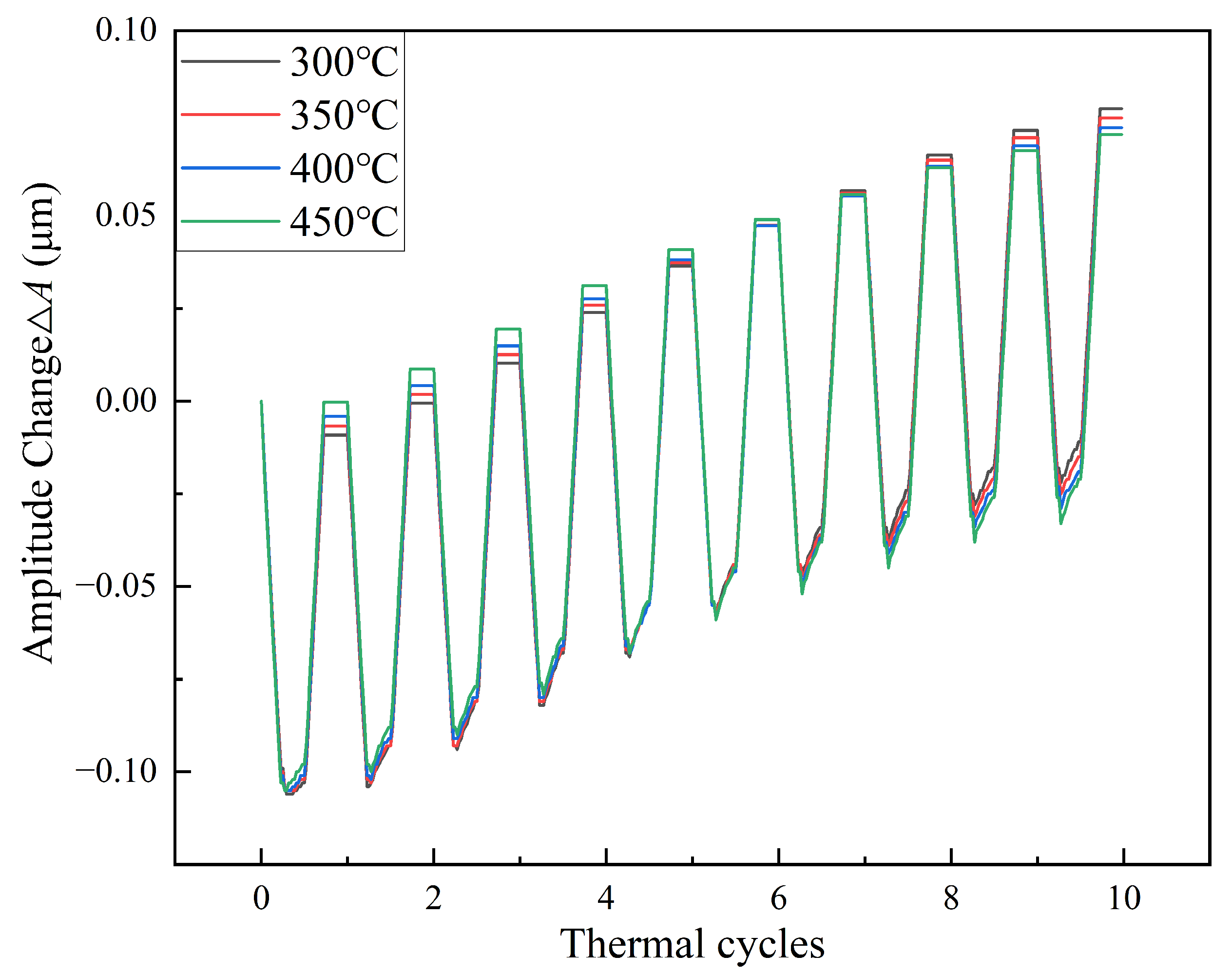
5.3. Stress and Morphology Evolution with Temperature of Cooling Steam
6. Concluding Remarks and Future Directions
- (1)
- The oxidation kinetics of TBCs in a high-temperature water vapor environment at 700 °C followed a parabolic growth pattern. The growth rate of the TGO layer decreased over time, with an oxidation rate constant taking .
- (2)
- As the TGO layer grew, its interfacial amplitude increase, resulting in greater interfacial curvature. This curvature enhanced the stress concentration at the TC/TGO and BC/TGO interfaces, significantly influencing the interfacial stress of the coated system.
- (3)
- The temperature of the cooling steam substantially affected the stress distribution at the TC/TGO and BC/TGO interfaces by altering the thermal stress within the coating system. When the cooling steam temperature rose from 300 °C to 450 °C, the stress values at the TC/TGO and BC/TGO interfaces decreased from −917 MPa and −379 MPa to −717 MPa and −219 MPa, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Ye, B.; Liu, J. Research on the peak of CO2 emissions in the developing world: Current progress and future prospect. Appl. Energy 2019, 235, 186–203. [Google Scholar] [CrossRef]
- Jianlan, Z.; Bo, A.; Yuqi, G. Thermal stress analysis on thermal barrier coatings based on real three-dimensional structure of thermally grown oxide. Rare Met. Mater. Eng. 2018, 47, 2100–2106. [Google Scholar]
- Guo, X.; Sun, W.; Becker, A.; Morris, A.; Pavier, M.; Flewitt, P.; Tierney, M.; Wales, C. Thermal and stress analyses of a novel coated steam dual pipe system for use in advanced ultra-supercritical power plant. Int. J. Press. Vessels Pip. 2019, 176, 103933. [Google Scholar] [CrossRef]
- Guo, X.; Benaarbia, A.; Sun, W.; Becker, A.; Morris, A.; Pavier, M.; Flewitt, P.; Tierney, M.; Wales, C. Optimisation and thermo-mechanical analysis of a coated steam dual pipe system for use in advanced ultra-supercritical power plant. Int. J. Press. Vessels Pip. 2020, 186, 104157. [Google Scholar] [CrossRef]
- Evans, A.G.; Mumm, D.; Hutchinson, J.; Meier, G.; Pettit, F. Mechanisms controlling the durability of thermal barrier coatings. Prog. Mater. Sci. 2001, 46, 505–553. [Google Scholar] [CrossRef]
- Wang, T.; Fan, X.; Sun, Y.; Su, L.; Song, Y.; Lv, B. The stresses and cracks in thermal barrier coating system: A review. Guti Lixue Xuebao/Acta Mech. Solida Sin. 2016, 37, 477–517. [Google Scholar]
- Bai, Y.; Ding, C.; Li, H.; Han, Z.; Ding, B.; Wang, T.; Yu, L. Isothermal oxidation behavior of supersonic atmospheric plasma-sprayed thermal barrier coating system. J. Therm. Spray Technol. 2013, 22, 1201–1209. [Google Scholar] [CrossRef]
- Liu, X.; Wang, T.; Li, C.; Lime, R.S.; Patnaik, P.C. Formation and growth behavior of TGO in air plasma sprayed thermal barrier coatings at high temperature. Surf. Technol. 2015, 11, 91–96. [Google Scholar]
- Poza, P.; Gómez-García, J.; Múnez, C. TEM analysis of the microstructure of thermal barrier coatings after isothermal oxidation. Acta Mater. 2012, 60, 7197–7206. [Google Scholar] [CrossRef]
- Li, Z.; Qian, S.; Wang, W.; Liu, J. Microstructure and oxidation resistance of magnetron-sputtered nanocrystalline NiCoCrAlY coatings on nickel-based superalloy. J. Alloys Compd. 2010, 505, 675–679. [Google Scholar] [CrossRef]
- Niranatlumpong, P.; Ponton, C.; Evans, H. The failure of protective oxides on plasma-sprayed NiCrAlY overlay coatings. Oxid. Met. 2000, 53, 241–258. [Google Scholar] [CrossRef]
- Tuan, W.; Wu, H.; Chen, R. Effect of sintering atmosphere on the mechanical properties of NiAl2O3 composites. J. Eur. Ceram. Soc. 1997, 17, 735–741. [Google Scholar] [CrossRef]
- Kumar, A.; Moledina, J.; Liu, Y.; Chen, K.; Patnaik, P.C. Nano-micro-structured 6%–8% YSZ thermal barrier coatings: A comprehensive review of comparative performance analysis. Coatings 2021, 11, 1474. [Google Scholar] [CrossRef]
- Wagner, C. Diffusion and high temperature oxidation of metals. At. Mov. 1951, 165. [Google Scholar]
- Freborg, A.; Ferguson, B.; Brindley, W.; Petrus, G. Modeling oxidation induced stresses in thermal barrier coatings. Mater. Sci. Eng. A 1998, 245, 182–190. [Google Scholar] [CrossRef]
- Karlsson, A.M.; Evans, A. A numerical model for the cyclic instability of thermally grown oxides in thermal barrier systems. Acta Mater. 2001, 49, 1793–1804. [Google Scholar] [CrossRef]
- Karlsson, A.M.; Levi, C.; Evans, A. A model study of displacement instabilities during cyclic oxidation. Acta Mater. 2002, 50, 1263–1273. [Google Scholar] [CrossRef]
- He, M.; Hutchinson, J.; Evans, A. Large deformation simulations of cyclic displacement instabilities in thermal barrier systems. Acta Mater. 2002, 50, 1063–1073. [Google Scholar] [CrossRef]
- He, M.; Hutchinson, J.; Evans, A. Simulation of stresses and delamination in a plasma-sprayed thermal barrier system upon thermal cycling. Mater. Sci. Eng. A 2003, 345, 172–178. [Google Scholar] [CrossRef]
- Clarke, D.R. The lateral growth strain accompanying the formation of a thermally grown oxide. Acta Mater. 2003, 51, 1393–1407. [Google Scholar] [CrossRef]
- Rhines, F.; Wolf, J. The role of oxide microstructure and growth stresses in the high-temperature scaling of nickel. Metall. Trans. 1970, 1, 1701–1710. [Google Scholar] [CrossRef]
- Su, L.; Zhang, W.; Sun, Y.; Wang, T. Effect of TGO creep on top-coat cracking induced by cyclic displacement instability in a thermal barrier coating system. Surf. Coatings Technol. 2014, 254, 410–417. [Google Scholar] [CrossRef]
- Ding, J.; Li, F.X.; Kang, K.J. Numerical simulation of displacement instabilities of surface grooves on an alumina forming alloy during thermal cycling oxidation. J. Mech. Sci. Technol. 2009, 23, 2308–2319. [Google Scholar] [CrossRef]
- Wang, X.; Atkinson, A.; Chirivì, L.; Nicholls, J.R. Evolution of stress and morphology in thermal barrier coatings. Surf. Coatings Technol. 2010, 204, 3851–3857. [Google Scholar] [CrossRef]
- Abdelgawad, A.; Al-Athel, K. Effect of TGO thickness, pores, and creep on the developed residual stresses in thermal barrier coatings under cyclic loading using SEM image-based finite element model. Ceram. Int. 2021, 47, 20064–20076. [Google Scholar] [CrossRef]

| C | Mn | P | S | Si | Cr | W | Mo | V |
| 0.114 | 0.392 | 0.011 | 0.004 | 0.315 | 9.21 | 1.93 | 0.475 | 0.189 |
| Nb | C | Mn | P | N | B | Ni | Al | |
| 0.073 | 0.114 | 0.392 | 0.01 | 0.037 | 0.003 | 0.275 | 0.011 |
| First Thermal Cycle | Second Thermal Cycle | |||||||
|---|---|---|---|---|---|---|---|---|
| Heating | HT dwell | Cooling | RT dwell | Heating | HT dwell | Cooling | RT dwell | |
| Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | |
| Conversion layer C1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Conversion layer C2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Layer No. | Time (Hour) | h (mm) | Lateral Growth Strain |
|---|---|---|---|
| 0 | 0 | 0.0000 | 0.0000 |
| 1 | 50 | 0.0047 | 0.0707 |
| 2 | 100 | 0.0020 | 0.0293 |
| 3 | 150 | 0.0015 | 0.0225 |
| 4 | 200 | 0.0013 | 0.0189 |
| 5 | 250 | 0.0011 | 0.0167 |
| 6 | 300 | 0.0010 | 0.0151 |
| 7 | 350 | 0.0009 | 0.0139 |
| 8 | 400 | 0.0009 | 0.0129 |
| 9 | 450 | 0.0008 | 0.0121 |
| 10 | 500 | 0.0008 | 0.0115 |
| Material | Temp. | E | Yield Strength | Density | CTE | Conductivity | Specific Heat | |
|---|---|---|---|---|---|---|---|---|
| (°C) | (GPa) | (MPa) | (kg/m3) | (10−6/°C) | (W/m°C) | (J/(kg°C)) | ||
| 8YSZ | 20 | 204 | 0.1 | 6037 | 9.68 | 1.2 | 500 | |
| 800 | 179 | 0.11 | 9.88 | |||||
| TGO | 20 | 400 | 0.23 | 1000 | 3984 | 8 | 10 | 755 |
| 1000 | 325 | 0.25 | 1 | 9.3 | 4 | |||
| NiCoCrAlY | 20 | 200 | 0.3 | 868 | 7711 | 12.5 | 5.8 | 628 |
| 800 | 145 | 0.32 | 191 | 14.3 | 14.5 | |||
| P92 | 20 | 218 | 0.3 | 488 | 7770 | 26 | 440 | |
| 100 | 213 | 461 | 10.9 | 27 | 480 | |||
| 200 | 207 | 441 | 11.3 | 28 | 510 | |||
| 300 | 199 | 427 | 11.7 | 28 | 550 | |||
| 400 | 190 | 396 | 12.1 | 29 | 630 | |||
| 450 | 186 | 12.1 | 29 | 630 | ||||
| 500 | 181 | 360 | 12.3 | 30 | 660 | |||
| 550 | 175 | 331 | 12.4 | 30 | 710 | |||
| 600 | 168 | 285 | 12.6 | 30 | 770 | |||
| 650 | 162 | 206 | 12.7 | 30 | 860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, B.; Wang, K.; Guo, X.; Gao, J.; Chen, P. Nonlinear Oxidation Behavior at Interfaces in Coated Steam Dual-Pipe with Initial Waviness and Cooling Temperature. Coatings 2024, 14, 1478. https://doi.org/10.3390/coatings14121478
Yuan B, Wang K, Guo X, Gao J, Chen P. Nonlinear Oxidation Behavior at Interfaces in Coated Steam Dual-Pipe with Initial Waviness and Cooling Temperature. Coatings. 2024; 14(12):1478. https://doi.org/10.3390/coatings14121478
Chicago/Turabian StyleYuan, Bo, Ke Wang, Xiaofeng Guo, Junxiang Gao, and Pengfei Chen. 2024. "Nonlinear Oxidation Behavior at Interfaces in Coated Steam Dual-Pipe with Initial Waviness and Cooling Temperature" Coatings 14, no. 12: 1478. https://doi.org/10.3390/coatings14121478
APA StyleYuan, B., Wang, K., Guo, X., Gao, J., & Chen, P. (2024). Nonlinear Oxidation Behavior at Interfaces in Coated Steam Dual-Pipe with Initial Waviness and Cooling Temperature. Coatings, 14(12), 1478. https://doi.org/10.3390/coatings14121478