Controlling Directional Liquid Transfer over a Ratchet-like Surface with Oriented Open-Wedges
Abstract
1. Introduction
2. Materials and Methods
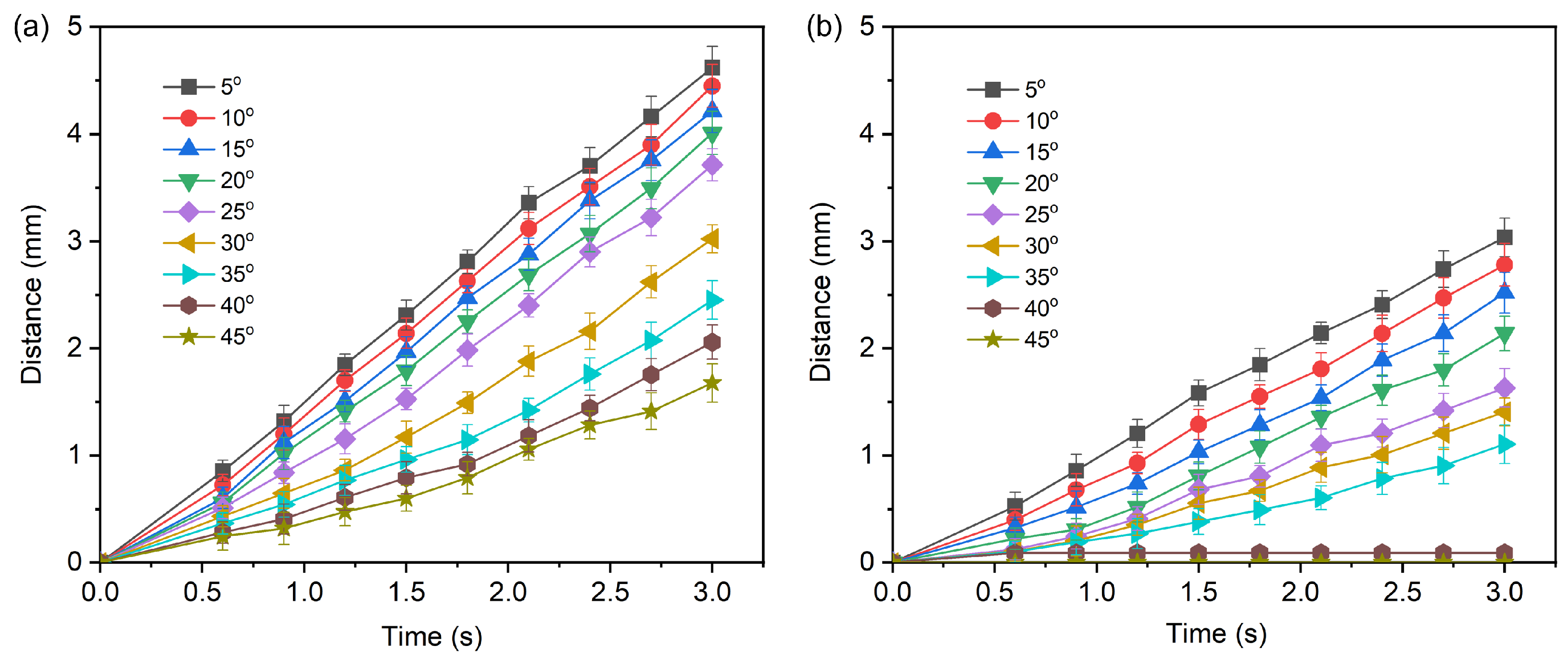
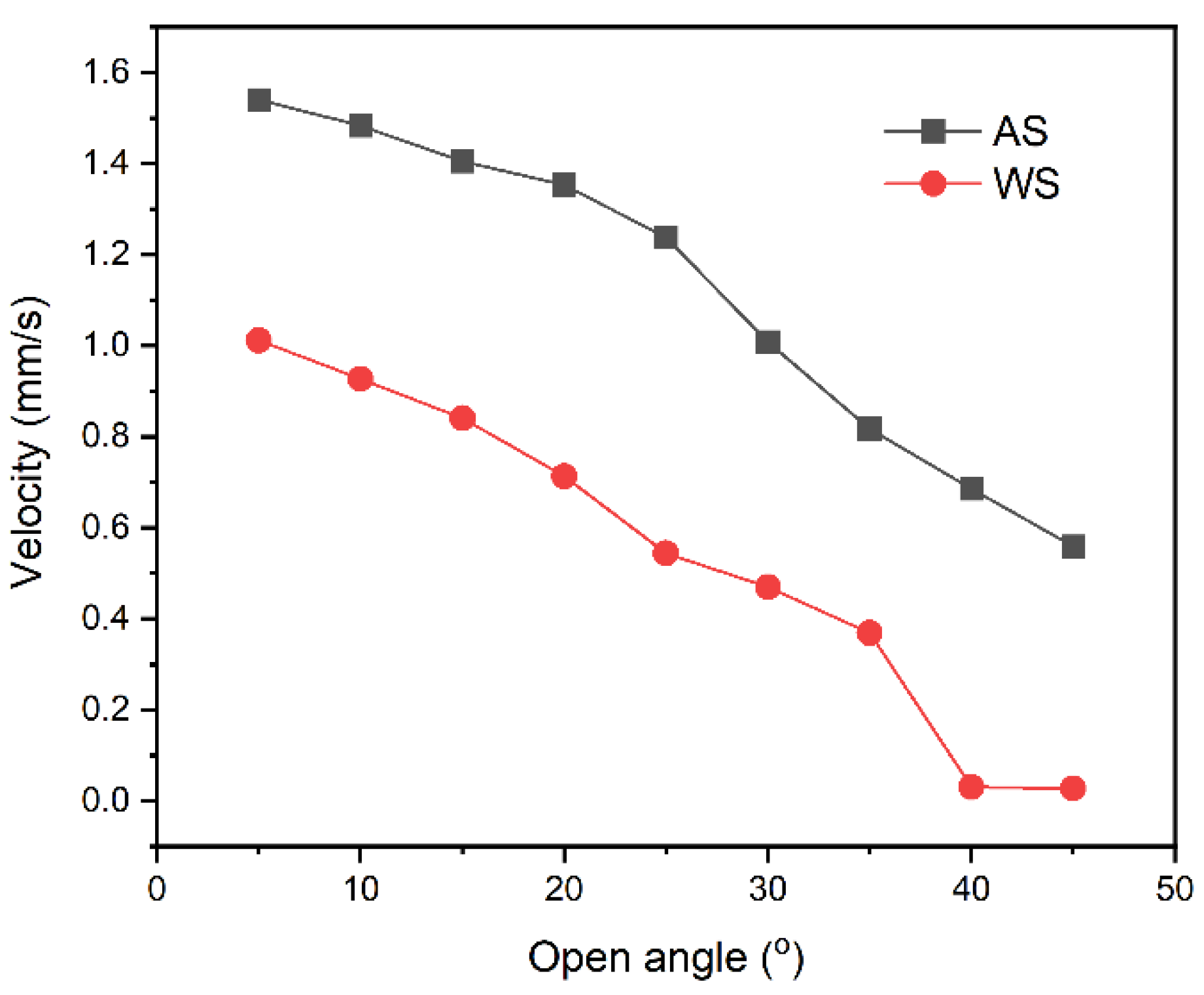
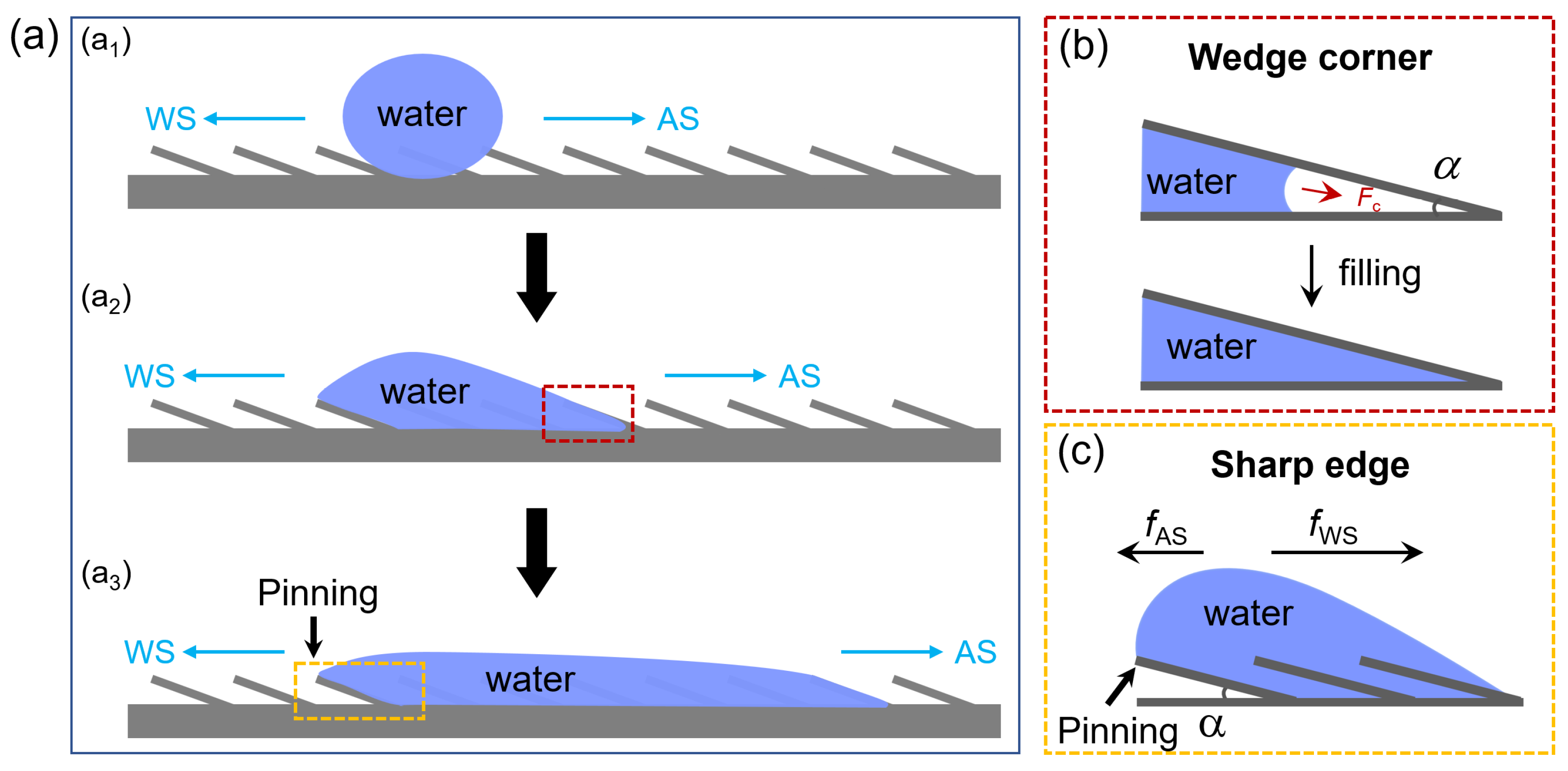
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Li, W.; Lian, J.; Zhu, H.; Deng, Q.; Zhang, Y.; Li, J.; Yin, X.; Wang, L. Selective Directional Liquid Transport on Shoot Surfaces of Crassula Muscosa. Science 2024, 384, 1344–1349. [Google Scholar] [CrossRef] [PubMed]
- Parker, A.R.; Lawrence, C.R. Water Capture by a Desert Beetle. Nature 2001, 414, 33–34. [Google Scholar] [CrossRef]
- Prakash, M.; Quere, D.; Bush, J.W.M. Surface Tension Transport of Prey by Feeding Shorebirds: The Capillary Ratchet. Science 2008, 320, 931–934. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Yao, X.; Liu, H.; Quere, D.; Jiang, L. Self-Removal of Condensed Water on the Legs of Water Striders. Proc. Natl. Acad. Sci. USA 2015, 112, 9247–9252. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, P.; Zhang, L.; Liu, H.; Jiang, Y.; Zhang, D.; Han, Z.; Jiang, L. Continuous Directional Water Transport on the Peristome Surface of Nepenthes Alata. Nature 2016, 532, 85–89. [Google Scholar] [CrossRef]
- Ju, J.; Bai, H.; Zheng, Y.; Zhao, T.; Fang, R.; Jiang, L. A Multi-Structural and Multi-Functional Integrated Fog Collection System in Cactus. Nat. Commun. 2012, 3, 1247. [Google Scholar] [CrossRef]
- Zheng, Y.; Bai, H.; Huang, Z.; Tian, X.; Nie, F.Q.; Zhao, Y.; Zhai, J.; Jiang, L. Directional Water Collection on Wetted Spider Silk. Nature 2010, 463, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Zhu, P.; Zheng, H.; Zhan, H.; Chen, C.; Li, J.; Wang, L.; Yao, X.; Liu, Y.; Wang, Z. Three-Dimensional Capillary Ratchet-Induced Liquid Directional Steering. Science 2021, 1348, 1344–1348. [Google Scholar] [CrossRef]
- Li, J.; Zhou, X.; Li, J.; Che, L.; Yao, J.; McHale, G.; Chaudhury, M.K.; Wang, Z. Topological Liquid Diode. Sci. Adv. 2017, 3, 19–25. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Chen, H.; Dong, Z.; Zhang, D. Surfaces Inspired by the Nepenthes Peristome for Unidirectional Liquid Transport. Adv. Mater. 2017, 29, 1702995. [Google Scholar] [CrossRef]
- Huang, Y.; Yin, S.; Li, H.; Liu, S.; Wong, T.N. One-Step Fabrication of Moon-Shaped Microrobots through in Situ Solidification of Magnetic Janus Droplets in Microchannels. Droplet 2023, 2, e56. [Google Scholar] [CrossRef]
- Shang, L.; Cheng, Y.; Zhao, Y. Emerging Droplet Microfluidics. Chem. Rev. 2017, 117, 7964–8040. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhan, H.; He, X.; Zhang, M.; Xue, J.; Ouyang, T.; Zhao, L.; Liu, Y.; Feng, S. Excellent Liquid Unidirectional Transport Inner Tilted-Sector Arrayed Tubes. Adv. Mater. Interfaces 2023, 10, 2300239. [Google Scholar] [CrossRef]
- Xu, Y.; Rather, A.M.; Yao, Y.; Fang, J.; Mamtani, R.S.; Bennett, R.K.A.; Atta, R.G.; Adera, S.; Tkalec, U.; Wang, X. Liquid Crystal—Based Open Surface Microfluidics Manipulate Liquid Mobility and Chemical Composition on Demand. Sci. Adv. 2021, 7, eabi7607. [Google Scholar] [CrossRef]
- Xu, Y.; Chang, Y.; Yao, Y.; Zhang, M.; Dupont, R.L.; Rather, A.M. Modularizable Liquid-Crystal-Based Open Surfaces Enable Programmable Chemical Transport and Feeding using Liquid Droplets. Adv. Mater. 2022, 34, 2108788. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Wang, L.; Ju, J.; Sun, R.; Zheng, Y.; Jiang, L. Efficient Water Collection on Integrative Bioinspired Surfaces with Star-Shaped Wettability Patterns. Adv. Mater. 2014, 26, 5025–5030. [Google Scholar] [CrossRef]
- Yu, Z.; Yun, F.F.; Wang, Y.; Yao, L.; Dou, S.; Liu, K.; Jiang, L.; Wang, X. Desert Beetle-Inspired Superwettable Patterned Surfaces for Water Harvesting. Small 2017, 13, 1701403. [Google Scholar] [CrossRef]
- Chen, Y.; Li, K.; Zhang, S.; Qin, L.; Deng, S.; Ge, L.; Xu, L.P.; Ma, L.; Wang, S.; Zhang, X. Bioinspired Superwettable Microspine Chips with Directional Droplet Transportation for Biosensing. ACS Nano 2020, 14, 4654–4661. [Google Scholar] [CrossRef]
- Ware, C.S.; Smith-Palmer, T.; Peppou-Chapman, S.; Scarratt, L.R.J.; Humphries, E.M.; Balzer, D.; Neto, C. Marine Antifouling Behavior of Lubricant-Infused Nanowrinkled Polymeric Surfaces. ACS Appl. Mater. Interfaces 2018, 10, 4173–4182. [Google Scholar] [CrossRef]
- Daniel, S. Fast Drop Movements Resulting from the Phase Change on a Gradient Surface. Science 2001, 291, 633–636. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Y.; Wu, S.; Wang, L. In Situ Multi-Directional Liquid Manipulation Enabled by 3D Asymmetric Fang-Structured Surface. Adv. Mater. 2024, 36, 2407034. [Google Scholar] [CrossRef] [PubMed]
- Kuang, X.; Zhang, Z.; Ma, X.; Zhu, L.; Li, Y.; Li, P.; Fu, Y.; Ma, T.; He, H.; Ramakrishna, S. Advances in Directional Liquid Transport Textiles: Mechanism, Construction, and Applications. Adv. Funct. Mater. 2024, 2406906. [Google Scholar] [CrossRef]
- Meng, Q.; Xu, B.; Tang, Z.; Wei, Y.; Jiang, L.; Liu, H. Controlling Directional Liquid Transport on Dual Cylindrical Fibers with Oriented Open-Wedges. Adv. Mater. Interfaces 2022, 9, 2101749. [Google Scholar] [CrossRef]
- Taylor, B. Part of a Letter from Mr. Brook Taylor, FRS to Dr. Hans Sloane RS Secr. Concerning the Ascent of Water between Two Glass Planes. Philos. Trans. R. Soc. 1710, 27, 538. [Google Scholar]
- Hauksbee, F.X. An Account of an Experiment Touching the Ascent of Water between Two Glass Planes, in an Hyperbolick Figure. Philos. Trans. R. Soc. 1710, 27, 539–540. [Google Scholar]
- Renvoisé, P.; Bush, J.W.M.; Prakash, M.; Quéré, D. Drop Propulsion in Tapered Tubes. EPL (Europhys. Lett.) 2009, 86, 64003. [Google Scholar] [CrossRef]
- Extrand, C.W. Retention Forces of a Liquid Slug in a Rough Capillary Tube with Symmetric or Asymmetric Features. Langmuir 2007, 23, 1867–1871. [Google Scholar] [CrossRef]
- Mori, Y.H.; Van de Ven, T.G.M.; Mason, S.G. Resistance to Spreading of Liquids by Sharp Edged Microsteps. Colloids Surf. 1982, 4, 1–15. [Google Scholar] [CrossRef]
- Oliver, J.F.; Huh, C.; Mason, S.G. Resistance to Spreading of Liquids by Sharp Edges. J. Colloid. Interface Sci. 1977, 59, 568–581. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Zhou, J.; Pang, J.; Qiu, W.; Wang, X.; Qin, W. Controlling Directional Liquid Transfer over a Ratchet-like Surface with Oriented Open-Wedges. Coatings 2024, 14, 1308. https://doi.org/10.3390/coatings14101308
Meng Q, Zhou J, Pang J, Qiu W, Wang X, Qin W. Controlling Directional Liquid Transfer over a Ratchet-like Surface with Oriented Open-Wedges. Coatings. 2024; 14(10):1308. https://doi.org/10.3390/coatings14101308
Chicago/Turabian StyleMeng, Qing’an, Junjie Zhou, Jie Pang, Wenli Qiu, Xiaopeng Wang, and Wenfeng Qin. 2024. "Controlling Directional Liquid Transfer over a Ratchet-like Surface with Oriented Open-Wedges" Coatings 14, no. 10: 1308. https://doi.org/10.3390/coatings14101308
APA StyleMeng, Q., Zhou, J., Pang, J., Qiu, W., Wang, X., & Qin, W. (2024). Controlling Directional Liquid Transfer over a Ratchet-like Surface with Oriented Open-Wedges. Coatings, 14(10), 1308. https://doi.org/10.3390/coatings14101308





