Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
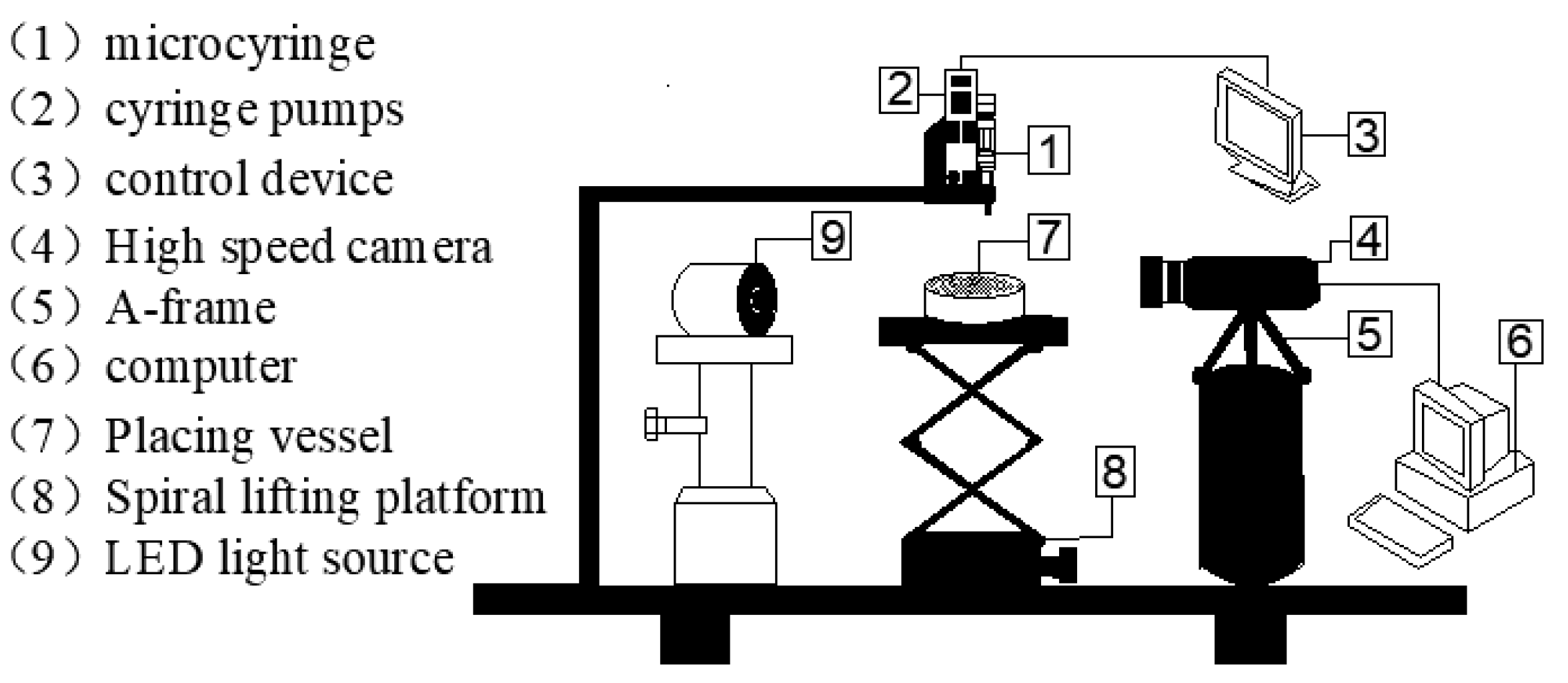
2.2. Apparatus
2.3. Testing Plan
2.4. Testing Items
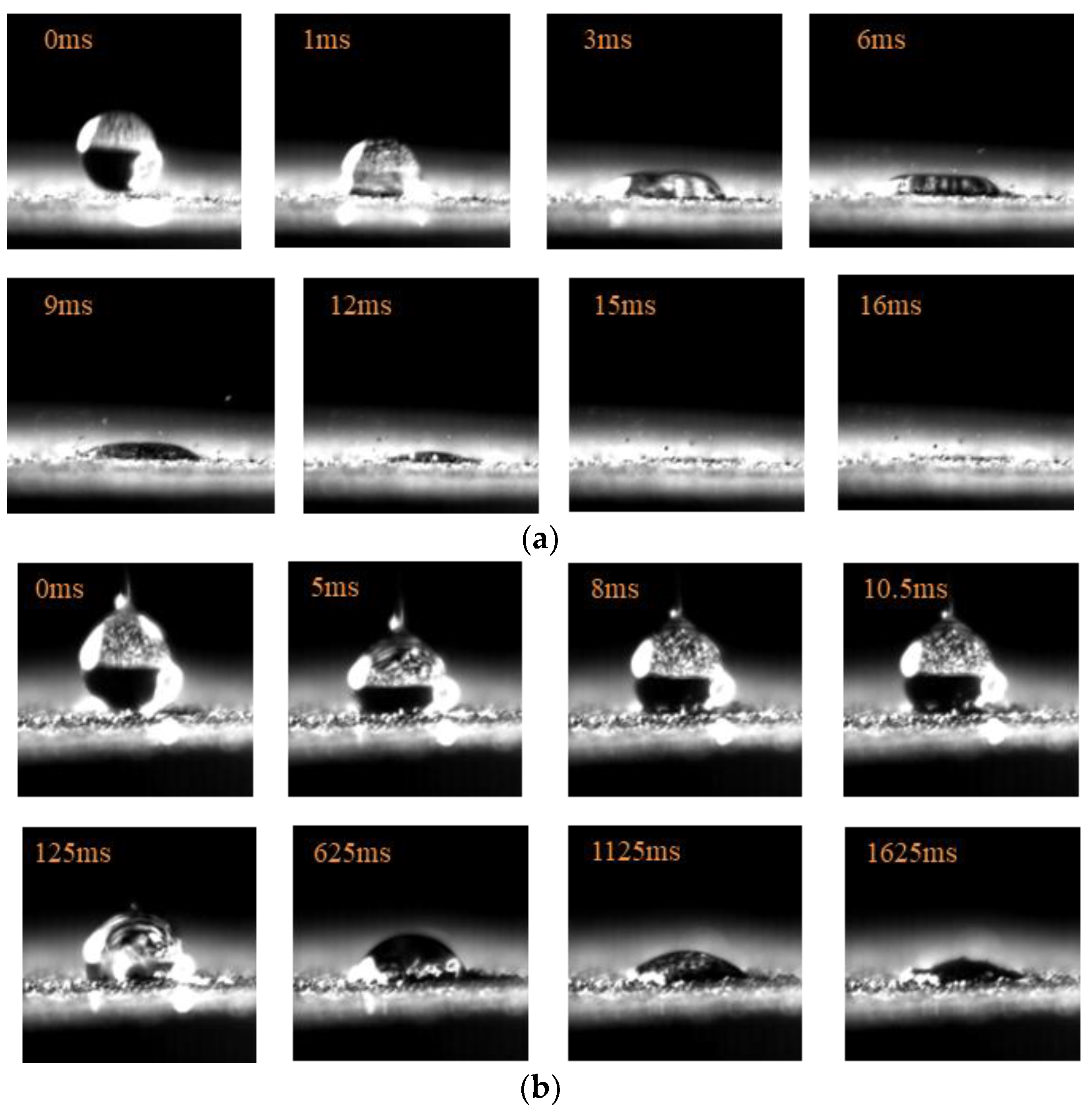
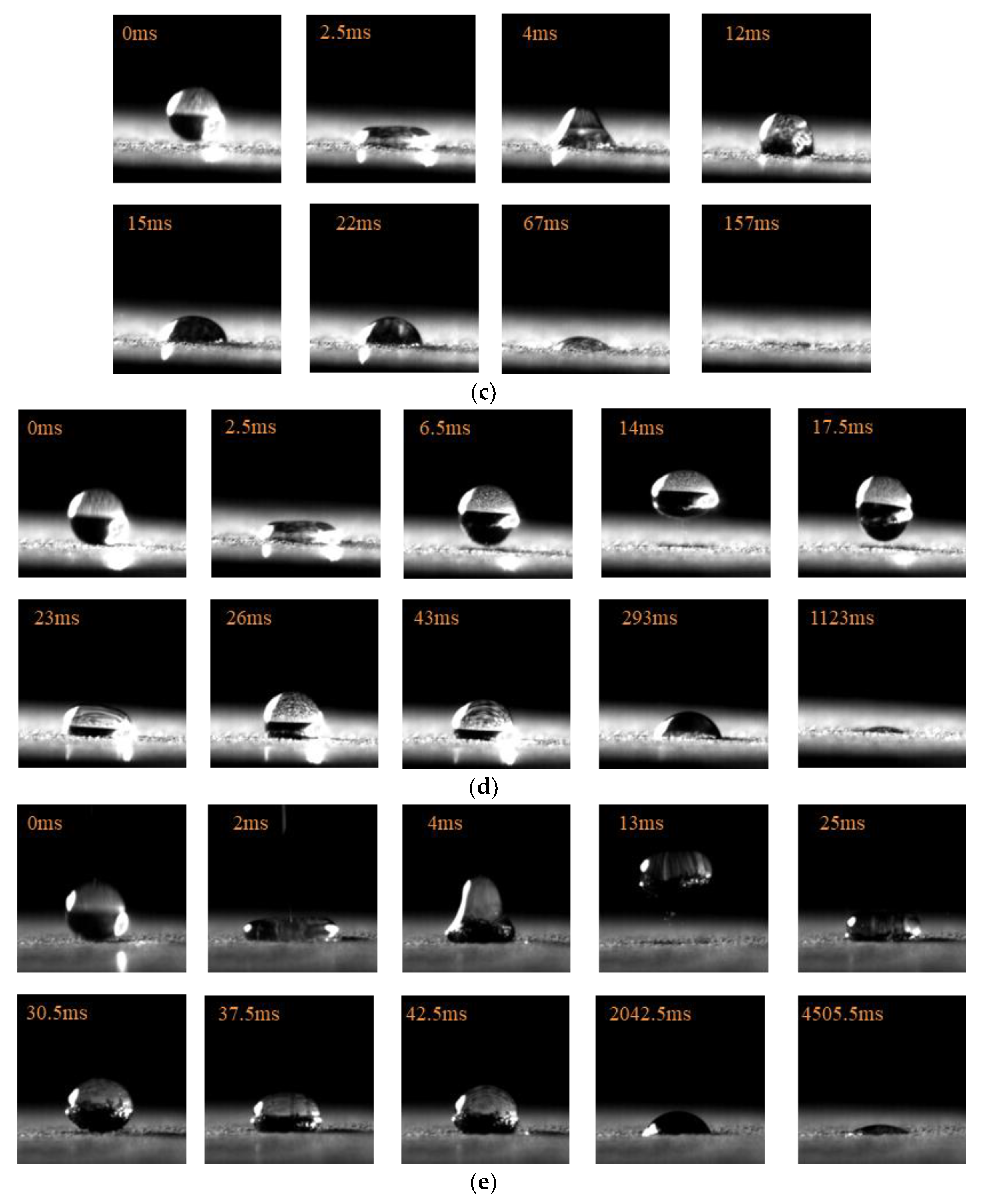
2.4.1. Droplet Behavior Types
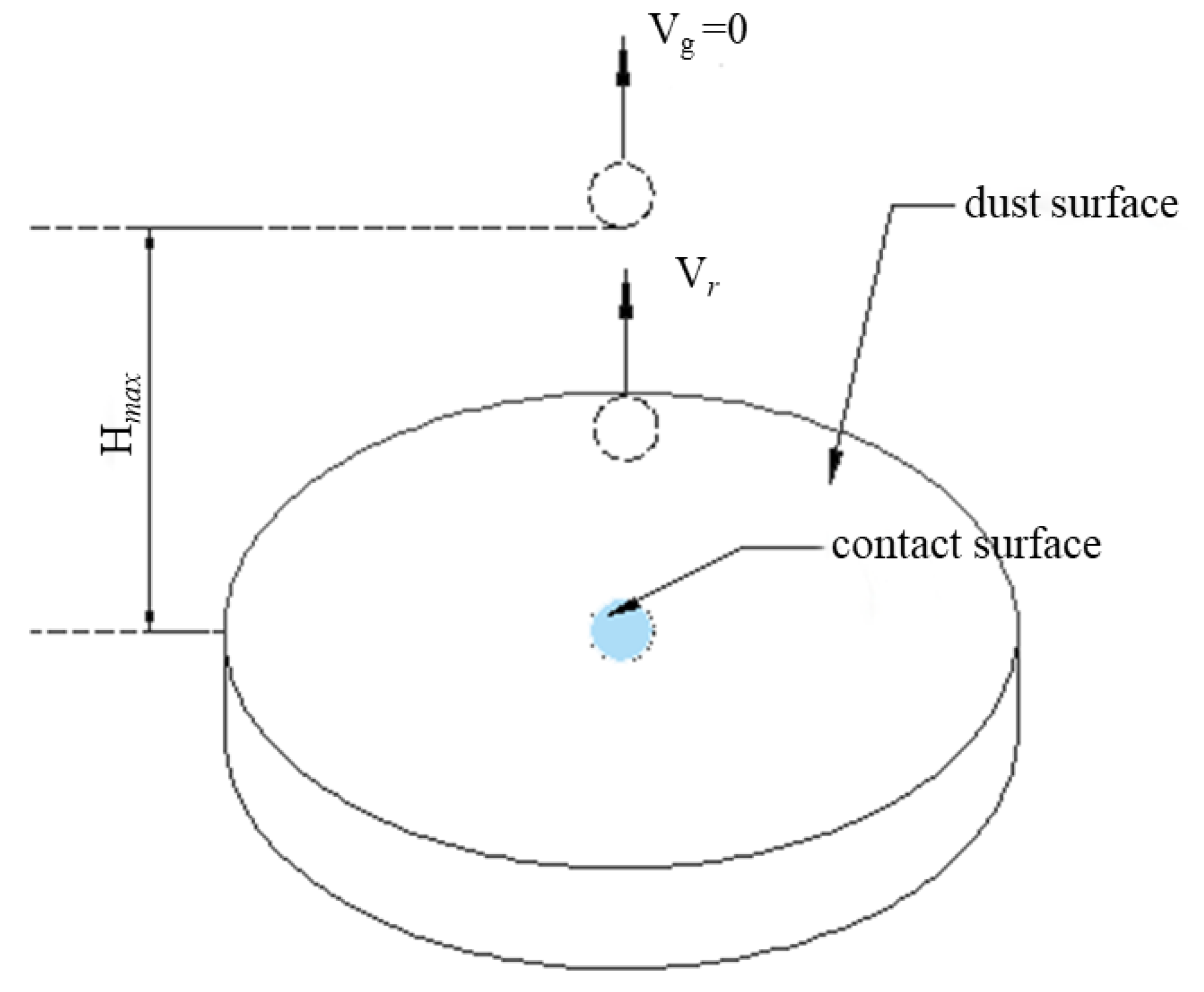
2.4.2. Maximum Spreading Coefficient
2.4.3. Maximum Acting Diameter and Acting Area
2.4.4. Maximum Bounce Height
3. Results and Discussion
3.1. Pattern of Contact Behavior
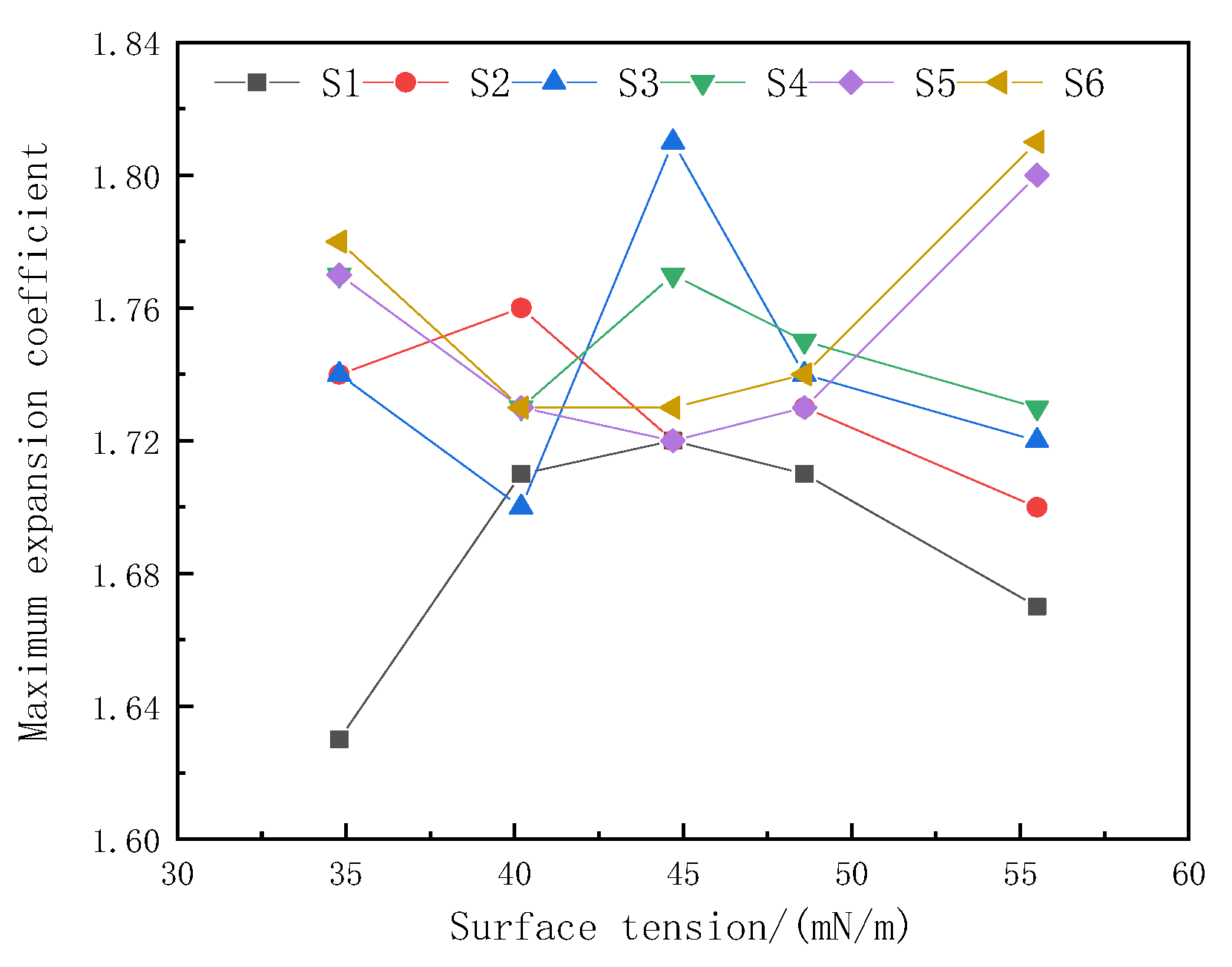
3.2. Maximum Spreading Diameter
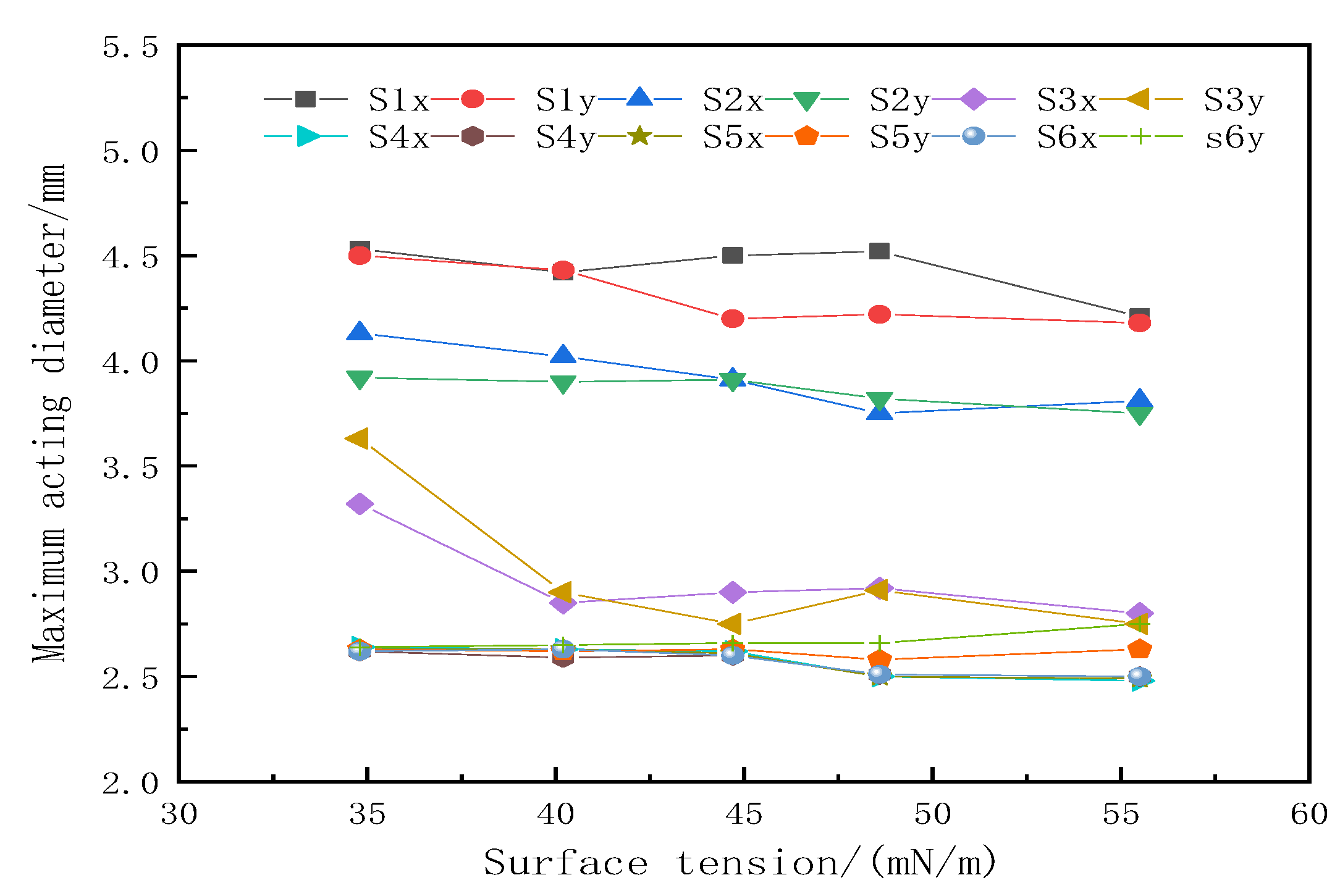
3.3. Maximum Acting Diameter and Acting Area
3.4. Maximum Vertical Bounce
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Zhou, F.; Li, S. Experimental study on the dust filtration performance with participation of water mist. Process Saf. Environ. Prot. 2017, 109, 357–364. [Google Scholar] [CrossRef]
- Werner, S.R.; Jones, J.R.; Paterson, A.H.; Archer, R.H.; Pearce, D.L. Droplet impact and spreading on lecithinated anhydrous milkfat surfaces. J. Food Eng. 2009, 90, 525–530. [Google Scholar] [CrossRef]
- van Dam, D.B.; Le Clerc, C. Experimental study of the impact of an ink-jet printed droplet on a solid substrate. Phys. Fluids 2004, 16, 3403–3414. [Google Scholar] [CrossRef]
- Jia, W.; Zhu, H.; Dong, X.; Xue, F. Study on spray droplets hitting soybean leaf surface. J. Agric. Mach. 2013, 44, 87–94. [Google Scholar]
- Kamgar, A.; Hassanajili, S. Super-hydrophobic Fe3O4@SiO2@MPS nanoparticles for oil remediation: The influence of pH and concentration on clustering phenomenon and oil sorption. J. Mol. Liq. 2020, 315, 113709. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Ganji, D.; Ommi, F. Effect of SiO2 super-hydrophobic coating and self-rewetting fluid on two phase closed thermosyphon heat transfer characteristics: An experimental and numerical study. J. Mol. Liq. 2020, 315, 113748. [Google Scholar] [CrossRef]
- Rein, M. Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 1993, 12, 61–93. [Google Scholar] [CrossRef]
- Worthington, A. On the forms assumed by drops of liquids falling vertically on a horizontal plate. Proc. R. Soc. Lond. 1876, 25, 261–272. [Google Scholar]
- Kai, R.; Feuillebois, F. Influence of surface roughness on liquid drop impact. J. Colloid Interface Sci. 1998, 203, 16–30. [Google Scholar]
- Sikalo, S.; Marengo, M.; Tropea, C.; Ganic, E. Analysis of impact of droplet on horizontal surface. Exp. Therm. Fluid Sci. 2002, 25, 503–510. [Google Scholar] [CrossRef]
- Huang, H.; Chen, X. Energetic analysis of drop’s maximum spreading on solid surface with low impact speed. Phys. Fluids 2018, 30, 022106. [Google Scholar] [CrossRef]
- Bi, F.; Guo, Y.; Shen, S.; Li, Y. Experimental study of spread characteristics of droplet impacting solid surface. Acta Phys. Sin. 2012, 61, 293–298. [Google Scholar]
- Andrade, R.; Skurtys, O.; Osorio, F. Experimental study of drop impacts and spreading on epicarps: Effect of fluid properties. J. Food Eng. 2011, 109, 430–437. [Google Scholar] [CrossRef]
- Rioboo, R.; Voue, M.; Vaillant, A.; Coninck, J. Drop impact on porous super-hydrophobic polymer surfaces. Langmuir ACS J. Surf. Colloids 2008, 24, 14074–14077. [Google Scholar] [CrossRef] [PubMed]
- Roeland, C.; Henderix, M.; Tran, T.; Sun, C.; Tsai, P.; Lohse, D. How microstructures affect air film dynamics prior to drop impact. Soft Matter 2014, 10, 3703. [Google Scholar]
- Roisman, I.; Rioboo, R.; Tropea, C. Normal impact of a liquid drop on a dry surface: Model for spreading and receding. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 458, 1411–1430. [Google Scholar] [CrossRef]
- Hardalupas, Y.; Okamoto, S.; Taylor, A.; Whitelaw, J. Application of a phase Doppler anemometer to a spray impinging on a disc. In Proceedings of the 6th International Symposium on the Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 20–23 July 1992; pp. 490–506. [Google Scholar]
- Wei, J.; Wang, H.; Si, L.; Xi, Y. Characteristics of solid-liquid contact between coal and water under gas atmosphere. J. Coal Sci. 2022, 47, 323–332. [Google Scholar]
- Xu, T.; Sun, H.; Dai, L. Research on the mechanism of the influence of fine coal particle size on coal seam gas content. Min. Res. Dev. 2023, 43, 138–142. [Google Scholar]
- Jin, L.; Guo, J.; Li, G.; Wang, T.; Liu, J. Research progress and prospect of dust poisoning Control Technology in Metal mine stope. Metal Mine 2021, 1, 120–134. [Google Scholar]
- Jin, L.; Wang, J.; Liu, J.; Guo, J.; Wang, T. Influence of dust surface characteristics on wettability of inlet roadway in Luoshan Gold Mine. Saf. Environ. 2019, 19, 1954–1962. [Google Scholar]
- Liu, J.; Jin, L.; Wang, J.; Ou, S.; Ghio, J.; Wang, T. Micromorphology and physicochemical properties of hydrophobic blasting dust in iron mines. Int. Miner. Met. Mater. 2019, 26, 665–672. [Google Scholar] [CrossRef]
- Jin, L.; Liu, J.; Guo, J.; Wang, J.; Wang, T. Physicochemical factors affecting the wettability of copper mine blasting dust. Int. Coal Sci. Technol. 2021, 8, 265–273. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. A computational method for free surface hydrodynamics. J. Press. Vessel Technol. 1981, 103, 136–141. [Google Scholar] [CrossRef]
- Pilch, M.; Erdman, C. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Ji, S.; Ge, J.; Tan, D. Research on Particle Wall Impact Collision Wall Effects in Liquid Solid Two Phase Fluids. J. Zhejiang Univ. Sci. A 2017, 18, 958–973. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Zhang, D. Dynamic response of turbine blades under high-speed impact of water droplets. J. Electr. Eng. China 2008, 280, 76–81. [Google Scholar]
- Xie, Y.; Han, Y.; Zhang, D.; Lan, J. Numerical simulation on elastic-plastic response of high speed liquid-solid impact. In Proceedings of the 10th National Conference on Impact Dynamics, Taiyuan, China, 26 July 2011. [Google Scholar]
- Yang, H.; Yi, H. Experimental study on hydraulic reduction of blasting dust toxicity. Met. Mines 2016, 8, 148–151. [Google Scholar]
- Wu, J.; Yuan, M. Research and Application of Underground High Air Flow Purification Technology in Metal Mines. Min. Res. Dev. 2014, 34, 78–81. [Google Scholar]
- Guo, F.; Yang, T.; Yang, J.; Mo, J. Design and application of exhaust ventilation and dust removal system for rock roadway excavation working face. Min. Saf. Environ. Prot. 2021, 48, 97–100+111. [Google Scholar]
- Li, G.; Wu, J.; Jin, L.; Guo, J. Research Status and Prospects of Dust Control Technology in Metal Mines in China. Met. Mines 2021, 1, 154–167. [Google Scholar]
- Wang, P.; Wang, X.; Liu, Y. Research Status and Prospects of Dust Suppressants for Coal Mines in China. Chem. Miner. Process. 2021, 50, 49–54+64. [Google Scholar]
- Wu, C. Chemical Dust Suppression; Central South University Press: Changsha, China, 2003. [Google Scholar]
- Wang, D. Mineralogy; Science Press: Beijing, China, 2015. [Google Scholar]
- Lu, X.; Wang, D.; Ren, W.; Wang, H. Experimental research on foam dust suppression technology in Zaozhuang Binhu Coal Mine. Coal Technol. 2012, 11, 35. [Google Scholar]
- Lu, X.; Wang, D.; Wang, H.; Ren, W.; Gao, Q. Experimental study on foam for mine dust removal. Coal Mine Saf. 2011, 42, 1–3. [Google Scholar]
- Zhang, H.; Nie, W.; Yan, J.; Bao, Q.; Liu, Q. Preparation and performance study of a novel polymeric spraying duet suppression agent with enhanced wetting and coagulation properties for coal mine. Powder Technol. 2020, 364, 901–914. [Google Scholar] [CrossRef]
- Bao, Q.; Nie, W.; Liu, C.; Zhang, H.; Liu, Q. The preparation of a novel hydrogel based on crosslinked polymers for suppressing coal dusts. J. Clean. Prod. 2020, 249, 119343. [Google Scholar] [CrossRef]
- Yang, C.; Wu, C. Study on chemical dust suppression performance of nano-fluids. China Saf. Sci. J. 2019, 29, 147–152. [Google Scholar]
- Gao, Y.; Jun, S.; Pan, L. Interaction and instability of air films between bituminous coal surfaces and surfactant droplets. Fuel 2020, 274, 117839. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, S.; Jiang, B. Wetting process and adsorption mechanism of surfactant solutions on coal dust surface. J. Chem. 2019, 2019, 9085310. [Google Scholar] [CrossRef]
- Li, M.; Guan, Z. Dust suppression of dynamic contact between droplets and dust heap surface behavior research. J. Saf. Environ. 2021, 21, 2550–2556. [Google Scholar]
- Wang, J.; Jin, L.; Guo, J.; Liu, J.; Wang, T.; Gong, Q. Key influencing factors on wettability of blasting dust in Meishan Iron Mine. J. Cent. South Univ. 2019, 50, 2527–2535. [Google Scholar]
- Dai, C.; Ji, X.; Zhou, D.; Wang, Y.; Xu, J. Behavioral characteristics of droplets colliding with different wetted surfaces. J. Zhejiang Univ. 2018, 52, 36–42. [Google Scholar]







| Dust Sample | Upper Screen Aperture (μm) | Lower Screen Aperture (μm) | D50/(μm) | D90/(μm) | D[4,3] |
|---|---|---|---|---|---|
| S1 | 150 | 125 | 160 | 237 | 155 |
| S2 | 125 | 105 | 131 | 196 | 127 |
| S3 | 105 | 100 | 113 | 170 | 110 |
| S4 | 100 | 90 | 65.4 | 140.7 | 72.5 |
| S5 | 90 | 74 | 5.23 | 91 | 30 |
| S6 | 74 | 65 | 0.68 | 63.9 | 21.9 |
| Number | Solution Type | Mass Fraction/% | Surface Tension/mN/m | Viscosity/mPa·s |
|---|---|---|---|---|
| Y0 | Pure water | 0 | 71.2 | 1.17 |
| Y1 | Multi-component wetting agent | 0.005 | 55.5 | 1.30 |
| Y2 | 0.01 | 48.6 | 1.28 | |
| Y3 | 0.05 | 44.7 | 1.26 | |
| Y4 | 0.1 | 40.2 | 1.27 | |
| Y5 | 0.15 | 34.8 | 1.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Jin, L.; Yang, Y.; Cui, R.; Khan, N.M.; Li, M.; Zhang, Q.; Yue, X. Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface. Coatings 2023, 13, 1146. https://doi.org/10.3390/coatings13071146
Guo J, Jin L, Yang Y, Cui R, Khan NM, Li M, Zhang Q, Yue X. Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface. Coatings. 2023; 13(7):1146. https://doi.org/10.3390/coatings13071146
Chicago/Turabian StyleGuo, Jingzhong, Longzhe Jin, Yuanzhong Yang, Ruoyu Cui, Naseer Muhammad Khan, Ming Li, Qipeng Zhang, and Xinran Yue. 2023. "Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface" Coatings 13, no. 7: 1146. https://doi.org/10.3390/coatings13071146
APA StyleGuo, J., Jin, L., Yang, Y., Cui, R., Khan, N. M., Li, M., Zhang, Q., & Yue, X. (2023). Study on Dynamic Contact Behavior of Multi-Component Droplet and Dust Surface. Coatings, 13(7), 1146. https://doi.org/10.3390/coatings13071146







