Abstract
We study the Josephson current (supercurrent) in a system consisting of two superconductors connected to a single-level quantum dot (QD), which is also side-coupled to a nanowire hosting Majorana bound states (MBSs). Our results show that the MBSs change both the peak height and position in the current-carrying density of states (CCDOS), and this determines the amplitude of the Josephson current due to the phase difference between the superconductors. By adjusting the energy level in the QD and MBSs-QD hybridization strengths, the magnetic flux penetrating through the closed circuit formed by the QD and the nanowire as well as the direct overlap between the MBSs, one can fully control the electron transport processes. The present results are useful in superconductor-based electrical devices and the newly developed area of superconducting coated conductors.
1. Introduction
Among diverse electrical materials, high-transition-temperature superconductors have been extensively investigated due to not only their applications in high-efficiency electronic instruments but also basic research values in solid-state condensed matter physics [1,2,3]. As a typical physical model, micro-nano tunnel junctions consist of a buffer layer (central scattering region) sandwiched between superconducting leads, which have attracted much attention [1,4,5,6,7]. Moreover, when the scattering regions between the electron reservoirs (leads) are confined in three dimensions, a quantum dot (QD) with adjustable quantized energy levels is realized, which enables the control of electrons one by one [8]. Various exotic phenomena contained in systems of superconductor–QD–superconductor (S–QD–S) have been continuously exploited and applied in electronic [1,5,9], optical [10], magnetic [11] and thermal devices [12,13,14]. In these structures, electrons and holes form Andreev bound states (ABSs) and are converted into each other at the interfaces between the QD and superconductors, from which the Andreev reflection processes occur and carry the Josephson current (supercurrent) [15,16,17,18]. The magnitude of the Josephson current is determined by the phase difference between the two superconductors, is adjustable by the energy levels of the QD and was used in various phase-coherent electronic apparatuses [1,5,10,11,12,13,14,19,20].
In recent years, Majorana bound states (MBSs) have been successfully prepared at the opposite ends of nanowires (Majorana wires) fabricated from various materials, including topological superconductors [21] and insulators [22], p-wave superconductors [23], ferromagnetic nanowires with Rashba spin–orbit interaction proximitized to s-wave superconductors [24] and Josephson junctions [25]. They were also realized in electrostatic defects in topological superconductors [26]. The MBSs are charge-neutral relativistic quasi-particles of Majorana fermions and emerge in pairs at zero energy state. Similar to the ABSs, a pair of MBSs can be viewed as superpositions of electrons and holes and are their own anti-particles with self-adjoint creation and annihilation operators [21,22,23,24,25,26,27,28]. Due to these exotic properties, MBSs are promising for fault-tolerant topological quantum computation immune to most decoherence [21,22,23,29] as well as in the subject of spintronics [30]. In spinful topological superconductors, MBSs can enforce the intrinsic -phase difference between spin-triplet pairings (spin phase), which is adjustable by changing the spin–orbit coupling strength in the superconductors with the help of electric gates [30]. The spin phase changes the direct hybridization amplitude between the MBSs and induces a fractional Josephson effect in the absence of magnetic flux. This provides an all-electrical way to manipulate and detect non-Abelian statistics properties of the MBSs. Recently, MBSs localized well away from the interface between helical ferromagnet–superconducting junctions were realized in experiments and are also prominent in spintronics [31].
To detect the existence and enrich the applications of MBSs, Majorana wires were proposed to side-couple to QD sandwiched between two normal metallic leads (N-QD-N). In such a system, the QD–MBSs coupling affects the nonlinear transport processes if the two modes of the MBSs overlap to each other with even a small relaxation rate [32]. In the presence of strong interaction between the MBSs, their lifetime can be read directly from the height of the current peak, which is crucial for topological quantum computing. When the dot is symmetrically coupled to the leads and its level is aligned to the Fermi energy, the peak value of the linear conductance maintains its half quantum value (i.e., ) as when driving the Majorana wire in the topological phase. Whereas, in the trivial phase, the linear conductance peak value is and is zero if a regular fermionic zero mode is located at the end of the Majorana wires [28]. This provides a non-invasive detection scheme for the existence of MBSs. Recently, MBSs were also studied in the fields of thermoelectric effect, which converts heat into electricity or vice verse. If the Majorana wire is directly subjected to a temperature gradient existed between two leads, the thermopower is vanishingly small because of the particle-hole symmetric nature of the MBSs [33,34]. If the Majorana nanowire is side-coupled to N-QD-N, however, the particle-hole symmetry is broken by changing the dot level, and the thermoelectric performance is quite different from that in the pure N-QD-N structure. For example, the sign of the thermopower can be reversed by changing either the direct hybridization between the MBSs [33] or the QD–MBSs coupling strength [35,36]. If the QD is coupled to only one nanowire hosting MBSs, the authors found in Ref. [35] that the value of the figure of merit (FOM), which measures the thermoelectric efficiency, is clearly enhanced under the conditions of both weak QD–MBS coupling and ultra-low temperatures. When the QD is connected simultaneously to two Majorana nanowires, however, the magnitude of the FOM can be efficiently adjusted by the QD–MBS coupling phase difference between the two nanowires or the difference between the MBS’s polarization directions [37]. These can also serve as detection means for the MBSs.
Although the system of MBSs side-coupled to N-QD-N have received much attention in the last two decades, issues about MBSs interacting with S–QD–S have seldom been studied yet. Here, we present theoretical investigations on electronic transport through this system with the help of non-equilibrium Green’s function technique. We consider that both the two ends of the Majorana wire are coupled to the QD with different strengths [28,38,39]. The Majorana wire and the QD then form a loop enabling a magnetic flux to penetrate through them. Our results show that the Josephson current through the system is sensitive to the MBSs and can be either enhanced or suppressed by changing the quantities related to the latter. When the overlap between the MBSs is strong enough, the peak of the Josephson current originally located at the Fermi level can be split into two, which is useful for identifying the existence of MBSs.
2. Model and Method
We consider the system with a QD sandwiched between the left and right Bardeen–Cooper–Schrieffer superconductor leads. The QD is simultaneously side-coupled to both of the two modes of the MBSs with different strengths as shown in Figure 1. The Hamiltonian of the system is divided into four parts [28,40,41,42], in which represents the QD with creation (annihilation) operator of electrons having the quantized energy level and spin state . The Hamiltonian is, for the MBSs, prepared at the ends of the nanowire with coupling between them. Due to the helical property of the MBSs, they usually couple only to a unique spin state in the QD, for example, the spin-up state we here choose [28,39]. The specific form of is as follows [27,28],
in which is the overlap energy of the two mode of the MBSs denoted individually by and . Its magnitude depends exponentially on the the length of the nanowire L as with the coherence length of the nanowire [27,29]. The MBS of couples to the spin-up electrons on the QD with strength of , which is complex due to the magnetic flux penetrating through the closed structure composing of the QD and the nanowire. The magnetic flux phase difference between and is related to via , in which . Here, we set , and . After preforming a unitary transformation of and to express the MBSs by regular fermionic operators f and [27,28], the Hamiltonian reads [41,42,43],
The terms and in the total Hamiltonian describe, respectively, the superconductor leads as well as tunneling between them and the QD:
in which annihilates (creates) an electron in the -th superconductor lead with momentum k and spin . The quantity is the energy gap in the superconductor leads, and is the phase factor.
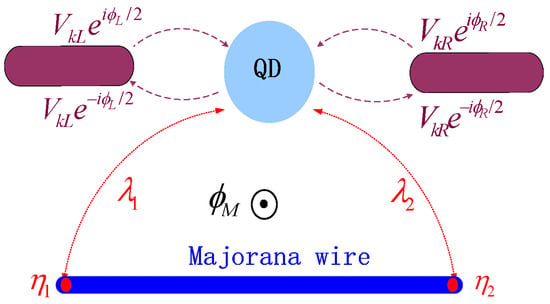
Figure 1.
(Color online) Schematic plot of the system composing of a QD connected to superconductor leads and a nanowire hosting Majorana bound states. The dot with discrete energy level is coupled to the leads with strengths of and to the MBSs with . The phase in the two superconductors are denoted by whose difference induces the Josephson current. If the dot is coupled simultaneously to both of the two modes of the MBSs, a magnetic flux emerges from the applied magnetic filed.
The Josephson current through each superconductor lead is calculated from the time evolution of the electron number operator , i.e., . Following Refs. [40,42,43,44], the Josephson current is expressed as , in which is the equilibrium Dirac–Fermi distribution function, with as the Boltzmann constant and T as the system’s equilibrium temperature, which is set to be zero in the present manuscript. The quantity in the current is the current-carrying density of states (CCDOS) [42,43,44]:
where is a matrix with as the usual Pauli matrix of component. The quantity represents the difference between the self-energies in the presence of the superconductor leads, and is the retarded (advanced) Green’s function of the dot. Here, we calculate the Green’s function by using the equation of motion technique combined with the Dyson equation method, i.e., we first calculate the free Green’s function of the QD by the equation of motion method and then include the couplings between the QD and the superconductor leads as well as the MBSs in the form of self-energies [40,42,44]. The matrix form of the total retarded (advanced) Green’s function is . In the generalized Nambu representation [40,42] , is diagonal with , and . The self-energies in the Green’s functions and the CCDOS are as follows,
where the Pauli matrix of -component, and and are, individually, the unit and zero matrices. and are the retarded Green’s functions of the MBSs in Nambu space, with . The quantity is the phase difference between the two superconductor leads that induces the Josephson current.
3. Numerical Results
In the following numerical investigations, we choose the energy gap of the superconductor leads as the energy unit. We first study the Josephson current varying with respect to the phase difference when the spin-up electrons on the QD interact only with one mode of the MBSs with different coupling strengths and MBS–MBS hybridizations. Figure 2a indicates that, when the dot is decoupled from the MBSs prepared on the nanowire, the system becomes the usual S–QD–S junction, and the Josephson current J has a discontinuous jump from positive to negative value at . Such a result has been found in some previous work [40,41,42,44]. When QD–MBS coupling is turned on, the maximums in the Josephson current are reduced and shifted away from the point of , while the jump therein remains unchanged. With increasing , the magnitude of the Josephson current is further suppressed as indicated in Figure 2a. To understand the physical reason for the current’s suppression by the MBSs, we display the CCDOS in Figure 2b for and . Since, at zero temperature, only the states of contribute to the current, we mainly show the CCDOS in that regime. Under the condition of , has two -function-type discrete states within the superconducting gap, which correspond to two ABSs. Here, we have broadened the -function by to show them more clearly [44]. These states carry currents with opposite signs, i.e., the state of the negative spectrum carries a positive supercurrent, whereas that of the positive spectrum carries a negative current (which is actually zero at zero temperature). The CCDOS also has a continuous spectrum outside the superconducting gap as indicated by the solid black line in Figure 2b, which is negative and positive individually for and . Since the CCDOS within the superconducting gap is much larger than that at , the Josephson current is positive for the chosen parameters.
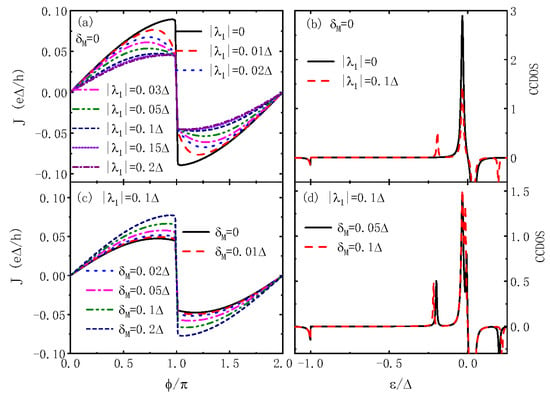
Figure 2.
(color online) Josephson current in (a,c) as a function of and the current-carrying density of states (CCDOS) in (b,d) versus the electron energy for and different values of , . Other parameters are , and .
In the presence of dot-MBS coupling ( for example), the peak of the CCDOS within the superconducting gap is lowered and split into two, while that at remains unchanged (the red dashed line in Figure 2b). This is in consistent with previous work that the coupling between the QD and the MBSs will induce new states at [28]. In Figure 2c, we show the Josephson current for different values of MBS–MBS coupling . The current is enhanced with increasing , which suggests that the impacts of the MBSs are reduced. The reason can be found in Figure 2d, in which the CCDOS within the superconducting gap and near to the zero energy is split into two with slightly suppressed magnitude. The two states induced by are located approximately at . The peak height of the CCDOS away from the zero energy state is almost unchanged, and then the magnitude of the current is enhanced with increasing MBS–MBS hybridization.
We now show, in Figure 3, the impacts of the QD energy level, which is tunable in experiments by metallic gate electrodes, with fixed values of the QD–MBS couplings and . Figure 3a shows that the current becomes a sinusoidal function with respect to the phase difference when the dot level is shifted away from the Fermi energy . With increasing , the current’s magnitude is further suppressed and almost vanishes for . This is in consistent with previous work in the absence of the MBSs [42,43,44]. The reduction in the current can be seen from the behavior of the CCDOS in Figure 3b, in which the two peaks within the superconducting gap are shifted toward a negative energy regime when the dot level is .
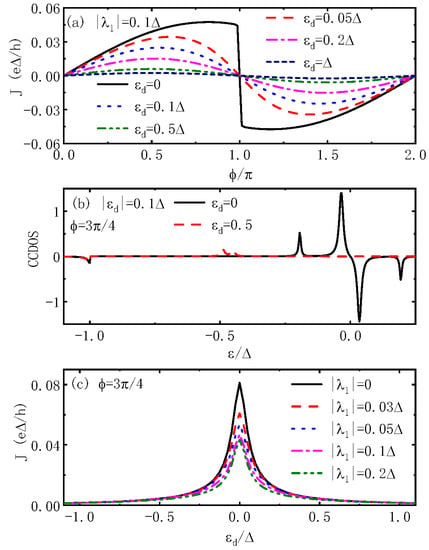
Figure 3.
(Color online) Josephson current varying with respect to in (a) for different values of dot level and the CCDOS versus electron energy in (b). (c) is for J as a function of for fixed and different . Unless listed in the figures, the parameters are the same as in Figure 2.
The height of the two peaks is clearly lowered with unchanged double-peak configuration, and hence the magnitude of the current is reduced. Note that, for unhybridized MBSs (), the lineshape of the current J for finite and, for , have mirror reflection symmetry around the axis [27,38,39]. We did not show the case of . Figure 3c shows that the Josephson current exhibits a symmetric resonant peak centered at , and the peak height is lowered by the QD–MBS coupling . This result can be attributed to the quantum interference effect of two paths [27,38]. In the absence of the MBSs, electrons are easy to transport through the system when the dot level is aligned to the Fermi energy in the leads, i.e., , inducing a resonant peak in the current (the black solid line in Figure 3c). When the Majorana nanowire is connected to the dot with coupling strength , however, some of the electrons transported through the QD will be injected into the nanowire. When , destructive interference occurs between electrons through the two paths, and the current is suppressed accordingly. Under this condition, the Majorana nanowire acts as an impurity to scatter the electrons or Cooper pairs injected from the leads. The results here resembles the transport through T-shaped double QDs sandwiched between normal metal or superconductor leads [42]. As is seen from Figure 2b,d and Figure 3b, for K, the CCDOS at positive energy regimes () will contribute to the Josephson current and lead to a reduction in the current. This is because, at finite temperature, the ABSs either below or above the Fermi level contribute to the Josephson current. This can be found in Ref. [44], in which the authors also found that the sharp edge between and was smeared out at finite temperatures.
The hybridization strength between the QD and MBS depends on the distance between them. In experiments, both of the two modes of the MBSs may interact with the QD [27,28,32,38,39]. For example, in Ref. [32], the author proposed to couple the QD to both ends of the Majorana nanowire and, hence, to the two modes of the MBSs. The system then forms an enclosed loop with a penetrating magnetic flux for implementing a phase gate. We then present, in Figure 4, the influences of and the magnetic flux for fixed . Figure 4a shows that the becomes a sinusoidal lineshape, and the current is suppressed as is increased. When comparing Figure 4a with Figure 2a, one can see that the introduction of additional QD–MBS coupling not only strengthens the hybridization between the QD and the MBSs but also changes the configuration of the electron transport path through the Majorana nanowire and then alters the quantum interference effect. More specifically, the function of the additional coupling resembles the variation of the QD level as in Figure 3a. Figure 4b shows the curves under the conditions of symmetrical QD–MBS couplings at six different MBS–MBS overlap values. The current J varies with respect to the phase difference still in a sinusoidal function form and increases with increasing . The reason is the same as in Figure 2c,d, where the MBS–MBS coupling splits the peak of the CCDOS within the superconducting gap and then enhances the magnitude of the current. In Figure 4c, we present the Josephson current varying with respect to the phase difference and magnetic flux penetrating through the loop composed of the QD and the Majorana nanowire. First, the abrupt jump at from positive to negative value in the curve is preserved for any value of . Second, the current’s magnitude is strongly enhanced around , with n as an integer. Similar results have been found in previous work [28,38]. In Ref. [28], the authors found that the linear conductance developed a peak of infinitely narrow width only at , which corresponds to the degenerate states in Flensberg’s qubit [27] and was zero at other values of . The peak in the linear conductance is widened by increasing system temperature, which was studied in Ref. [37] in the presence of electron–phonon interaction.
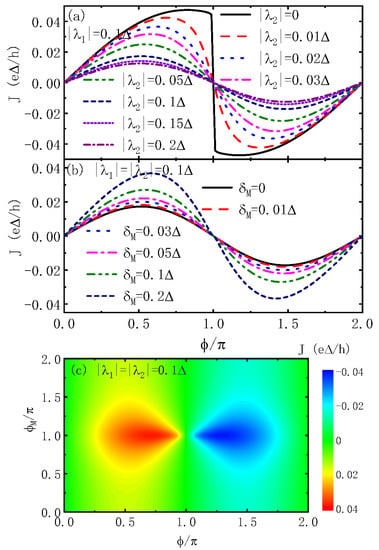
Figure 4.
(color online) Josephson current as a function of for different in (a) and in (b). (c) The counter plot of the Josephson current as a function of and . Other parameters are as in Figure 2.
We present, in Figure 5, the variation of the current with respect to the dot level for different values of , , and magnetic flux for the fixed phase difference and . Figure 5a indicates that the current develops a resonant peak centered at for any value of and decreases with increasing . This result resembles that in Figure 3c. The reason is also similar as, when the dot is coupled only to one mode of the MBSs, this induces destructive interference between electrons transporting through the two paths. When the two modes of the MBSs are overlapped () as shown in Figure 5b, the central peak in the current is split into two as . When , the current is suppressed to zero if the dot level is tuned between the two peaks. Moreover interestingly, the additional peak emerges in occupied states (), and the lineshape of the current in empty states () is unchanged by the variation of . We emphasize that the splitting of the central peak occurs only in the case of symmetrical QD–MBS coupling, whereas it is absent when the QD is coupled only to one mode of the MBSs. Figure 5c shows that the peak value of the current is clearly enhanced when the magnetic flux is , which is in consistent with the result in Figure 4c.
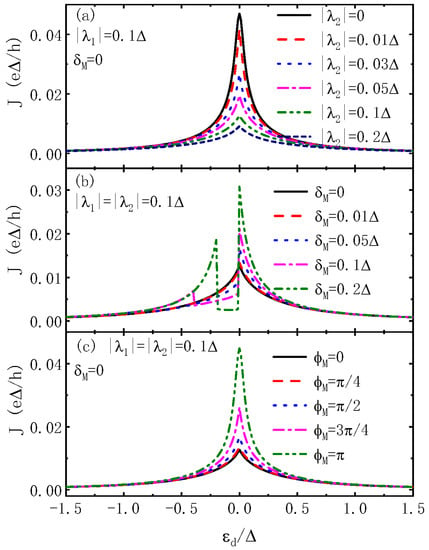
Figure 5.
(Color online) Josephson current as a function of the dot level for varying in (a), different in (b) and different in (c). Other parameters are as in Figure 2.
4. Summary
In summary, we studied electronic transport through a hybridized superconductors/QD structure under the influence of MBSs theoretically within the framework of non-equilibrium Green’s function method. We found that, when the QD was coupled to only one mode of the MBSs, the magnitude of the Josephson current was monotonously suppressed (enhanced) by increasing the QD–MBS (MBS–MBS) coupling strength due to the destructive interference effect induced by the additional transport channel through the Majorana nanowire. If the QD was symmetrically coupled to both the two modes of the MBSs, perfect constructive interference occurred with the help of suitable magnetic flux penetrating through the loop formed by the QD and the Majorana nanowire. The magnitude of the Josephson current at a zero-energy state can clearly be enhanced. Moreover, by adjusting the dot level and the parameters related to the MBSs, the central peak in the Josephson current can be split and shifted to the occupied states, whereas that in the empty states remains unchanged. This is useful in detecting the existence of MBSs. Our results also show that the abrupt jump at from a positive to negative value in the Josephson current remains unchanged for any value of . The strength of the current is significantly enhanced around , with n being an integer. The above results can be attributed to the dependence of the CCDOS on the MBSs.
Author Contributions
Writing—original draft preparation, F.C., Q.-S.J., J.L. and Q.-G.G.; writing—review and editing, F.C., L.-M.L., Z.-C.Y. and Q.-G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China under Grant Nos. 12264037, 62075035 and 62104033; Guangdong Province Education Department under Grant Nos. 2021GCZX005 and 2021KCXTD040. L.-M.L. was supported by the GuangDong Basic and Applied Basic Research Foundation under Grant No. 2021B1515420001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data included in this study are available upon request by contact with the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cybart, S.A.; Cho, E.Y.; Wong, T.J.; Wehlin, B.H.; Ma, M.K.; Huynh, C.; Dynes, R.C. Nano Josephson superconducting tunnel junctions in YBaCuO directly patterned with a focused helium ion beam. Nat. Nanotechnol. 2015, 10, 598. [Google Scholar] [CrossRef]
- Zhou, X.J.; Lee, W.S.; Imada, M.; Trivedi, N.; Phillips, P.; Kee, H.Y.; Torma, P.; Eremets, M. High-temperature superconductivity. Nat. Rev. Phys. 2021, 3, 462. [Google Scholar] [CrossRef]
- Thimont, Y.; Xing, Y.T.; Bernstein, P.; Miryala, M.; Noudem, J. Joining Superconducting MgB Parts by Spark Plasma Sintering: A New Technique with High Potential for Manufacturing Future Superconducting Devices. Coatings 2022, 12, 1151. [Google Scholar] [CrossRef]
- Friedrich, S. Superconducting Tunnel Junction Photon Detectors: Theory and Applications. J. Low. Temp. Phys. 2008, 151, 277. [Google Scholar] [CrossRef]
- Strambini, E.; Spies, M.; Ligato, N.; Ilic, S.; Rouco, S.M.; Gonzalez-Orellana, C.; Ilyn, M.; Rogero, C.; Bergeret, F.S.; Moodera, J.S.; et al. Superconducting spintronic tunnel diode. Nat. Commun. 2022, 13, 2431. [Google Scholar] [CrossRef]
- Ando, F.; Miyasaka, Y.; Li, T.; Ishizuka, J.; Arakawa, T.; Shiota, Y.; Moriyama, T.; Yanase, Y.; Ono, T. Observation of superconducting diode effect. Nature 2020, 584, 373. [Google Scholar] [CrossRef]
- Legg, H.F.; Loss, D.; Klinovaja, J. Superconducting diode effect due to magnetochiral anisotropy in topological insulators and Rashba nanowire. Phys. Rev. B 2022, 106, 104501. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217. [Google Scholar] [CrossRef]
- De Franceschi, S.; Kouwenhoven, L.; Schonenberger, C.; Wernsdorfer, W. Hybrid superconductor-quantum dot devices. Nat. Nanotechnol. 2010, 5, 703. [Google Scholar] [CrossRef]
- Burkard, G.; Gullans, M.J.; Mi, X.; Petta, J.R. Superconductor–Csemiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2020, 2, 129. [Google Scholar] [CrossRef]
- Bordoloi, A.; Zannier, V.; Sorba, L.; Schonenberger, C.; Baumgartner, A. A double quantum dot spin valve. Commun. Phys. 2020, 3, 135. [Google Scholar] [CrossRef]
- Kleeorin, Y.; Meir, Y.; Giazotto, F.; Dubi, Y. Large Tunable Thermophase in Superconductor-Quantum Dot-Superconductor Josephson Junctions. Sci. Rep. 2016, 6, 35116. [Google Scholar] [CrossRef]
- Hwang, S.Y.; Sanchez, D.; Lopez, R. A hybrid superconducting quantum dot acting as an efficient charge and spin Seebeck diode. New J. Phys. 2016, 18, 093024. [Google Scholar] [CrossRef]
- Kamp, M.; Sothmann, B. Phase-dependent heat and charge transport through superconductor–Cquantum dot hybrids. Phys. Rev. B 2019, 99, 045428. [Google Scholar] [CrossRef]
- Sun, Q.F.; Wang, J.; Lin, T.H. Photon-assisted Andreev tunneling through a mesoscopic hybrid system. Phys. Rev. B 1999, 59, 13126. [Google Scholar] [CrossRef]
- Pan, H.; Lin, T.H. Control of the supercurrent through a parallel-coupled double quantum dot system. Phys. Rev. B 2006, 74, 235312. [Google Scholar] [CrossRef]
- Rodero, A.M.; Yeyati, A.L. Josephson and Andreev transport through quantum dot. Adv. Phys. 2011, 60, 899. [Google Scholar] [CrossRef]
- Pala, M.G.; Governale, M.; Konig, J. Nonequilibrium Josephson and Andreev current through interacting quantum dots. New. J. Phys. 2007, 9, 278. [Google Scholar] [CrossRef]
- Szombati, D.; Nadj-Perge, S.; Car, D.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Josephson ϕ0-junction in nanowire quantum dots. Nat. Phys. 2016, 12, 568. [Google Scholar] [CrossRef]
- Germanese, G.; Paolucci, F.; Marchegiani, G.; Braggio, A.; Giazotto, F. Bipolar thermoelectric Josephson engine. Nat. Nanotechnol. 2022, 17, 1084. [Google Scholar] [CrossRef]
- Sato, M.; Fujimoto, S. Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics. Phys. Rev. B 2009, 79, 094504. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Sau, J.D.; Lutchyn, R.M.; Tewari, S.; Sarma, S.D. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 2010, 104, 040502. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.P.; Edge, J.M.; Akhmerov, A.R.; Beenakker, C.W.J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin–orbit coupling. Phys. Rev. B 2011, 84, 195442. [Google Scholar] [CrossRef]
- San-Jose, P.; Prada, E.; Aguado, R. AC Josephson effect in finite-length nanowire junctions with Majorana modes. Phys. Rev. Lett. 2012, 108, 257001. [Google Scholar] [CrossRef]
- Wimmer, M.; Akhmerov, A.R.; Medvedyeva, M.V.; Tworzydło, J.; Beenakker, C.W.J. Majorana bound states without vortices in topological superconductors with electrostatic defects. Phys. Rev. Lett. 2010, 105, 046803. [Google Scholar] [CrossRef]
- Flensberg, K. Tunneling characteristics of a chain of Majorana bound states. Phys. Rev. B 2010, 82, 180516. [Google Scholar] [CrossRef]
- Liu, D.E.; Baranger, H.U. Detecting a majorana-fermion zero mode using a quantum dot. Phys. Rev. B 2011, 84, 201308. [Google Scholar] [CrossRef]
- Flensberg, K. Non-Abelian Operations on Majorana Fermions via Single-Charge Control. Phys. Rev. Lett. 2011, 106, 090503. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Deng, D.L.; Liu, X.J.; Das, S.D. Majorana spintronics. Phys. Rev. B 2016, 94, 014511. [Google Scholar] [CrossRef]
- Wu, C.T.; Anderson, B.M.; Hsiao, W.H.; Levin, K. Majorana zero modes in spintronics device. Phys. Rev. B 2017, 95, 014519. [Google Scholar] [CrossRef]
- Leijnse, M.; Flensberg, K. Scheme to measure Majorana fermion lifetimes using a quantum dot. Phys. Rev. B 2011, 84, 140501. [Google Scholar] [CrossRef]
- Lopez, R.; Lee, M.; Serra, L.; Lim, J. Thermoelectrical detection of majorana states. Phys. Rev. B 2014, 89, 205418. [Google Scholar] [CrossRef]
- Leijnse, M. Thermoelectric signatures of a Majorana bound state coupled to a quantum dot. New J. Phys. 2014, 16, 015029. [Google Scholar] [CrossRef]
- Hong, L.; Chi, F.; Fu, Z.G.; Hou, Y.F.; Wang, Z. Large enhancement of thermoelectric effect by majorana bound states coupled to a quantum dot. J. Appl. Phys. 2020, 127, 124302. [Google Scholar] [CrossRef]
- Chi, F.; Fu, Z.G.; Liu, J.; Li, K.; Wang, Z.; Zhang, P. Thermoelectric effect in a quantum dot side-coupled to Majorana bound states. Nanoscale Res. Lett. 2020, 15, 79. [Google Scholar] [CrossRef]
- Wang, X.Q.; Zhang, S.F.; Han, Y.; Yi, G.Y.; Gong, W.J. Efficient enhancement of the thermoelectric effect due to the Majorana zero modes coupled to one quantum-dot system. Phys. Rev. B 2019, 99, 155424. [Google Scholar] [CrossRef]
- Mathe, L.; Sticlet, D.; Zarbo, L.P. Quantum transport through a quantum dot side-coupled to a Majorana bound state pair in the presence of electron-phonon interaction. Phys. Rev. B 2022, 105, 155409. [Google Scholar] [CrossRef]
- Ricco, L.S.; de Souza, M.; Figueira, M.S. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: Distinguishing isolated majorana fermions from Andreev bound states. Phys. Rev. B 2019, 99, 155159. [Google Scholar] [CrossRef]
- Xu, L.T.; Li, X.Q.; Sun, Q.F. Majorana dc Josephson current mediated by a quantum dot. J. Phys. Condens. Matter 2017, 29, 195301. [Google Scholar] [CrossRef]
- Stefanski, P. Properties of the Majorana-state tunneling Josephson junction mediated by an interacting quantum dot. J. Phys. Condens. Matter 2019, 31, 185301. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.G.; Sun, Q.F. Josephson current transport through T-shaped double quantum dots. J. Phys. Condens. Matter 2008, 20, 505202. [Google Scholar] [CrossRef]
- Sun, Q.F.; Wang, J.; Lin, T.H. Control of the supercurrent in a mesoscopic four-terminal Josephson junction. Phys. Rev. B 2000, 62, 648. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev bound states and the π-junction transition in a superconductor/quantum-dot/superconductor system. J. Phys. Condens. Matter 2001, 13, 8783. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).