Prediction Model of Aluminized Coating Thicknesses Based on Monte Carlo Simulation by X-ray Fluorescence
Abstract
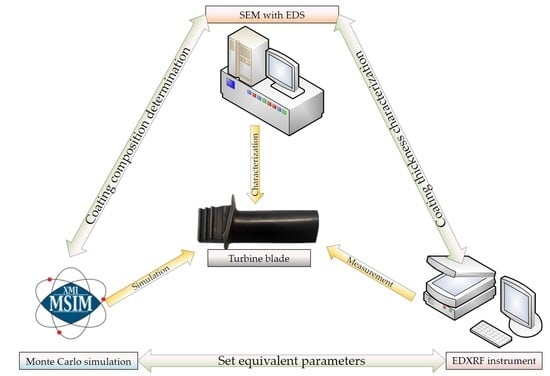
1. Introduction
2. Materials and Methods
2.1. Principle of XRF Thickness Measurement
- Emission method: The research object of the emission method is the coating element. The thicker the coating, the greater the XRF intensity of the coating element.
- Absorption method: The research object of the absorption method is the substrate element. The thicker the coating, the more the XRF of the substrate element is absorbed, and the smaller the intensity.
- Relative method: The relative method calculates the ratio of the XRF intensity of the coating element and the substrate element to determine the thickness [16]. Since the method uses relative values to calculate thickness, variations in measurement conditions have little effect on the calculation error.
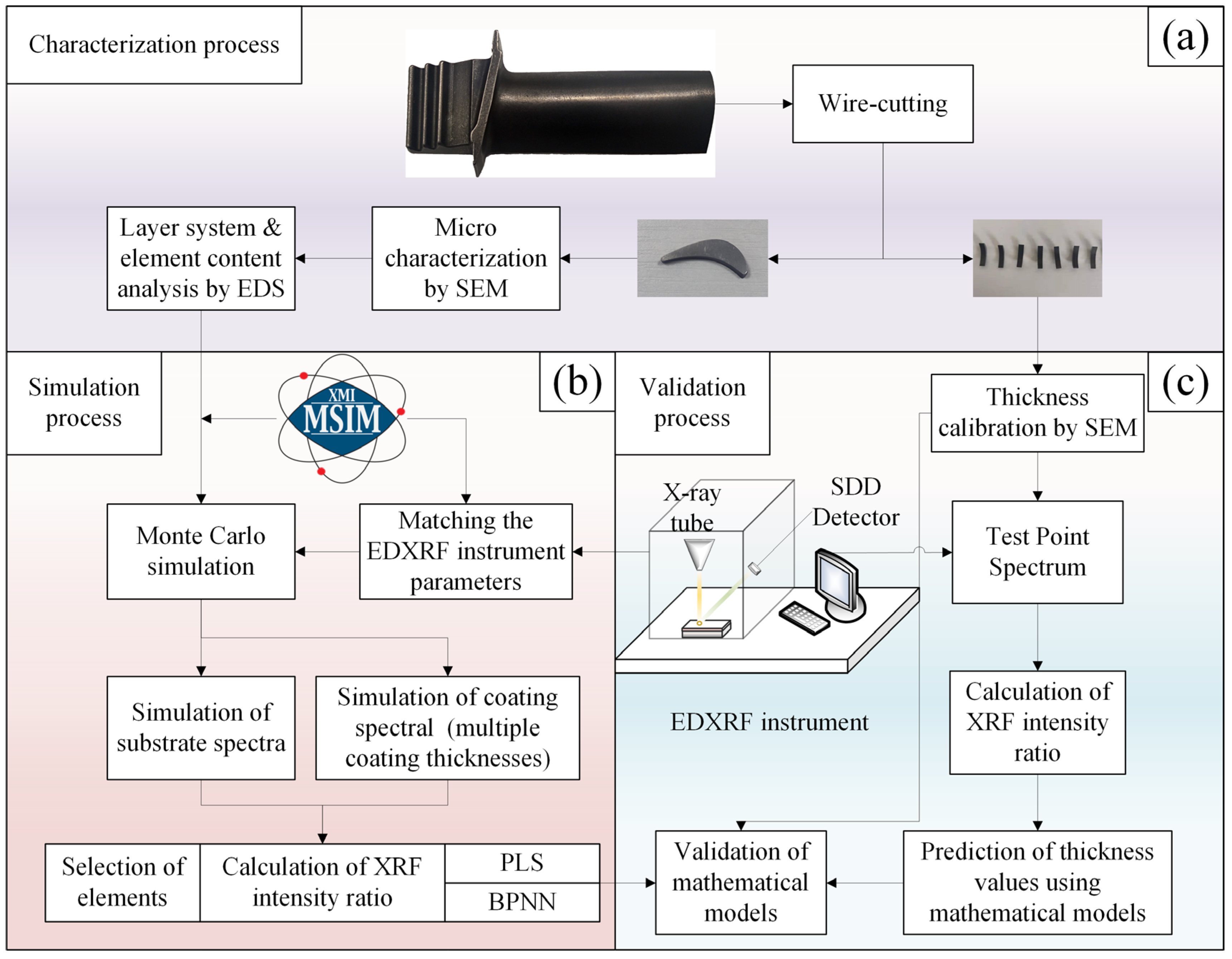
2.2. Experimental Procedure
| Project | Segmentation | Parameter | Density (g/cm3) | Thickness (cm) |
|---|---|---|---|---|
| General | Number photons per interval | 10,000 | ||
| Number of photons per discrete line | 100,000 | |||
| Number of interactions per trajectory | 4 | |||
| Geometry | Sample-source distance (cm) | 2 | ||
| Primary X-ray incidence angle (°) | 90 | |||
| X-ray fluorescence emission angle (°) | 45 | |||
| Active detector area (cm2) | 0.0531 | |||
| Excitation | Tube voltage (kV) | 40 | ||
| Tube current (mA) | 1.00 | |||
| Anode | W | 19.3 | 0.0002 | |
| window | Be | 1.848 | 0.0125 | |
| Composition | Air, Dry | C, N, O, Ar | 0.001205 | 2 |
| Al-rich layer | Reference Table 2 | 5.24 | 0~0.0022 | |
| Al-poor layer | 6.05 | 0~0.0040 | ||
| IDZ layer | 6.83 | 0~0.0060 | ||
| Substrate | 7.28 | 1 | ||
| Detection | Detector type | SDD | ||
| Number of spectrum channels | 4096 | |||
| Active detector area (cm2) | 0.25 |
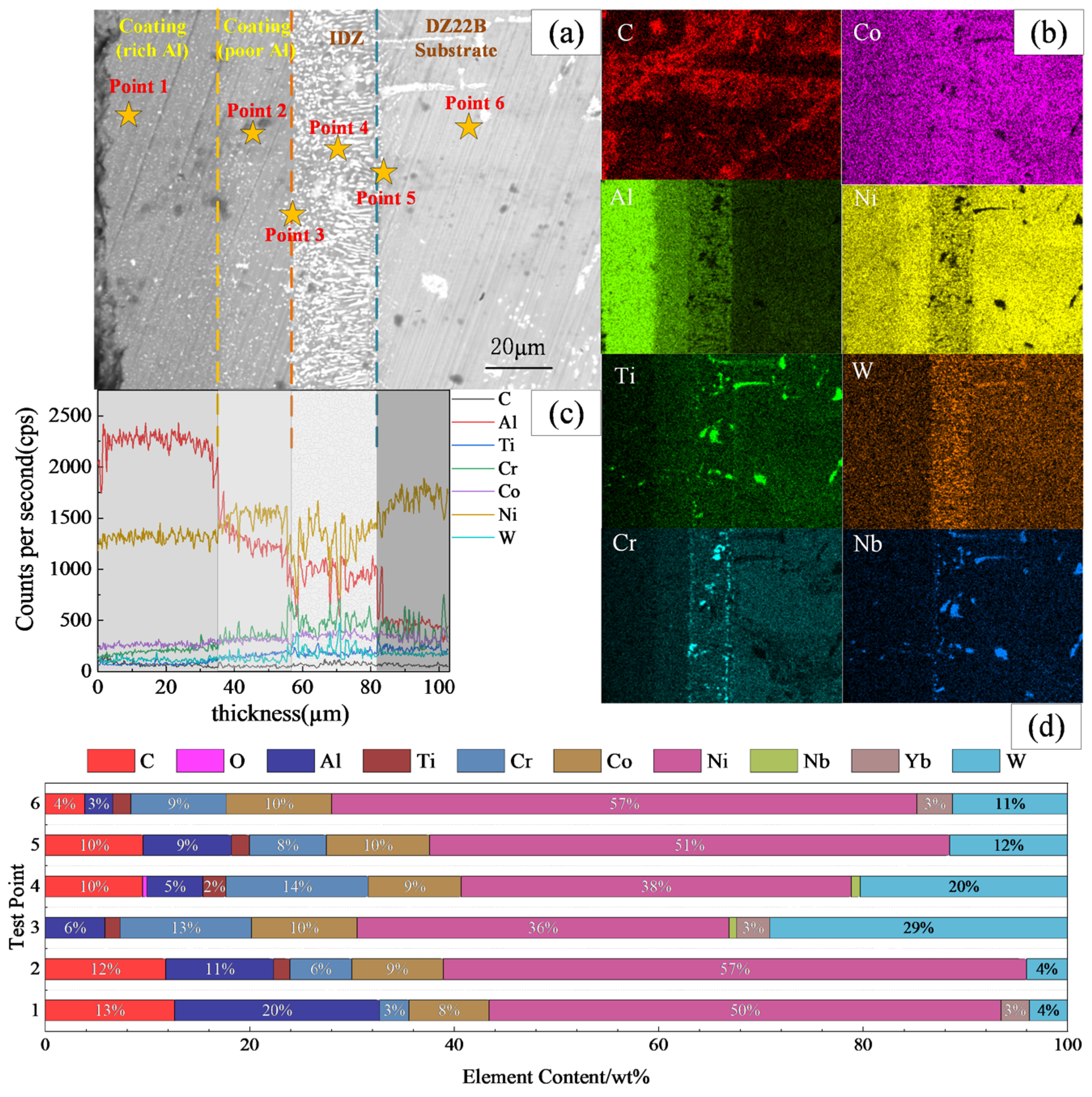
| Element | C | Al | Cl | K | Ti | Cr | Co | Ni | Nb | Yb | Hf | W |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al-rich layer | 7.64 | 20.52 | 0.33 | 0.16 | 0.42 | 3.54 | 8.20 | 53.68 | 0 | 0 | 0 | 5.51 |
| Al-poor layer | 6.47 | 11.47 | 0.25 | 0 | 1.71 | 6.36 | 9.51 | 60.35 | 0.38 | 0 | 0 | 3.51 |
| IDZ layer | 7.16 | 6.21 | 0.21 | 0 | 2.80 | 11.21 | 9.39 | 41.57 | 1.40 | 0 | 0 | 20.06 |
| Substrate | 5.37 | 2.81 | 0.22 | 0.09 | 2.48 | 8.25 | 9.48 | 56.14 | 1.01 | 2.07 | 1.47 | 10.61 |
3. Results and Discussion
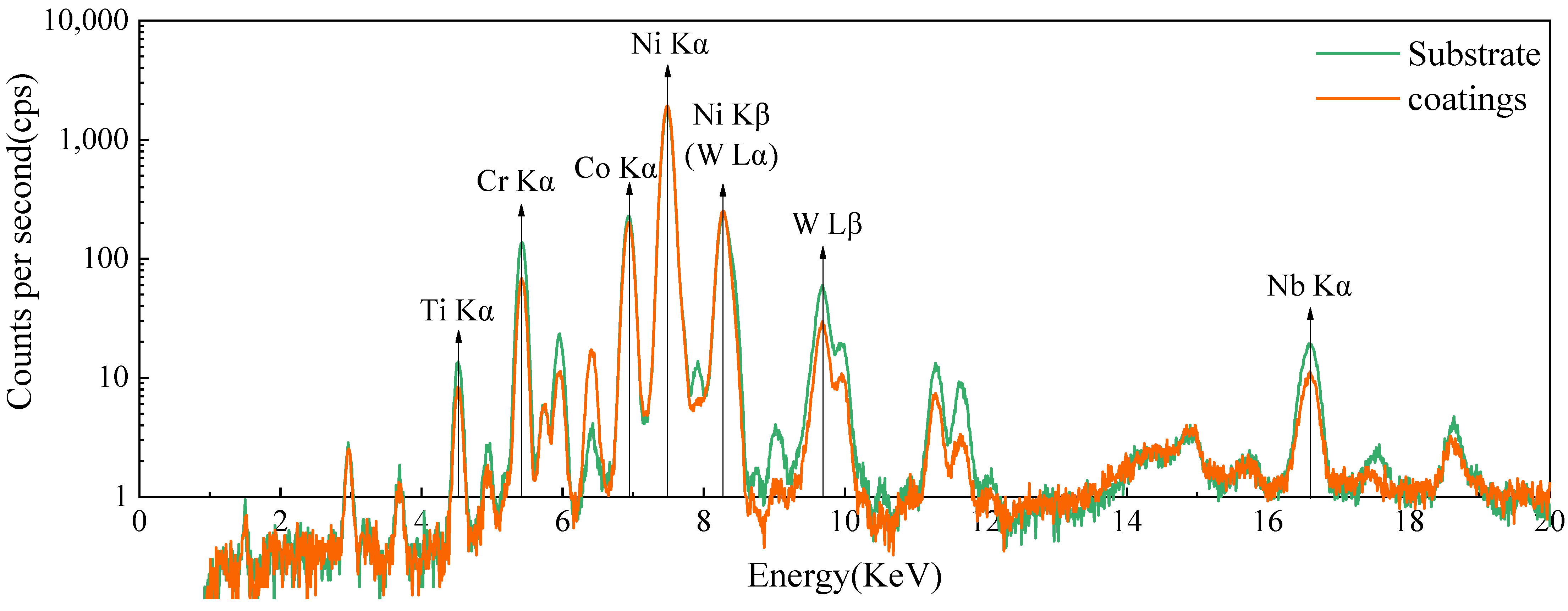
3.1. Characterization of the Coating System
3.2. Monte Carlo Simulation
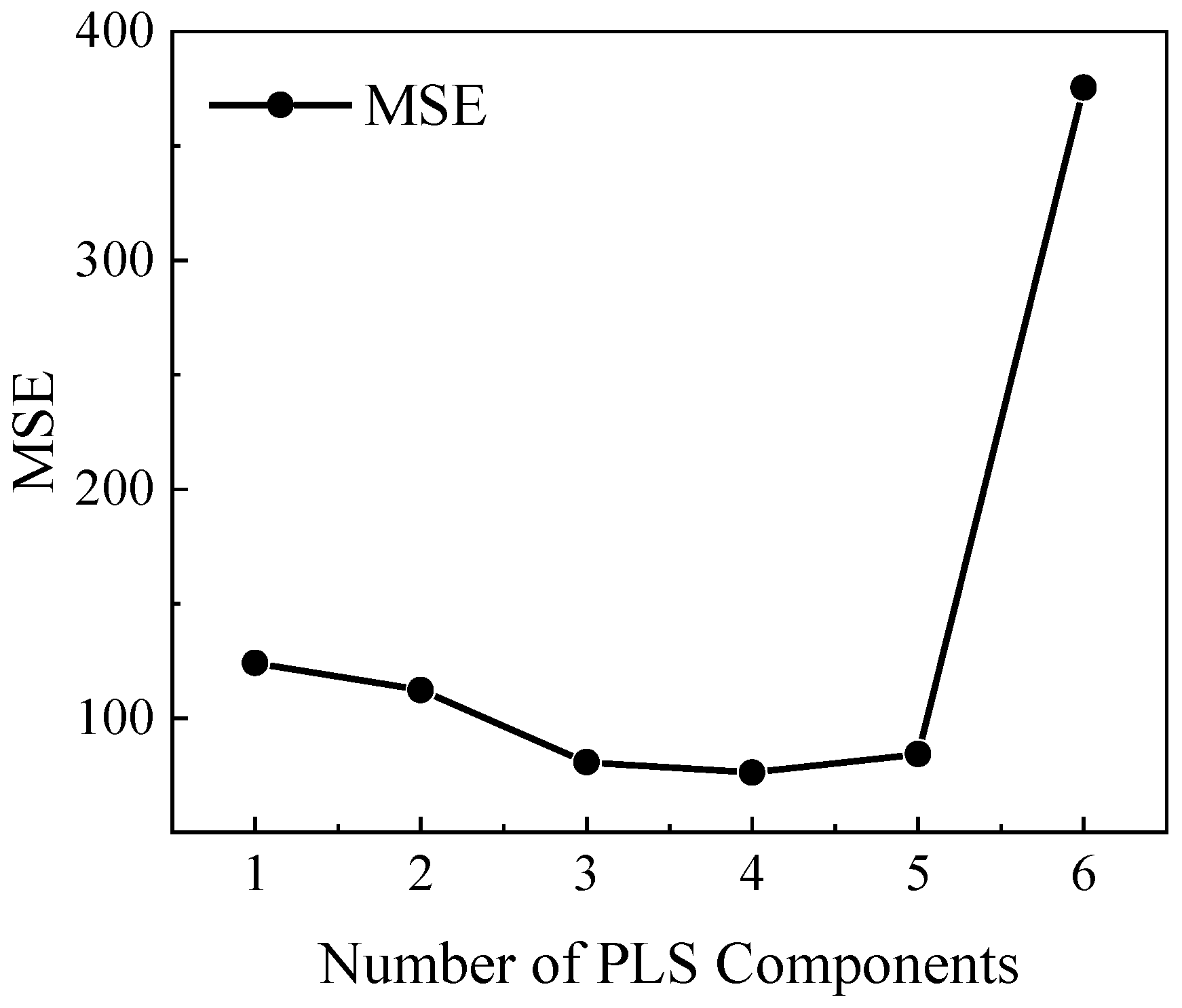
3.3. Thickness Prediction Modeling
3.3.1. Thickness Prediction Model based on PLS
3.3.2. Thickness Prediction Model Based on BPNN
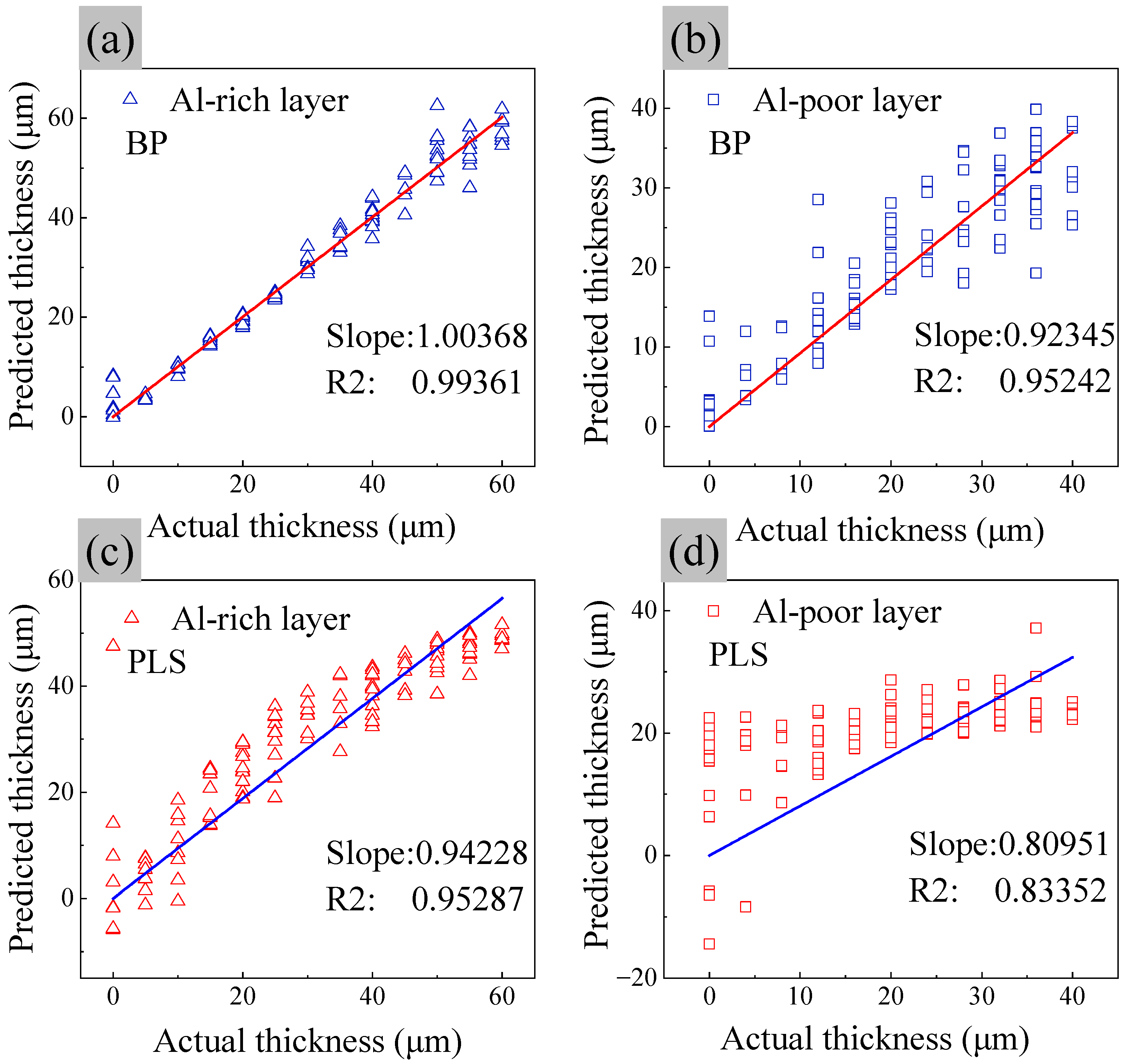
3.3.3. Comparison of Model Results
3.4. Experimental Validation
4. Conclusions
- The layering of aluminized layers. EDS analysis reveals that the aluminized layer on the in-service turbine blade surface can be divided into three layers with relatively stable elemental content: an Al-rich layer, an Al-poor layer, and an IDZ layer.
- Variation of XRF intensity for the different elements with coating thickness. The results of Monte Carlo simulations show that as the coating thickness increases, the spectral lines with lower XRF energy gradually reached the maximum information depth, while the spectral lines with higher XRF energy did not.
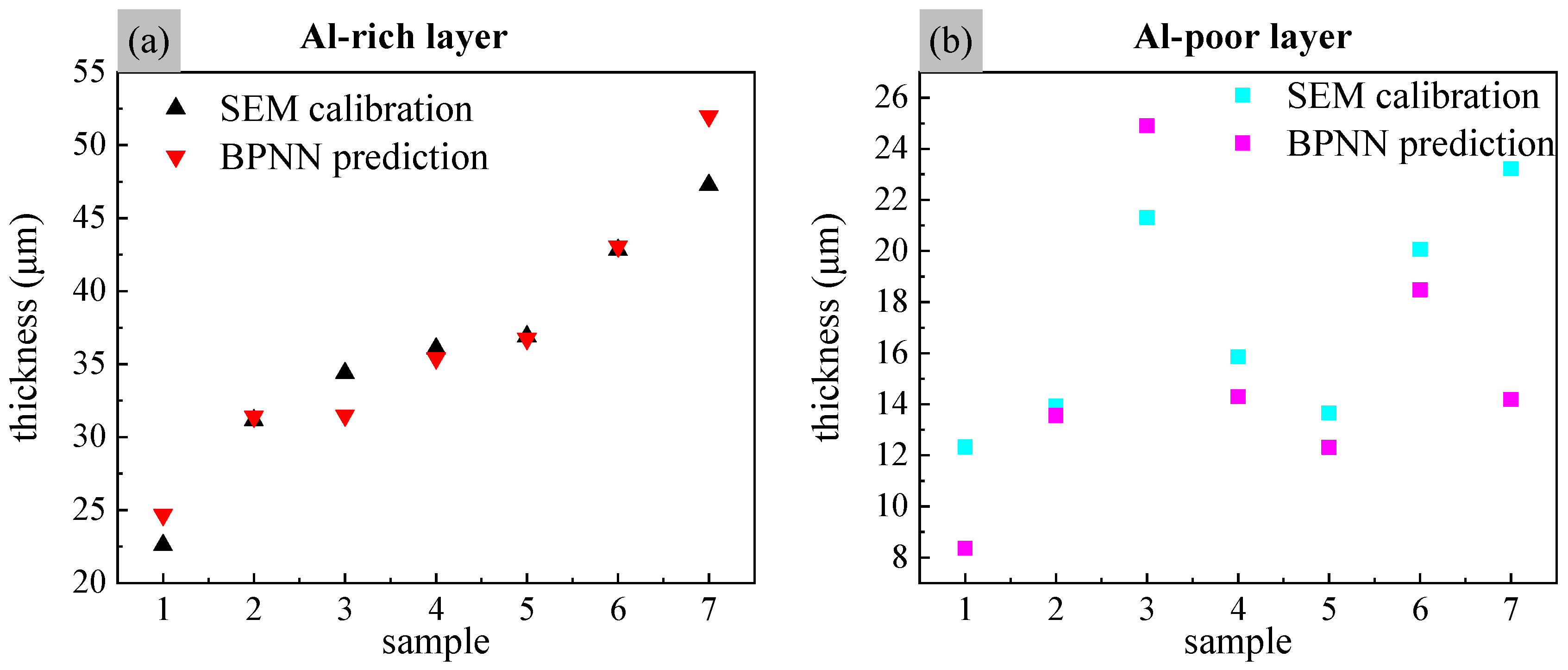
- The BNPP model is superior to the PLS model. In terms of the consistency between the predicted and actual thickness of the coating from the mathematical model, the BPNN model has the best consistency with a slope of 1.00368 and an R2 of 0.99361 for the Al-rich layer, and the PLS model has a slope of 0.94228 and an R2 of 0.95287. For the Al-poor layer, the BPNN model has a slope of 0.92345 and R2 of 0.95242, and the PLS model has a slope of 0.80951 and R2 of 0.83352. Comparing the coating thickness, prediction models show that the nonlinear BPNN model is superior to the linear PLS model.
- The Al-rich layer thickness prediction accuracy is higher than that of the Al-poor layer. The average relative errors of the BPNN model to predict the actual blade coating thicknesses were 4.45% for the Al-rich layer and 16.89% for the Al-poor layer, respectively. According to the prediction results, the prediction accuracy of the Al-rich layer is significantly higher than that of the Al-poor layer for both simulated and measured samples.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carter, T.J. Common failures in gas turbine blades. Eng. Fail. Anal. 2005, 12, 237–247. [Google Scholar] [CrossRef]
- Xie, Y.-J.; Wang, M.-C.; Zhang, G.; Chang, M. Analysis of superalloy turbine blade tip cracking during service. Eng. Fail. Anal. 2006, 13, 1429–1436. [Google Scholar] [CrossRef]
- Salwan, G.K.; Subbarao, R.; Mondal, S. Comparison and selection of suitable materials applicable for gas turbine blades. Mater. Today Proc. 2021, 46, 8864–8870. [Google Scholar] [CrossRef]
- Bhagi, L.K.; Gupta, P.; Rastogi, V. A brief review on failure of turbine blades. In Proceedings of the STME-2013 Smart Technologies for Mechanical Engineering, Delhi, India, 26–27 October 2013; pp. 25–26. [Google Scholar]
- Hetmańczyk, M.; Swadźba, L.; Mendala, B. Advanced materials and protective coatings in aero-engines application. J. Achiev. Mater. Manuf. Eng. 2007, 24, 372–381. [Google Scholar]
- Mazur, Z.; Luna-Ramírez, A.; Juárez-Islas, J.A.; Campos-Amezcua, A. Failure analysis of a gas turbine blade made of Inconel 738LC alloy. Eng. Fail. Anal. 2005, 12, 474–486. [Google Scholar] [CrossRef]
- Giurlani, W.; Zangari, G.; Gambinossi, F.; Passaponti, M.; Salvietti, E.; Di Benedetto, F.; Caporali, S.; Innocenti, M. Electroplating for Decorative Applications: Recent Trends in Research and Development. Coatings 2018, 8, 260. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, P.A. Advances and Researches on Non Destructive Testing: A Review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Giovani, C.; Giurlani, W.; Galvanetto, E.; Calisi, N.; Casale, M.; Fontanesi, C.; Ciattini, S.; Innocenti, M. A robust and cost-effective protocol to fabricate calibration standards for the thickness determination of metal coatings by XRF. Spectrochim. Acta Part B At. Spectrosc. 2021, 182, 106255. [Google Scholar] [CrossRef]
- Brocchieri, J.; Sabbarese, C. Thickness determination of the gilding on brass materials by XRF technique. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2021, 496, 29–36. [Google Scholar] [CrossRef]
- Giurlani, W.; Berretti, E.; Innocenti, M.; Lavacchi, A. Coating Thickness Determination Using X-ray Fluorescence Spectroscopy: Monte Carlo Simulations as an Alternative to the Use of Standards. Coatings 2019, 9, 79. [Google Scholar] [CrossRef]
- Giurlani, W.; Berretti, E.; Lavacchi, A.; Innocenti, M. Thickness determination of metal multilayers by ED-XRF multivariate analysis using Monte Carlo simulated standards. Anal Chim Acta 2020, 1130, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Giurlani, W.; Innocenti, M.; Lavacchi, A. X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination. Coatings 2018, 8, 84. [Google Scholar] [CrossRef]
- Lachance, G.R.; Traill, R.J. Practical solution to the matrix problem in X-ray analysis. Can. Spectrosc. 1966, 11, 43–48. [Google Scholar]
- Rousseau, R. The quest for a fundamental algorithm in X-ray fluorescence analysis and calibration. Open Spectrosc. J. 2009, 3, 31–42. [Google Scholar] [CrossRef][Green Version]
- Haschke, M.; Flock, J.; Haller, M. X-ray Fluorescence Spectroscopy for Laboratory Applications; John Wiley & Sons: Weinheim, Germany, 2021. [Google Scholar]
- Brocchieri, J.; Scialla, E.; Sabbarese, C. Estimation of Ag coating thickness by different methods using a handheld XRF instrument. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2021, 486, 73–84. [Google Scholar] [CrossRef]
- Takahara, H. Thickness and composition analysis of thin film samples using F.P. method by XRF analysis. Rigaku J. 2017, 33, 17–21. [Google Scholar]
- Han, L.; Zheng, S.; Tao, M.; Fei, C.; Hu, Y.; Huang, B.; Yuan, L. Service damage mechanism and interface cracking behavior of Ni-based superalloy turbine blades with aluminized coating. Int. J. Fatigue 2021, 153, 106500. [Google Scholar] [CrossRef]
- Schoonjans, T.; Vincze, L.; Solé, V.A.; del Rio, M.S.; Brondeel, P.; Silversmit, G.; Appel, K.; Ferrero, C. A general Monte Carlo simulation of energy dispersive X-ray fluorescence spectrometers—Part 5: Polarized radiation, stratified samples, cascade effects, M-lines. Spectrochim. Acta Part B At. Spectrosc. 2012, 70, 10–23. [Google Scholar] [CrossRef]
- Schoonjans, T.; Solé, V.A.; Vincze, L.; del Rio, M.S.; Appel, K.; Ferrero, C. A general Monte Carlo simulation of energy-dispersive X-ray fluorescence spectrometers—Part 6. Quantification through iterative simulations. Spectrochim. Acta Part B At. Spectrosc. 2013, 82, 36–41. [Google Scholar] [CrossRef]
- Golosio, B.; Schoonjans, T.; Brunetti, A.; Oliva, P.; Masala, G.L. Monte Carlo simulation of X-ray imaging and spectroscopy experiments using quadric geometry and variance reduction techniques. Comput. Phys. Commun. 2014, 185, 1044–1052. [Google Scholar] [CrossRef]
- Trojek, T. Iterative Monte Carlo procedure for quantitative X-ray fluorescence analysis of copper alloys with a covering layer. Radiat. Phys. Chem. 2020, 167, 108294. [Google Scholar] [CrossRef]
- Nocco, C.; Brunetti, A.; Barcellos Lins, S.A. Monte Carlo Simulations of ED-XRF Spectra as an Authentication Tool for Nuragic Bronzes. Heritage 2021, 4, 1912–1919. [Google Scholar] [CrossRef]
- Brunetti, A.; Fabian, J.; La Torre, C.W.; Schiavon, N. A combined XRF/Monte Carlo simulation study of multilayered Peruvian metal artifacts from the tomb of the Priestess of Chornancap. Appl. Phys. A 2016, 122, 571. [Google Scholar] [CrossRef]
- Brunetti, A.; Golosio, B.; Schoonjans, T.; Oliva, P. Use of Monte Carlo simulations for cultural heritage X-ray fluorescence analysis. Spectrochim. Acta Part B At. Spectrosc. 2015, 108, 15–20. [Google Scholar] [CrossRef]
- Markowicz, A. An overview of quantification methods in energy-dispersive X-ray fluorescence analysis. Pramana 2011, 76, 321–329. [Google Scholar] [CrossRef]
- Tiseanu, I.; Mayer, M.; Craciunescu, T.; Hakola, A.; Koivuranta, S.; Likonen, J.; Ruset, C.; Dobrea, C. X-ray microbeam transmission/fluorescence method for non-destructive characterization of tungsten coated carbon materials. Surf. Coat. Technol. 2011, 205, S192–S197. [Google Scholar] [CrossRef]
- Panchuk, V.; Yaroshenko, I.; Legin, A.; Semenov, V.; Kirsanov, D. Application of chemometric methods to XRF-data—A tutorial review. Anal. Chim. Acta 2018, 1040, 19–32. [Google Scholar] [CrossRef]
- Rakotondrajoa, A.; Buzanich, G.; Radtke, M.; Reinholz, U.; Riesemeier, H.; Vincze, L.; Raboanary, R. Improvement of PLS regression-based XRF spectroscopy quantification using multiple step procedure and Monte Carlo simulation. X-ray Spectrom. 2013, 42, 183–188. [Google Scholar] [CrossRef]
- Liang, W.; Wang, G.; Ning, X.; Zhang, J.; Li, Y.; Jiang, C.; Zhang, N. Application of B.P. neural network to the prediction of coal ash melting characteristic temperature. Fuel 2020, 260, 116324. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Tang, B.; Ma, Y.; Xing, J.; Liu, L. Lithology identification technology using B.P. neural network based on XRF. Acta Geophys. 2021, 69, 2231–2240. [Google Scholar] [CrossRef]
- Li, F.; Gu, Z.; Ge, L.; Sun, D.; Deng, X.; Wang, S.; Hu, B.; Xu, J. Application of artificial neural networks to X-ray fluorescence spectrum analysis. X-ray Spectrom. 2018, 48, 138–150. [Google Scholar] [CrossRef]
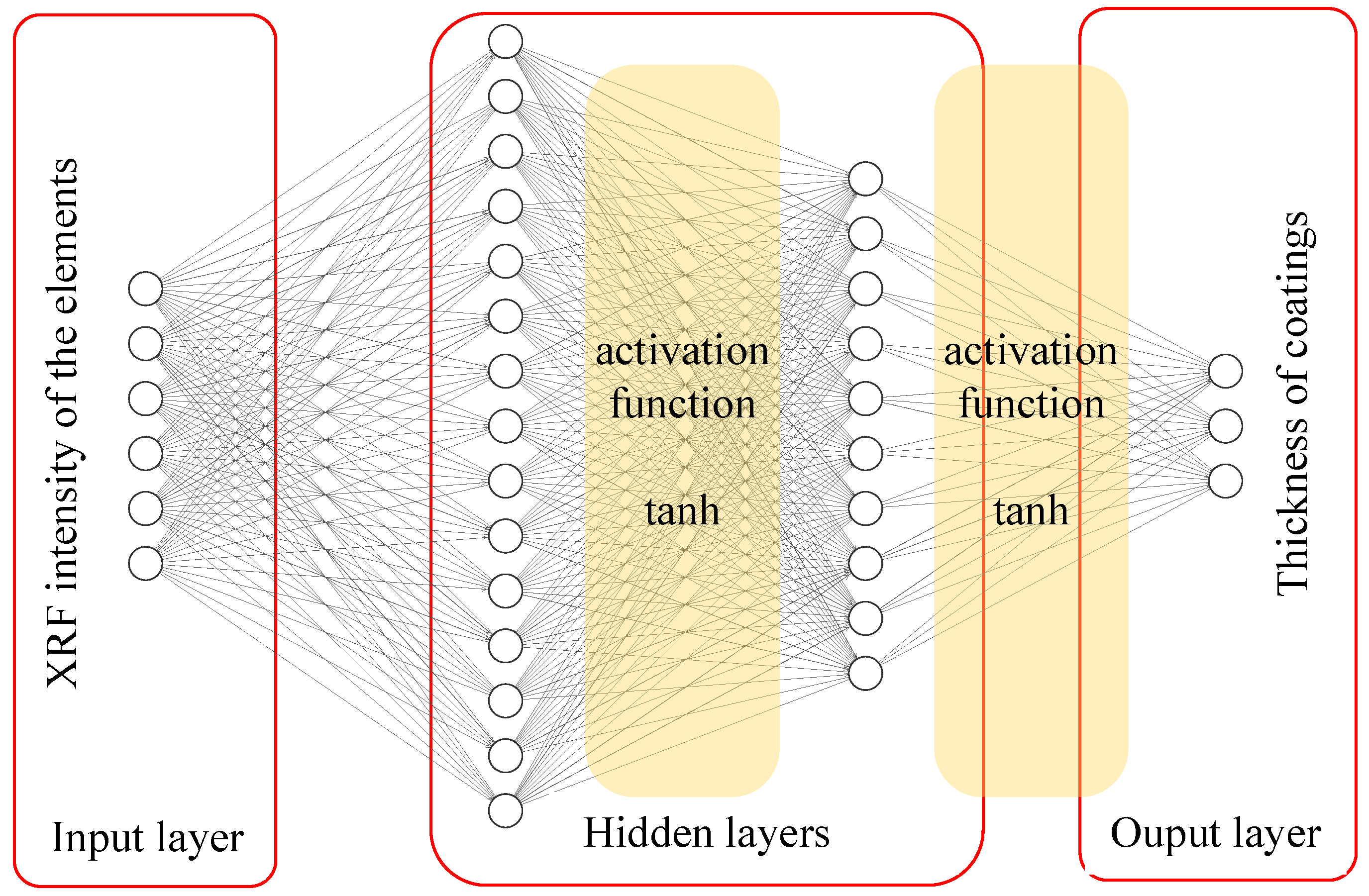
| Parameters | Values |
|---|---|
| Activation function | tanh |
| Hidden layer sizes | (15, 10) |
| Learning rate | 0.02 |
| Max iteration | 5000 |
| Sample | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Al-rich layer | 22.6 | 31.15 | 34.39 | 36.07 | 36.89 | 42.81 | 47.27 |
| Al-poor layer | 12.32 | 13.93 | 21.31 | 15.85 | 13.66 | 20.06 | 23.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, C.; Ju, H.; Li, X.; Qu, Y.; Yu, J. Prediction Model of Aluminized Coating Thicknesses Based on Monte Carlo Simulation by X-ray Fluorescence. Coatings 2022, 12, 764. https://doi.org/10.3390/coatings12060764
Li Z, Wang C, Ju H, Li X, Qu Y, Yu J. Prediction Model of Aluminized Coating Thicknesses Based on Monte Carlo Simulation by X-ray Fluorescence. Coatings. 2022; 12(6):764. https://doi.org/10.3390/coatings12060764
Chicago/Turabian StyleLi, Zhuoyue, Cheng Wang, Haijuan Ju, Xiangrong Li, Yi Qu, and Jiabo Yu. 2022. "Prediction Model of Aluminized Coating Thicknesses Based on Monte Carlo Simulation by X-ray Fluorescence" Coatings 12, no. 6: 764. https://doi.org/10.3390/coatings12060764
APA StyleLi, Z., Wang, C., Ju, H., Li, X., Qu, Y., & Yu, J. (2022). Prediction Model of Aluminized Coating Thicknesses Based on Monte Carlo Simulation by X-ray Fluorescence. Coatings, 12(6), 764. https://doi.org/10.3390/coatings12060764