Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film
Abstract
:1. Introduction
2. Modeling and Computational Details
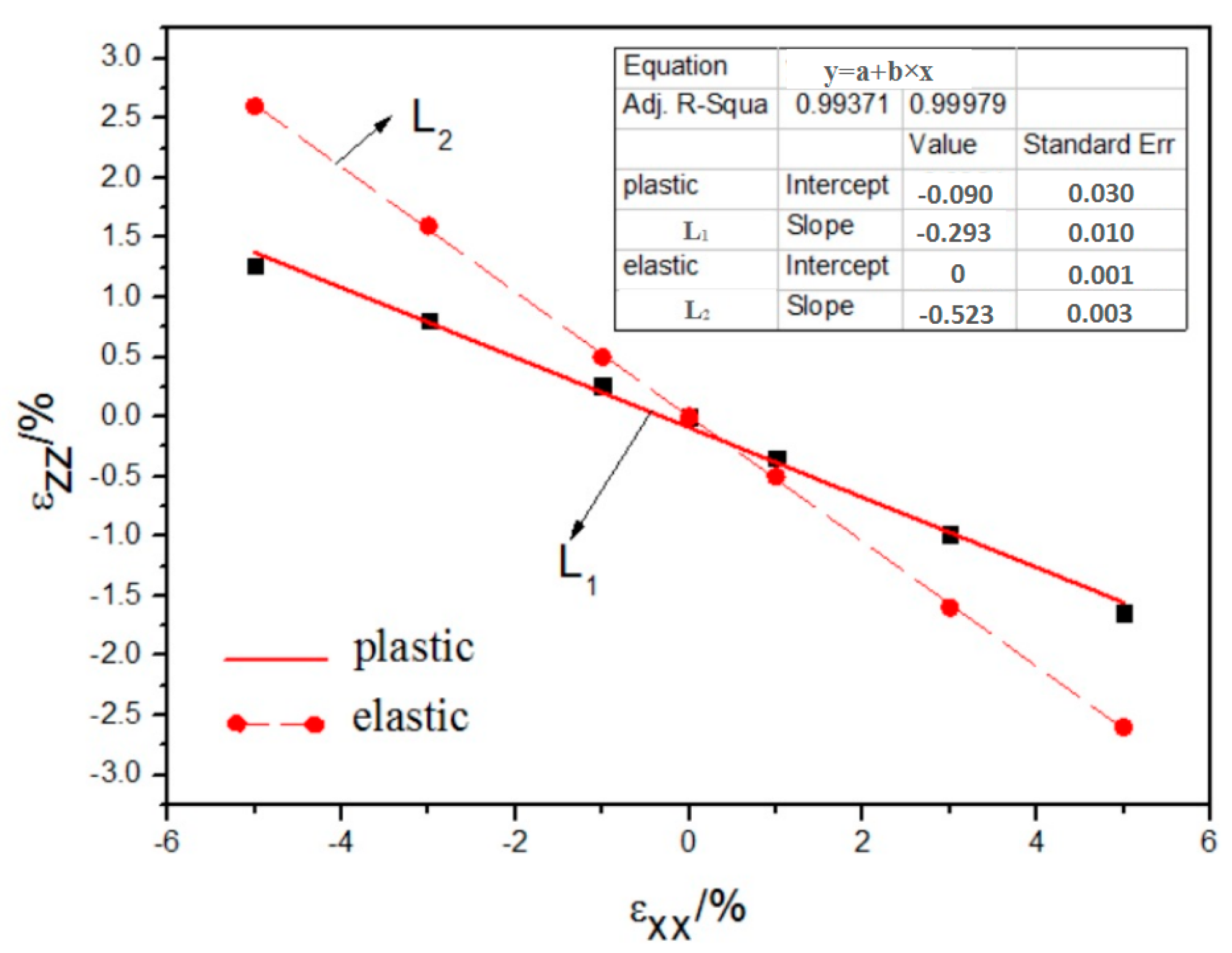
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arifin, P.; Sutanto, H.; Subagio, A. Plasma-Assisted MOCVD Growth of Non-Polar GaN and AlGaN on Si(111) Substrates Utilizing GaN-AlN Buffer Layer. Coatings 2022, 12, 94. [Google Scholar] [CrossRef]
- Hu, H.; Tang, B.; Wan, H.; Sun, H.; Zhou, S.; Dai, J.; Chen, C.; Liu, S.; Guo, L.J. Boosted ultraviolet electroluminescence of InGaN/AlGaN quantum structures grown on high-index contrast patterned sapphire with silica array. Nano Energy 2020, 69, 104427. [Google Scholar] [CrossRef]
- Khan, M.A.K.; Alim, M.A.; Gaquiere, C. 2DEG transport properties over temperature for AlGaN/GaN HEMT and AlGaN/InGaN/GaN pHEMT. Microelectron. Eng. 2021, 238, 111508. [Google Scholar] [CrossRef]
- Song, W.; Li, T.; Zhang, L.; Zhu, W.; Wang, L. Influence of growth parameters on microstructures and electrical properties of InxAl1−xN thin films using sputtering. J. Alloys Compd. 2021, 885, 160977. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, W.; Li, J.; Liu, Y.; Zhu, X.; Wei, J.; Wang, H.; Zhao, Y. Substrate temperature induced physical property variation of InxAl1−xN alloys prepared on Al2O3 by magnetron sputtering. Vacuum 2020, 179, 109512. [Google Scholar] [CrossRef]
- Taylor, E.; Smith, M.D.; Sadler, T.C.; Lorenz, K.; Li, H.N.; Alves, E.; Parbrook, P.J.; Martin, R.W. Structural and optical properties of Ga auto-incorporated InAlN epilayers. J. Cryst. Growth 2014, 408, 97–101. [Google Scholar] [CrossRef] [Green Version]
- Gonschorek, M.; Carlin, J.F.; Feltin, E.; Py, M.A.; Grandjean, N.; Darakchieva, V.; Monemar, B.; Lorenz, M.; Ramm, G. Two-dimensional electron gas density in Al1−x InxN/AlN/GaN heterostructures (0.03 ≤ x ≤ 0.23). J. Appl. Phys. 2008, 103, 93714. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Ni, X.; Wu, M.; Leach, J.H.; Özgür, Ü.; Morkoç, H. High electron mobility in nearly lattice-matched AlInN∕AlN∕GaN heterostructure field effect transistors. Appl. Phys. Lett. 2007, 91, 132116. [Google Scholar] [CrossRef] [Green Version]
- Guoqiang, Q.; Guanglei, Z.; Dongchun, L.; Shimin, L. Lattice and internal relaxation of ZnO thin film under in-plane strain. Thin Solid Film. 2010, 519, 378–384. [Google Scholar] [CrossRef]
- Paszkowicz, W.; Černý, R.; Krukowski, S. Rietveld refinement for indium nitride in the 105–295 K range. Powder Diffr. 2012, 18, 114–121. [Google Scholar] [CrossRef] [Green Version]
- Angerer, H.; Brunner, D.; Freudenberg, F.; Ambacher, O.; Stutzmann, M.; Höpler, R.; Metzger, T.; Born, E.; Dollinger, G.; Bergmaier, A.; et al. Determination of the Al mole fraction and the band gap bowing of epitaxial AlxGa1−xN films. Appl. Phys. Lett. 1997, 71, 1504–1506. [Google Scholar] [CrossRef]
- Sapa, L.; Bożek, B.; Danielewski, M. Remarks on Parabolicity in a One-Dimensional Interdiffusion Model with the Vegard Rule. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 2135–2147. [Google Scholar] [CrossRef]
- Fan, Q.; Li, C.; Yang, R.; Yu, X.; Zhang, W.; Yun, S. Stability, mechanical, anisotropic and electronic properties of oP8 carbon: A superhard carbon allotrope in orthorhombic phase. J. Solid State Chem. 2021, 294, 121894. [Google Scholar] [CrossRef]
- Kilic, M.E.; Lee, K.-R. First-Principles Study of Fluorinated Tetrahexcarbon: Stable Configurations, Thermal, Mechanical, and Electronic Properties. J. Phys. Chem. C 2020, 124, 8225–8235. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Toma, M.; Kuvek, T.; Vrček, V. Ionization Energy and Reduction Potential in Ferrocene Derivatives: Comparison of Hybrid and Pure DFT Functionals. J. Phys. Chem. A 2020, 124, 8029–8039. [Google Scholar] [CrossRef]
- Darakchieva, V.; Xie, M.Y.; Tasnádi, F.; Abrikosov, I.A.; Hultman, L.; Monemar, B.; Kamimura, J.; Kishino, K. Lattice parameters, deviations from Vegard’s rule, and E2 phonons in InAlN. Appl. Phys. Lett. 2008, 93, 261908. [Google Scholar] [CrossRef] [Green Version]
- Polian, A.; Grimsditch, M.; Grzegory, I. Elastic constants of gallium nitride. J. Appl. Phys. 1996, 79, 3343–3344. [Google Scholar] [CrossRef]
- Caro, M.A.; Schulz, S.; O’Reilly, E.P. Hybrid functional study of the elastic and structural properties of wurtzite and zinc-blende group-III nitrides. Phys. Rev. B 2012, 86, 14117. [Google Scholar] [CrossRef]
- Serrano, J.; Bosak, A.; Krisch, M.; Manjón, F.J.; Romero, A.H.; Garro, N.; Wang, X.; Yoshikawa, A.; Kuball, M. InN Thin Film Lattice Dynamics by Grazing Incidence Inelastic X-Ray Scattering. Phys. Rev. Lett. 2011, 106, 205501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Łepkowski, S.P.; Gorczyca, I. Elastic properties of InGaN and InAlN from first-principles calculations. AIP Conf. Proc. 2013, 1566, 83–84. [Google Scholar]
- Ashrafi, A.B.M.A.; Binh, N.T.; Zhang, B.P.; Segawa, Y. Strain relaxation and its effect in exciton resonance energies of epitaxial ZnO layers grown on 6H-SiC substrates. Appl. Phys. Lett. 2004, 84, 2814–2816. [Google Scholar] [CrossRef]
- Ahmed, H.; Hashim, A. Geometry Optimization, Optical and Electronic Characteristics of Novel PVA/PEO/SiC Structure for Electronics Applications. Silicon 2021, 13, 2639–2644. [Google Scholar] [CrossRef]
- Alam, S.N.; Zubialevich, V.Z.; Ghafary, B.; Parbrook, P.J. Bandgap and refractive index estimates of InAlN and related nitrides across their full composition ranges. Nature 2020, 10, 16205. [Google Scholar] [CrossRef]
- Xie, M. Structural and elastic properties of InN and InAlN with different surface orientations and doping. Ph.D. Thesis, Linköping University Electronic Press, Linköping, Sweden, 2012; p. 79. [Google Scholar]
- Yang, S.; Prendergast, D.; Neaton, J.B. Nonlinear variations in the electronic structure of II–VI and III–V wurtzite semiconductors with biaxial strain. Appl. Phys. Lett. 2011, 98, 152108. [Google Scholar] [CrossRef]




| Name | Method | a = b/Å | c/Å | C11/GPa | C12/GPa | C13/GPa | C33/GPa | C44/GPa |
|---|---|---|---|---|---|---|---|---|
| AlN | Experimental [19] | 3.112 | 4.982 | 396 | 137 | 108 | 373 | 116 |
| This work | 3.126 | 5.002 | 428.8 | 93.2 | 64.1 | 418.3 | 125.0 | |
| HSE [20] | 3.103 | 4.970 | 410.2 | 142.4 | 110.1 | 385.0 | 122.9 | |
| InN | Experimental [21] | 3.548 | 5.760 | 225 | 109 | 108 | 265 | 55 |
| This work | 3.593 | 5.835 | 246.0 | 67.6 | 45.7 | 264.8 | 59.6 | |
| HSE [20] | 3.542 | 5.711 | 233.8 | 110.0 | 91 | 238.3 | 55.4 | |
| In0.5Al0.5N | This work | 3.348 | 5.527 | 256.5 | 89.3 | 84.1 | 321.0 | 69.2 |
| Others | 3.35 [18] | 5.37 [18] | 293 [22] | 128.3 [22] | 105.3 [22] | 298.25 [22] | 73.75 [22] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Qin, G.; Zhang, F. Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film. Coatings 2022, 12, 598. https://doi.org/10.3390/coatings12050598
Zhang G, Qin G, Zhang F. Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film. Coatings. 2022; 12(5):598. https://doi.org/10.3390/coatings12050598
Chicago/Turabian StyleZhang, Guanglei, Guoqiang Qin, and Feipeng Zhang. 2022. "Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film" Coatings 12, no. 5: 598. https://doi.org/10.3390/coatings12050598
APA StyleZhang, G., Qin, G., & Zhang, F. (2022). Effects of Internal Relaxation of Biaxial Strain on Structural and Electronic Properties of In0.5Al0.5N Thin Film. Coatings, 12(5), 598. https://doi.org/10.3390/coatings12050598







