Optimization of the Thickness and Interface Structure of Al2O3-YAG/ZrO1.5-YO1.5-TaO1.5/8YSZ/NiCoCrAlY Multilayer Thermal Barrier Coatings: A Finite Element Simulation
Abstract
:Highlights
- (1)
- The thickness and interface structure of the multilayer ceramic layers were optimized using the finite element method, which significantly saved the cost of experiments.
- (2)
- The failure mechanism and thickness selection range of the multilayer coatings were determined, providing theoretical guidance for the coating process.
- (3)
- The effects of different roughness on the magnitude and distribution of interfacial residual stresses were investigated to provide theoretical guidance for the selection of interfacial roughness of thermal sprayed coatings.
Abstract
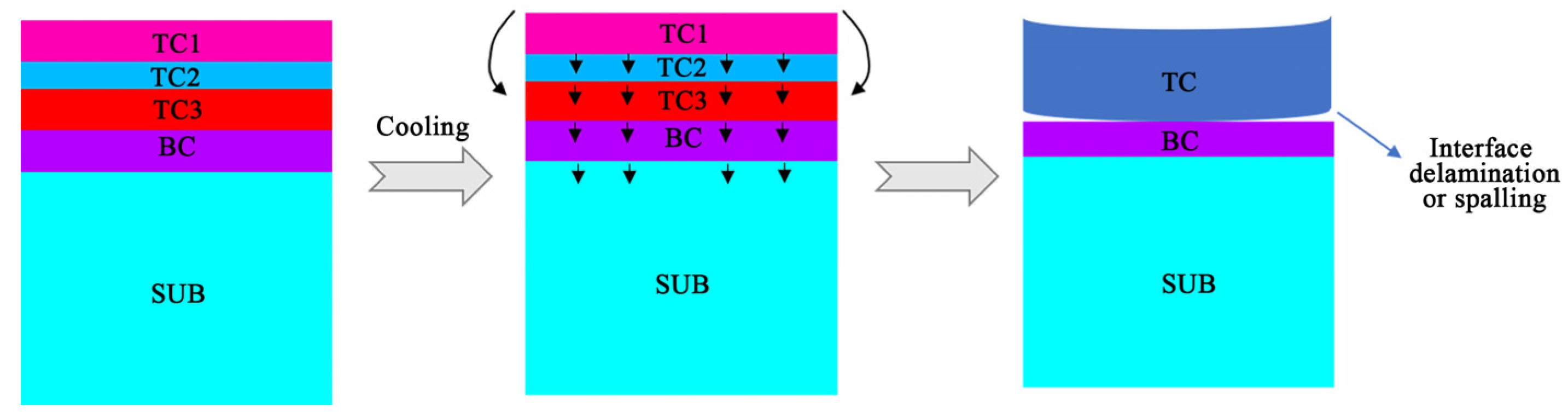
1. Introduction
2. Materials and Methods
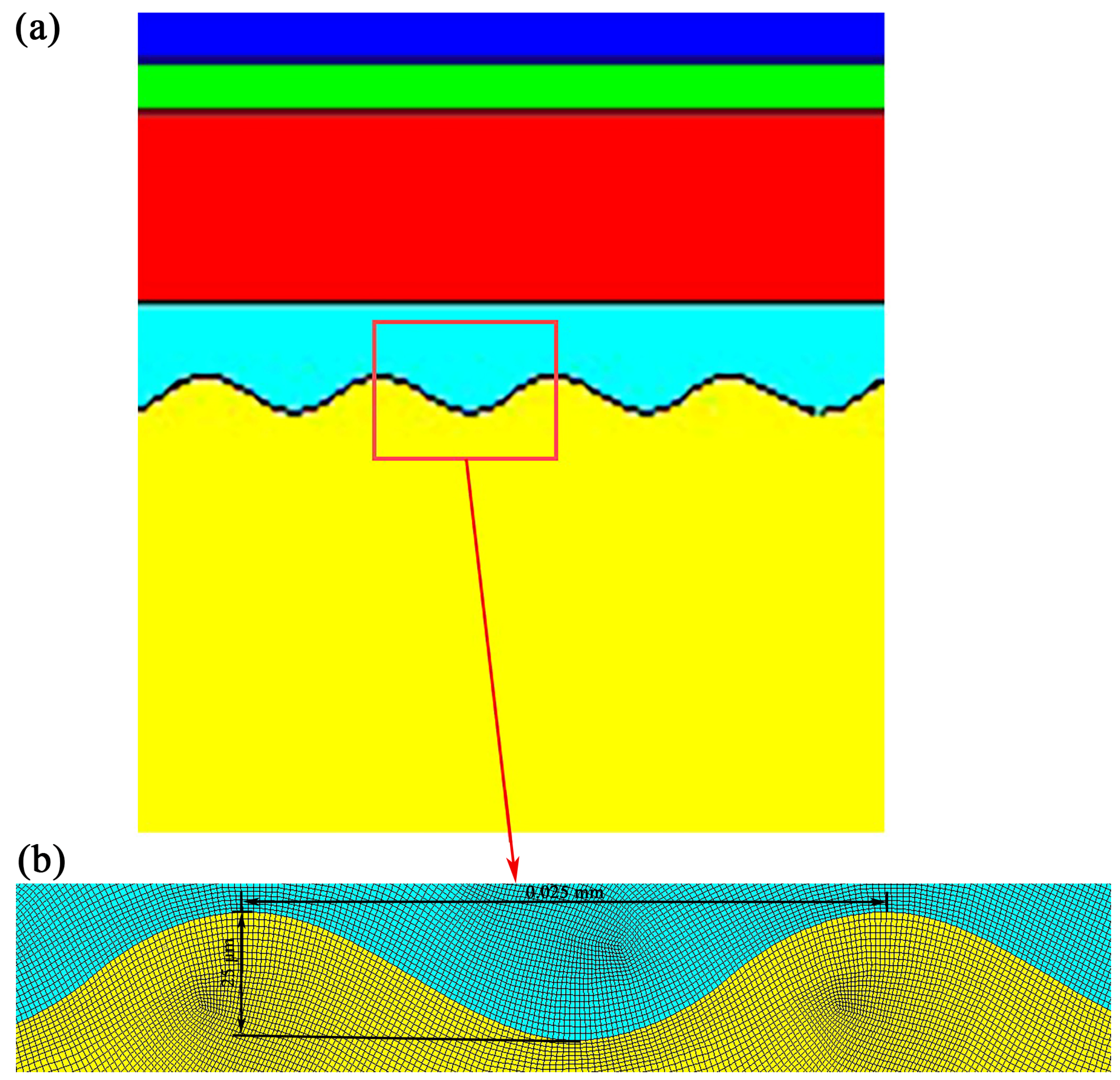
2.1. Finite Element Simulation Model
2.2. Boundary Conditions
2.3. Material Thermo-Physical Performance Parameters
3. Results and Discussion
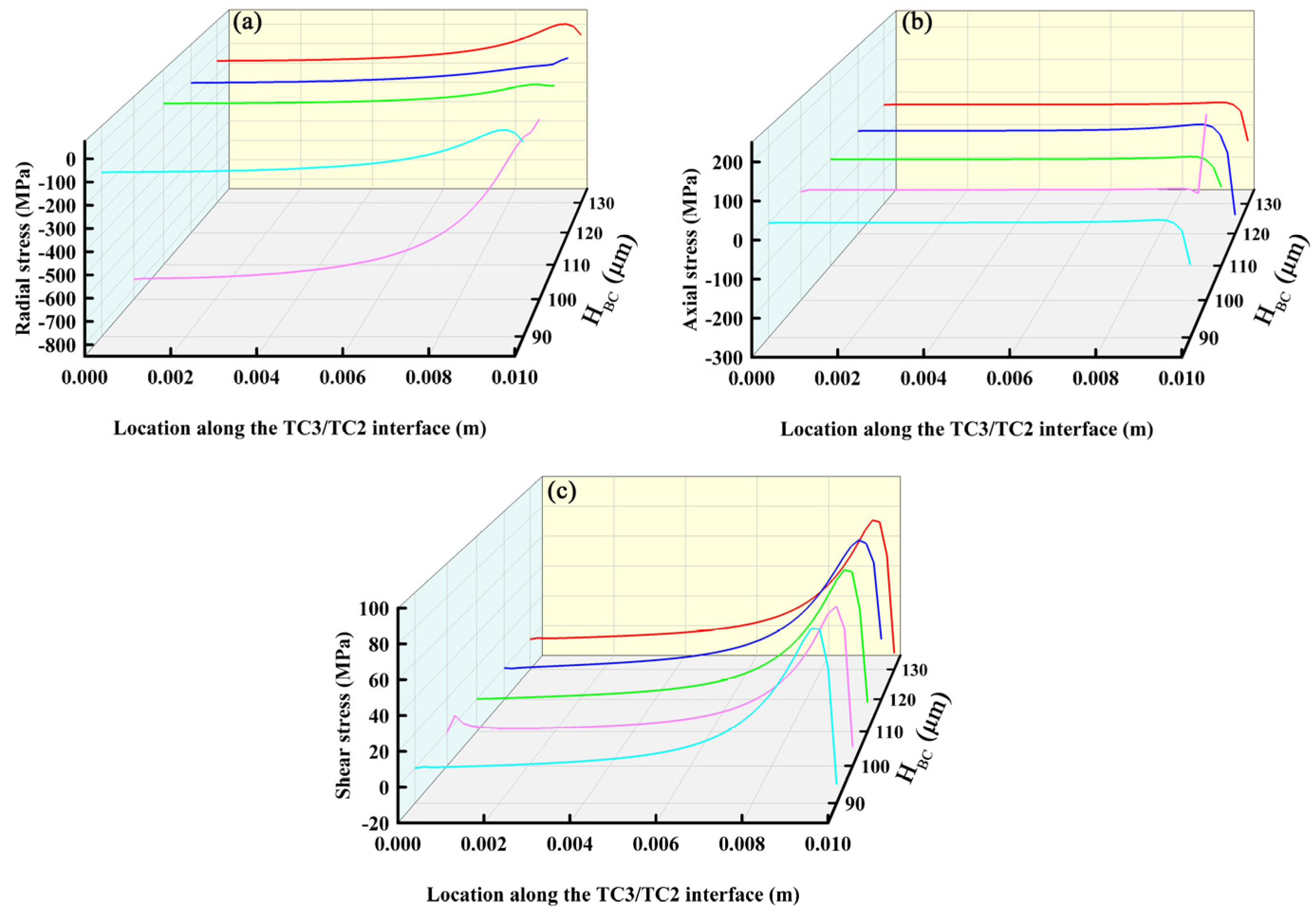
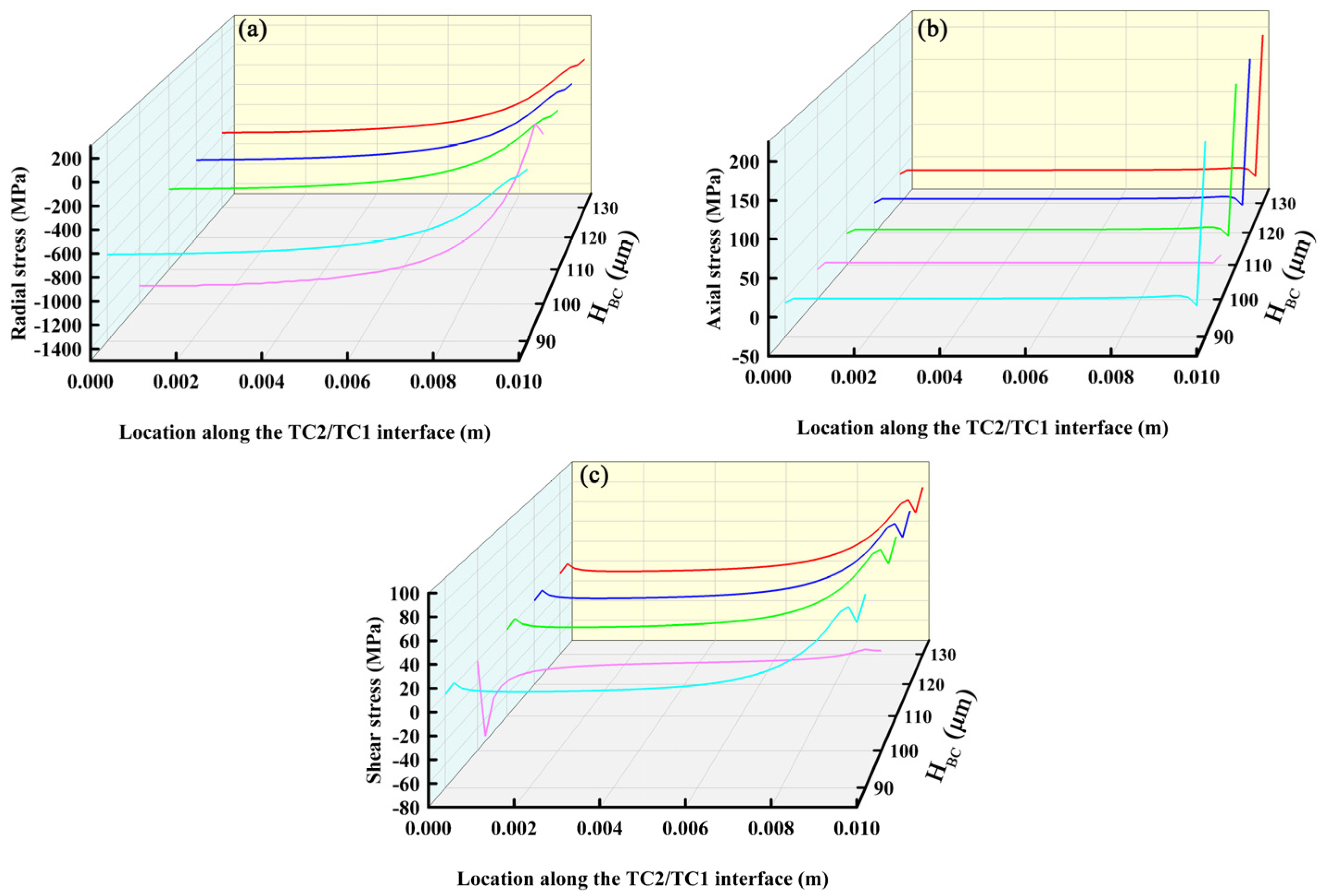
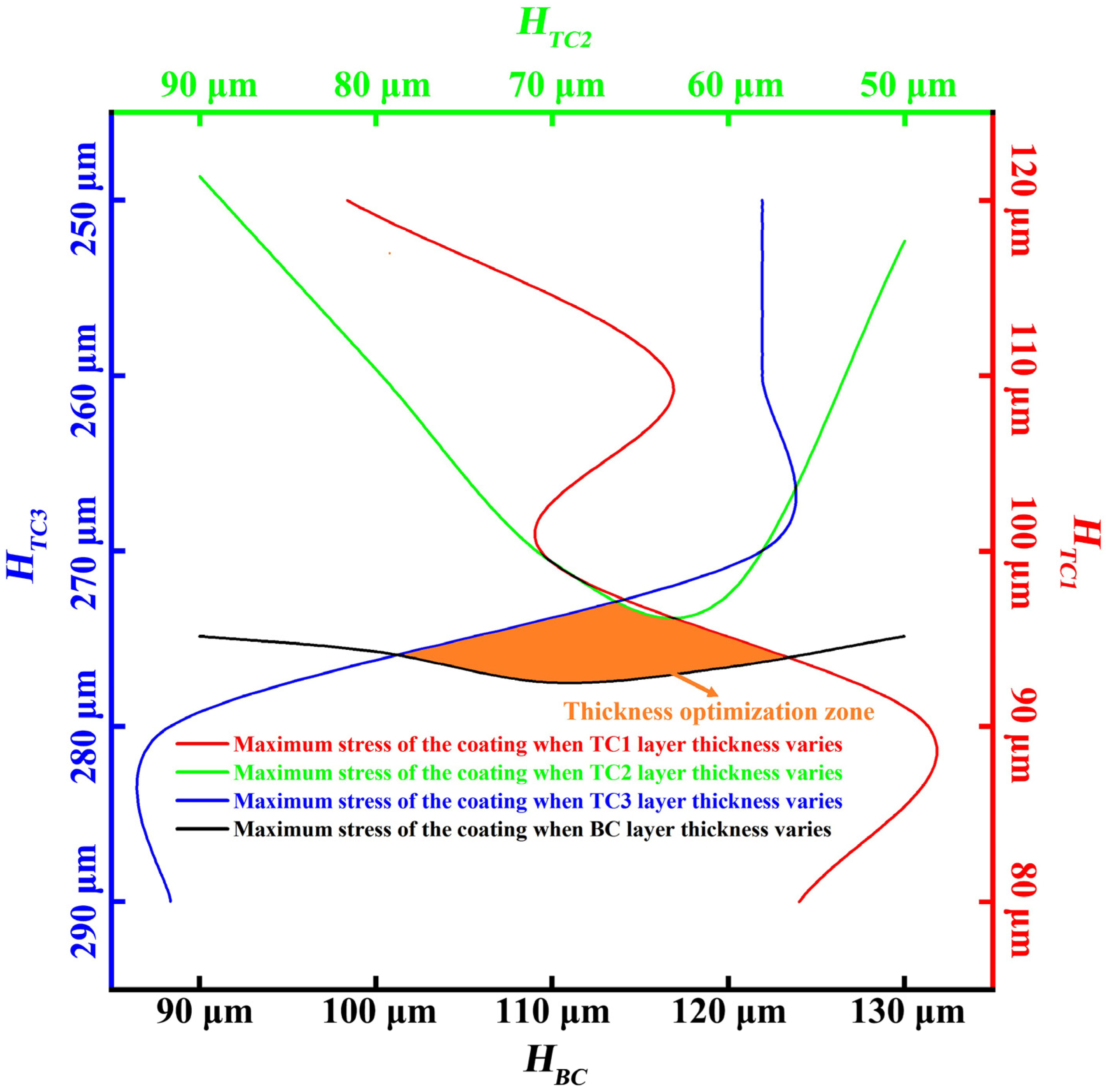
3.1. Influence of Thickness of Each Ceramic Layer on Interfacial Stress
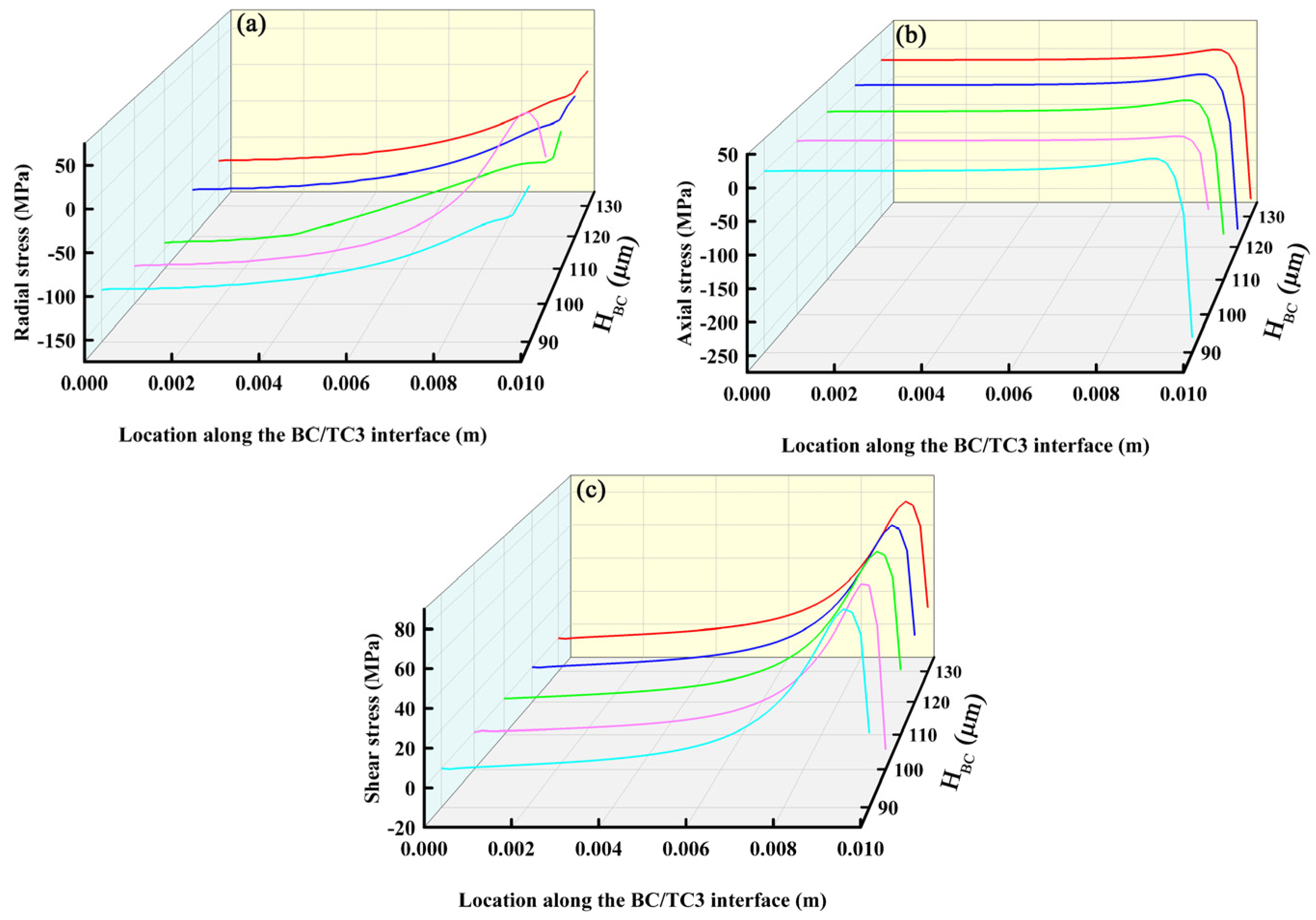
3.1.1. Effect of Bond Layer Thickness on Interfacial Stress
3.1.2. Summary of This Section
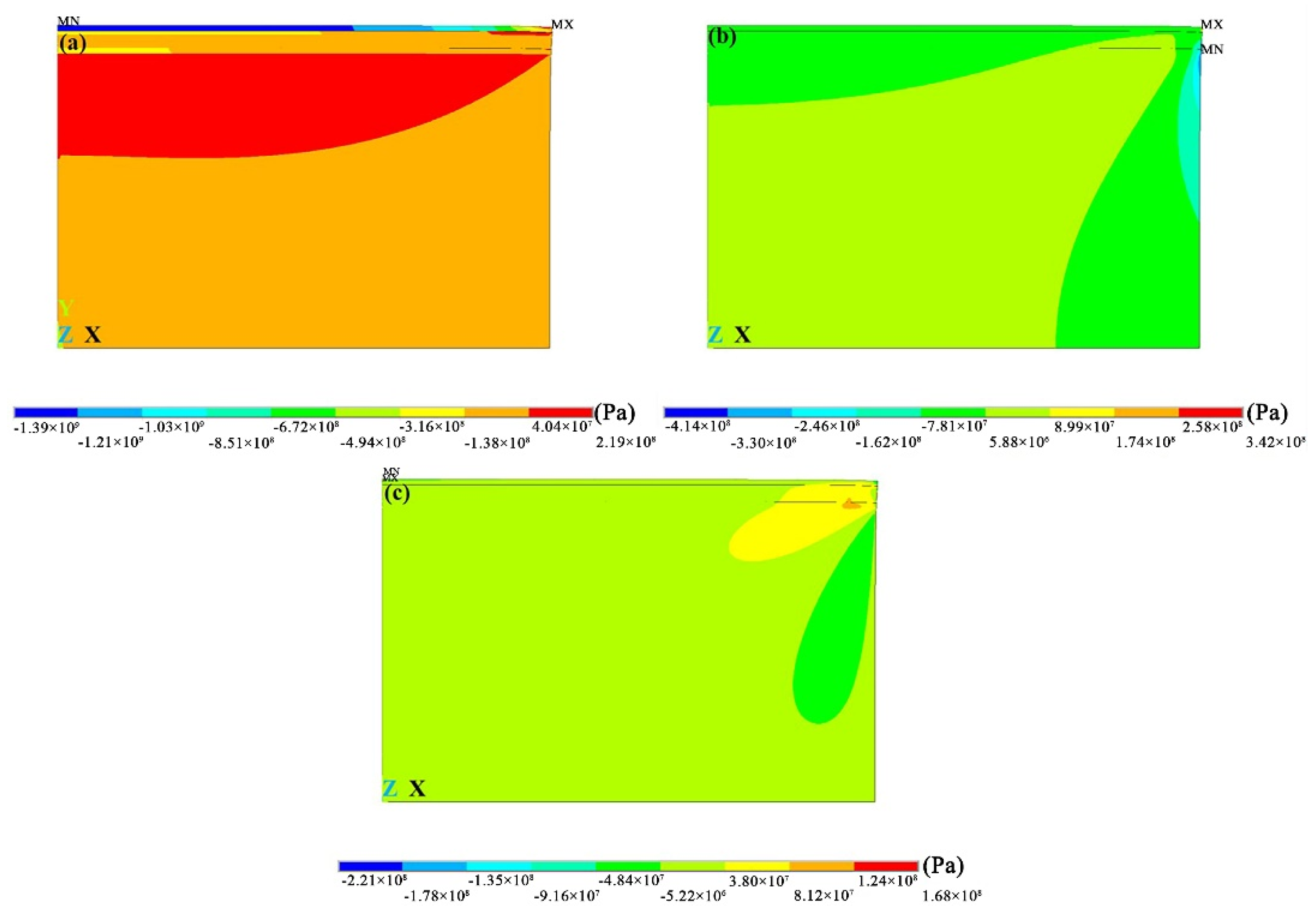
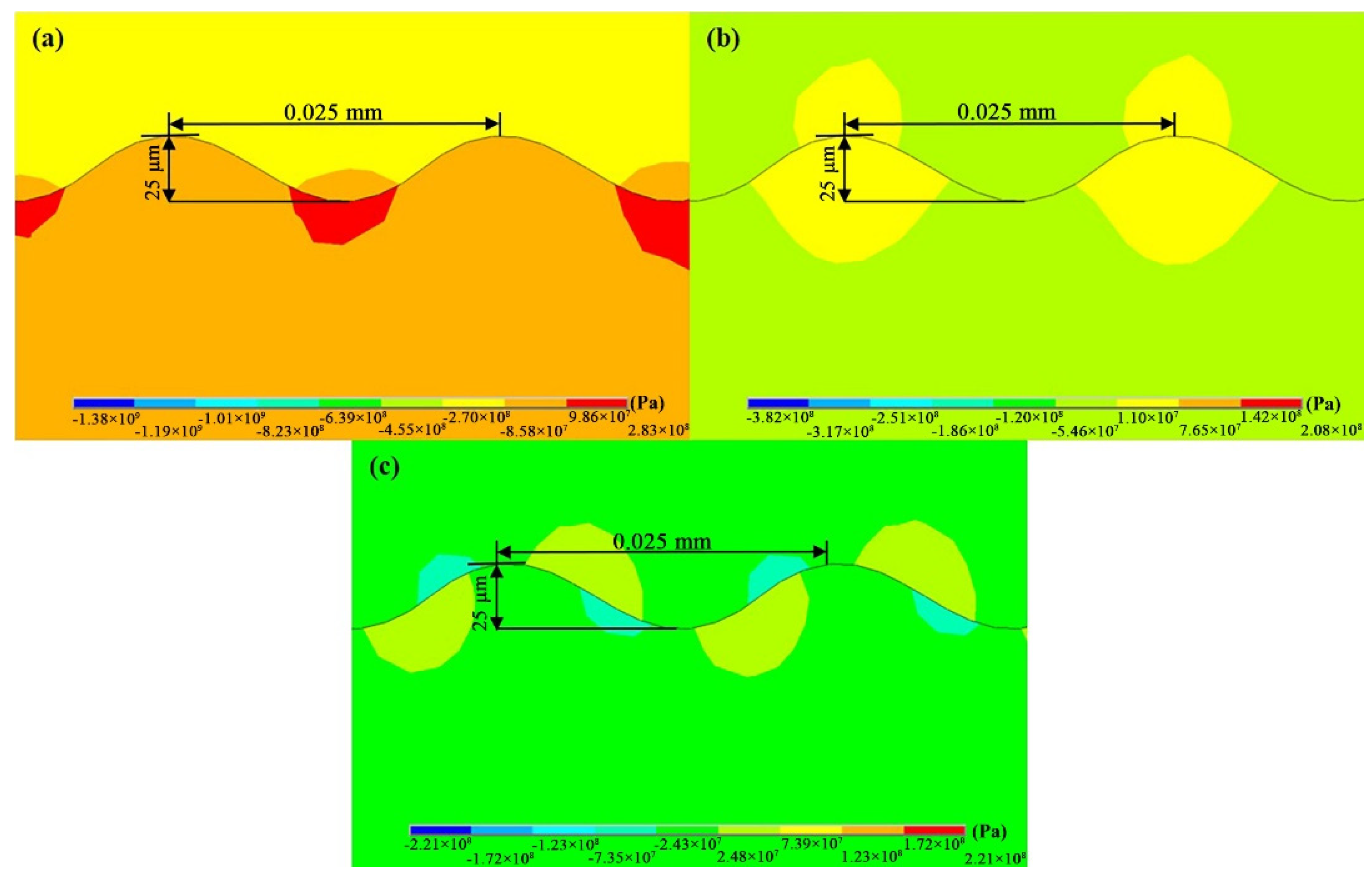
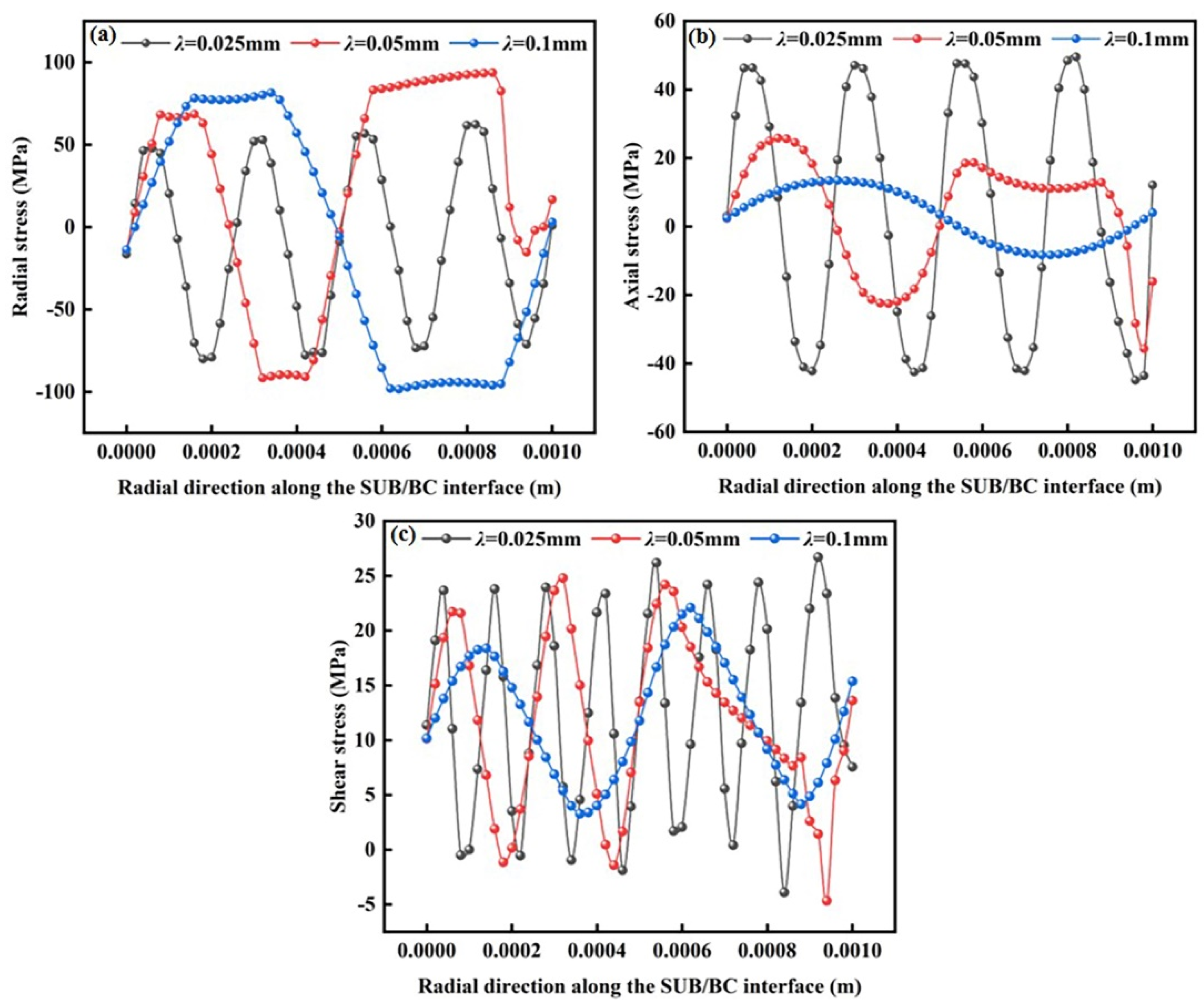
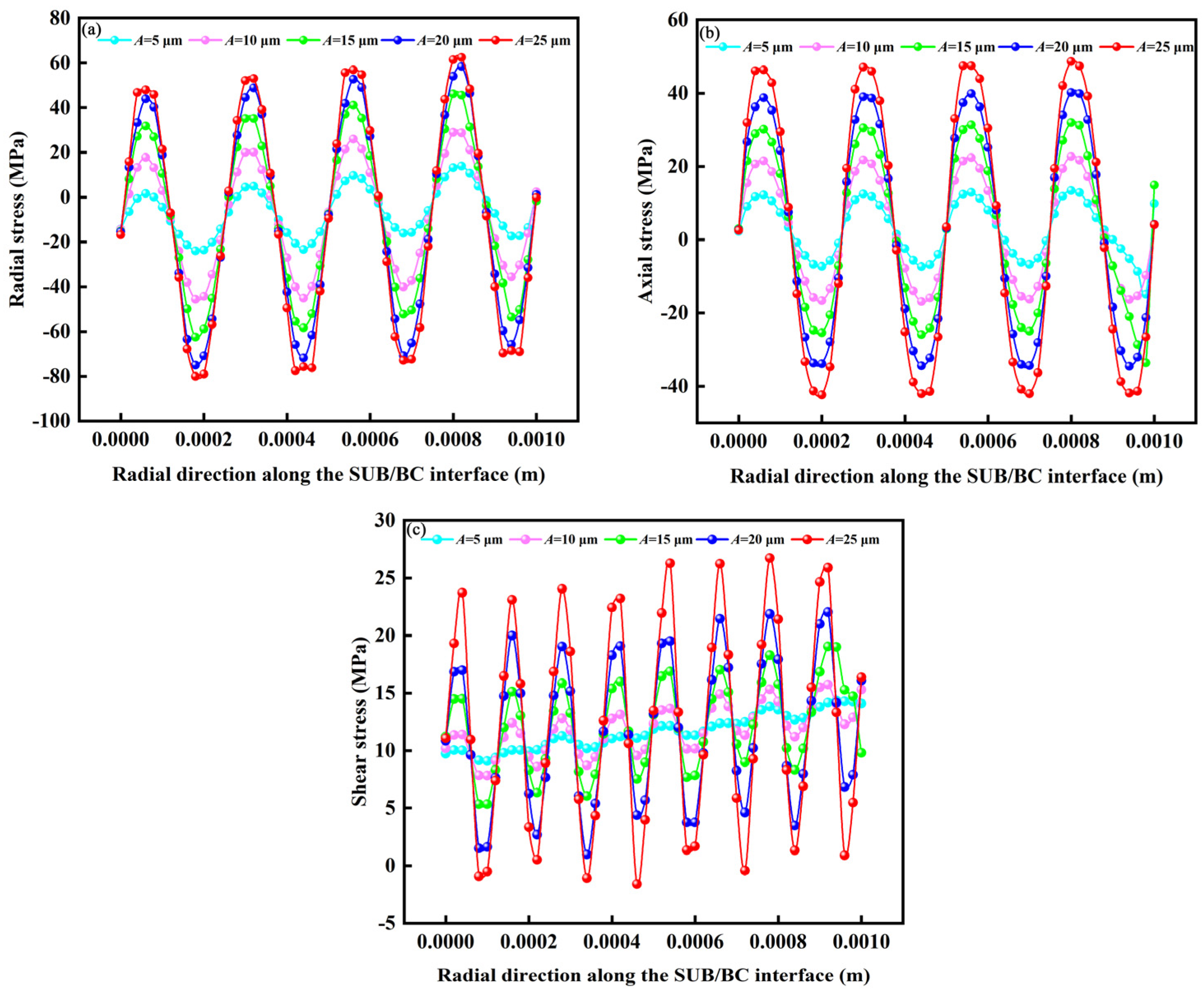
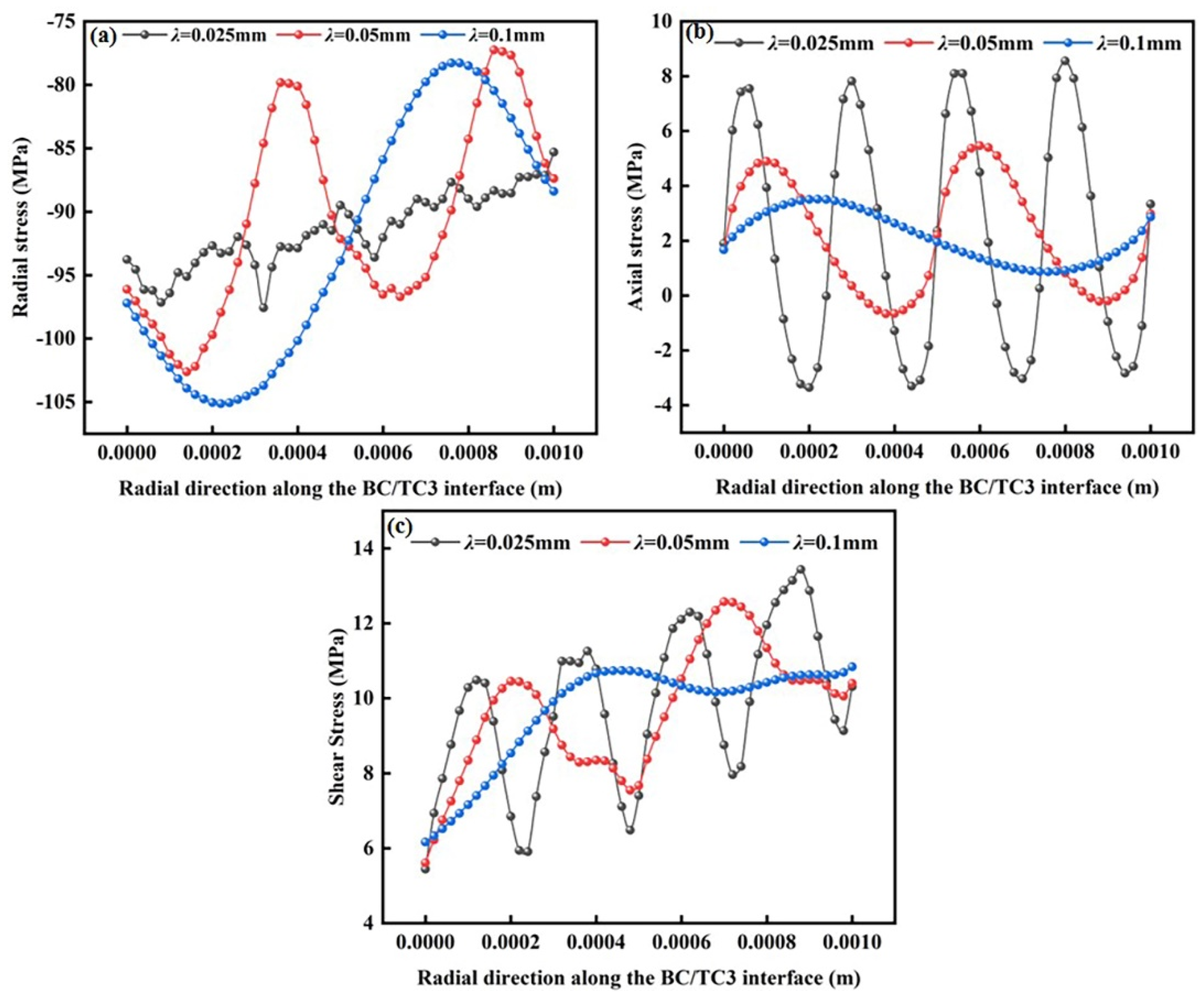
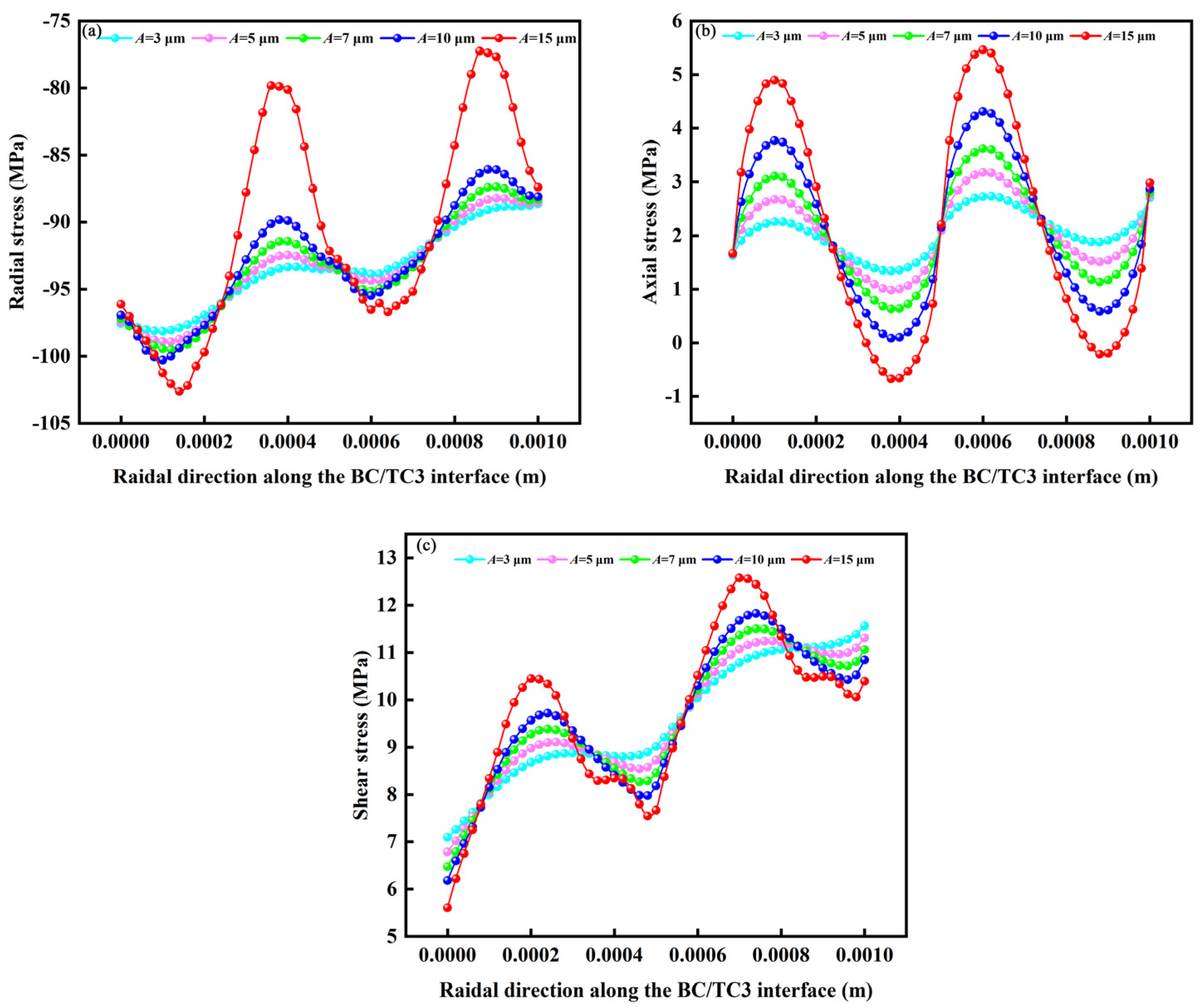
3.2. Influence of Interface Morphology on Interfacial Stress
3.2.1. Effect of Interface Morphology of Substrate on Interfacial Stress
3.2.2. Effect of Interface Morphology of Bond Layer on Interfacial Stress
3.2.3. Summary of This Section
4. Conclusions
- Based on the influence of the thickness optimization of each layer on the stress distributions of each interface, it can be concluded that to ensure that the residual stress of the coating is small and that it has good thermal insulation performance, the thicknesses of the BC, TC3, TC2, and TC1 layers should be approximately 110, 270, 70, and 100 μm, respectively. The thickness ratio was approximately 11:27:7:10.
- A periodic sine function was constructed to simulate the interface morphology of the coating during the plasma spraying. Based on the influence of a change in the interface morphology on the distributions of the interfacial stress, a relatively smooth interface could effectively reduce the concentration of the interfacial residual stress.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thakare, J.G. Thermal Barrier Coatings—A State of the Art Review. Met. Mater. Int. 2021, 27, 1947–1968. [Google Scholar] [CrossRef]
- Kanwal, S.; Thakare, J.G.; Pandey, C.; Singh, I.; Mahapatra, M.M. Characterization of slurry-based mullite coating deposited on P91 steel welds. J. Aust. Ceram. Soc. 2019, 55, 519–528. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Ming, Y.; Yuhua, L.; Ming, L. Research review of thermal barrier coatings preparation methods. J. Hubei Polytech. Univ. 2021, 37, 33–38. [Google Scholar] [CrossRef]
- Mercer, C. On a ferroelastic mechanism governing the toughness of metastable tetragonal-prime (t′) yttria-stabilized zirconia. Proc. R. Soc. A 2007, 463, 1393–1408. [Google Scholar] [CrossRef]
- Zhao, M.; Pan, W. Effect of lattice defects on thermal conductivity of Ti-doped, Y2O3-stabilized ZrO2. Acta Mater. 2013, 61, 5496–5503. [Google Scholar] [CrossRef]
- Zhao, M.; Ren, X.; Yang, J.; Pan, W. Thermo-mechanical properties of ThO2-doped Y2O3 stabilized ZrO2 for thermal barrier coatings. Ceram. Int. 2016, 42, 501–508. [Google Scholar] [CrossRef]
- Schelling, P.K. Mechanism of the cubic-to-tetragonal phase transition in zirconia and yttria-stabilized zirconia. J. Am. Ceram. 2001, 84, 2997–3007. [Google Scholar] [CrossRef]
- Fengling, L. The structure design of thermal barrier coating for 21 century. Mater. Prot. 2000, 33, 86–88. [Google Scholar] [CrossRef]
- Clarke, D.R.; Levi, C.G. Materials design for the next generation thermal battier coatings. Annu. Rev. Mater. Res. 2003, 33, 383–417. [Google Scholar] [CrossRef]
- Thakarea, J.G. Mechanical property evaluation of carbon nanotubes reinforced plasma sprayed YSZ-alumina composite coating. Ceram. Int. 2018, 44, 6980–6989. [Google Scholar] [CrossRef]
- Kim, D.J.; Tien, T.Y. Phase stability and physical properties of cubic and tetragonal ZrO2 in the system ZrO2–Y2O3–Ta2O5. J. Am. Ceram. Soc. 1991, 74, 3061–3065. [Google Scholar] [CrossRef]
- Pitek, F.M.; Levi, C.G. Opportunities for TBCs in the ZrO2-YO1.5-TaO2.5 system. Surf. Coat. Technol. 2007, 201, 6044–6050. [Google Scholar] [CrossRef]
- Shian, S. The tetragonal–monoclinic, ferroelastic transformation in yttrium tantalate and effect of zirconia alloying. Acta Mater. 2014, 69, 196–202. [Google Scholar] [CrossRef]
- Wu, J.; Wei, X.; Padture, N.P. Low-thermal-conductivity rare-earth zirconates for potential thermal-barrier-coating applications. J. Am. Ceram. Soc. 2002, 85, 3031–3035. [Google Scholar] [CrossRef]
- Lin, C.; Jing, F. Research progress on thermal mechanical properties of rare earth tantalate RE3TaO7 and RE3TaO9 ceramics. Mod. Tech. Ceram. 2019, 40, 31. [Google Scholar] [CrossRef]
- Muller, J.; Schierling, M. Chemical vapor deposition of smooth α-Al2O3 films on nickel base superalloys as diffusion barriers. Surf. Coat. Technol. 1999, 120, 16–21. [Google Scholar] [CrossRef]
- Pint, B.A. High-temperature oxidation-resistant alloys: Recent developments in science and applications. JOM 2009, 61, 42–43. [Google Scholar] [CrossRef]
- Ren, C.; He, Y.; Wang, D. High-temperature cyclic oxidation behavior of Al2O3-YAG composite coating prepared by EPD and microwave sintering. Appl. Surf. Sci. 2012, 258, 5739–5745. [Google Scholar] [CrossRef]
- Pereira, P.F.S. Red, green and blue (RGB) emission doped Y3Al5O12 (YAG) phosphors prepared by non-hydrolytic sol–gel route. J. Lumin. 2010, 130, 488–493. [Google Scholar] [CrossRef]
- Zheyi, Z. Study on process optimization of sprayable powders and deposition performance of amorphous Al2O3–YAG coatings. Coatings 2020, 10, 1158. [Google Scholar] [CrossRef]
- Yang, K.; Rong, J.; Feng, J. In-situ fabrication of amorphous/eutectic Al2O3-YAG ceramic composite coating via atmospheric plasma spraying. J. Eur. Ceram. Soc. 2016, 36, 4261–4267. [Google Scholar] [CrossRef]
- Parthasarathy, T.A.; Mah, T.I.; Keller, K. Creep mechanism of polycrystalline yttrium aluminum garnet. J. Am. Ceram. Soc. 1992, 75, 1756–1759. [Google Scholar] [CrossRef]
- Waku, Y.; Ohtsubo, H.; Nakagawa, N. Sapphire matrix composites reinforced with single crystal YAG phases. J. Mater. Sci. 1996, 31, 4663–4670. [Google Scholar] [CrossRef]
- Ochiai, S.; Ueda, T.; Sato, K. Deformation and fracture behavior of an Al2O3/YAG composite from room temperature to 2023 K. Compos. Sci. Technol. 2001, 61, 2117–2128. [Google Scholar] [CrossRef]
- Miyazaki, N.; Ikeda, T.; Komura, T. Estimation of steady-state creep behavior of Al2O3/YAG eutectic composite by image-based finite element analysis. J. Eng. Mater. Technol. 2003, 125, 277–282. [Google Scholar] [CrossRef]
- Sommer, F.; Kern, F.; El-Maghraby, F.H. Effect of preparation route on the properties of slip-casted Al2O3/YAG composites. Ceram. Int. 2012, 38, 4819–4826. [Google Scholar] [CrossRef]
- Lim, G.; Kar, A. Radiative properties of thermal barrier coatings at high temperatures. J. Phys. D Appl. Phys. 2009, 42, 155412. [Google Scholar] [CrossRef]
- Lee, G.; Atkinson, A.; Selçuk, A. Development of residual stress and damage in thermal barrier coatings. Surf. Coat. Technol. 2006, 201, 3931–3936. [Google Scholar] [CrossRef]
- Mao, W.G.; Zhou, Y.C.; Yang, L. Modeling of residual stresses variation with thermal cycling in thermal barrier coatings. Mech. Mater. 2006, 38, 1118–1127. [Google Scholar] [CrossRef]
- Faruk, S. Stress analysis of high temperature ZrO2 insulation coatings on Ag using finite element method. J. Mater. Process. Technol. 2006, 180, 239–245. [Google Scholar] [CrossRef]
- Ranjbar-Far, M. Impact of the non-homogenous temperature distribution and the coatings process modeling on the thermal barrier coatings system. Mater. Des. 2011, 32, 728–735. [Google Scholar] [CrossRef]
- Ozkan, S.; Yasar, I.; Erdal, C. Finite element modeling of the effect of the ceramic coatings on heat transfer characteristics in thermal barrier applications. Mater. Des. 2005, 26, 357–362. [Google Scholar] [CrossRef]
- Rätzer-Scheibe, H.J.; Schulz, U.; Krell, T. The effect of coating thickness on the thermal conductivity of EB-PVD PYSZ thermal barrier coatings. Surf. Coat. Technol. 2006, 200, 5636–5644. [Google Scholar] [CrossRef]
- Guo, H.B.; Vaßen, R.; Stöver, D. Atmospheric plasma sprayed thick thermal barrier coatings with high segmentation crack density. Surf. Coat. Technol. 2004, 186, 353–363. [Google Scholar] [CrossRef]
- Ranjbar-Far, M. Simulation of the effect of material properties and interface roughness on the stress distribution in thermal barrier coatings using finite element method. Mater. Des. 2010, 31, 772–781. [Google Scholar] [CrossRef]
- Białas, M. Finite element analysis of stress distribution in thermal barrier coatings. Surf. Coat. Technol. 2008, 202, 6002–6010. [Google Scholar] [CrossRef]
- Han, M.; Huang, J.; Chen, S. The influence of interface morphology on the stress distribution in double-ceramic-layer thermal barrier coatings. Ceram. Int. 2015, 41, 4312–4325. [Google Scholar] [CrossRef]
- Ahrens, M.; Vaßen, R.; Stöver, D. Stress distributions in plasma-sprayed thermal barrier coatings as a function of interface roughness and oxide scale thickness. Surf. Coat. Technol. 2002, 161, 26–35. [Google Scholar] [CrossRef]
- Zhang, W.X.; Fan, X.L.; Wang, T.J. The surface cracking behavior in air plasma sprayed thermal barrier coating system incorporating interface roughness effect. Appl. Surf. Sci. 2011, 258, 811–817. [Google Scholar] [CrossRef]
- Zhang, D. Effect of bond coat surface roughness on the thermal cyclic behavior of thermal barrier coatings. Surf. Coat. Technol. 2006, 201, 649–653. [Google Scholar] [CrossRef]
- Han, M. A parametric study of the double-ceramic-layer thermal barrier coatings part I: Optimization design of the ceramic layer thickness ratio based on the finite element analysis of thermal insulation (take LZ7C3/8YSZ/NiCoAlY DCL-TBCs for an example). Surf. Coat. Technol. 2013, 236, 500–509. [Google Scholar] [CrossRef]
- Zhuang, M.X. Design and optimization of coating structure for plasma sprayed self-healing MgO coating via finite element method. Ceram. Int. 2021, 47, 2414–2429. [Google Scholar] [CrossRef]
- Wu, Q.; Dong, Y.F.; Wang, Z.; Song, D.Y.; Ji, Y.X. Computational modal analysis of circular saw blade based on APDL method. For. Mach. Woodwork. Equip. 2022, 50, 97–105. [Google Scholar] [CrossRef]
- Han, M. Optimization selection of the thermal conductivity of the top ceramic layer in the Double-Ceramic-Layer Thermal Barrier Coatings based on the finite element analysis of thermal insulation. Surf. Coat. Technol. 2014, 240, 320–326. [Google Scholar] [CrossRef]
- Lou, S.Y.; Shan, X.; Zhao, X.F. Composition and thickness optimization of anti-CMAS layer on air plasma sprayed thermal barrier coatings. Surf. Coat. Technol. 2018, 47, 208–217. [Google Scholar] [CrossRef]
- Han, M.; Huang, J.H.; Chen, S.H. Behavior and mechanism of the stress buffer effect of the inside ceramic layer to the top ceramic layer in a double-ceramic-layer thermal barrier coating. Ceram. Int. 2014, 40, 2901–2914. [Google Scholar] [CrossRef]
- Zhou, C.G.; Wang, C.L.; Song, Y.X. Evaluation of cyclic oxidation of thermal barrier coatings exposed to NaCl vapor by finite element method. Mater. Sci. Eng. A 2008, 490, 351–358. [Google Scholar] [CrossRef]
- Zhou, C.G. Cyclic-oxidation behavior of thermal-barrier coatings exposed to NaCl vapor. Oxid. Met. 2008, 69, 119–130. [Google Scholar] [CrossRef]
- Zhou, C.G. Influence of service temperature on grain growth and thermal diffusivity of nanostructured thermal barrier coating. Mater. Sci. Forum. 2005, 510, 3985–3988. [Google Scholar] [CrossRef]
- Han, M.; Huang, J.H.; Chen, S.H. A parametric study of the Double- Ceramic-Layer Thermal Barrier Coating Part II: Optimization selection of mechanical parameters of the inside ceramic layer based on the effect on the stress distribution. Surf. Coat. Technol. 2014, 238, 93–117. [Google Scholar] [CrossRef]
- Wang, L. Finite element simulation of stress distribution and development in 8YSZ and double-ceramic-layer La2Zr2O7/8YSZ thermal barrier coatings during thermal shock. Appl. Surf. Sci. 2012, 258, 3540–3551. [Google Scholar] [CrossRef]
- Ren, C.; He, Y.D.; Wang, D.R. Cyclic oxidation behavior and thermal barrier effect of YSZ-(Al2O3/YAG) double-layer TBCs prepared by the composite sol–gel method. Surf. Coat. Technol. 2011, 206, 1461–1468. [Google Scholar] [CrossRef]
- Hsuch, C.H.; Jong, H.; Lee, C.S. Modeling of thermal stresses in joining two layers with multi- and graded interlayers. J. Am. Ceram. Soc. 2006, 9, 251–257. [Google Scholar] [CrossRef]
- Gao, X.Y. Study of residual stresses and stability of thermal barrier coatings under thermal cycling. N. P. U. 2007, 6, 77–79. [Google Scholar] [CrossRef]
- Liu, D.D. Research and numerical simulation of thermal of thermal mechanical behavior of thermal barrier coating micromorphology. Southwest Jiaotong Univ. 2018. [Google Scholar]
- Zhang, H.S.; Zhang, Z.; Chen, X.G.; Liu, J.Y. Plasma spraying Sm2Zr2O7 Residual thermal stress in thermal barrier coatings. China’s Ceram. 2010, 46, 38–41. [Google Scholar] [CrossRef]
- Han, Z.Y.; Wang, H. Relation between concave cone 3 dimension topography and residual stress in thermal barrier coatings. Adv. Mat. Res. 2011, 291, 172–175. [Google Scholar] [CrossRef]
- Hou, P.J.; Wang, H.G.; Zha, B.L.; Yuan, X.J. Numerical simulation for effect of interface roughness on residual stress of double-layer thermal barrier coatings. Hot Work. Technol. 2007, 36, 82–85. [Google Scholar]



| T (°C) | E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 20 | 220 | 0.31 | 14.8 | 4.3 | 658 | 8.15 × 103 |
| 200 | 210 | 0.32 | 15.2 | 5.2 | 667 | 8.15 × 103 |
| 400 | 190 | 0.33 | 15.6 | 6.4 | 680 | 8.15 × 103 |
| 600 | 170 | 0.33 | 16.2 | 8.6 | 690 | 8.15 × 103 |
| 800 | 155 | 0.33 | 16.9 | 10.2 | 696 | 8.15 × 103 |
| 900 | 140 | 0.34 | 11 | 16.1 | 703 | 8.15 × 103 |
| 1100 | 130 | 0.35 | 17.5 | 16.9 | 716 | 8.15 × 103 |
| T (°C) | E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 20 | 152.4 | 0.1 | 12.3 | 4.3 | 501 | 5.28 × 103 |
| 200 | 143.3 | 0.1 | 13.2 | 5.2 | 547 | 5.28 × 103 |
| 400 | 136.7 | 0.11 | 14.7 | 6.4 | 598 | 5.28 × 103 |
| 600 | 126.4 | 0.11 | 15.9 | 8.6 | 638 | 5.28 × 103 |
| 800 | 41.3 | 0.12 | 17.7 | 10.2 | 781 | 5.28 × 103 |
| 900 | 22 | 0.12 | 18.2 | 16.1 | 764 | 5.28 × 103 |
| 1100 | 15 | 0.12 | 18.6 | 16.9 | 779 | 5.28 × 103 |
| T (°C) | E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 20 | 48 | 0.1 | 10.4 | 9.8 | 640 | 5.90 × 103 |
| 200 | 47 | 0.1 | 10.5 | 7.79 | 640 | 5.90 × 103 |
| 400 | 43 | 0.1 | 10.7 | 6.21 | 640 | 5.90 × 103 |
| 600 | 39 | 0.1 | 10.8 | 5.42 | 640 | 5.90 × 103 |
| 800 | 25 | 0.1 | 10.9 | 5.38 | 640 | 5.90 × 103 |
| 900 | 22 | 0.1 | 11 | 5.26 | 640 | 5.90 × 103 |
| 1100 | 15 | 0.1 | 11.3 | 5.23 | 640 | 5.90 × 103 |
| E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|
| 130 | 0.27 | 12 | 1.34 | 320 | 6.20 × 103 |
| T (°C) | E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 20 | 400 | 0.23 | 7.13 | 9.8 | 980 | 4.20 × 103 |
| 200 | 390 | 0.23 | 7.47 | 7.79 | 980 | 4.20 × 103 |
| 400 | 376 | 0.25 | 8.57 | 6.21 | 980 | 4.20 × 103 |
| 600 | 355 | 0.25 | 9 | 5.42 | 980 | 4.20 × 103 |
| 800 | 325 | 0.25 | 9.5 | 5.38 | 980 | 4.20 × 103 |
| 900 | 315 | 0.25 | 9.7 | 5.26 | 980 | 4.20 × 103 |
| 1100 | 310 | 0.26 | 9.8 | 5.23 | 980 | 4.20 × 103 |
| E (GPa) | v | α (×10−6 °C−1) | k | c (J/(Kg·°C)) | ρ (kg/m3) |
|---|---|---|---|---|---|
| 310 | 0.3 | 7.8 | 14 | 590 | 4.55 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.-Y.; Zhou, H.-X.; Cao, Z.-J.; Wan, J.-B.; Liu, Y.; Sun, X.-W.; Su, J.-H.; Wu, Q.; Wang, L. Optimization of the Thickness and Interface Structure of Al2O3-YAG/ZrO1.5-YO1.5-TaO1.5/8YSZ/NiCoCrAlY Multilayer Thermal Barrier Coatings: A Finite Element Simulation. Coatings 2022, 12, 1660. https://doi.org/10.3390/coatings12111660
Su H-Y, Zhou H-X, Cao Z-J, Wan J-B, Liu Y, Sun X-W, Su J-H, Wu Q, Wang L. Optimization of the Thickness and Interface Structure of Al2O3-YAG/ZrO1.5-YO1.5-TaO1.5/8YSZ/NiCoCrAlY Multilayer Thermal Barrier Coatings: A Finite Element Simulation. Coatings. 2022; 12(11):1660. https://doi.org/10.3390/coatings12111660
Chicago/Turabian StyleSu, Huai-Yu, Hong-Xia Zhou, Zhi-Jun Cao, Jia-Bao Wan, Yao Liu, Xiao-Wen Sun, Jia-Hui Su, Qian Wu, and Liang Wang. 2022. "Optimization of the Thickness and Interface Structure of Al2O3-YAG/ZrO1.5-YO1.5-TaO1.5/8YSZ/NiCoCrAlY Multilayer Thermal Barrier Coatings: A Finite Element Simulation" Coatings 12, no. 11: 1660. https://doi.org/10.3390/coatings12111660
APA StyleSu, H.-Y., Zhou, H.-X., Cao, Z.-J., Wan, J.-B., Liu, Y., Sun, X.-W., Su, J.-H., Wu, Q., & Wang, L. (2022). Optimization of the Thickness and Interface Structure of Al2O3-YAG/ZrO1.5-YO1.5-TaO1.5/8YSZ/NiCoCrAlY Multilayer Thermal Barrier Coatings: A Finite Element Simulation. Coatings, 12(11), 1660. https://doi.org/10.3390/coatings12111660







