Research on Mechanical Properties of 210Cr12 Shaft Surface Processed with Rolling
Abstract
1. Introduction
2. Material and Method
2.1. Sample Preparation
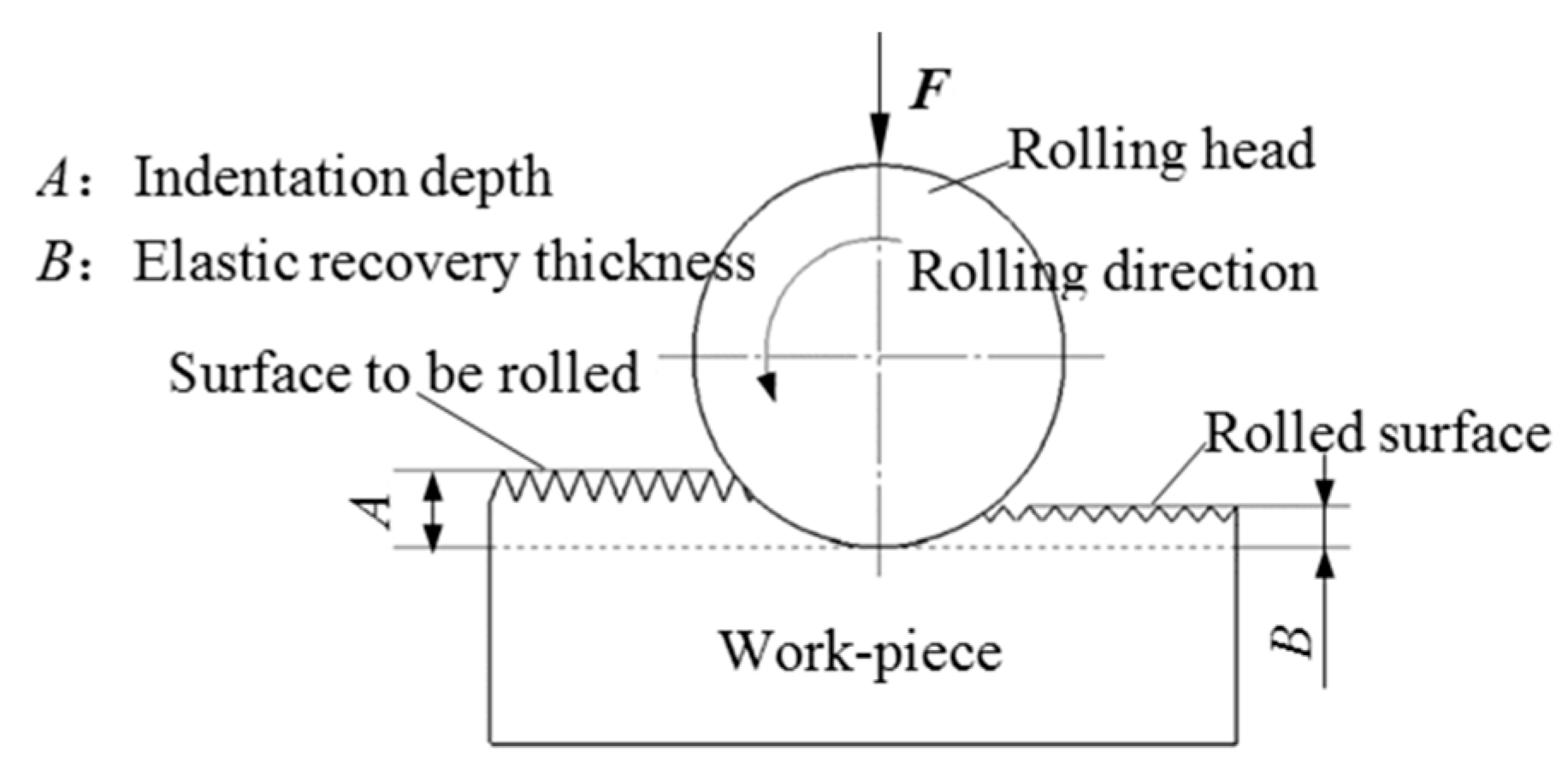
2.2. Rolling Equipment
2.3. Experimental Design
2.4. Measurement Conditions
3. Experimental Investigation on Rolling Process for 210Cr12 Shaft
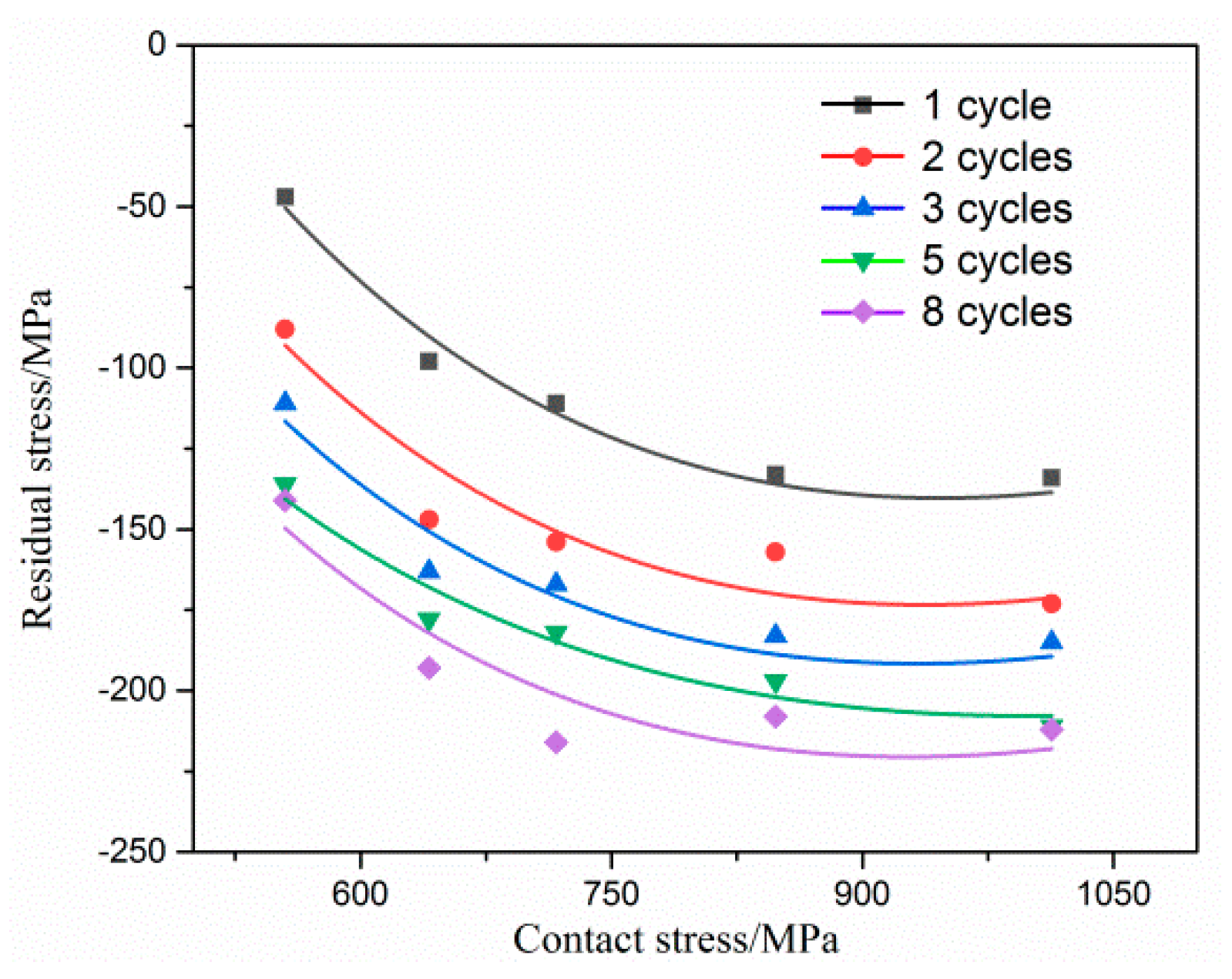
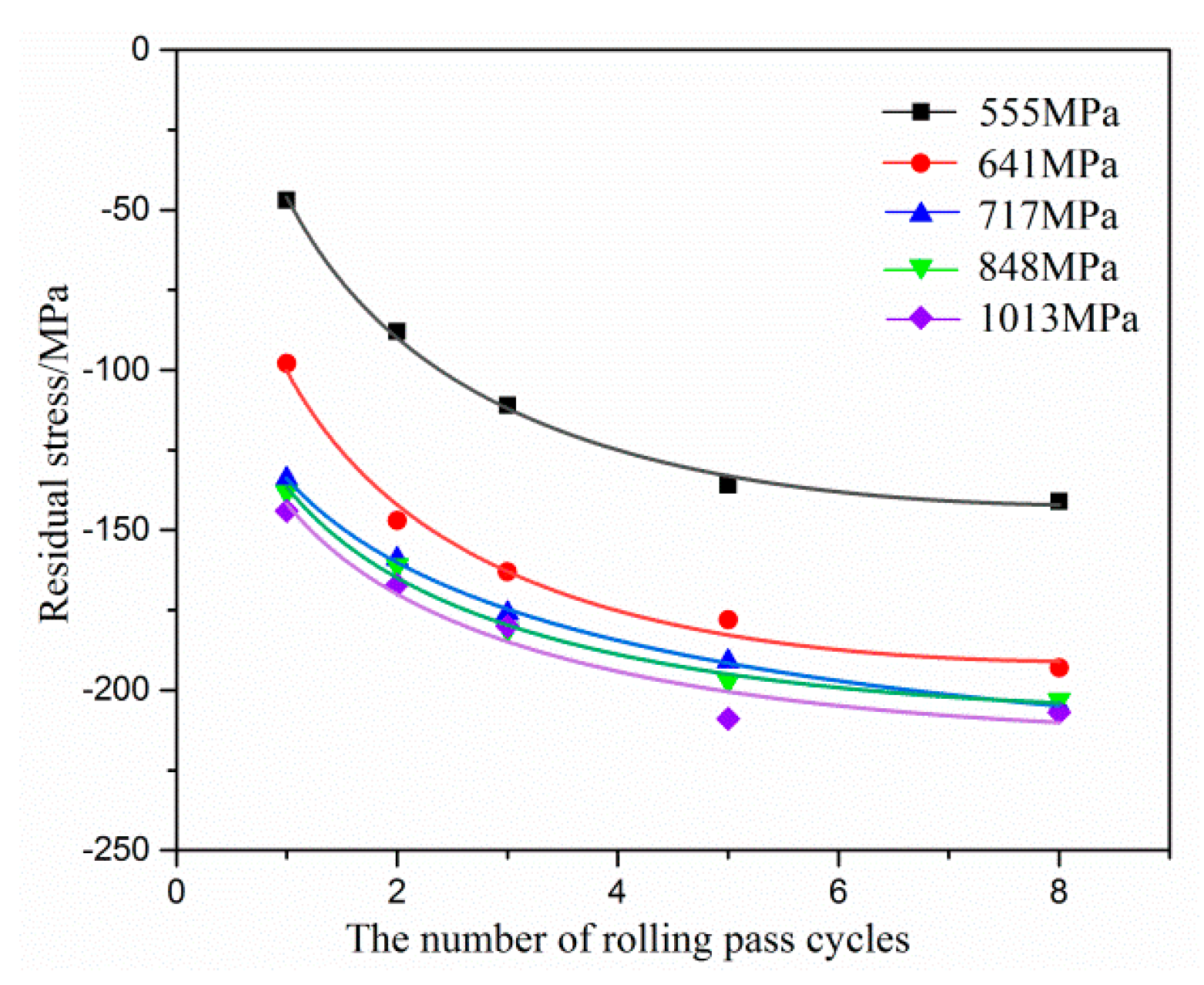
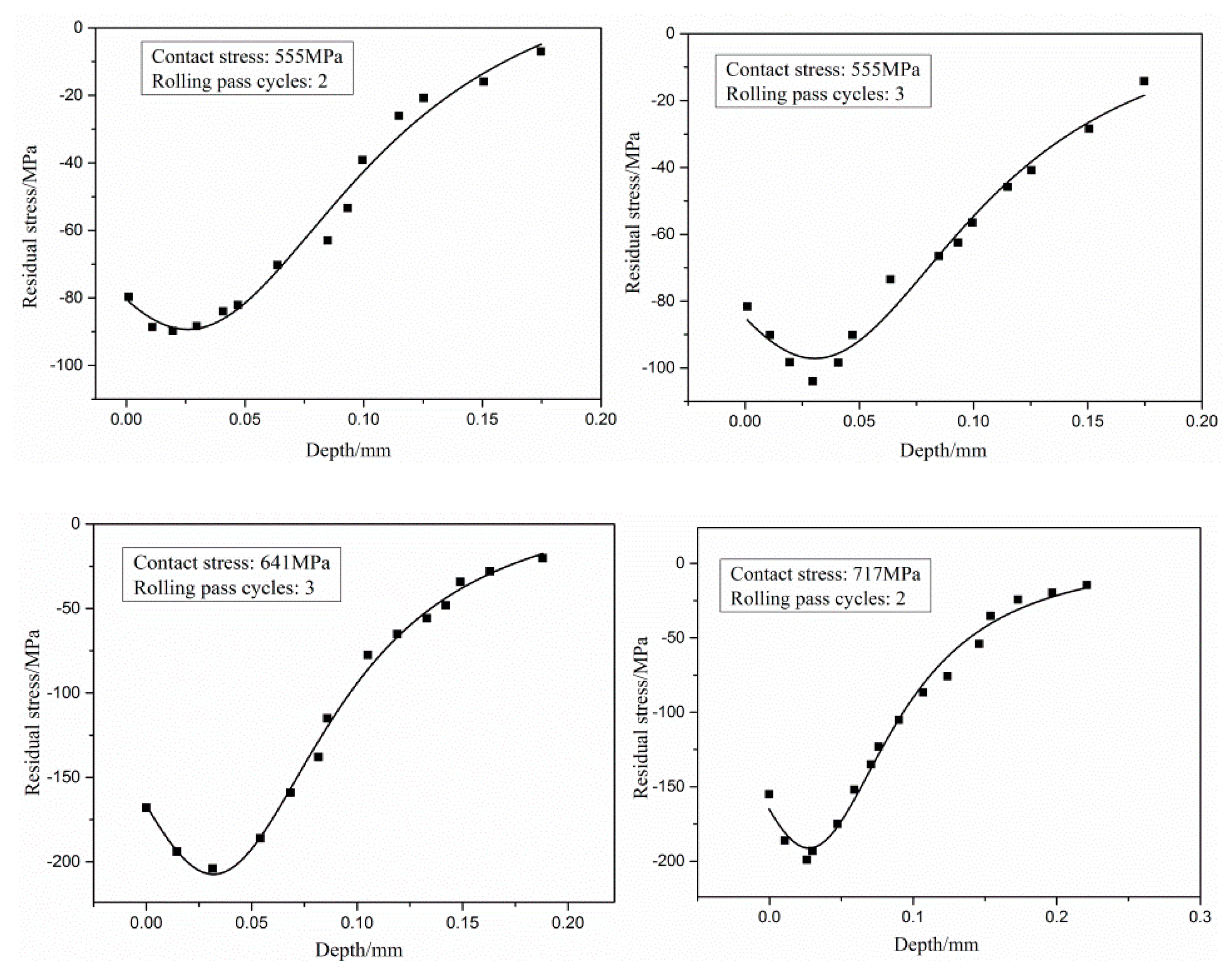
3.1. Effect of Rolling on Residual Stress
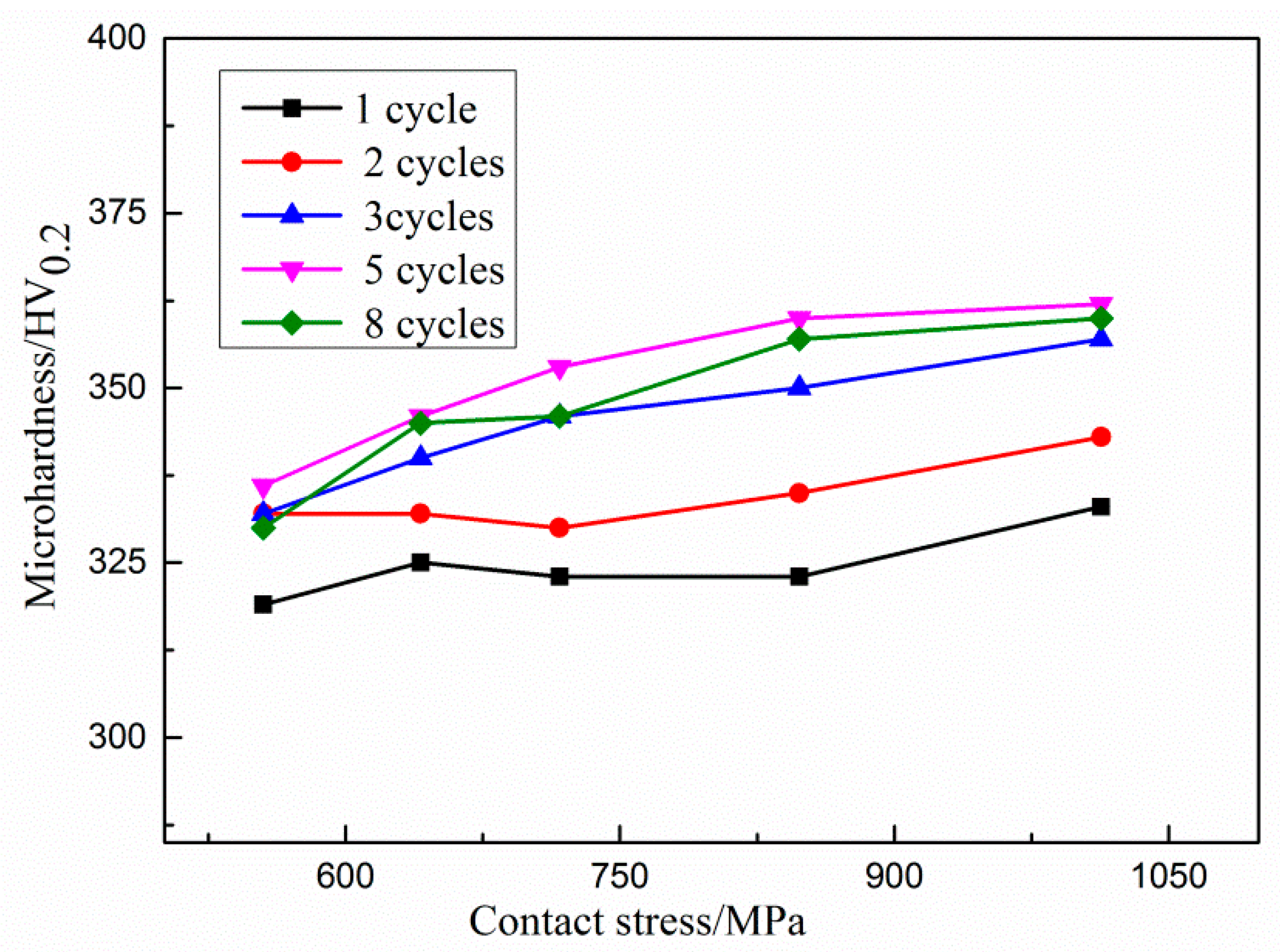
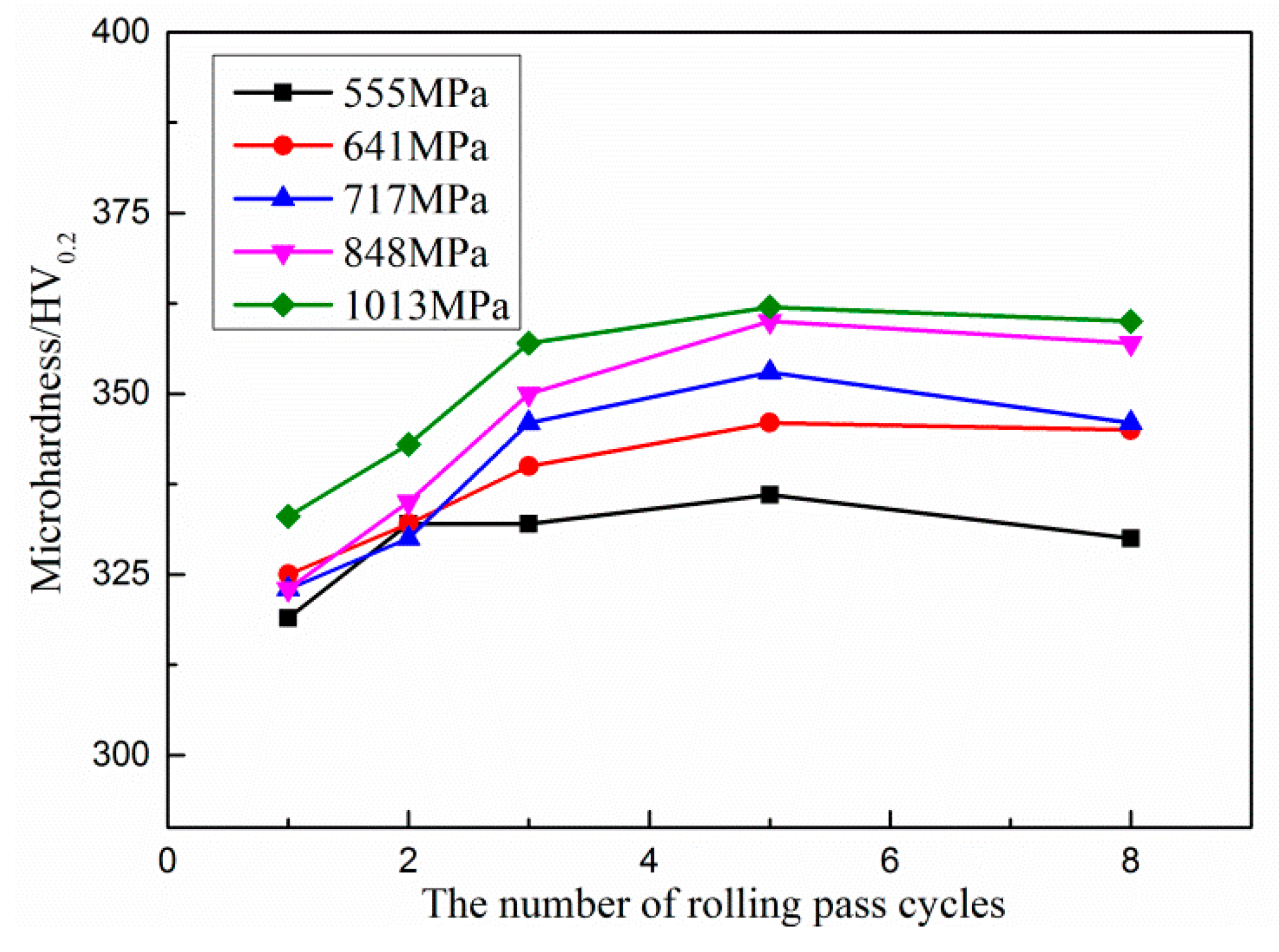
3.2. Effect of Rolling on Surface Microhardness
3.3. Effect of Rolling on Surface Roughness
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Priyadarsini, C.; Ramana, V.V.; Prabha, K.A.; Swetha, S. A review on ball, roller, low plasticity burnishing process. Mater. Today Proc. 2019, 18, 5087–5099. [Google Scholar] [CrossRef]
- Tang, J.; Luo, H.Y.; Zhang, Y.B. Enhancing the surface integrity and corrosion resistance of Ti-6Al-4V titanium alloy through cryogenic burnishing. Int. J. Adv. Manuf. Technol. 2017, 88, 2785–2793. [Google Scholar] [CrossRef]
- Swirad, S.; Wdowik, R. Determining the effect of ball burnishing parameters on surface roughness using the Taguchi method. Procedia Manuf. 2019, 34, 287–292. [Google Scholar] [CrossRef]
- Stöckmann, R.; Putz, M. Modelling of surface formation mechanism during burnishing of aluminium. Procedia CIRP 2019, 82, 450–454. [Google Scholar] [CrossRef]
- Teimouri, R.; Amini, S.; Bami, A.B. Evaluation of optimized surface properties and residual stress in ultrasonic assisted ball burnishing of AA6061-T6. Measurement 2018, 116, 129–139. [Google Scholar] [CrossRef]
- Abuzaid, W.Z.; Sehitoglu, H.; Lambros, J. Localisation of plastic strain at the microstructurlal level in Hastelloy X subjected to monotonic, fatigue, and creep loading: The role of grain boundaries and slip transmission. Mater. High Temp. 2016, 33, 384–400. [Google Scholar] [CrossRef]
- Saldaña-Robles, A.; Plascencia-Mora, H.; Aguilera-Gómez, E.; Saldaña-Robles, A.; Marquez-Herrera, A.; Diosdado-De la Peña, J.A. Influence of ball-burnishing on roughness, hardness and corrosion resistance of AISI 1045 steel. Surf. Coat. Technol. 2018, 339, 191–198. [Google Scholar] [CrossRef]
- Dwivedi, S.P.; Sharma, S.; Mishra, R.K. Effects of roller burnishing process parameters on surface roughness of A356/5%SiC composite using response surface methodology. Adv. Manuf. 2014, 2, 303–317. [Google Scholar] [CrossRef]
- Juijerm, P.; Altenberger, I. Fatigue behavior of deep rolled Al–Mg–Si–Cu alloy at elevated temperature. Scr. Mater. 2006, 55, 943–946. [Google Scholar] [CrossRef]
- Avilés, R.; Albizuri, J.; Rodríguez, A.; De Lacalle, L.L. Influence of low-plasticity ball burnishing on the high-cycle fatigue strength of medium carbon AISI 1045 steel. Int. J. Fatigue 2013, 55, 230–244. [Google Scholar] [CrossRef]
- Wong, C.C.; Hartawan, A.; Teo, W.K. Deep cold rolling of features on aero-engine components. Procedia CIRP 2014, 13, 350–354. [Google Scholar] [CrossRef]
- Moussa, N.B.; Gharbi, K.; Chaieb, I.; Fredj, N.B. Improvement of AISI 304 austenitic stainless steel low-cycle fatigue life by initial and intermittent deep rolling. Int. J. Adv. Manuf. Technol. 2019, 101, 435–449. [Google Scholar] [CrossRef]
- Bouzid, W.; Tsoumarev, O.; Saï, K. An investigation of surface roughness of burnished AISI 1042 steel. Int. J. Adv. Manuf. Technol. 2004, 24, 120–125. [Google Scholar] [CrossRef]
- Hiegemann, L.; Weddeling, C.; Khalifa, N.B.; Tekkaya, A.E. Analytical Prediction of Roughness after Ball Burnishing of Thermally Coated Surfaces. Procedia Eng. 2014, 81, 1921–1926. [Google Scholar] [CrossRef]
- Korzynski, M. Modeling and experimental validation of the force–surface roughness relation for smoothing burnishing with a spherical tool. Int. J. Mach. Tools Manuf. 2007, 47, 1956–1964. [Google Scholar] [CrossRef]
- Zhang, P.; Lindemann, J.; Ding, W.J.; Leyens, C. Effect of roller burnishing on fatigue properties of the hot-rolled Mg–12Gd–3Y magnesium alloy. Mater. Chem. Phys. 2010, 124, 835–840. [Google Scholar] [CrossRef]
- Jing, Z.H.A.O.; Wei, X.I.A.; Ning, L.I.; Li, F.L. A gradient nano/micro-structured surface layer on copper induced by severe plasticity roller burnishing. Trans. Nonferrous Met. Soc. China 2014, 24, 441–448. [Google Scholar]
- Chen, B.; Zhang, G.; Zhang, L.; Xu, T. A new approach of a gradient nanograined surface layer for Mg-3Al-1Zn alloy induced by SMRGT. Int. J. Adv. Manuf. Technol. 2018, 94, 2659–2665. [Google Scholar] [CrossRef]
- Shiou, F.J.; Huang, S.J.; Shih, A.J.; Zhu, J.; Yoshino, M. Fine surface finish of a hardened stainless steel using a new burnishing tool. Procedia Manuf. 2017, 10, 208–217. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Rodríguez, A.; Lamikiz, A.; Celaya, A.; Alberdi, R. Five-axis machining and burnishing of complex parts for the improvement of surface roughness. Mater. Manuf. Process. 2011, 26, 997–1003. [Google Scholar] [CrossRef]
- Meyer, D. Cryogenic deep rolling—An energy based approach for enhanced cold surface hardening. CIRP Ann. Manuf. Technol. 2012, 61, 543–546. [Google Scholar] [CrossRef]
- Scheil, J.; Müller, C.; Steitz, M.; Groche, P. Influence of process parameters on surface hardening in hammer peening and deep rolling. Key Eng. Mater. 2013, 554–557, 1819–1827. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, K.M.; Jia, Y.F.; Zhang, C.C.; Zhang, X.C.; Ma, X.F.; Tu, S.T. Effect of thermal annealing on the microstructure, mechanical properties and residual stress relaxation of pure titanium after deep rolling treatment. J. Mater. Sci. Technol. 2019, 35, 409–417. [Google Scholar] [CrossRef]
- Saalfeld, S.; Oevermann, T.; Niendorf, T.; Scholtes, B. Consequences of deep rolling on the fatigue behavior of steel SAE 1045 at high loading amplitudes. Int. J. Fatigue 2019, 118, 192–201. [Google Scholar] [CrossRef]
- Saalfeld, S.; Scholtes, B.; Niendorf, T. On the influence of overloads on the fatigue performance of deep rolled steel SAE 1045. Int. J. Fatigue 2019, 126, 221–230. [Google Scholar] [CrossRef]



| Element | C | Cr | Mn | Si | P | S | Others |
|---|---|---|---|---|---|---|---|
| Weight percentage wt % | 2.00–2.30 | 11.50–13.00 | ≤0.40 | ≤0.40 | ≤0.030 | ≤0.030 | ≤0.025 |
| Rolling Pass Cycles | Contact Stress /MPa | ||||
|---|---|---|---|---|---|
| 555 | 641 | 717 | 848 | 1013 | |
| 1 | −47 | −98 | −111 | −133 | −134 |
| 2 | −88 | −147 | −154 | −157 | −173 |
| 3 | −111 | −163 | −167 | −183 | −180 |
| 5 | −136 | −178 | −182 | −197 | −211 |
| 8 | −141 | −193 | −216 | −205 | −212 |
| Contact Stress/MPa | 555 | 641 | 717 | 848 | 1013 | |
|---|---|---|---|---|---|---|
| Rolling Pass Cycles | ||||||
| 1 | 319 | 325 | 323 | 323 | 333 | |
| 2 | 332 | 332 | 330 | 335 | 343 | |
| 3 | 332 | 340 | 346 | 350 | 357 | |
| 5 | 336 | 346 | 353 | 360 | 362 | |
| 8 | 330 | 345 | 346 | 357 | 360 | |
| Contact Stress/MPa | 555 | 641 | 717 | 848 | 1013 | |
|---|---|---|---|---|---|---|
| Rolling Pass Cycles | ||||||
| 1 | 2.326 | 2.102 | 2.181 | 2.269 | 2.072 | |
| 2 | 2.243 | 2.243 | 2.297 | 2.006 | 1.572 | |
| 3 | 2.185 | 2.031 | 2.226 | 2.074 | 1.795 | |
| 5 | 2.211 | 2.019 | 2.176 | 1.954 | 1.346 | |
| 8 | 1.94 | 2.001 | 2.124 | 1.769 | 1.019 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Y.; Chen, H.; Qi, K.; Guo, P. Research on Mechanical Properties of 210Cr12 Shaft Surface Processed with Rolling. Coatings 2020, 10, 611. https://doi.org/10.3390/coatings10070611
Qiao Y, Chen H, Qi K, Guo P. Research on Mechanical Properties of 210Cr12 Shaft Surface Processed with Rolling. Coatings. 2020; 10(7):611. https://doi.org/10.3390/coatings10070611
Chicago/Turabian StyleQiao, Yang, Hongtang Chen, Kaihua Qi, and Peiquan Guo. 2020. "Research on Mechanical Properties of 210Cr12 Shaft Surface Processed with Rolling" Coatings 10, no. 7: 611. https://doi.org/10.3390/coatings10070611
APA StyleQiao, Y., Chen, H., Qi, K., & Guo, P. (2020). Research on Mechanical Properties of 210Cr12 Shaft Surface Processed with Rolling. Coatings, 10(7), 611. https://doi.org/10.3390/coatings10070611





