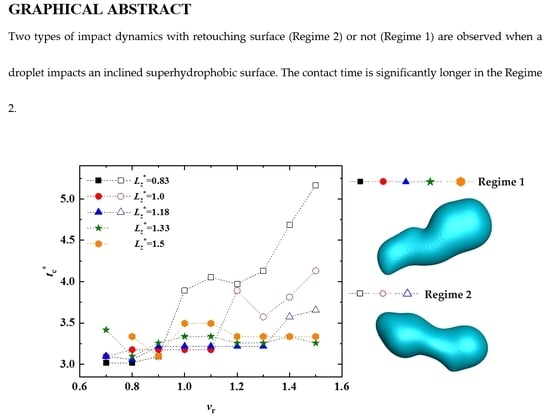
Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface
Abstract
1. Introduction
2. Mathematical Model
2.1. Shan-Chen Lattice Boltzmann Model
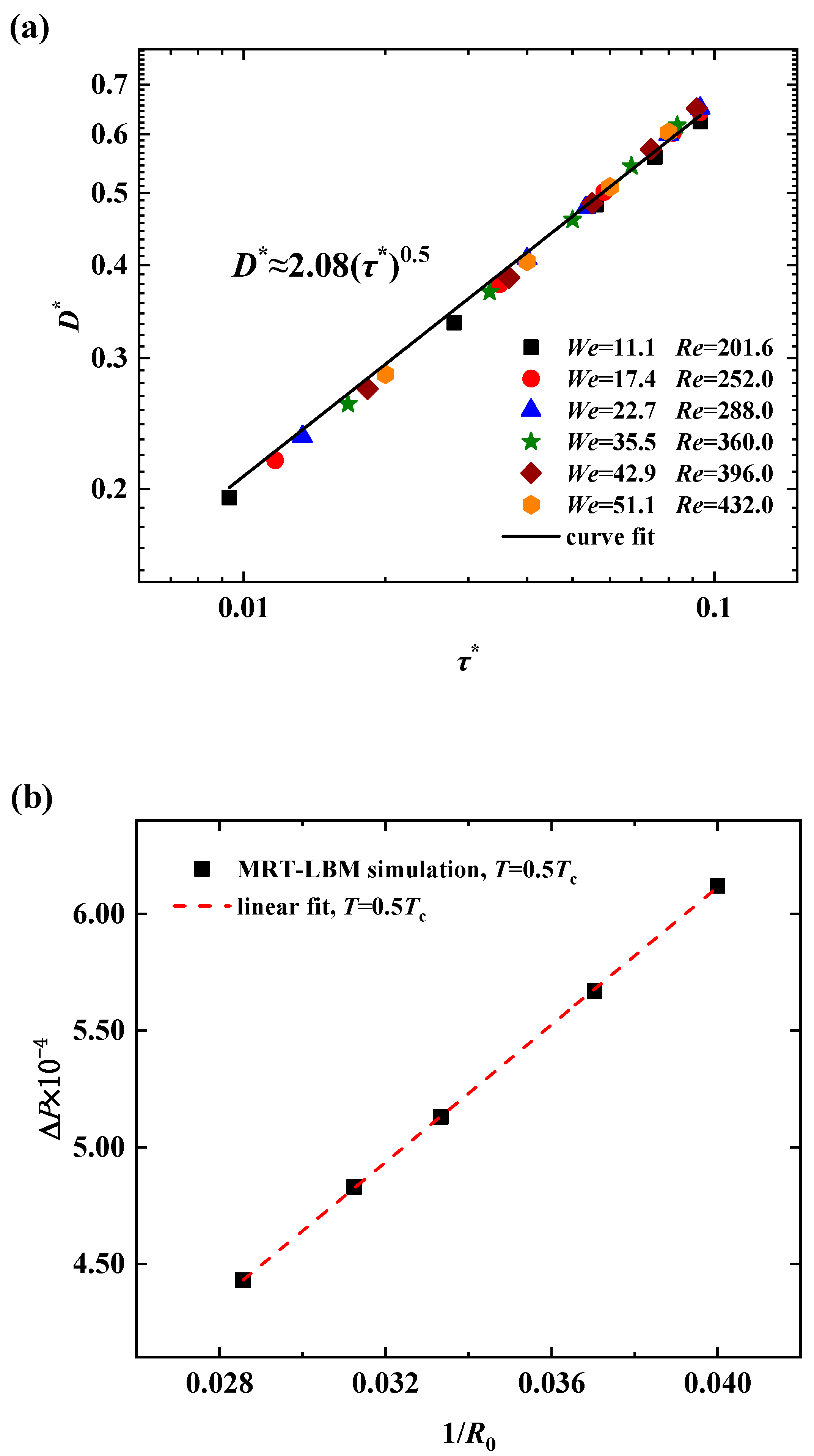
2.2. Model validation
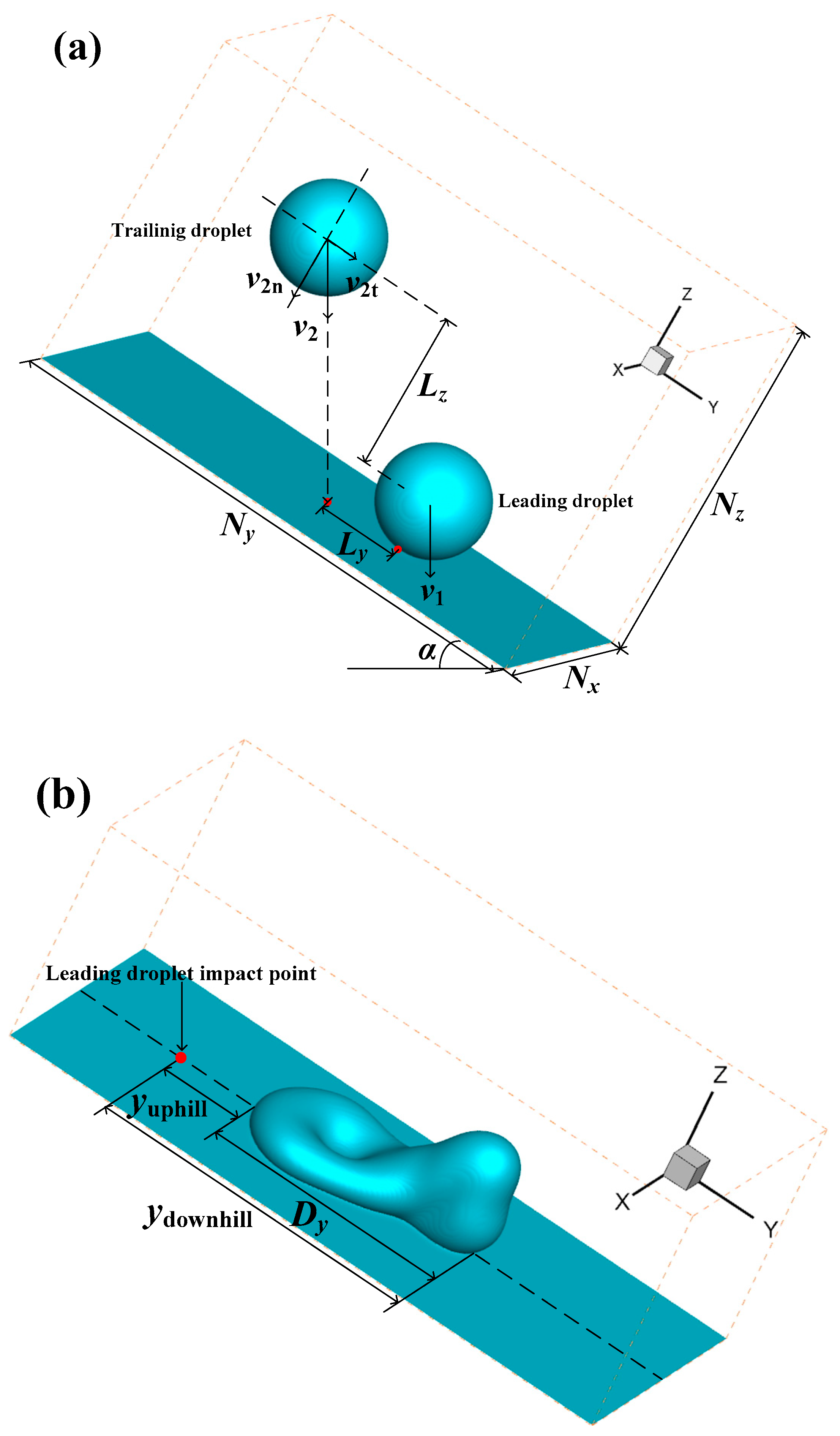
2.3. The Simulation Setup
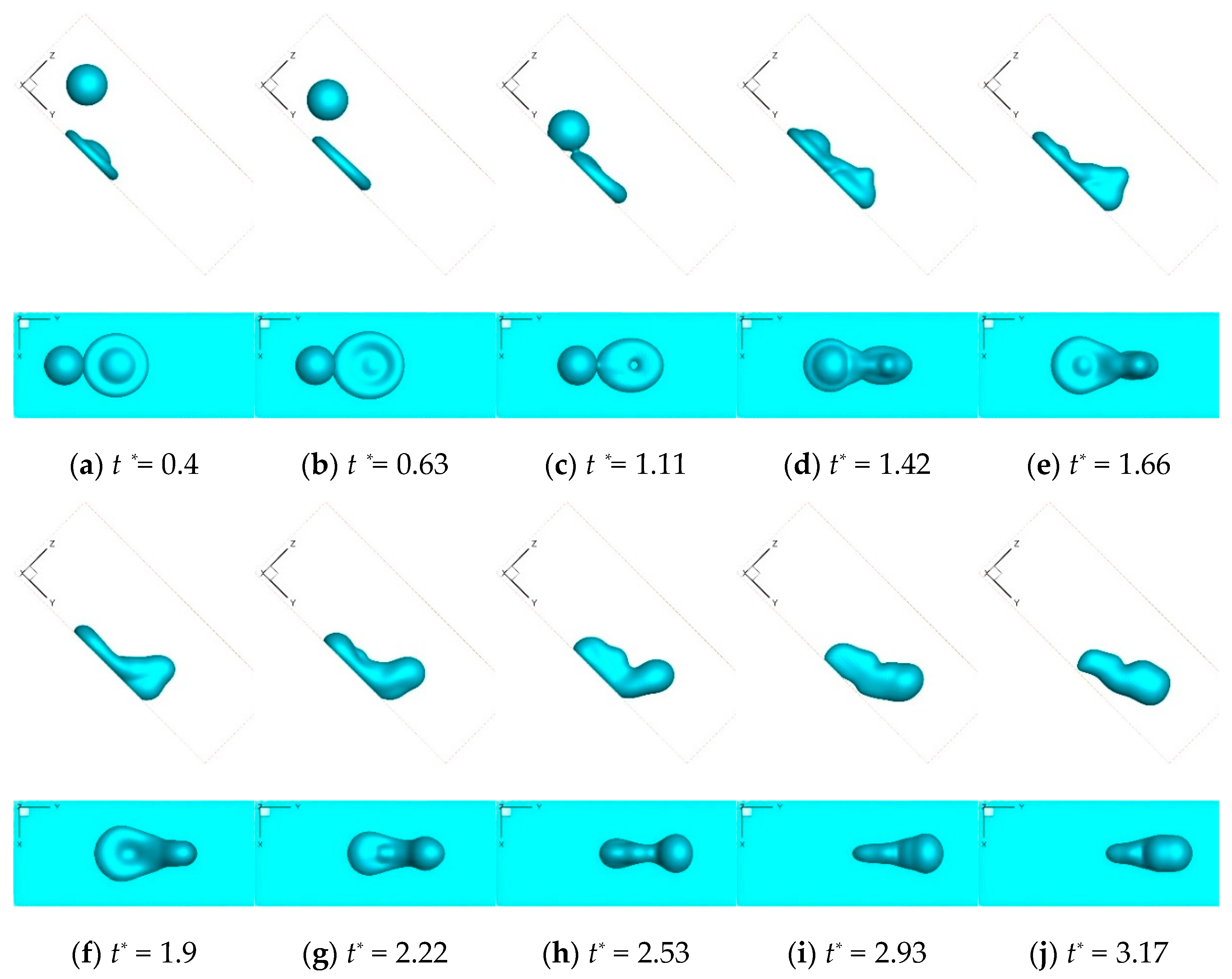
3. Results and Discussion
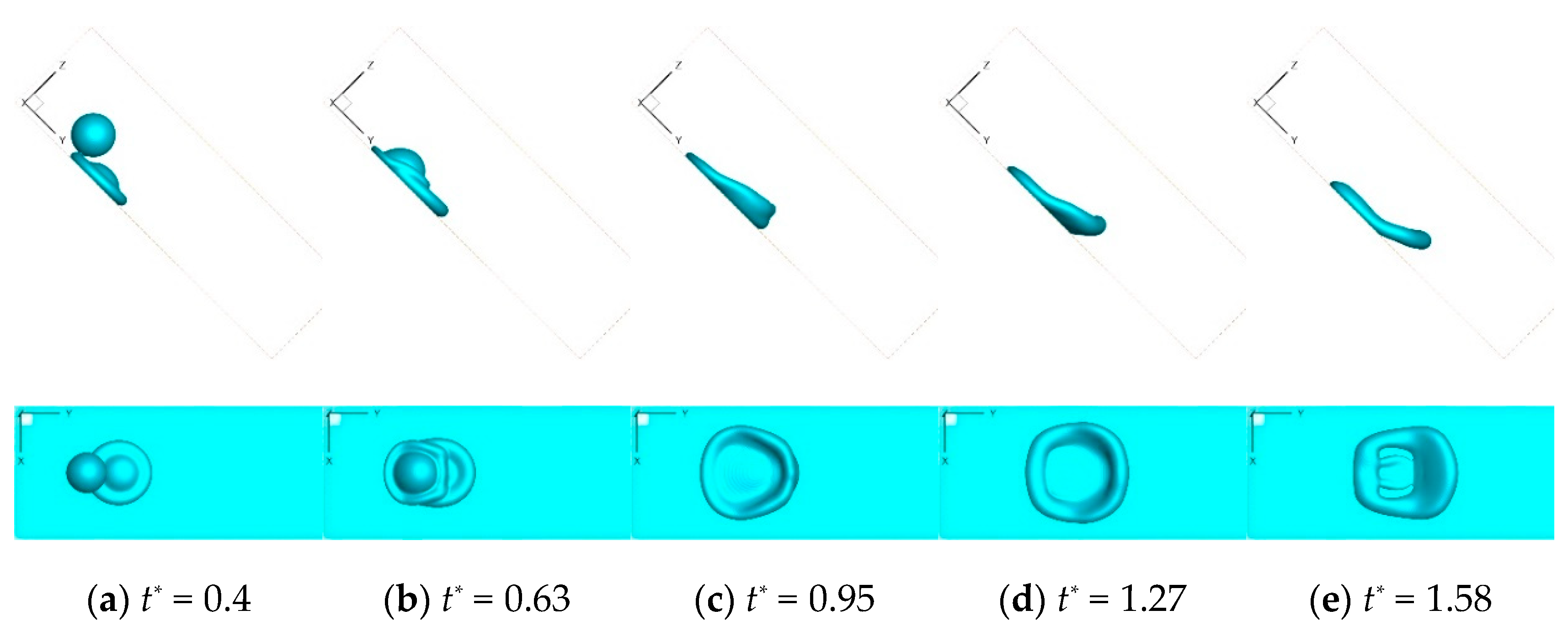
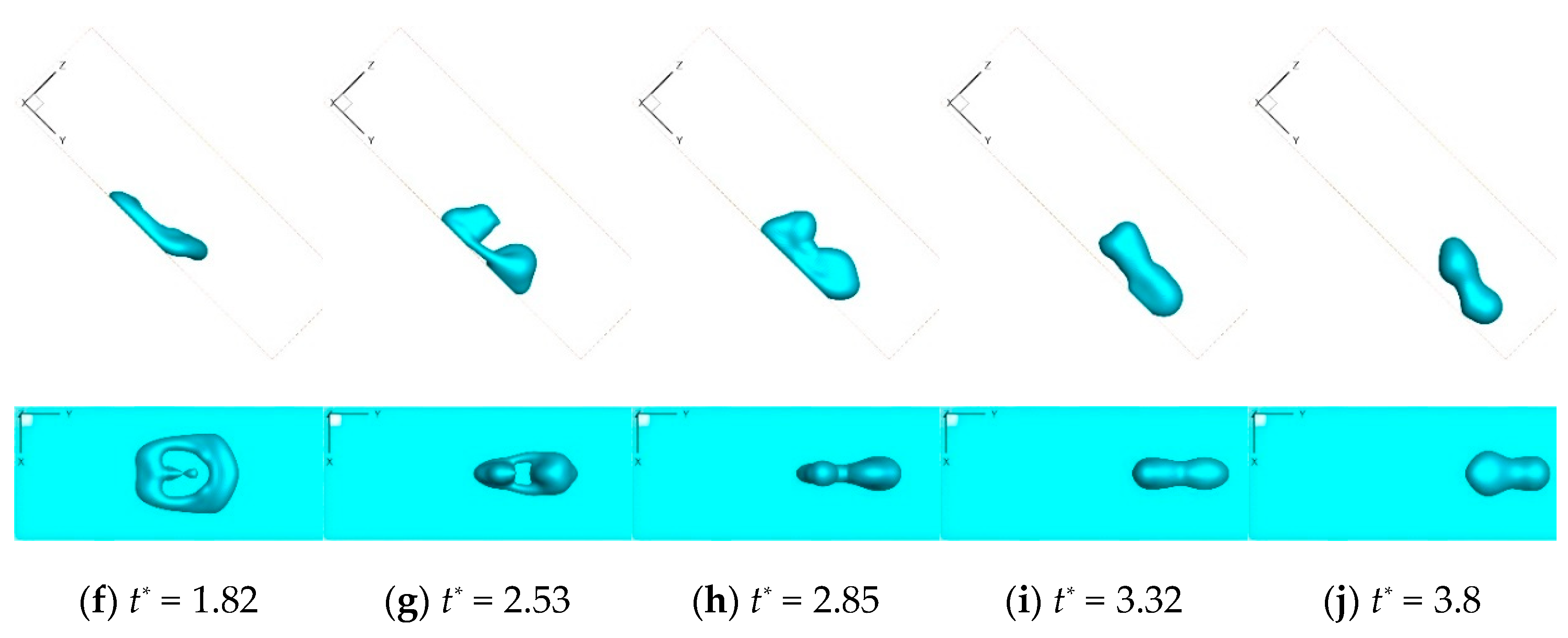
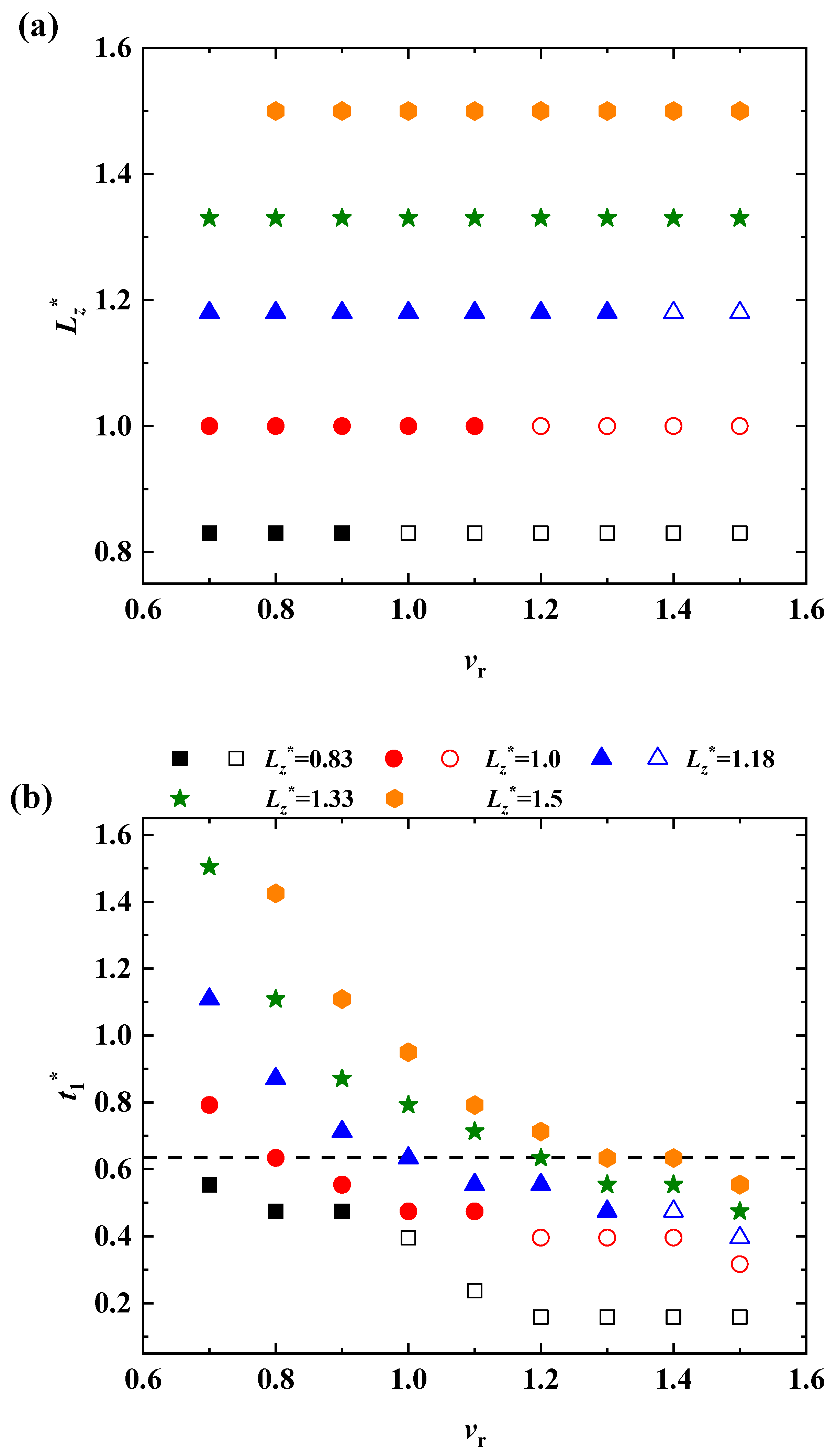
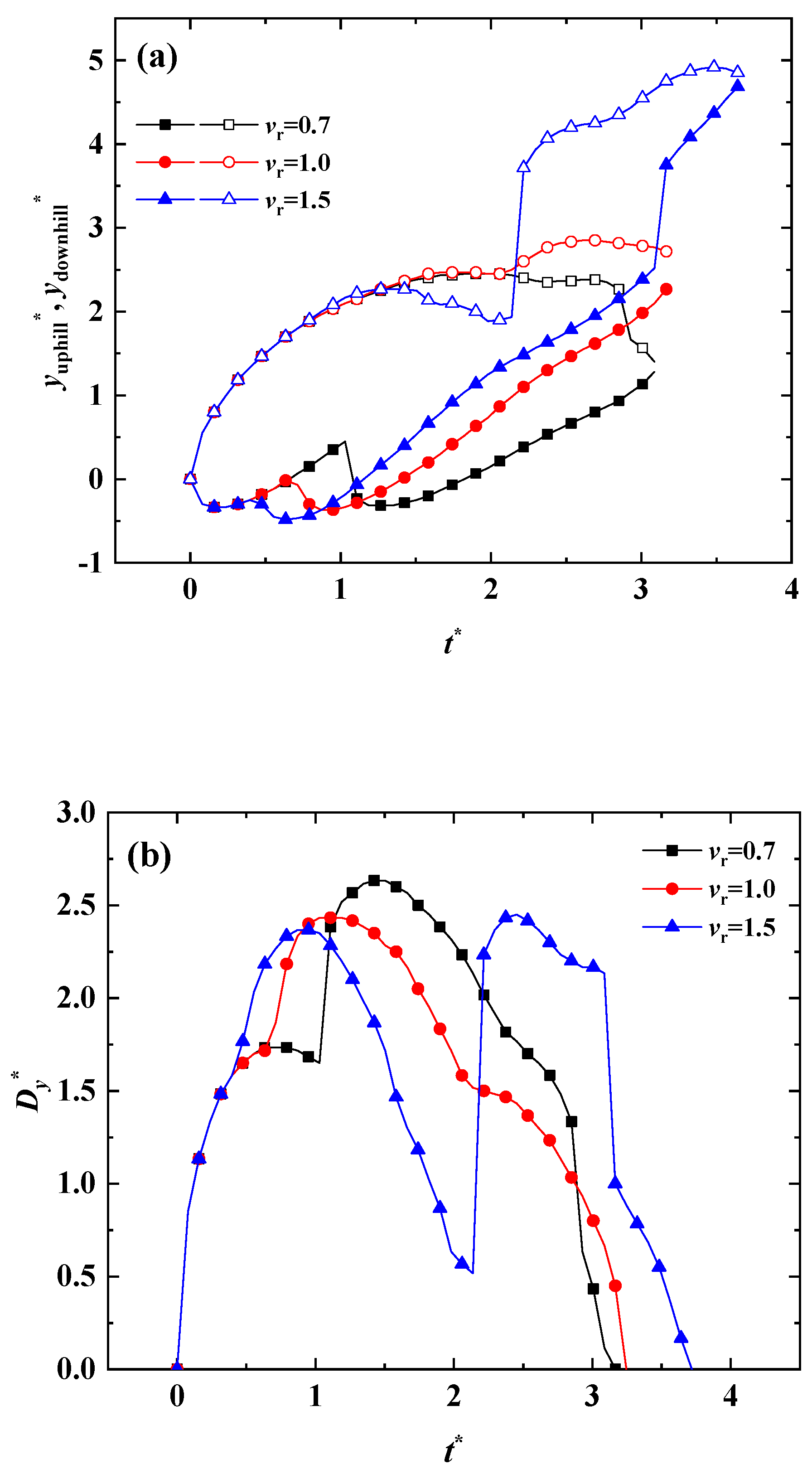
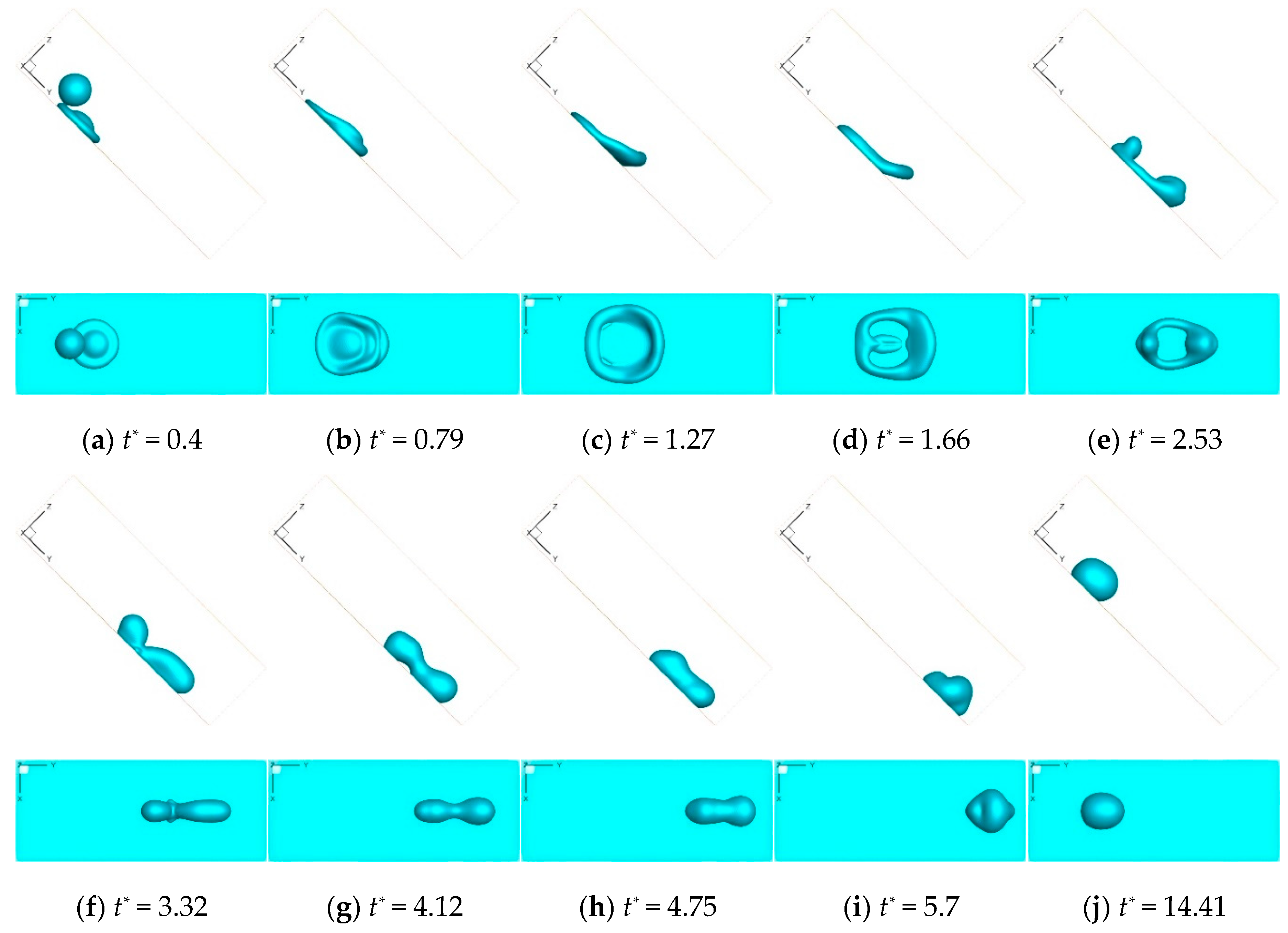
3.1. Effect of Velocity Ratio on Contact Time
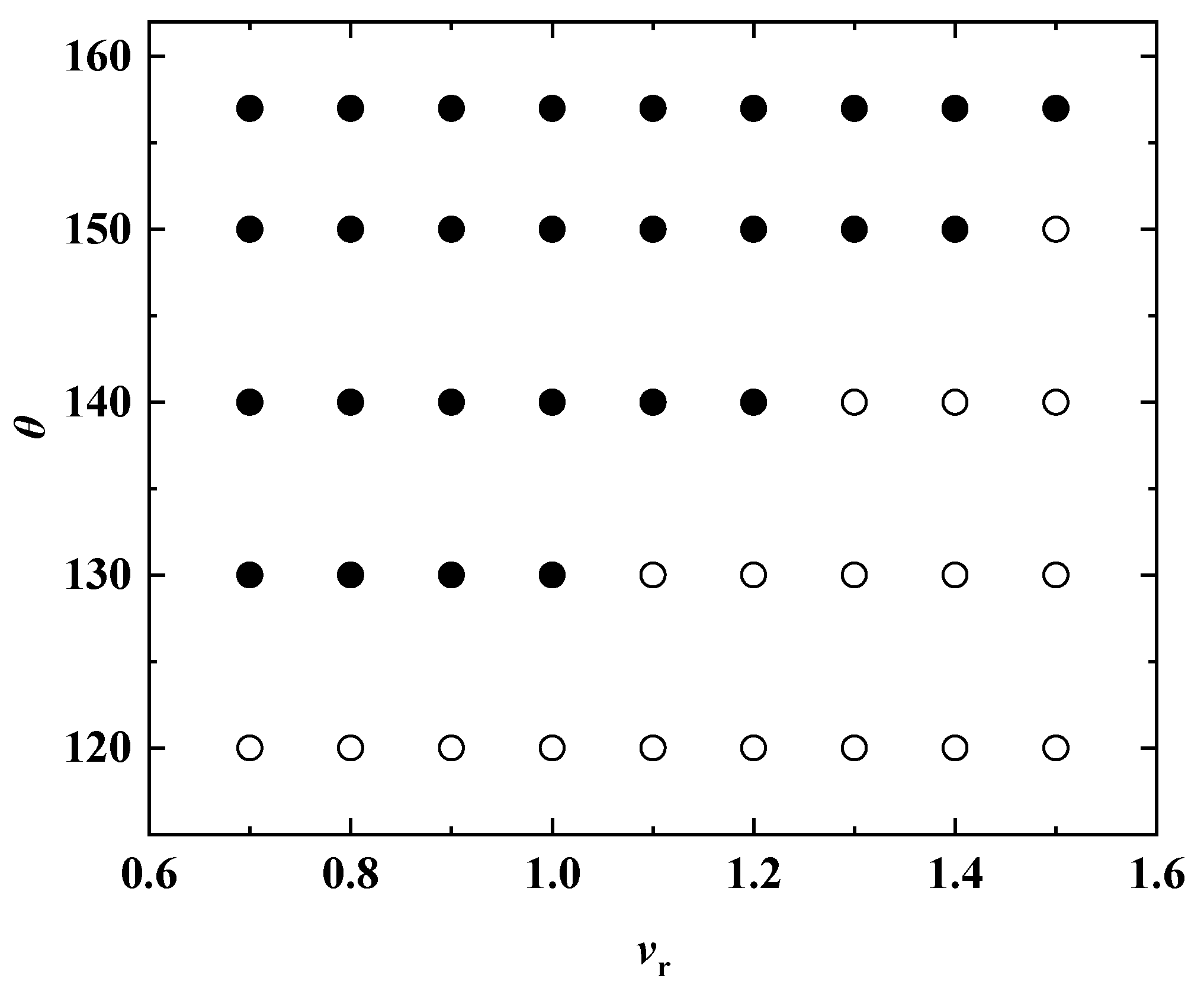
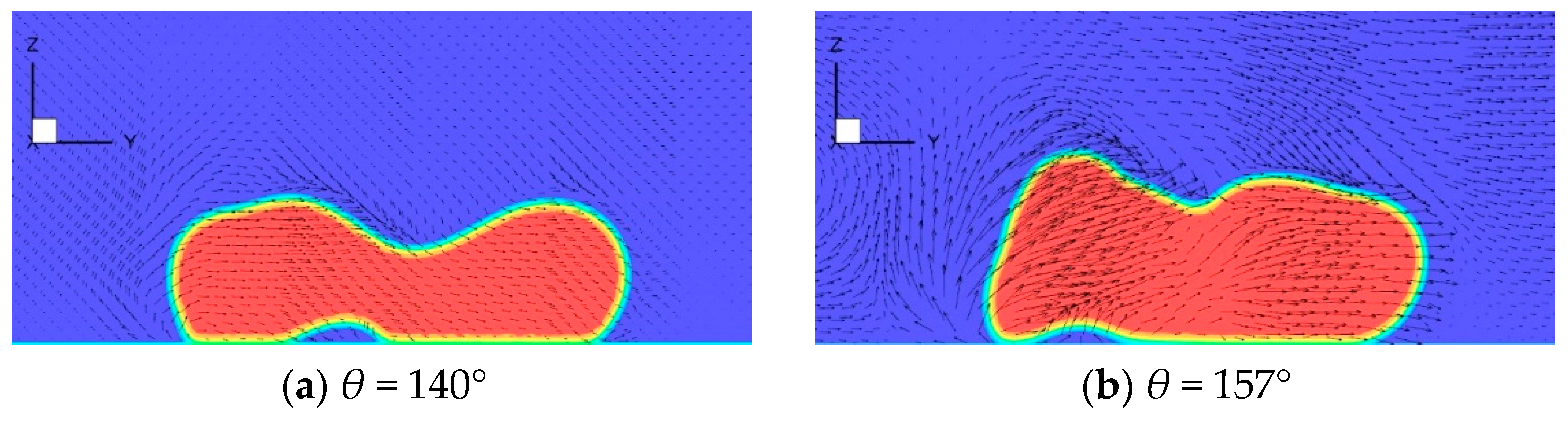
3.2. Outcome Map of Rebounding
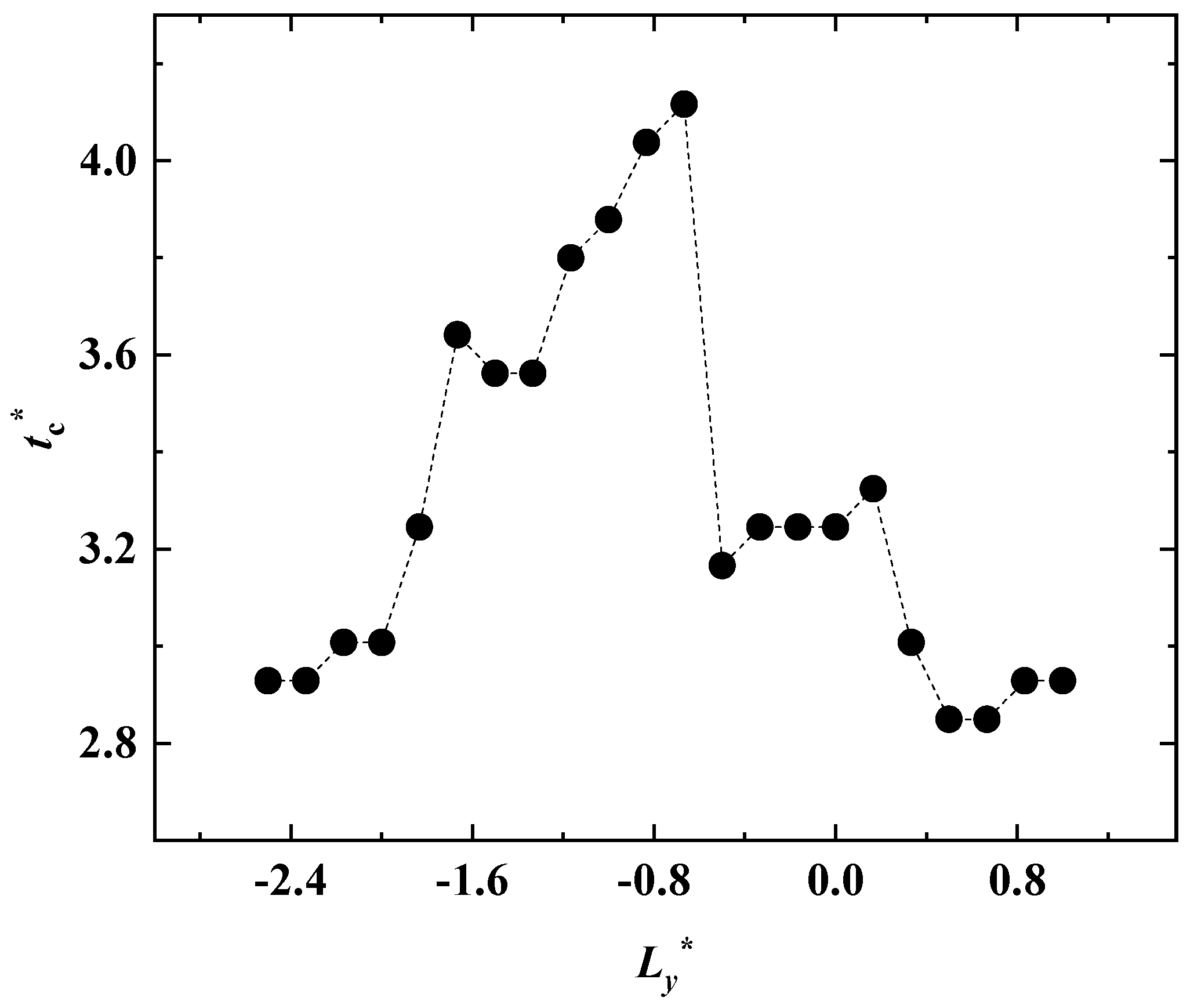
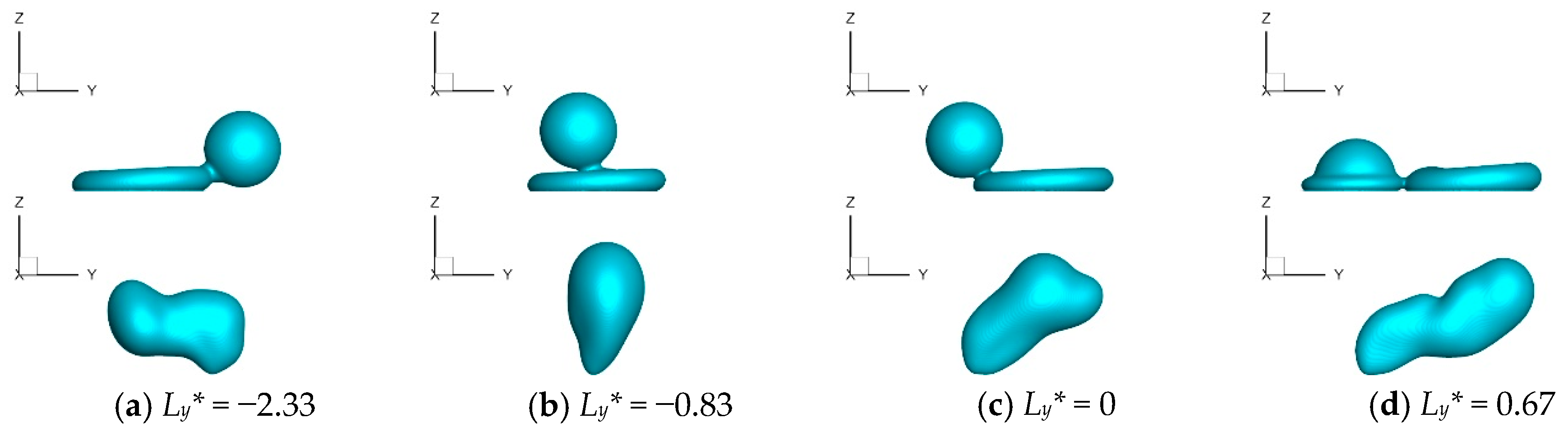
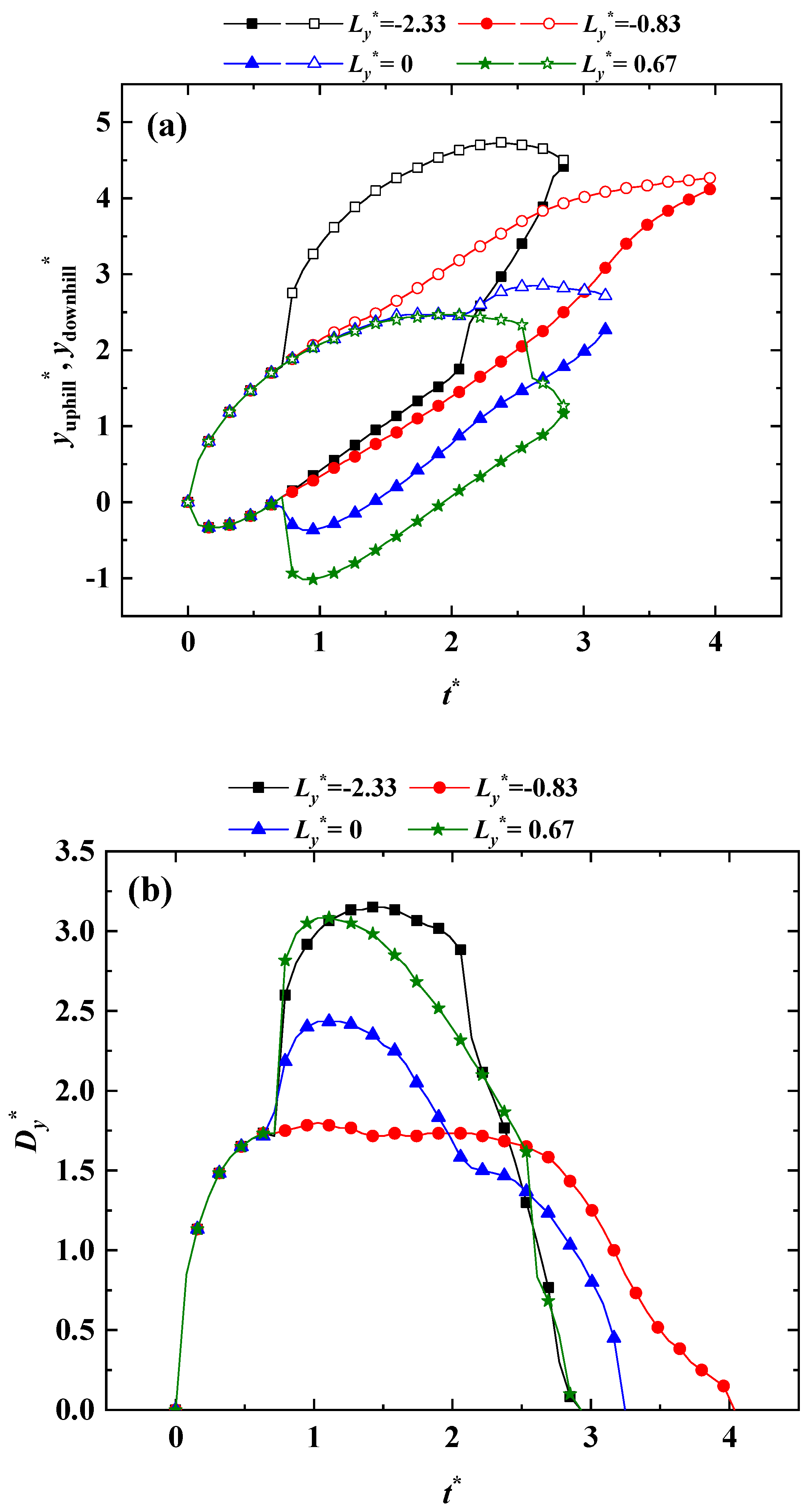
3.3. Effect of Length Between Impact Points on Contact Time
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodič, P.; Kapun, B.; Panjan, M.; Milošev, I. Easy and Fast Fabrication of Self-Cleaning and Anti-Icing Perfluoroalkyl Silane Film on Aluminium. Coatings 2020, 10, 234. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Liu, Y. Superhydrophobic Surface with Gamma Irradiation Resistance and Self-Cleaning Effect in Air and Oil. Coatings 2020, 10, 106. [Google Scholar] [CrossRef]
- Yoo, H.; Kim, C. Experimental studies on formation, spreading and drying of inkjet drop of colloidal suspensions. Colloids Surf. A Physicochem. Eng. Asp. 2015, 468, 234–245. [Google Scholar] [CrossRef]
- Zhao, X.; Yin, Z.; Zhang, B.; Yang, Z. Experimental investigation of surface temperature non-uniformity in spray cooling. Int. J. Heat Mass Transf. 2020, 146, 118819. [Google Scholar] [CrossRef]
- Kim, J. Spray cooling heat transfer: The state of the art. Int. J. Heat Fluid Flow 2007, 28, 753–767. [Google Scholar] [CrossRef]
- Khojasteh, D.; Kazerooni, M.; Salarian, S.; Kamali, R.; Kazerooni, N.M. Droplet impact on superhydrophobic surfaces: A review of recent developments. J. Ind. Eng. Chem. 2016, 42, 1–14. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys. Fluids 2012, 24, 102104. [Google Scholar] [CrossRef]
- Yarin, A. Drop impact dynamics: Splashing, Spreading, Receding, Bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; Betton, E.S.; Kubiak, K.; Wilson, M.C.T.; Hutchings, I.M. The dynamics of the impact and coalescence of droplets on a solid surface. Biomicrofluidics 2011, 5, 14112. [Google Scholar] [CrossRef]
- Fujimoto, H.; Ogino, T.; Takuda, H.; Hatta, N. Collision of a droplet with a hemispherical static droplet on a solid. Int. J. Multiph. Flow 2001, 27, 1227–1245. [Google Scholar] [CrossRef]
- Fujimoto, H.; Ito, S.; Takezaki, I. Experimental study of successive collision of two water droplets with a solid. Exp. Fluids 2002, 33, 500–502. [Google Scholar] [CrossRef]
- Raman, K.A.; Jaiman, R.K.; Lee, T.-S.; Low, H.-T. Lattice Boltzmann study on the dynamics of successive droplets impact on a solid surface. Chem. Eng. Sci. 2016, 145, 181–195. [Google Scholar] [CrossRef]
- Soltman, D.; Subramanian, V. Inkjet-Printed Line Morphologies and Temperature Control of the Coffee Ring Effect. Langmuir 2008, 24, 2224–2231. [Google Scholar] [CrossRef] [PubMed]
- Stringer, J.; Derby, B. Formation and Stability of Lines Produced by Inkjet Printing. Langmuir 2010, 26, 10365–10372. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhu, Y.; Cheng, X. Numerical investigation of multi-droplets deposited lines morphology with a multiple-relaxation-time lattice Boltzmann model. Chem. Eng. Sci. 2017, 171, 534–544. [Google Scholar] [CrossRef]
- Raman, K.A.; Jaiman, R.K.; Lee, T.-S.; Low, H.-T. Dynamics of simultaneously impinging drops on a dry surface: Role of impact velocity and air inertia. J. Colloid Interface Sci. 2017, 486, 265–276. [Google Scholar] [CrossRef]
- Ahmad, S.; Tang, H.; Yao, H. Oblique impact of two successive droplets on a flat surface. Int. J. Heat Mass Transf. 2018, 119, 433–445. [Google Scholar] [CrossRef]
- Graham, P.J.; Farhangi, M.M.; Dolatabadi, A. Dynamics of droplet coalescence in response to increasing hydrophobicity. Phys. Fluids 2012, 24, 112105. [Google Scholar] [CrossRef]
- Damak, M.; Varanasi, K.K. Expansion and retraction dynamics in drop-on-drop impacts on nonwetting surfaces. Phys. Rev. Fluids 2018, 3, 093602. [Google Scholar] [CrossRef]
- Yuan, Z.P.; Wu, X.M.; Hu, Z.F. Rotation of a rebounding-coalescing droplet on a superhydrophobic surface. Phys. Fluids 2019, 31, 062109. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Wang, K.; Liu, H.; Shen, S. Numerical study on dynamic characteristics of double droplets impacting a super-hydrophobic tube with different impact velocities. Int. J. Comput. Fluid Dyn. 2019, 33, 222–233. [Google Scholar] [CrossRef]
- Farhangi, M.M.; Graham, P.J.; Choudhury, N.R.; Dolatabadi, A. Induced Detachment of Coalescing Droplets on Superhydrophobic Surfaces. Langmuir 2012, 28, 1290–1303. [Google Scholar] [CrossRef] [PubMed]
- Mitra, S.; Sathe, M.J.; Doroodchi, E.; Utikar, R.; Shah, M.; Pareek, V.; Joshi, J.B.; Evans, G.M. Droplet impact dynamics on a spherical particle. Chem. Eng. Sci. 2013, 100, 105–119. [Google Scholar] [CrossRef]
- Malgarinos, I.; Nikolopoulos, N.; Gavaises, M. A numerical study on droplet-particle collision dynamics. Int. J. Heat Fluid Flow 2016, 61, 499–509. [Google Scholar] [CrossRef]
- Malgarinos, I.; Nikolopoulos, N.; Gavaises, M. Numerical investigation of heavy fuel droplet-particle collisions in the injection zone of a Fluid Catalytic Cracking reactor, Part I: Numerical model and 2D simulations. Fuel Process. Technol. 2017, 156, 317–330. [Google Scholar] [CrossRef]
- Malgarinos, I.; Nikolopoulos, N.; Gavaises, M. Numerical investigation of heavy fuel droplet-particle collisions in the injection zone of a Fluid Catalytic Cracking reactor, part II: 3D simulations. Fuel Process. Technol. 2017, 156, 43–53. [Google Scholar] [CrossRef]
- Mitra, S.; Evans, G. Dynamic Surface Wetting and Heat Transfer in a Droplet-Particle System of Less Than Unity Size Ratio. Front. Chem. 2018, 6, 259. [Google Scholar] [CrossRef]
- Liu, Y.; Moevius, L.; Xu, X.; Qian, T.; Yeomans, J.M.; Wang, Z. Pancake bouncing on superhydrophobic surfaces. Nat. Phys. 2014, 10, 515–519. [Google Scholar] [CrossRef]
- Regulagadda, K.; Bakshi, S.; Das, S.K. Morphology of drop impact on a superhydrophobic surface with macro-structures. Phys. Fluids 2017, 29, 82104. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Zhan, H.; Liu, Y. Droplet Asymmetric Bouncing on Inclined Superhydrophobic Surfaces. ACS Omega 2019, 4, 12238–12243. [Google Scholar] [CrossRef] [PubMed]
- Aboud, D.G.K.; Kietzig, A.-M. On the Oblique Impact Dynamics of Drops on Superhydrophobic Surfaces. Part I: Sliding Length and Maximum Spreading Diameter. Langmuir 2018, 34, 9879–9888. [Google Scholar] [CrossRef] [PubMed]
- Aboud, D.G.K.; Kietzig, A.-M. On the Oblique Impact Dynamics of Drops on Superhydrophobic Surfaces. Part II: Restitution Coefficient and Contact Time. Langmuir 2018, 34, 9889–9896. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. EPL Europhysics Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Zheng, S.; Eimann, F.; Philipp, C.; Fieback, T.; Gross, U. Single droplet condensation in presence of non-condensable gas by a multi-component multi-phase thermal lattice Boltzmann model. Int. J. Heat Mass Transf. 2019, 139, 254–268. [Google Scholar] [CrossRef]
- Zheng, S.; Eimann, F.; Fieback, T.; Xie, G.; Gross, U. Numerical investigation of convective dropwise condensation flow by a hybrid thermal lattice Boltzmann method. Appl. Therm. Eng. 2018, 145, 590–602. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.; He, Y.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef]
- Mohamad, A.A. The Boltzmann Equation. In Lattice Boltzmann Method; Springer: London, UK, 2011; Volume 70, pp. 23–24. [Google Scholar]
- Zhang, D.; Papadikis, K.; Gu, S. Three-dimensional multi-relaxation time lattice-Boltzmann model for the drop impact on a dry surface at large density ratio. Int. J. Multiph. Flow 2014, 64, 11–18. [Google Scholar] [CrossRef]
- Shi, Y.; Tang, G.; Xia, H. Investigation of coalescence-induced droplet jumping on superhydrophobic surfaces and liquid condensate adhesion on slit and plain fins. Int. J. Heat Mass Transf. 2015, 88, 445–455. [Google Scholar] [CrossRef]
- Lin, D.-J.; Wang, L.; Wang, X.-D.; Yan, W.-M. Reduction in the contact time of impacting droplets by decorating a rectangular ridge on superhydrophobic surfaces. Int. J. Heat Mass Transf. 2019, 132, 1105–1115. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Li, X.J. Lattice Boltzmann modeling of multiphase flows at large density ratio with an improved pseudopotential model. Phys. Rev. E 2013, 87, 053301. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 42101. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Zhang, D.; Papadikis, K.; Gu, S. Application of a high density ratio lattice-Boltzmann model for the droplet impingement on flat and spherical surfaces. Int. J. Therm. Sci. 2014, 84, 75–85. [Google Scholar] [CrossRef]
- Gu, X.; Gupta, A.; Kumar, R. Lattice Boltzmann Simulation of Surface Impingement at High-Density Ratio. J. Thermophys. Heat Transf. 2009, 23, 773–785. [Google Scholar] [CrossRef]
- Caviezel, D.; Narayanan, C.; Lakehal, D. Adherence and bouncing of liquid droplets impacting on dry surfaces. Microfluid. Nanofluidics 2008, 5, 469–478. [Google Scholar] [CrossRef]


| Case | Ly* | Lz* | vr | θ0 |
|---|---|---|---|---|
| Section 3.1 | 0 | 0.83 | 0.7~1.5 | 157° |
| Section 3.1 | 0 | 1.0 | 0.7~1.5 | 157° |
| Section 3.1 | 0 | 1.18 | 0.7~1.5 | 157° |
| Section 3.1 | 0 | 1.33 | 0.7~1.5 | 157° |
| Section 3.1 | 0 | 1.5 | 0.8~1.5 | 157° |
| Section 3.2 | 0 | 1.18 | 0.7~1.5 | 120°~157° |
| Section 3.3 | −2.5~1 | 1.18 | 1.0 | 157° |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.-J.; Zhang, L.-Z.; Yi, M.-C.; Wang, X.; Gao, S.-R.; Yang, Y.-R.; Wang, X.-D. Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface. Coatings 2020, 10, 592. https://doi.org/10.3390/coatings10060592
Lin D-J, Zhang L-Z, Yi M-C, Wang X, Gao S-R, Yang Y-R, Wang X-D. Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface. Coatings. 2020; 10(6):592. https://doi.org/10.3390/coatings10060592
Chicago/Turabian StyleLin, Dian-Ji, Ling-Zhe Zhang, Meng-Chao Yi, Xin Wang, Shu-Rong Gao, Yan-Ru Yang, and Xiao-Dong Wang. 2020. "Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface" Coatings 10, no. 6: 592. https://doi.org/10.3390/coatings10060592
APA StyleLin, D.-J., Zhang, L.-Z., Yi, M.-C., Wang, X., Gao, S.-R., Yang, Y.-R., & Wang, X.-D. (2020). Rebound Dynamics of Two Droplets Successively Impacting an Inclined Surface. Coatings, 10(6), 592. https://doi.org/10.3390/coatings10060592