Numerical Modeling of Gentamicin Transport in Agricultural Soils: Implications for Environmental Pollution
Abstract
1. Introduction
2. Results and Discussion
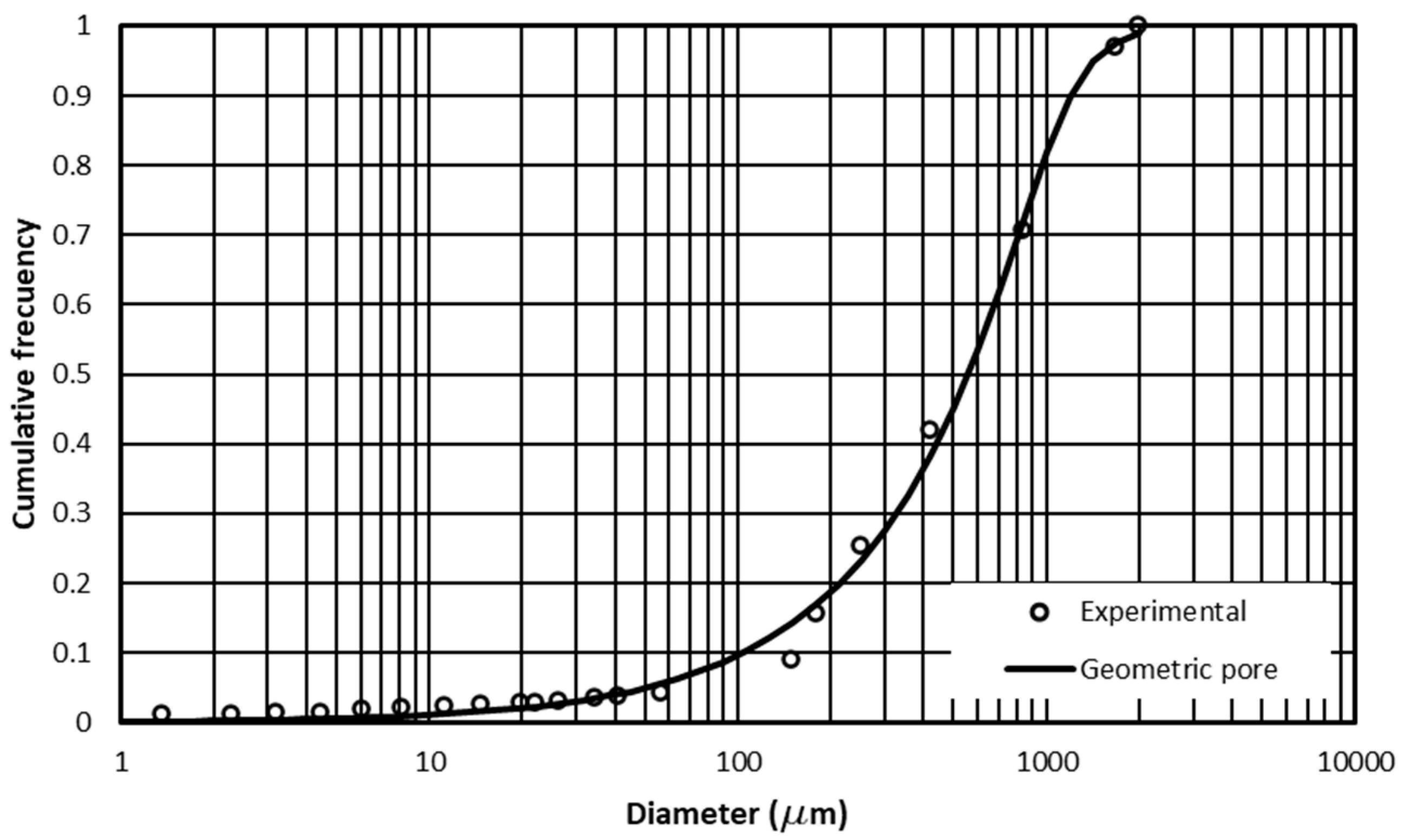
2.1. Retention Curve and Granulometric Curve Parameters
2.2. Infiltration Tests
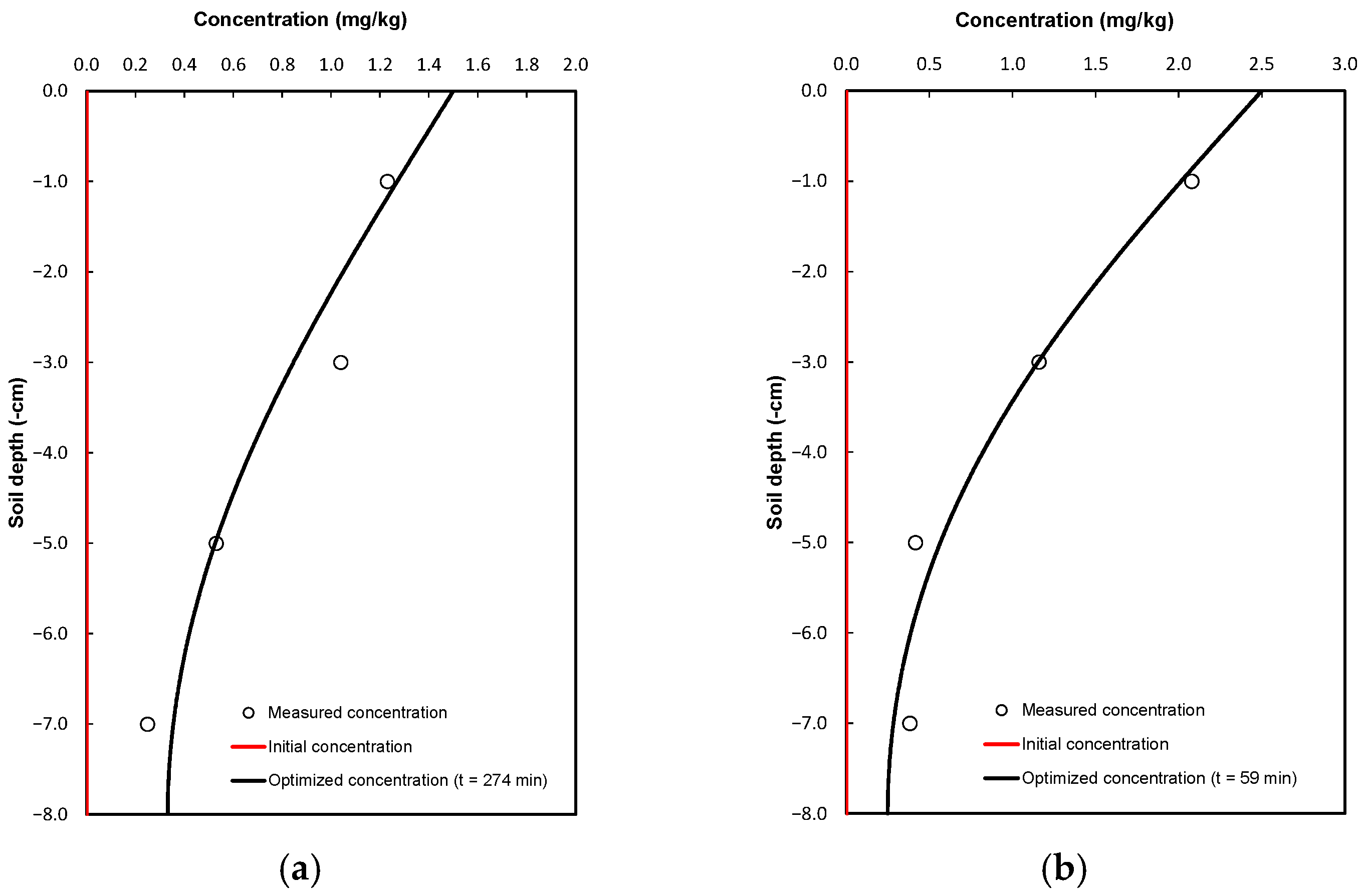
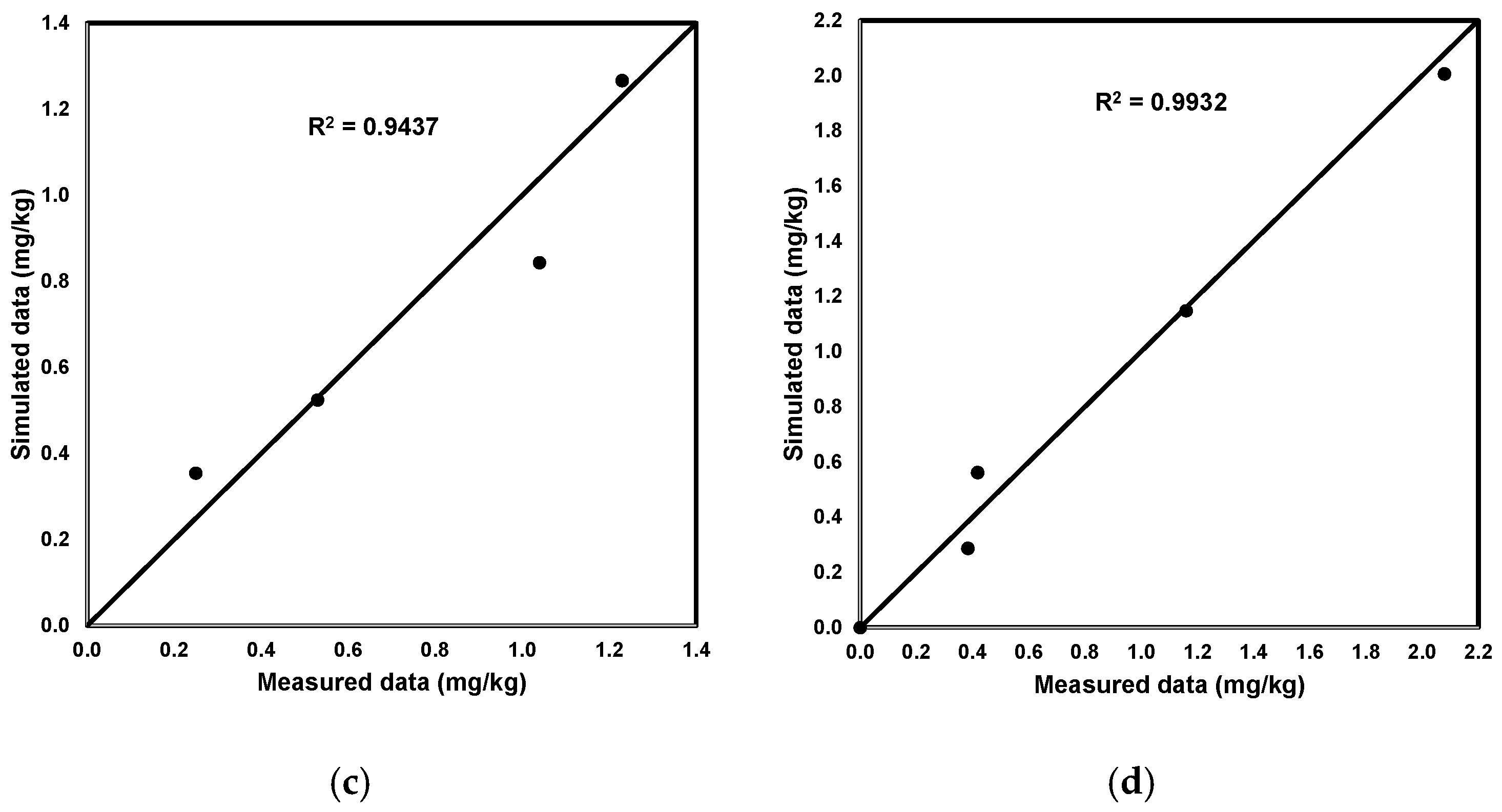
2.3. The Transport Process and the Chemical Parameters of the Soil
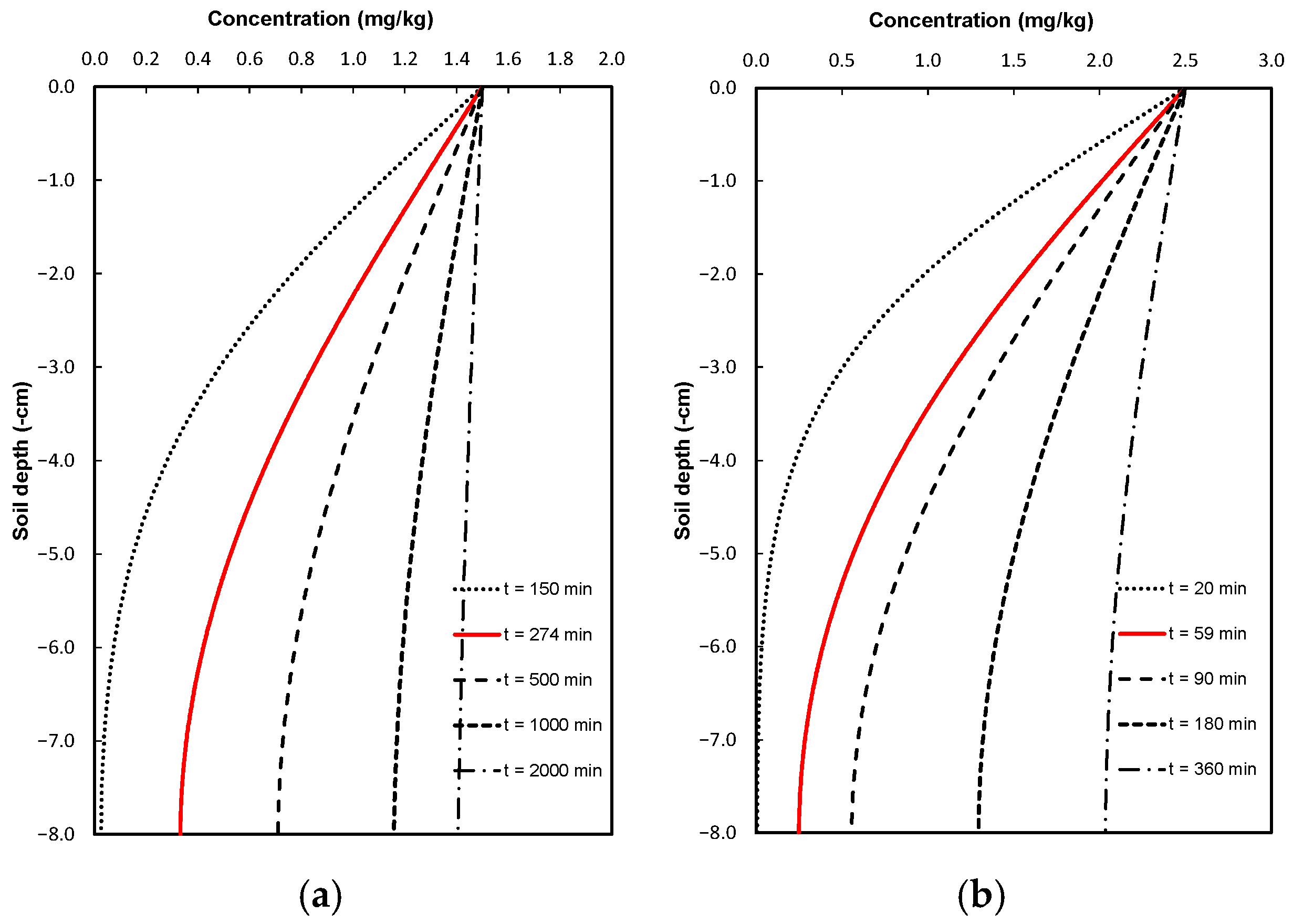
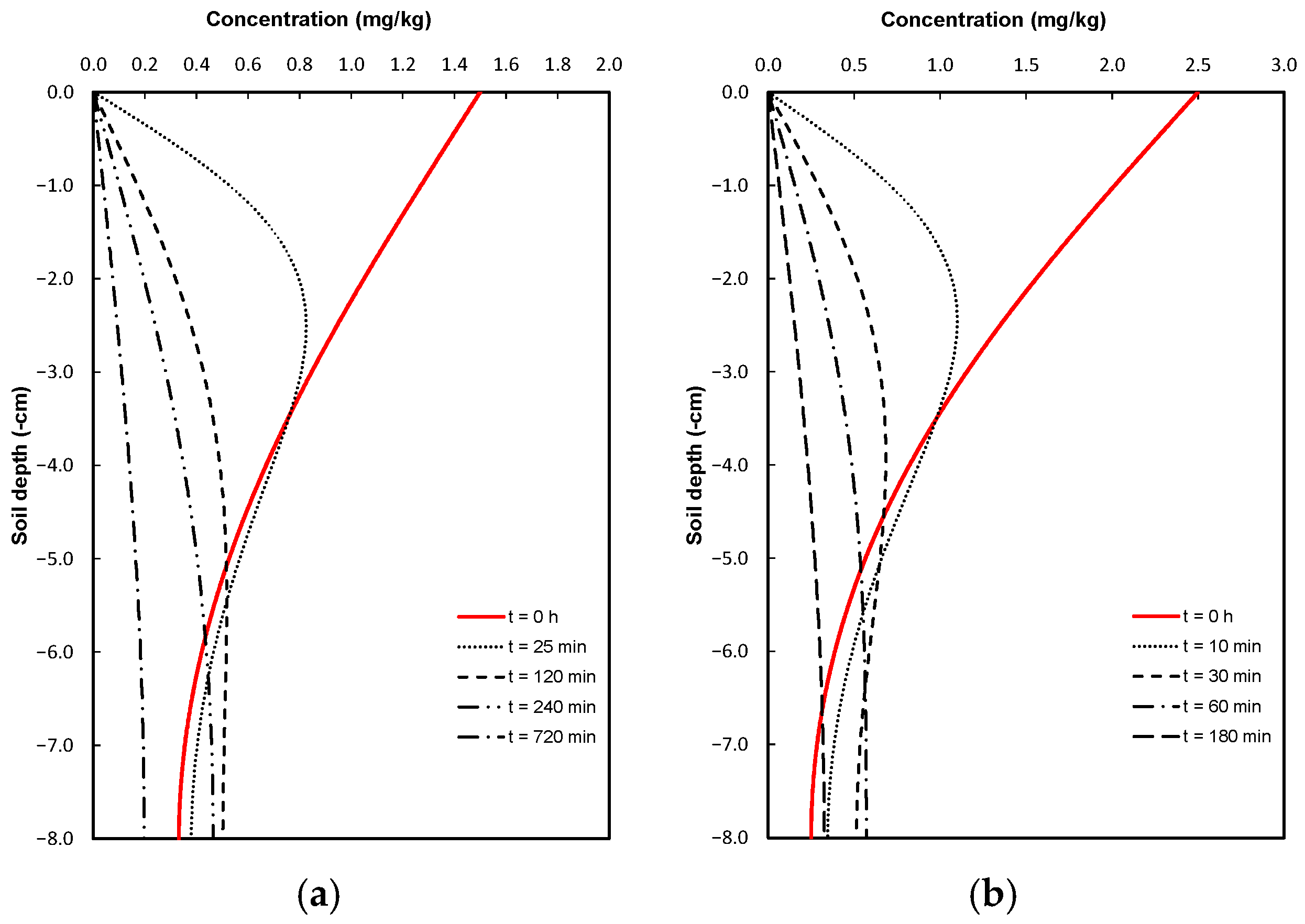
2.4. Simulation Scenarios
3. Discussion
4. Materials and Methods
4.1. Transference Model
4.2. Transport Model
4.3. Characteristics of the Gentamicin Used in the Experiment
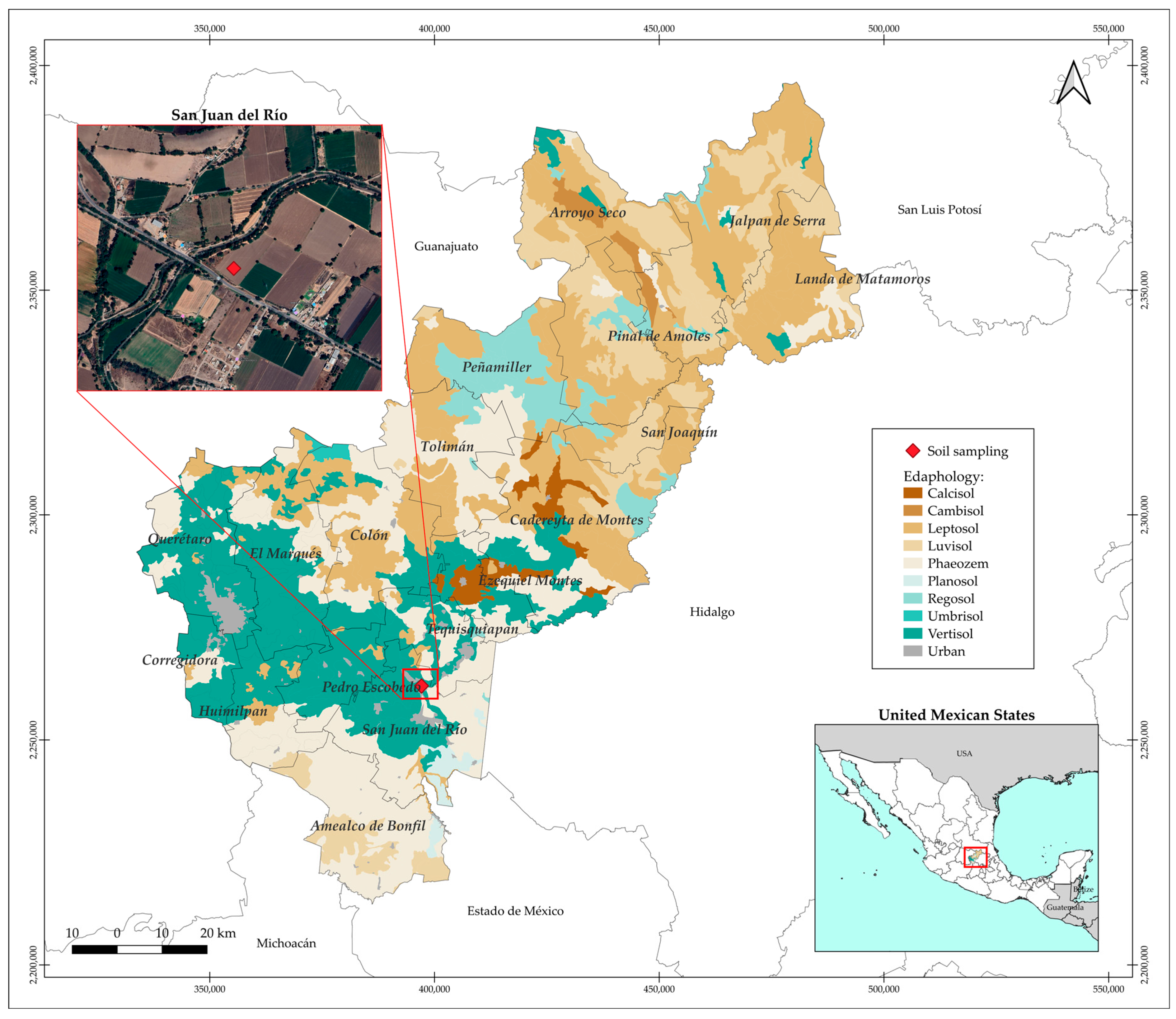
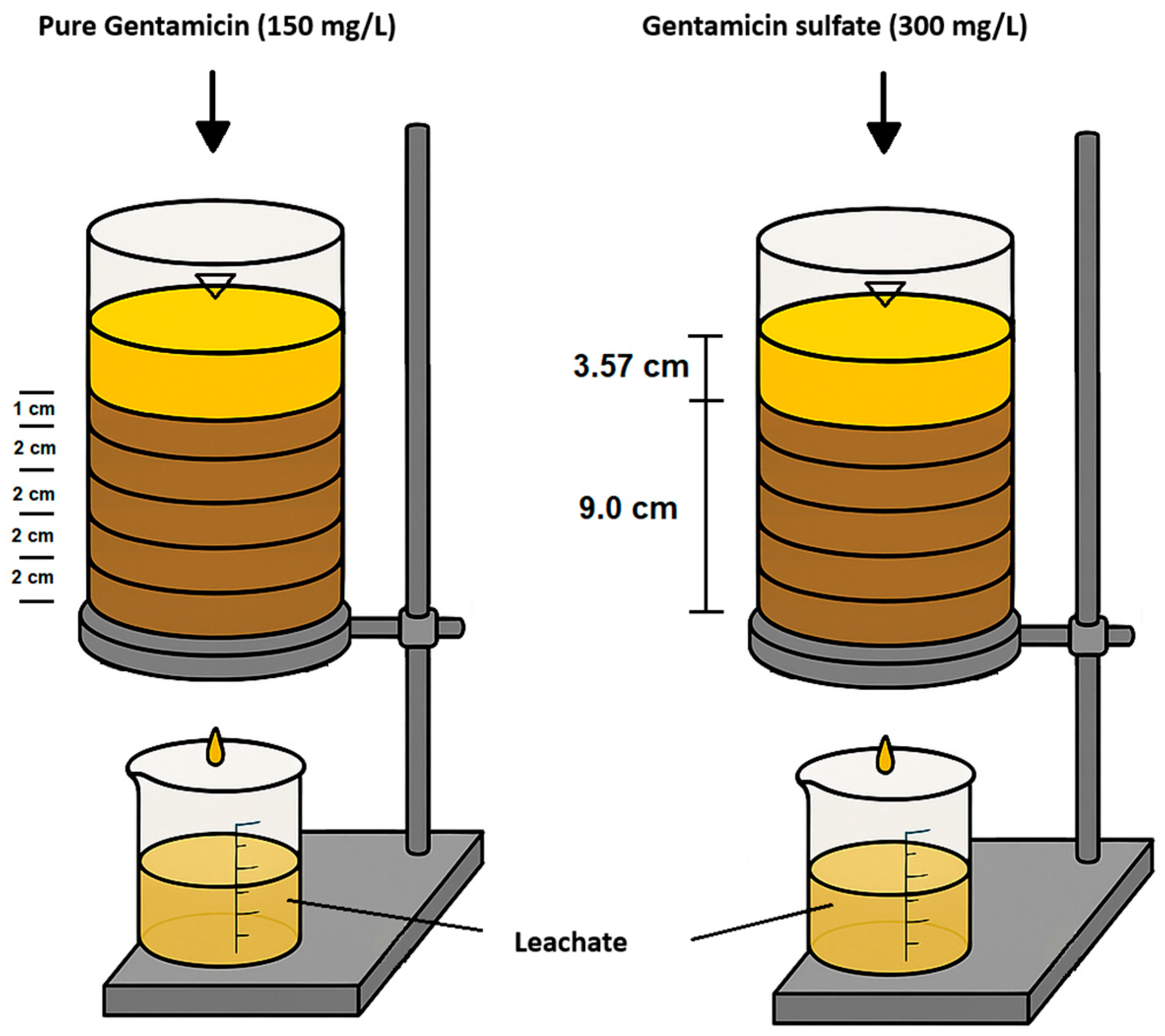
4.4. Experiment
4.5. Determination of Gentamicin Concentration in Soil
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Boeckel, T.P.; Brower, C.; Gilbert, M.; Grenfell, B.T.; Levin, S.A.; Robinson, T.P.; Teillant, A.; Laxminarayan, R. Global Trends in Antimicrobial Use in Food Animals. Proc. Natl. Acad. Sci. USA 2015, 112, 5649–5654. [Google Scholar] [CrossRef]
- Gogoi, A.; Mazumder, P.; Tyagi, V.K.; Tushara Chaminda, G.G.; An, A.K.; Kumar, M. Occurrence and Fate of Emerging Contaminants in Water Environment: A Review. Groundw. Sustain. Dev. 2018, 6, 169–180. [Google Scholar] [CrossRef]
- Massey, L.B.; Haggard, B.E.; Galloway, J.M.; Loftin, K.A.; Meyer, M.T.; Green, W.R. Antibiotic Fate and Transport in Three Effluent-Dominated Ozark Streams. Ecol. Eng. 2010, 36, 930–938. [Google Scholar] [CrossRef]
- Li, S.; Shi, W.; Li, H.; Xu, N.; Zhang, R.; Chen, X.; Sun, W.; Wen, D.; He, S.; Pan, J.; et al. Antibiotics in Water and Sediments of Rivers and Coastal Area of Zhuhai City, Pearl River Estuary, South China. Sci. Total Environ. 2018, 636, 1009–1019. [Google Scholar] [CrossRef]
- Nemergut, D.R.; Schmidt, S.K.; Fukami, T.; O’Neill, S.P.; Bilinski, T.M.; Stanish, L.F.; Knelman, J.E.; Darcy, J.L.; Lynch, R.C.; Wickey, P.; et al. Patterns and Processes of Microbial Community Assembly. Microbiol. Mol. Biol. Rev. 2013, 77, 342–356. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chi, Y.; Song, S. Important Soil Microbiota’s Effects on Plants and Soils: A Comprehensive 30-Year Systematic Literature Review. Front. Microbiol. 2024, 15, 1347745. [Google Scholar] [CrossRef]
- Pepper, I.L.; Gerba, C.P.; Gentry, T.J. (Eds.) Environmental Microbiology, 3rd ed.; Academic Press: San Diego, CA, USA, 2015; ISBN 978-0-12-394626-3. [Google Scholar]
- Bayranvand, M.; Akbarinia, M.; Salehi Jouzani, G.; Gharechahi, J.; Kooch, Y.; Baldrian, P. Composition of Soil Bacterial and Fungal Communities in Relation to Vegetation Composition and Soil Characteristics along an Altitudinal Gradient. FEMS Microbiol. Ecol. 2021, 97, fiaa201. [Google Scholar] [CrossRef] [PubMed]
- Batuman, O.; Britt-Ugartemendia, K.; Kunwar, S.; Yilmaz, S.; Fessler, L.; Redondo, A.; Chumachenko, K.; Chakravarty, S.; Wade, T. The Use and Impact of Antibiotics in Plant Agriculture: A Review. Phytopathology 2024, 114, 885–909. [Google Scholar] [CrossRef] [PubMed]
- Coates, J.; Bostick, K.J.; Jones, B.A.; Caston, N.; Ayalew, M. What Is the Impact of Aminoglycoside Exposure on Soil and Plant Root-Associated Microbiota? A Systematic Review Protocol. Environ. Evid. 2022, 11, 18. [Google Scholar] [CrossRef]
- Sanchez-Cid, C.; Guironnet, A.; Wiest, L.; Vulliet, E.; Vogel, T.M. Gentamicin Adsorption onto Soil Particles Prevents Overall Short-Term Effects on the Soil Microbiome and Resistome. Antibiotics 2021, 10, 191. [Google Scholar] [CrossRef]
- Cycoń, M.; Mrozik, A.; Piotrowska-Seget, Z. Antibiotics in the Soil Environment—Degradation and Their Impact on Microbial Activity and Diversity. Front. Microbiol. 2019, 10, 338. [Google Scholar] [CrossRef]
- Le-Minh, N.; Khan, S.J.; Drewes, J.E.; Stuetz, R.M. Fate of Antibiotics during Municipal Water Recycling Treatment Processes. Water Res. 2010, 44, 4295–4323. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Cid, C.; Guironnet, A.; Keuschnig, C.; Wiest, L.; Vulliet, E.; Vogel, T.M. Gentamicin at Sub-Inhibitory Concentrations Selects for Antibiotic Resistance in the Environment. ISME Commun. 2022, 2, 29. [Google Scholar] [CrossRef] [PubMed]
- Bassil, R.J.; Bashour, I.I.; Sleiman, F.T.; Abou-Jawdeh, Y.A. Antibiotic Uptake by Plants from Manure-Amended Soils. J. Environ. Sci. Health B 2013, 48, 570–574. [Google Scholar] [CrossRef]
- Miller, S.A.; Ferreira, J.P.; LeJeune, J.T. Antimicrobial Use and Resistance in Plant Agriculture: A One Health Perspective. Agriculture 2022, 12, 289. [Google Scholar] [CrossRef]
- Kushner, B.; Allen, P.D.; Crane, B.T. Frequency and Demographics of Gentamicin Use. Otol. Neurotol. 2016, 37, 190–195. [Google Scholar] [CrossRef]
- National Center for Biotechnology Information PubChem Compound Summary for Gentamicin Sulfate. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Gentamicin-Sulfate (accessed on 13 March 2025).
- Barrios, R.E.; Bartelt-Hunt, S.L.; Li, Y.; Li, X. Modeling the Vertical Transport of Antibiotic Resistance Genes in Agricultural Soils Following Manure Application. Environ. Pollut. 2021, 285, 117480. [Google Scholar] [CrossRef]
- Tong, X.; Mohapatra, S.; Zhang, J.; Tran, N.H.; You, L.; He, Y.; Gin, K.Y.-H. Source, Fate, Transport and Modelling of Selected Emerging Contaminants in the Aquatic Environment: Current Status and Future Perspectives. Water Res. 2022, 217, 118418. [Google Scholar] [CrossRef]
- Zheng, C.; Bennett, G.D. Applied Contaminant Transport Modeling; Wiley-Interscience: New York, NY, USA, 2002; Volume 2. [Google Scholar]
- Jamal, M.S.; Awotunde, A.A.; Al-Kobaisi, M.S.; Al-Yousef, H.Y.; Sadeed, A.; Patil, S. Interwell Simulation Model for the Advection Dispersion Equation. Comput. Geosci. 2023, 171, 105283. [Google Scholar] [CrossRef]
- Fuentes, S.; Trejo-Alonso, J.; Quevedo, A.; Fuentes, C.; Chávez, C. Modeling Soil Water Redistribution under Gravity Irrigation with the Richards Equation. Mathematics 2020, 8, 1581. [Google Scholar] [CrossRef]
- Chen, J.-S.; Chen, J.-T.; Liu, C.-W.; Liang, C.-P.; Lin, C.-W. Analytical Solutions to Two-Dimensional Advection–Dispersion Equation in Cylindrical Coordinates in Finite Domain Subject to First- and Third-Type Inlet Boundary Conditions. J. Hydrol. 2011, 405, 522–531. [Google Scholar] [CrossRef]
- Moranda, A.; Cianci, R.; Paladino, O. Analytical Solutions of One-Dimensional Contaminant Transport in Soils with Source Production-Decay. Soil Syst. 2018, 2, 40. [Google Scholar] [CrossRef]
- Fuentes, S.; Chávez, C.; Brambila-Paz, F.; Trejo-Alonso, J. Hydrodynamic Border Irrigation Model: Comparison of Infiltration Equations. Water 2022, 14, 2111. [Google Scholar] [CrossRef]
- Morales-Durán, N.; Fuentes, S.; Chávez, C. A Soil Database from Queretaro, Mexico for Assessment of Crop and Irrigation Water Requirements. Sci. Data 2023, 10, 429. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating Two-and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media. Tech. Man. Version 2006, 1, 241. [Google Scholar]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Mertz, S.; Devau, N.; Thouin, H.; Battaglia-Brunet, F.; Norini, M.-P.; Crampon, M.; Le Forestier, L. Leaching of Pollutant Metals (Pb, Zn) from Abandoned Mine Tailings: A Multicomponent Reactive Transport Model of a Pilot-Scale Experiment. Sci. Total Environ. 2025, 960, 178248. [Google Scholar] [CrossRef]
- Kamil, H.; Soulaïmani, A.; Beljadid, A. A Comparative Study of Physics-Informed Neural Network Strategies for Modeling Water and Nitrogen Transport in Unsaturated Soils. J. Hydrol. 2025, 661, 133624. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Jia, X.; Zhu, Y.; Shao, M.; Binley, A. A Comparative Study of Conceptual Model Complexity to Describe Water Flow and Nitrate Transport in Deep Unsaturated Loess. Water Resour. Res. 2021, 57, e2020WR029250. [Google Scholar] [CrossRef]
- Wehbe, S.; Zewge, F.; Inagaki, Y.; Sievert, W.; Nutakki, T.U.K.; Deshpande, A. A Mechanistic Model for Simulation of Carbendazim and Chlorothalonil Transport through a Two-Stage Vertical Flow Constructed Wetland. Water 2023, 16, 142. [Google Scholar] [CrossRef]
- Fuentes, C.; Brambila-Paz, F.; Haverkamp, R. Soil Hydrodynamic Characteristics. In Gravity Irrigation; National Association of Irrigation Specialists: Mexico City, Mexico, 2017; pp. 67–150. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Fuentes, S.; Fuentes, C.; Chávez, C. Parameter Optimization of Green and Ampt Equation Using a Nonlinear Algorithm. INAGBI 2022, 14, 47–63. [Google Scholar] [CrossRef]
- Haverkamp, R.; Leij, F.J.; Fuentes, C.; Sciortino, A.; Ross, P.J. Soil Water Retention: I. Introduction of a Shape Index. Soil Sci. Soc. Am. J. 2005, 69, 1881–1890. [Google Scholar] [CrossRef]
- Samreen; Ahmad, I.; Malak, H.A.; Abulreesh, H.H. Environmental Antimicrobial Resistance and Its Drivers: A Potential Threat to Public Health. J. Glob. Antimicrob. Resist. 2021, 27, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Sambaza, S.S.; Naicker, N. Contribution of Wastewater to Antimicrobial Resistance: A Review Article. J. Glob. Antimicrob. Resist. 2023, 34, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Fu, Y.-H.; Sheng, H.-J.; Topp, E.; Jiang, X.; Zhu, Y.-G.; Tiedje, J.M. Antibiotic Resistance in the Soil Ecosystem: A One Health Perspective. Curr. Opin. Environ. Sci. Health 2021, 20, 100230. [Google Scholar] [CrossRef]
- Fernández Rodríguez, R.E. Antibiotic resistance: The role of man, animals and the environment. Sun 2021, 36, 298–324. [Google Scholar] [CrossRef]
- Forsberg, K.J.; Reyes, A.; Wang, B.; Selleck, E.M.; Sommer, M.O.A.; Dantas, G. The Shared Antibiotic Resistome of Soil Bacteria and Human Pathogens. Science 2012, 337, 1107–1111. [Google Scholar] [CrossRef]
- Han, B.; Ma, L.; Yu, Q.; Yang, J.; Su, W.; Hilal, M.G.; Li, X.; Zhang, S.; Li, H. The Source, Fate and Prospect of Antibiotic Resistance Genes in Soil: A Review. Front. Microbiol. 2022, 13, 976657. [Google Scholar] [CrossRef]
- Telo da Gama, J. The Role of Soils in Sustainability, Climate Change, and Ecosystem Services: Challenges and Opportunities. Ecologies 2023, 4, 552–567. [Google Scholar] [CrossRef]
- Ahmed, S.K.; Hussein, S.; Qurbani, K.; Ibrahim, R.H.; Fareeq, A.; Mahmood, K.A.; Mohamed, M.G. Antimicrobial Resistance: Impacts, Challenges, and Future Prospects. J. Med. Surg. Public Health 2024, 2, 100081. [Google Scholar] [CrossRef]
- Reygaert, W.C. An Overview of the Antimicrobial Resistance Mechanisms of Bacteria. AIMS Microbiol. 2018, 4, 482–501. [Google Scholar] [CrossRef]
- Guo, K.; Han, L.; Luo, J.; Lu, G.; Li, Y.; Liu, J. Occurrence and Accumulation Characteristics of Antibiotics in Soil and Effects of Carbon and Nitrogen Cycle. Curr. Opin. Environ. Sci. Health 2025, 45, 100619. [Google Scholar] [CrossRef]
- Jia, W.-L.; Song, C.; He, L.-Y.; Wang, B.; Gao, F.-Z.; Zhang, M.; Ying, G.-G. Antibiotics in Soil and Water: Occurrence, Fate, and Risk. Curr. Opin. Environ. Sci. Health 2023, 32, 100437. [Google Scholar] [CrossRef]
- Chow, L.K.M.; Ghaly, T.M.; Gillings, M.R. A Survey of Sub-Inhibitory Concentrations of Antibiotics in the Environment. J. Environ. Sci. 2021, 99, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Grenni, P.; Ancona, V.; Barra Caracciolo, A. Ecological Effects of Antibiotics on Natural Ecosystems: A Review. Microchem. J. 2018, 136, 25–39. [Google Scholar] [CrossRef]
- Li, Y.; Li, R.; Hou, J.; Sun, X.; Wang, Y.; Li, L.; Yang, F.; Yao, Y.; An, Y. Mobile Genetic Elements Affect the Dissemination of Antibiotic Resistance Genes (ARGs) of Clinical Importance in the Environment. Environ. Res. 2024, 243, 117801. [Google Scholar] [CrossRef]
- Westhoff, S.; van Leeuwe, T.M.; Qachach, O.; Zhang, Z.; van Wezel, G.P.; Rozen, D.E. The Evolution of No-Cost Resistance at Sub-MIC Concentrations of Streptomycin in Streptomyces Coelicolor. ISME J. 2017, 11, 1168–1178. [Google Scholar] [CrossRef]
- Parras-Moltó, M.; Lund, D.; Ebmeyer, S.; Larsson, D.G.J.; Johnning, A.; Kristiansson, E. The Transfer of Antibiotic Resistance Genes between Evolutionarily Distant Bacteria. mSphere 2025, 10, e00114–e00125. [Google Scholar] [CrossRef]
- Zhou, Y.; Niu, L.; Zhu, S.; Lu, H.; Liu, W. Occurrence, Abundance, and Distribution of Sulfonamide and Tetracycline Resistance Genes in Agricultural Soils across China. Sci. Total Environ. 2017, 599–600, 1977–1983. [Google Scholar] [CrossRef]
- Vydrin, A.F.; Shikhaleev, I.V.; Makhortov, V.L.; Shcherenko, N.N.; Kolchanova, N.V. Component Composition of Gentamicin Sulfate Preparations. Pharm. Chem. J. 2003, 37, 448–450. [Google Scholar] [CrossRef]
- Doucette, W.J.; Andren, A.W. Aqueous Solubility of Selected Biphenyl, Furan, and Dioxin Congeners. Chemosphere 1988, 17, 243–252. [Google Scholar] [CrossRef]
- Puzyn, T.; Mostrąg, A.; Falandysz, J.; Kholod, Y.; Leszczynski, J. Predicting Water Solubility of Congeners: Chloronaphthalenes—A Case Study. J. Hazard. Mater. 2009, 170, 1014–1022. [Google Scholar] [CrossRef] [PubMed]
- Zuluaga, A.F.; Agudelo, M.; Cardeño, J.J.; Rodriguez, C.A.; Vesga, O. Determination of Therapeutic Equivalence of Generic Products of Gentamicin in the Neutropenic Mouse Thigh Infection Model. PLoS ONE 2010, 5, e10744. [Google Scholar] [CrossRef]
- Khaled, E.; Khalil, M.M.; Abed El Aziz, G.M. Calixarene/Carbon Nanotubes Based Screen Printed Sensors for Potentiometric Determination of Gentamicin Sulphate in Pharmaceutical Preparations and Spiked Surface Water Samples. Sens. Actuators B Chem. 2017, 244, 876–884. [Google Scholar] [CrossRef]
- Pisani, S.; Piazza, A.; Dorati, R.; Genta, I.; Rosalia, M.; Chiesa, E.; Bruni, G.; Migliavacca, R.; Conti, B. Investigating Electrospun Shape Memory Patches as Gentamicin Drug Delivery System. Int. J. Pharm. 2025, 673, 125393. [Google Scholar] [CrossRef]
- Sandaoui, M.; Aboulfadile, M.A.; Sakoui, S.; Derdak, R.; El Khalfi, B.; El Ghachtouli, S.; Azzi, M.; Zaroual, Z. The Ultrasonic Degradation of a Pharmaceutical Formulation Including Gentamicin Sulfate and Parabens: Optimization of Operational Parameters, Antibacterial Activity Assessment, and Analysis of Resulting by-Products. J. Water Process Eng. 2024, 58, 104875. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Sun, Z.; Li, Y.; Xie, X.; Xin, S.; Liu, G.; Liu, H.; Xin, Y. Decoding the Fate of Antibiotic Resistance Genes in Soil with the Application of Thermally Treated Gentamicin Mycelial Residues. Bioresour. Technol. Rep. 2025, 30, 102169. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, D.; Xue, J.; Feng, Y.; Wakelin, S.A.; Weaver, L.; Shehata, E.; Li, Z. Fate of Bacterial Community, Antibiotic Resistance Genes and Gentamicin Residues in Soil after Three-Year Amendment Using Gentamicin Fermentation Waste. Chemosphere 2022, 291, 132734. [Google Scholar] [CrossRef]
- Arshad, M.S.; Zafar, S.; Rana, S.J.; Nazari, K.; Chang, M.-W.; Ahmad, Z. Fabrication of Gentamicin Sulphate Laden Stimulus Responsive Polymeric Microarray Patches for the Treatment of Bacterial Biofilms. J. Drug Deliv. Sci. Technol. 2023, 84, 104504. [Google Scholar] [CrossRef]
- Koestel, J.K.; Moeys, J.; Jarvis, N.J. Meta-Analysis of the Effects of Soil Properties, Site Factors and Experimental Conditions on Solute Transport. Hydrol. Earth Syst. Sci. 2012, 16, 1647–1665. [Google Scholar] [CrossRef]
- Mojid, M.A.; Hossain, A.B.M.Z.; Wyseure, G.C.L. Relation of Reactive Solute-Transport Parameters to Basic Soil Properties. Eurasian J. Soil Sci. 2018, 7, 326–336. [Google Scholar] [CrossRef][Green Version]
- Merck KGaA (Sigma-Aldrich) Gentamicin Solution—Product Information: 50 Mg/mL, BioReagent, Suitable for Cell Culture. Available online: https://www.sigmaaldrich.com/MX/es/product/sigma/g1397 (accessed on 22 February 2025).
- Tabuada, M.A.; Rego, Z.J.C.; Vachaud, G.; Pereira, L.S. Two-Dimensional Infiltration under Furrow Irrigation: Modelling, Its Validation and Applications. Agric. Water Manag. 1995, 27, 105–123. [Google Scholar] [CrossRef]
- Castanedo, V.; Saucedo, H.; Fuentes, C. Modeling Two-Dimensional Infiltration with Constant and Time-Variable Water Depth. Water 2019, 11, 371. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de La Ville de Dijon; Victor Dalmont: Paris, France, 1856; p. 647. [Google Scholar]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C.; Brambila, F. Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model. Mathematics 2020, 8, 2201. [Google Scholar] [CrossRef]
- Zerihun, D.; Furman, A.; Warrick, A.W.; Sanchez, C.A. Coupled Surface-Subsurface Flow Model for Improved Basin Irrigation Management. J. Irrig. Drain. Eng. 2005, 131, 111–128. [Google Scholar] [CrossRef]
- Chávez, C.; Fuentes, C.; Brambila-Paz, F.; Castañeda, A. Numerical Solution of the Advection-Dispersion Equation: Application to the Agricultural Drainage. J. Agr. Sci. Tech. 2014, 16, 1357–1388. [Google Scholar]
- Sigma-Aldrich. Protocol Guide: WST-1 Assay for Cell Proliferation and Viability; Sigma-Aldrich: St. Louis, MO, USA; Available online: https://www.sigmaaldrich.cn/CN/zh/technical-documents/protocol/cell-culture-and-cell-culture-analysis/cell-counting-and-health-analysis/cell-proliferation-reagent-wst-1 (accessed on 15 December 2024).
- AMSA Laboratorios. Gentamicina Solución Inyectable 160 Mg/2 mL: Información Técnica del Producto; AMSA Laboratorios: Mexico City, Mexico, 2025. [Google Scholar]
- World Health Organization. WHO Model List of Essential Medicines—2023 Update; World Health Organization: Geneva, Switzerland, 2024. [Google Scholar]
- Kim, S.H.; Park, S.Y.; Kim, G.E.; Jho, E.H. Effect of pH and Temperature on the Biodegradation of Oxytetracycline, Streptomycin, and Validamycin A in Soil. Appl. Biol. Chem. 2023, 66, 63. [Google Scholar] [CrossRef]
- SEMARNAT. Norma Oficial Mexicana NOM-021-SEMARNAT-2000 Que Establece las Especificaciones de Fertilidad, Salinidad y Clasificación de Suelos. Estudios, Muestreo y Análisis [Official Mexican Standard NOM-021-SEMARNAT-2000: Specifications of Fertility, Salinity and Soil Classification. Studies, Sampling and Analysis]; Diario Oficial de la Federación: Mexico City, Mexico, 31 December 2002; Available online: https://dof.gob.mx/nota_detalle.php?codigo=717582&fecha=31/12/2002 (accessed on 20 November 2024).
- Rashtbari, M.; Safari Sinegani, A.A. Efficiency of Soil Extracellular Enzymes in Soils Treated by Organic and Mineral Conditioners Against Mostly Applied Veterinary Antibiotics (Gentamicin, Oxytetracycline and Penicillin). J. Soil Manag. Sustain. Prod. 2020, 10, 1–26. [Google Scholar]
- Naveed, S.; Shah, S.N.; Qamar, F.; Waheed, N.; Nazeer, S. Simple UV Spectrophotometric Assay of New Formulation Gentamycin. J. App. Pharm. 2014, 6, 407–410. [Google Scholar]
- Pareja-Aivar, L. Desarrollo y Validación de Un Método Análitico Para La Cuantificación de Gentamicina En Un Producto Farmacéutico En Crema Por Potencia Antibiotica; Universidad Nacional de San Antonio Abad del Cusco: Cusco, Peru, 2012. [Google Scholar]
- Hernández-García, R.G. Determinación de La Cinética de Liberación de Gentamicina En Cemento Óseo Afectado Por El Desgaste y La Influencia de La Materia Orgánica; Universidad Autónoma de Nuevo León: San Nicolás de los Garza, Mexico, 2019. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Sand | 15.23 | 0.7019 | |
| Clay | 61.43 | 0.0166 | |
| Texture | 23.34 | 3.5 | |
| 8 | 0.9481 | ||
| 1.35 | 92.8674 | ||
| 0.4906 | 0.3084 | ||
| 1136.6942 | 1.4689 | ||
| 0.18609 | 47.0628 | ||
| 3.1784 | 0.2170 |
| Parameter | Value |
|---|---|
| 6.05 | |
| Organic matter (%) | 2.61 |
| Total organic carbon (%) | 1.58 |
| Parameter | Pure Gentamicin | Gentamicin Sulfate |
|---|---|---|
| Dispersion coefficient D (m2/s) | 9.55 × 10−3 | 2.97 × 10−2 |
| RMSE | 0.2257 | 0.1889 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales-Durán, N.; Fuentes, S.; García-Gallego, J.; Treviño-Reséndez, J.; García-Espinoza, J.D.; Morones-Ramírez, R.; Chávez, C. Numerical Modeling of Gentamicin Transport in Agricultural Soils: Implications for Environmental Pollution. Antibiotics 2025, 14, 786. https://doi.org/10.3390/antibiotics14080786
Morales-Durán N, Fuentes S, García-Gallego J, Treviño-Reséndez J, García-Espinoza JD, Morones-Ramírez R, Chávez C. Numerical Modeling of Gentamicin Transport in Agricultural Soils: Implications for Environmental Pollution. Antibiotics. 2025; 14(8):786. https://doi.org/10.3390/antibiotics14080786
Chicago/Turabian StyleMorales-Durán, Nami, Sebastián Fuentes, Jesús García-Gallego, José Treviño-Reséndez, Josué D. García-Espinoza, Rubén Morones-Ramírez, and Carlos Chávez. 2025. "Numerical Modeling of Gentamicin Transport in Agricultural Soils: Implications for Environmental Pollution" Antibiotics 14, no. 8: 786. https://doi.org/10.3390/antibiotics14080786
APA StyleMorales-Durán, N., Fuentes, S., García-Gallego, J., Treviño-Reséndez, J., García-Espinoza, J. D., Morones-Ramírez, R., & Chávez, C. (2025). Numerical Modeling of Gentamicin Transport in Agricultural Soils: Implications for Environmental Pollution. Antibiotics, 14(8), 786. https://doi.org/10.3390/antibiotics14080786







