A Variable Cross-Section Microfluidic Channel for Simultaneous Reproduction of Low Oscillatory and Pulsatile Wall Shear Stress at the Carotid Bifurcation: A Computational Fluid Dynamics-Based Study
Abstract
1. Introduction
2. Materials and Methods
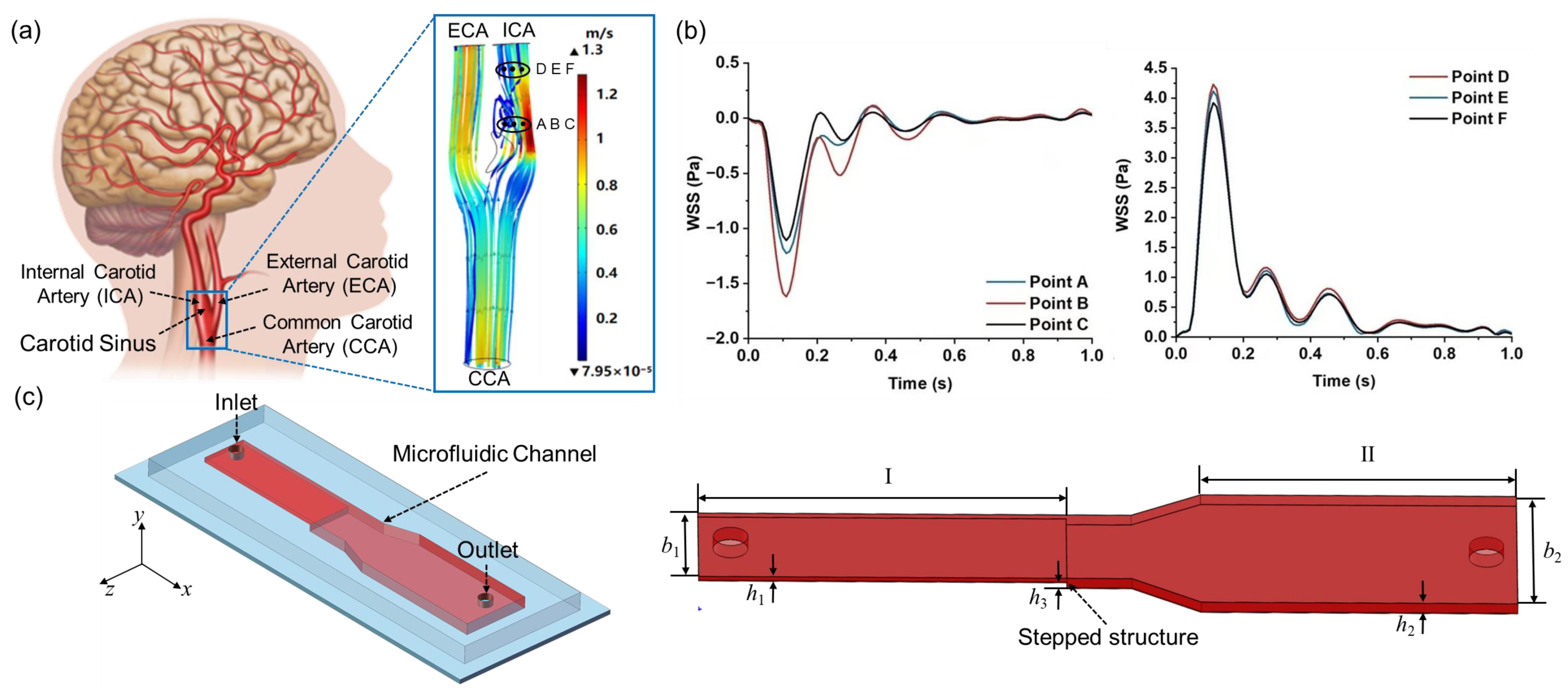
2.1. Extraction of WSS Patterns at the Carotid Bifurcation
2.2. Design of the Variable Cross-Section Microfluidic Channel
2.3. Governing Equations of Fluid Motion in the Microchannel
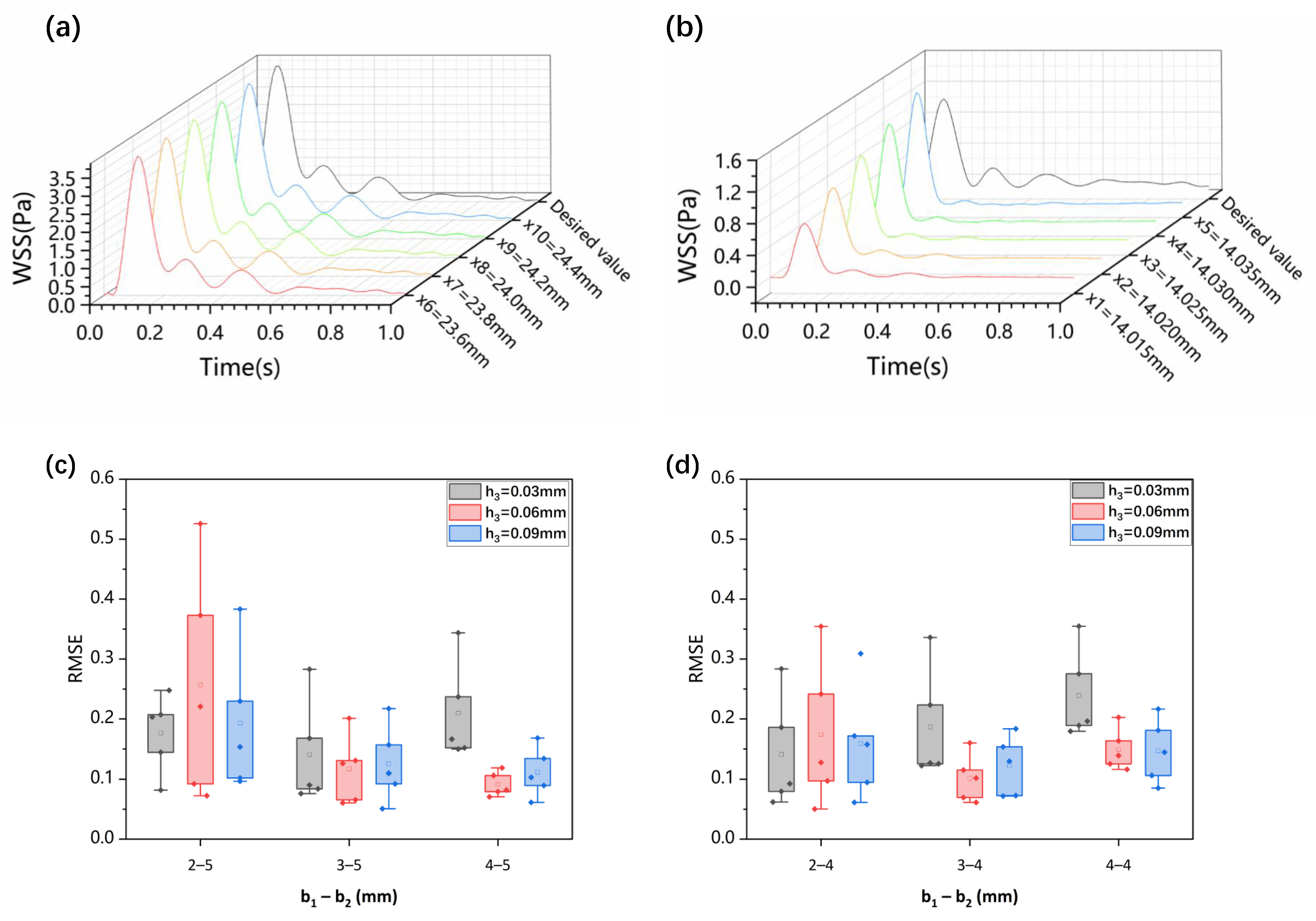
2.4. CFD Simulation and Optimization of WSS in the Microchannel
3. Results
3.1. Carotid Artery WSS Waveform Simulation in the Variable Cross-Section Microchannel
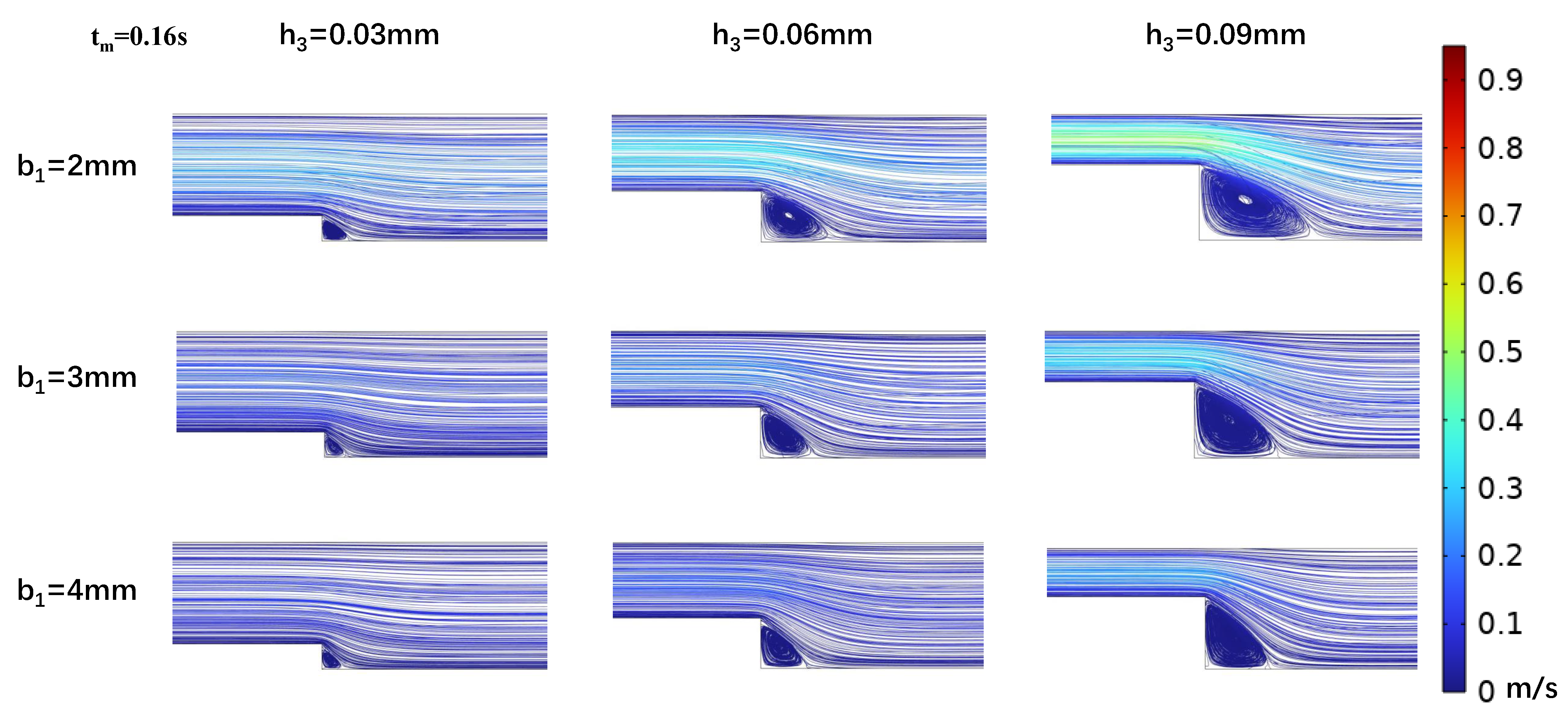
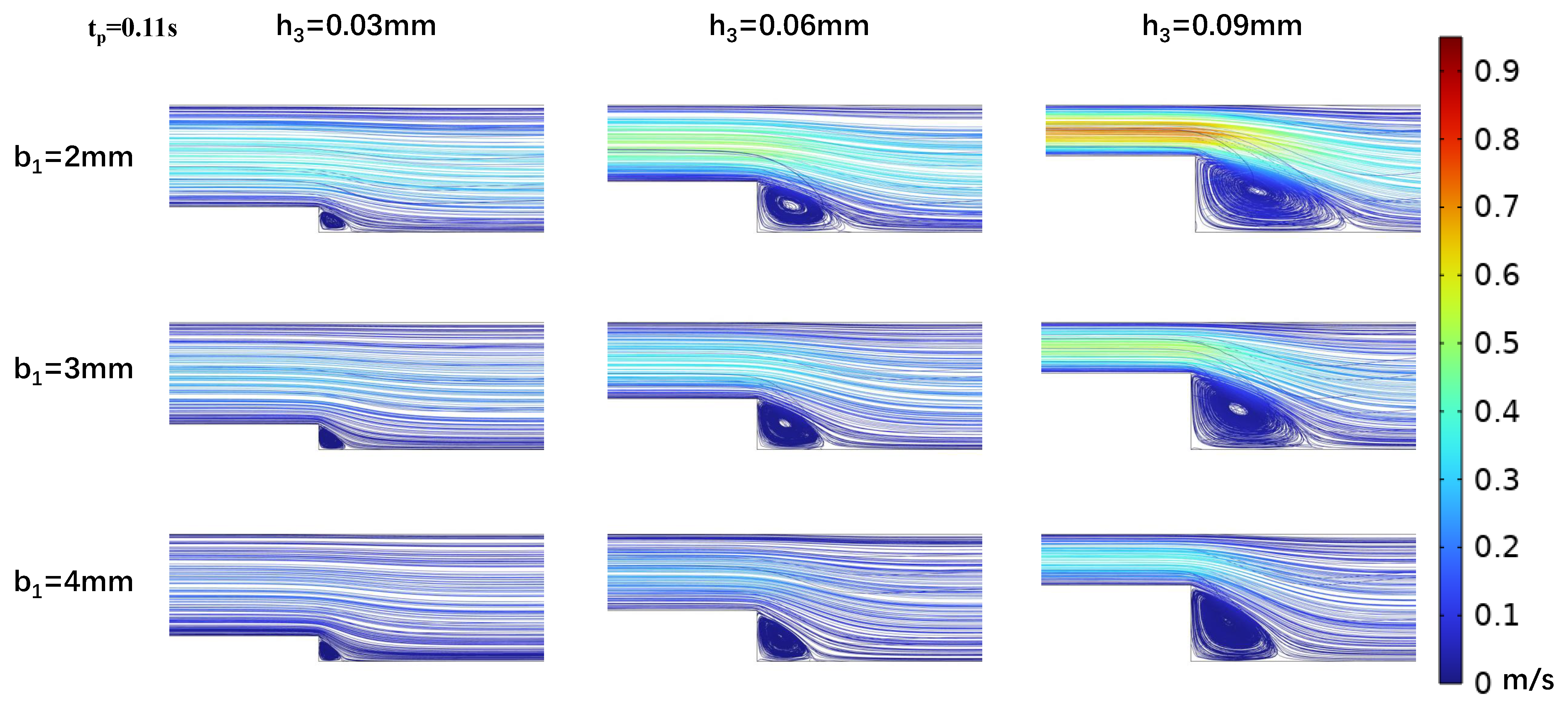
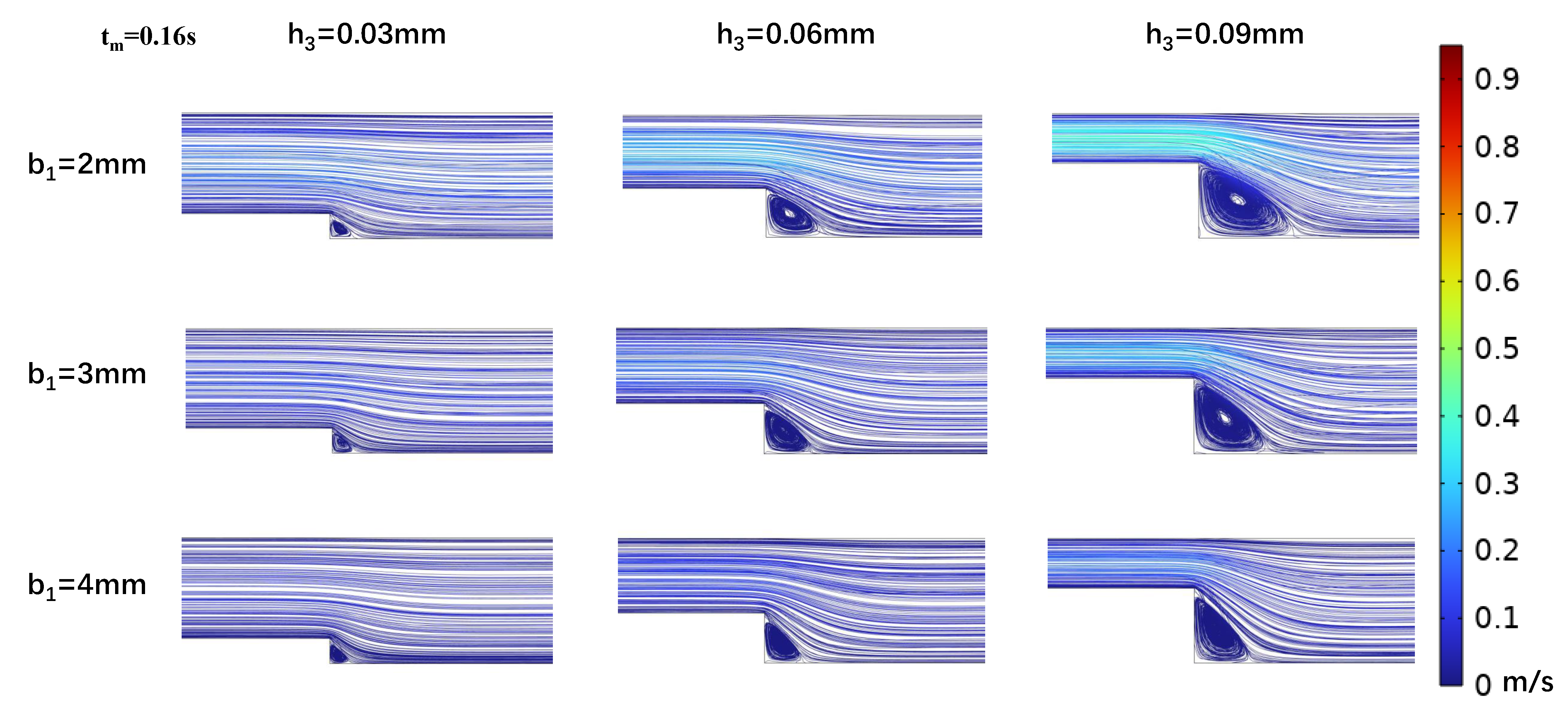
3.2. Impact of Step Size on Low Oscillatory WSS
3.3. Influence of Wide Area Channel Size on Low Oscillatory WSS
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WSS | Wall shear stress |
| CFD | Computational fluid dynamics |
| OWSS | Oscillatory wall shear stress |
| PWSS | Pulsatile wall shear stress |
| 3D | Three-dimensional |
| CCA | Common carotid artery |
| ICA | Internal carotid artery |
| ECA | External carotid artery |
| RMSE | Root mean square error |
References
- Baratchi, S.; Khoshmanesh, K.; Woodman, O.L.; Potocnik, S.; Peter, K.; McIntyre, P. Molecular sensors of blood flow in endothelial cells. Trends Mol. Med. 2017, 23, 850–868. [Google Scholar] [CrossRef]
- Bharadvaj, B.; Mabon, R.; Giddens, D. Steady flow in a model of the human carotid bifurcation. Part II—laser-Doppler anemometer measurements. J. Biomech. 1982, 15, 363–378. [Google Scholar] [CrossRef]
- Calò, K.; De Nisco, G.; Gallo, D.; Chiastra, C.; Hoogendoorn, A.; Steinman, D.A.; Scarsoglio, S.; Wentzel, J.J.; Morbiducci, U. Exploring wall shear stress spatiotemporal heterogeneity in coronary arteries combining correlation-based analysis and complex networks with computational hemodynamics. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2020, 234, 1209–1222. [Google Scholar] [CrossRef]
- Caro, C.; Fitz-Gerald, J.; Schroter, R. Arterial wall shear and distribution of early atheroma in man. Nature 1969, 223, 1159–1161. [Google Scholar] [CrossRef] [PubMed]
- Dhawan, S.S.; Avati Nanjundappa, R.P.; Branch, J.R.; Taylor, W.R.; Quyyumi, A.A.; Jo, H.; McDaniel, M.C.; Suo, J.; Giddens, D.; Samady, H. Shear stress and plaque development. Expert Rev. Cardiovasc. Ther. 2010, 8, 545–556. [Google Scholar] [CrossRef] [PubMed]
- Genuardi, L.; Chatzizisis, Y.S.; Chiastra, C.; Sgueglia, G.; Samady, H.; Kassab, G.S.; Migliavacca, F.; Trani, C.; Burzotta, F. Local fluid dynamics in patients with bifurcated coronary lesions undergoing percutaneous coronary interventions. Cardiol. J. 2021, 28, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Malik, J.; Novakova, L.; Valerianova, A.; Chytilova, E.; Lejsek, V.; Buryskova Salajova, K.; Lambert, L.; Grus, T.; Porizka, M.; Michalek, P. Wall shear stress alteration: A local risk factor of atherosclerosis. Curr. Atheroscler. Rep. 2022, 24, 143–151. [Google Scholar] [CrossRef]
- Suo, J.; Oshinski, J.N.; Giddens, D.P. Blood flow patterns in the proximal human coronary arteries: Relationship to atherosclerotic plaque occurrence. Mol. Cell. Biomech. 2008, 5, 9. [Google Scholar]
- Zalud, N.C.; Bulusu, K.V.; Plesniak, M.W. Shear stress metrics associated with pro-atherogenic high-risk anatomical features in a carotid artery bifurcation model. Clin. Biomech. 2023, 105, 105956. [Google Scholar] [CrossRef]
- Early, K.S.; Stewart, A.; Johannsen, N.; Lavie, C.J.; Thomas, J.R.; Welsch, M. The effects of exercise training on brachial artery flow-mediated dilation: A meta-analysis. J. Cardiopulm. Rehabil. Prev. 2017, 37, 77–89. [Google Scholar] [CrossRef]
- Maeda, S.; Miyauchi, T.; Kakiyama, T.; Sugawara, J.; Iemitsu, M.; Irukayama-Tomobe, Y.; Murakami, H.; Kumagai, Y.; Kuno, S.; Matsuda, M. Effects of exercise training of 8 weeks and detraining on plasma levels of endothelium-derived factors, endothelin-1 and nitric oxide, in healthy young humans. Life Sci. 2001, 69, 1005–1016. [Google Scholar] [CrossRef] [PubMed]
- Laufs, U.; Werner, N.; Link, A.; Endres, M.; Wassmann, S.; Jürgens, K.; Miche, E.; Böhm, M.; Nickenig, G. Physical training increases endothelial progenitor cells, inhibits neointima formation, and enhances angiogenesis. Circulation 2004, 109, 220–226. [Google Scholar] [CrossRef]
- Na, J.-T.; Xue, C.-D.; Wang, Y.-X.; Li, Y.-J.; Wang, Y.; Liu, B.; Qin, K.R. Fabricating a multi-component microfluidic system for exercise-induced endothelial cell mechanobiology guided by hemodynamic similarity. Talanta 2023, 253, 123933. [Google Scholar] [CrossRef]
- Chiu, J.J.; Wang, D.; Chien, S.; Skalak, R.; Usami, S. Effects of disturbed flow on endothelial cells. J. Biomech. Eng. 1998, 120, 2–8. [Google Scholar] [CrossRef]
- Alford, A.; Jacobs, C.; Donahue, H. Oscillating fluid flow regulates gap junction communication in osteocytic MLO-Y4 cells by an ERK1/2 MAP kinase-dependent mechanism. Bone 2003, 33, 64–70. [Google Scholar] [CrossRef]
- Chien, S. Effects of disturbed flow on endothelial cells. Ann. Biomed. Eng. 2008, 36, 554–562. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; He, Y.; Bu, H.; Wang, M.; Yu, J.; Li, L.; Li, H.; Zhang, X.; Cui, X.; Cheng, M. Oscillating shear stress mediates mesenchymal transdifferentiation of EPCs by the Kir2. 1 channel. Heart Vessel. 2020, 35, 1473–1482. [Google Scholar] [CrossRef]
- Wang, Y.X.; Liu, H.B.; Li, P.S.; Yuan, W.X.; Liu, B.; Liu, S.T.; Qin, K.R. ROS and NO dynamics in endothelial cells exposed to exercise-induced wall shear stress. Cell. Mol. Bioeng. 2019, 12, 107–120. [Google Scholar] [CrossRef]
- Wang, Y.X.; Xiang, C.; Liu, B.; Zhu, Y.; Luan, Y.; Liu, S.T.; Qin, K.R. A multi-component parallel-plate flow chamber system for studying the effect of exercise-induced wall shear stress on endothelial cells. Biomed. Eng. Online 2016, 15, 659–672. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Cornwell, J.; Zhang, H.; Lim, T.; Resurreccion, R.; Port, T.; Rosengarten, G.; Nordon, R.E. Cardiac-like flow generator for long-term imaging of endothelial cell responses to circulatory pulsatile flow at microscale. Lab A Chip 2013, 13, 2999–3007. [Google Scholar] [CrossRef]
- Lee, J.; Estlack, Z.; Somaweera, H.; Wang, X.; Lacerda, C.M.; Kim, J. A microfluidic cardiac flow profile generator for studying the effect of shear stress on valvular endothelial cells. Lab A Chip 2018, 18, 2946–2954. [Google Scholar] [CrossRef]
- Roy, B.; Das, T.; Mishra, D.; Maiti, T.K.; Chakraborty, S. Oscillatory shear stress induced calcium flickers in osteoblast cells. Integr. Biol. 2014, 6, 289–299. [Google Scholar] [CrossRef]
- Shao, J.; Wu, L.; Wu, J.; Zheng, Y.; Zhao, H.; Jin, Q.; Zhao, J. Integrated microfluidic chip for endothelial cells culture and analysis exposed to a pulsatile and oscillatory shear stress. Lab A Chip 2009, 9, 3118–3125. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.K.; Koomson, E.; Zou, H.; Yi, C.; Li, C.W.; Xu, T.; Yang, M. Recent advances in microfluidic technology for manipulation and analysis of biological cells (2007–2017). Anal. Chim. Acta 2018, 1044, 29–65. [Google Scholar] [CrossRef] [PubMed]
- Chai, H.; Feng, Y.; Liang, F.; Wang, W. A microfluidic device enabling deterministic single cell trapping and release. Lab A Chip 2021, 21, 2486–2494. [Google Scholar] [CrossRef] [PubMed]
- Pattanayak, P.; Singh, S.K.; Gulati, M.; Vishwas, S.; Kapoor, B.; Chellappan, D.K.; Anand, K.; Gupta, G.; Jha, N.K.; Gupta, P.K.; et al. Microfluidic chips: Recent advances, critical strategies in design, applications and future perspectives. Microfluid. Nanofluidics 2021, 25, 99. [Google Scholar] [CrossRef]
- Saupe, M.; Wiedemeier, S.; Gastrock, G.; Römer, R.; Lemke, K. Flexible Toolbox of High-Precision Microfluidic Modules for Versatile Droplet-Based Applications. Micromachines 2024, 15, 250. [Google Scholar] [CrossRef]
- Bozzi, S.; Morbiducci, U.; Gallo, D.; Ponzini, R.; Rizzo, G.; Bignardi, C.; Passoni, G. Uncertainty propagation of phase contrast-MRI derived inlet boundary conditions in computational hemodynamics models of thoracic aorta. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1104–1112. [Google Scholar] [CrossRef]
- Mariotti, A.; Boccadifuoco, A.; Celi, S.; Salvetti, M. Hemodynamics and stresses in numerical simulations of the thoracic aorta: Stochastic sensitivity analysis to inlet flow-rate waveform. Comput. Fluids 2021, 230, 105123. [Google Scholar] [CrossRef]
- Fojas, J.J.R.; De Leon, R.L. Carotid artery modeling using the Navier-Stokes equations for an incompressible, Newtonian and axisymmetric flow. APCBEE Procedia 2013, 7, 86–92. [Google Scholar] [CrossRef][Green Version]
- Markl, M.; Wegent, F.; Zech, T.; Bauer, S.; Strecker, C.; Schumacher, M.; Weiller, C.; Hennig, J.; Harloff, A. In vivo wall shear stress distribution in the carotid artery: Effect of bifurcation geometry, internal carotid artery stenosis, and recanalization therapy. Circ. Cardiovasc. Imaging 2010, 3, 647–655. [Google Scholar] [CrossRef]
- Na, J.T.; Hu, S.Y.; Xue, C.D.; Wang, Y.X.; Chen, K.J.; Li, Y.J.; Wang, Y.; Qin, K.R. A microfluidic system for precisely reproducing physiological blood pressure and wall shear stress to endothelial cells. Analyst 2021, 146, 5913–5922. [Google Scholar] [CrossRef]
- Zhan, C.L.; Li, Y.J.; Chen, D.; Qin, K.R. Numerical Simulation of Blood Flow Conductivity and Electrical Impedance in Common Carotid Artery Affected by Internal Carotid Artery Stenosis. Shui Dongli Xue Yanjiu Yujinzhan A Ji 2023, 38, 637–645. [Google Scholar]
- Shen, B.Y.; Liu, H.B.; Cao, L.; Qin, K.R. Acute effects of different intensities of cycling acute exercise on carotid arterial apparent elasticity and hemodynamic variables. BioMed Res. Int. 2020, 2020, 9027560. [Google Scholar] [CrossRef] [PubMed]
- Rezazadeh, M.; Ostadi, R. Numerical simulation of the wall shear stress distribution in a carotid artery bifurcation. J. Mech. Sci. Technol. 2022, 36, 5035–5046. [Google Scholar] [CrossRef]
- Xu, G.; Qin, K.; Liu, Z. Calculation of the shear stress in the parallel-plate flow chamber under pulsatile flow condition. Chin. Q. Mech 2000, 21, 45–51. [Google Scholar]
- Kim, S.; Kim, H.J.; Jeon, N.L. Biological applications of microfluidic gradient devices. Integr. Biol. 2010, 2, 584–603. [Google Scholar] [CrossRef]
- Li, Z.; Guan, X.; Zhang, J.; Guo, Q.; Xu, Q.; Yang, N. Bayesian optimization of operational and geometric parameters of microchannels for targeted droplet generation. Chin. J. Chem. Eng. 2025, 84, 244–253. [Google Scholar] [CrossRef]
- Sugii, Y.; Okuda, R.; Okamoto, K.; Madarame, H. Velocity measurement of both red blood cells and plasma of in vitro blood flow using high-speed micro PIV technique. Meas. Sci. Technol. 2005, 16, 1126. [Google Scholar] [CrossRef]
- Gimbrone, M.A.; García-Cardeña, G. Endothelial Cell Dysfunction and the Pathobiology of Atherosclerosis. Circ. Res. 2016, 118, 620–636. [Google Scholar] [CrossRef]



| Symbols | Expression | Unit |
|---|---|---|
| Part (I) width | mm | |
| Part (I) height | mm | |
| Part (I) length | mm | |
| Part (II) width | mm | |
| Part (II) height | mm | |
| Part (II) length | mm | |
| Step height | mm | |
| Time of maximum velocity | s | |
| Mean time of velocity | s | |
| l | Distance from the step | mm |
| x(1–5) | 5 observation points downstream from the step | mm |
| x(6–10) | 5 observation points at part (II) | mm |
| Fluid velocity | m/s | |
| Fluid viscosity | Pa · s | |
| Liquid density | kg/m | |
| Inlet velocity | m/s2 | |
| Q(t) | Volume flow rate of the inlet fluid | m3/s |
| Velocity at channel wall | m/s | |
| Pressure at the outlet | Pa | |
| (t) | WSS at the channel bottom of Part (I) | Pa |
| (t) | WSS at the channel bottom of Part (II) | Pa |
| Unit vector in the y direction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-J.; Hou, H.-M.; Hu, Q.-F.; Yuan, L.-J.; Xue, C.-D.; Chen, D.; Hu, X.-Q.; Qin, K.-R. A Variable Cross-Section Microfluidic Channel for Simultaneous Reproduction of Low Oscillatory and Pulsatile Wall Shear Stress at the Carotid Bifurcation: A Computational Fluid Dynamics-Based Study. Biosensors 2025, 15, 648. https://doi.org/10.3390/bios15100648
Li Y-J, Hou H-M, Hu Q-F, Yuan L-J, Xue C-D, Chen D, Hu X-Q, Qin K-R. A Variable Cross-Section Microfluidic Channel for Simultaneous Reproduction of Low Oscillatory and Pulsatile Wall Shear Stress at the Carotid Bifurcation: A Computational Fluid Dynamics-Based Study. Biosensors. 2025; 15(10):648. https://doi.org/10.3390/bios15100648
Chicago/Turabian StyleLi, Yong-Jiang, Hui-Min Hou, Qi-Fei Hu, Li-Jin Yuan, Chun-Dong Xue, Dong Chen, Xu-Qu Hu, and Kai-Rong Qin. 2025. "A Variable Cross-Section Microfluidic Channel for Simultaneous Reproduction of Low Oscillatory and Pulsatile Wall Shear Stress at the Carotid Bifurcation: A Computational Fluid Dynamics-Based Study" Biosensors 15, no. 10: 648. https://doi.org/10.3390/bios15100648
APA StyleLi, Y.-J., Hou, H.-M., Hu, Q.-F., Yuan, L.-J., Xue, C.-D., Chen, D., Hu, X.-Q., & Qin, K.-R. (2025). A Variable Cross-Section Microfluidic Channel for Simultaneous Reproduction of Low Oscillatory and Pulsatile Wall Shear Stress at the Carotid Bifurcation: A Computational Fluid Dynamics-Based Study. Biosensors, 15(10), 648. https://doi.org/10.3390/bios15100648






