Microfluidic Systems for Blood and Blood Cell Characterization
Abstract
:1. Introduction
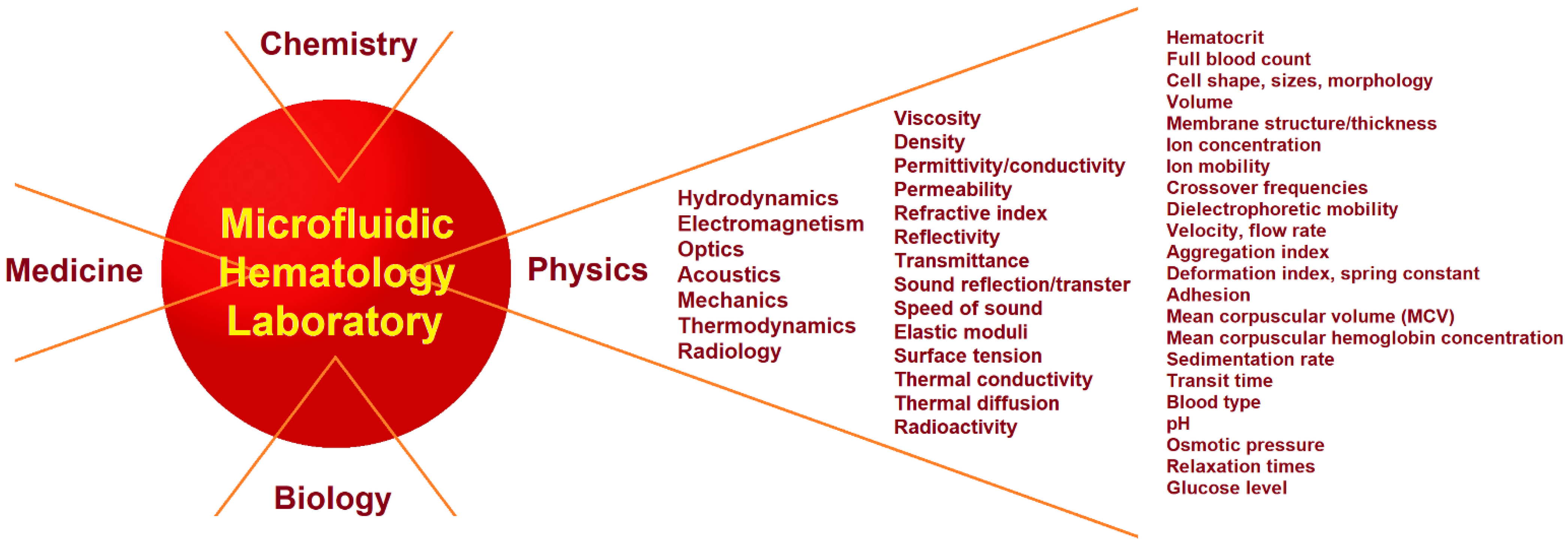
2. Physics and Physical Experiments in Hematology
2.1. Clinical Hematology Laboratory
2.2. Physical Measurements in a Microfluidic Hematology Laboratory
3. Theory and Physical Principles
3.1. Hydrodynamic Forces in Microfluidic Systems
3.1.1. Reynolds Number
3.1.2. Wall Interaction and Shear-Gradient Lift and Drag Forces
3.1.3. The Force Balance
3.1.4. Measurement of Whole Blood and Plasma Viscosities
3.2. Electromagnetic Characterization of Blood and Blood Cells
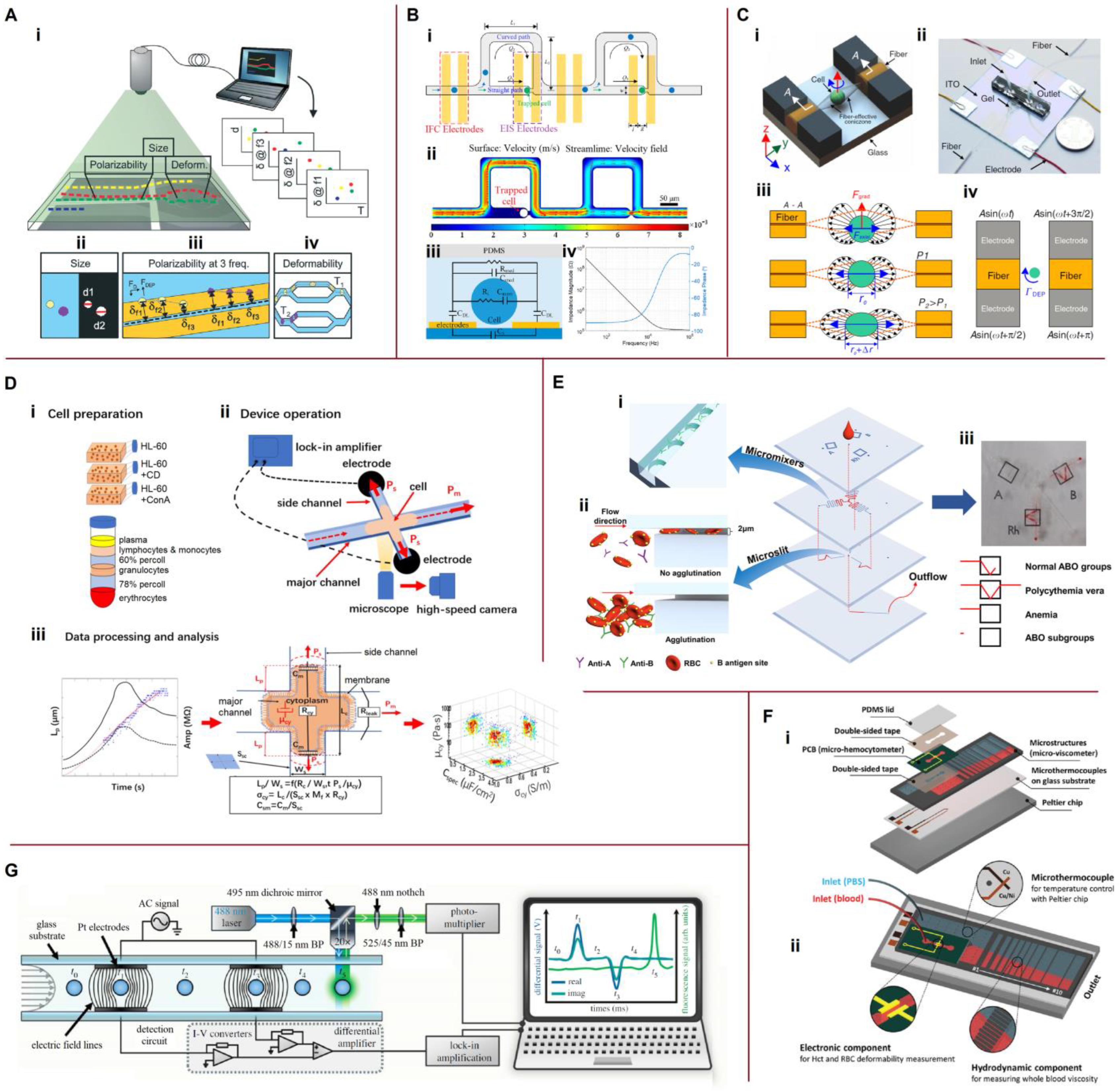
3.2.1. Electrochemical Impedance Spectroscopy
3.2.2. Effective Properties of a Two-Phase System
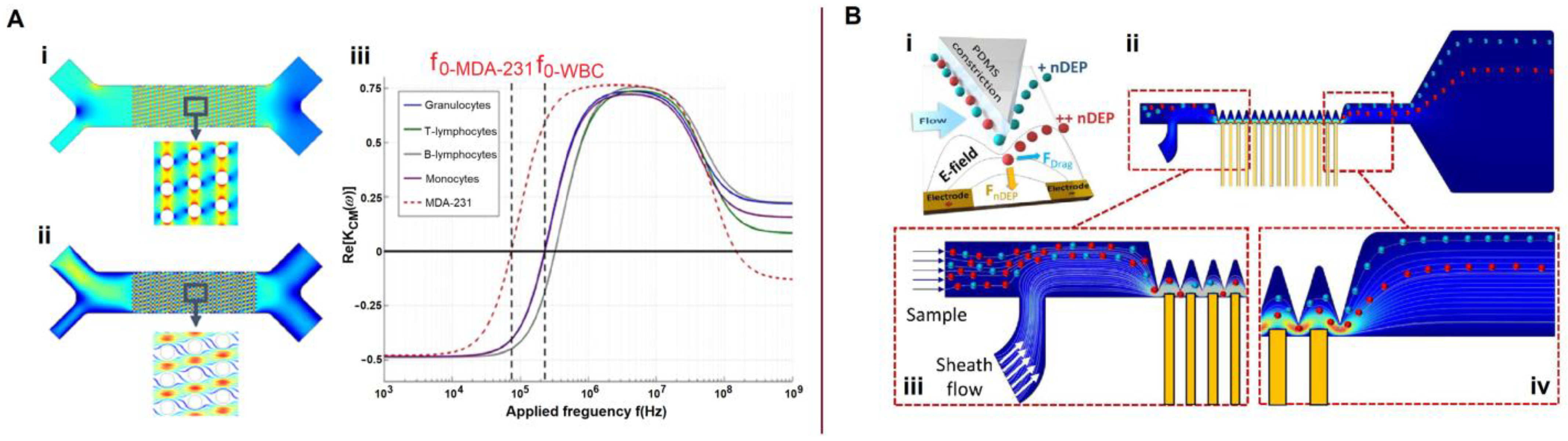
3.2.3. Dielectrophoretic Forces
3.2.4. Electrorotation
3.2.5. Magnetic Force
3.3. Optical Methods
3.3.1. Laser Tweezers and Optical Forces
3.3.2. Image Analysis
3.4. Acoustic Radiation Force
3.5. Mechanical Properties
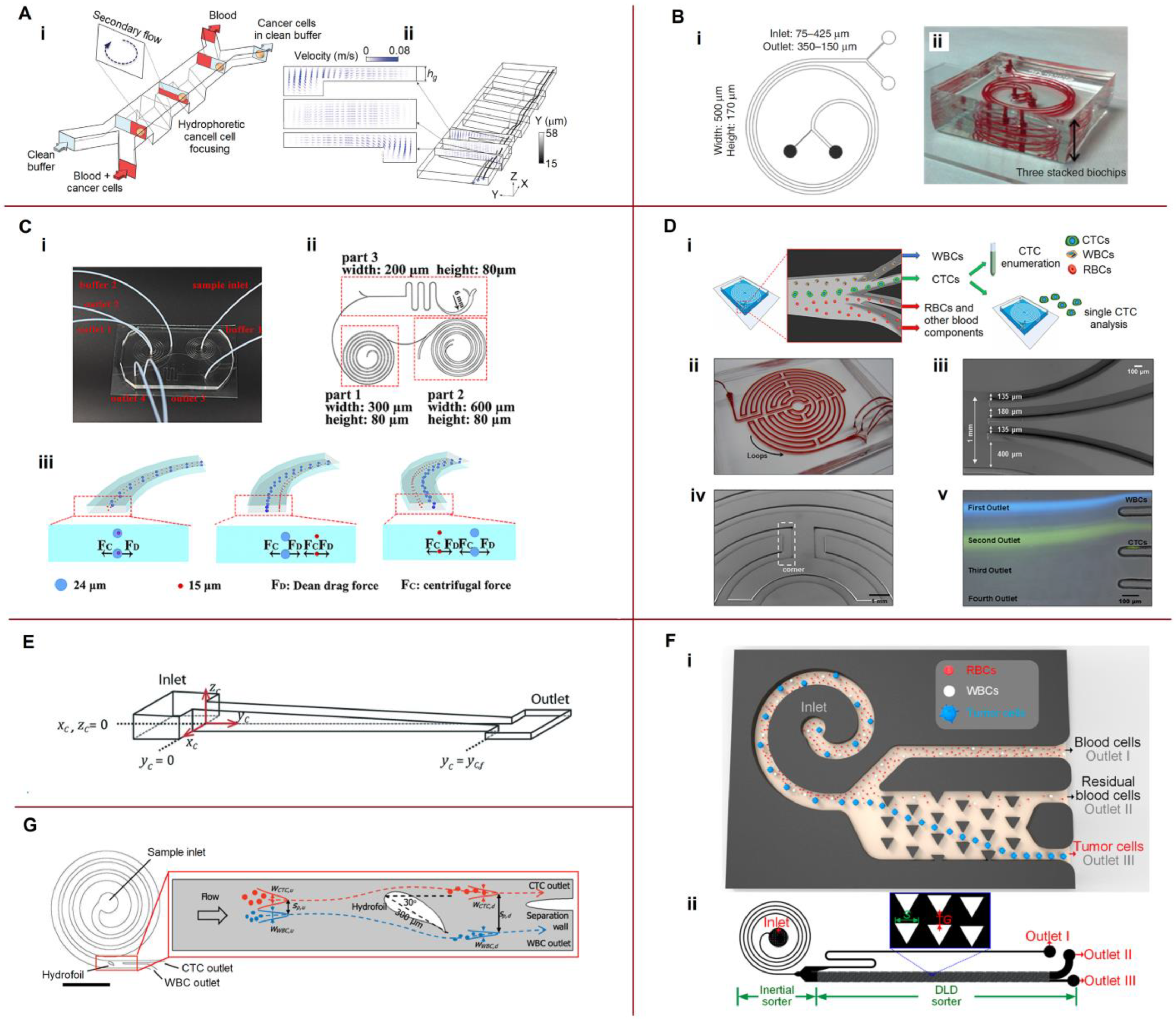
4. Separation and Sorting
4.1. Separation by a Combination of Hydrodynamic Forces
4.2. Coupling Hydrophoresis with Other Techniques
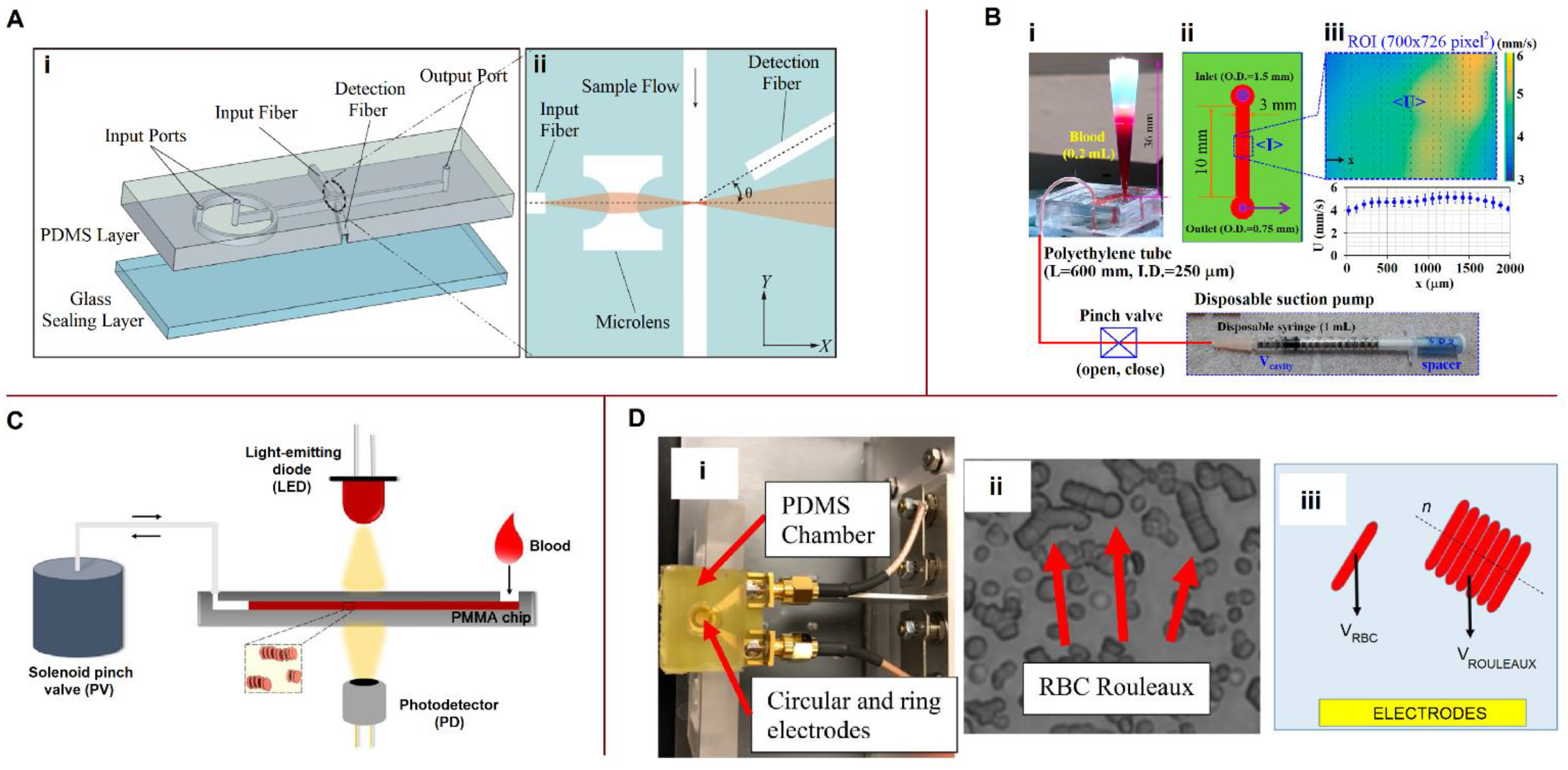
5. Cytometry and Biophysical Characterization of Blood
5.1. Microfluidic Impedance Cytometry
5.2. Photoacoustic Flow Cytometry
5.3. Optical Characterization of Blood
5.3.1. Optical Cell Counting
5.3.2. Erythrocyte Aggregation and Sedimentation Rates
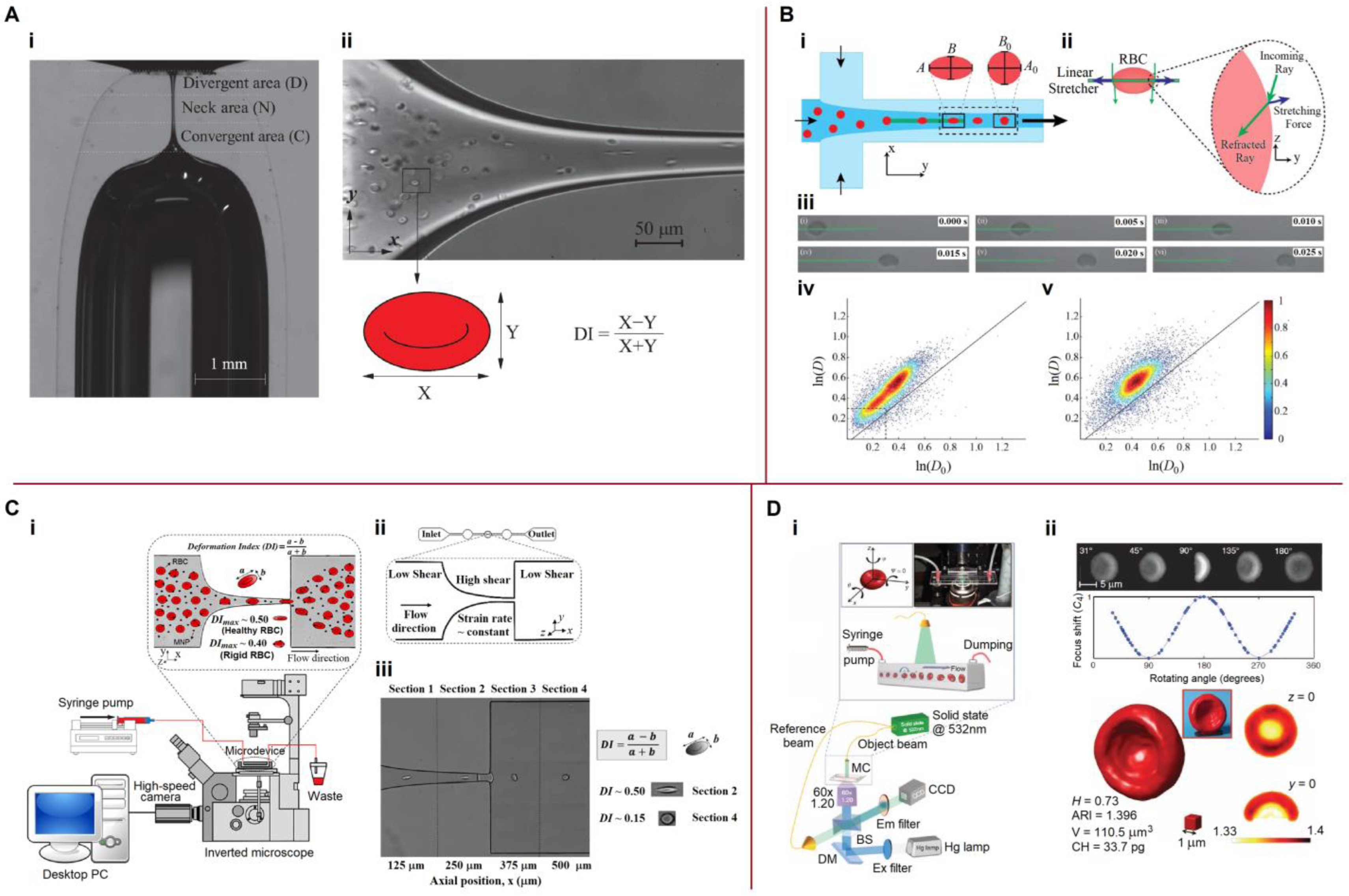
5.3.3. Mechanical Properties, Deformability
6. Physical Properties of Blood and Blood Cells
6.1. Dielectric Properties, Ion Concentration and Ion Mobility
6.2. Elastic Characteristics of Cells
6.3. Viscosity
6.4. Multidisciplinary Methods, Multiparameter Devices
6.4.1. Multifunctional Microfluidic Platforms
6.4.2. Microfluidic Hematology on a Single Platform
6.4.3. Neural Networks
7. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Aggregation index |
| CTC | Circulating tumor cell |
| CM factor | Clausius–Mossotti factor |
| DEP | Dielectrophoresis |
| DI | Deformation index |
| DLD | Deterministic lateral displacement |
| dRT-DC | Dynamic real-time deformability cytometry |
| ESR | Erythrocyte sedimentation rate |
| HCT | Hematocrit |
| IFC | Impedance flow cytometry |
| iRBC | Infected red blood cell |
| MCH | Mean corpuscular hemoglobin |
| MCHC | Mean corpuscular hemoglobin concentration |
| MCV | Mean corpuscular volume |
| MNP | Magnetic nanoparticle |
| μ-LaFF | Microfluidic lateral flow filtration |
| μ-PIV | Microparticle image velocimetry |
| nDEP | Negative dielectrophoresis |
| NIQPM | Non-interferometric quantitative phase microscopy |
| PA | Photoacoustic |
| PAFC | Photoacoustic flow cytometry |
| PBMC | Peripheral blood mononuclear cell |
| pDEP | Positive dielectrophoresis |
| PBS | Phosphate-buffered saline |
| PIV | Particle image velocity |
| PLT | Platelet |
| POC | Point of care |
| R-TPM | Rolling tomographic phase microscopy |
| RBC | Red blood cell |
| RT-DC | Real-time deformability cytometry |
| SAWs | Surface acoustic waves |
| SSAWs | Standing surface acoustic waves |
| TPM | Tomographic phase microscopy |
| TSAWs | Traveling pulsed surface acoustic waves |
| WBC | White blood cell |
References
- Geyer, P.E.; Holdt, L.M.; Teupser, D.; Mann, M. Revisiting biomarker discovery by plasma proteomics. Mol. Syst. Biol. 2017, 13, 942. [Google Scholar] [CrossRef] [PubMed]
- Blay, A. Introduction to routine blood tests, normal values and relevance to clinical practice. In Venepuncture and Cannulation; Phillips, S., Collins, M., Dougherty, L.L., Eds.; Wiley Online Books; Wiley-Blackwell: Oxford, UK, 2011; Chapter 9; pp. 223–280. [Google Scholar] [CrossRef]
- Burklund, A.; Tadimety, A.; Nie, Y.; Hao, N.; Zhang, J.X.J.; Makowski, G.S. Chapter One—Advances in diagnostic microfluidics. Adv. Clin. Chem. 2020, 95, 1–72. [Google Scholar] [CrossRef] [PubMed]
- Akceoglu, G.A.; Saylan, Y.; Inci, F. A snapshot of microfluidics in point-of-care diagnostics: Multifaceted integrity with materials and sensors. Adv. Mater. Technol. 2021, 6, 2100049. [Google Scholar] [CrossRef]
- Abbasi, U.; Chowdhury, P.; Subramaniam, S.; Jain, P.; Muthe, N.; Sheikh, F.; Banerjee, S.; Kumaran, V. A cartridge based Point-of-Care device for complete blood count. Sci. Rep. 2019, 9, 18583. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, R.; Sarkar, A.; Bhowmik, A.; Mukherjee, D.; Chakraborty, S. A portable spinning disc for complete blood count (CBC). Biosens. Bioelectron. 2020, 150, 111935. [Google Scholar] [CrossRef]
- Luo, J.; Chen, C.; Li, Q. White blood cell counting at point-of-care testing: A review. Electrophoresis 2020, 41, 1450–1468. [Google Scholar] [CrossRef]
- Wang, M.; Liang, H.; Chen, X.; Chen, D.; Wang, J.; Zhang, Y.; Chen, J. Developments of conventional and microfluidic flow cytometry enabling high-throughput characterization of single cells. Biosensors 2022, 12, 443. [Google Scholar] [CrossRef]
- Béné, M.C. Microfluidics in flow cytometry and related techniques. Int. J. Lab. Hematol. 2017, 39, 93–97. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.-J.; Fu, L.-M.; Hou, H.-H. Review and perspectives on microfluidic flow cytometers. Sens. Actuator B-Chem. 2018, 266, 26–45. [Google Scholar] [CrossRef]
- Daguerre, H.; Solsona, M.; Cottet, J.; Gauthier, M.; Renaud, P.; Bolopion, A. Positional dependence of particles and cells in microfluidic electrical impedance flow cytometry: Origin, challenges and opportunities. Lab Chip 2020, 20, 3665–3689. [Google Scholar] [CrossRef]
- Kuan, D.-H.; Huang, N.-T. Recent advancements in microfluidics that integrate electrical sensors for whole blood analysis. Anal. Methods 2020, 12, 3318–3332. [Google Scholar] [CrossRef] [PubMed]
- Honrado, C.; Bisegna, P.; Swami, N.S.; Caselli, F. Single-cell microfluidic impedance cytometry: From raw signals to cell phenotypes using data analytics. Lab Chip 2021, 21, 22–54. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Zhang, X.; Zhou, Z.; Han, Y.; Xiang, N.; Ni, Z. Microfluidic impedance cytometry for single-cell sensing: Review on electrode configurations. Talanta 2021, 233, 122571. [Google Scholar] [CrossRef]
- Liu, Z.; Lan, X. Microfluidic radiobioassays: A radiometric detection tool for understanding cellular physiology and pharmacokinetics. Lab Chip 2019, 19, 2315–2339. [Google Scholar] [CrossRef]
- Jackson, J.M.; Witek, M.A.; Kamande, J.W.; Soper, S.A. Materials and microfluidics: Enabling the efficient isolation and analysis of circulating tumour cells. Chem. Soc. Rev. 2017, 46, 4245–4280. [Google Scholar] [CrossRef]
- Yu, X.; Wu, N.; Chen, F.; Wei, J.; Zhao, Y. Engineering microfluidic chip for circulating tumor cells: From enrichment, release to single cell analysis. Trac-Trends Anal. Chem. 2019, 117, 27–38. [Google Scholar] [CrossRef]
- Coluccio, M.L.; Perozziello, G.; Malara, N.; Parrotta, E.; Zhang, P.; Gentile, F.; Limongi, T.; Raj, P.M.; Cuda, G.; Candeloro, P.; et al. Microfluidic platforms for cell cultures and investigations. Microelectron. Eng. 2019, 208, 14–28. [Google Scholar] [CrossRef]
- Darwish, N.T.; Sekaran, S.D.; Khor, S.M. Point-of-care tests: A review of advances in the emerging diagnostic tools for dengue virus infection. Sens. Actuator B-Chem. 2018, 255, 3316–3331. [Google Scholar] [CrossRef]
- Qureshi, A.; Niazi, J.H. Biosensors for detecting viral and bacterial infections using host biomarkers: A review. Analyst 2020, 145, 7825–7848. [Google Scholar] [CrossRef]
- Yue, W.-Q.; Tan, Z.; Li, X.-P.; Liu, F.-F.; Wang, C. Micro/nanofluidic technologies for efficient isolation and detection of circulating tumor cells. Trac-Trends Anal. Chem. 2019, 117, 101–115. [Google Scholar] [CrossRef]
- Farshchi, F.; Hasanzadeh, M. Microfluidic biosensing of circulating tumor cells (CTCs): Recent progress and challenges in efficient diagnosis of cancer. Biomed. Pharmacother. 2021, 134, 111153. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Zhang, L.; Liu, J.; Li, Z.; Li, J.; Zhou, W.; Wang, H.; Li, J.; Liu, D.; Yu, X.; et al. Multifunctional microfluidic chip for cancer diagnosis and treatment. Nanotheranostics 2021, 5, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Hussain, S.H.; Huertas, C.S.; Mitchell, A.; Deman, A.-L.; Laurenceau, E. Biosensors for circulating tumor cells (CTCs)-biomarker detection in lung and prostate cancer: Trends and prospects. Biosens. Bioelectron. 2022, 197, 113770. [Google Scholar] [CrossRef]
- Belotti, Y.; Lim, C.T. Microfluidics for liquid biopsies: Recent advances, current challenges, and future directions. Anal. Chem. 2021, 93, 4727–4738. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Li, Y.; Yan, H.; Wen, Y.; Zhou, X.; Friedman, L.; Zeng, Y. Advances in microfluidic extracellular vesicle analysis for cancer diagnostics. Lab Chip 2021, 21, 3219–3243. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.-Y.; Choi, J.-H.; Lim, J.; Lee, S.-N.; Choi, J.-W. Microfluidic chip-based cancer diagnosis and prediction of relapse by detecting circulating tumor cells and circulating cancer stem cells. Cancers 2021, 13, 1385. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Zhang, Z.; Wang, S. Immunomagnetic separation of circulating tumor cells with microfluidic chips and their clinical applications. Biomicrofluidics 2020, 14, 041502. [Google Scholar] [CrossRef]
- Habli, Z.; AlChamaa, W.; Saab, R.; Kadara, H.; Khraiche, M.L. Circulating tumor cell detection technologies and clinical utility: Challenges and opportunities. Cancers 2020, 12, 1930. [Google Scholar] [CrossRef]
- Sachdeva, S.; Davis, R.W.; Saha, A.K. Microfluidic point-of-care testing: Commercial landscape and future directions. Front. Bioeng. Biotechnol. 2021, 8, 1537. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Shehata Draz, M.; Zarghooni, M.; Sanati-Nezhad, A.; Ghavami, S.; Shafiee, H.; Akbari, M. Microfluidic approaches for isolation, detection, and characterization of extracellular vesicles: Current status and future directions. Biosens. Bioelectron. 2017, 91, 588–605. [Google Scholar] [CrossRef] [Green Version]
- Sebastian, B.; Dittrich, P.S. Microfluidics to mimic blood flow in health and disease. Ann. Rev. Fluid Mech. 2018, 50, 483–504. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Y.; Zhao, Y.; Zhang, L.; Zhang, L.; Mao, H.; Huang, C. Nanotechnology-assisted isolation and analysis of circulating tumor cells on microfluidic devices. Micromachines 2020, 11, 774. [Google Scholar] [CrossRef] [PubMed]
- Hochstetter, A. Lab-on-a-chip technologies for the single cell level: Separation, analysis, and diagnostics. Micromachines 2020, 11, 468. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Liu, J.; Yang, X.; Zhang, Q.; Yang, W.; Zhang, H.; Liu, L. Microfluidic-based cancer cell separation using active and passive mechanisms. Microfluid. Nanofluid. 2020, 24, 26. [Google Scholar] [CrossRef]
- Van Berkel, C.; Gwyer, J.D.; Deane, S.; Green, N.G.; Holloway, J.; Hollis, V.; Morgan, H. Integrated systems for rapid point of care (POC) blood cell analysis. Lab Chip 2011, 11, 1249–1255. [Google Scholar] [CrossRef] [Green Version]
- Shukla, V.C.; Kuang, T.-R.; Senthilvelan, A.; Higuita-Castro, N.; Duarte-Sanmiguel, S.; Ghadiali, S.N.; Gallego-Perez, D. Lab-on-a-chip platforms for biophysical studies of cancer with single-cell resolution. Trends Biotechnol. 2018, 36, 549–561. [Google Scholar] [CrossRef]
- Martel, J.M.; Toner, M. Inertial focusing in microfluidics. Ann. Rev. Biomed. Eng. 2014, 16, 371–396. [Google Scholar] [CrossRef] [Green Version]
- Nieuwstadt, H.A.; Seda, R.; Li, D.S.; Fowlkes, J.B.; Bull, J.L. Microfluidic particle sorting utilizing inertial lift force. Biomed. Microdevices 2011, 13, 97–105. [Google Scholar] [CrossRef]
- Dalili, A.; Sattati, A.; Tasnim, N.; Hoorfar, M. Sheath-assisted focusing of microparticles on lab-on-a-chip platforms. Electrophoresis 2020, 41, 2188–2196. [Google Scholar] [CrossRef]
- Reichel, F.; Mauer, J.; Nawaz, A.A.; Gompper, G.; Guck, J.; Fedosov, D.A. High-throughput microfluidic characterization of erythrocyte shapes and mechanical variability. Biophys. J. 2019, 117, 14–24. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Effects of aggregation on blood sedimentation and conductivity. PLoS ONE 2015, 10, e0129337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ying, Y.; Lin, Y. Inertial focusing and separation of particles in similar curved channels. Sci. Rep. 2019, 9, 16575. [Google Scholar] [CrossRef] [Green Version]
- Dincau, B.; Dressaire, E.; Sauret, A. Pulsatile flow in microfluidic systems. Small 2020, 16, 1904032. [Google Scholar] [CrossRef] [PubMed]
- Laxmi, V.; Joshi, S.S.; Agrawal, A. Effect of various parameters on the distribution and extraction of platelets in a microfluidic system. Microfluid. Nanofluid. 2021, 25, 65. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press Inc.: New York, NY, USA, 2008. [Google Scholar]
- Son, Y. Determination of shear viscosity and shear rate from pressure drop and flow rate relationship in a rectangular channel. Polymer 2007, 48, 632–637. [Google Scholar] [CrossRef]
- Pipe, C.J.; Majmudar, T.S.; McKinley, G.H. High shear rate viscometry. Rheol. Acta 2008, 47, 621–642. [Google Scholar] [CrossRef]
- Jung, T.; Yang, S. Highly stable liquid metal-based pressure sensor integrated with a microfluidic channel. Sensors 2015, 15, 11823–11835. [Google Scholar] [CrossRef] [Green Version]
- Chevalier, J.; Ayela, F. Microfluidic on chip viscometers. Rev. Sci. Instrum. 2008, 79, 076102. [Google Scholar] [CrossRef]
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef]
- Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef]
- Asami, K. Characterization of heterogeneous systems by dielectric spectroscopy. Prog. Polym. Sci. 2002, 27, 1617–1659. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical impedance characterization of blood cell suspensions. Part 1: Basic theory and application to two-phase systems. IEEE Trans. Biomed. Eng. 2020, 67, 2956–2978. [Google Scholar] [CrossRef] [PubMed]
- Zhbanov, A.; Yang, S. Electrochemical impedance characterization of blood cell suspensions. Part 2: Three-phase systems with single-shelled particles. IEEE Trans. Biomed. Eng. 2020, 67, 2979–2989. [Google Scholar] [CrossRef] [PubMed]
- Pennock, B.E.; Schwan, H.P. Further observations on the electrical properties of hemoglobin-bound water. J. Phys. Chem. 1969, 73, 2600–2610. [Google Scholar] [CrossRef]
- Xu, J.; Xie, W.; Chen, Y.; Wang, L.; Ma, Q. Dielectric properties of nucleated erythrocytes as simulated by the double spherical-shell model. Chin. Phys. B 2020, 29, 128703. [Google Scholar] [CrossRef]
- Jones, T.B. Basic theory of dielectrophoresis and electrorotation. IEEE Eng. Med. Biol. Mag. 2003, 22, 33–42. [Google Scholar] [CrossRef]
- Lenshof, A.; Laurell, T. Continuous separation of cells and particles in microfluidic systems. Chem. Soc. Rev. 2010, 39, 1203–1217. [Google Scholar] [CrossRef]
- Adekanmbi, E.O.; Srivastava, S.K. Dielectric characterization of bioparticles via electrokinetics: The past, present, and the future. Appl. Phys. Rev. 2019, 6, 041313. [Google Scholar] [CrossRef]
- Yildizhan, Y.; Erdem, N.; Islam, M.; Martinez-Duarte, R.; Elitas, M. Dielectrophoretic separation of live and dead monocytes using 3D carbon-electrodes. Sensors 2017, 17, 2691. [Google Scholar] [CrossRef]
- Afshar, S.; Fazelkhah, A.; Braasch, K.; Salimi, E.; Butler, M.; Thomson, D.J.; Bridges, G.E. Full beta-dispersion region dielectric spectra and dielectric models of viable and non-viable CHO cells. IEEE J. Electromagn. RF Microw. Med. Biol. 2021, 5, 70–77. [Google Scholar] [CrossRef]
- Crowther, C.V.; Hilton, S.H.; Kemp, L.; Hayes, M.A. Isolation and identification of Listeria monocytogenes utilizing DC insulator-based dielectrophoresis. Anal. Chim. Acta 2019, 1068, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Elitas, M.; Sengul, E. Quantifying heterogeneity according to deformation of the U937 monocytes and U937-differentiated macrophages using 3D carbon dielectrophoresis in microfluidics. Micromachines 2020, 11, 576. [Google Scholar] [CrossRef] [PubMed]
- Punjiya, M.; Nejad, H.R.; Mathews, J.; Levin, M.; Sonkusale, S. A flow through device for simultaneous dielectrophoretic cell trapping and AC electroporation. Sci. Rep. 2019, 9, 11988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benhal, P.; Quashie, D.; Kim, Y.; Ali, J. Insulator based dielectrophoresis: Micro, nano, and molecular scale biological applications. Sensors 2020, 20, 5095. [Google Scholar] [CrossRef] [PubMed]
- Ou, X.; Chen, P.; Huang, X.; Li, S.; Liu, B.-F. Microfluidic chip electrophoresis for biochemical analysis. J. Sep. Sci. 2020, 43, 258–270. [Google Scholar] [CrossRef]
- Benhal, P.; Chase, J.G.; Gaynor, P.; Oback, B.; Wang, W. AC electric field induced dipole-based on-chip 3D cell rotation. Lab Chip 2014, 14, 2717–2727. [Google Scholar] [CrossRef]
- Sun, J.; Moore, L.; Xue, W.; Kim, J.; Zborowski, M.; Chalmers, J.J. Correlation of simulation/finite element analysis to the separation of intrinsically magnetic spores and red blood cells using a microfluidic magnetic deposition system. Biotechnol. Bioeng. 2018, 115, 1288–1300. [Google Scholar] [CrossRef]
- Li, F.; Xu, H.; Zhao, Y. Magnetic particles as promising circulating tumor cell catchers assisting liquid biopsy in cancer diagnosis: A review. Trac-Trends Anal. Chem. 2021, 145, 116453. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; González-Fernández, C.; Real, E.; Iles, A.; Bringas, E.; Furlani, E.P.; Ortiz, I. Computational modeling and fluorescence microscopy characterization of a two-phase magnetophoretic microsystem for continuous-flow blood detoxification. Lab Chip 2018, 18, 1593–1606. [Google Scholar] [CrossRef]
- Li, S.; Plouffe, B.D.; Belov, A.M.; Ray, S.; Wang, X.; Murthy, S.K.; Karger, B.L.; Ivanov, A.R. An integrated platform for isolation, processing, and mass spectrometry-based proteomic profiling of rare cells in whole blood. Mol. Cell. Proteom. 2015, 14, 1672–1683. [Google Scholar] [CrossRef] [Green Version]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wottawah, F.; Schinkinger, S.; Lincoln, B.; Ebert, S.; Müller, K.; Sauer, F.; Travis, K.; Guck, J. Characterizing single suspended cells by optorheology. Acta Biomater. 2005, 1, 263–271. [Google Scholar] [CrossRef] [PubMed]
- Atajanov, A.; Zhbanov, A.; Yang, S. Sorting and manipulation of biological cells and the prospects for using optical forces. Micro Nano Syst. Lett. 2018, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Zhu, R.; Avsievich, T.; Popov, A.; Meglinski, I. Optical tweezers in studies of red blood cells. Cells 2020, 9, 545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avsievich, T.; Zhu, R.; Popov, A.; Bykov, A.; Meglinski, I. The advancement of blood cell research by optical tweezers. Rev. Phys. 2020, 5, 100043. [Google Scholar] [CrossRef]
- Shi, Y.; Xiong, S.; Chin, L.K.; Zhang, J.; Ser, W.; Wu, J.; Chen, T.; Yang, Z.; Hao, Y.; Liedberg, B.; et al. Nanometer-precision linear sorting with synchronized optofluidic dual barriers. Sci. Adv. 2018, 4, eaao0773. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Microfluidic-based measurement method of red blood cell aggregation under hematocrit variations. Sensors 2017, 17, 2037. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Dai, L.; Yu, N.; Wu, Y. Red blood cell recognition and posture estimation in microfluidic chip based on lensless imaging. Biomicrofluidics 2021, 15, 034109. [Google Scholar] [CrossRef]
- Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, M.; Ren, L.; Liu, J.; Whitley, P.H.; Wang, L.; Huang, T.J. High-throughput acoustic separation of platelets from whole blood. Lab Chip 2016, 16, 3466–3472. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Ozcelik, A.; Rufo, J.; Wang, Z.; Fang, R.; Huang, T.J. Acoustofluidic separation of cells and particles. Microsyst. Nanoeng. 2019, 5, 32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carey, T.R.; Cotner, K.L.; Li, B.; Sohn, L.L. Developments in label-free microfluidic methods for single-cell analysis and sorting. Wiley Interdiscip. Rev.-Nanomed. Nanobiotechnol. 2019, 11, e1529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catarino, S.O.; Rodrigues, R.O.; Pinho, D.; Miranda, J.M.; Minas, G.; Lima, R. Blood cells separation and sorting techniques of passive microfluidic devices: From fabrication to applications. Micromachines 2019, 10, 593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dalili, A.; Samiei, E.; Hoorfar, M. A review of sorting, separation and isolation of cells and microbeads for biomedical applications: Microfluidic approaches. Analyst 2019, 144, 87–113. [Google Scholar] [CrossRef]
- Shen, Y.; Yalikun, Y.; Tanaka, Y. Recent advances in microfluidic cell sorting systems. Sens. Actuator B-Chem. 2019, 282, 268–281. [Google Scholar] [CrossRef]
- Sun, L.; Yang, W.; Cai, S.; Chen, Y.; Chu, H.; Yu, H.; Wang, Y.; Liu, L. Recent advances in microfluidic technologies for separation of biological cells. Biomed. Microdevices 2020, 22, 55. [Google Scholar] [CrossRef]
- Witek, M.A.; Freed, I.M.; Soper, S.A. Cell separations and sorting. Anal. Chem. 2020, 92, 105–131. [Google Scholar] [CrossRef]
- Pang, L.; Ding, J.; Liu, X.-X.; Yuan, H.; Ge, Y.; Fan, J.; Fan, S.-K. Microstructure-based techniques for single-cell manipulation and analysis. Trac-Trends Anal. Chem. 2020, 129, 115940. [Google Scholar] [CrossRef]
- Pei, H.; Li, L.; Han, Z.; Wang, Y.; Tang, B. Recent advance in microfluidic technologies for circulating tumor cells: From enrichment, single cell analysis to liquid biopsy for clinical applications. Lab Chip 2020, 20, 3854–3875. [Google Scholar] [CrossRef]
- Zhu, S.; Jiang, F.; Han, Y.; Xiang, N.; Ni, Z. Microfluidics for label-free sorting of rare circulating tumor cells. Analyst 2020, 145, 7103–7124. [Google Scholar] [CrossRef]
- Akpe, V.; Kim, T.H.; Brown, C.L.; Cock, I.E. Circulating tumour cells: A broad perspective. J. R. Soc. Interface 2020, 17, 20200065. [Google Scholar] [CrossRef]
- Farahinia, A.; Zhang, W.J.; Badea, I. Novel microfluidic approaches to circulating tumor cell separation and sorting of blood cells: A review. J. Sci. 2021, 6, 303–320. [Google Scholar] [CrossRef]
- He, S.; Wei, J.; Ding, L.; Yang, X.; Wu, Y. State-of-the-arts techniques and current evolving approaches in the separation and detection of circulating tumor cell. Talanta 2022, 239, 123024. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Lee, J.K.; Choi, S. Continuous sorting and washing of cancer cells from blood cells by hydrophoresis. BioChip J. 2016, 10, 81–87. [Google Scholar] [CrossRef]
- Warkiani, M.E.; Khoo, B.L.; Wu, L.; Tay, A.K.P.; Bhagat, A.A.S.; Han, J.; Lim, C.T. Ultra-fast, label-free isolation of circulating tumor cells from blood using spiral microfluidics. Nat. Protoc. 2016, 11, 134–148. [Google Scholar] [CrossRef]
- Abdulla, A.; Liu, W.; Gholamipour-Shirazi, A.; Sun, J.; Ding, X. High-throughput isolation of circulating tumor cells using cascaded inertial focusing microfluidic channel. Anal. Chem. 2018, 90, 4397–4405. [Google Scholar] [CrossRef]
- Lin, E.; Rivera-Báez, L.; Fouladdel, S.; Yoon, H.J.; Guthrie, S.; Wieger, J.; Deol, Y.; Keller, E.; Sahai, V.; Simeone, D.M.; et al. High-throughput microfluidic labyrinth for the label-free isolation of circulating tumor cells. Cell Syst. 2017, 5, 295–304. [Google Scholar] [CrossRef] [Green Version]
- Mena, S.E.; de Beer, M.P.; McCormick, J.; Habibi, N.; Lahann, J.; Burns, M.A. Variable-height channels for microparticle characterization and display. Lab Chip 2020, 20, 2510–2519. [Google Scholar] [CrossRef]
- Xiang, N.; Wang, J.; Li, Q.; Han, Y.; Huang, D.; Ni, Z. Precise size-based cell separation via the coupling of inertial microfluidics and deterministic lateral displacement. Anal. Chem. 2019, 91, 10328–10334. [Google Scholar] [CrossRef]
- Özkayar, G.; Mutlu, E.; Şahin, Ş.; Demircan Yalçın, Y.; Töral, T.; Külah, H.; Yildirim, E.; Zorlu, Ö.; Özgür, E. A novel microfluidic method utilizing a hydrofoil structure to improve circulating tumor cell enrichment: Design and analytical validation. Micromachines 2020, 11, 981. [Google Scholar] [CrossRef]
- Ahmed, H.; Ramesan, S.; Lee, L.; Rezk, A.R.; Yeo, L.Y. On-chip generation of vortical flows for microfluidic centrifugation. Small 2020, 16, 1903605. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Zhu, S.; Cheng, W.; Ni, Z.; Xiang, N. Efficient bioparticle extraction using a miniaturized inertial microfluidic centrifuge. Lab Chip 2022, 22, 3545–3554. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Tian, C.; Li, T.; Xu, J.; Chen, S.-W.; Tu, Q.; Yuan, M.-S.; Liu, W.; Wang, J. Spiral microchannel with ordered micro-obstacles for continuous and highly-efficient particle separation. Lab Chip 2017, 17, 3578–3591. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Zhang, F.; Wang, S.; Wang, J.; Long, D.; Wang, D.; Niu, Y. Ultra-low aspect ratio spiral microchannel with ordered micro-bars for flow-rate insensitive blood plasma extraction. Sens. Actuator B-Chem. 2019, 287, 320–328. [Google Scholar] [CrossRef]
- Bazaz, S.R.; Mihandust, A.; Salomon, R.; Joushani, H.A.N.; Li, W.; Amiri, H.A.; Mirakhorli, F.; Zhand, S.; Shrestha, J.; Miansari, M.; et al. Zigzag microchannel for rigid inertial separation and enrichment (Z-RISE) of cells and particles. Lab Chip 2022, 22, 4093–4109. [Google Scholar] [CrossRef]
- Tang, W.; Zhu, S.; Jiang, D.; Zhu, L.; Yang, J.; Xiang, N. Channel innovations for inertial microfluidics. Lab Chip 2020, 20, 3485–3502. [Google Scholar] [CrossRef]
- Xiang, N.; Ni, Z. Inertial microfluidics: Current status, challenges, and future opportunities. Lab Chip 2022, in press. [CrossRef]
- Jack, R.M.; Grafton, M.M.G.; Rodrigues, D.; Giraldez, M.D.; Griffith, C.; Cieslak, R.; Zeinali, M.; Kumar Sinha, C.; Azizi, E.; Wicha, M.; et al. Ultra-specific isolation of circulating tumor cells enables rare-cell RNA profiling. Adv. Sci. 2016, 3, 1600063. [Google Scholar] [CrossRef]
- Kim, S.H.; Ito, H.; Kozuka, M.; Hirai, M.; Fujii, T. Localization of low-abundant cancer cells in a sharply expanded microfluidic step-channel using dielectrophoresis. Biomicrofluidics 2017, 11, 054114. [Google Scholar] [CrossRef]
- Lee, S.-W.; Hyun, K.-A.; Kim, S.-I.; Kang, J.-Y.; Jung, H.-I. Continuous enrichment of circulating tumor cells using a microfluidic lateral flow filtration chip. J. Chromatogr. A 2015, 1377, 100–105. [Google Scholar] [CrossRef]
- Faustino, V.; Catarino, S.O.; Pinho, D.; Lima, R.A.; Minas, G. A passive microfluidic device based on crossflow filtration for cell separation measurements: A spectrophotometric characterization. Biosensors 2018, 8, 125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, D.; Yi, Q.; Shen, C.; Lan, Y.; Urban, G.; Du, W. Direct enrichment of pathogens from physiological samples of high conductivity and viscosity using H-filter and positive dielectrophoresis. Biomicrofluidics 2018, 12, 014109. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Zhao, H.; Chen, J.; Liu, W.; Li, E.; Wang, Q.; Zhang, L. An integrated microfluidic chip and its clinical application for circulating tumor cell isolation and single-cell analysis. Cytom. Part A 2020, 97, 46–53. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, W.; Lin, Z.; Cai, F.; Li, F.; Wu, J.; Meng, L.; Niu, L.; Zheng, H. Sorting of tumour cells in a microfluidic device by multi-stage surface acoustic waves. Sens. Actuator B-Chem. 2018, 258, 1174–1183. [Google Scholar] [CrossRef]
- Nguyen, N.-V.; Jen, C.-P. Impedance detection integrated with dielectrophoresis enrichment platform for lung circulating tumor cells in a microfluidic channel. Biosens. Bioelectron. 2018, 121, 10–18. [Google Scholar] [CrossRef]
- Cha, H.; Fallahi, H.; Dai, Y.; Yuan, D.; An, H.; Nguyen, N.-T.; Zhang, J. Multiphysics microfluidics for cell manipulation and separation: A review. Lab Chip 2022, 22, 423–444. [Google Scholar] [CrossRef]
- Guo, J.; Chen, L.; Ai, Y.; Cheng, Y.; Li, C.M.; Kang, Y.; Wang, Z. Numerical and experimental characterization of solid-state micropore-based cytometer for detection and enumeration of biological cells. Electrophoresis 2015, 36, 737–743. [Google Scholar] [CrossRef]
- Nguyen, J.; Wei, Y.; Zheng, Y.; Wang, C.; Sun, Y. On-chip sample preparation for complete blood count from raw blood. Lab Chip 2015, 15, 1533–1544. [Google Scholar] [CrossRef]
- Caselli, F.; Reale, R.; De Ninno, A.; Spencer, D.; Morgan, H.; Bisegna, P. Deciphering impedance cytometry signals with neural networks. Lab Chip 2022, 22, 1714–1722. [Google Scholar] [CrossRef]
- Cai, C.; Carey, K.A.; Nedosekin, D.A.; Menyaev, Y.A.; Sarimollaoglu, M.; Galanzha, E.I.; Stumhofer, J.S.; Zharov, V.P. In vivo photoacoustic flow cytometry for early malaria diagnosis. Cytom. Part A 2016, 89, 531–542. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Fernandez, O.; Rodriguez-Trujillo, R.; Gomila, G.; Samitier, J. High-speed counting and sizing of cells in an impedance flow microcytometer with compact electronic instrumentation. Microfluid. Nanofluid. 2014, 16, 91–99. [Google Scholar] [CrossRef]
- Ghassemi, P.; Ren, X.; Foster, B.M.; Kerr, B.A.; Agah, M. Post-enrichment circulating tumor cell detection and enumeration via deformability impedance cytometry. Biosens. Bioelectron. 2020, 150, 111868. [Google Scholar] [CrossRef] [PubMed]
- Reale, R.; De Ninno, A.; Businaro, L.; Bisegna, P.; Caselli, F. High-throughput electrical position detection of single flowing particles/cells with non-spherical shape. Lab Chip 2019, 19, 1818–1827. [Google Scholar] [CrossRef] [PubMed]
- de Bruijn, D.S.; Jorissen, K.F.A.; Olthuis, W.; van den Berg, A. Determining particle size and position in a coplanar electrode setup using measured opacity for microfluidic cytometry. Biosensors 2021, 11, 353. [Google Scholar] [CrossRef] [PubMed]
- Serhatlioglu, M.; Asghari, M.; Tahsin Guler, M.; Elbuken, C. Impedance-based viscoelastic flow cytometry. Electrophoresis 2019, 40, 906–913. [Google Scholar] [CrossRef] [Green Version]
- Kong, C.; Hu, M.; Weerakoon-Ratnayake, K.M.; Witek, M.A.; Dathathreya, K.; Hupert, M.L.; Soper, S.A. Label-free counting of affinity-enriched circulating tumor cells (CTCs) using a thermoplastic micro-Coulter counter (µCC). Analyst 2020, 145, 1677–1686. [Google Scholar] [CrossRef] [PubMed]
- Gnyawali, V.; Strohm, E.M.; Wang, J.-Z.; Tsai, S.S.H.; Kolios, M.C. Simultaneous acoustic and photoacoustic microfluidic flow cytometry for label-free analysis. Sci. Rep. 2019, 9, 1585. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Yu, H.; Wen, Y.; Luo, H.; Jia, B.; Wang, X.; Liu, L.; Li, W.J. Real-time red blood cell counting and osmolarity analysis using a photoacoustic-based microfluidic system. Lab Chip 2021, 21, 2586–2593. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Q.; Hu, X.; Lo, Y. Microfluidic cytometers with integrated on-chip optical systems for red blood cell and platelet counting. Biomicrofluidics 2016, 10, 064119. [Google Scholar] [CrossRef]
- Isiksacan, Z.; Asghari, M.; Elbuken, C. A microfluidic erythrocyte sedimentation rate analyzer using rouleaux formation kinetics. Microfluid. Nanofluid. 2017, 21, 44. [Google Scholar] [CrossRef]
- Sabuncu, A.C.; Muldur, S.; Cetin, B.; Usta, O.B.; Aubry, N. β -Dispersion of blood during sedimentation. Sci. Rep. 2021, 11, 2642. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-S.; Price, H.; Ceballos, S.; Chi, J.-T.; Wax, A. Single cell analysis of stored red blood cells using ultra-high throughput holographic cytometry. Cells 2021, 10, 2455. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Su, X.; Cheng, X.; Wei, Z.; Su, X.; Li, Q. A microfluidic cytometer for white blood cell analysis. Cytom. Part A 2021, 99, 1107–1113. [Google Scholar] [CrossRef] [PubMed]
- Kaliviotis, E.; Dusting, J.; Sherwood, J.M.; Balabani, S. Quantifying local characteristics of velocity, aggregation and hematocrit of human erythrocytes in a microchannel flow. Clin. Hemorheol. Microcirc. 2016, 63, 123–148. [Google Scholar] [CrossRef] [Green Version]
- Isiksacan, Z.; Serhatlioglu, M.; Elbuken, C. In vitro analysis of multiple blood flow determinants using red blood cell dynamics under oscillatory flow. Analyst 2020, 145, 5996–6005. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood. Part 3: A study of the correlation between blood conductivity and sedimentation to shorten the erythrocyte sedimentation rate test. Anal. Methods 2018, 10, 180–189. [Google Scholar] [CrossRef]
- Rubio, A.; Faustino, V.; Cabezas, M.G.; Lima, R.; Vega, E.J. Fire-shaped cylindrical glass micronozzles to measure cell deformability. J. Micromech. Microeng. 2019, 29, 105001. [Google Scholar] [CrossRef]
- Roth, K.B.; Neeves, K.B.; Squier, J.; Marr, D.W.M. High-throughput linear optical stretcher for mechanical characterization of blood cells. Cytom. Part A 2016, 89, 391–397. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, R.O.; Bañobre-López, M.; Gallo, J.; Tavares, P.B.; Silva, A.M.T.; Lima, R.; Gomes, H.T. Haemocompatibility of iron oxide nanoparticles synthesized for theranostic applications: A high-sensitivity microfluidic tool. J. Nanopart. Res. 2016, 18, 194. [Google Scholar] [CrossRef]
- Merola, F.; Memmolo, P.; Miccio, L.; Savoia, R.; Mugnano, M.; Fontana, A.; D’Ippolito, G.; Sardo, A.; Iolascon, A.; Gambale, A.; et al. Tomographic flow cytometry by digital holography. Light-Sci. Appl. 2017, 6, e16241. [Google Scholar] [CrossRef] [Green Version]
- Besedina, N.A.; Skverchinskaya, E.A.; Ivanov, A.S.; Kotlyar, K.P.; Morozov, I.A.; Filatov, N.A.; Mindukshev, I.V.; Bukatin, A.S. Microfluidic characterization of red blood cells microcirculation under oxidative stress. Cells 2021, 10, 3552. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Guo, K.; Jiang, L.; Zhu, S.; Ni, Z.; Xiang, N. Microfluidic deformability cytometry: A review. Talanta 2023, 251, 123815. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Li, J.; Wen, J.; Cheng, L.; Hu, Y.; Zhang, Y.; Wan, N.; Takei, M. Quantitative evaluation of burn injuries based on electrical impedance spectroscopy of blood with a seven-parameter equivalent circuit. Sensors 2021, 21, 1496. [Google Scholar] [CrossRef] [PubMed]
- Caduff, A.; Ben Ishai, P.; Feldman, Y. Continuous noninvasive glucose monitoring; water as a relevant marker of glucose uptake in vivo. Biophys. Rev. 2019, 11, 1017–1035. [Google Scholar] [CrossRef]
- Pedro, B.G.; Marcôndes, D.W.; Bertemes-Filho, P. Analytical model for blood glucose detection using electrical impedance spectroscopy. Sensors 2020, 20, 6928. [Google Scholar] [CrossRef]
- Lee, Y.S.; Son, M.; Zhbanov, A.; Jung, Y.; Jung, M.H.; Eom, K.; Nam, S.H.; Park, J.; Yang, S. Temperature correction to enhance blood glucose monitoring accuracy using electrical impedance spectroscopy. Sensors 2020, 20, 6231. [Google Scholar] [CrossRef]
- Liu, J.; Qiang, Y.; Alvarez, O.; Du, E. Electrical impedance characterization of erythrocyte response to cyclic hypoxia in sickle cell disease. ACS Sensors 2019, 4, 1783–1790. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Qiang, Y.; Du, E. Dielectric spectroscopy of red blood cells in sickle cell disease. Electrophoresis 2021, 42, 667–675. [Google Scholar] [CrossRef]
- Aghaamoo, M.; Aghilinejad, A.; Chen, X.; Xu, J. On the design of deterministic dielectrophoresis for continuous separation of circulating tumor cells from peripheral blood cells. Electrophoresis 2019, 40, 1486–1493. [Google Scholar] [CrossRef]
- Torres-Castro, K.; Honrado, C.; Varhue, W.B.; Farmehini, V.; Swami, N.S. High-throughput dynamical analysis of dielectrophoretic frequency dispersion of single cells based on deflected flow streamlines. Anal. Bioanal. Chem. 2020, 412, 3847–3857. [Google Scholar] [CrossRef]
- Pradhan, R.; Raisa, S.A.; Kumar, P.; Kalkal, A.; Kumar, N.; Packirisamy, G.; Manhas, S. Optimization, fabrication, and characterization of four electrode-based sensors for blood impedance measurement. Biomed. Microdev. 2021, 23, 9. [Google Scholar] [CrossRef] [PubMed]
- Puttaswamy, S.V.; Bhalla, N.; Kelsey, C.; Lubarsky, G.; Lee, C.; McLaughlin, J. Independent and grouped 3D cell rotation in a microfluidic device for bioimaging applications. Biosens. Bioelectron. 2020, 170, 112661. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Murillo, C.J.; de los Santos-Ramirez, J.M.; Perez-Gonzalez, V.H. Toward low-voltage dielectrophoresis-based microfluidic systems: A review. Electrophoresis 2021, 42, 565–587. [Google Scholar] [CrossRef] [PubMed]
- Yalçın, Y.D.; Sukas, S.; Töral, T.B.; Gündüz, U.; Külah, H. Exploring the relationship between cytoplasmic ion content variation and multidrug resistance in cancer cells via ion-release based impedance spectroscopy. Sens. Actuator B-Chem. 2019, 290, 180–187. [Google Scholar] [CrossRef]
- Li, W.; Zhu, B.; Cai, Y.; Wu, Z.; Sun, L.; Yang, H. Analysis of red blood cell deformability using parallel ladder electrodes in a microfluidic manipulation system. Int. J. Adv. Manuf. Technol. 2019, 105, 4919–4928. [Google Scholar] [CrossRef]
- Yao, Z.; Kwan, C.C.; Poon, A.W. An optofluidic “tweeze-and-drag” cell stretcher in a microfluidic channel. Lab Chip 2020, 20, 601–613. [Google Scholar] [CrossRef] [Green Version]
- Fregin, B.; Czerwinski, F.; Biedenweg, D.; Girardo, S.; Gross, S.; Aurich, K.; Otto, O. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun. 2019, 10, 415. [Google Scholar] [CrossRef] [Green Version]
- Jacobi, A.; Rosendahl, P.; Kräter, M.; Urbanska, M.; Herbig, M.; Guck, J. Analysis of biomechanical properties of hematopoietic stem and progenitor cells using real-time fluorescence and deformability cytometry. In Stem Cell Mobilization. Methods in Molecular Biology; Klein, G.G., Wuchter, P., Eds.; Springer: New York, NY, USA, 2019; Volume 2017, pp. 135–148. [Google Scholar] [CrossRef]
- Feng, Y.; Chai, H.; He, W.; Liang, F.; Cheng, Z.; Wang, W. Impedance-Enabled Camera-Free Intrinsic Mechanical Cytometry. Small Methods 2022, 6, 2200325. [Google Scholar] [CrossRef]
- Mietke, A.; Otto, O.; Girardo, S.; Rosendahl, P.; Taubenberger, A.; Golfier, S.; Ulbricht, E.; Aland, S.; Guck, J.; Fischer-Friedrich, E. Extracting cell stiffness from real-time deformability cytometry: Theory and experiment. Biophys. J. 2015, 109, 2023–2036. [Google Scholar] [CrossRef] [Green Version]
- Mokbel, M.; Mokbel, D.; Mietke, A.; Träber, N.; Girardo, S.; Otto, O.; Guck, J.; Aland, S. Numerical simulation of real-time deformability cytometry to extract cell mechanical properties. ACS Biomater. Sci. Eng. 2017, 3, 2962–2973. [Google Scholar] [CrossRef]
- Kucukal, E.; Man, Y.; Hill, A.; Liu, S.; Bode, A.; An, R.; Kadambi, J.; Little, J.A.; Gurkan, U.A. Whole blood viscosity and red blood cell adhesion: Potential biomarkers for targeted and curative therapies in sickle cell disease. Am. J. Hematol. 2020, 95, 1246–1256. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J. Microfluidic-based biosensor for blood viscosity and erythrocyte sedimentation rate using disposable fluid delivery system. Micromachines 2020, 11, 215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, Y.J. Blood viscoelasticity measurement using interface variations in coflowing streams under pulsatile blood flows. Micromachines 2020, 11, 245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, Y.J. Experimental investigation of air compliance effect on measurement of mechanical properties of blood sample flowing in microfluidic channels. Micromachines 2020, 11, 460. [Google Scholar] [CrossRef]
- Pinho, D.; Carvalho, V.; Gonçalves, I.M.; Teixeira, S.; Lima, R. Visualization and measurements of blood cells flowing in microfluidic systems and blood rheology: A personalized medicine perspective. J. Pers. Med. 2020, 10, 249. [Google Scholar] [CrossRef]
- Solomon, D.E.; Abdel-Raziq, A.; Vanapalli, S.A. A stress-controlled microfluidic shear viscometer based on smartphone imaging. Rheol. Acta 2016, 55, 727–738. [Google Scholar] [CrossRef]
- Kim, B.J.; Lee, S.Y.; Jee, S.; Atajanov, A.; Yang, S. Micro-viscometer for measuring shear-varying blood viscosity over a wide-ranging shear rate. Sensors 2017, 17, 1442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, B.J.; Lee, S.Y.; Zhbanov, A.; Yang, S. A physiometer for simultaneous measurement of whole blood viscosity and its determinants: Hematocrit and red blood cell deformability. Analyst 2019, 144, 3144–3157. [Google Scholar] [CrossRef]
- Trejo-Soto, C.; Lázaro, G.R.; Pagonabarraga, I.; Hernández-Machado, A. Microfluidics approach to the mechanical properties of red blood cell membrane and their effect on blood rheology. Membranes 2022, 12, 217. [Google Scholar] [CrossRef]
- Pinho, D.; Yaginuma, T.; Lima, R. A microfluidic device for partial cell separation and deformability assessment. BioChip J. 2013, 7, 367–374. [Google Scholar] [CrossRef] [Green Version]
- King, M.R.; Phillips, K.G.; Mitrugno, A.; Lee, T.-R.; de Guillebon, A.M.E.; Chandrasekaran, S.; McGuire, M.J.; Carr, R.T.; Baker-Groberg, S.M.; Rigg, R.A.; et al. A physical sciences network characterization of circulating tumor cell aggregate transport. Am. J. Physiol.-Cell Physiol. 2015, 308, C792–C802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, W.; Zhang, K.; Yang, X.; Liu, L.; Yu, H.; Zhang, W. Distinctive translational and self-rotational motion of lymphoma cells in an optically induced non-rotational alternating current electric field. Biomicrofluidics 2015, 9, 014121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, W.; Wang, Y.; Zhang, H.; Liu, L. Characterization of the self-rotational motion of stored red blood cells by using optically-induced electrokinetics. Opt. Lett. 2016, 41, 2763–2766. [Google Scholar] [CrossRef] [PubMed]
- Apichitsopa, N.; Jaffe, A.; Voldman, J. Multiparameter cell-tracking intrinsic cytometry for single-cell characterization. Lab Chip 2018, 18, 1430–1439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, Y.; Huang, L.; Zhao, P.; Liang, F.; Wang, W. A microfluidic device integrating impedance flow cytometry and electric impedance spectroscopy for high-efficiency single-cell electrical property measurement. Anal. Chem. 2019, 91, 15204–15212. [Google Scholar] [CrossRef]
- Huang, L.; Liang, F.; Feng, Y.; Zhao, P.; Wang, W. On-chip integrated optical stretching and electrorotation enabling single-cell biophysical analysis. Microsyst. Nanoeng. 2020, 6, 57. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Sun, X.; Chen, D.; Wang, J.; Chen, J. Development of microfluidic platform capable of characterizing cytoplasmic viscosity, cytoplasmic conductivity and specific membrane capacitance of single cells. Microfluid. Nanofluid. 2020, 24, 45. [Google Scholar] [CrossRef]
- Lin, J.-H.; Tsai, T.-T.; Zeng, Q.; Chang, C.-Y.; Guo, J.-Y.; Lin, C.-J.; Chen, C.-F. A multifunctional microfluidic device for blood typing and primary screening of blood diseases. ACS Sens. 2020, 5, 3082–3090. [Google Scholar] [CrossRef]
- Honrado, C.; Ciuffreda, L.; Spencer, D.; Ranford-Cartwright, L.; Morgan, H. Dielectric characterization of Plasmodium falciparum-infected red blood cells using microfluidic impedance cytometry. J. R. Soc. Interface 2018, 15, 20180416. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yang, D.; Zhou, Y.; Khoo, B.L.; Han, J. Characterizing deformability and electrical impedance of cancer cells in a microfluidic device. Anal. Chem. 2018, 90, 912–919. [Google Scholar] [CrossRef]
- Wang, K.; Sun, X.; Zhang, Y.; Wei, Y.; Chen, D.; Wu, H.; Song, Z.; Long, R.; Wang, J.; Chen, J. Microfluidic cytometry for high-throughput characterization of single cell cytoplasmic viscosity using crossing constriction channels. Cytom. Part A 2020, 97, 630–637. [Google Scholar] [CrossRef] [PubMed]
- Sharifi Noghabi, H.; Soo, M.; Khamenehfar, A.; Li, P.C.H. Dielectrophoretic trapping of single leukemic cells using the conventional and compact optical measurement systems. Electrophoresis 2019, 40, 1478–1485. [Google Scholar] [CrossRef] [PubMed]
- Doan, M.; Vorobjev, I.; Rees, P.; Filby, A.; Wolkenhauer, O.; Goldfeld, A.E.; Lieberman, J.; Barteneva, N.; Carpenter, A.E.; Hennig, H. Diagnostic potential of imaging flow cytometry. Trends Biotechnol. 2018, 36, 649–652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Li, S.; Liu, Y. Machine learning-driven multiobjective optimization: An opportunity of microfluidic platforms applied in cancer research. Cells 2022, 11, 905. [Google Scholar] [CrossRef]
- Honrado, C.; McGrath, J.S.; Reale, R.; Bisegna, P.; Swami, N.S.; Caselli, F. A neural network approach for real-time particle/cell characterization in microfluidic impedance cytometry. Anal. Bioanal. Chem. 2020, 412, 3835–3845. [Google Scholar] [CrossRef]
- Herbig, M.; Nawaz, A.A.; Urbanska, M.; Nötzel, M.; Kräter, M.; Rosendahl, P.; Herold, C.; Töpfner, N.; Kubankova, M.; Goswami, R.; et al. Image-based cell sorting using artificial intelligence. Proc. SPIE 2020, 11250, 112500J. [Google Scholar] [CrossRef]
- Rizzuto, V.; Mencattini, A.; Álvarez-González, B.; Di Giuseppe, D.; Martinelli, E.; Beneitez-Pastor, D.; del Mar Mañú-Pereira, M.; Lopez-Martinez, M.J.; Samitier, J. Combining microfluidics with machine learning algorithms for RBC classification in rare hereditary hemolytic anemia. Sci. Rep. 2021, 11, 13553. [Google Scholar] [CrossRef]
- Jou, H.-J.; Chou, L.-Y.; Chang, W.-C.; Ho, H.-C.; Zhang, W.-T.; Ling, P.-Y.; Tsai, K.-H.; Chen, S.-H.; Chen, T.-H.; Lo, P.-H.; et al. An automatic platform based on nanostructured microfluidic chip for isolating and identification of circulating tumor cells. Micromachines 2021, 12, 473. [Google Scholar] [CrossRef]
- Baur, M.; Reisbeck, M.; Hayden, O.; Utschick, W. Joint particle detection and analysis by a cnn and adaptive norm minimization approach. IEEE Trans. Biomed. Eng. 2022. early access. [Google Scholar] [CrossRef]
- Szydzik, C.; Brazilek, R.J.; Nesbitt, W.S. A review of design considerations for hemocompatibility within microfluidic systems. Semin. Thromb. Hemost. 2020, 46, 622–636. [Google Scholar] [CrossRef]
- Nie, J.; Fu, J.; He, Y. Hydrogels: The next generation body materials for microfluidic chips? Small 2020, 16, 2003797. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, C.; Chu, P.K.; Gelinsky, M. 3D printing of hydrogels: Rational design strategies and emerging biomedical applications. Mater. Sci. Eng. R-Rep. 2020, 140, 100543. [Google Scholar] [CrossRef]
- Lui, Y.S.; Sow, W.T.; Tan, L.P.; Wu, Y.; Lai, Y.; Li, H. 4D printing and stimuli-responsive materials in biomedical applications. Acta Biomater. 2019, 92, 19–36. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Qiao, Z.; Nazarzadeh Zare, E.; Huang, J.; Zheng, X.; Sun, X.; Shao, M.; Wang, H.; Wang, X.; Chen, D.; et al. 4D-printed dynamic materials in biomedical applications: Chemistry, challenges, and their future perspectives in the clinical sector. J. Med. Chem. 2020, 63, 8003–8024. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Onck, P.; den Toonder, J. A concise review of microfluidic particle manipulation methods. Microfluid. Nanofluid. 2020, 24, 24. [Google Scholar] [CrossRef] [Green Version]
- Soto, F.; Wang, J.; Ahmed, R.; Demirci, U. Medical micro/nanorobots in precision medicine. Adv. Sci. 2020, 7, 2002203. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Zhbanov, A.; Yang, S. Microfluidic Systems for Blood and Blood Cell Characterization. Biosensors 2023, 13, 13. https://doi.org/10.3390/bios13010013
Kim H, Zhbanov A, Yang S. Microfluidic Systems for Blood and Blood Cell Characterization. Biosensors. 2023; 13(1):13. https://doi.org/10.3390/bios13010013
Chicago/Turabian StyleKim, Hojin, Alexander Zhbanov, and Sung Yang. 2023. "Microfluidic Systems for Blood and Blood Cell Characterization" Biosensors 13, no. 1: 13. https://doi.org/10.3390/bios13010013
APA StyleKim, H., Zhbanov, A., & Yang, S. (2023). Microfluidic Systems for Blood and Blood Cell Characterization. Biosensors, 13(1), 13. https://doi.org/10.3390/bios13010013







