Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes
Abstract
:1. Introduction
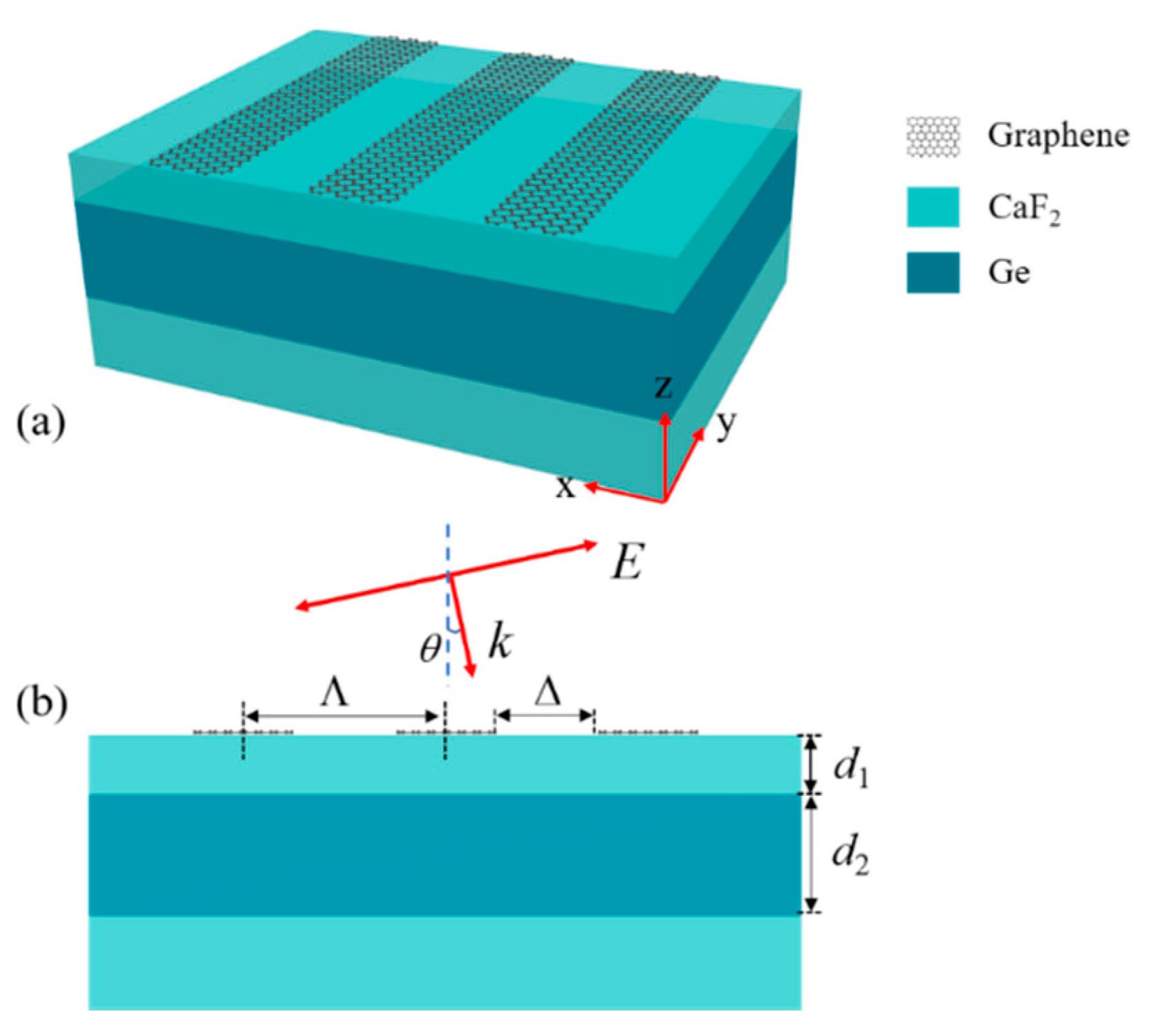
2. Structure and Theoretical Model
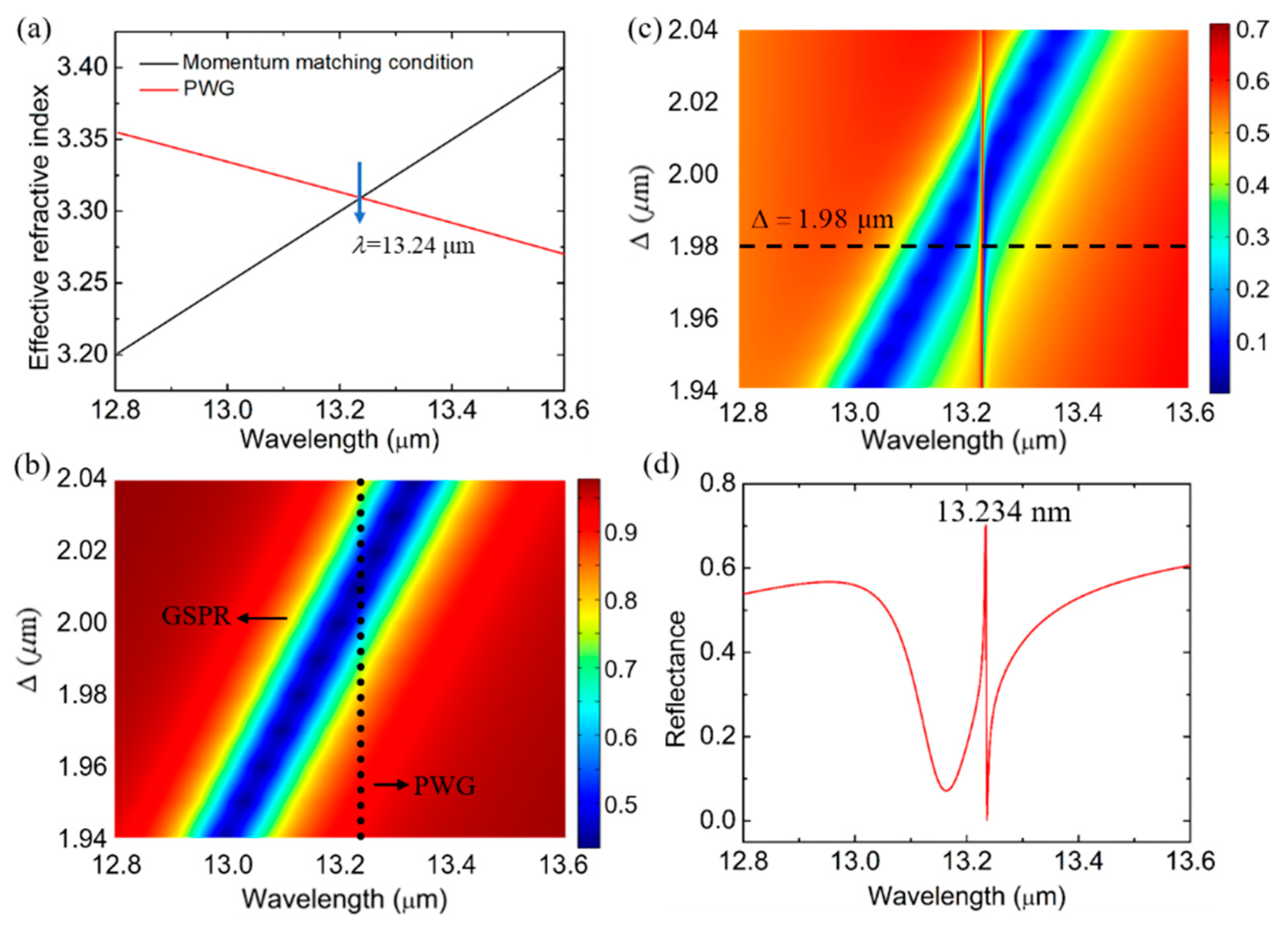
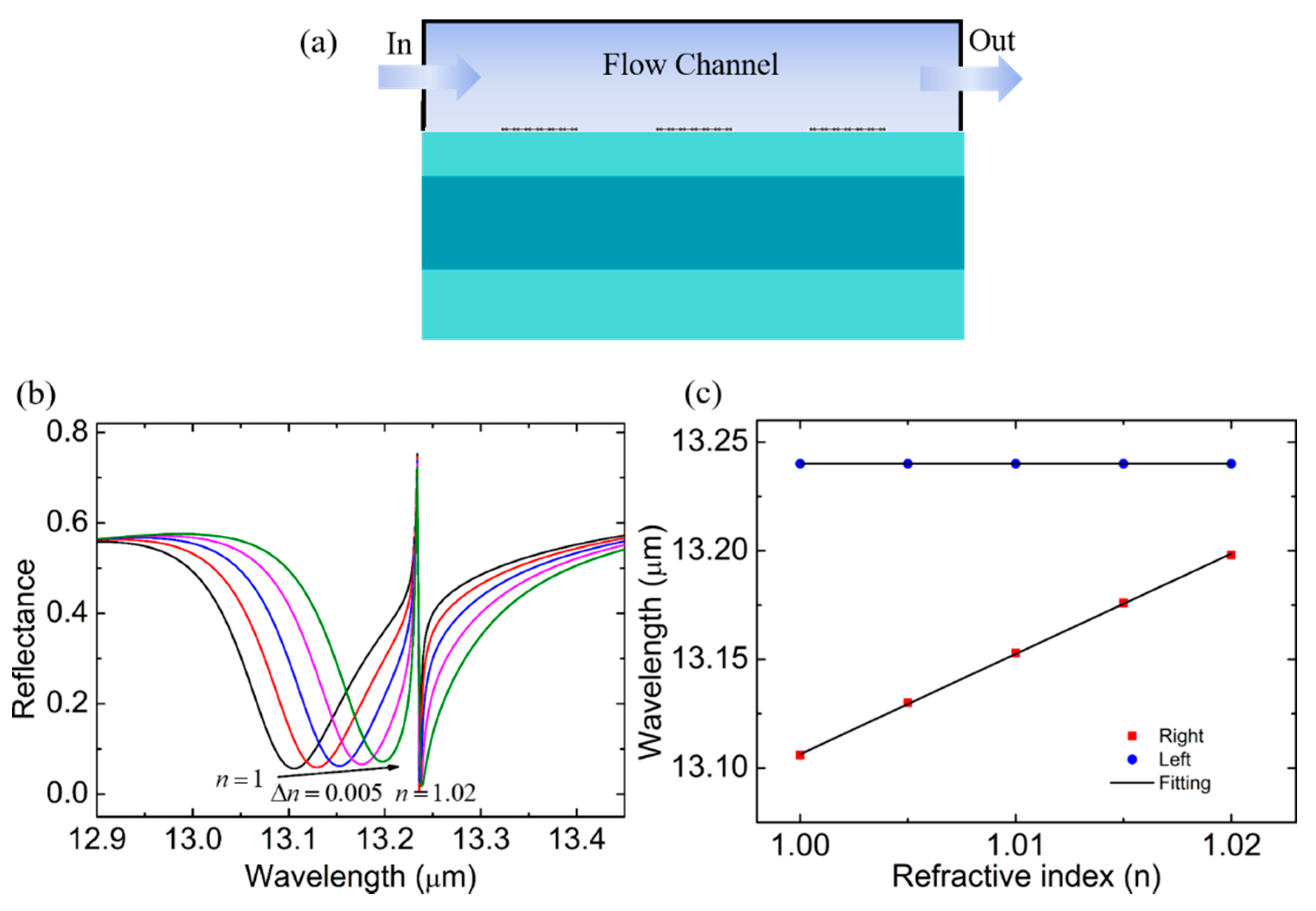
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Liu, L.; Han, Z.; He, S. Novel surface plasmon waveguide for high integration. Opt. Express 2005, 13, 6645–6650. [Google Scholar] [CrossRef]
- Tyagi, D.; Chen, T.; Huang, C. Polarization-Enabled Steering of Surface Plasmons Using Crossed Reciprocal Nanoantennas. Laser Photonics Rev. 2020, 14, 2000076. [Google Scholar] [CrossRef]
- Gao, E.; Liu, Z.; Li, H.; Xu, H.; Zhang, Z.; Luo, X.; Xiong, C.; Liu, C.; Zhang, B.; Zhou, F. Dynamically tunable dual plasmon-induced transparency and absorption based on a single-layer patterned graphene metamaterial. Opt. Express 2019, 27, 13884–13894. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Li, M.; Ruan, B.; Zhang, B.; Wu, K. Plasmonic biosensor based on excellently absorbable adjustable plasmon-induced transparency in black phosphorus and graphene metamaterials. New J. Phys. 2020, 22, 073049. [Google Scholar] [CrossRef]
- Xiong, C.; Li, H.; Xu, H.; Zhao, M.; Zhang, B.; Liu, C.; Wu, K. Coupling effects in single-mode and multimode resonator-coupled system. Opt. Express 2019, 27, 17718–17728. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Li, Z.; Li, C.; Xue, W.; Cui, W. Ultra-high sensitivity sensing based on ultraviolet plasmonic enhancements in semiconductor triangular prism meta-antenna systems. Opt. Express 2020, 28, 17595–17610. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, E.; Zhang, X.; Li, H.; Xu, H.; Zhang, Z.; Luo, X.; Zhou, F. Terahertz electro-optical multi-functional modulator and its coupling mechanisms based on upper-layer double graphene ribbons and lower-layer a graphene strip. New J. Phys. 2020, 22, 053039. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, Z.; Zhu, M.; Huang, T.; Zeng, S.; Pan, J.; Song, C.; Wang, Y.; Shum, P.P. Study on the dual-Fano resonance generation and its potential for self-calibrated sensing. Opt. Express 2020, 28, 23703–23716. [Google Scholar] [CrossRef]
- Wu, L.; Guo, J.; Xu, H.; Dai, X.; Xiang, Y. Ultrasensitive biosensors based on long-range surface plasmon polariton and dielectric waveguide modes. Photonics Res. 2016, 4, 262–266. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Sekkat, Z. Fano resonance and plasmon-induced transparency in waveguide-coupled surface plasmon resonance sensors. Appl. Phys. Express 2015, 8, 022201. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Song, C.; Hang, J.; Hu, Z.; Zhang, F. Tunable Fano resonance based on grating coupled and graphene-based Otto configuration. Opt. Express 2017, 25, 23880–23892. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Jiang, L.; Dai, X.; Xiang, Y. Tunable Fano resonances of a graphene/waveguide hybrid structure at mid-infrared wavelength. Opt. Express 2016, 24, 4740–4748. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Guo, X.; Zhang, G.; Balakin, A.; Shkurinov, A.; Yu, A.; Zhun, Y. Excitation of graphene surface plasmons polaritons by guided-mode resonances with high efficiency. Opt. Express 2020, 28, 13224–13233. [Google Scholar] [CrossRef] [PubMed]
- Briones-Torres, J.A.; Perez-Alvarez, R.; Pernas-Salomon, R.; Rodriguez-Vargas, I. Enhancement of the Fano-resonance response in bilayer graphene single and double barriers induced by bandgap opening. Phys. E Low Dimens. Syst. Nanostruct. 2020, 119, 113999. [Google Scholar] [CrossRef]
- Arruda, T.; Bachelard, R.; Weiner, J.; Courteille, P. Tunable Fano resonances in the decay rates of a pointlike emitter near a graphene-coated nanowire. Phys. Rev. B 2018, 98, 245419. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.; Zeng, S.; Zhao, X.; Cheng, Z.; Shum, P. Fano Resonance Enhanced Surface Plasmon Resonance Sensors Operating in Near-Infrared. Photonics 2018, 5, 23. [Google Scholar] [CrossRef] [Green Version]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Yadav, S.; Devi, A.; De, A.K. Synergistic effect of Fano resonance and optical nonlinearity in laser trapping of silver nanoparticles. Phys. Rev. A 2020, 102, 043511. [Google Scholar] [CrossRef]
- Fu, T.; Liu, F.; An, Y.B.; Li, Q.; Li, H.; Sun, T.; Xiao, G.; Muhammad, N. Separately tuning of double Fano resonances in facile asymmetric slit metasurface. Appl. Phys. Express 2020, 13, 052009. [Google Scholar] [CrossRef]
- Zheng, S.; Cao, X.; Wang, J. Multimode Fano resonances for low-power mode switching. Opt. Lett. 2020, 45, 1035–1038. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, H.; Lin, W.; Wang, Y.; Liu, B. Laser-Controlled Fano Resonance Sensing Based on WGM Coupling in Eccentric Hole Fibers Integrated with Azobenzene. J. Lightwave Technol. 2021, 39, 320–327. [Google Scholar] [CrossRef]
- Lalanne, P. Improved formulation of the coupled-wave method for two dimensional gratings. J. Opt. Soc. Am. A 1997, 14, 1592–1598. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Tan, K.H. The profile optimization of periodic nano-structures for wavelength-selective thermophotovoltaic emitters. Int. J. Heat Mass Transf. 2010, 53, 5542–5551. [Google Scholar] [CrossRef]
- Soydan, M.C.; Ghobadi, A.; Yildirim, D.U.; Duman, E.S.; Bek, A.; Erturk, V.B.; Ozbay, E. Lithography-Free Random Bismuth Nanostructures for Full Solar Spectrum Harvesting and Mid-Infrared Sensing. Adv. Opt. Mater. 2020, 8, 1901203. [Google Scholar] [CrossRef]
- Babayigit, C.; Boztug, C.; Kurt, H.; Turduev, M. Fabry–Pérot Microtube Cavity Structure for Optical Sensing at Mid-infrared Spectrum. IEEE Sens. J. 2020, 20, 2390–2397. [Google Scholar] [CrossRef]
- Chau, Y.F.C. Mid-infrared sensing properties of a plasmonic metal–insulator–metal waveguide with a single stub including defects. J. Phys. D Appl. Phys. 2020, 53, 115401. [Google Scholar] [CrossRef]
- Li, H.; Ying, Z.; Lyu, B.; Deng, A.; Wang, L.; Taniguchi, T.; Watanabe, K.; Shi, Z. Electrode-Free Anodic Oxidation Nanolithography of Low-Dimensional Materials. Nano Lett. 2018, 18, 8011–8015. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, L.; Cui, W.; Chen, M.; Zou, S. Ultra-narrow electromagnetically induced transparency in the visible and near-infrared regions. Appl. Phys. Lett. 2019, 114, 213103. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Ruan, B.; Xiang, Y. Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes. Biosensors 2021, 11, 400. https://doi.org/10.3390/bios11100400
Dai X, Ruan B, Xiang Y. Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes. Biosensors. 2021; 11(10):400. https://doi.org/10.3390/bios11100400
Chicago/Turabian StyleDai, Xiaoyu, Banxian Ruan, and Yuanjiang Xiang. 2021. "Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes" Biosensors 11, no. 10: 400. https://doi.org/10.3390/bios11100400
APA StyleDai, X., Ruan, B., & Xiang, Y. (2021). Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes. Biosensors, 11(10), 400. https://doi.org/10.3390/bios11100400




