Nanoparticle Deposition in Rhythmically Moving Acinar Models with Interalveolar Septal Apertures
Abstract
1. Introduction
2. Methods
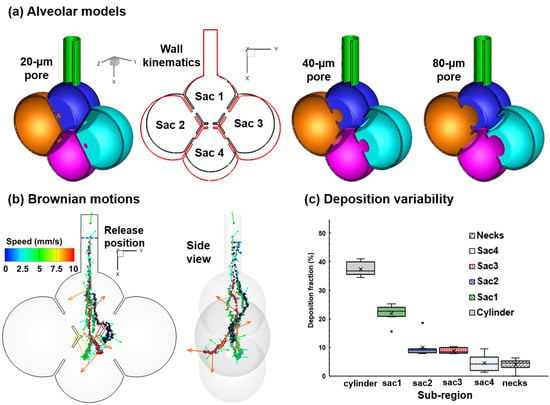
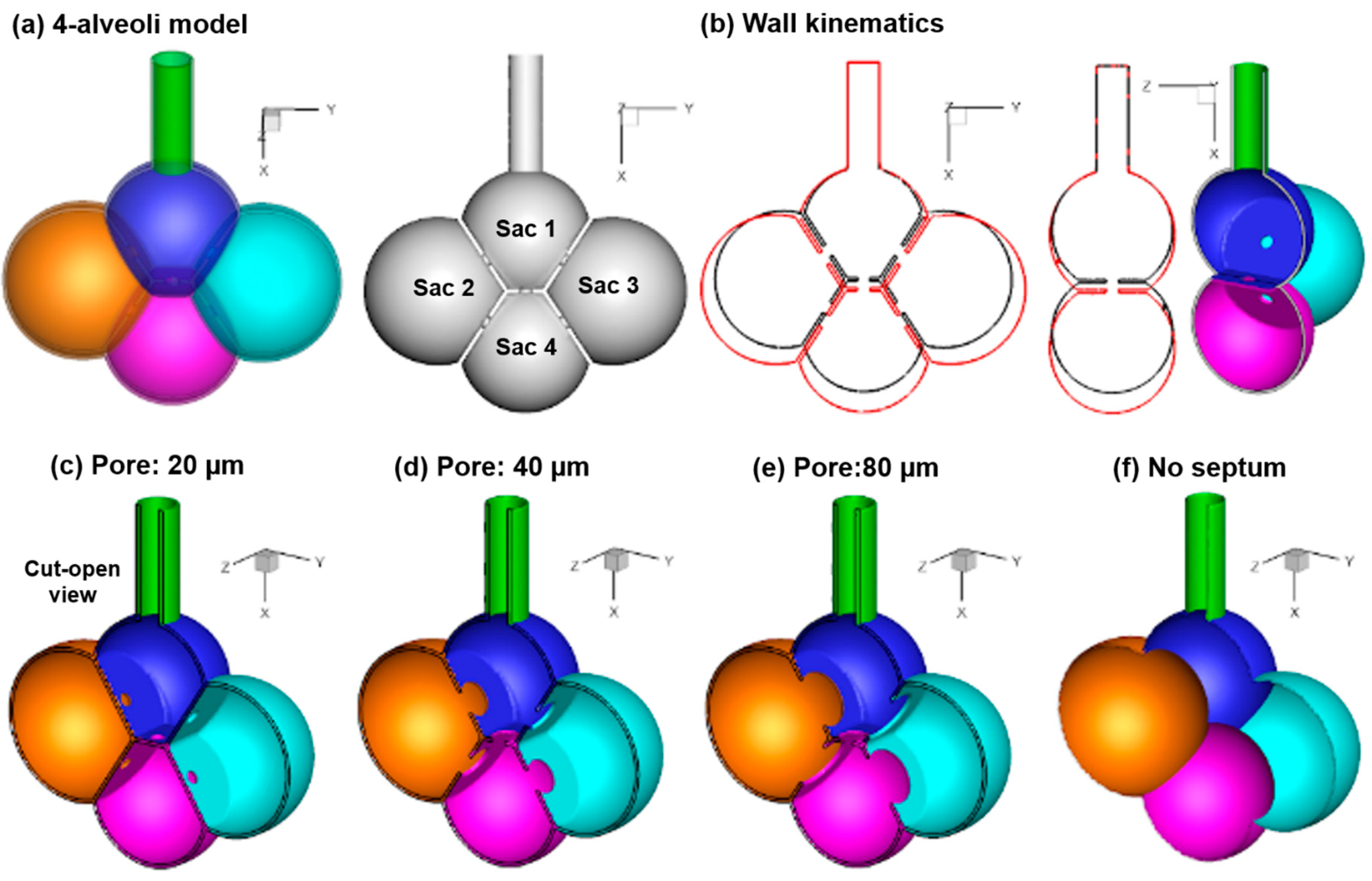
2.1. Alveolar Model and Wall Kinematics
2.2. Airflow and Nanoparticle Transport Models
2.3. Numerical Methods
3. Results
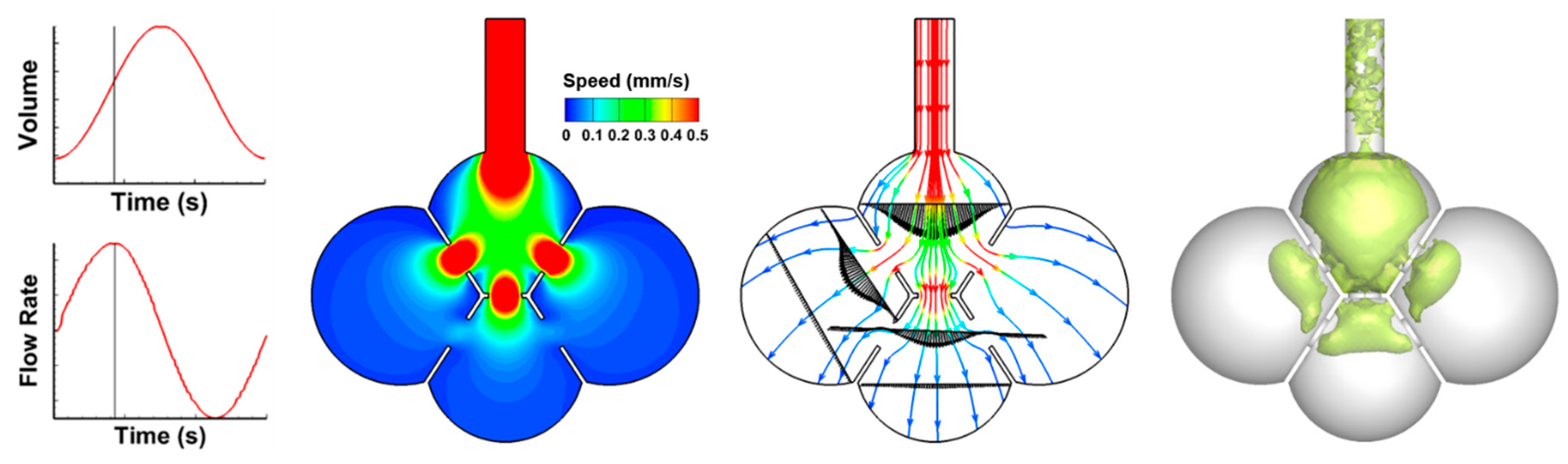
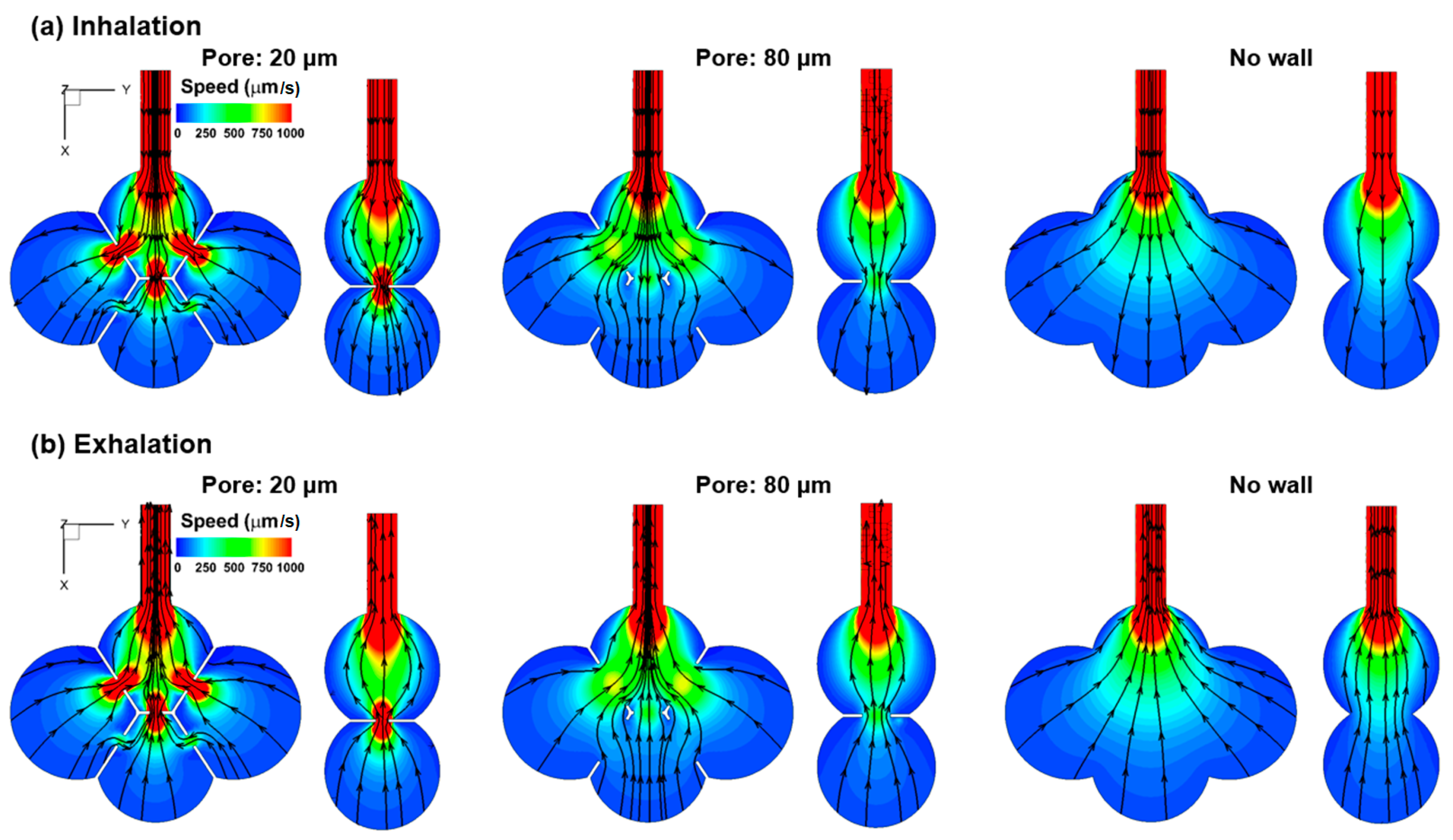
3.1. Airflow Field
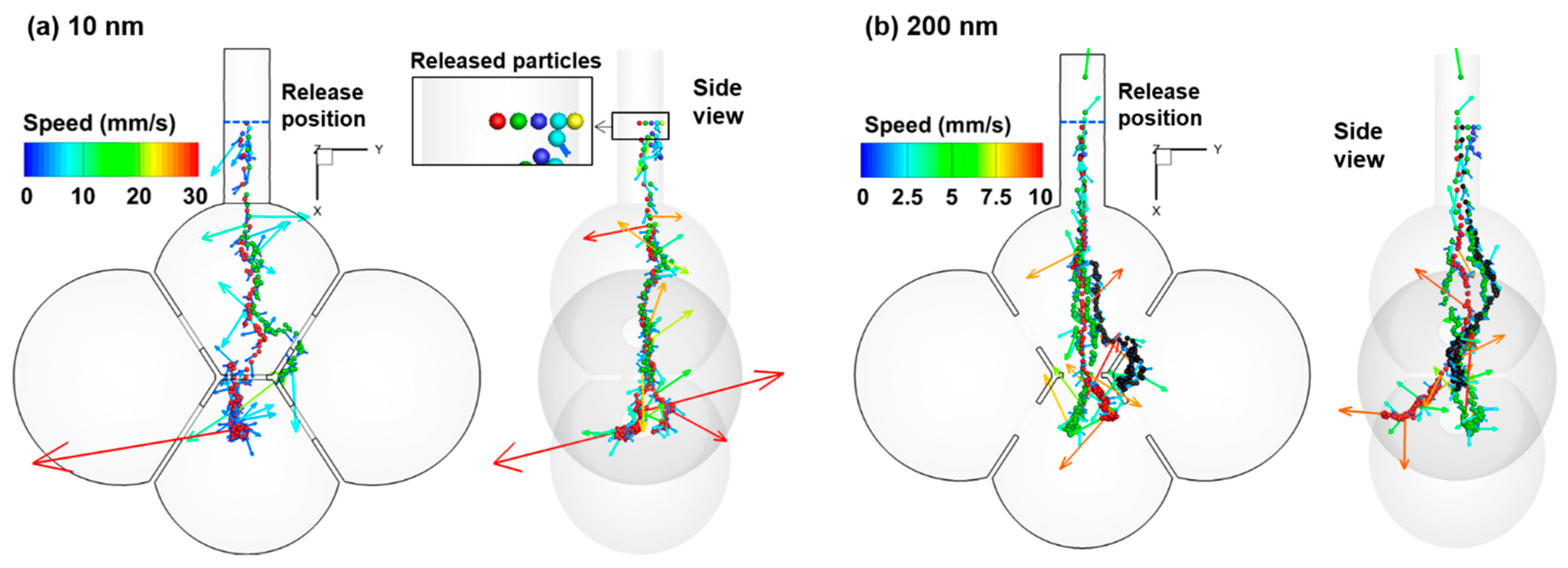
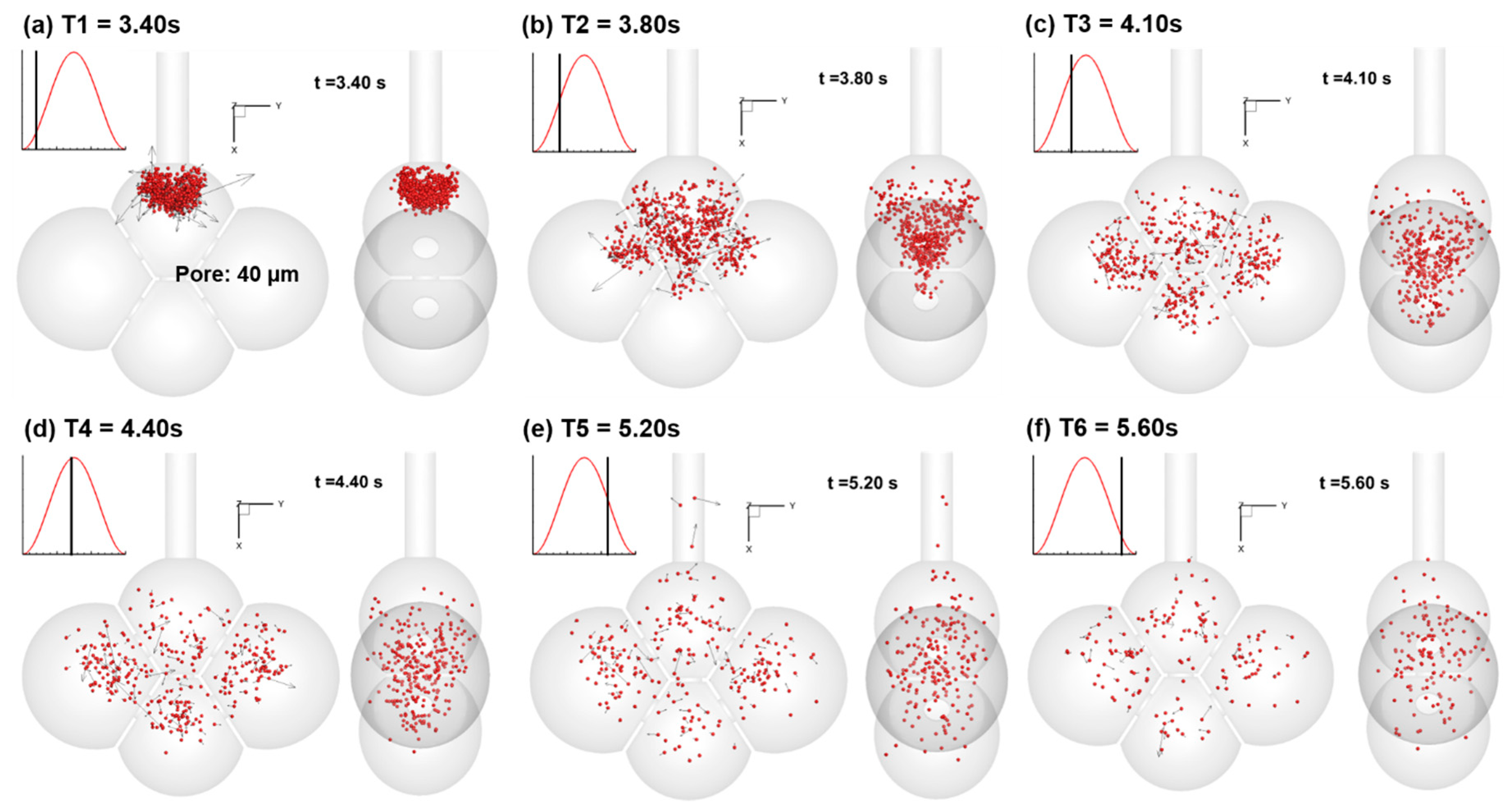
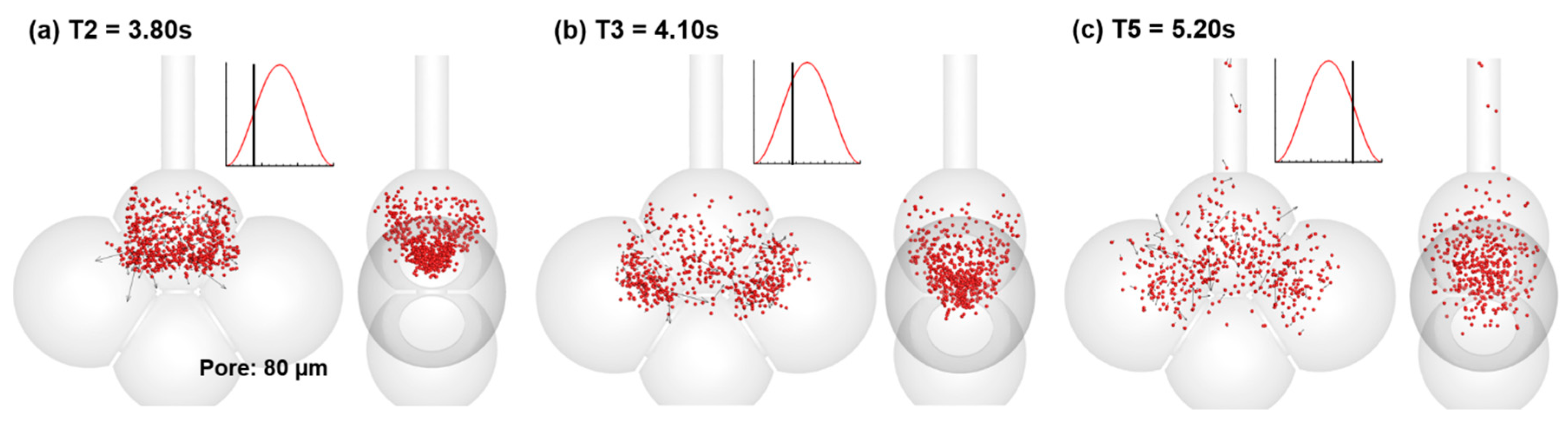
3.2. Particle Motion
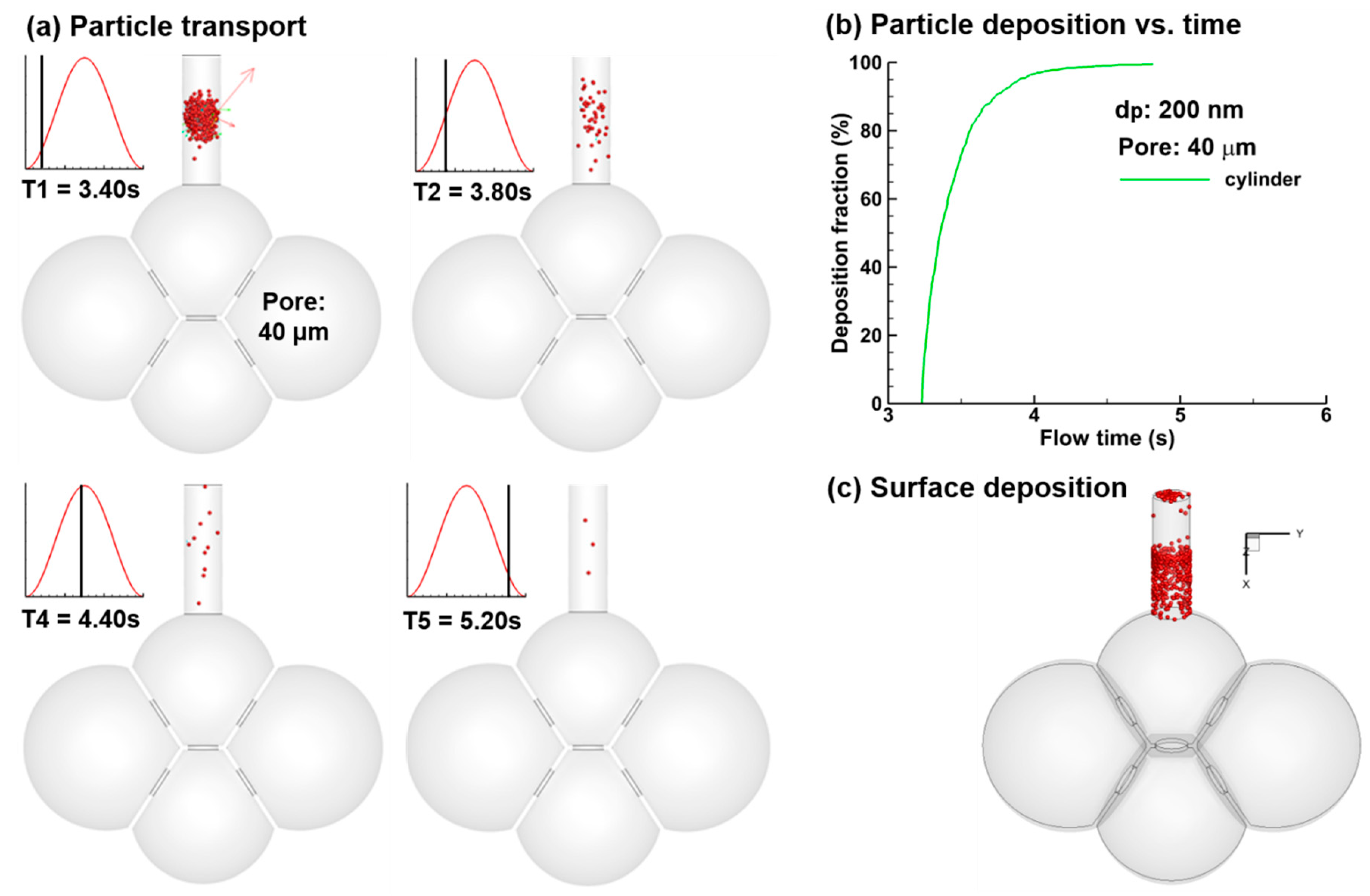
3.3. Particle Deposition
4. Discussion and Summary
4.1. Effects of Wall Motion on Nanoparticle Deposition
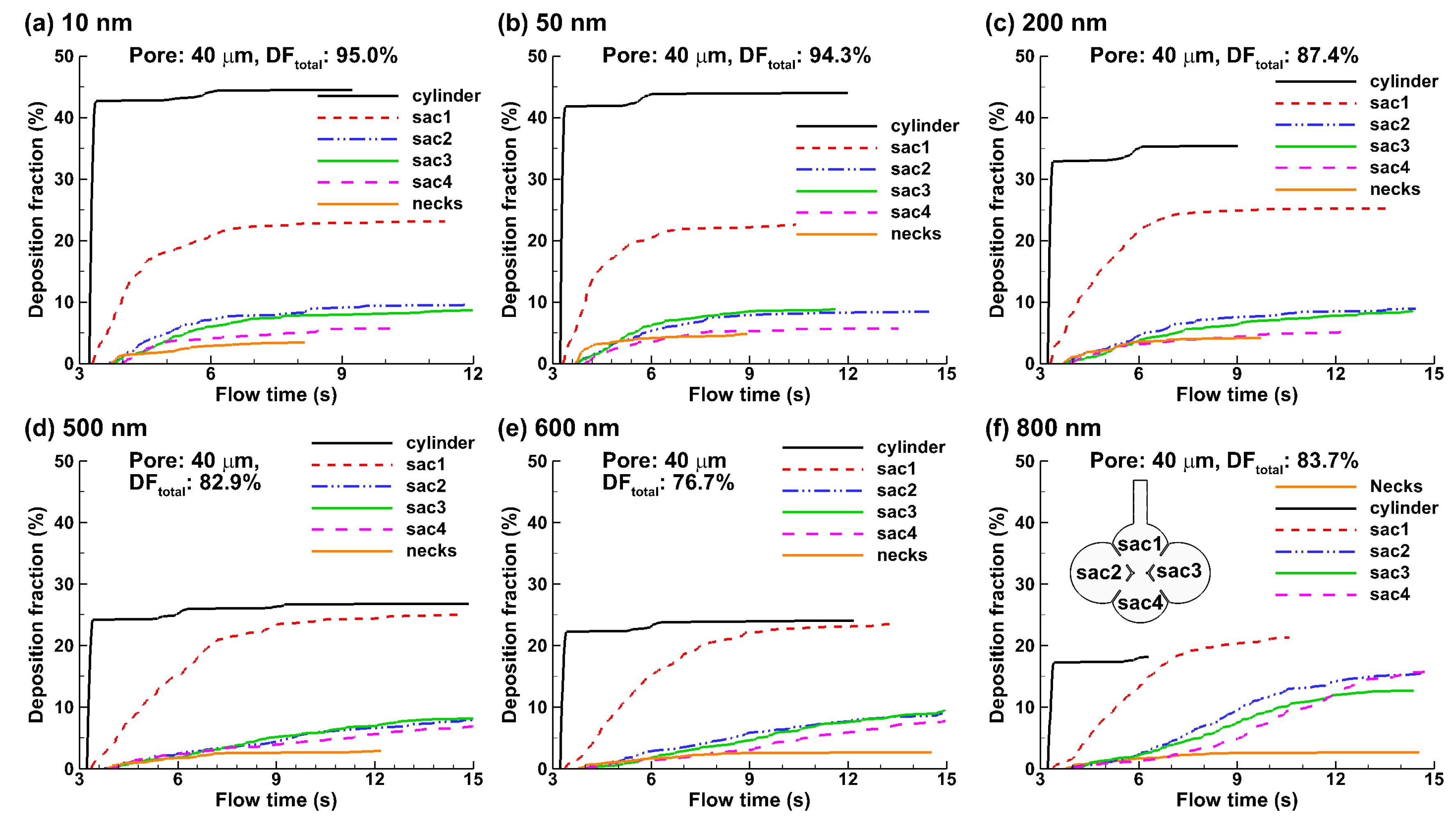
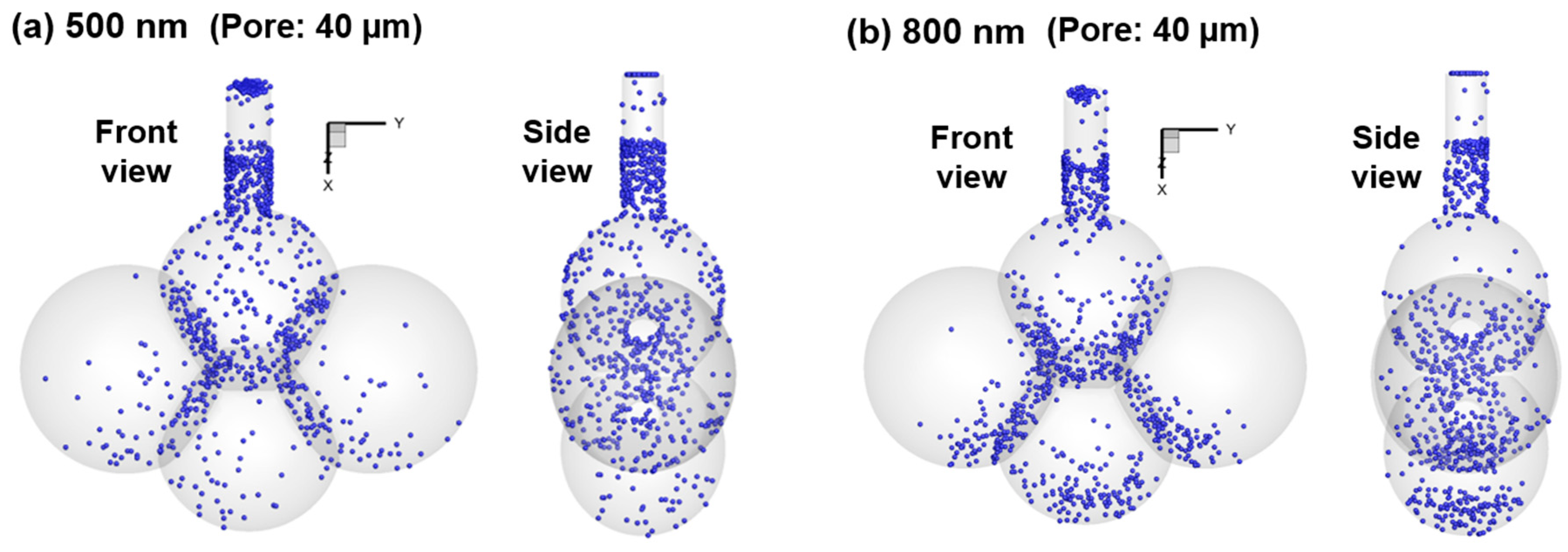
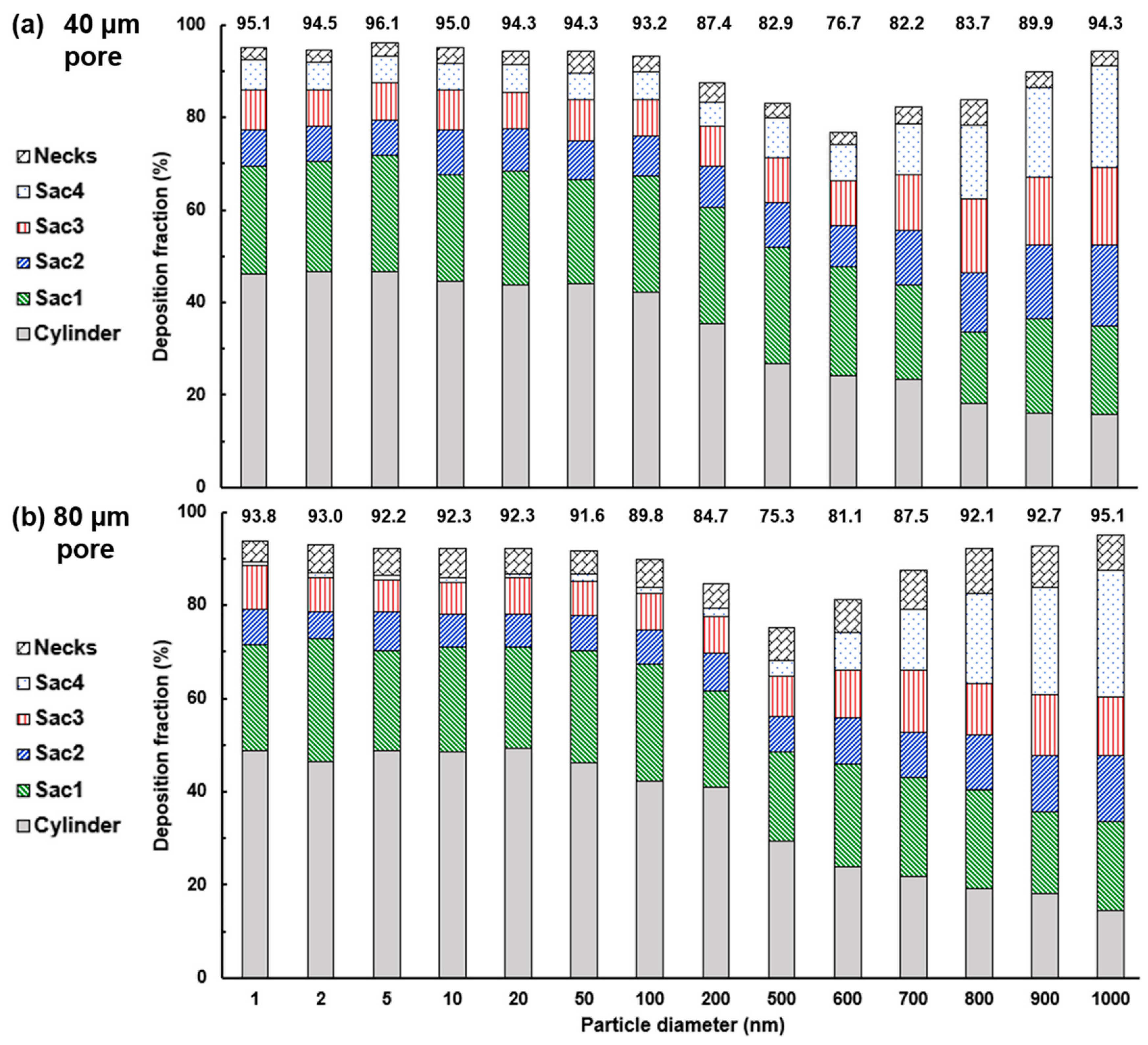
4.2. Effects of Particle Size on Nanoparticle Deposition
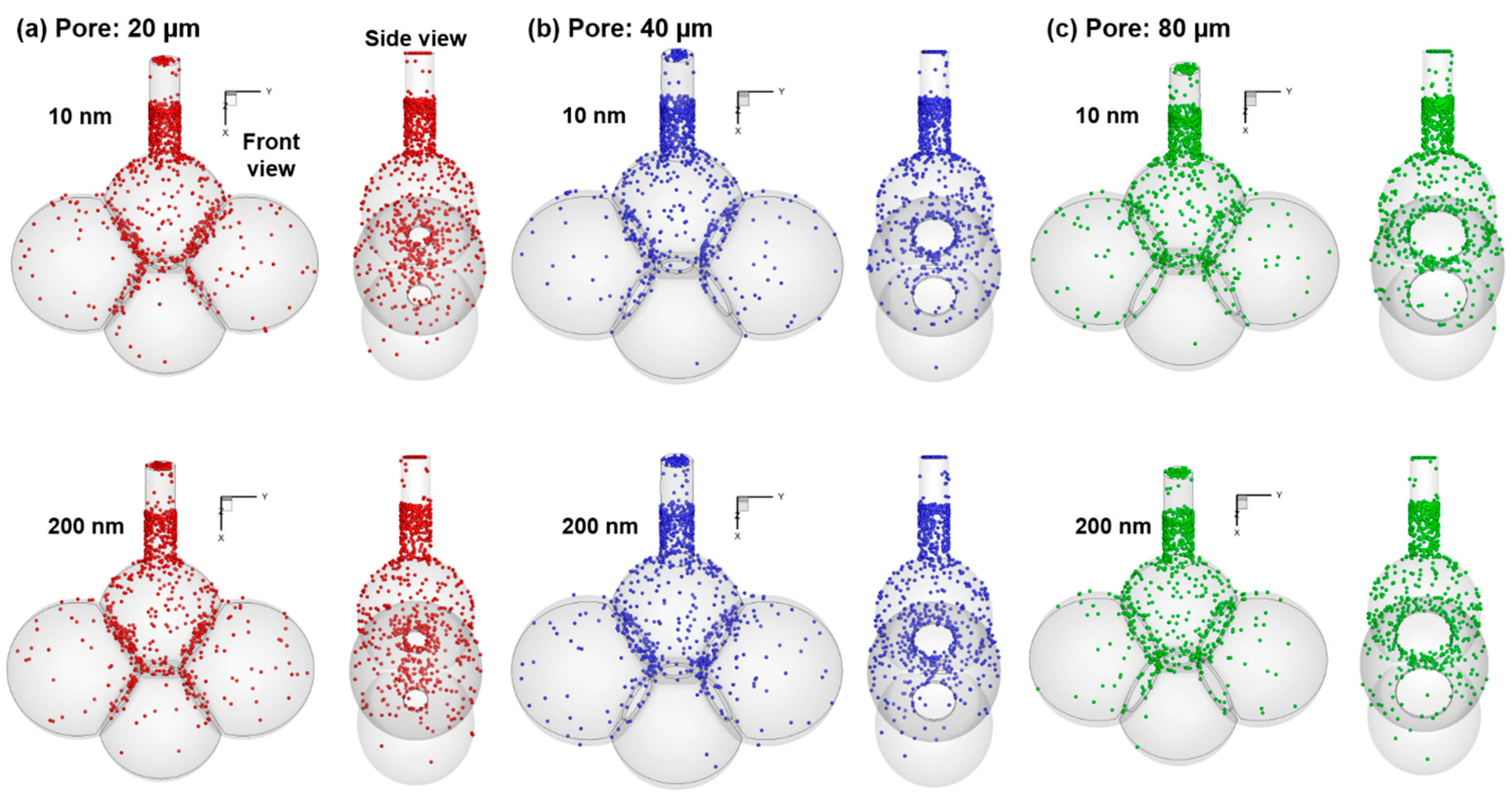
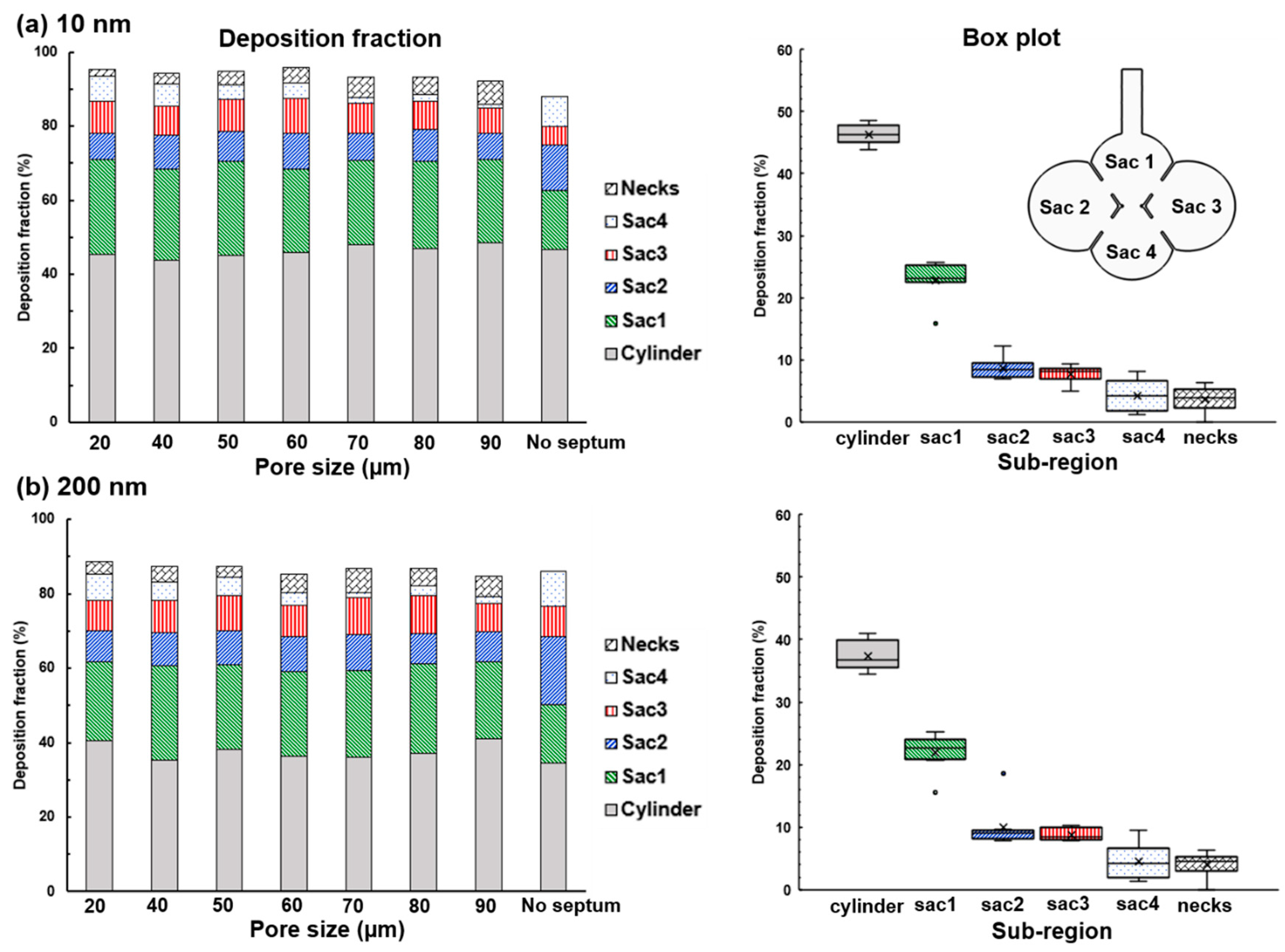
4.3. Effects of Inter-Septal Pore Size on Nanoparticle Deposition
Elevated Nanoparticle Deposition When Released at Early Inhalation
4.4. Limitations
- Rhythmic alveolar wall motion is indispensable for inhaled nanomedicine to deposit in the distal alveoli.
- Diffusion-driven mixing of inhaled nanoparticles with residual air in the alveoli (termed as aerosol irreversibility) is the primary mechanism that keeps particles from being exhaled out of the alveoli.
- Concentrated deposition occurs in the alveolar entrance and pore size due to diffusional screening effect.
- Elevated deposition fractions (~85%, as the ratio of particles depositing in the alveolar model over the particles entering the alveolar model) were predicted for nanoparticles released at the beginning of the inhalation. Improved pulmonary doses of nanomedicine can be achieved by optimizing their release time.
- The intra-septal pore size was found to have an insignificant impact on nanoparticle deposition on both the total and sub-regional basis, indicating a potentially consistent dose of nanomedicine if the patient can perform the required breathing maneuver.
Author Contributions
Funding
Conflicts of Interest
References
- Gross, N.J.; Barnes, P.J. New therapies for asthma and chronic obstructive pulmonary disease. Am. J. Respir. Crit. Care Med. 2016, 195, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Mansour, H.M.; Rhee, Y.-S.; Wu, X. Nanomedicine in pulmonary delivery. Int. J. Nanomed. 2009, 4, 299–319. [Google Scholar] [CrossRef]
- Fröhlich, E.; Mercuri, A.; Wu, S.; Salar-Behzadi, S. Measurements of deposition, lung surface area and lung fluid for simulation of inhaled compounds. Front. Pharmacol. 2016, 7, 181. [Google Scholar] [CrossRef] [PubMed]
- Borghardt, J.M.; Kloft, C.; Sharma, A. Inhaled therapy in respiratory disease: The complex interplay of pulmonary kinetic processes. Can. Respir. J. 2018, 2018, 2732017. [Google Scholar] [CrossRef]
- Lakshmi, S.P.; Reddy, A.T.; Reddy, R.C. Emerging pharmaceutical therapies for COPD. Int. J. Chronic Obstruct. Pulmon. Dis. 2017, 12, 2141–2156. [Google Scholar] [CrossRef]
- Solaro, R.; Chiellini, F.; Battisti, A. Targeted Delivery of Protein Drugs by Nanocarriers. Materials 2010, 3, 1928–1980. [Google Scholar] [CrossRef]
- Chiuchiolo, M.J.; Crystal, R.G. Gene therapy for alpha-1 antitrypsin deficiency lung disease. Ann. Am. Thorac. Soc. 2016, 13 (Suppl. 4), S352–S369. [Google Scholar] [CrossRef]
- Flotte, T.R.; Mueller, C. Gene therapy for alpha-1 antitrypsin deficiency. Hum. Mol. Genet. 2011, 20, R87–R92. [Google Scholar] [CrossRef]
- Villate-Beitia, I.; Zarate, J.; Puras, G.; Pedraz, J.L. Gene delivery to the lungs: Pulmonary gene therapy for cystic fibrosis. Drug Dev. Ind. Pharm. 2017, 43, 1071–1081. [Google Scholar] [CrossRef]
- Mathieu, M.; Demoly, P. Gene Therapy for Asthma. In Gene Therapy for Acute and Acquired Diseases; Factor, P., Ed.; Springer: Boston, MA, USA, 2001; pp. 107–126. [Google Scholar]
- Chuquimia, O.D.; Petursdottir, D.H.; Periolo, N.; Fernández, C. Alveolar epithelial cells are critical in protection of the respiratory tract by secretion of factors able to modulate the activity of pulmonary macrophages and directly control bacterial growth. Infect. Immun. 2013, 81, 381–389. [Google Scholar] [CrossRef]
- Heckel, K.; Kiefmann, R.; Dorger, M.; Stoeckelhuber, M.; Goetz, A.E. Colloidal gold particles as a new in vivo marker of early acute lung injury. Am. J. Physiol. Lung Cell Mol. Physiol. 2004, 287, L867–L878. [Google Scholar] [CrossRef] [PubMed]
- Kato, T.; Yashiro, T.; Murata, Y.; Herbert, D.C.; Oshikawa, K.; Bando, M.; Ohno, S.; Sugiyama, Y. Evidence that exogenous substances can be phagocytized by alveolar epithelial cells and transported into blood capillaries. Cell Tissue Res. 2003, 311, 47–51. [Google Scholar] [CrossRef] [PubMed]
- Chono, S.; Tanino, T.; Seki, T.; Morimoto, K. Influence of particle size on drug delivery to rat alveolar macrophages following pulmonary administration of ciprofloxacin incorporated into liposomes. J. Drug Target. 2006, 14, 557–566. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Peters, J.I.; Williams, R.O., 3rd. Inhaled nanoparticles—A current review. Int. J. Pharm. 2008, 356, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environ. Health Perspect. 2005, 113, 823–839. [Google Scholar] [CrossRef] [PubMed]
- Ochs, M.; Nyengaard, J.R.; Jung, A.; Knudsen, L.; Voigt, M.; Wahlers, T.; Richter, J.; Gundersen, H.J. The number of alveoli in the human lung. Am. J. Respir. Crit. Care Med. 2004, 169, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Desplechain, C.; Foliguet, B.; Barrat, E.; Grignon, G.; Touati, F. The pores of Kohn in pulmonary alveoli. Bull. Eur. Physiopathol. Respir. 1983, 19, 59–68. [Google Scholar]
- Namati, E.; Thiesse, J.; de Ryk, J.; McLennan, G. Alveolar dynamics during respiration: Are the pores of Kohn a pathway to recruitment? Am. J. Respir. Cell Mol. Biol. 2008, 38, 572–578. [Google Scholar] [CrossRef]
- Terry, P.B.; Traystman, R.J. The Clinical Significance of Collateral Ventilation. Ann. Am. Thorac Soc. 2016, 13, 2251–2257. [Google Scholar] [CrossRef]
- Nagai, A.; Inano, H.; Matsuba, K.; Thurlbeck, W.M. Scanning electronmicroscopic morphometry of emphysema in humans. Am. J. Respir. Crit. Care Med. 1994, 150, 1411–1415. [Google Scholar] [CrossRef]
- Van Allen, C.M.; Lindskog, G.E.; Richter, H.G. Gaseous Interchange Between Adjacent Lung Lobules. Yale J. Biol. Med. 1930, 2, 297–300. [Google Scholar] [PubMed]
- Terry, P.B.; Traystman, R.J.; Newball, H.H.; Batra, G.; Menkes, H.A. Collateral ventilation in man. N. Engl. J. Med. 1978, 298, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Hogg, J.C. Pathophysiology of airflow limitation in chronic obstructive pulmonary disease. Lancet 2004, 364, 709–721. [Google Scholar] [CrossRef]
- Shimura, S.; Boatman, E.S.; Martin, C.J. Effects of ageing on the alveolar pores of Kohn and on the cytoplasmic components of alveolar type II cells in monkey lungs. J. Pathol. 1986, 148, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Gillett, N.A.; Gerlach, R.F.; Muggenburg, B.A.; Harkema, J.R.; Griffith, W.C.; Mauderly, J.L. Relationship between collateral flow resistance and alveolar pores in the aging beagle dog. Exp. Lung Res. 1989, 15, 709–719. [Google Scholar] [CrossRef]
- Finlay, W.H. The Mechanics of Inhaled Pharmaceutical Aerosols; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Rudolf, G.; Gebhart, J.; Heyder, J.; Schiller, C.F.; Stahlhofen, W. An empirical formula describing aerosol deposition in man for any particle size. J. Aerosol Sci. 1986, 17, 350–355. [Google Scholar] [CrossRef]
- Isaacs, K.K.; Rosati, J.A.; Martonen, T.B. Mechanisms of particle deposition. In Aerosols Handbook; Ruzer, L.S., Harley, N.H., Eds.; CRC Press: New York, NY, USA, 2005; pp. 75–99. [Google Scholar]
- Kojic, M.; Tsuda, A. A simple model for gravitational deposition of non-diffusing particles in oscillatory laminar pipe flow and its application to small airways. J. Aerosol Sci. 2004, 35, 245–261. [Google Scholar] [CrossRef]
- Choi, J.I.; Kim, C.S. Mathematical analysis of particle deposition in human lungs: An improved single path transport model. Inhal. Toxicol. 2007, 19, 925–939. [Google Scholar] [CrossRef]
- Kim, C.S. Deposition of aerosol particles in human lungs: In vivo measurement and modelling. Biomarkers 2009, 14, 54–58. [Google Scholar] [CrossRef]
- Kumar, H.; Tawhai, M.H.; Hoffman, E.A.; Lin, C.L. The effects of geometry on airflow in the acinar region of the human lung. J. Biomech. 2009, 42, 1635–1642. [Google Scholar] [CrossRef]
- Talaat, K.; Xi, J. Computational modeling of aerosol transport, dispersion, and deposition in rhythmically expanding and contracting terminal alveoli. J. Aerosol Sci. 2017, 112, 19–33. [Google Scholar] [CrossRef]
- Haber, S.; Yitzhak, D.; Tsuda, A. Gravitational deposition in a rhythmically expanding and contracting alveolus. J. Appl. Physiol. 2003, 95, 657–671. [Google Scholar] [CrossRef] [PubMed]
- Haber, S.; Butler, J.P.; Brenner, H.; Emanuel, I.; Tsuda, A. Shear flow over a self-similar expanding pulmonary alveolus during rhythmical breathing. J. Fluid Mech. 2000, 405, 243–268. [Google Scholar] [CrossRef]
- Chhabra, S.; Prasad, A.K. Flow and particle dispersion in a pulmonary alveolus—Part I: Velocity measurements and convective particle transport. J. Biomech. Eng. 2010, 132, 4001112. [Google Scholar] [CrossRef] [PubMed]
- Sznitman, J.; Heimsch, T.; Wildhaber, J.H.; Tsuda, A.; Rösgen, T. Respiratory flow phenomena and gravitational deposition in a three-dimensional space-filling model of the pulmonary acinar tree. J. Biomech. Eng. 2009, 131, 031010. [Google Scholar] [CrossRef] [PubMed]
- Khajeh-Hosseini-Dalasm, N.; Longest, P.W. Deposition of particles in the alveolar airways: Inhalation and breath-hold with pharmaceutical aerosols. J. Aerosol Sci. 2015, 79, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Hofemeier, P.; Koshiyama, K.; Wada, S.; Sznitman, J. One (sub-)acinus for all: Fate of inhaled aerosols in heterogeneous pulmonary acinar structures. Eur. J. Pharm. Sci. 2018, 113, 53–63. [Google Scholar] [CrossRef]
- Xi, J.; Talaat, M.; Tanbour, H.; Talaat, K. Airflow and particle deposition in acinar models with interalveolar septal walls and different alveolar numbers. Comput. Math. Methods Med. 2018, 2018, 3649391. [Google Scholar] [CrossRef]
- Xi, J.; Talaat, K.; Si, X. Deposition of bolus and continuously inhaled aerosols in rhythmically moving terminal alveoli. J. Comput. Multiph. Flow 2018, 10. [Google Scholar] [CrossRef]
- Plathow, C.; Ley, S.; Fink, C.; Puderbach, M.; Heilmann, M.; Zuna, I.; Kauczor, H.U. Evaluation of chest motion and volumetry during the breathing cycle by dynamic MRI in healthy subjects: Comparison with pulmonary function tests. Investig. Radiol. 2004, 39, 202–209. [Google Scholar] [CrossRef]
- De Groote, A.; Wantier, M.; Cheron, G.; Estenne, M.; Paiva, M. Chest wall motion during tidal breathing. J. Appl. Physiol. 1997, 83, 1531–1537. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.L.; Nzekwu, M.M. The effects of body mass index on lung volumes. Chest 2006, 130, 827–833. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Si, X.; Kim, J.; Su, G.; Dong, H. Modeling the pharyngeal anatomical effects on breathing resistance and aerodynamically generated sound. Med. Biol. Eng. Comput. 2014, 52, 567–577. [Google Scholar] [CrossRef] [PubMed]
- Si, X.; Xi, J.; Kim, J. Effect of laryngopharyngeal anatomy on expiratory airflow and submicrometer particle deposition in human extrathoracic airways. Open J. Fluid Dyn. 2013, 2013, 40441. [Google Scholar] [CrossRef]
- Longest, P.W.; Xi, J. Computational investigation of particle inertia effects on submicron aerosol deposition in the respiratory tract. J. Aerosol Sci. 2007, 38, 111–130. [Google Scholar] [CrossRef]
- Longest, P.W.; Xi, J. Effectiveness of direct Lagrangian tracking models for simulating nanoparticle deposition in the upper airways. Aerosol Sci. Technol. 2007, 41, 380–397. [Google Scholar] [CrossRef]
- Kim, J.; Xi, J.; Si, X.; Berlinski, A.; Su, W.C. Hood nebulization: Effects of head direction and breathing mode on particle inhalability and deposition in a 7-month-old infant model. J. Aerosol Med. Pulm. Drug Deliv. 2014, 27, 209–218. [Google Scholar] [CrossRef]
- Li, Z.; Kleinstreuer, C.; Zhang, Z. Simulation of airflow fields and microparticle deposition in realistic human lung airway models. Part II: Particle transport and deposition. Eur. J. Mech. B/Fluids 2007, 26, 650–668. [Google Scholar] [CrossRef]
- Allen, M.D.; Raabe, O.G. Slip correction measurements of spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Xi, J.; Longest, P.W. Transport and deposition of micro-aerosols in realistic and simplified models of the oral airway. Ann. Biomed. Eng. 2007, 35, 560–581. [Google Scholar] [CrossRef]
- Xi, J.; Yuan, J.E.; Yang, M.; Si, X.; Zhou, Y.; Cheng, Y.-S. Parametric study on mouth–throat geometrical factors on deposition of orally inhaled aerosols. J. Aerosol Sci. 2016, 99, 94–106. [Google Scholar] [CrossRef]
- Felici, M.; Filoche, M.; Sapoval, B. Diffusional screening in the human pulmonary acinus. J. Appl. Physiol. 2003, 94, 2010–2016. [Google Scholar] [CrossRef]
- Bennett, W.D.; Smaldone, G.C. Use of aerosols to estimate mean air-space size in chronic obstructive pulmonary disease. J. Appl. Physiol. 1985, 64, 1554–1560. [Google Scholar] [CrossRef]
- Xi, J.; Si, X.; Longest, P.W. Electrostatic Charge Effects on Pharmaceutical Aerosol Deposition in Human Nasal-Laryngeal Airways. Pharmaceutics 2013, 6, 26–35. [Google Scholar] [CrossRef]
- Xi, J.; Si, X.A.; Gaide, R. Electrophoretic Particle Guidance Significantly Enhances Olfactory Drug Delivery: A Feasibility Study. PLoS ONE 2014, 9, e86593. [Google Scholar] [CrossRef]
- Si, X.A.; Xi, J.; Kim, J.; Zhou, Y.; Zhong, H. Modeling of release position and ventilation effects on olfactory aerosol drug delivery. Respir. Physiol. Neurobiol. 2013, 186, 22–32. [Google Scholar] [CrossRef]
- Kim, J.W.; Xi, J.; Si, X.A. Dynamic growth and deposition of hygroscopic aerosols in the nasal airway of a 5-year-old child. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 17–39. [Google Scholar] [CrossRef]
- Smaldone, G.C.; Mitzner, W. Viewpoint: Unresolved mysteries. J. Appl. Physiol. 2012, 113, 1945–1947. [Google Scholar] [CrossRef]
- Haefeli-Bleuer, B.; Weibel, E.R. Morphometry of the human pulmonary acinus. Anat. Rec. 1988, 220, 401–414. [Google Scholar] [CrossRef]
- Berg, E.J.; Weisman, J.L.; Oldham, M.J.; Robinson, R.J. Flow field analysis in a compliant acinus replica model using particle image velocimetry (PIV). J. Biomech. 2010, 43, 1039–1047. [Google Scholar] [CrossRef]
- Kumar, H.; Vasilescu, D.M.; Yin, Y.; Hoffman, E.A.; Tawhai, M.H.; Lin, C.-L. Multiscale imaging and registration-driven model for pulmonary acinar mechanics in the mouse. J. Appl. Physiol. 2013, 114, 971–978. [Google Scholar] [CrossRef][Green Version]
- Yoshikawa, A.; Sato, S.; Tanaka, T.; Hashisako, M.; Kashima, Y.; Tsuchiya, T.; Yamasaki, N.; Nagayasu, T.; Yamamoto, H.; Fukuoka, J. Breakdown of lung framework and an increase in pores of Kohn as initial events of emphysema and a cause of reduction in diffusing capacity. Int. J. Chronic Obstruct. Pulmon. Dis. 2016, 11, 2287–2294. [Google Scholar]
- Ryan, S.F. The structure of the interalveolar septum of the mammalian lung. Anat. Rec. 1969, 165, 467–483. [Google Scholar] [CrossRef]
- Cordingley, J.L. Pores of Kohn. Thorax 1972, 27, 433–441. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, J.; Talaat, M. Nanoparticle Deposition in Rhythmically Moving Acinar Models with Interalveolar Septal Apertures. Nanomaterials 2019, 9, 1126. https://doi.org/10.3390/nano9081126
Xi J, Talaat M. Nanoparticle Deposition in Rhythmically Moving Acinar Models with Interalveolar Septal Apertures. Nanomaterials. 2019; 9(8):1126. https://doi.org/10.3390/nano9081126
Chicago/Turabian StyleXi, Jinxiang, and Mohamed Talaat. 2019. "Nanoparticle Deposition in Rhythmically Moving Acinar Models with Interalveolar Septal Apertures" Nanomaterials 9, no. 8: 1126. https://doi.org/10.3390/nano9081126
APA StyleXi, J., & Talaat, M. (2019). Nanoparticle Deposition in Rhythmically Moving Acinar Models with Interalveolar Septal Apertures. Nanomaterials, 9(8), 1126. https://doi.org/10.3390/nano9081126