Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter
Abstract
1. Introduction
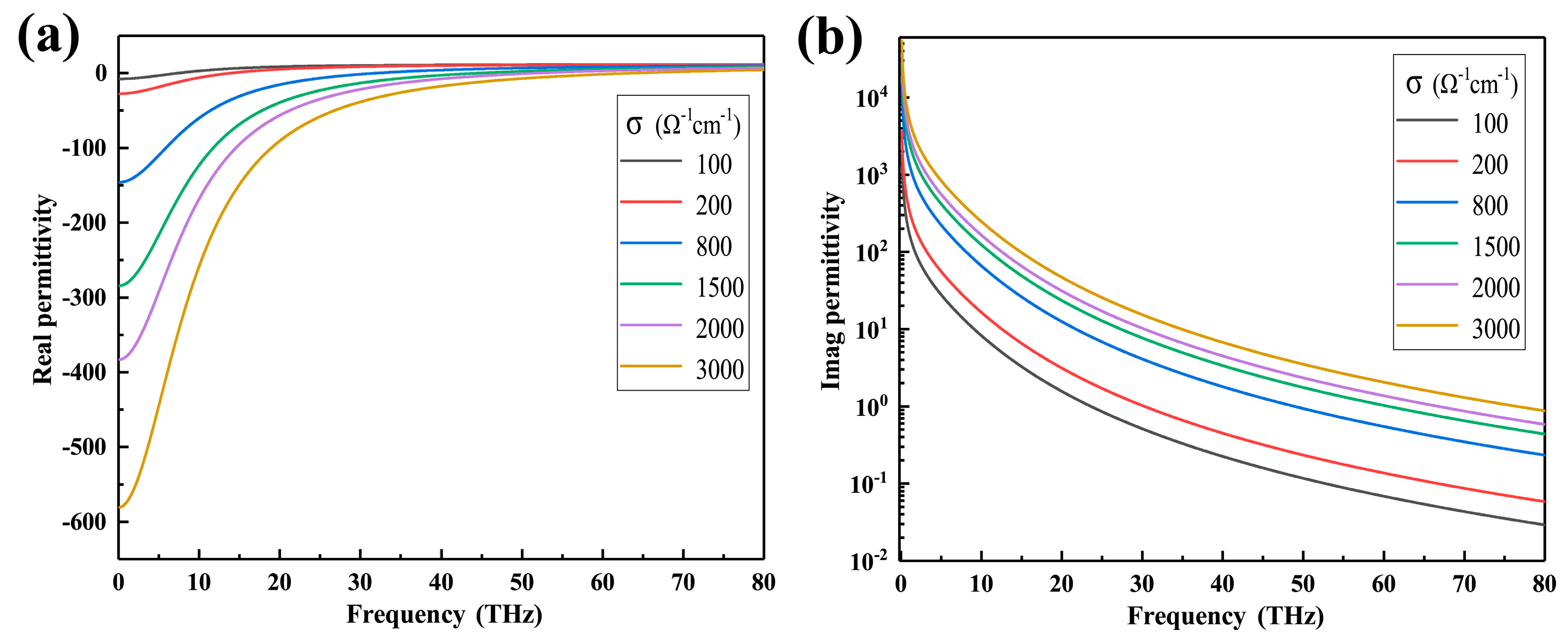
2. Material Model Analysis
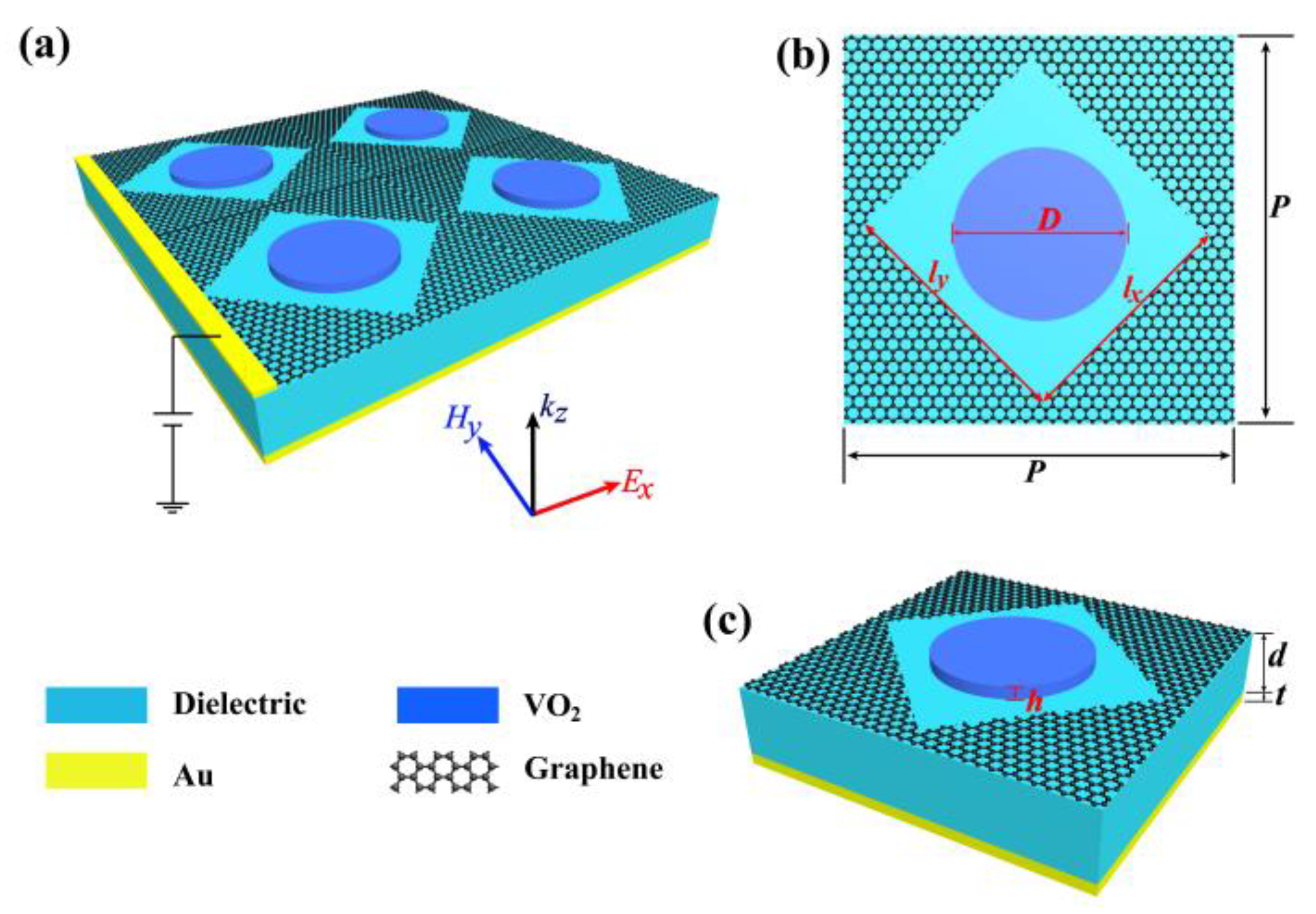
3. Design of Structure
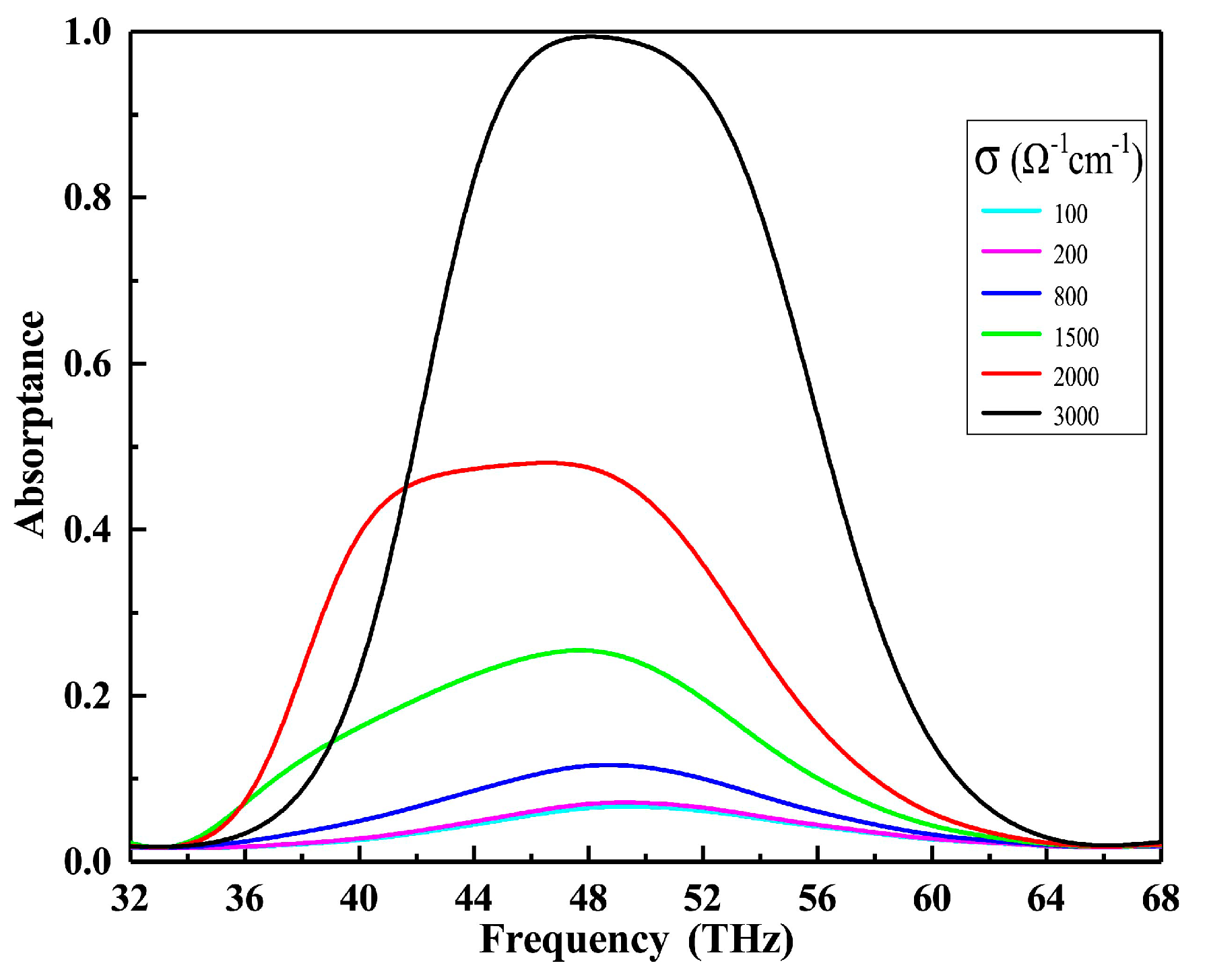
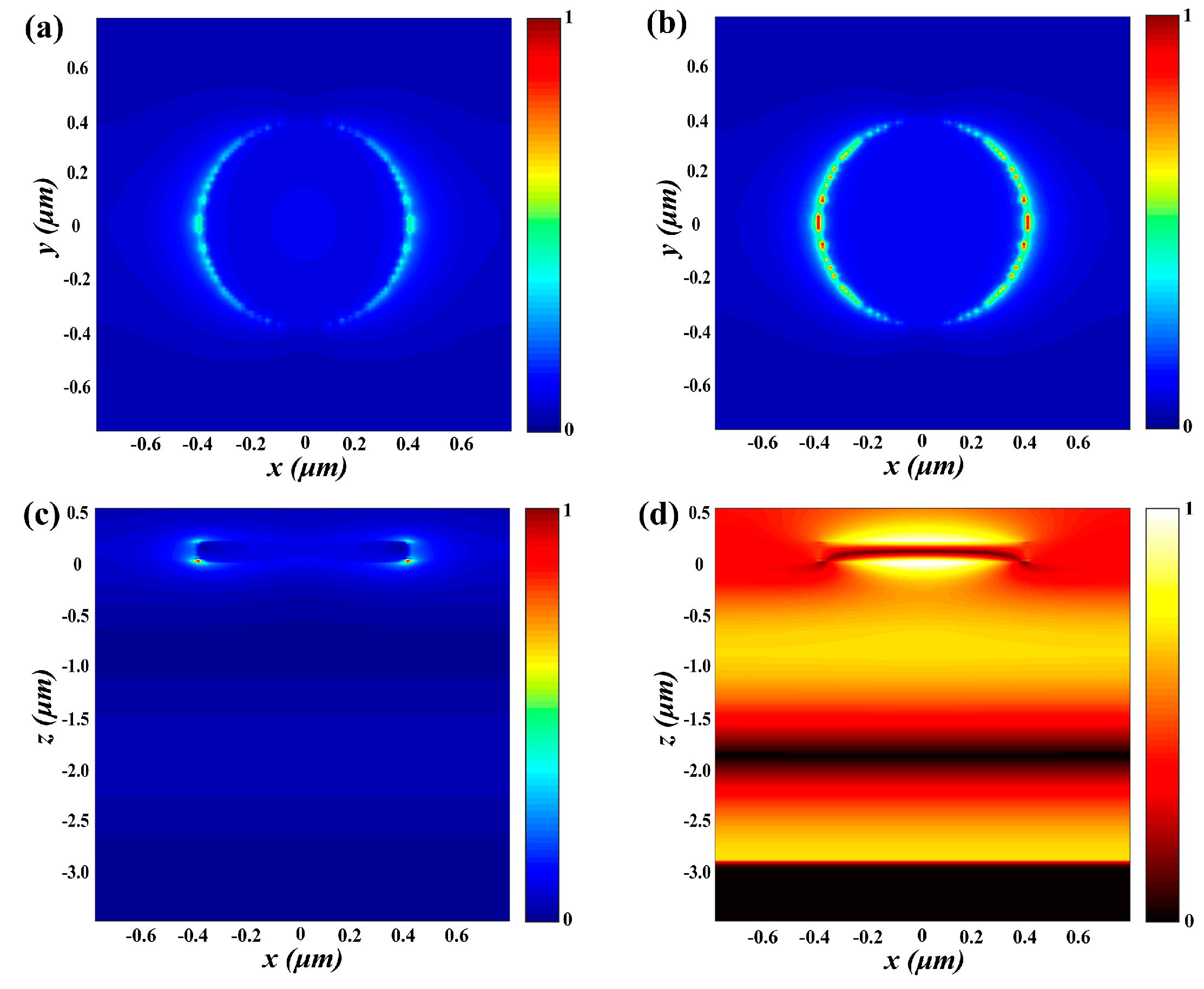
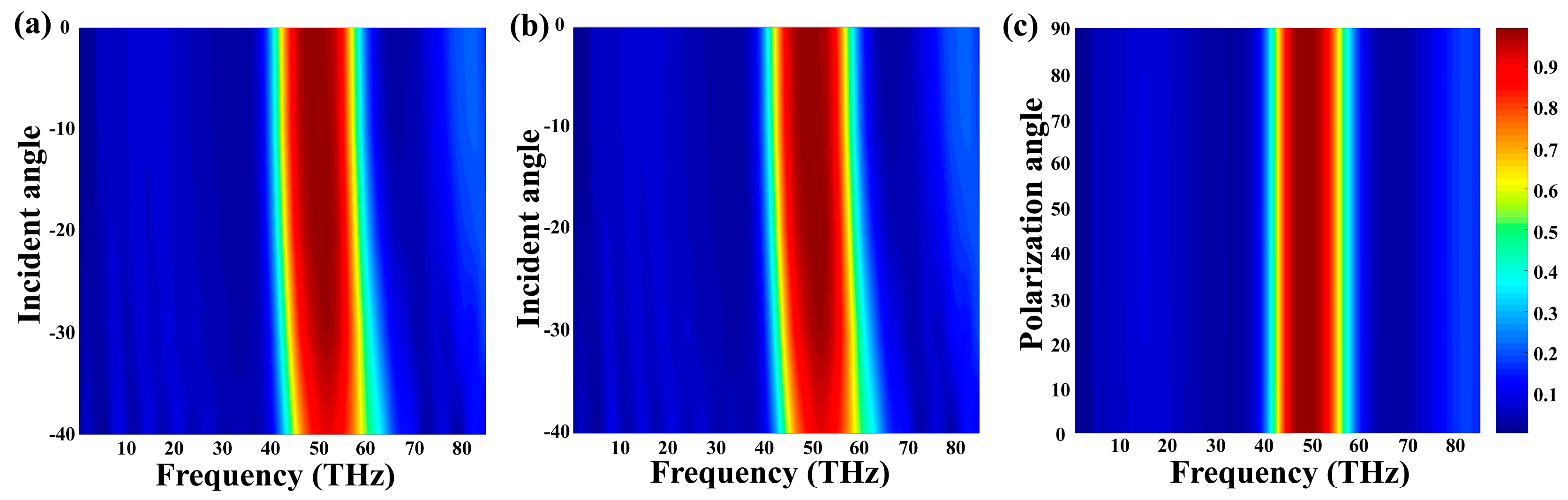
3.1. VO2-Based Tunable Metamaterial Absorber
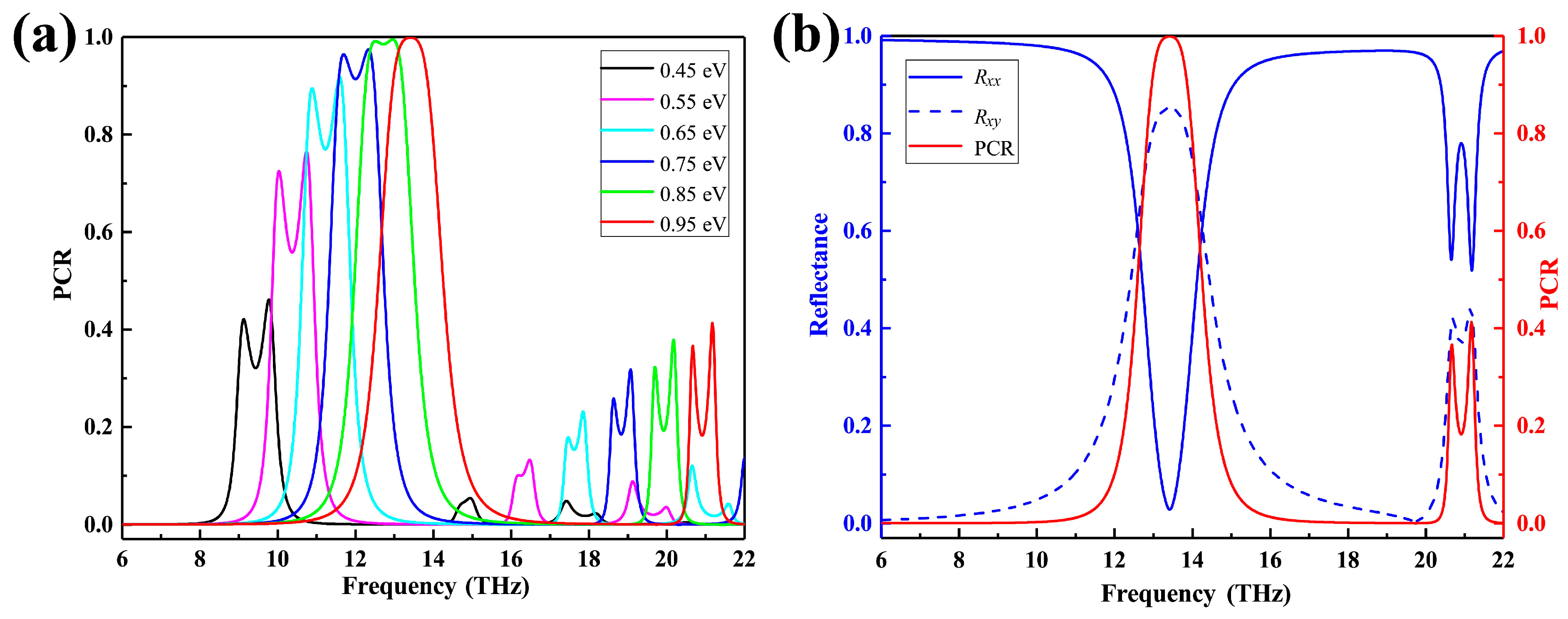
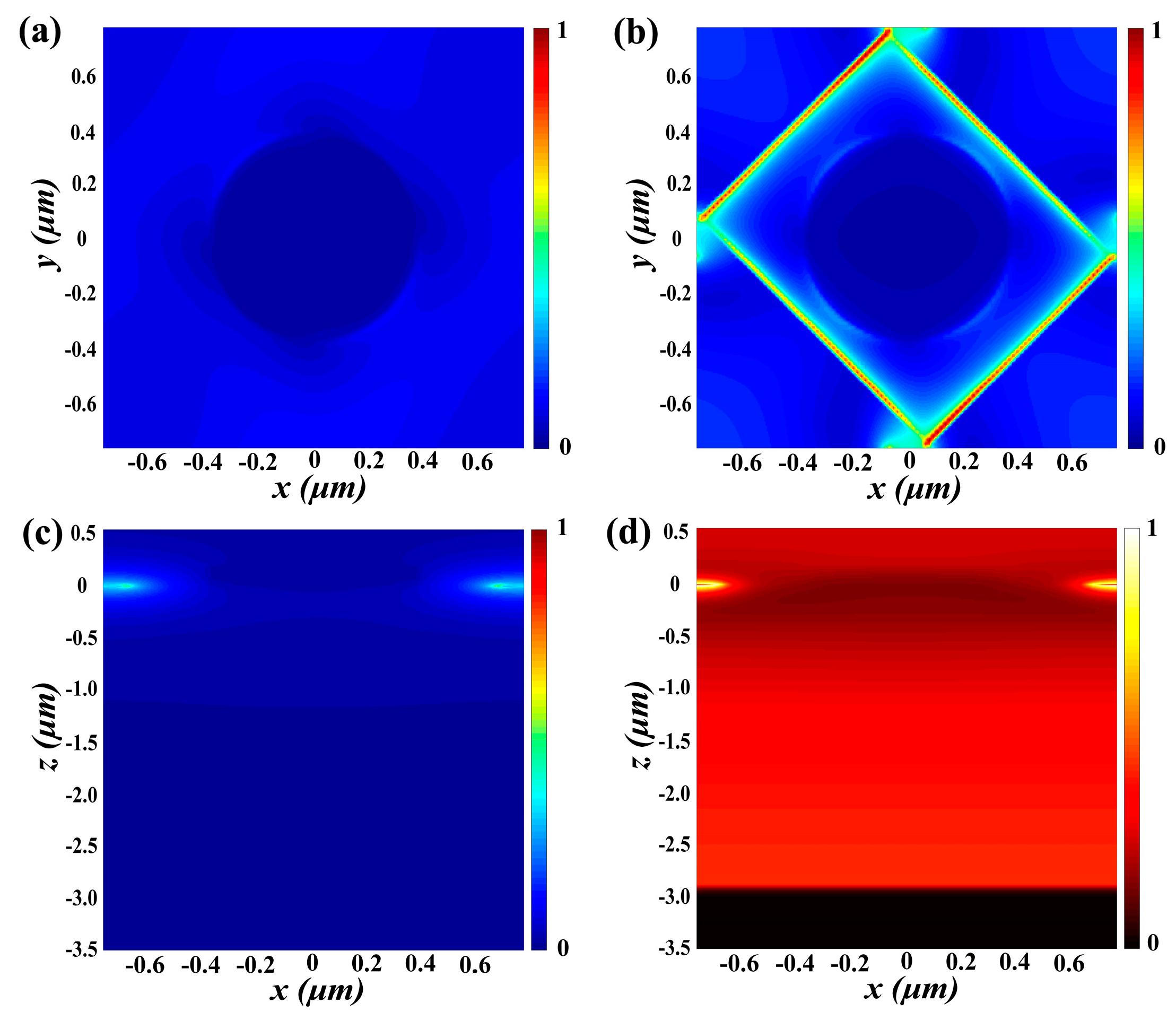
3.2. Graphene-Based Tunable Metamaterial Polarization Converter
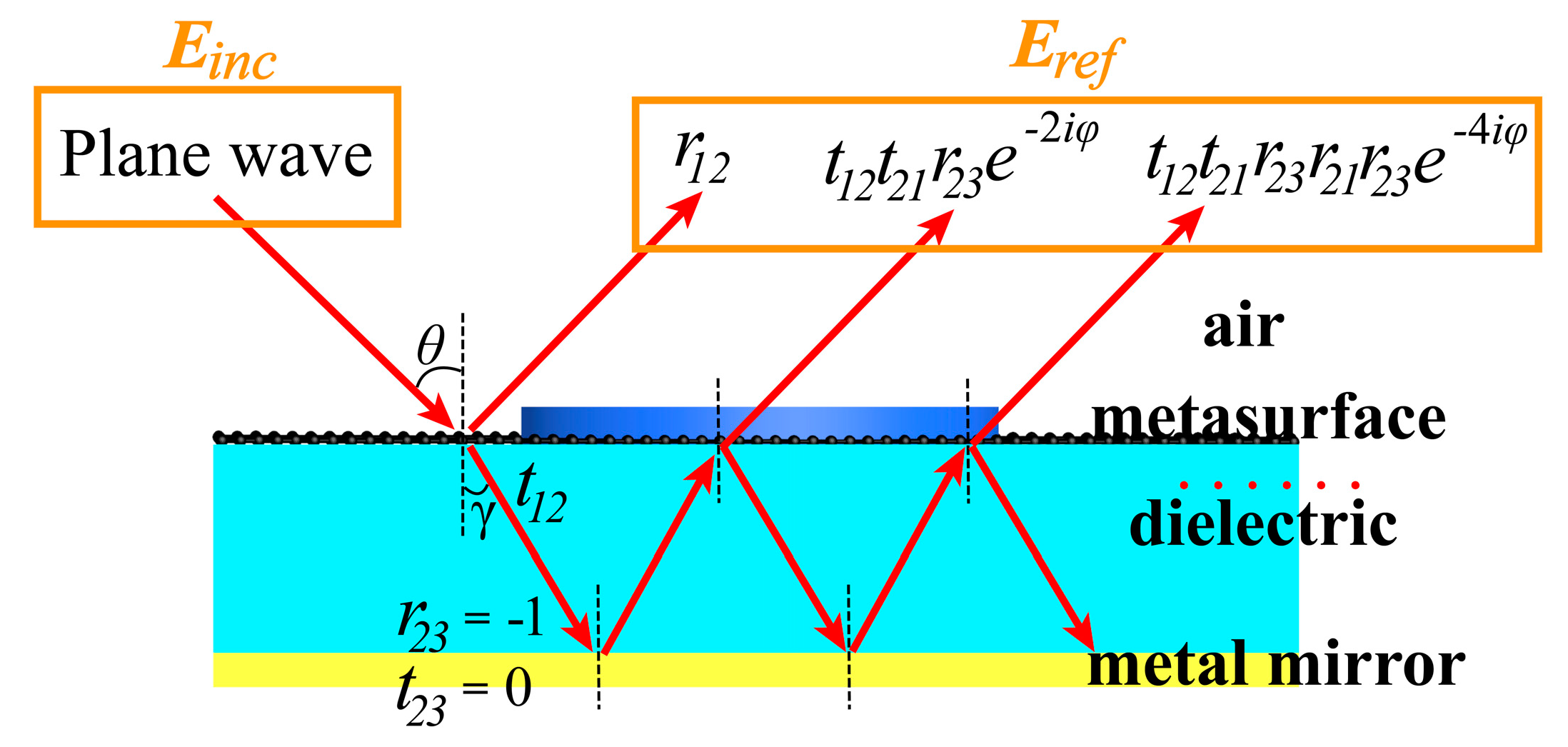
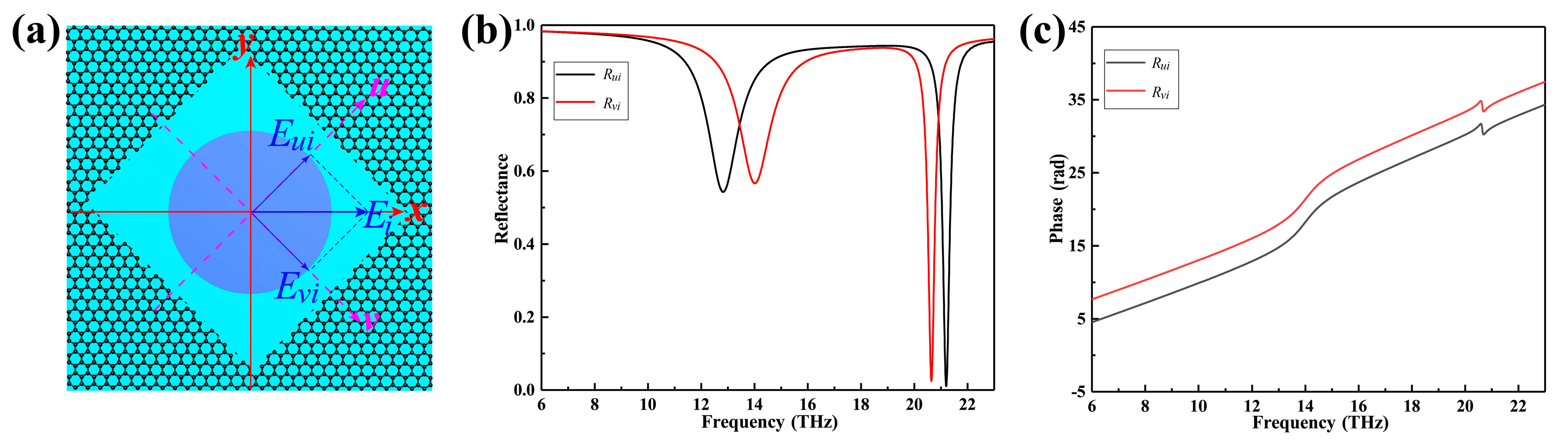
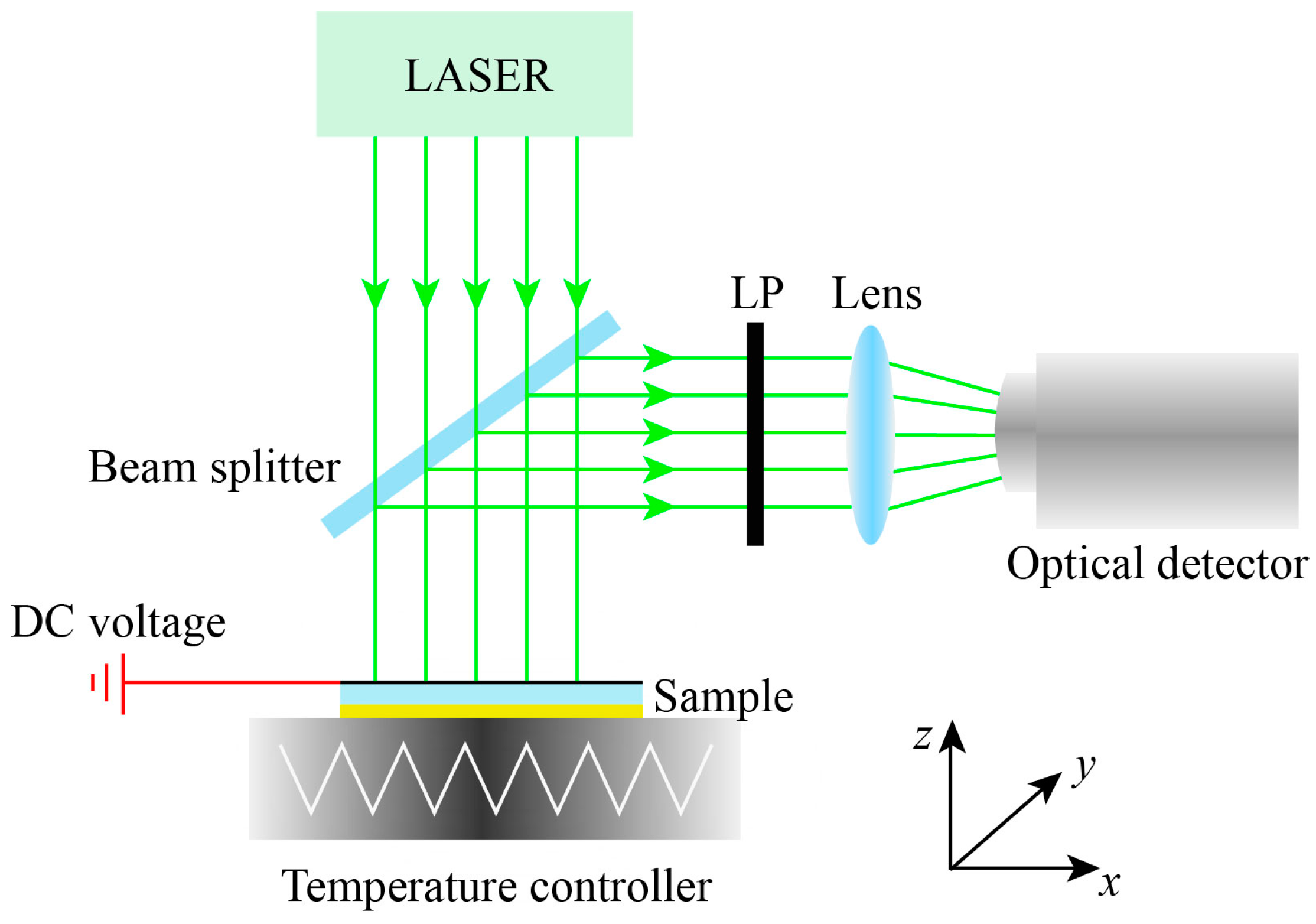
4. Experimental Feasibility
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pradhan, J.K.; Anantha Ramakrishna, S.; Rajeswaran, B.; Umarji, A.M.; Achanta, V.G.; Agarwal, A.K.; Ghosh, A. High contrast switchability of vo2 based metamaterial absorbers with ito ground plane. Opt. Express 2017, 25, 9116–9121. [Google Scholar] [CrossRef]
- Wang, S.; Kang, L.; Werner, D.H. Hybrid resonators and highly tunable terahertz metamaterials enabled by vanadium dioxide (vo2). Sci. Rep. 2017, 7, 4326. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Wang, X.R. Metamaterials based on the phase transition of vo2. Nanotechnology 2018, 29, 024002. [Google Scholar] [CrossRef]
- Casu, E.A.; Oliva, N.; Cavalieri, M.; Muller, A.A.; Fumarola, A.; Vitale, W.A.; Krammer, A.; Schuler, A.; Fernandez-Bolanos, M.; Ionescu, A.M. Tunable rf phase shifters based on vanadium dioxide metal insulator transition. IEEE J. Electron Devices Soc. 2018, 6, 965–971. [Google Scholar] [CrossRef]
- KuanChang, P.; Weisong, W.; Eunsung, S.; Freeman, K.; Subramanyam, G. Vanadium oxide thin-film variable resistor-based rf switches. IEEE Trans. Electron Devices 2015, 62, 2959–2965. [Google Scholar] [CrossRef]
- Choi, H.S.; Ahn, J.S.; Jung, J.H.; Noh, T.W.; Kim, D.H. Mid-infrared properties of a vo2 film near the metal-insulator transition. Phys. Rev. B Condens. Matter 1996, 54, 4621–4628. [Google Scholar] [CrossRef]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef]
- Tony, L.; Phaedon, A. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar]
- Chen, K.; Dao, T.D.; Ishii, S.; Aono, M.; Nagao, T. Infrared aluminum metamaterial perfect absorbers for plasmon-enhanced infrared spectroscopy. Adv. Funct. Mater. 2015, 25, 6637–6643. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Dao, T.D.; Kai, C.; Ishii, S.; Ohi, A.; Nabatame, T.; Kitajima, M.; Nagao, T. Infrared perfect absorbers fabricated by colloidal mask etching of al−al2o3−al trilayers. ACS Photonics 2015, 2, 964–970. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Schlather, A.E.; Liu, Z.; Ajayan, P.M.; de Abajo, F.J.; Nordlander, P.; Zhu, X.; Halas, N.J. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 2014, 14, 299–304. [Google Scholar] [CrossRef]
- Gao, X.; Yang, W.; Cao, W.; Chen, M.; Jiang, Y.; Yu, X.; Li, H. Bandwidth broadening of a graphene-based circular polarization converter by phase compensation. Opt. Express 2017, 25, 23945–23954. [Google Scholar] [CrossRef]
- Ding, F.; Wang, Z.; He, S.; Shalaev, V.M.; Kildishev, A.V. Broadband high-efficiency half-wave plate: A supercell-based plasmonic metasurface approach. ACS Nano 2015, 9, 4111–4119. [Google Scholar] [CrossRef]
- Yu, X.; Gao, X.; Qiao, W.; Wen, L.; Yang, W. Broadband tunable polarization converter realized by graphene-based metamaterial. IEEE Photonics Technol. Lett. 2016, 28, 2399–2402. [Google Scholar] [CrossRef]
- Ding, J.; Arigong, B.; Ren, H.; Zhou, M.; Shao, J.; Lin, Y.; Zhang, H. Efficient multiband and broadband cross polarization converters based on slotted l-shaped nanoantennas. Opt. Express 2014, 22, 29143–29151. [Google Scholar] [CrossRef]
- Ding, J.; Arigong, B.; Han, R.; Mi, Z.; Jin, S.; Lin, Y.; Zhang, H. Multi-wavelength near infrared cross polarization converters. In Proceedings of the Wireless & Microwave Circuits & Systems, Waco, TX, USA, 23–24 April 2015; IEEE: Waco, TX, USA, 2015. [Google Scholar]
- Liu, W.; Chen, S.; Li, Z.; Cheng, H.; Yu, P.; Li, J.; Tian, J. Realization of broadband cross-polarization conversion in transmission mode in the terahertz region using a single-layer metasurface. Opt. Lett. 2015, 40, 3185–3188. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, Y.; Zhang, W.; Wang, J.; Wang, Y.; Gong, S.; Liao, G. Ultra-wideband metasurface with linear-to-circular polarization conversion of an electromagnetic wave. Opt. Mater. Express 2018, 8, 597–604. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, D.; Liu, Y.; Liu, C.; Yu, Z.; Yu, L.; Ye, H. Design of a tunable ultra-broadband terahertz absorber based on multiple layers of graphene ribbons. Nanoscale Res. Lett. 2018, 13, 143. [Google Scholar] [CrossRef]
- Guo, W.; Liu, Y.; Han, T. Ultra-broadband infrared metasurface absorber. Opt. Express 2016, 24, 20586–20592. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Fischer, B.M.; Thoman, A.; Helm, H.; Suh, J.Y.; Lopez, R.; Haglund, R.F. Metal-insulator phase transition in a vo2 thin film observed with terahertz spectroscopy. Phys. Rev. B 2006, 74, 3840–3845. [Google Scholar] [CrossRef]
- Wen, Q.-Y.; Zhang, H.-W.; Yang, Q.-H.; Chen, Z.; Long, Y.; Jing, Y.-L.; Lin, Y.; Zhang, P.-X. A tunable hybrid metamaterial absorber based on vanadium oxide films. J. Phys. D: Appl. Phys. 2012, 45, 235106. [Google Scholar] [CrossRef]
- Zheng, X.; Xiao, Z.; Ling, X. A tunable hybrid metamaterial reflective polarization converter based on vanadium oxide film. Plasmonics 2017, 13, 287–291. [Google Scholar] [CrossRef]
- Xiao, Z.; Zou, H.; Zheng, X.; Ling, X.; Wang, L. A tunable reflective polarization converter based on hybrid metamaterial. Opt. Quantum Electron. 2017, 49, 401. [Google Scholar] [CrossRef]
- Smith, N. Classical generalization of the drude formula for the optical conductivity. Phys. Rev. B 2001, 64, 155106. [Google Scholar] [CrossRef]
- Guo, T.; Argyropoulos, C. Broadband polarizers based on graphene metasurfaces. Opt. Lett. 2016, 41, 5592–5595. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of plasmonic waves in graphene by guided-mode resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, Y.; Liang, C.-H. Broadband tunable graphene-based metamaterial absorber. Opt. Mater. Express 2016, 6, 3036–3044. [Google Scholar] [CrossRef]
- Song, Z.; Wang, K.; Li, J.; Liu, Q.H. Broadband tunable terahertz absorber based on vanadium dioxide metamaterials. Opt. Express 2018, 26, 7148–7154. [Google Scholar] [CrossRef]
- Piper, J.R.; Fan, S. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance. ACS Photonics 2014, 1, 347–353. [Google Scholar] [CrossRef]
- Lv, T.T.; Li, Y.X.; Ma, H.F.; Zhu, Z.; Li, Z.P.; Guan, C.Y.; Shi, J.H.; Zhang, H.; Cui, T.J. Hybrid metamaterial switching for manipulating chirality based on vo2 phase transition. Sci. Rep. 2016, 6, 23186. [Google Scholar] [CrossRef]
- Zhu, Y.; Vegesna, S.; Zhao, Y.; Kuryatkov, V.; Holtz, M.; Fan, Z.; Saed, M.; Bernussi, A.A. Tunable dual-band terahertz metamaterial bandpass filters. Opt. Lett. 2013, 38, 2382–2384. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 2014, 22, 22743–22752. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Dibakar Roy, C.; Yong, Z.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Hou-Tong, C. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef]
| Parameter | Absorber | Polarization Converter |
|---|---|---|
| VO2 thickness (µm) | 0.2 | |
| VO2 radius (µm) | 0.4 | |
| Size of hole in graphene (µm) | 1.0 × 1.2 | |
| Refractive index of dielectric | 1.5 | |
| The thickness of the dielectric (µm) | 2.9 | |
| Graphene Fermi level (µ = 1 m2/Vs) | EF = 0.1 – 0.95 eV | EF = 0.95 eV |
| Permittivity of VO2 | Drude model | ε = 9, σ = 200 S/m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, M.; Liang, Y.; Liang, R.; Zhao, L.; Xu, N.; Guo, J.; Wang, F.; Meng, H.; Liu, H.; Wei, Z. Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter. Nanomaterials 2019, 9, 1101. https://doi.org/10.3390/nano9081101
Mao M, Liang Y, Liang R, Zhao L, Xu N, Guo J, Wang F, Meng H, Liu H, Wei Z. Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter. Nanomaterials. 2019; 9(8):1101. https://doi.org/10.3390/nano9081101
Chicago/Turabian StyleMao, Min, Yaoyao Liang, Ruisheng Liang, Lin Zhao, Ning Xu, Jianping Guo, Faqiang Wang, Hongyun Meng, Hongzhan Liu, and Zhongchao Wei. 2019. "Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter" Nanomaterials 9, no. 8: 1101. https://doi.org/10.3390/nano9081101
APA StyleMao, M., Liang, Y., Liang, R., Zhao, L., Xu, N., Guo, J., Wang, F., Meng, H., Liu, H., & Wei, Z. (2019). Dynamically Temperature-Voltage Controlled Multifunctional Device Based on VO2 and Graphene Hybrid Metamaterials: Perfect Absorber and Highly Efficient Polarization Converter. Nanomaterials, 9(8), 1101. https://doi.org/10.3390/nano9081101









