Extreme and Topological Dissipative Solitons with Structured Matter and Structured Light
Abstract
1. Introduction
2. Structuring of a Medium
2.1. Molecular J-Aggregates
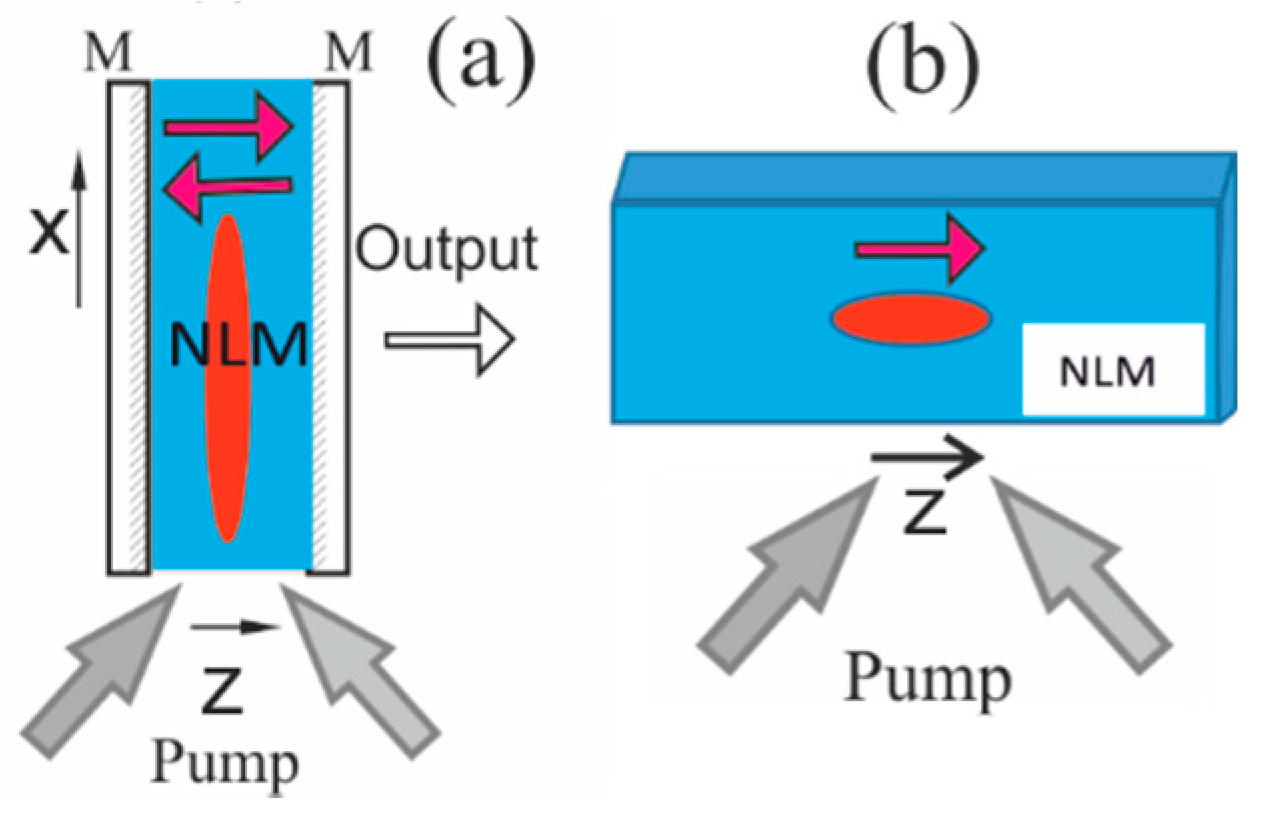
2.1.1. Model of J-Aggregate and Governing Equations
2.1.2. Governing Equations
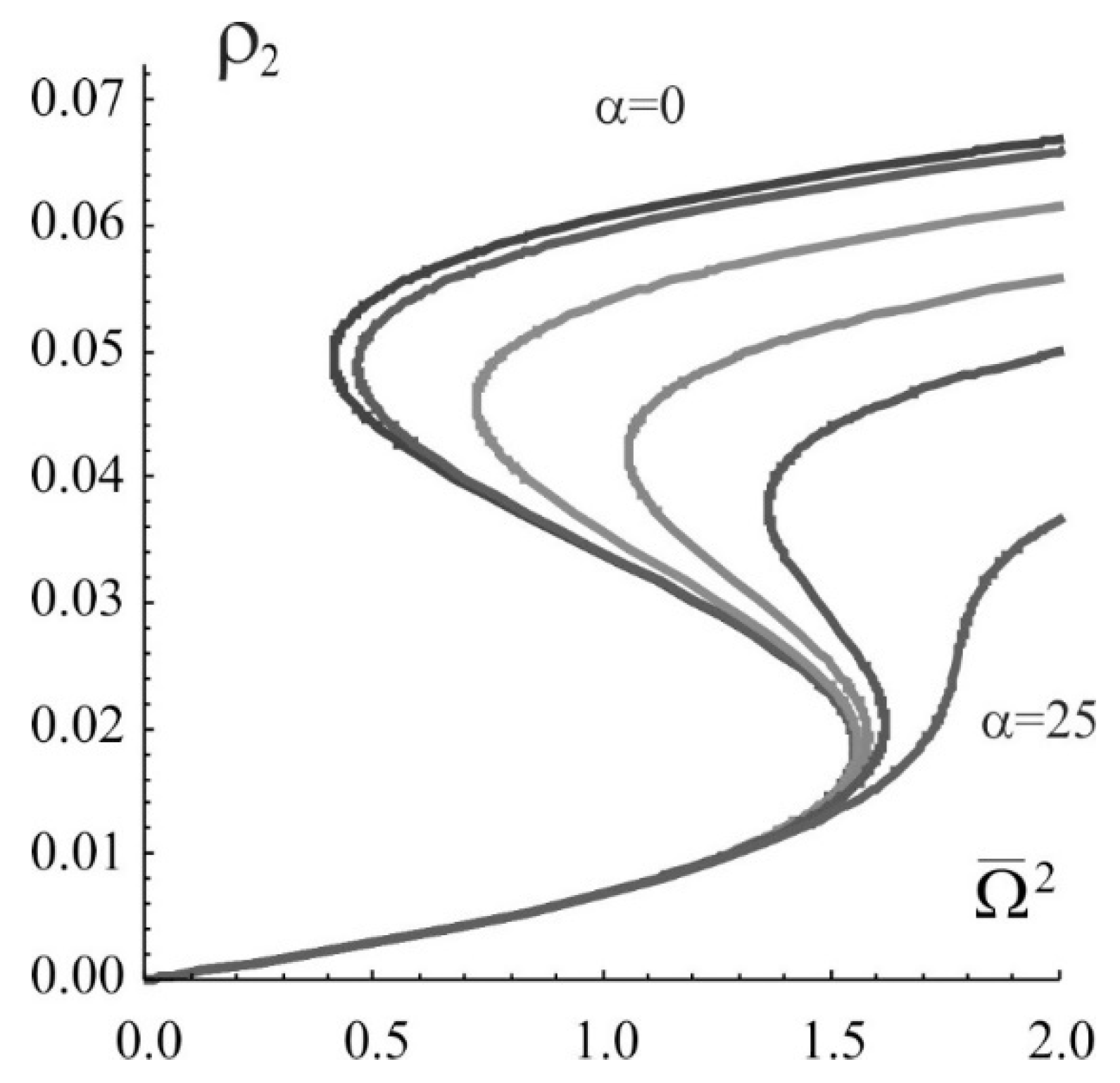
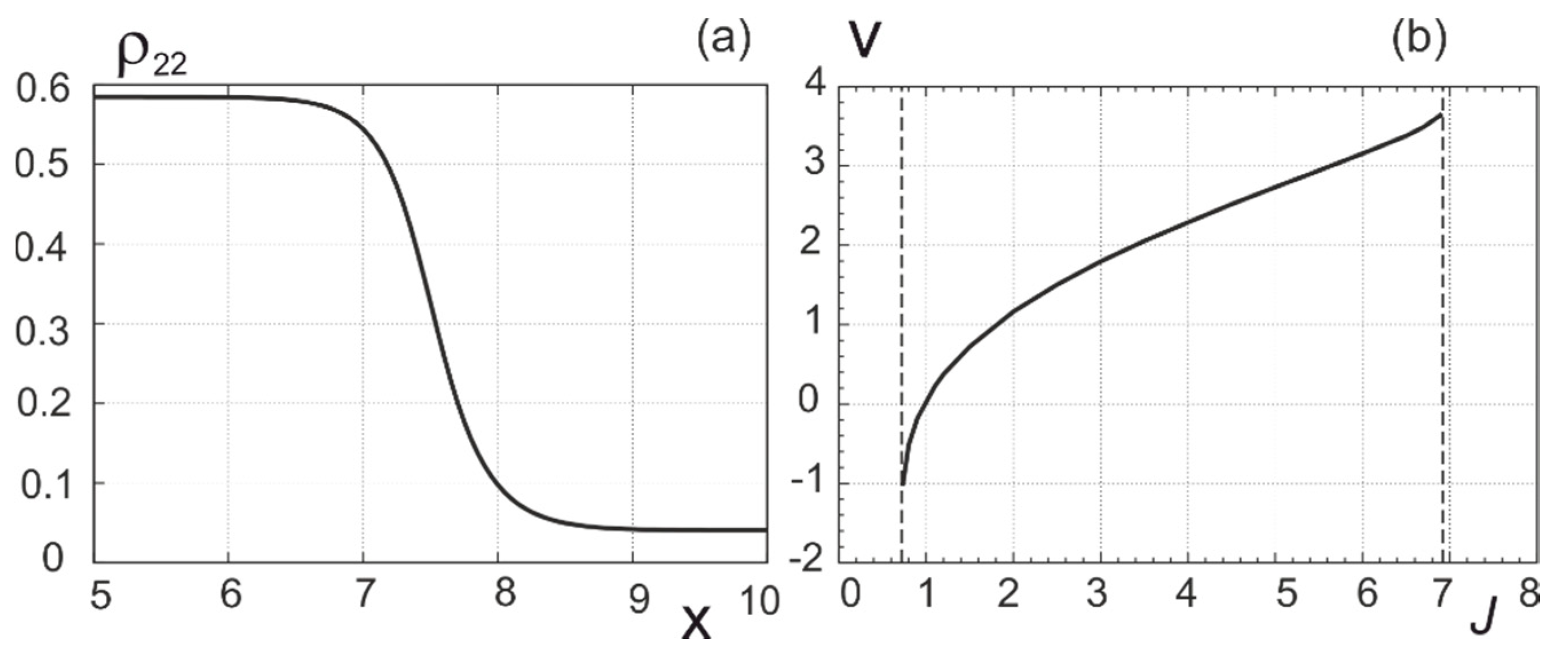
2.1.3. Bistability for Molecular J-Aggregates
2.1.4. Stability of Homogeneous Distributions
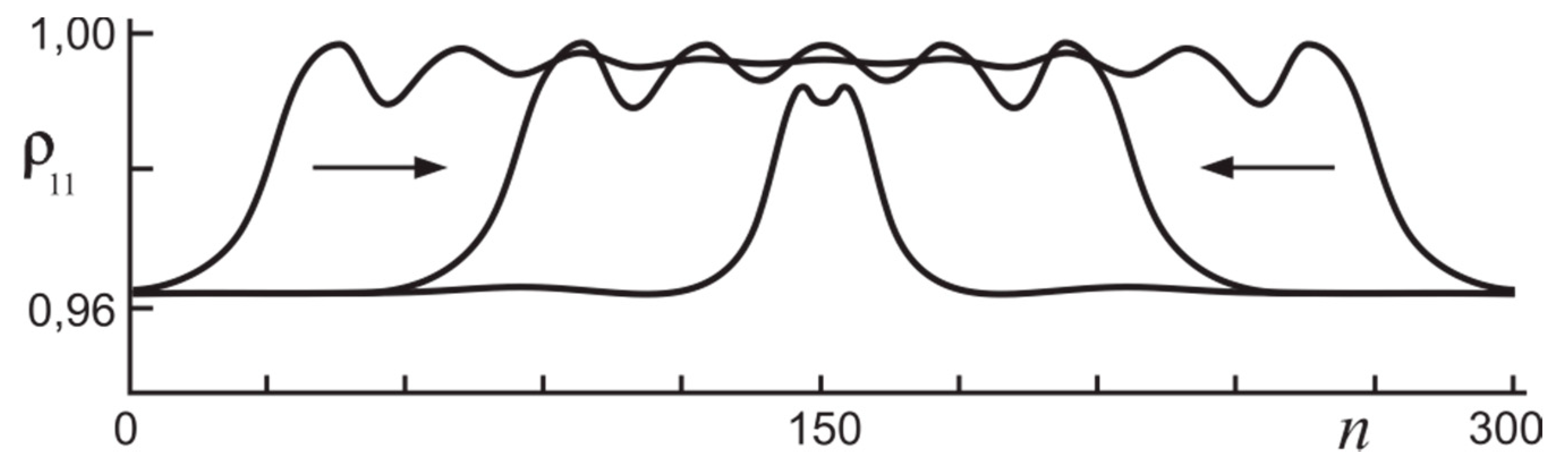
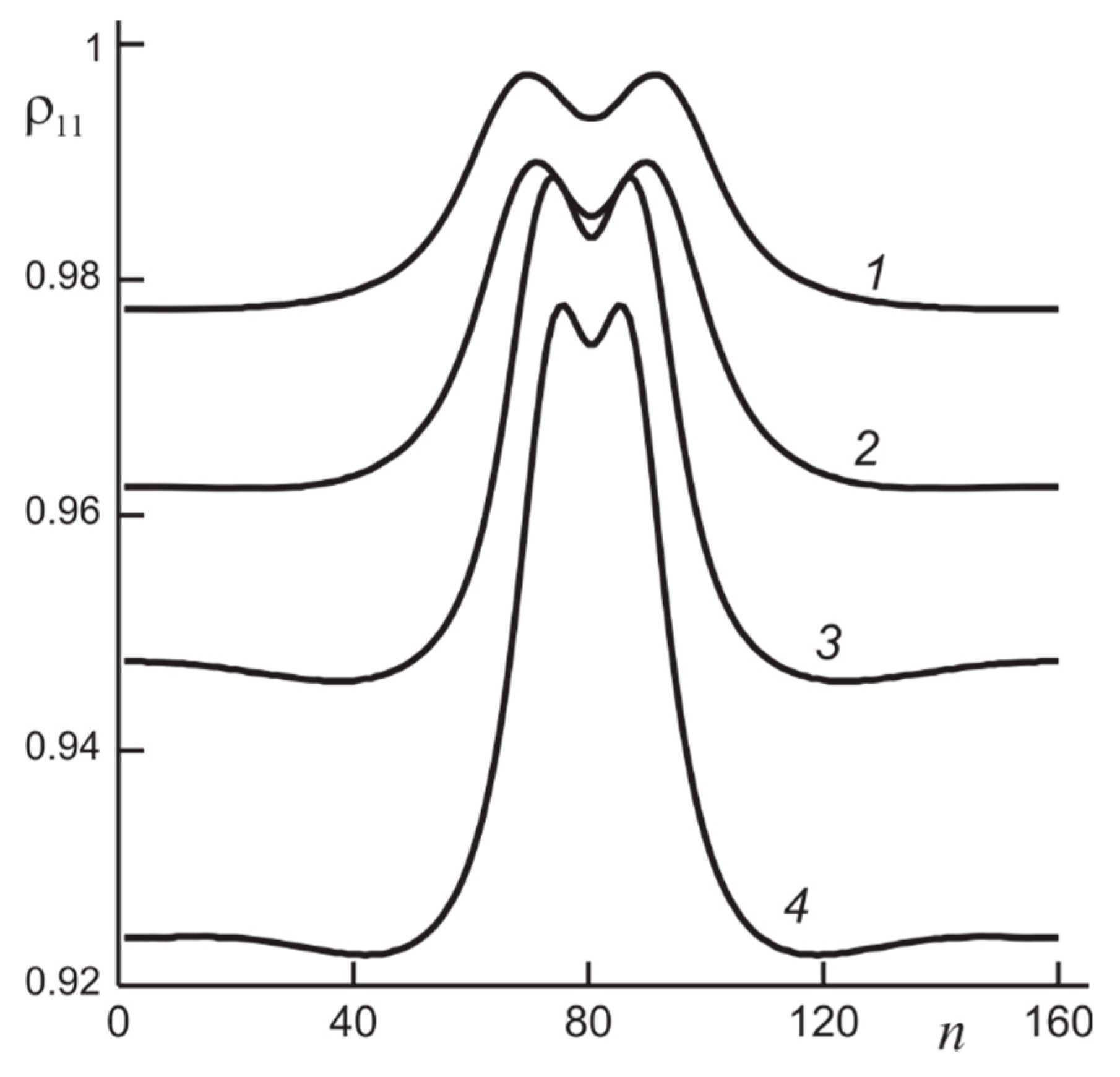
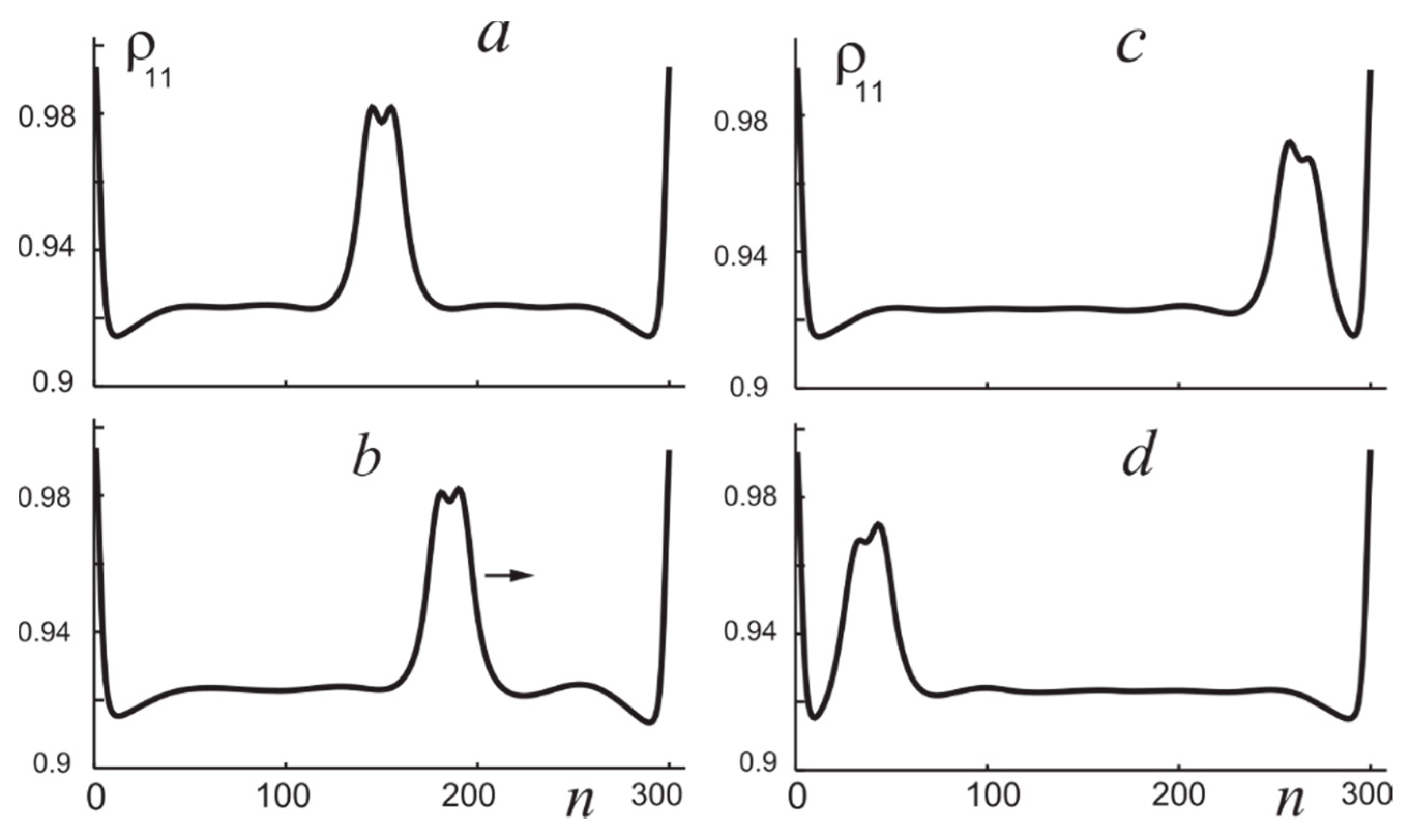
2.1.5. Discrete Switching Waves and Dissipative Molecular Solitons
2.2. Organic Thin Films: Bistability and Switching Waves
3. Light Structuring
3.1. Model of a Laser with Saturable Absorption and Governing Equations
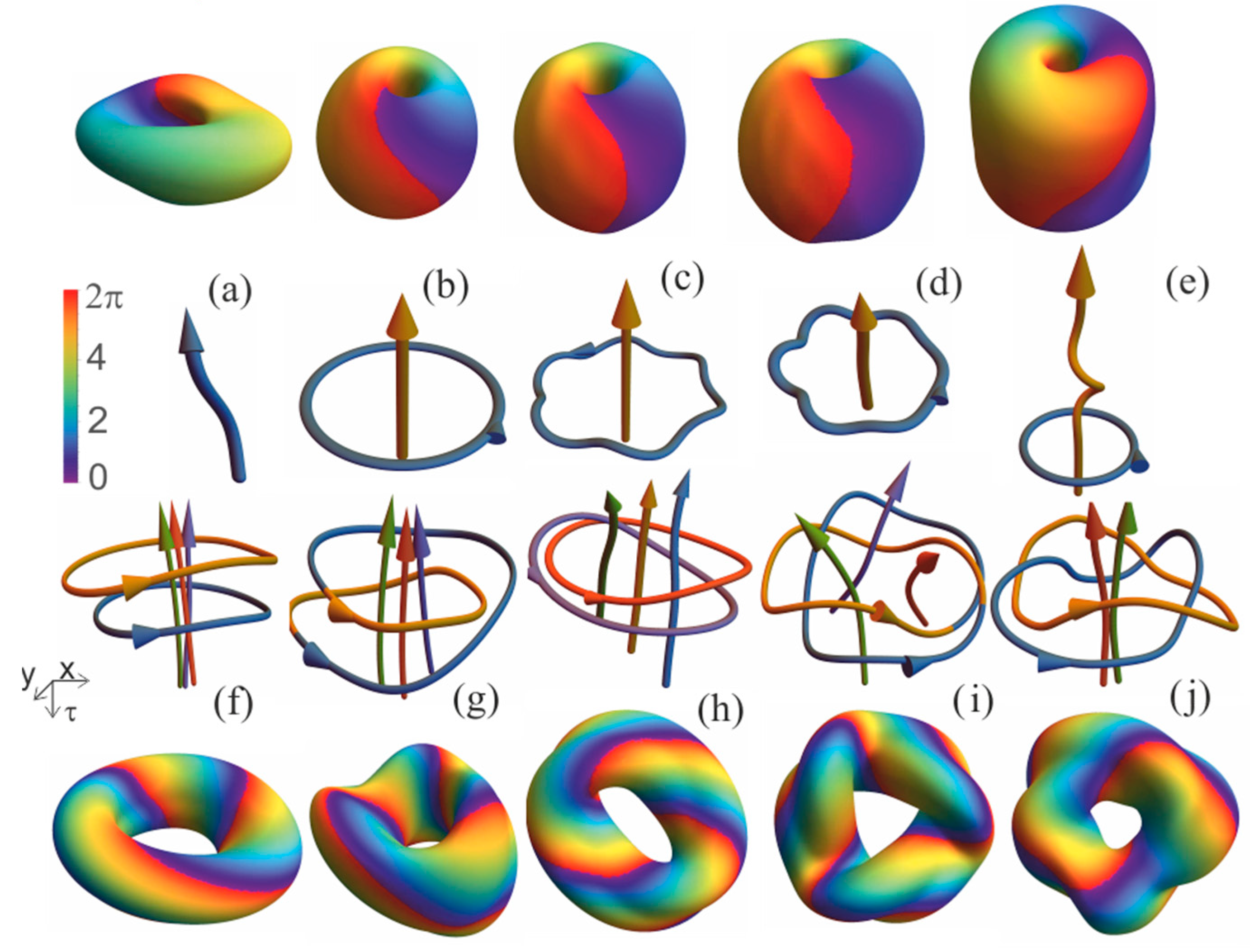
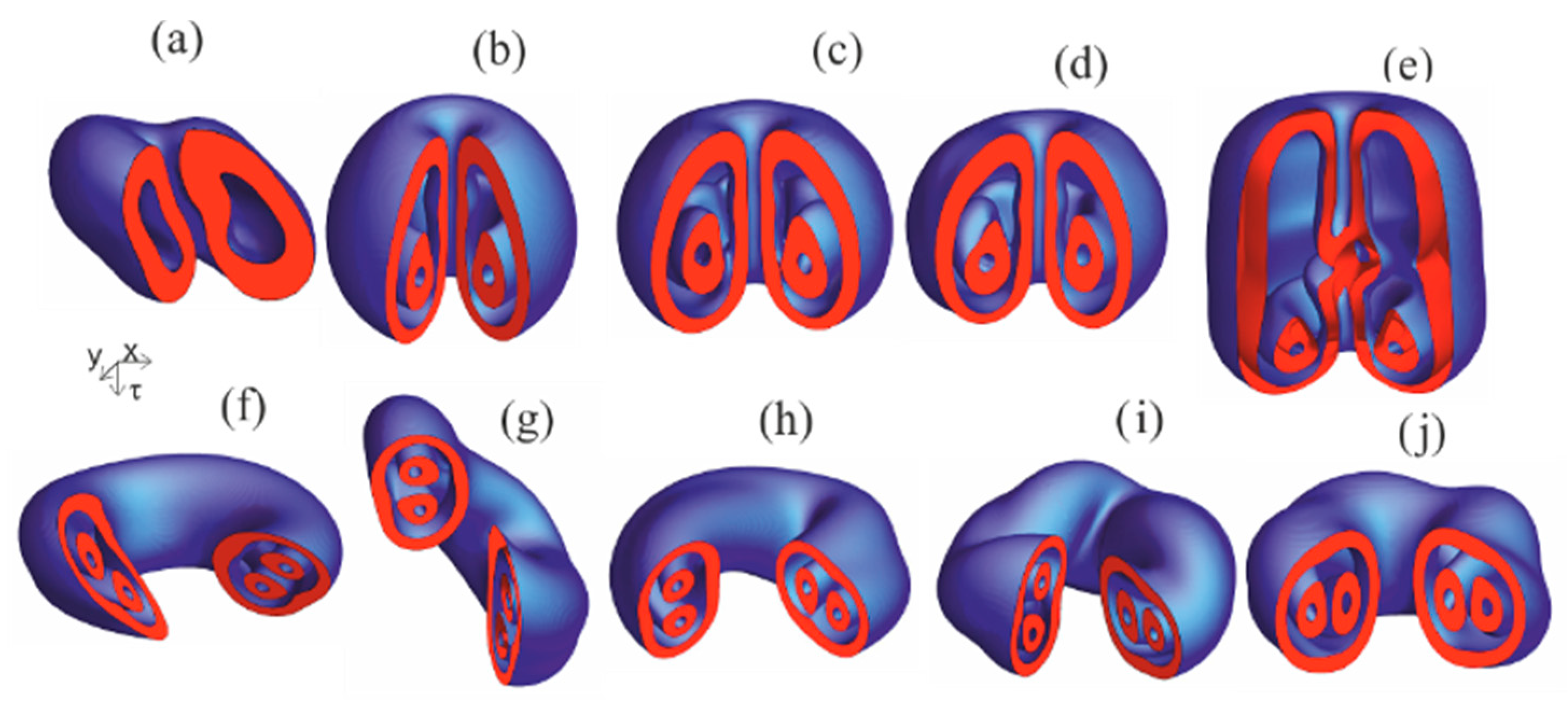
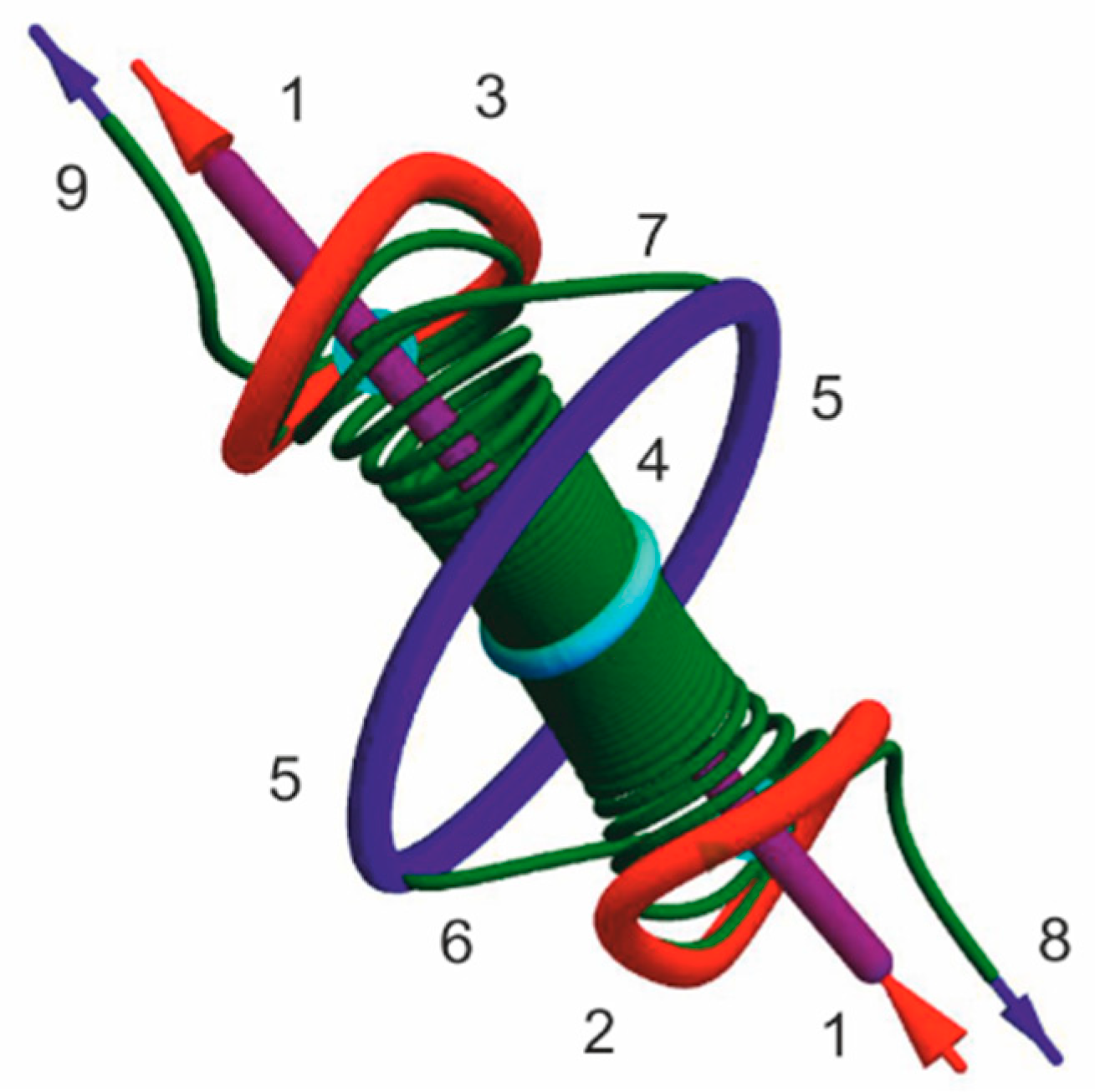
3.2. Topological Laser Solitons
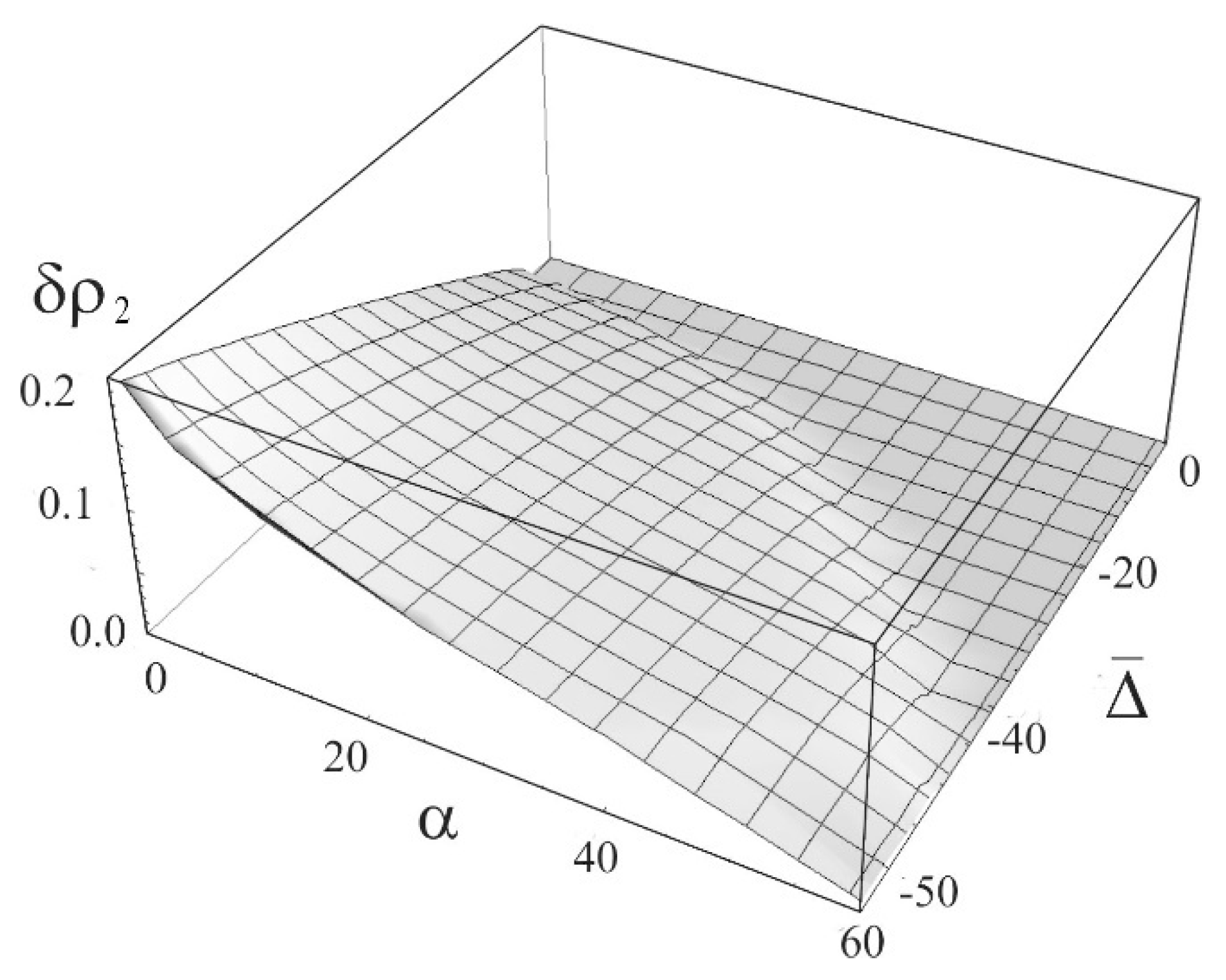
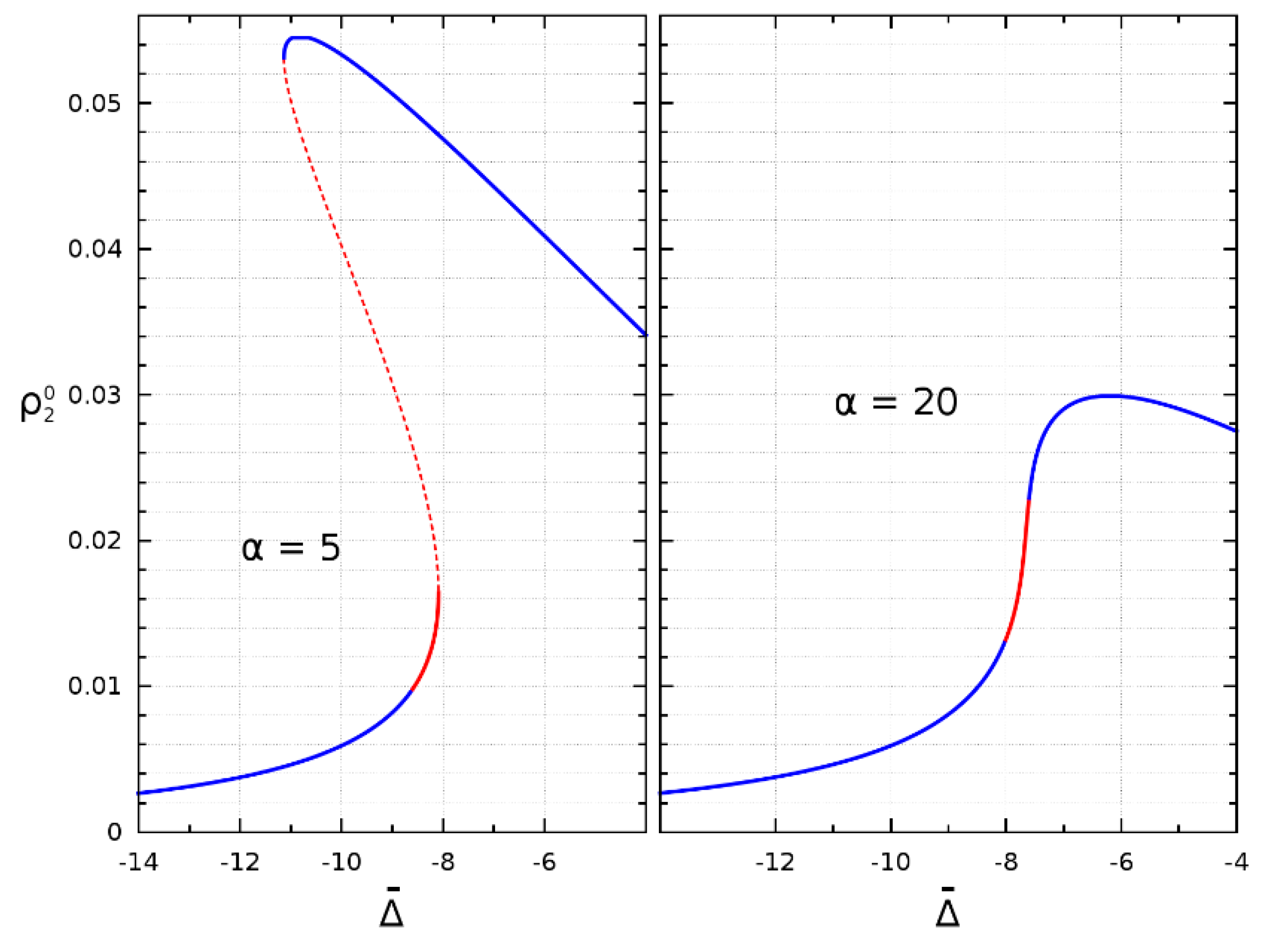
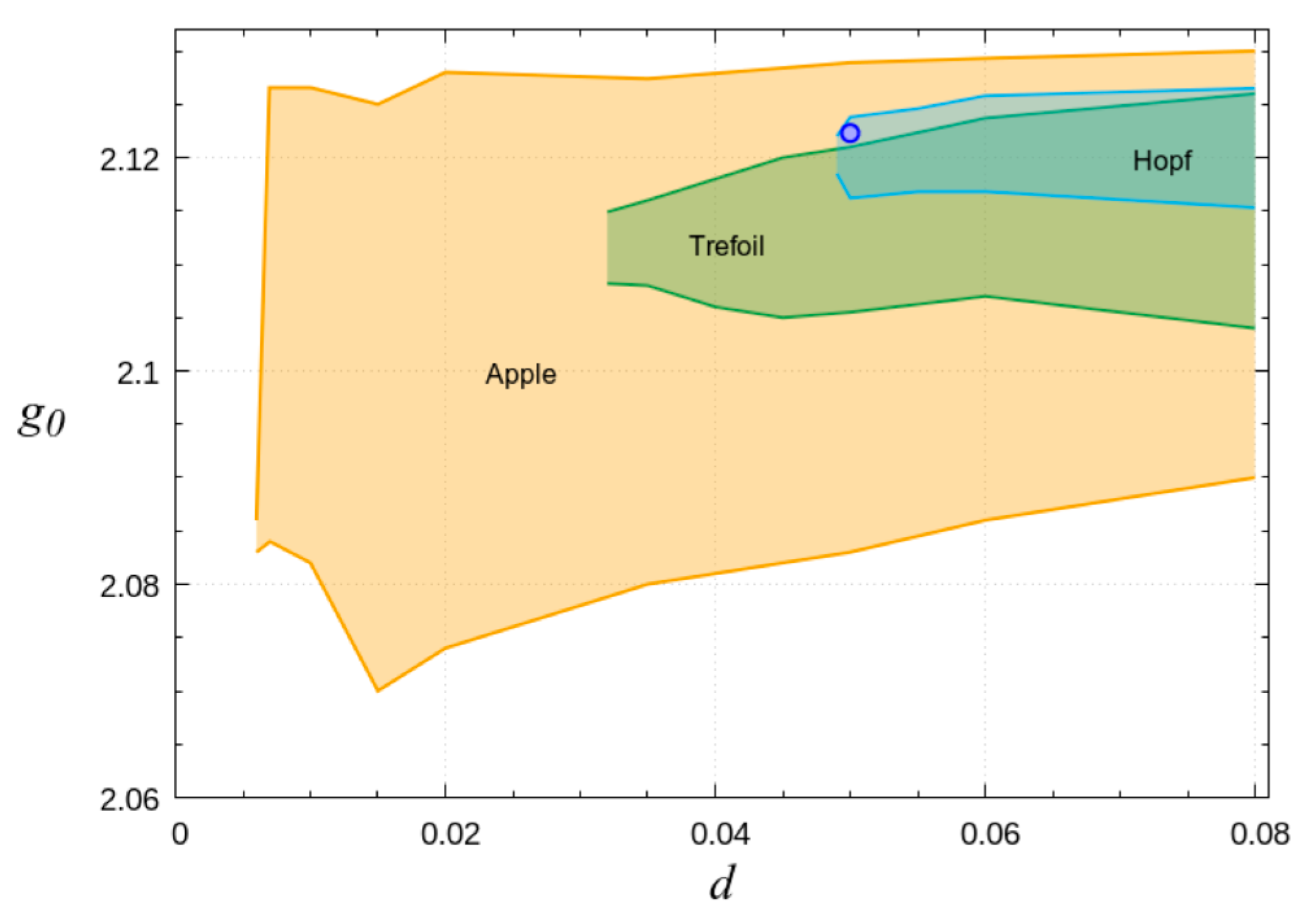
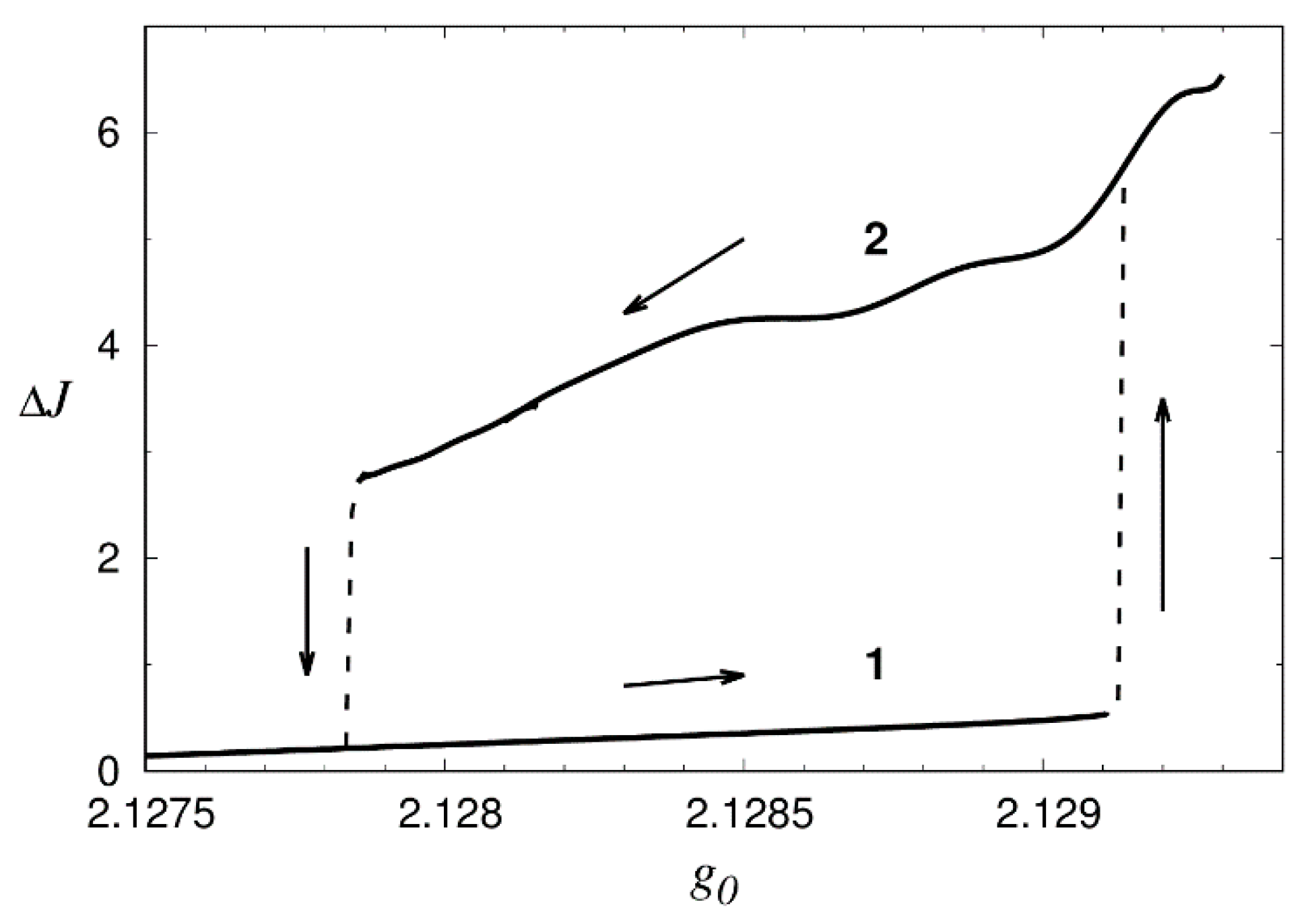
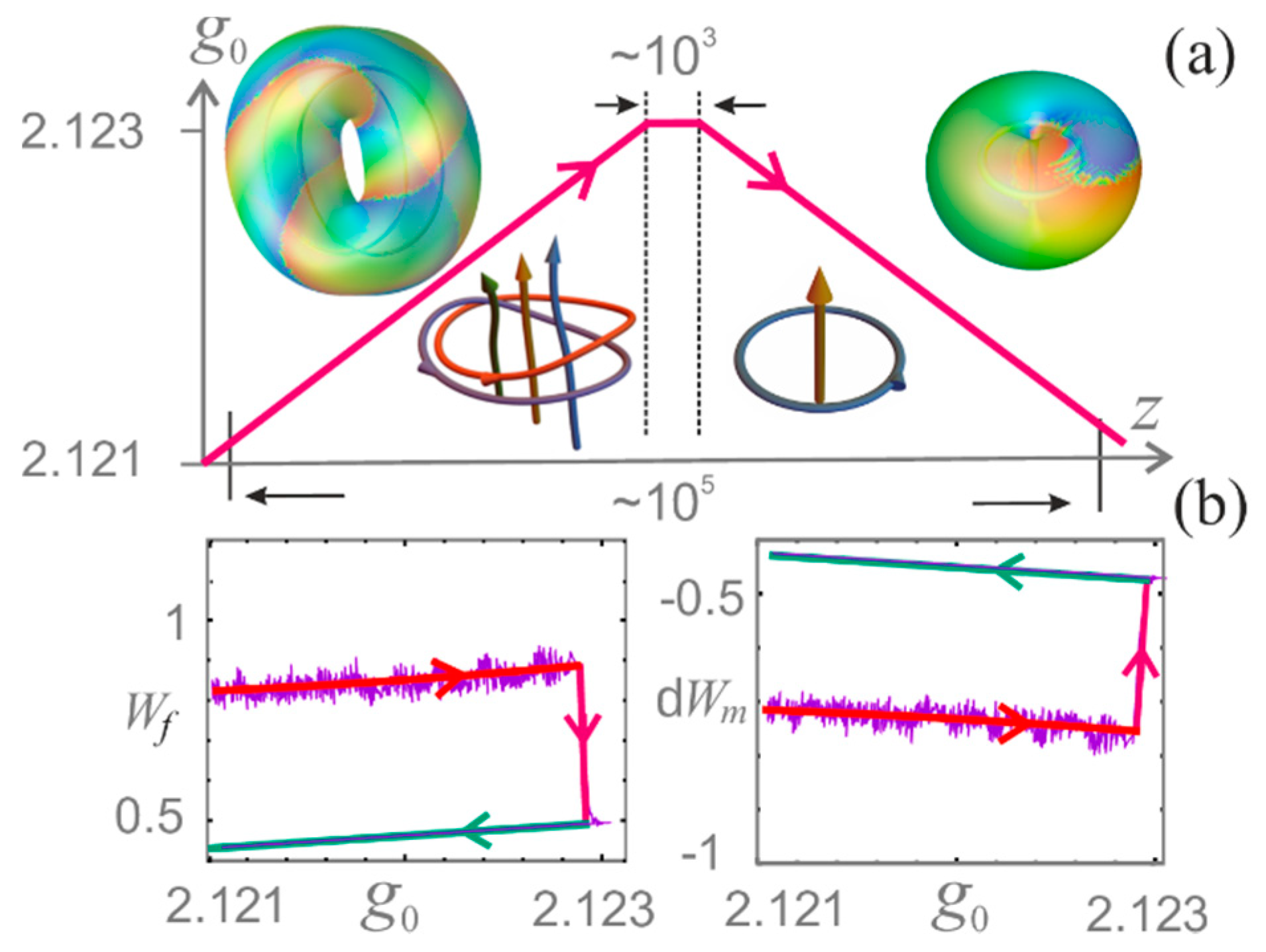
3.3. Hysteresis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science + Business Media LLC: New York, NY, USA, 2007; ISBN 978-0-387-37825-1. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2012; ISBN 978-0-123-97023-7. [Google Scholar]
- Gu, L.; Livenery, J.; Zhu, G.; Narimanov, E.E.; Noginov, M.A. Quest for organic plasmonics. Appl. Phys. Lett. 2013, 103, 021104. [Google Scholar] [CrossRef]
- Gentile, M.J.; Núñez-Sánchez, S.; Barnes, W.L. Optical field-enhancement and subwavelength field-confinement using excitonic nanostructures. Nano Lett. 2014, 14, 2339–2344. [Google Scholar] [CrossRef]
- English, L.Q.; Sato, M.; Sievers, A.J. Nanoscale intrinsic localized modes in an antiferromagnetic lattice. J. Appl. Phys. 2001, 89, 6707. [Google Scholar] [CrossRef][Green Version]
- Slavin, A.; Tiberkevich, V. Spin wave mode excited by spin-polarized current in a magnetic nanocontact is a standing self-localized wave bullet. Phys. Rev. Lett. 2005, 95, 237201. [Google Scholar] [CrossRef]
- Frenkel, Y.; Kontorova, T. On the theory of plastic deformation and twining. Phys. Z. Sowjetunion 1938, 13, 1–10. [Google Scholar]
- Fermi, E.; Pasta, J.; Ulam, S.M. Studies in Nonlinear Problems; Technique Report LA-1940; Los Alamos Sci. Lab.: Los Alamos, NM, USA, 1955. [Google Scholar]
- Davydov, A.S.; Kislukha, N.I. Solitary excitons in one-dimensional molecular chains. Phys. Stat. Sol. B 1973, 59, 465–470. [Google Scholar] [CrossRef]
- Kobayashi, T. (Ed.) J-Aggregats; Word Scientific: Singapore, 1996; ISBN 978-981-02-2737-1. [Google Scholar]
- Furuki, M.; Tian, M.; Sato, Y.; Pu, L.S.; Tatsuura, S.; Wada, O. Terahertz demultiplexing by a single shot time to space conversion using a film of squarylium dye J-aggregates. Appl. Phys. Lett. 2000, 77, 472–474. [Google Scholar] [CrossRef]
- Bricker, W.P.; Banal, J.L.; Stone, M.B.; Bathe, M. Molecular model of J-aggregated pseudoisocyanine fibers. J. Chem. Phys. 2018, 149, 024905. [Google Scholar] [CrossRef]
- Malyshev, V.A.; Glaeske, H.; Feller, K.-H. Optical bistable response of an open Frenkel chain: Exciton-exciton annihilation and boundary effects. Phys. Rev. A 1998, 58, 670–678. [Google Scholar] [CrossRef]
- Malyshev, V.A.; Moreno, P. Mirrorless optical bistability of linear molecular aggregates. Phys. Rev. A 1996, 53, 416–423. [Google Scholar] [CrossRef] [PubMed]
- Malyshev, V.; Glaeske, H.; Feller, K. Effects of higher exciton manifolds and exciton-exciton annihilation on optical bistable response of an ultrathin glassy film comprised of oriented linear Frenkel chains. Phys. Rev. A 2002, 65, 033821. [Google Scholar] [CrossRef]
- Klugkist, J.A.; Malyshev, V.; Knoester, J. Intrinsic optical bistability of thin films of linear molecular aggregates: The one-exciton approximation. J. Chem. Phys. 2007, 127, 164705. [Google Scholar] [CrossRef]
- Klugkist, J.A.; Malyshev, V.; Knoester, J. Intrinsic optical bistability of thin films of linear molecular aggregates: The two-exciton approximation. J. Chem. Phys 2008, 128, 084706. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, A.S.; Kiselev, A.S.; Rozanov, N.N. Nanosized discrete dissipative solitons in resonantly excited molecular J-aggregates. JETP Lett. 2008, 87, 663–666. [Google Scholar] [CrossRef]
- Vysotina, N.V.; Malyshev, V.A.; Maslov, V.G.; Nesterov, L.A.; Rosanov, N.N.; Fedorov, S.V.; Shatsev, A.N. Simulation of interaction of oriented J aggregates with resonance laser radiation. Opt. Spectrosc. 2010, 109, 112–119. [Google Scholar] [CrossRef]
- Vysotina, N.V.; Rosanov, N.N.; Fedorov, S.V.; Shatsev, A.N. Motion of molecular dissipative solitons in oriented linear J aggregates upon oblique incidence of exciting laser radiation. Opt. Spectrosc. 2010, 109, 120–122. [Google Scholar] [CrossRef]
- Rosanov, N.N.; Fedorov, S.V.; Shatsev, A.N.; Vyssotina, N.V. Dissipative molecular solitons. Eur. Phys. J. 2010, 59, 3–12. [Google Scholar] [CrossRef]
- Rosanov, N.N. Dissipativnye Opticheskie Solitony. Ot Mikro-k Nano-i Atto-[Dissipative Optical Solitons. From Micro to Nano and Atto]; Fizmatlit Publ.: Moscow, Russia, 2011; 536p. (In Russian) [Google Scholar]
- Levinsky, B.N.; Nesterov, L.A.; Fainberg, B.D.; Rosanov, N.N. Derivation of the equation of motion for resonantly excited molecular J aggregates taking into account multiparticle effects. Opt. Spectrosc. 2013, 115, 406–419. [Google Scholar] [CrossRef]
- Nesterov, L.A.; Fedorov, S.V.; Rosanov, N.N.; Levinsky, B.N.; Fainberg, B.D. Analysis of bistability in molecular J aggregates under their resonant optical excitation taking into account multiparticle effects. Opt. Spectrosc. 2013, 115, 499–507. [Google Scholar] [CrossRef]
- Veretenov, N.A.; Nesterov, L.A.; Rosanov, N.N.; Fedorov, S.V. Modulation instability of the homogeneous mode resonant excitation of molecular J-aggregates. Opt. Spectrosc. 2014, 117. [Google Scholar] [CrossRef]
- Veretenov, N.A.; Levinsky, B.N.; Nesterov, L.A.; Rosanov, N.N.; Fainberg, B.D.; Fedorov, S.V. Accounting of many-particle interactions in molecular J-aggregates and nonlinear optical effects in these systems. Sci. Tech. J. Inf. Technol. Mech. Opt. 2014, 93, 1–17. [Google Scholar]
- Mukamel, S.; Abramavicius, D. Many-body approaches for simulating coherent nonlinear spectroscopies of electronic and vibrational excitons. Chem. Rev. 2004, 104, 2073–2098. [Google Scholar] [CrossRef] [PubMed]
- Renger, T.; May, V.; Kuhn, O. Ultrafast excitation energy transfer dynamics in photosynthetic pigment–protein complexes. Phys. Rep. 2001, 343, 137–254. [Google Scholar] [CrossRef]
- Spano, F.; Mukamel, S. Nonlinear susceptibilities of molecular aggregates: Enhancement of χ3 by size. Phys. Rev. A 1989, 40, 5783–5801. [Google Scholar] [CrossRef]
- Spano, F.; Mukamel, S. Excitons in confined geometries: Size scaling of nonlinear susceptibilities. J. Chem. Phys. 1991, 95, 7526–7540. [Google Scholar] [CrossRef][Green Version]
- Lemberg, R. Radiation from an N-atom system. I. general formalism. Phys. Rev. A 1970, 2, 883–888. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: New York, NY, USA, 1999; ISBN 9780195132915. [Google Scholar]
- Fainberg, B.; Jouravlev, M.; Nitzan, A. Light-induced current in molecular tunneling junctions excited with intense shaped pulses. Phys. Rev. B 2007, 76, 245329. [Google Scholar] [CrossRef]
- Rozanov, N.N. Hysteresis phenomena in distributed optical systems. Sov. Phys. JETP 1981, 53, 47. [Google Scholar]
- Rosanov, N.N. Spatial Hysteresis and Optical Patterns; Springer: Berlin, Germany, 2002; ISBN 978-3-662-04792-7. [Google Scholar]
- Durach, M.; Rusina, A.; Klimov, V.I.; Stockman, M.I. Nanoplasmonic renormalization and enhancement of Coulomb interactions. New J. Phys. 2008, 10, 105011. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.-S.; Link, S.; Nordlander, P. Plasmons in strongly coupled metallic nanostructures. Chem. Rev. 2011, 111, 3913. [Google Scholar] [CrossRef]
- Leonhardt, U.; Philbin, T. Geometry and Light. The Science of Invisibility; Dover Publications: Mineola, NY, USA, 2010; ISBN 0486476936. [Google Scholar]
- Fainberg, B.D.; Li, G. Nonlinear organic plasmonics: Applications to optical control of Coulomb blocking in nanojunctions. Appl. Phys. Lett. 2015, 107, 109902, Erratum in 2015, 107, 109902. [Google Scholar] [CrossRef]
- Fainberg, B.D.; Rosanov, N.N.; Veretenov, N.A. Light-induced “plasmonic” properties of organic materials: Surface polaritons and switching waves in bistable organic thin films. Appl. Phys. Lett. 2017, 110, 203301. [Google Scholar] [CrossRef]
- Fainberg, B.D.; Li, G. Nonlinear organic plasmonics. arXiv 2015, arXiv:1510.00205. [Google Scholar] [CrossRef]
- Agranovich, V.M.; Galanin, M.D. Electronic Excitation Energy Transfer in Condensed Matter; North-Holland: Amsterdam, NY, USA, 1983. [Google Scholar]
- Fainberg, B.D. Nonperturbative analytic approach to the interaction of intense ultrashort chirped pulses with molecules in solution: Picture of “moving” potentials. J. Chem. Phys. 1998, 109, 4523. [Google Scholar] [CrossRef]
- Brasselet, E.; Gervinskas, G.; Seniutinas, G.; Juodkazis, S. Topological shaping of light by closed-path nanoslits. Phys. Rev. Lett. 2013, 111, 193901. [Google Scholar] [CrossRef] [PubMed]
- Faddeev, L.D. Quantization of Solitons; Princeton Report; No. IAS-75-QS70; Institute for Advanced Study: Princeton, NJ, USA, 1975. [Google Scholar]
- Faddeev, L.D. Einstein and several contemporarytendences in the field theory of elementary particle. In Relativity, Quanta and Cosmology; Pantaleo, M., de Finis, F., Eds.; Johnson Reprint Corporation: New York, NY, USA, 1979; Volume 1. [Google Scholar]
- Babaev, E. Dual neutral variables and knot solitons in triplet superconductors. Phys. Rev. Lett. 2002, 88, 177002. [Google Scholar] [CrossRef] [PubMed]
- Garaud, J.; Carlstrom, J.; Babaev, E. Topological solitons in three-band superconductors with broken time reversal symmetry. Phys. Rev. Lett. 2011, 107, 197001. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Heatley, D.R.; Wright, E.M.; Akhmediev, N.N. Stability of the higher-bound states in a saturable self-focusing medium. Phys. Rev. A 1991, 44, 636–644. [Google Scholar] [CrossRef] [PubMed]
- Quiroga-Teixeiro, M.; Michinel, H. Stable azimuthal stationary state in quintic nonlinear media. J. Opt. Soc. Am. B 1997, 14, 2004–2009. [Google Scholar] [CrossRef]
- Quiroga-Teixeiro, M.L.; Berntson, A.; Michinel, H. Internal dynamics of nonlinear beams in their ground states: Short- and long-lived excitation. J. Opt. Soc. Am. B 1999, 16, 1697–1704. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Crasovan, L.C.; Towers, I.; Buryak, A.V.; Malomed, B.A.; Torner, L.; Torres, J.P.; Lederer, F. Stable spinning optical solitons in three dimensions. Phys. Rev. Lett. 2002, 88, 073902. [Google Scholar] [CrossRef]
- Desyatnikov, A.; Maimistov, A.; Malomed, B. Three-dimensional spinning solitons in dispersive media with the cubic-quintic nonlinearity. Phys. Rev. E 2000, 61, 3107–3113. [Google Scholar] [CrossRef]
- Grelu, P.; Soto-Crespo, J.M.; Akhmediev, N. Light bullets and dynamic pattern formation in nonlinear dissipative systems. Opt. Express 2005, 13, 9352–9360. [Google Scholar] [CrossRef] [PubMed]
- Mihalache, D.; Mazilu, D.; Lederer, F.; Kartashov, Y.V.; Crasovan, L.C.; Torner, L.; Malomed, B.A. Stable vortex tori in the three dimensional cubic-quintic Ginzburg-Landau equation. Phys. Rev. Lett. 2006, 97, 073904. [Google Scholar] [CrossRef] [PubMed]
- Gustave, F.; Radwell, N.; McIntyre, C.; Toomey, J.P.; Kane, D.M.; Barland, S.; Firth, W.J.; Oppo, G.-L.; Ackemann, T. Observation of mode-locked spatial laser solitons. Phys. Rev. Lett. 2017, 118, 044102. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.V.; Astrakharchik, G.E.; Malomed, B.A.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Veretenov, N.A.; Rosanov, N.N.; Fedorov, S.V. Rotating and precessing dissipative-optical-topological-3D solitons. Phys. Rev. Lett. 2016, 117, 183901. [Google Scholar] [CrossRef] [PubMed]
- Veretenov, N.A.; Fedorov, S.V.; Rosanov, N.N. Topological vortex and knotted dissipative optical 3D solitons generated by 2D vortex solitons. Phys. Rev. Lett. 2017, 119, 263901. [Google Scholar] [CrossRef]
- Fedorov, S.V.; Veretenov, N.A.; Rosanov, N.N. Irreversible hysteresis of internal structure of tangle dissipative optical solitons. Phys. Rev. Lett. 2019, 122, 023903. [Google Scholar] [CrossRef] [PubMed]
- Veretenov, N.A.; Fedorov, S.V.; Rosanov, N.N. Topological three-dimensional dissipative optical solitons. Philos. Trans. R. Soc. A 2018, 376, 20170367. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, S.V.; Rosanov, N.N.; Veretenov, N.A. Structure of energy fluxes in topological three-dimensional dissipative solitons. JETP Lett. 2018, 107, 327–331. [Google Scholar] [CrossRef]
- Rosanov, N.N. Quasi-optical equation in media with weak absorption. Opt. Spectr. 2019, 127. in press. [Google Scholar]
- Veretenov, N.A.; Fedorov, S.V.; Rosanov, N.N. Reversible and irreversible hysteresis with three-dimensional topological laser solitons. 2019; in preparation. [Google Scholar]
- Kawauchi, A. A Survey of Knot Theory; Birkhauser: Basel, Switzerland, 1996; ISBN 3-7643-5048-2. [Google Scholar]
- Zabusky, N.J.; Melander, M.V. Three-dimensional vortex tube reconnection: Morphology for orthogonally-offset tubes. Phys. D Nonlinear Phenom. 1989, 37, 555–562. [Google Scholar] [CrossRef]
- Pontin, D.I. Three-dimensional magnetic reconnection regimes: A review. Adv. Space Res. 2011, 47, 1508. [Google Scholar] [CrossRef]
- Zuccher, S.; Caliari, M.; Baggaley, A.W.; Barenghi, C.F. Quantum vortex reconnections. Phys. Fluids 2012, 24, 125108. [Google Scholar] [CrossRef]
- Laing, C.E.; Ricca, R.L.; Sumners, D.W.L. Conservation of writhe helicity under anti-parallel reconnection. Sci. Rep. 2015, 5, 9224. [Google Scholar] [CrossRef]
- Scheeler, M.W.; Kleckner, D.; Proment, D.; Kindlmann, G.L.; Irvine, W.T.M. Helicity conservation by flow across scales in reconnecting vortex links and knots. Proc. Natl. Acad. Sci. USA 2014, 111, 15350. [Google Scholar] [CrossRef]
- Barenghi, C.F.; Ricca, R.L.; Samuels, D.C. How tangled is a tangle? Physica (Amst.) 2001, 157, 197–206. [Google Scholar] [CrossRef]
- Kleckner, D.; Kauffman, L.H.; Irvine, W.T.M. How superfluid vortex knots untie. Nat. Phys. 2016, 12, 650. [Google Scholar] [CrossRef]
- Vysotina, N.V.; Rosanov, N.N.; Semenov, V.E. Extremely short dissipative solitons in an active nonlinear medium with quantum dots. Opt. Spectrosc. 2009, 106, 713–717. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosanov, N.N.; Fedorov, S.V.; Nesterov, L.A.; Veretenov, N.A. Extreme and Topological Dissipative Solitons with Structured Matter and Structured Light. Nanomaterials 2019, 9, 826. https://doi.org/10.3390/nano9060826
Rosanov NN, Fedorov SV, Nesterov LA, Veretenov NA. Extreme and Topological Dissipative Solitons with Structured Matter and Structured Light. Nanomaterials. 2019; 9(6):826. https://doi.org/10.3390/nano9060826
Chicago/Turabian StyleRosanov, Nikolay N., Sergey V. Fedorov, Leonid A. Nesterov, and Nikolay A. Veretenov. 2019. "Extreme and Topological Dissipative Solitons with Structured Matter and Structured Light" Nanomaterials 9, no. 6: 826. https://doi.org/10.3390/nano9060826
APA StyleRosanov, N. N., Fedorov, S. V., Nesterov, L. A., & Veretenov, N. A. (2019). Extreme and Topological Dissipative Solitons with Structured Matter and Structured Light. Nanomaterials, 9(6), 826. https://doi.org/10.3390/nano9060826




