Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications
Abstract
1. Introduction
2. Perfect Absorption Theory
2.1. Critical Coupling Concept
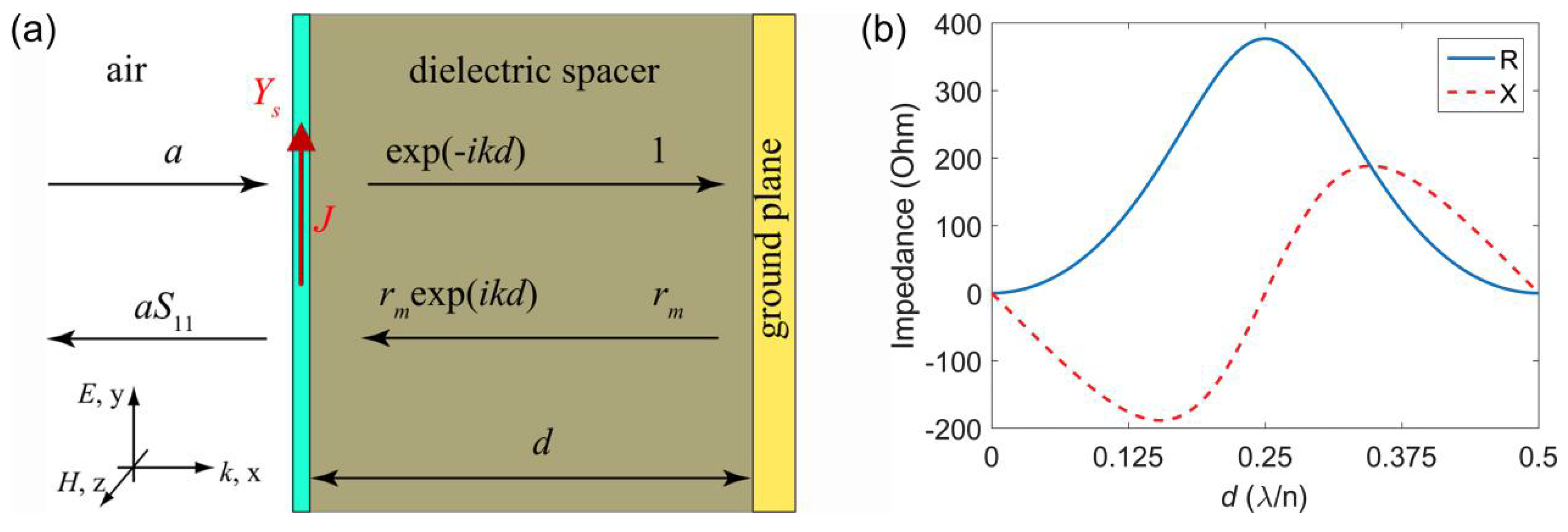
2.2. Impedance Matching Concept
3. Perfect Absorption in the Mid-IR to THz Band
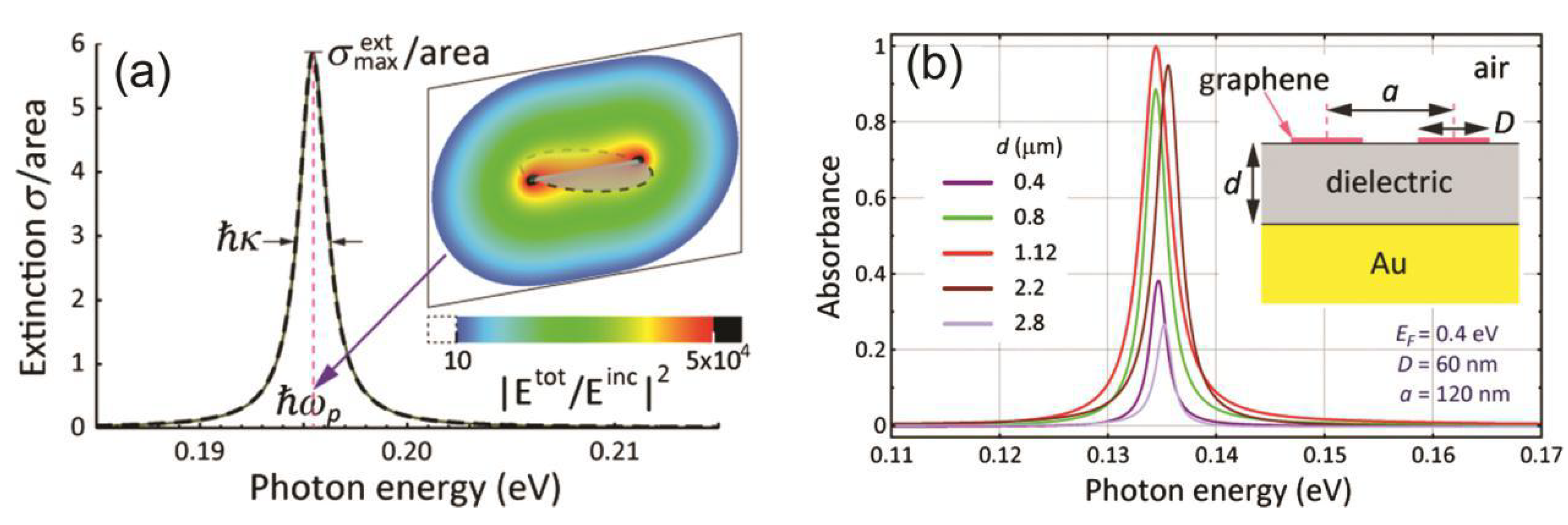
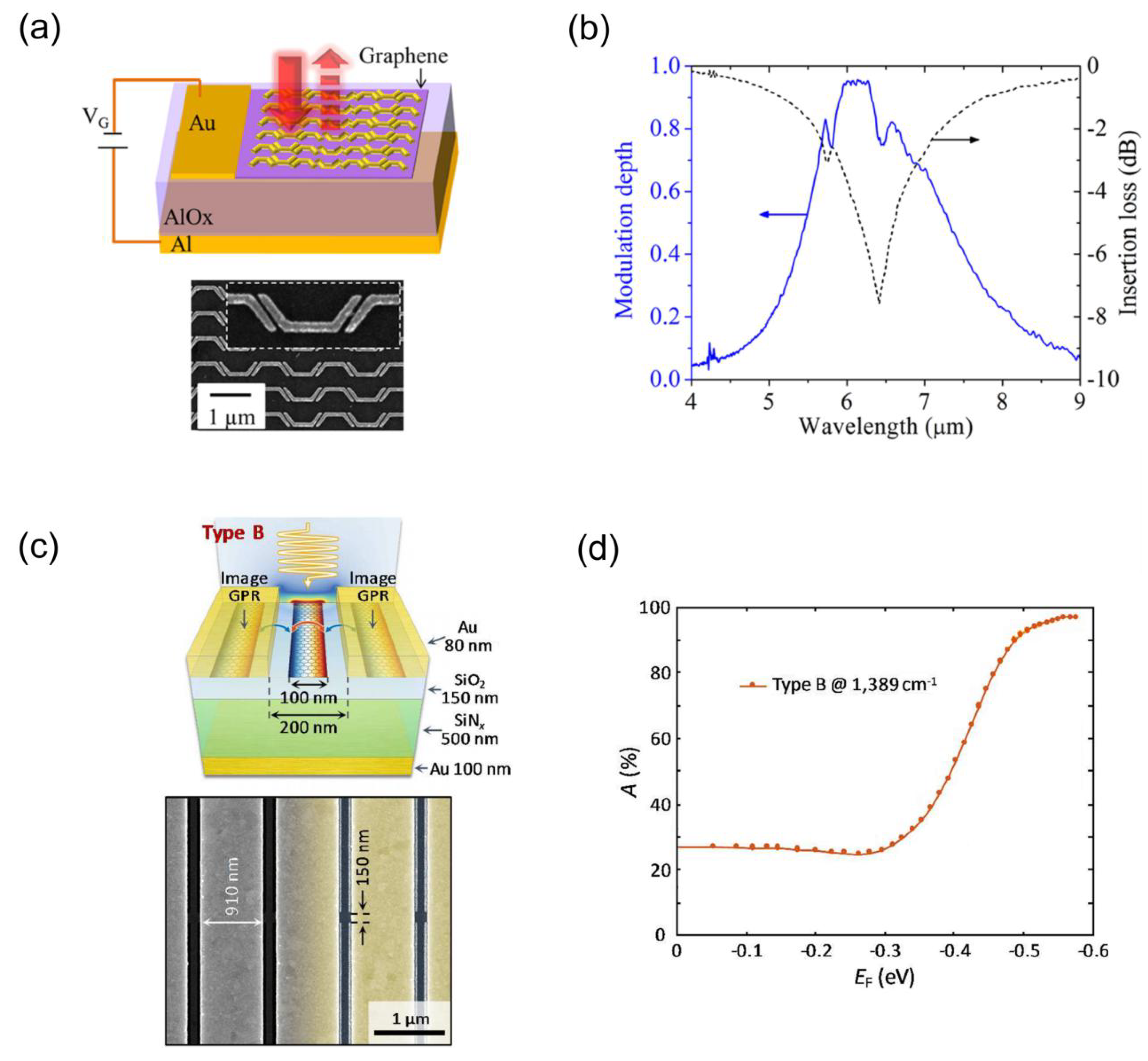
3.1. Graphene Plasmons Induced Perfect Absorption
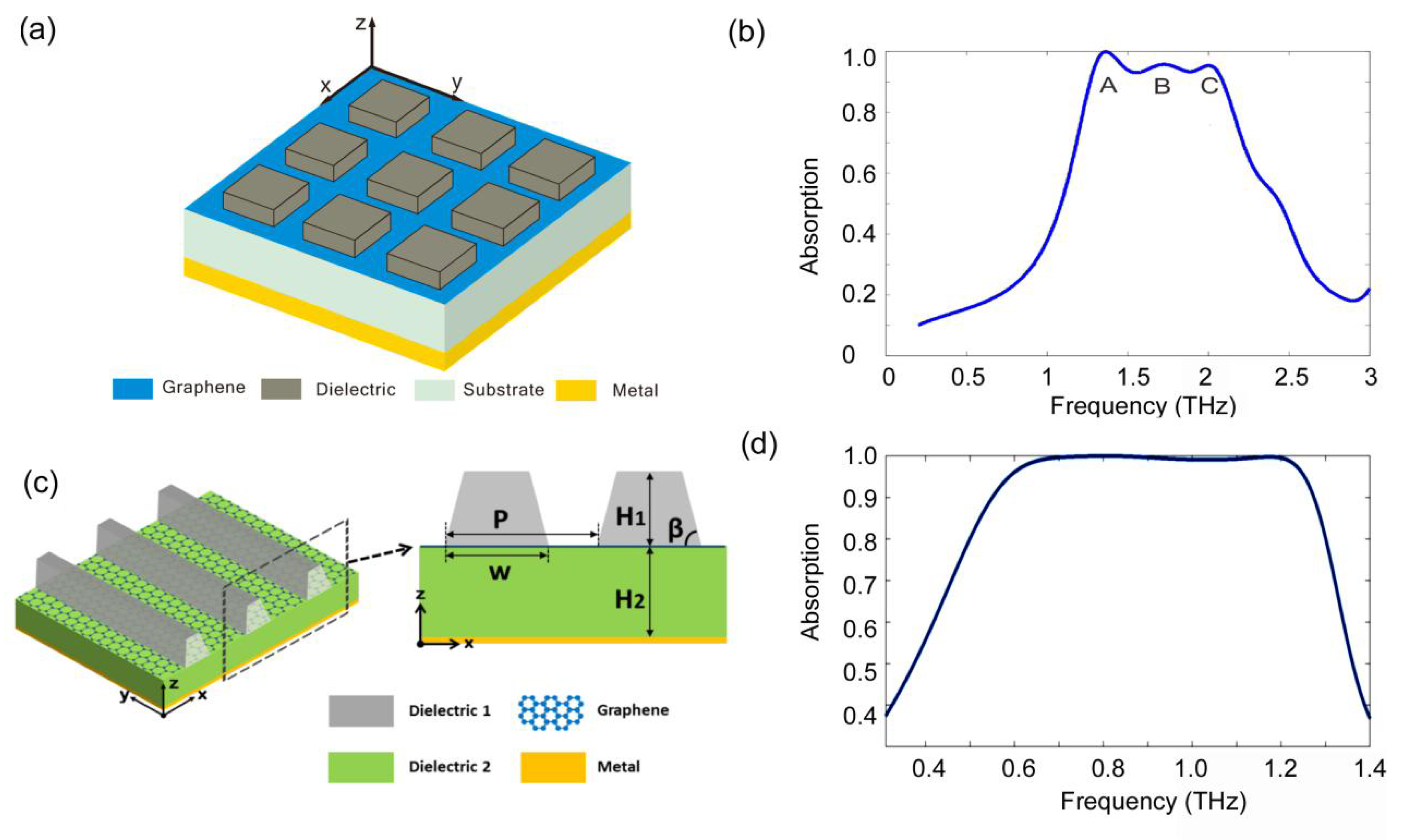
3.2. Broadband Perfect Absorption
3.3. Coherent Perfect Absorption
4. Perfect Absorption in the Visible and Near-IR Band
4.1. Graphene Coupled with Metallic Nanostructures
4.2. Graphene Coupled with Dielectric-Mode Structures
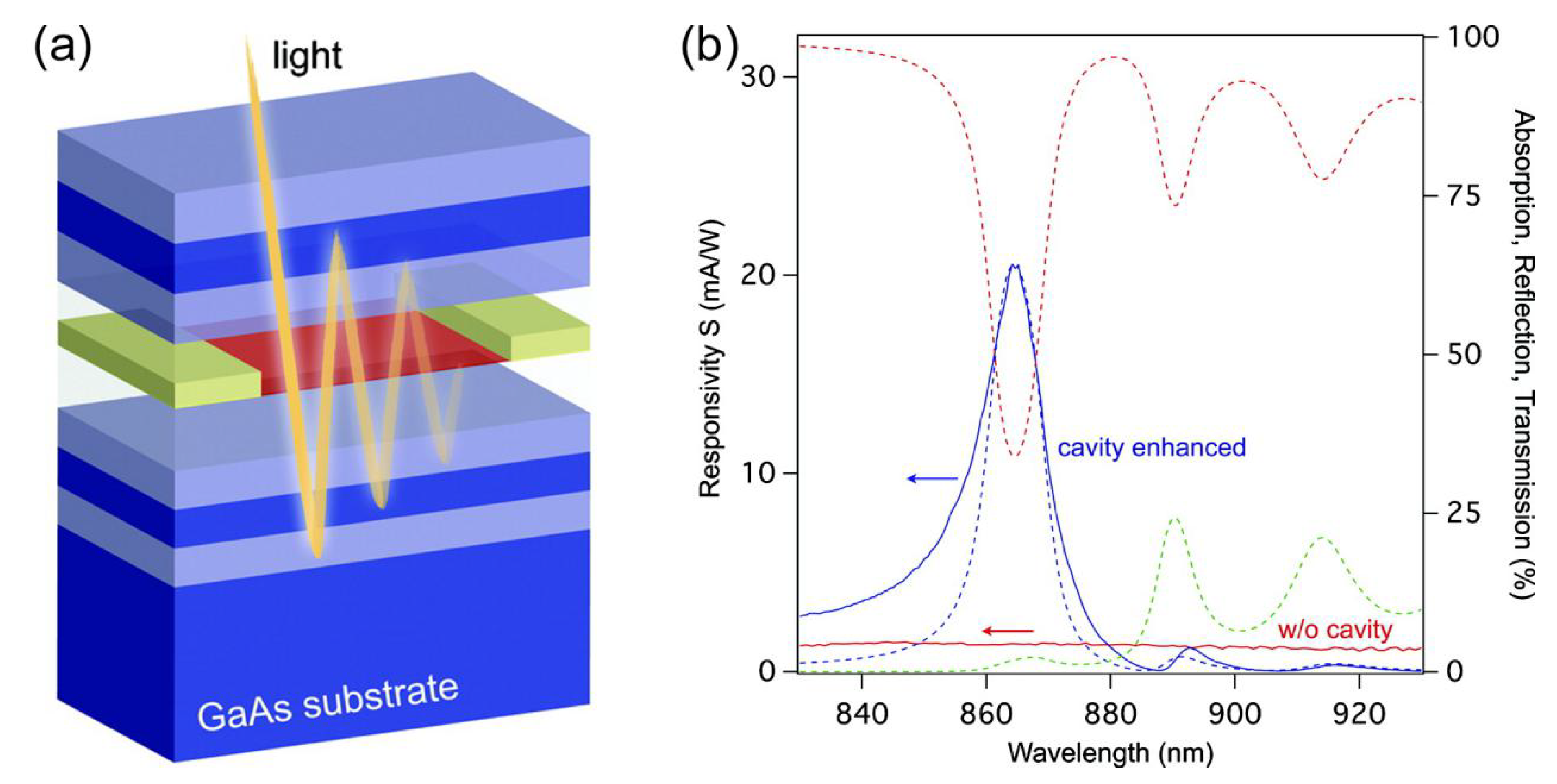
4.3. Chip-Integrated Graphene-Based Perfect Absorption Structure
5. Optoelecronic Applications
5.1. Photodetectors
5.2. Modulators
6. Outlook and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Xia, F.N.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Xia, F.N.; Mueller, T.; Lin, Y.M.; Valdes-Garcia, A.; Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 2009, 4, 839–843. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Mueller, T.; Xia, F.N.; Avouris, P. Graphene photodetectors for high-speed optical communications. Nat. Photonics 2010, 4, 297–301. [Google Scholar] [CrossRef]
- Urich, A.; Unterrainer, K.; Mueller, T. Intrinsic response time of graphene photodetectors. Nano Lett. 2011, 11, 2804–2808. [Google Scholar] [CrossRef] [PubMed]
- Schall, D.; Neumaier, D.; Mohsin, M.; Chmielak, B.; Bolten, J.; Porschatis, C.; Prinzen, A.; Matheisen, C.; Kuebart, W.; Junginger, B.; et al. 50 GBit/s Photodetectors Based on Wafer-Scale Graphene for Integrated Silicon Photonic Communication Systems. ACS Photonics 2014, 1, 781–784. [Google Scholar] [CrossRef]
- Gan, X.T.; Shiue, R.J.; Gao, Y.D.; Meric, I.; Heinz, T.F.; Shepard, K.; Hone, J.; Assefa, S.; Englund, D. Chip-integrated ultrafast graphene photodetector with high responsivity. Nat. Photonics 2013, 7, 883–887. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Koester, S.J.; Li, M. High-speed waveguide-coupled graphene-on-graphene optical modulators. Appl. Phys. Lett. 2012, 100, 171107. [Google Scholar] [CrossRef]
- Gosciniak, J.; Tan, D.T. Theoretical investigation of graphene-based photonic modulators. Sci. Rep. 2013, 3, 1897. [Google Scholar] [CrossRef]
- Phare, C.T.; Daniel, L.Y.H.; Cardenas, J.; Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. [Google Scholar] [CrossRef]
- Lee, C.C.; Suzuki, S.; Xie, W.; Schibli, T.R. Broadband graphene electro-optic modulators with sub-wavelength thickness. Opt. Express 2012, 20, 5264–5269. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.P.; Martinez, A.; Wang, F. Optical modulators with 2D layered materials. Nat. Photonics 2016, 10, 227–238. [Google Scholar] [CrossRef]
- Hu, Y.; Pantouvaki, M.; Van Campenhout, J.; Brems, S.; Asselberghs, I.; Huyghebaert, C.; Absil, P.; Van Thourhout, D. Broadband 10 Gb/s operation of graphene electro-absorption modulator on silicon. Laser Photonics Rev. 2016, 10, 307–316. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Balci, O.; Polat, E.O.; Kakenov, N.; Kocabas, C. Graphene-enabled electrically switchable radar-absorbing surfaces. Nat. Commun. 2015, 6, 6628. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Duan, Q.; Li, S.; Yin, Q.; Lu, W.; Li, L.; Gu, B.; Hou, B.; Wen, W. Perfect electromagnetic absorption at one-atom-thick scale. Appl. Phys. Lett. 2015, 107, 181112. [Google Scholar] [CrossRef]
- Li, H.J.; Wang, L.L.; Zhai, X. Tunable graphene-based mid-infrared plasmonic wide-angle narrowband perfect absorber. Sci. Rep. 2016, 6, 36651. [Google Scholar] [CrossRef]
- Yao, G.; Ling, F.R.; Yue, J.; Luo, C.Y.; Ji, J.; Yao, J.Q. Dual-band tunable perfect metamaterial absorber in the THz range. Opt. Express 2016, 24, 1518–1527. [Google Scholar] [CrossRef]
- Huang, M.L.; Cheng, Y.Z.; Cheng, Z.Z.; Chen, H.R.; Mao, X.S.; Gong, R.Z. Based on graphene tunable dual-band terahertz metamaterial absorber with wide-angle. Opt. Commun. 2018, 415, 194–201. [Google Scholar] [CrossRef]
- Xia, S.X.; Zhai, X.; Huang, Y.; Liu, J.Q.; Wang, L.L.; Wen, S.C. Multi-band perfect plasmonic absorptions using rectangular graphene gratings. Opt. Lett. 2017, 42, 3052–3055. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.Y.; Xue, X.X.; Lin, Q.; Liu, G.D.; Zhai, X.; Wang, L.L. Tunable and multi-channel perfect absorber based on graphene at mid-infrared region. Appl. Phys. Express 2018, 11, 052002. [Google Scholar] [CrossRef]
- Andryieuski, A.; Lavrinenko, A.V. Graphene metamaterials based tunable terahertz absorber: Effective surface conductivity approach. Opt. Express 2013, 21, 9144–9155. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhu, Z.; Zhang, J.; Xu, W.; Guo, C.; Liu, K.; Zhu, M.; Chen, H.; Zhang, R.; Yuan, X.; et al. Mie resonance induced broadband near-perfect absorption in nonstructured graphene loaded with periodical dielectric wires. Opt. Express 2018, 26, 20174–20182. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.F.; Guo, C.C.; Liu, K.; Zhu, Z.H.; Ye, W.M.; Yuan, X.D.; Qin, S.Q. Coherent perfect absorption and transparency in a nanostructured graphene film. Opt. Express 2014, 22, 12524–12532. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Wang, J. High-speed gate-tunable terahertz coherent perfect absorption using a split-ring graphene. Opt. Lett. 2015, 40, 5538–5541. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.B.; Chen, P.; Wang, Y.Q.; Zhao, Z.Y.; Wang, C.T.; Huang, C.; Hu, C.G.; Luo, X.G. Strong enhancement of light absorption and highly directive thermal emission in graphene. Opt. Express 2013, 21, 11618–11627. [Google Scholar] [CrossRef] [PubMed]
- Ning, R.X.; Liu, S.B.; Zhang, H.F.; Kong, X.K.; Bian, B.R.; Bao, J. Wideband absorption in fibonacci quasi-periodic graphene-based hyperbolic metamaterials. J. Opt. 2014, 16, 125108. [Google Scholar] [CrossRef]
- Deng, X.H.; Liu, J.T.; Yuan, J.R.; Wang, T.B.; Liu, N.H. Tunable THz absorption in graphene-based heterostructures. Opt. Express 2014, 22, 30177–30183. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.P.; Jiang, L.Y.; Guo, J.; Dai, X.Y.; Xiang, Y.J.; Wen, S.C. Turnable perfect absorption at infrared frequencies by a Graphene-hBN Hyper Crystal. Opt. Express 2016, 24, 17103–17114. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.X.; Liu, F.Y.; Lin, H.T.; Hu, J.J.; Yu, Z.F.; Wang, X.R.; Fan, S.H. Angle-selective perfect absorption with two-dimensional materials. Light Sci. Appl. 2016, 5, e16052. [Google Scholar] [CrossRef] [PubMed]
- Song, S.C.; Chen, Q.; Jin, L.; Sun, F.H. Great light absorption enhancement in a graphene photodetector integrated with a metamaterial perfect absorber. Nanoscale 2013, 5, 9615–9619. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.J.; Zhu, J.F.; Liu, Q.H. Tunable enhanced optical absorption of graphene using plasmonic perfect absorbers. Appl. Phys. Lett. 2015, 106, 917–989. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, J.M.; Zhang, Z.M. Enhancement of near-infrared absorption in graphene with metal gratings. Appl. Phys. Lett. 2014, 105, 031905. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, J.M.; Zhang, Z.M. Resonance enhanced absorption in a graphene monolayer using deep metal gratings. J. Opt. Soc. Am. B 2015, 32, 1176–1185. [Google Scholar] [CrossRef]
- Xiong, F.; Zhang, J.F.; Zhu, Z.H.; Yuan, X.D.; Qin, S.Q. Ultrabroadband, More than One Order Absorption Enhancement in Graphene with Plasmonic Light Trapping. Sci. Rep. 2015, 5, 16998. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Zheng, G.G.; Xu, L.H.; Xian, F.L.; Lai, M. Broad-band and polarization-independent perfect absorption in graphene-gold cylinder arrays at visible and near-infrared wavelengths. Opt. Mater. 2018, 81, 59–63. [Google Scholar] [CrossRef]
- Liu, B.; Tang, C.J.; Chen, J.; Xie, N.Y.; Tang, H.; Zhu, X.Q.; Park, G.S. Multiband and Broadband Absorption Enhancement of Monolayer Graphene at Optical Frequencies from Multiple Magnetic Dipole Resonances in Metamaterials. Nanoscale Res. Lett. 2018, 13, 153. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Guo, C.; Zhu, Z.; Xu, W.; Wu, F.; Yuan, X.; Qin, S. Monolayer-graphene-based broadband and wide-angle perfect absorption structures in the near infrared. Sci. Rep. 2018, 8, 13709. [Google Scholar] [CrossRef]
- Ning, R.X.; Bao, J.; Jiao, Z.; Xu, Y. Omnidirectional polarization-insensitive tunable absorption in graphene metamaterial of nanodisk structure. J. Appl. Phys. 2015, 118, 203101. [Google Scholar] [CrossRef]
- Zare, M.S.; Nozhat, N.; Rashiditabar, R. Tunable graphene based plasmonic absorber with grooved metal film in near infrared region. Opt. Commun. 2017, 398, 56–61. [Google Scholar] [CrossRef]
- Liu, B.; Tang, C.J.; Chen, J.; Wang, Q.G.; Pei, M.X.; Tang, H. Dual-band light absorption enhancement of monolayer graphene from surface plasmon polaritons and magnetic dipole resonances in metamaterials. Opt. Express 2017, 25, 12061–12068. [Google Scholar] [CrossRef] [PubMed]
- Zare, M.S.; Nozhat, N.; Rashiditabar, R. Improving the absorption of a plasmonic absorber using a single layer of graphene at telecommunication wavelengths. Appl. Opt. 2016, 55, 9764–9768. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.; Peres, N.M.R.; Ribeiro, R.M.; Stauber, T. Graphene-based photodetector with two cavities. Phys. Rev. B 2012, 85, 115438. [Google Scholar] [CrossRef]
- Furchi, M.; Urich, A.; Pospischil, A.; Lilley, G.; Unterrainer, K.; Detz, H.; Klang, P.; Andrews, A.M.; Schrenk, W.; Strasser, G.; et al. Microcavity-integrated graphene photodetector. Nano Lett. 2012, 12, 2773–2777. [Google Scholar] [CrossRef] [PubMed]
- Vincenti, M.A.; de Ceglia, D.; Grande, M.; D’Orazio, A.; Scalora, M. Nonlinear control of absorption in one-dimensional photonic crystal with graphene-based defect. Opt. Lett. 2013, 38, 3550–3553. [Google Scholar] [CrossRef] [PubMed]
- Piper, J.R.; Fan, S.H. Total Absorption in a Graphene Monolayer in the Optical Regime by Critical Coupling with a Photonic Crystal Guided Resonance. ACS Photonics 2014, 1, 347–353. [Google Scholar] [CrossRef]
- Piper, J.R.; Liu, V.; Fan, S.H. Total absorption by degenerate critical coupling. Appl. Phys. Lett. 2014, 104, 251110. [Google Scholar] [CrossRef]
- Liu, Y.H.; Chadha, A.; Zhao, D.Y.; Piper, J.R. Approaching total absorption at near infrared in a large area monolayer graphene by critical coupling. Appl. Phys. Lett. 2014, 105, 181105. [Google Scholar] [CrossRef]
- Hu, J.H.; Huang, Y.Q.; Duan, X.F.; Wang, Q.; Zhang, X.; Wang, J.; Ren, X.M. Enhanced absorption of graphene strips with a multilayer subwavelength grating structure. Appl. Phys. Lett. 2014, 105, 221113. [Google Scholar] [CrossRef]
- Wang, W.Y.; Klots, A.; Yang, Y.M.; Li, W.; Kravchenko, I.I.; Briggs, D.P.; Bolotin, K.I.; Valentine, J. Enhanced absorption in two-dimensional materials via Fano-resonant photonic crystals. Appl. Phys. Lett. 2015, 106, 181104. [Google Scholar] [CrossRef]
- Grande, M.; Vincenti, M.A.; Stomeo, T.; Bianco, G.V.; De Ceglia, D.; Aközbek, N.; Petruzzelli, V.; Bruno, G.; De Vittorio, M.; Scalora, M.; et al. Graphene-based perfect optical absorbers harnessing guided mode resonances. Opt. Express 2015, 23, 21032–21042. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Chen, L.; Guo, Q.; Chen, J.; Zhao, X.; Shi, W. Enhanced graphene absorption and linewidth sharpening enabled by Fano-like geometric resonance at near-infrared wavelengths. Opt. Express 2015, 23, 21097–21106. [Google Scholar] [CrossRef] [PubMed]
- Long, Y.B.; Liang, S.; Xu, H.T.; Deng, H.D.; Li, Y.X. Achieving ultranarrow graphene perfect absorbers by exciting guided-mode resonance of one-dimensional photonic crystals. Sci. Rep. 2016, 6, 32312. [Google Scholar] [CrossRef] [PubMed]
- Wu, J. Enhancement of Absorption in Graphene Strips with Cascaded Grating Structures. IEEE Photonics Technol. Lett. 2016, 28, 1332–1335. [Google Scholar] [CrossRef]
- Long, Y.B.; Li, Y.X.; Shen, L.; Liang, W.Y.; Deng, H.D.; Xu, H.T. Dually guided-mode-resonant graphene perfect absorbers with narrow bandwidth for sensors. J. Phys. D Appl. Phys. 2016, 49, 32LT01. [Google Scholar] [CrossRef]
- Jiang, X.Y.; Wang, T.; Xiao, S.Y.; Yan, X.C.; Cheng, L. Tunable ultra-high-efficiency light absorption of monolayer graphene using critical coupling with guided resonance. Opt. Express 2017, 25, 27028–27036. [Google Scholar] [CrossRef]
- Hu, J.Q.; Qing, Y.M.; Yang, S.Y.; Ren, Y.Z.; Wu, X.H.; Gao, W.Q.; Wu, C.Y. Tailoring total absorption in a graphene monolayer covered subwavelength multilayer dielectric grating structure at near-infrared frequencies. J. Opt. Soc. Am. B 2017, 34, 861–868. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zheng, G.G.; Xian, F.L.; Zou, X.J.; Wang, J.C. Near-unity absorption of graphene monolayer with a triple-layer waveguide coupled grating. Opt. Mater. 2017, 72, 476–481. [Google Scholar] [CrossRef]
- Yildirim, D.U.; Ghobadi, A.; Ozbay, E. Near-absolute polarization insensitivity in grapheme based ultra-narrowband perfect visible light absorber. Sci. Rep. 2018, 8, 15210. [Google Scholar] [CrossRef]
- Sang, T.; Wang, R.; Li, J.L.; Zhou, J.Y.; Wang, Y.K. Approaching total absorption of graphene strips using a c-Si subwavelength periodic membrane. Opt. Commun. 2018, 413, 255–260. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.C.; Lu, C.Y. Sensitive perfect absorber with monolayer graphene-based multi-layer dielectric grating structure. Optik 2018, 158, 508–513. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Li, G.H.; Yu, F.L.; Yang, H.; Chen, X.S.; Lu, W. Sub-Wavelength Grating Enhanced Ultra-Narrow Graphene Perfect Absorber. Plasmonics 2018, 1–6. [Google Scholar] [CrossRef]
- Guo, C.C.; Zhu, Z.H.; Yuan, X.D.; Ye, W.M.; Liu, K.; Zhang, J.F.; Xu, W.; Qin, S.Q. Experimental Demonstration of Total Absorption over 99% in the Near Infrared for Monolayer-Graphene-Based Subwavelength Structures. Adv. Opt. Mater. 2016, 4, 1955–1960. [Google Scholar] [CrossRef]
- Fan, Y.S.; Guo, C.C.; Zhu, Z.H.; Xu, W.; Wu, F.; Yuan, X.D.; Qin, S.Q. Monolayer-graphene-based perfect absorption structures in the near infrared. Opt. Express 2017, 25, 13079–13086. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.J.; Zheng, G.G.; Cong, J.W.; Xu, L.H.; Chen, Y.Y.; Lai, M. Polarization-insensitive and wide-incident-angle optical absorber with periodically patterned graphene-dielectric arrays. Opt. Lett. 2018, 43, 46–49. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, S.G. Practical Perfect Absorption in Monolayer Graphene by Prism Coupling. IEEE Photonics J. 2017, 9, 2700810. [Google Scholar] [CrossRef]
- Zou, X.J.; Zheng, G.G.; Chen, Y.Y.; Xu, L.H.; Lai, M. Multiple resonant absorber with prism-incorporated graphene and one-dimensional photonic crystals in the visible and near-infrared spectral range. Superlattices Microstruct. 2018, 116, 88–94. [Google Scholar] [CrossRef]
- Zand, I.; Dalir, H.; Chen, R.T.; Dowling, J.P. Multispectral selective near-perfect light absorption by graphene monolayer using aperiodic multilayer microstructures. Appl. Phys. Express 2018, 11, 035101. [Google Scholar] [CrossRef]
- Rao, S.M.; Heitz, J.J.F.; Roger, T.; Westerberg, N.; Faccio, D. Coherent control of light interaction with graphene. Opt. Lett. 2014, 39, 5345–5347. [Google Scholar] [CrossRef]
- Xiong, F.; Zou, J.; Xu, W.; Zhu, Z.; Yuan, X.; Zhang, J.; Qin, S. Coherent perfect absorption and asymmetric interferometric light-light control in graphene with resonant dielectric nanostructures. Opt. Express 2018, 26, 29183–29191. [Google Scholar]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jang, M.S.; Brar, V.W.; Mauser, K.W.; Kim, L.; Atwater, H.A. Electronically Tunable Perfect Absorption in Graphene. Nano Lett. 2018, 18, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.Y.; Alu, A. Terahertz Metamaterial Devices Based on Graphene Nanostructures. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 748–756. [Google Scholar] [CrossRef]
- Meng, H.Y.; Wang, L.L.; Liu, G.D.; Xue, X.X.; Lin, Q.; Zhai, X. Tunable graphene-based plasmonic multispectral and narrowband perfect metamaterial absorbers at the mid-infrared region. Appl. Opt. 2017, 56, 6022–6027. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.H.; Guo, C.C.; Liu, K.; Zhang, J.F.; Ye, W.M.; Yuan, X.D.; Qin, S.Q. Electrically controlling the polarizing direction of a graphene polarizer. J. Appl. Phys. 2014, 116, 104304. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Guo, C.C.; Liu, K.; Zhang, J.F.; Ye, W.M.; Yuan, X.D.; Qin, S.Q. Electrically tunable polarizer based on anisotropic absorption of graphene ribbons. Appl. Phys. A 2014, 114, 1017–1021. [Google Scholar] [CrossRef]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; pp. 200–211. [Google Scholar]
- Pu, M.; Hu, C.; Wang, M.; Huang, C.; Zhao, Z.; Wang, C.; Feng, Q.; Luo, X. Design principles for infrared wide-angle perfect absorber based on plasmonic structure. Opt. Express 2011, 19, 17413–17420. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal optical conductance of graphite. Phys. Rev. Lett. 2008, 100, 117401. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Khavasi, A. Design of ultra-broadband graphene absorber using circuit theory. J. Opt. Soc. Am. B 2015, 32, 1941–1946. [Google Scholar] [CrossRef]
- Koppens, F.H.; Chang, D.E.; Garcia de Abajo, F.J. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Wang, Y.; Schlather, A.E.; Liu, Z.; Ajayan, P.M.; García de Abajo, F.J.; Nordlander, P.; Zhu, X.; Halas, N.J. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 2013, 14, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Thongrattanasiri, S.; Koppens, F.H.; Garcia de Abajo, F.J. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.F.; Ma, Q.X.; Yan, S.T.; Wu, F.M.; He, X.J.; Jiang, J.X. Tunable terahertz absorption in graphene-based metamaterial. Opt. Commun. 2015, 353, 70–75. [Google Scholar] [CrossRef]
- Tang, L.L.; Shi, H.F.; Yang, J.; Du, C.L.; Gao, F.H.; Zhu, J.H.; Du, J.L. Complete optical absorption in graphene by using nano-gratings to excite graphene surface plasmons. Microelectron. Eng. 2015, 145, 58–61. [Google Scholar] [CrossRef]
- Ye, C.Y.; Zhu, Z.H.; Xu, W.; Yuan, X.D.; Qin, S.Q. Electrically tunable absorber based on nonstructured graphene. J. Opt. 2015, 17, 125009. [Google Scholar] [CrossRef]
- Wang, F.L.; Huang, S.; Li, L.; Chen, W.D.; Xie, Z.W. Dual-band tunable perfect metamaterial absorber based on graphene. Appl. Opt. 2018, 57, 6916–6922. [Google Scholar] [CrossRef]
- Yue, J.; Luo, X.; Zhai, X.; Wang, L.L.; Lin, Q. A tunable dual-band graphene-based perfect absorber in the optical communication band. Opt. Laser Technol. 2018, 108, 404–408. [Google Scholar] [CrossRef]
- Zhang, J.G.; Tian, J.P.; Li, L. A Dual-Band Tunable Metamaterial Near-Unity Absorber Composed of Periodic Cross and Disk Graphene Arrays. IEEE Photonics J. 2018, 10, 4800512. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, Y. Ultra-multiband absorption enhancement of graphene in a metal-dielectric-graphene sandwich structure covering terahertz to mid-infrared regime. Opt. Express 2017, 25, 19185–19194. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.X.; Li, L.; Liu, J.L.; Yan, F.; Tian, F.J.; Tian, H.; Zhang, J.Z.; Sun, W.M. Triple-band tunable perfect terahertz metamaterial absorber with liquid crystal. Opt. Express 2017, 25, 32280. [Google Scholar] [CrossRef]
- Ferreira, A.; Peres, N.M.R. Complete light absorption in graphene-metamaterial corrugated structures. Phys. Rev. B 2012, 86, 205401. [Google Scholar] [CrossRef]
- Alaee, R.; Farhat, M.; Rockstuhl, C.; Lederer, F. A perfect absorber made of a graphene micro-ribbon metamaterial. Opt. Express 2012, 20, 28017–28024. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J.; Zhou, M.; Lin, X.; Liu, H.X.; Wang, H.P.; Yu, F.X.; Lin, S.S.; Li, E.P.; Chen, H.S. A circuit method to integrate metamaterial and graphene in absorber design. Opt. Commun. 2014, 329, 76–80. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.Q.; Pu, M.B.; Hu, C.G.; Wu, X.Y.; Zhao, Z.Y.; Luo, X.G. Circular dichroism of graphene-based absorber in static magnetic field. J. Appl. Phys. 2014, 115, 154312. [Google Scholar] [CrossRef]
- He, X.J.; Yao, Y.; Zhu, Z.H.; Chen, M.H.; Zhu, L.; Yang, W.L.; Yang, Y.Q.; Wu, F.M.; Jiang, J.X. Active graphene metamaterial absorber for terahertz absorption bandwidth, intensity and frequency control. Opt. Mater. Express 2018, 8, 1031–1042. [Google Scholar] [CrossRef]
- Jiang, L.Y.; Guo, J.; Wang, Q.K.; Dai, X.Y.; Xiang, Y.J. Perfect Terahertz Absorption with Graphene Surface Plasmons in the Modified Otto Configuration. Plasmonics 2017, 12, 1825–1831. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 2014, 22, 22743–22752. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.; Farhat, M.; Bagci, H. An ultra-broadband multilayered graphene absorber. Opt. Express 2013, 21, 29938–29948. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.B.; Yang, J.B.; Zhang, J.J.; Huang, J.; Zhang, Z.J. Section 1Tunable broadband terahertz absorbers based on multiple layers of graphene ribbons. Sci. Rep. 2017, 7, 15836. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.H.; Wu, D.; Liu, Y.M.; Liu, C.; Yu, Z.Y.; Yu, L.; Ye, H. Design of a Tunable Ultra-Broadband Terahertz Absorber Based on Multiple Layers of Graphene Ribbons. Nanoscale Res. Lett. 2018, 13, 143. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.; Liu, F.; Ren, G.J.; Su, F.; Li, D.; Yao, J.Q. A broadband metamaterial absorber based on multi-layer graphene in the terahertz region. Opt. Commun. 2018, 417, 62–66. [Google Scholar] [CrossRef]
- Rahmanzadeh, M.; Rajabalipanah, H.; Abdolali, A. Multilayer graphene-based metasurfaces: Robust design method for extremely broadband, wide-angle, and polarization-insensitive terahertz absorbers. Appl. Opt. 2018, 57, 959–968. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.G.; Gu, M.Y.; Xiao, S.S. Broadband, wide-angle and tunable terahertz absorber based on cross-shaped graphene arrays. Appl. Opt. 2017, 56, 5458–5462. [Google Scholar] [CrossRef]
- Fardoost, A.; Vanani, F.G.; Amirhosseini, S.A.; Safian, R. Design of Multi-Layer Graphene Based Ultra Wideband Terahertz Absorber. IEEE Trans. Nanotechnol. 2016, 16, 68–74. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Guo, C.C.; Zhang, J.F.; Liu, K.; Yuan, X.D.; Qin, S.Q. Broadband single-layered graphene absorber using periodic arrays of graphene ribbons with gradient width. Appl. Phys. Express 2015, 8, 015102. [Google Scholar]
- Ye, L.F.; Chen, Y.; Cai, G.X.; Liu, N.; Zhu, J.F.; Song, Z.Y.; Liu, Q.H. Broadband absorber with periodically sinusoidally-patterned graphene layer in terahertz range. Opt. Express 2017, 25, 11223–11232. [Google Scholar] [CrossRef]
- Huang, M.L.; Cheng, Y.Z.; Cheng, Z.Z.; Chen, H.R.; Mao, X.S.; Gong, R.Z. Design of a Broadband Tunable Terahertz Metamaterial Absorber Based on Complementary Structural Graphene. Materials 2018, 11, 540. [Google Scholar] [CrossRef] [PubMed]
- Mou, N.; Sun, S.; Dong, H.; Dong, S.; He, Q.; Zhou, L.; Zhang, L. Hybridization-induced broadband terahertz wave absorption with graphene metasurfaces. Opt. Express 2018, 26, 11728–11736. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.H.; Liu, P.G.; Bian, L.A.; Liu, H.Q.; Liu, C.X.; Chen, G.H. Controlling enhanced absorption in graphene metamaterial. Opt. Commun. 2018, 413, 310–316. [Google Scholar] [CrossRef]
- Huang, X.J.; Hu, Z.R.; Aqeeli, M.; Zhang, X.; Alburaikan, A. Design of broadband and tunable terahertz absorbers based on graphene metasurface: Equivalent circuit model approach. IET Microw. Antennas Propag. 2015, 9, 307–312. [Google Scholar] [CrossRef]
- Liu, C.; Qi, L.M.; Zhang, X. Broadband graphene-based metamaterial absorbers. AIP Adv. 2018, 8, 015301. [Google Scholar] [CrossRef]
- Arik, K.; AbdollahRamezani, S.; Khavasi, A. Polarization Insensitive and Broadband Terahertz Absorber Using Graphene Disks. Plasmonics 2016, 12, 393–398. [Google Scholar] [CrossRef]
- Gao, F.; Zhu, Z.H.; Xu, W.; Zhang, J.F.; Guo, C.C.; Liu, K.; Yuan, X.D.; Qin, S.Q. Broadband wave absorption in single-layered and nonstructured graphene based on far-field interaction effect. Opt. Express 2017, 25, 9579–9586. [Google Scholar] [CrossRef]
- Yang, J.W.; Zhu, Z.Z.; Zhang, J.F.; Guo, C.C.; Xu, W.; Liu, K.; Yuan, X.D.; Qin, S.Q. Broadband terahertz absorber based on multi-band continuous plasmon resonances in geometrically gradient dielectric-loaded graphene plasmon structure. Sci. Rep. 2018, 8, 3239. [Google Scholar] [CrossRef]
- Nefedov, I.S.; Valagiannopoulos, C.A.; Melnikov, L.A. Perfect absorption in graphene multilayers. J. Opt. 2013, 15, 114003. [Google Scholar] [CrossRef]
- Chen, P.Y.; Farhat, M.; Bagci, H. Graphene metascreen for designing compact infrared absorbers with enhanced bandwidth. Nanotechnology 2015, 26, 164002. [Google Scholar] [CrossRef]
- Yao, G.; Ling, F.R.; Yue, J.; Luo, C.Y.; Luo, Q.; Yao, J.Q. Dynamically Electrically Tunable Broadband Absorber Based on Graphene Analog of Electromagnetically Induced Transparency. IEEE Photonics J. 2016, 8, 7800808. [Google Scholar] [CrossRef]
- Chong, Y.; Ge, L.; Cao, H.; Stone, A.D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Chong, Y.; Ge, L.; Noh, H.; Stone, A.D.; Cao, H. Time-Reversed Lasing and Interferometric Control of Absorption. Science 2011, 331, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; MacDonald, K.F.; Zheludev, N.I. Controlling light-with-light without nonlinearity. Light Sci. Appl. 2012, 1, e18. [Google Scholar] [CrossRef]
- Fan, Y.C.; Liu, Z.; Zhang, F.L.; Zhao, Q.; Wei, Z.Y.; Fu, Q.H.; Li, J.; Gu, C.Z.; Li, H.Q. Tunable mid-infrared coherent perfect absorption in a graphene meta-surface. Sci. Rep. 2015, 5, 13956. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.Y.; Dong, Z.W.; Si, J.N.; Deng, X.X. Tunable polarization-independent coherent perfect absorber based on a metal-graphene nanostructure. Opt. Express 2017, 25, 32467–32474. [Google Scholar] [CrossRef]
- Fan, Y.C.; Zhang, F.L.; Zhao, Q.; Wei, Z.Y.; Li, H.Q. Tunable terahertz coherent perfect absorption in a monolayer graphene. Opt. Lett. 2014, 39, 6269–6272. [Google Scholar] [CrossRef]
- Liu, F.L.; Chong, Y.D.; Adam, S.; Polini, M. Gate-tunable coherent perfect absorption of terahertz radiation in graphene. 2D Mater. 2014, 1, 031001. [Google Scholar] [CrossRef]
- Kakenov, N.; Balci, O.; Takan, T.; Ozkan, V.A.; Altan, H.; Kocabas, C. Observation of Gate-Tunable Coherent Perfect Absorption of Terahertz Radiation in Graphene. ACS Photonics 2016, 3, 1531–1535. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, Z.H.; Liu, K.; Zhang, J.F.; Yuan, X.D.; Lu, Q.S.; Qin, S.Q. Chip-integrated nearly perfect absorber at telecom wavelengths by graphene coupled with nanobeam cavity. Opt. Lett. 2015, 40, 3256–3259. [Google Scholar] [CrossRef] [PubMed]
- Konstantatos, G.; Badioli, M.; Gaudreau, L.; Osmond, J.; Bernechea, M.; De Arquer, F.P.G.; Gatti, F.; Koppens, F.H. Hybrid graphene–quantum dot phototransistors with ultrahigh gain. Nat. Nanotechnol. 2012, 7, 363–368. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, C.; Wu, S.; Li, S.; Bao, Q.; Giannini, V.; Maier, S.A.; Li, X. Photonic surface waves enabled perfect infrared absorption by monolayer graphene. Nano Energy 2018, 48, 161–169. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Fukazawa, Y.; Amasaka, Y.; Reckmann, R.; Yokoi, T.; Ishida, K.; Kawahara, K.; Ago, H.; Maki, H. High-speed and on-chip graphene blackbody emitters for optical communications by remote heat transfer. Nat. Commun. 2018, 9, 1279. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhu, Z.H.; Li, X.J.; Zhang, J.F.; Yuan, X.D.; Guo, C.C.; Xu, W.; Qin, S.Q. Bright multicolored photoluminescence of hybrid graphene/silicon optoelectronics. ACS Photonics 2015, 2, 797–804. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Zhang, J.; Xu, W.; Liu, K.; Yuan, X.; Qin, S.; Zhu, Z. Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications. Nanomaterials 2018, 8, 1033. https://doi.org/10.3390/nano8121033
Guo C, Zhang J, Xu W, Liu K, Yuan X, Qin S, Zhu Z. Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications. Nanomaterials. 2018; 8(12):1033. https://doi.org/10.3390/nano8121033
Chicago/Turabian StyleGuo, Chucai, Jianfa Zhang, Wei Xu, Ken Liu, Xiaodong Yuan, Shiqiao Qin, and Zhihong Zhu. 2018. "Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications" Nanomaterials 8, no. 12: 1033. https://doi.org/10.3390/nano8121033
APA StyleGuo, C., Zhang, J., Xu, W., Liu, K., Yuan, X., Qin, S., & Zhu, Z. (2018). Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications. Nanomaterials, 8(12), 1033. https://doi.org/10.3390/nano8121033





