Theoretical Study of the BaTiO3 Powder’s Volume Ratio’s Influence on the Output of Composite Piezoelectric Nanogenerator
Abstract
:1. Introduction
2. Methods and Structure
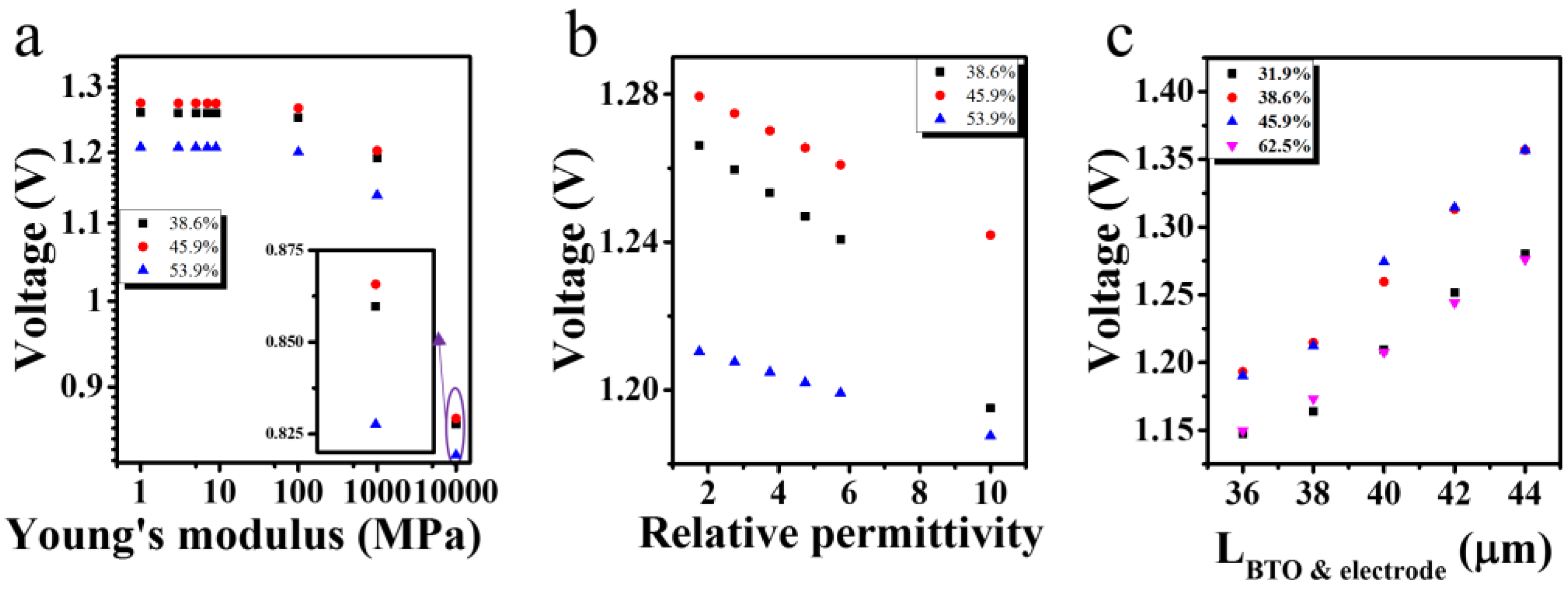
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Z.L.; Song, J.H. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Wang, T.; Lee, C. MEMS based broadband Piezoelectric Ultrasonic Energy Harvester (PUEH) for enabling self-powered implantable biomedical devices. Sci. Rep. 2016, 6, 24946. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Chen, Y.; Ou, D.; Chen, H.; Diao, L.; Zhang, W.; Zheng, J.; Ma, W.; Sun, L.; Feng, X. Ultra-flexible piezoelectric devices integrated with heart to harvest the biomechanical energy. Sci. Rep. 2015, 5, 16065. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Xue, X.; Ma, Y.; Han, M.; Zhang, W.; Xu, Z.; Zhang, H.; Zhang, H. Implantable and self-powered blood pressure monitoring based on a piezoelectric thinfilm: Simulated, in vitro and in vivo studies. Nano Energy 2016, 22, 453–460. [Google Scholar] [CrossRef]
- Hwang, G.-T.; Park, H.; Lee, J.-H.; Oh, S.; Park, K.-I.; Byun, M.; Park, H.; Ahn, G.; Jeong, C.K.; No, K.; et al. Self-powered cardiac pacemaker enabled by flexible single crystalline PMN-PT piezoelectric energy harvester. Adv. Mater. 2014, 26, 4880–4887. [Google Scholar] [CrossRef] [PubMed]
- Yuan, M.; Cheng, L.; Xu, Q.; Wu, W.; Bai, S.; Gu, L.; Wang, Z.; Lu, J.; Li, H.; Qin, Y.; et al. Biocompatible nanogenerators through high piezoelectric coefficient 0.5Ba(Zr0.2Ti0.8)O3-0.5(Ba0.7Ca0.3)TiO3 nanowires for in vivo applications. Adv. Mater. 2014, 26, 7432–7437. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.-Y.; Lee, W.-H.; Hwang, H.-G.; Kim, D.-H.; Kim, J.-H.; Lee, S.-H.; Nahm, S. Resistive switching memory integrated with nanogenerator for self-powered bioimplantable devices. Adv. Funct. Mater. 2016, 26, 5211–5221. [Google Scholar] [CrossRef]
- Siddiqui, S.; Kim, D.-I.; Le Thai, D.; Minh Triet, N.; Muhammad, S.; Yoon, W.-S.; Lee, N.-E. High-performance flexible lead-free nanocomposite piezoelectric nanogenerator for biomechanical energy harvesting and storage. Nano Energy 2015, 15, 177–185. [Google Scholar] [CrossRef]
- Siddiqui, S.; Kim, D.-I.; Roh, E.; Duy, L.T.; Trung, T.Q.; Nguyen, M.T.; Lee, N.-E. A durable and stable piezoelectric nanogenerator with nanocomposite nanofibers embedded in an elastomer under high loading for a self-powered sensor system. Nano Energy 2016, 30, 434–442. [Google Scholar] [CrossRef]
- Proto, A.; Penhaker, M.; Bibbo, D.; Vala, D.; Conforto, S.; Schmid, M. Measurements of generated energy/electrical quantities from locomotion activities using piezoelectric wearable sensors for body motion energy harvesting. Sensors 2016, 16, 524. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Cheng, L.; Wang, Z.; Zheng, Y.; Bai, S.; Qin, Y. A transparent antipeep Piezoelectric nanogenerator to harvest tapping energy on screen. Small 2016, 12, 1315–1321. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Hinchet, R.; Lee, Y.; Yang, Y.; Lin, Z.H.; Ardila, G.; Montes, L.; Mouis, M.; Wang, Z.L. Ultrathin nanogenerators as self-powered/active skin sensors for tracking eye ball motion. Adv. Funct. Mater. 2014, 24, 1163–1168. [Google Scholar] [CrossRef]
- Delnavaz, A.; Voix, J. Flexible piezoelectric energy harvesting from jaw movements. Smart Mater. Struct. 2014, 23, 105020. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, H.; Lu, Y.; Li, S.; Lin, L.; Du, Y.; Wang, X. In vitro cardiomyocyte-driven biogenerator based on aligned piezoelectric nanofibers. Nanoscale 2016, 8, 7278–7286. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Deng, P.; Nie, Y.; Hu, Y.; Xing, L.; Zhang, Y.; Xue, X. Room-temperature self-powered ethanol sensing of a Pd/ZnO nanoarray nanogenerator driven by human finger movement. Nanoscale 2014, 6, 4604–4610. [Google Scholar] [CrossRef] [PubMed]
- Park, K.-I.; Lee, M.; Liu, Y.; Moon, S.; Hwang, G.-T.; Zhu, G.; Kim, J.E.; Kim, S.O.; Kim, D.K.; Wang, Z.L.; et al. Flexible nanocomposite generator made of BaTiO3 nanoparticles and graphitic carbons. Adv. Mater. 2012, 24, 2999–3004. [Google Scholar] [CrossRef] [PubMed]
- Park, K.-I.; Jeong, C.K.; Ryu, J.; Hwang, G.-T.; Lee, K.J. Flexible and large-area nanocomposite generators based on lead zirconate titanate particles and carbon nanotubes. Adv. Energy Mater. 2013, 3, 1539–1544. [Google Scholar] [CrossRef]
- Jeong, C.K.; Park, K.-I.; Ryu, J.; Hwang, G.-T.; Lee, K.J. Large-Area and flexible lead-free nanocomposite generator using alkaline niobate particles and metal nanorod filler. Adv. Funct. Mater. 2014, 24, 2620–2629. [Google Scholar] [CrossRef]
- Sultana, A.; Alam, M.M.; Garain, S.; Sinha, T.K.; Middya, T.R.; Mandal, D. An effective electrical throughput from PANI supplement ZnS nanorods and PDMS-based flexible piezoelectric nanogenerator for power up portable electronic devices: An alternative of MWCNT filler. ACS Appl. Mater. Interfaces 2015, 7, 19091–19097. [Google Scholar] [CrossRef] [PubMed]
- Jeong, C.K.; Kim, I.; Park, K.-I.; Oh, M.H.; Paik, H.; Hwang, G.-T.; No, K.; Nam, Y.S.; Lee, K.J. Virus-directed design of a flexible BaTiO3 nanogenerator. ACS Nano 2013, 7, 11016–11025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Liao, Q.; Zhang, Z.; Liang, Q.; Zhao, Y.; Zheng, X.; Zhang, Y. Novel piezoelectric paper-based flexible nanogenerators composed of BaTiO3 nanoparticles and bacterial cellulose. Adv. Sci. 2016, 3, 1500257. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.Y.; Kim, D.; Lee, J.-H.; Kim, T.Y.; Gupta, M.K.; Kim, S.-W. Unidirectional high-power generation via stress-induced dipole alignment from ZnSnO3 nanocubes/polymer hybrid piezoelectric nanogenerator. Adv. Funct. Mater. 2014, 24, 37–43. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.L. Electrostatic potential in a bent piezoelectric nanowire. The fundamental theory of nanogenerator and nanopiezotronics. Nano Lett. 2007, 7, 2499–2505. [Google Scholar] [CrossRef] [PubMed]
- Andrianov, A.V.; Aleshin, A.N.; Khripunov, A.K.; Trukhin, V.N. Terahertz properties of bacterial cellulose films and its composite with conducting polymer PEDOT/PSS. Synth. Met. 2015, 205, 201–205. [Google Scholar] [CrossRef]
- Henriksson, M.; Berglund, L.A.; Isaksson, P.; Lindstrom, T.; Nishino, T. Cellulose nanopaper structures of high toughness. Biomacromolecules 2008, 9, 1579–1585. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Liu, W.; Huang, X.; Zhang, A.; Zhang, Y.; Wang, Z.L. Theoretical study on two-dimensional MoS2 piezoelectric nanogenerators. Nano Res. 2016, 9, 800–807. [Google Scholar] [CrossRef]
- Xu, Q.; Qin, Y. Theoretical study of enhancing the piezoelectric nanogenerator’s output power by optimizing the external force’s shape. APL Mater. 2017, 5, 074101. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Xu, Q.; Bai, S.; Qin, Y.; Liu, W. Theoretical Study of the BaTiO3 Powder’s Volume Ratio’s Influence on the Output of Composite Piezoelectric Nanogenerator. Nanomaterials 2017, 7, 143. https://doi.org/10.3390/nano7060143
Zhou X, Xu Q, Bai S, Qin Y, Liu W. Theoretical Study of the BaTiO3 Powder’s Volume Ratio’s Influence on the Output of Composite Piezoelectric Nanogenerator. Nanomaterials. 2017; 7(6):143. https://doi.org/10.3390/nano7060143
Chicago/Turabian StyleZhou, Xi, Qi Xu, Suo Bai, Yong Qin, and Weisheng Liu. 2017. "Theoretical Study of the BaTiO3 Powder’s Volume Ratio’s Influence on the Output of Composite Piezoelectric Nanogenerator" Nanomaterials 7, no. 6: 143. https://doi.org/10.3390/nano7060143
APA StyleZhou, X., Xu, Q., Bai, S., Qin, Y., & Liu, W. (2017). Theoretical Study of the BaTiO3 Powder’s Volume Ratio’s Influence on the Output of Composite Piezoelectric Nanogenerator. Nanomaterials, 7(6), 143. https://doi.org/10.3390/nano7060143