Stress Waves and Characteristics of Zigzag and Armchair Silicene Nanoribbons
Abstract
:1. Introduction
2. Simulation Method
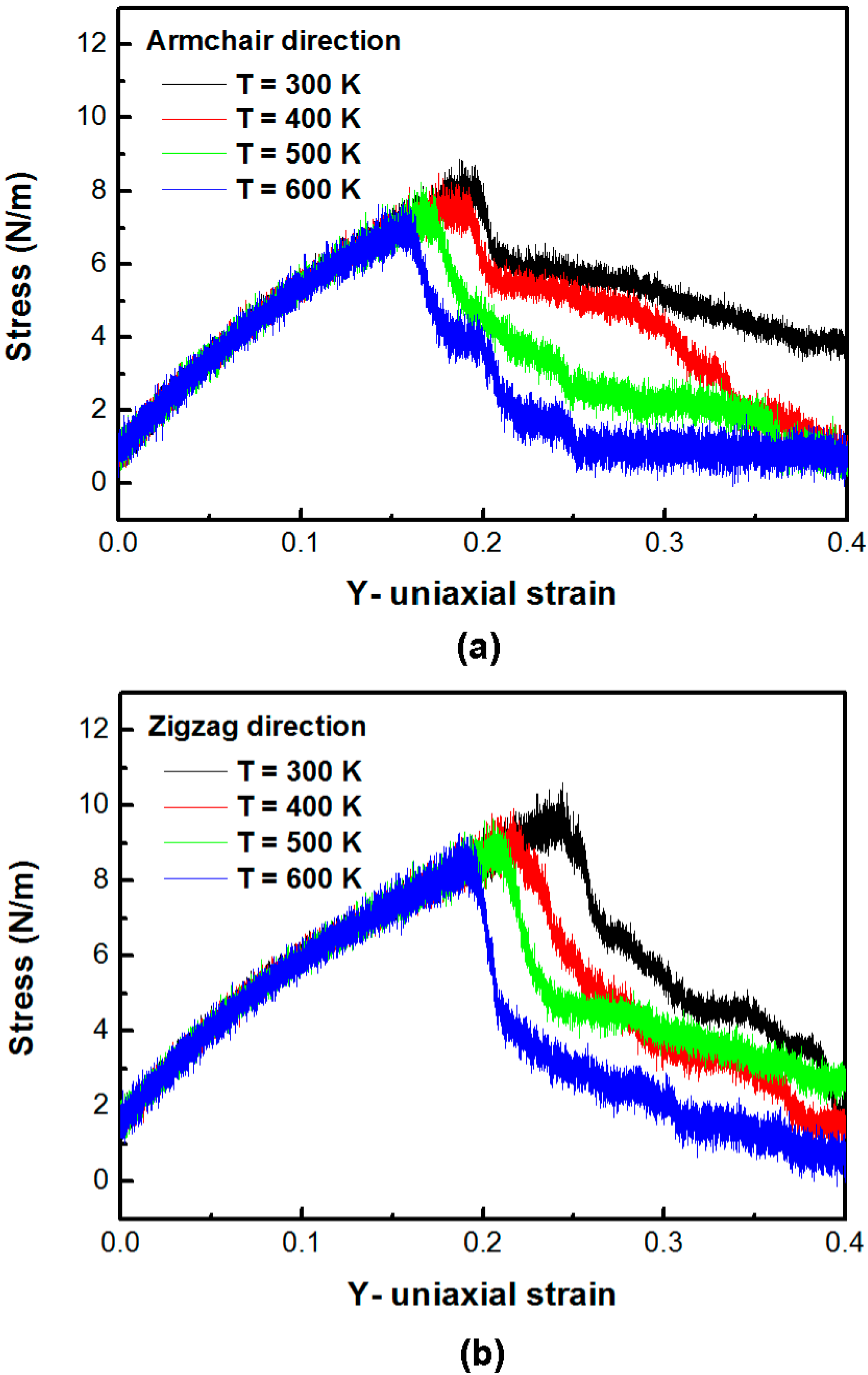
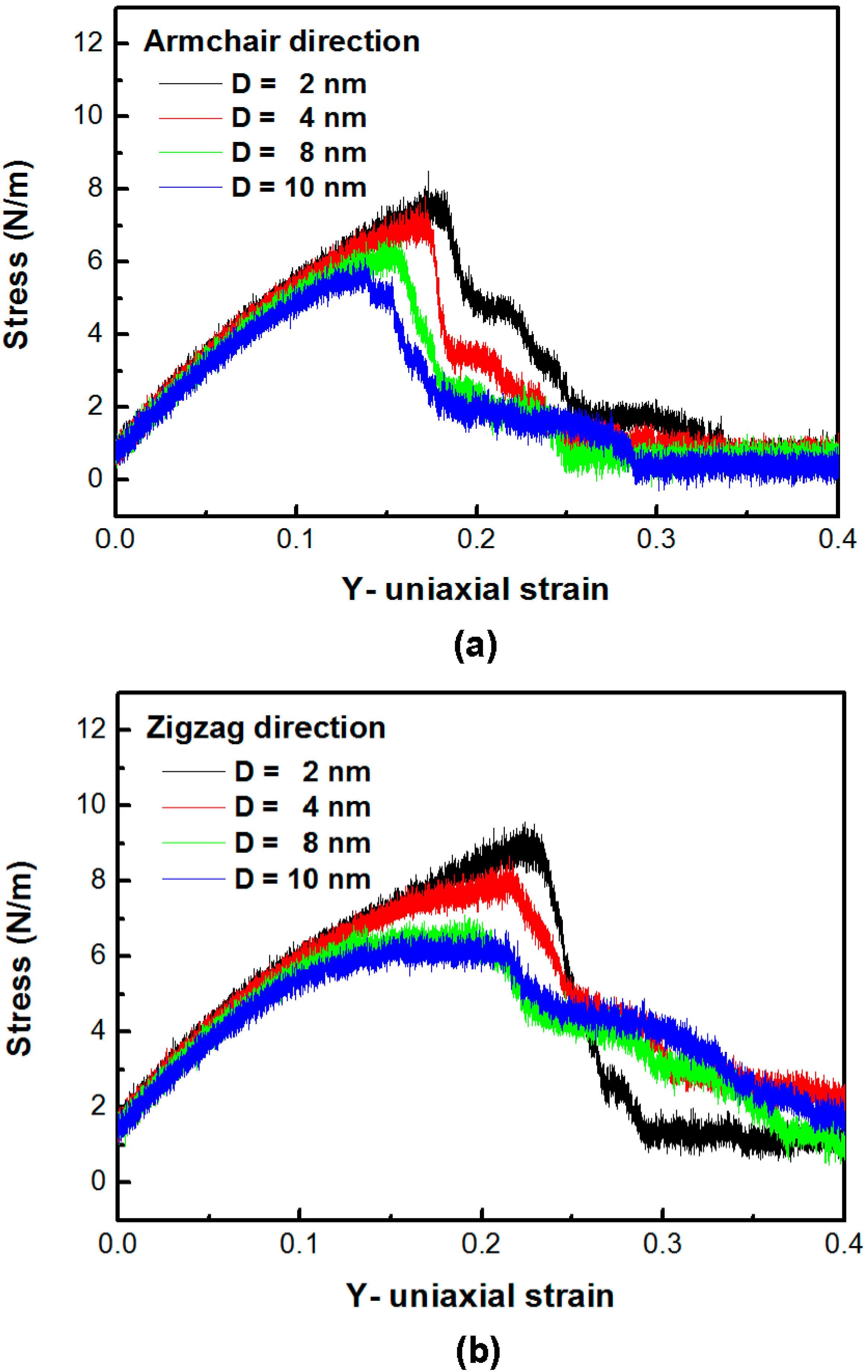
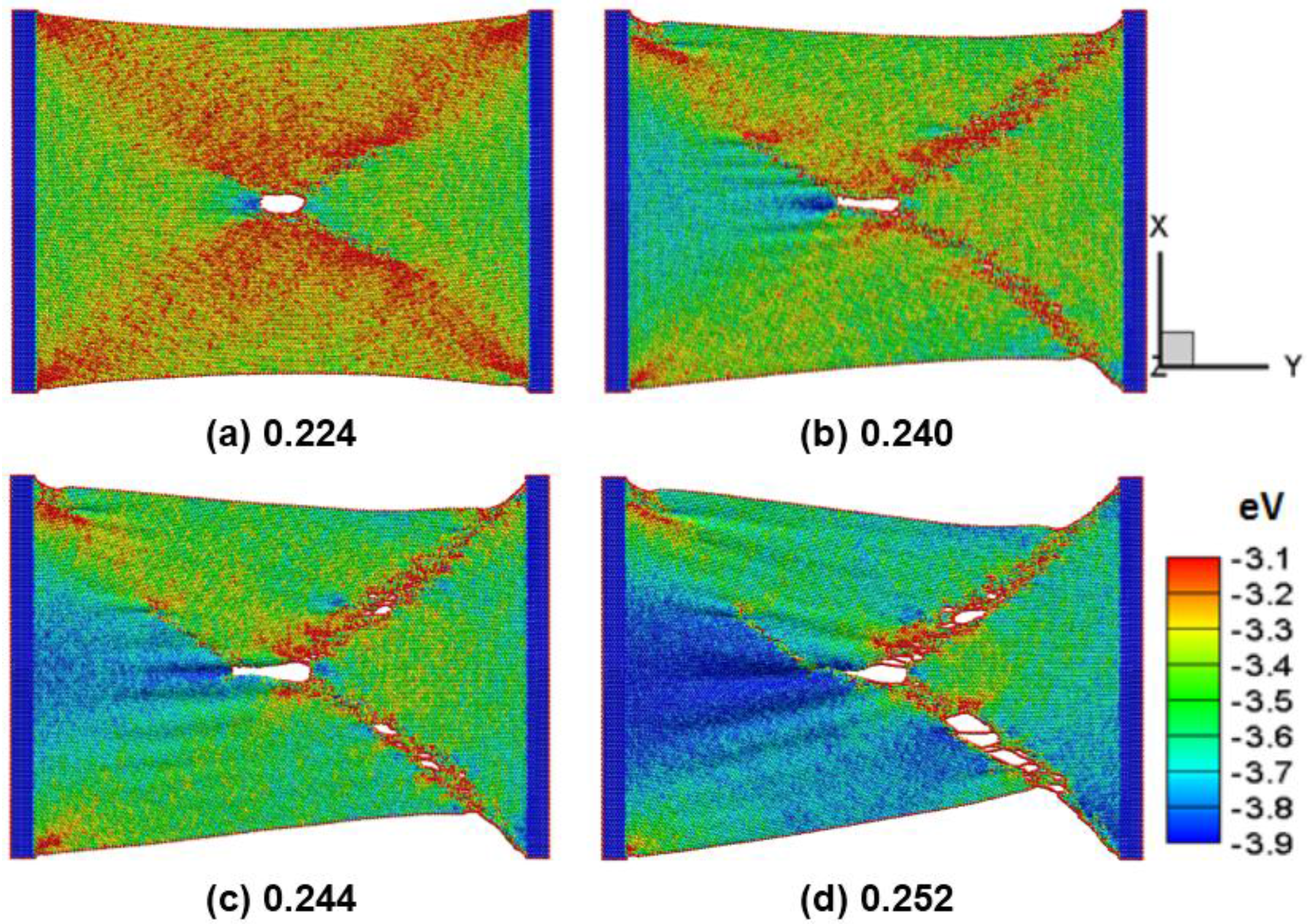
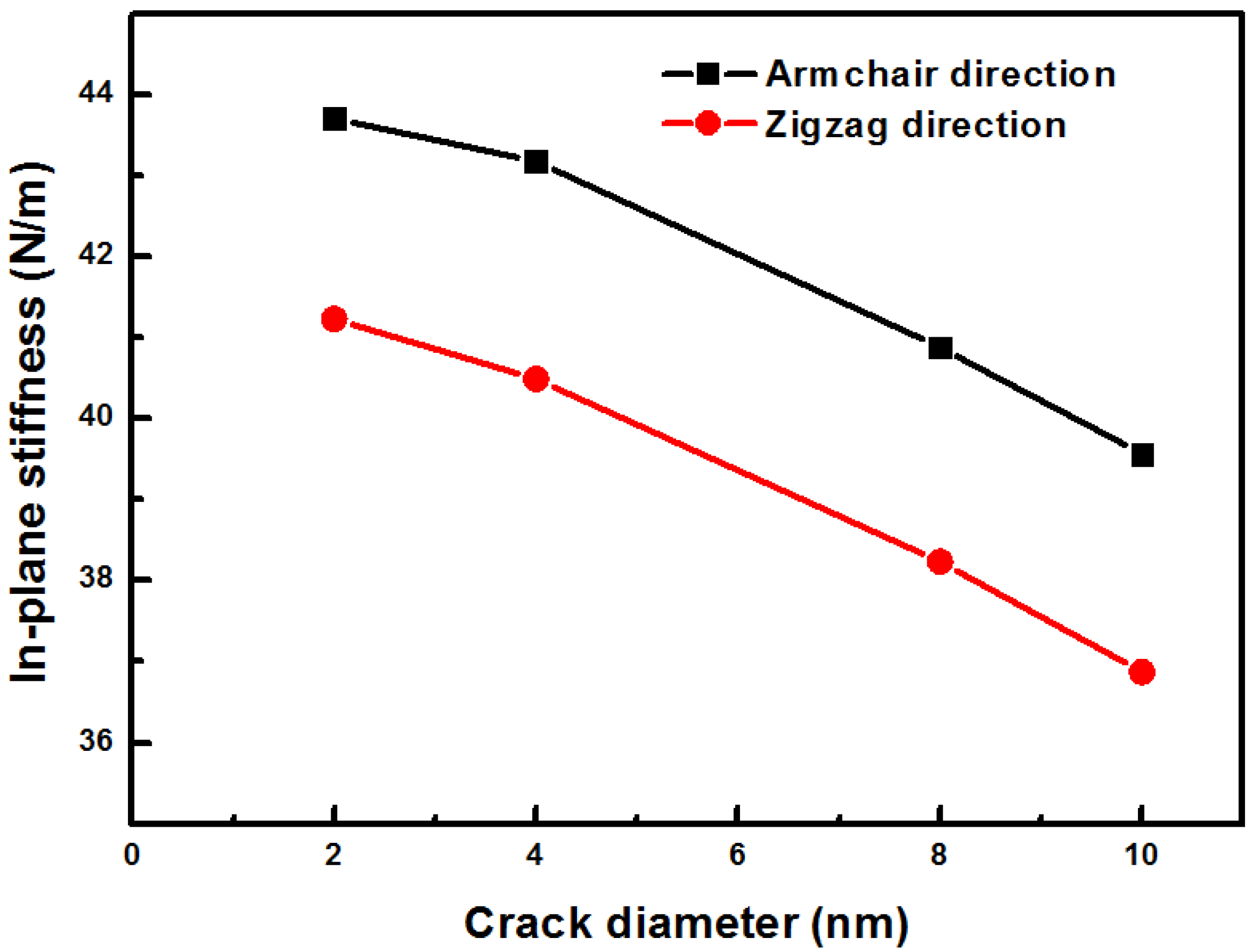
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Chiappe, D.; Grazianetti, C.; Tallarida, G.; Fanciulli, M.; Molle, A. Local electronic properties of corrugated silicene phases. Adv. Mater. 2012, 24, 5088–5093. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.J.; Ding, Z.J.; Meng, S.; Yao, Y.G.; He, X.Y.; Cheng, P.; Chen, L.; Wu, K.H. Evidence of silicene in honeycomb structures of silicon on Ag (111). Nano Lett. 2012, 12, 3507–3511. [Google Scholar] [CrossRef] [PubMed]
- Kara, A.; Enriquez, H.; Seitsonen, A.P.; Voon, L.C.L.Y.; Vizzini, S.; Aufray, B.; Oughaddou, H. A review on silicone—New candidate for electronics. Surf. Sci. Rep. 2012, 67, 1–18. [Google Scholar] [CrossRef]
- Xu, M.S.; Liang, T.; Shi, M.M.; Chen, H.Z. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.H.; Yu, Z.Y.; Lu, P.F.; Liu, Y.M.; Ye, H.; Gao, T. Phonon instability and ideal strength of silicene under tension. Comput. Mater. Sci. 2014, 95, 420–428. [Google Scholar] [CrossRef]
- Zhang, C.H.; Ran, Q.; Shen, J. Structural stability of silicene-like nanotubes. Comput. Phys. Commun. 2012, 183, 30–33. [Google Scholar] [CrossRef]
- Li, R.; Liu, Z.L.; Gu, Y.; Zhang, W.; Tan, Y. Oxygen- and hydroxyl-edge termination of silicene nanoribbons studied by first-principles calculations. Phys. E 2016, 79, 152–159. [Google Scholar] [CrossRef]
- Fan, Y.C.; Wu, C.D.; Fang, T.H.; Chen, T.H. Thermal relaxation and deformation of indented graphene. Comput. Mater. Sci. 2013, 79, 105–109. [Google Scholar] [CrossRef]
- Huang, C.C.; Chiang, T.C.; Fang, T.H. Grain size effect on indentation of nanocrystalline copper. Appl. Surf. Sci. 2015, 353, 494–498. [Google Scholar] [CrossRef]
- Fang, T.H.; Liu, C.H.; Lu, D.M.; Kua, L.M. Analysis and nanomold design for aluminum nanoimprinting. Smart Sci. 2014, 2, 168–172. [Google Scholar] [CrossRef]
- Duoc, N.T.; Nhung, N.T.A.; Duong, T.; Tat, P.V. Ab initio intermolecular potential energy surface and calculation of second virial coefficients for the Cl2-Cl2 Dimer. Smart Sci. 2015, 3, 193–201. [Google Scholar]
- Ansari, R.; Rouhi, S.; Ajori, S. Elastic properties and large deformation of two-dimensional silicene nanosheets using molecular dynamics. Superlattices Microstruct. 2014, 65, 64–70. [Google Scholar] [CrossRef]
- Ince, A.; Erkoc, S. Silicene nanoribbons: Molecular-dynamics simulations. Comput. Mater. Sci. 2011, 50, 865–870. [Google Scholar] [CrossRef]
- Roman, R.E.; Cranford, S.W. Mechanical properties of silicene. Comput. Mater. Sci. 2014, 82, 50–55. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, H.J.; Lee, D.B.; Lee, J.S.; Choi, Y.K.; Kwon, O.M. Heterogeneous crystallization of amorphous silicon expedited by external force fields: A molecular dynamics study. Superlattices Microstruct. 2004, 35, 205–215. [Google Scholar] [CrossRef]
- Pei, Q.X.; Sha, Z.D.; Zhang, Y.Y.; Zhang, Y.W. Effects of temperature and strain rate on the mechanical properties of silicene. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Le, M.Q.; Nguyen, D.T. The role of defects in the tensile properties of silicene. Appl. Phys. A 2015, 118, 1437–1445. [Google Scholar] [CrossRef]
- Sahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III–V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Peng, Q.; Wen, X.; De, S. Mechanical stabilities of silicene. RSC Adv. 2013, 3, 13772–13781. [Google Scholar] [CrossRef]
- Fan, Y.C.; Fang, T.H.; Huang, C.C.; Chen, T.H. Atomic simulation of wrinkling and deformation in curved graphene nanoribbons under boundary confinement. Mater. Des. 2016, 89, 470–475. [Google Scholar] [CrossRef]
- Fang, T.H.; Chang, W.J.; Lin, K.P. Stability and wrinkling of defective graphene sheets under shear deformation. Curr. Appl. Phys. 2014, 14, 533–537. [Google Scholar] [CrossRef]
- Wu, W.C.; Ao, Z.M.; Yang, C.H.; Li, S.; Wang, G.X.; Li, C.M.; Li, S. Hydrogenation of silicene with tensile strains. J. Mater. Chem. C 2015, 3, 2593–2602. [Google Scholar] [CrossRef]
- Wong, C.H.; Vijayaraghavan, V. Nanomechanics of free form and water submerged single layer graphene sheet under axial tension by using molecular dynamics simulation. Mater. Sci. Eng. A 2012, 556, 420–428. [Google Scholar] [CrossRef]
- Zhao, H.; Min, K.; Aluru, N.R. Size and chirality dependent elastic properties of graphene nanoribbons under uniaxial tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.J. Strain and chirality effects on the mechanical and electronic properties of silicene and silicane under uniaxial tension. Phys. Lett. A 2012, 376, 3546–3550. [Google Scholar] [CrossRef]
- Fang, T.H.; Chang, W.J.; Yang, J.C. Molecular dynamics study on mechanical properties of graphene sheets with a hole. Dig. J. Nanomater. Biostruct. 2014, 9, 1207–1214. [Google Scholar]

| References | Lattice Constant (Å) | Bond Length (Å) | Bond Angle (°) | Buckling Height (Å) |
|---|---|---|---|---|
| The present simulation | 4.00 | 2.32 | 117.98 | 0.38 |
| MD simulations with MEAM potential [17] | 4.05 | 2.5 | - | 0.85 |
| MD simulations with Tersoff Potential [18] | 3.932 | 2.313 | 116.4 | 0.4444 |
| DFT [19] | 3.83 | 2.25 | 116.4 | 0.44 |
| DFT [20] | 3.865 | 2.277 | 116.134 | 0.454 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.-C.; Fang, T.-H.; Chen, T.-H. Stress Waves and Characteristics of Zigzag and Armchair Silicene Nanoribbons. Nanomaterials 2016, 6, 120. https://doi.org/10.3390/nano6070120
Fan Y-C, Fang T-H, Chen T-H. Stress Waves and Characteristics of Zigzag and Armchair Silicene Nanoribbons. Nanomaterials. 2016; 6(7):120. https://doi.org/10.3390/nano6070120
Chicago/Turabian StyleFan, Yu-Cheng, Te-Hua Fang, and Tao-Hsing Chen. 2016. "Stress Waves and Characteristics of Zigzag and Armchair Silicene Nanoribbons" Nanomaterials 6, no. 7: 120. https://doi.org/10.3390/nano6070120
APA StyleFan, Y.-C., Fang, T.-H., & Chen, T.-H. (2016). Stress Waves and Characteristics of Zigzag and Armchair Silicene Nanoribbons. Nanomaterials, 6(7), 120. https://doi.org/10.3390/nano6070120








