Characterization of Nanoparticle Dispersion in Red Blood Cell Suspension by the Lattice Boltzmann-Immersed Boundary Method
Abstract
:1. Introduction
2. Fluid-Structure Interaction Model
2.1. Lattice Boltzmann Fluid Model
2.2. Spring Connected Network Cell Membrane Model

2.3. Immersed Boundary Coupling Scheme
2.4. Nanoparticle Model
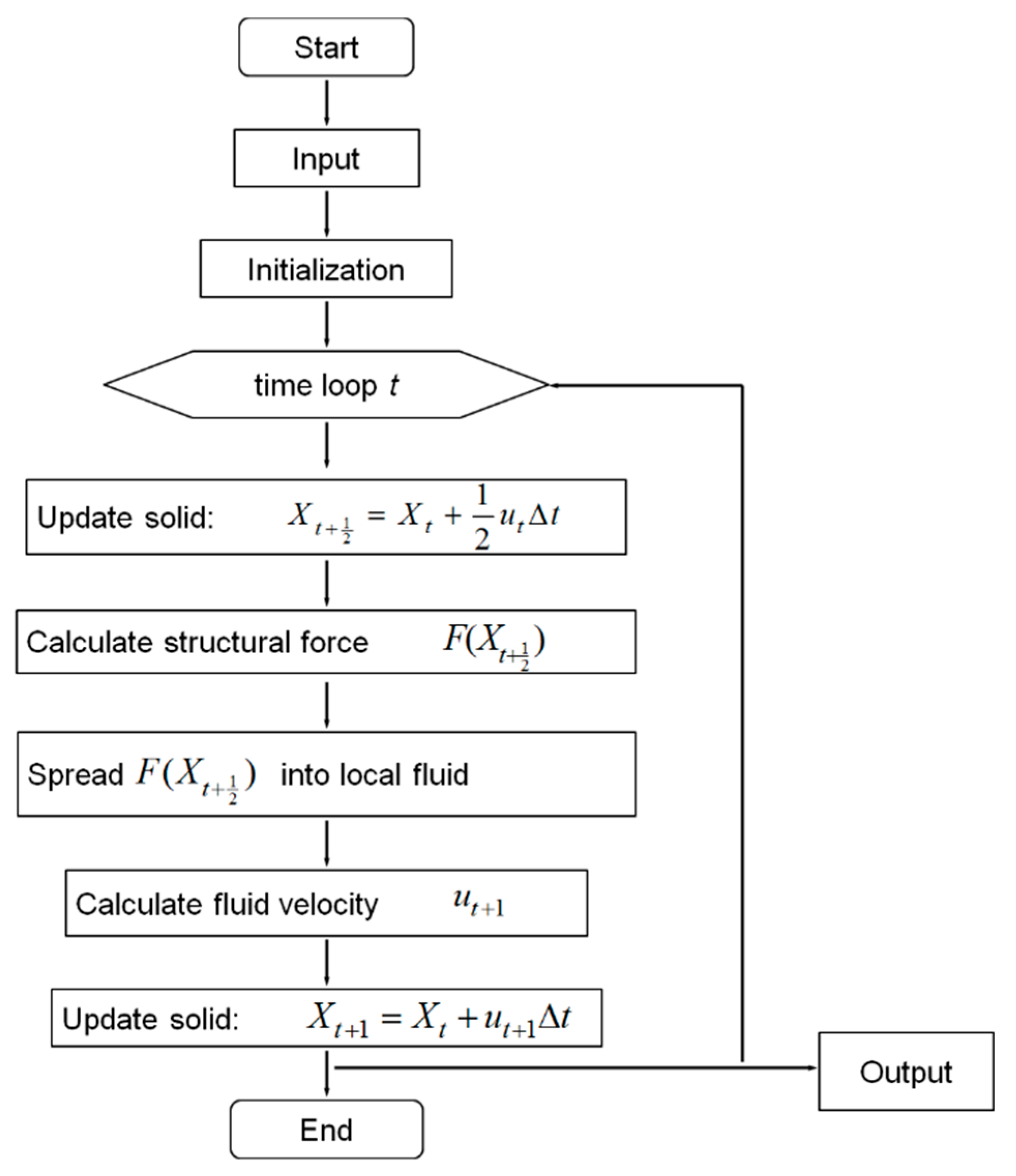
3. Model Setup and Parametric Study
4. Results and Discussion
4.1. NP Dispersion under Pure Shear Flow
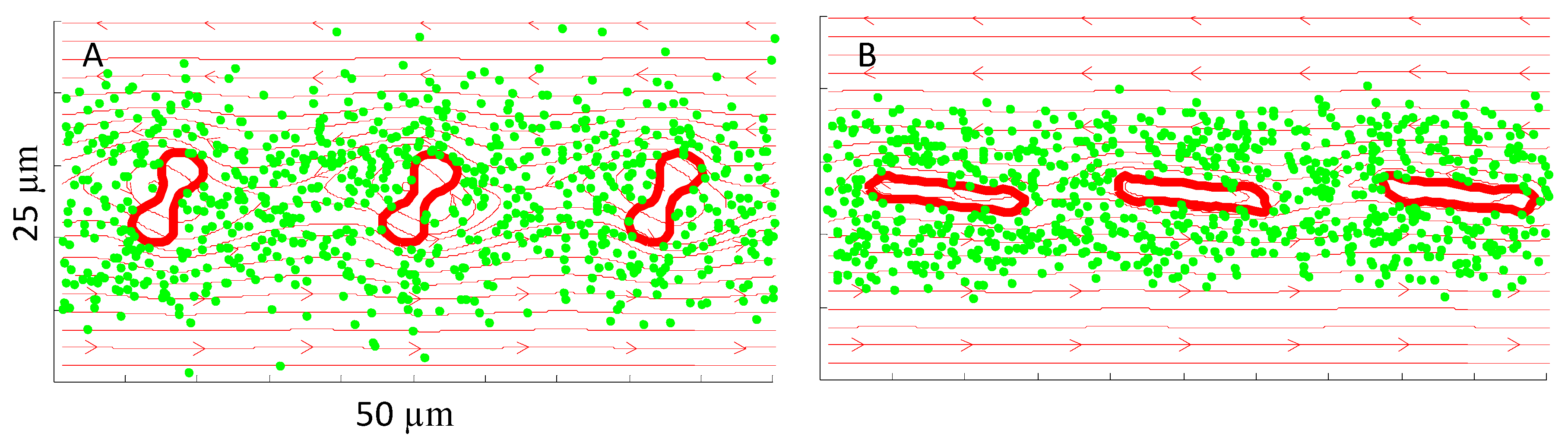
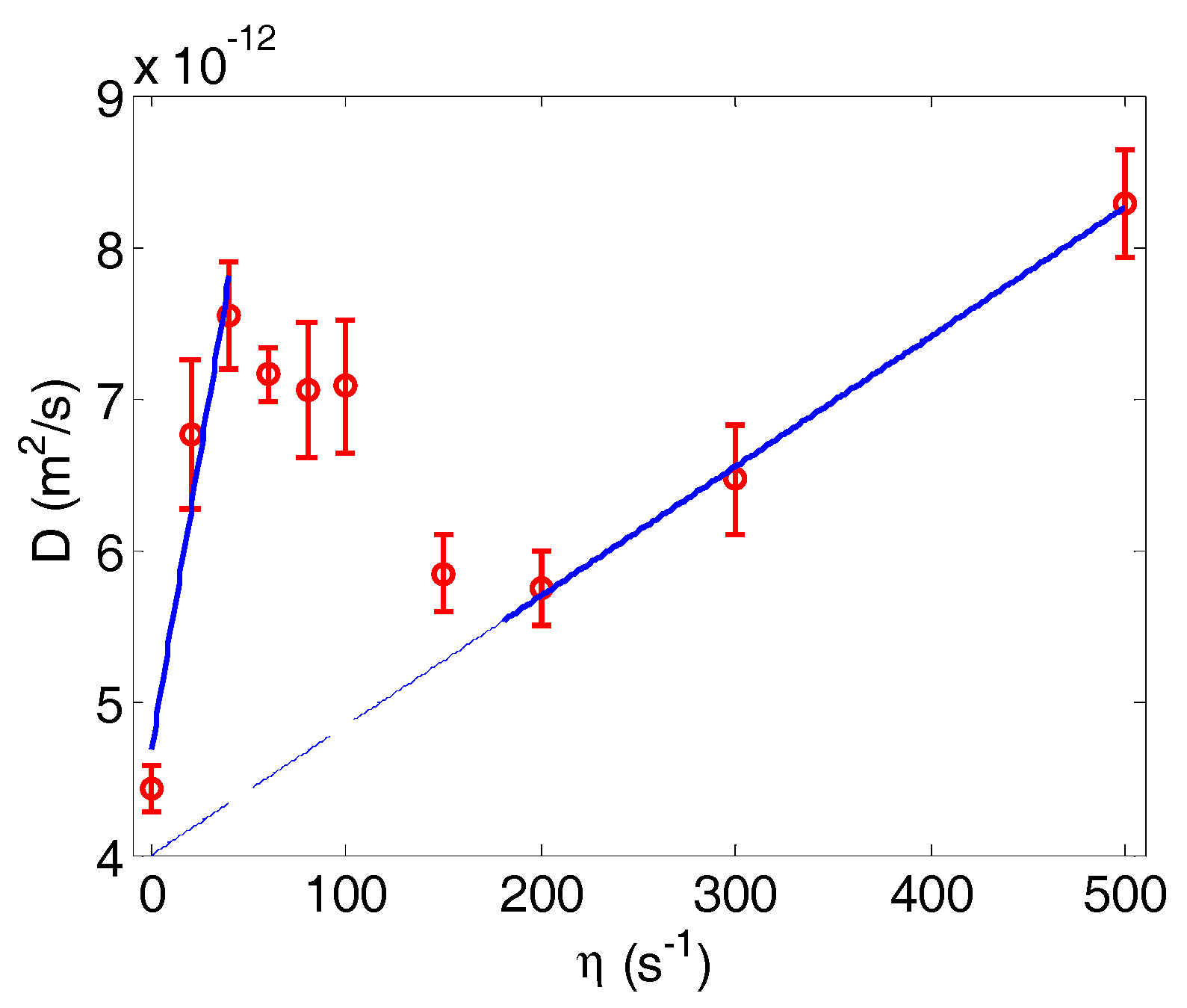
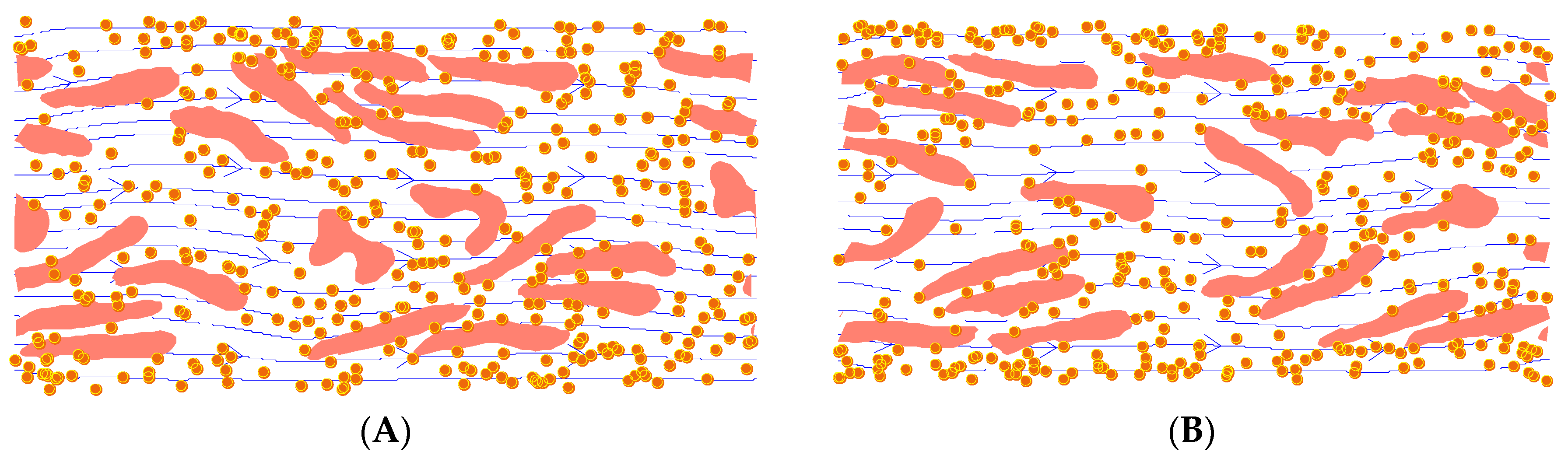
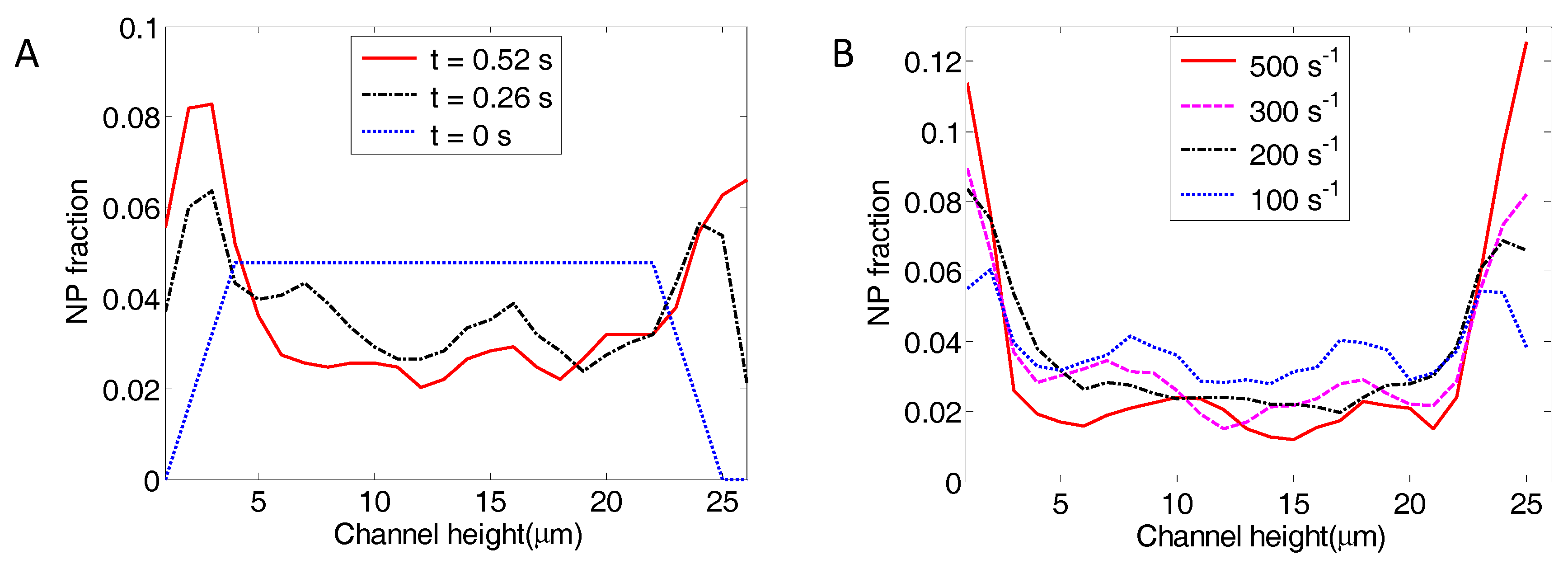
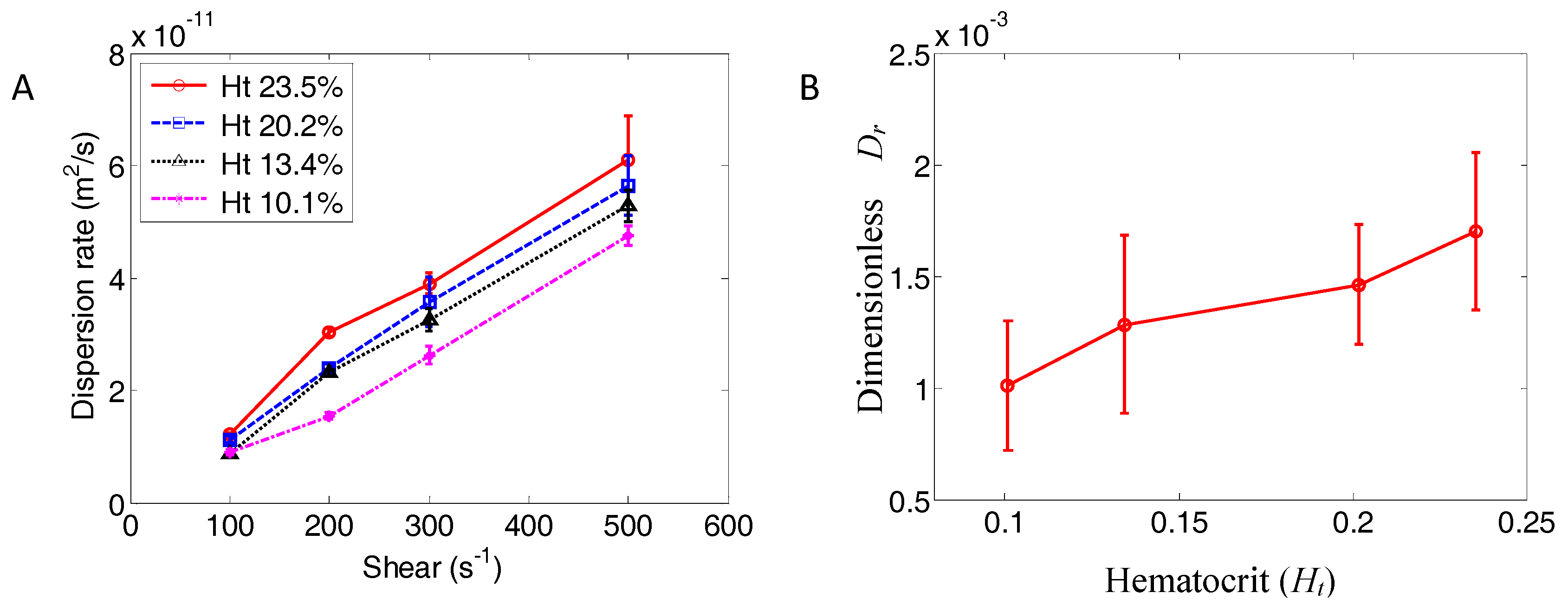
4.2. NP Dispersion under Channel Flow
| Ht | Shear (s−1) | Dispersion Rate (cm2/s) | Prediction (cm2/s) | Reference |
|---|---|---|---|---|
| [0.2, 0.4] | 400 | [0.5, 0.68] × 10−6 | [0.39, 0.63] × 10−6 | [76] |
| [0.2, 0.4] | 1100 | [1.5, 2.1] × 10−6 | [1.1, 1.7] × 10−6 | [76] |
| [0.1, 0.15, 0.2] | 44.8 | [8.2, 11.9, 17.2] × 10−9 | [31.3, 37.9, 44.6] × 10−9 | [13] |
| [0.1, 0.2] | 804 | [0.9, 1.4] × 10−7 | [5.4, 7.8] × 10−7 | [15] |
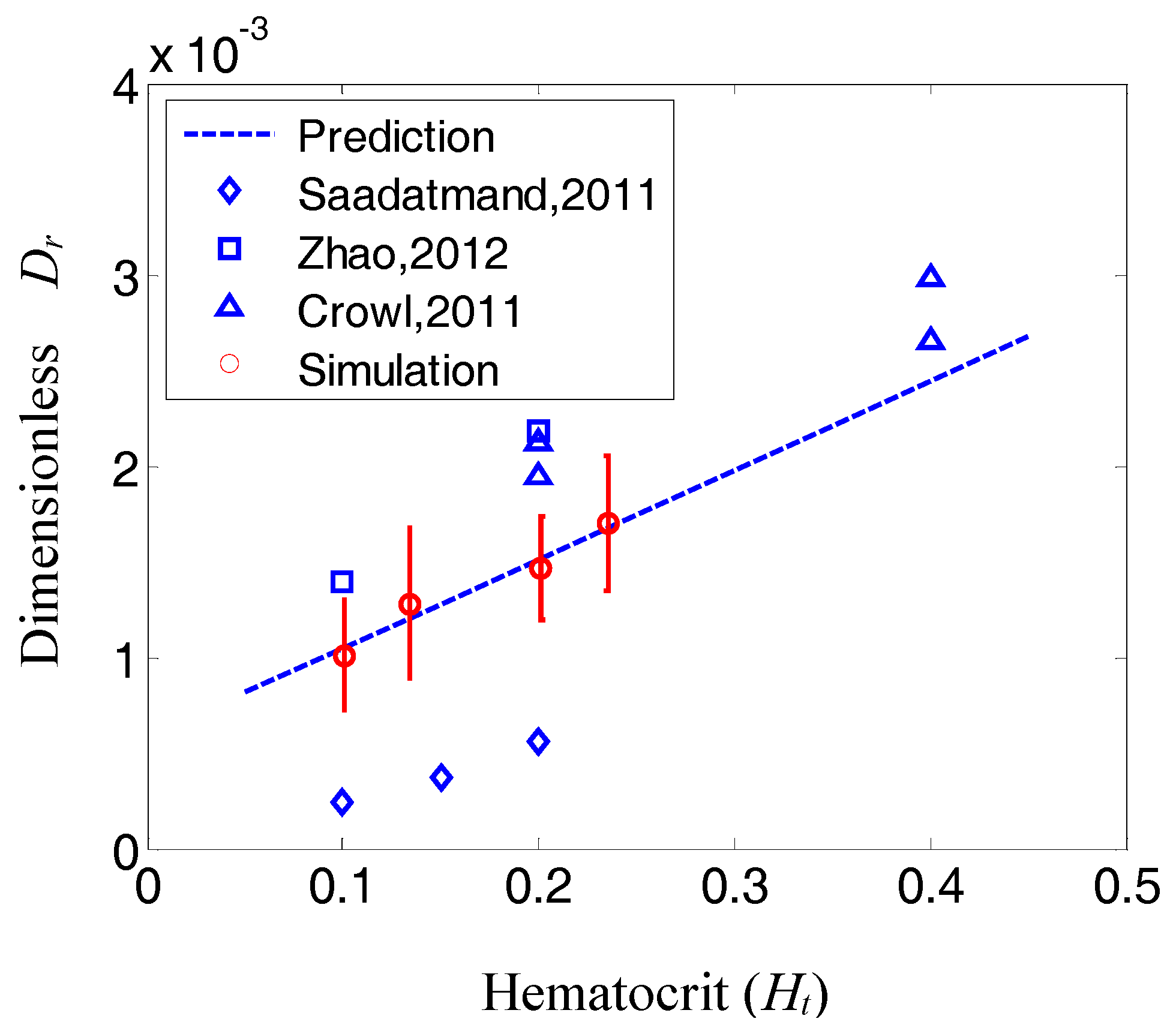
5. Conclusion and Future Work
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sanhai, W.R.; Sakamoto, J.H.; Canady, R.; Ferrari, M. Seven Challenges for Nanomedicine. Nat. Nano 2008, 3, 242–244. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Bradley, R.; Eckmann, D.M.; Ayyaswamy, P.S.; Radhakrishnan, R. Multiscale Modeling of Functionalized Nanocarriers in Targeted Drug Delivery. Curr. Nanosci. 2011, 7, 727–735. [Google Scholar] [CrossRef] [PubMed]
- Muller, K.; Fedosov, D.A.; Gompper, G. Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Thomas, A.; Liu, Y. Influence of red blood cells on nanoparticle targeted delivery in microcirculation. Soft Matter 2012, 8, 1934–1946. [Google Scholar] [CrossRef] [PubMed]
- Doshi, N.; Prabhakarpandian, B.; Rea-Ramsey, A.; Pant, K.; Sundaram, S.; Mitragotri, S. Flow and adhesion of drug carriers in blood vessels depend on their shape: A study using model synthetic microvascular networks. J. Control. Release 2010, 146, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Shah, S.; Thomas, A.; Ou-Yang, H.D.; Liu, Y. The influence of size, shape and vessel geometry on nanoparticle distribution. Microfluid. Nanofluid. 2013, 14, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Wang, S.; Yang, J.; Liu, Y. Coupled particulate and continuum model for nanoparticle targeted delivery. Comput. Struct. 2013, 122, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.; Dalhaimer, P.; Cai, S.; Tsai, R.; Tewari, M.; Minko, T.; Discher, D.E. Shape effects of filaments versus spherical particles in flow and drug delivery. Nat. Nanotechnol. 2007, 2, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Shah, S.; Tan, J. Computational Modeling of Nanoparticle Targeted Drug Delivery. Rev. Nanosci. Nanotechnol. 2010, 1, 66–83. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Y.; Tan, J.; Xu, J.; Yang, J.; Liu, Y. Computational modeling of magnetic nanoparticle targeting to stent surface under high gradient field. Comput. Mech. 2014, 53, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Guduru, R.; Liang, P.; Runowicz, C.; Nair, M.; Atluri, V.; Khizroev, S. Magneto-electric Nanoparticles to Enable Field-controlled High-Specificity Drug Delivery to Eradicate Ovarian Cancer Cells. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Reasor, D.A.; Mehrabadi, M.; Ku, D.N.; Aidun, C.K. Determination of Critical Parameters in Platelet Margination. Ann. Biomed. Eng. 2013, 41, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Saadatmand, M.; Ishikawa, T.; Matsuki, N.; Abdekhodaie, M.J.; Imai, Y.; Ueno, H.; Yamaguchi, T. Fluid particle diffusion through high-hematocrit blood flow within a capillary tube. J. Biomech. 2011, 44, 170–175. [Google Scholar] [CrossRef] [PubMed]
- Crowl, L.M.; Fogelson, A.L. Computational model of whole blood exhibiting lateral platelet motion induced by red blood cells. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 471–487. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shaqfeh, E.S.G.; Narsimhan, V. Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 2012, 24. [Google Scholar] [CrossRef]
- Lee, T.-R.; Choi, M.; Kopacz, A.M.; Yun, S.-H.; Liu, W.K.; Decuzzi, P. On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Eckstein, E.C.; Bailey, D.G.; Shapiro, A.H. Self-Diffusion of Particles in Shear-Flow of a Suspension. J. Fluid Mech. 1977, 79, 191–208. [Google Scholar] [CrossRef]
- Leighton, D.; Acrivos, A. The Shear-Induced Migration of Particles in Concentrated Suspensions. J. Fluid Mech. 1987, 181, 415–439. [Google Scholar] [CrossRef]
- Aarts, P.A.M.M.; Steendijk, P.; Sixma, J.J.; Heethaar, R.M. Fluid shear as a possible mechanism for platelet diffusivity in flowing blood. J. Biomech. 1986, 19, 799–805. [Google Scholar] [CrossRef]
- Gentile, F.; Ferrari, M.; Decuzzi, P. The Transport of Nanoparticles in Blood Vessels: The Effect of Vessel Permeability and Blood Rheology. Ann. Biomed. Eng. 2008, 36, 254–261. [Google Scholar] [CrossRef] [PubMed]
- Gentile, F.; Decuzzi, P. Time dependent dispersion of nanoparticles in blood vessels. J. Biomed. Sci. Eng. 2010, 3, 517–524. [Google Scholar] [CrossRef]
- Hossain, S.S.; Zhang, Y.J.; Liang, X.H.; Hussain, F.; Ferrari, M.; Hughes, T.J.R.; Decuzzi, P. In silico vascular modeling for personalized nanoparticle delivery. Nanomedicine 2013, 8, 343–357. [Google Scholar] [CrossRef] [PubMed]
- Kruger, T.; Gross, M.; Raabe, D.; Varnik, F. Crossover from tumbling to tank-treading-like motion in dense simulated suspensions of red blood cells. Soft Matter 2013, 9, 9008–9015. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.F.; Johnson, P.C.; Popel, A.S. Red blood cell aggregation and dissociation in shear flows simulated by lattice Boltzmann method. J. Biomech. 2008, 41, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, W.K. Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 2006, 220, 139–154. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, W.K.; Belytschko, T.; Patankar, N.; To, A.C.; Kopacz, A.; Chung, J.H. Immersed electrokinetic finite element method. Int. J. Numer. Methods Eng. 2007, 71, 379–405. [Google Scholar] [CrossRef]
- Liu, Y.; Oh, K.; Bai, J.G.; Chang, C.; Chung, J.; Lee, K.; Liu, W.K. Manipulation of Nanoparticles and Biomolecules by Electric Field and Surface Tension. Comput. Methods Appl. Mech. Eng. 2008, 197, 2156–2172. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.T.; Wang, X.; Liu, W.K. Coupling of Navier-Stokes Equations with Protein Molecular Dynamics and Its Application to Hemodynamics. Int. J. Numer. Methods Fluids 2004, 46. [Google Scholar] [CrossRef]
- Liu, Y.L.; Chung, J.H.; Liu, W.K.; Ruoff, R.S. Dielectrophoretic assembly of nanowires. J. Phys. Chem. B 2006, 110, 14098–14106. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shu, C.; Zhao, N.; Yan, W.W. Fluid Dynamics of Flapping Insect Wing in Ground Effect. J. Bionic Eng. 2014, 11, 52–60. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.C.; Shu, C.; Zhao, N.; Yan, W.W. Ground effect on the power extraction performance of a flapping wing biomimetic energy generator. J. Fluids Struct. 2015, 54, 247–262. [Google Scholar] [CrossRef]
- Suzuki, K.; Minami, K.; Inamuro, T. Lift and thrust generation by a butterfly-like flapping wing-body model: Immersed boundary-lattice Boltzmann simulations. J. Fluid Mech. 2015, 767, 659–695. [Google Scholar] [CrossRef]
- De Rosis, A.; Leveque, E. Harmonic oscillations of a thin lamina in a quiescent viscous fluid: A numerical investigation within the framework of the lattice Boltzmann method. Comput. Struct. 2015, 157, 209–217. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Teo, C.J.; Wu, J. An immersed boundary-lattice Boltzmann flux solver and its applications to fluid-structure interaction problems. J. Fluids Struct. 2015, 54, 440–465. [Google Scholar] [CrossRef]
- Tölke, J. Implementation of a Lattice Boltzmann kernel using the Compute Unified Device Architecture developed by nVIDIA. Comput. Vis. Sci. 2010, 13, 29–39. [Google Scholar] [CrossRef]
- Takashi, N.; Hughes, T.J. An arbitrary Lagrangian-Eulerian finite element method for interaction of fluid and a rigid body. Comput. Methods Appl. Mech. Eng. 1992, 95, 115–138. [Google Scholar] [CrossRef]
- Kruger, T.; Varnik, F.; Raabe, D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 2011, 61, 3485–3505. [Google Scholar] [CrossRef]
- Sui, Y.; Chew, Y.T.; Roy, P.; Low, H.T. A hybrid method to study flow-induced deformation of three-dimensional capsules. J. Comput. Phys. 2008, 227, 6351–6371. [Google Scholar] [CrossRef]
- Reasor, D.A.; Clausen, J.R.; Aidun, C.K. Coupling the lattice-Boltzmann and spectrin-link methods for the direct numerical simulation of cellular blood flow. Int. J. Numer. Methods Fluids 2012, 68, 767–781. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Luo, L.S. The lattice-gas and lattice boltzmann methods: Past, present, and future. In Proceedings of the International Conference on Applied Computational Fluid Dynamics, Beijing, China, 17–20 October 2000; pp. 52–83.
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Ladd, A.J.C. Numerical Simulations of Particulate Suspensions via a Discretized Boltzmann-Equation. 1. Theoretical Foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Latt, J. Hydrodynamic Limit of Lattice Boltzmann Equations; University of Geneva: Geneva, Switzerland, 2007. [Google Scholar]
- Qian, Y.; D’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL 1992, 17. [Google Scholar] [CrossRef]
- Zou, Q.S.; He, X.Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B. Lattice Boltzmann method with regularized pre-collision distribution functions. Math. Comput. Simul. 2006, 72, 165–168. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Malaspinas, O.; Deville, M.; Michler, A. Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Pozrikidis, C. Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 2001, 440, 269–291. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.P.; Chien, S. Strain Energy Function of Red Blood-Cell Membranes. Biophys. J. 1973, 13, 245–280. [Google Scholar] [CrossRef]
- Kruger, T. Computer Simulation Study of Collective Phenomena in Dense Suspensions of Red Blood Cells under Shear; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Dao, M.; Li, J.; Suresh, S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Eng. C 2006, 26, 1232–1244. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Lei, H.; Caswell, B.; Suresh, S.; Karniadakis, G.E. Multiscale Modeling of Red Blood Cell Mechanics and Blood Flow in Malaria. PLoS Comput. Biol. 2011, 7. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, M.; Bessho, S.; Wada, S. Spring-network-based model of a red blood cell for simulating mesoscopic blood flow. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 114–128. [Google Scholar] [CrossRef] [PubMed]
- Fedosov, D.A.; Caswell, B.; Karniadakis, G.E. A Multiscale Red Blood Cell Model with Accurate Mechanics, Rheology, and Dynamics. Biophys. J. 2010, 98, 2215–2225. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, M.; Bessho, S.; Wada, S. Analysis of Red Blood Cell Deformation under Fast Shear Flow for Better Estimation of Hemolysis. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Fung, Y.-C. Improved measurements of the erythrocyte geometry. Microvasc. Res. 1972, 4, 335–347. [Google Scholar] [CrossRef]
- Peskin, C.S.; McQueen, D.M. A three-dimensional computational method for blood flow in the heart I. Immersed elastic fibers in a viscous incompressible fluid. J. Comput. Phys. 1989, 81, 372–405. [Google Scholar] [CrossRef]
- Herschlag, G.; Miller, L. Reynolds number limits for jet propulsion: A numerical study of simplified jellyfish. J. Theor. Biol. 2011, 285, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Iaccarino, G. Immersed Boundary Methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Ladd, A.J. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311–339. [Google Scholar] [CrossRef]
- Aidun, C.K.; Lu, Y.N.; Ding, E.J. Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 1998, 373, 287–311. [Google Scholar] [CrossRef]
- Basagaoglu, H.; Allwein, S.; Succi, S.; Dixon, H.; Carrola, J.T.; Stothoff, S. Two- and three-dimensional lattice Boltzmann simulations of particle migration in microchannels. Microfluid. Nanofluid. 2013, 15, 785–796. [Google Scholar] [CrossRef]
- Brańka, A.; Heyes, D. Algorithms for Brownian dynamics simulation. Phys. Rev. E 1998, 58. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Uma, B.; Liu, J.; Ayyaswamy, P.S.; Eckmann, D.M. Temporal multiscale approach for nanocarrier motion with simultaneous adhesion and hydrodynamic interactions in targeted drug delivery. J. Comput. Phys. 2013, 244, 252–263. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Gerstenberger, A.; Wang, X.D.; Liu, W.K. Immersed finite element method. Comput. Methods Appl. Mech. Eng. 2004, 193, 2051–2067. [Google Scholar] [CrossRef]
- Feng, J.; Hu, H.H.; Joseph, D.D. Direct Simulation of Initial-Value Problems for the Motion of Solid Bodies in a Newtonian Fluid. 1. Sedimentation. J. Fluid Mech. 1994, 261, 95–134. [Google Scholar] [CrossRef]
- Fischer, T.; Stohr-Lissen, M.; Schmid-Schonbein, H. The red cell as a fluid droplet: tank tread-like motion of the human erythrocyte membrane in shear flow. Science 1978, 202, 894–896. [Google Scholar] [CrossRef] [PubMed]
- Sui, Y.; Low, H.T.; Chew, Y.T.; Roy, P. Tank-treading, swinging, and tumbling of liquid-filled elastic capsules in shear flow. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Pozrikidis, C. Numerical simulation of the flow-induced deformation of red blood cells. Ann. Biomed. Eng. 2003, 31, 1194–1205. [Google Scholar] [CrossRef] [PubMed]
- Decuzzi, P.; Ferrari, M. The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 2006, 27, 5307–5314. [Google Scholar] [CrossRef] [PubMed]
- Kruger, T.; Varnik, F.; Raabe, D. Shear stress in lattice Boltzmann simulations. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef] [PubMed]
- Holdych, D.J.; Noble, D.R.; Georgiadis, J.G.; Buckius, R.O. Truncation error analysis of lattice Boltzmann methods. J. Comput. Phys. 2004, 193, 595–619. [Google Scholar] [CrossRef]
- Fedosov, D.A. Multiscale modeling of Blood flow and soft matter. In Applied Mathematics; Brown University: Providence, RI, USA, 2010. [Google Scholar]
- Crowl, L.; Fogelson, A.L. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 2011, 676, 348–375. [Google Scholar] [CrossRef]
- Wang, W.W.; King, M.R. Multiscale Modeling of Platelet Adhesion and Thrombus Growth. Ann. Biomed. Eng. 2012, 40, 2345–2354. [Google Scholar] [CrossRef] [PubMed]
- Mody, N.A.; King, M.R. Platelet adhesive dynamics. Part I: Characterization of platelet hydrodynamic collisions and wall effects. Biophys. J. 2008, 95, 2539–2555. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Keller, W.; Sohrabi, S.; Yang, J.; Liu, Y. Characterization of Nanoparticle Dispersion in Red Blood Cell Suspension by the Lattice Boltzmann-Immersed Boundary Method. Nanomaterials 2016, 6, 30. https://doi.org/10.3390/nano6020030
Tan J, Keller W, Sohrabi S, Yang J, Liu Y. Characterization of Nanoparticle Dispersion in Red Blood Cell Suspension by the Lattice Boltzmann-Immersed Boundary Method. Nanomaterials. 2016; 6(2):30. https://doi.org/10.3390/nano6020030
Chicago/Turabian StyleTan, Jifu, Wesley Keller, Salman Sohrabi, Jie Yang, and Yaling Liu. 2016. "Characterization of Nanoparticle Dispersion in Red Blood Cell Suspension by the Lattice Boltzmann-Immersed Boundary Method" Nanomaterials 6, no. 2: 30. https://doi.org/10.3390/nano6020030
APA StyleTan, J., Keller, W., Sohrabi, S., Yang, J., & Liu, Y. (2016). Characterization of Nanoparticle Dispersion in Red Blood Cell Suspension by the Lattice Boltzmann-Immersed Boundary Method. Nanomaterials, 6(2), 30. https://doi.org/10.3390/nano6020030





