Effects of G-Quadruplex Topology on Electronic Transfer Integrals
Abstract
:1. Introduction
2. Results
2.1. Choice of Relevant G4 Structures, Spanning Viable Topologies
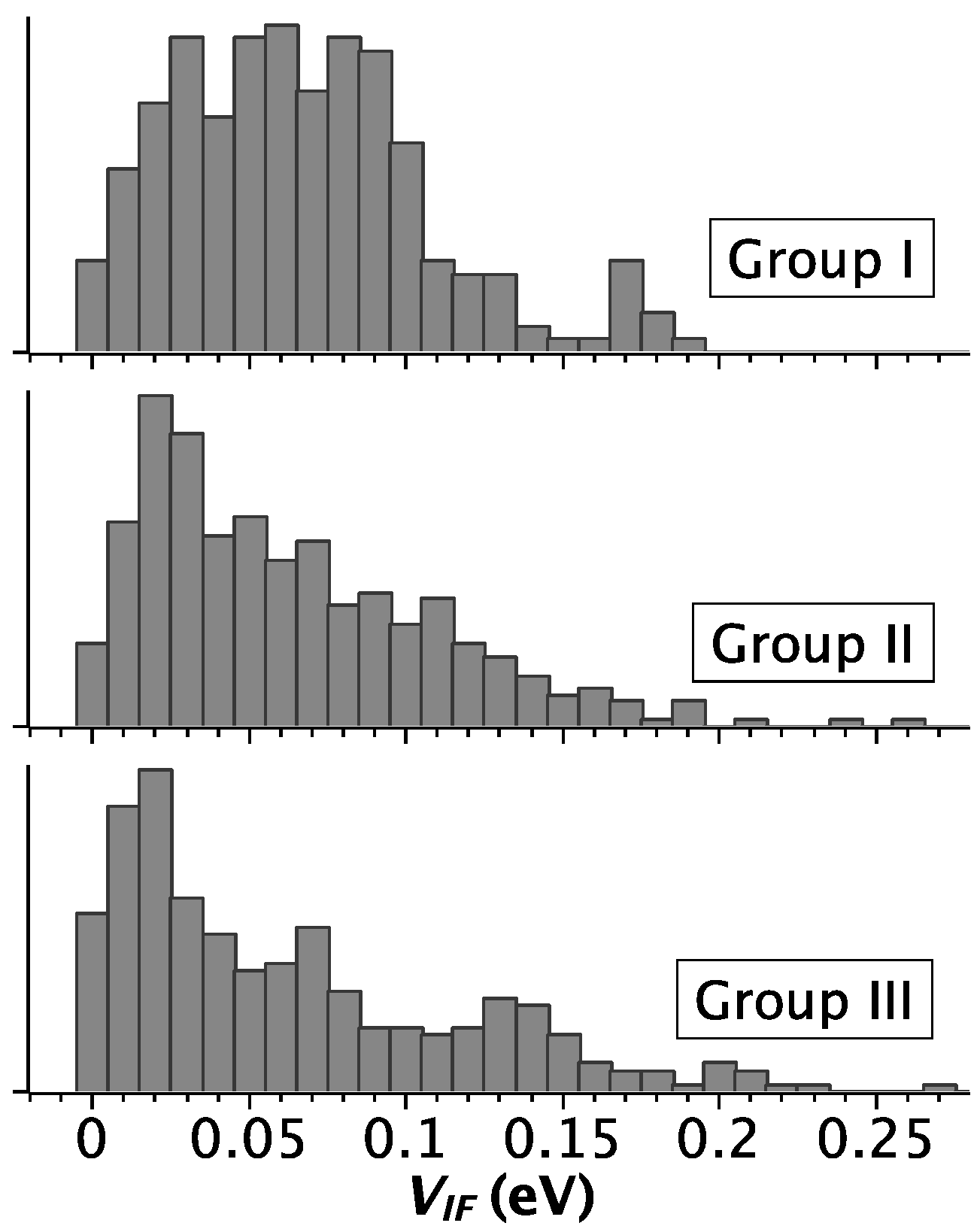
2.2. Strength of Electronic Coupling
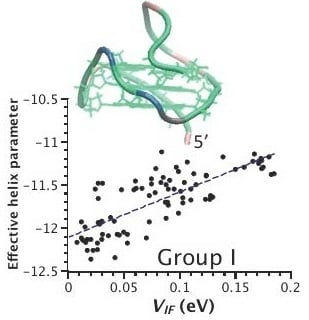
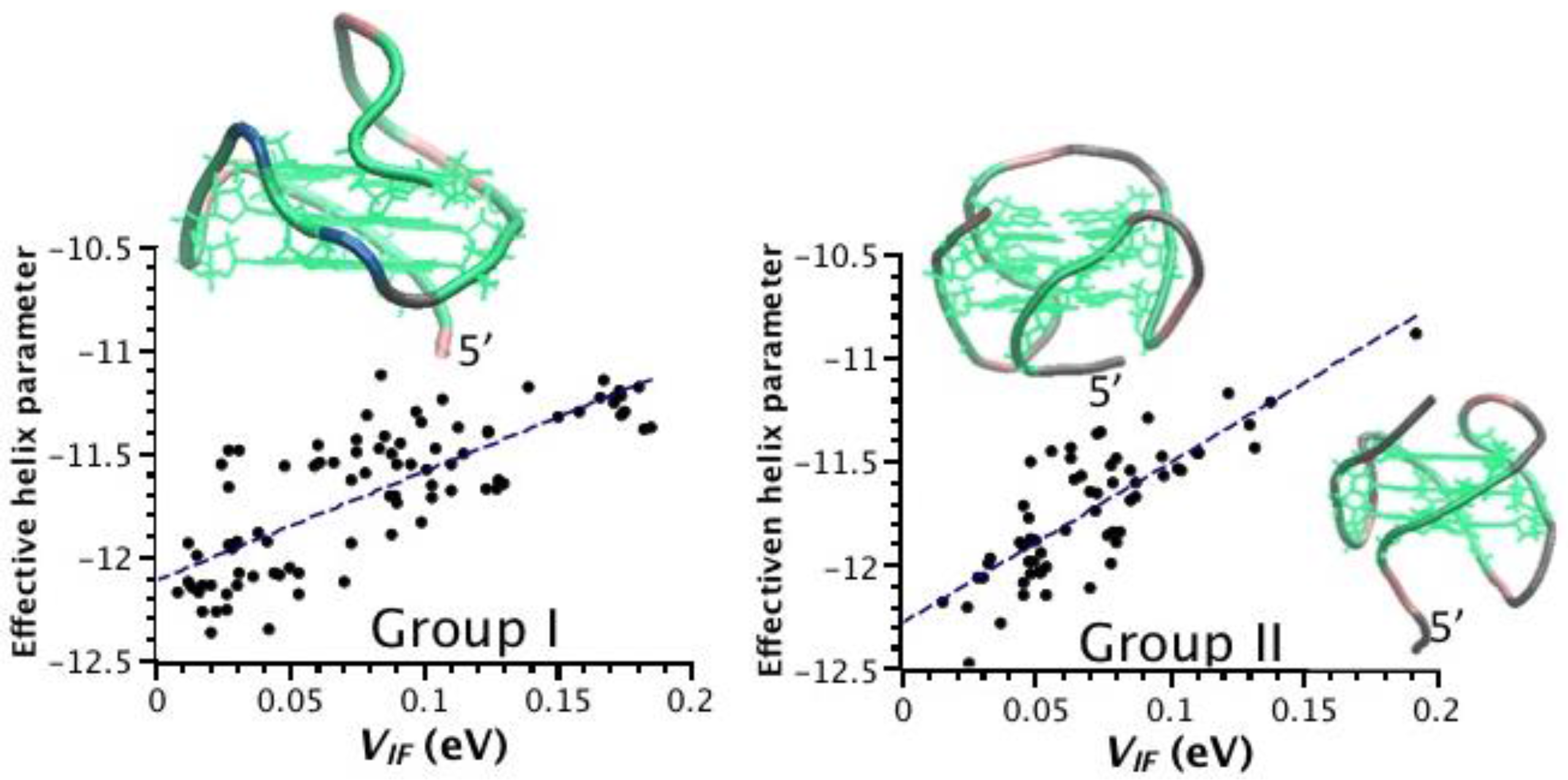
2.3. Correlation between Helix Shape Parameters and Electronic Coupling Parameters
3. Discussion
4. Materials and Methods
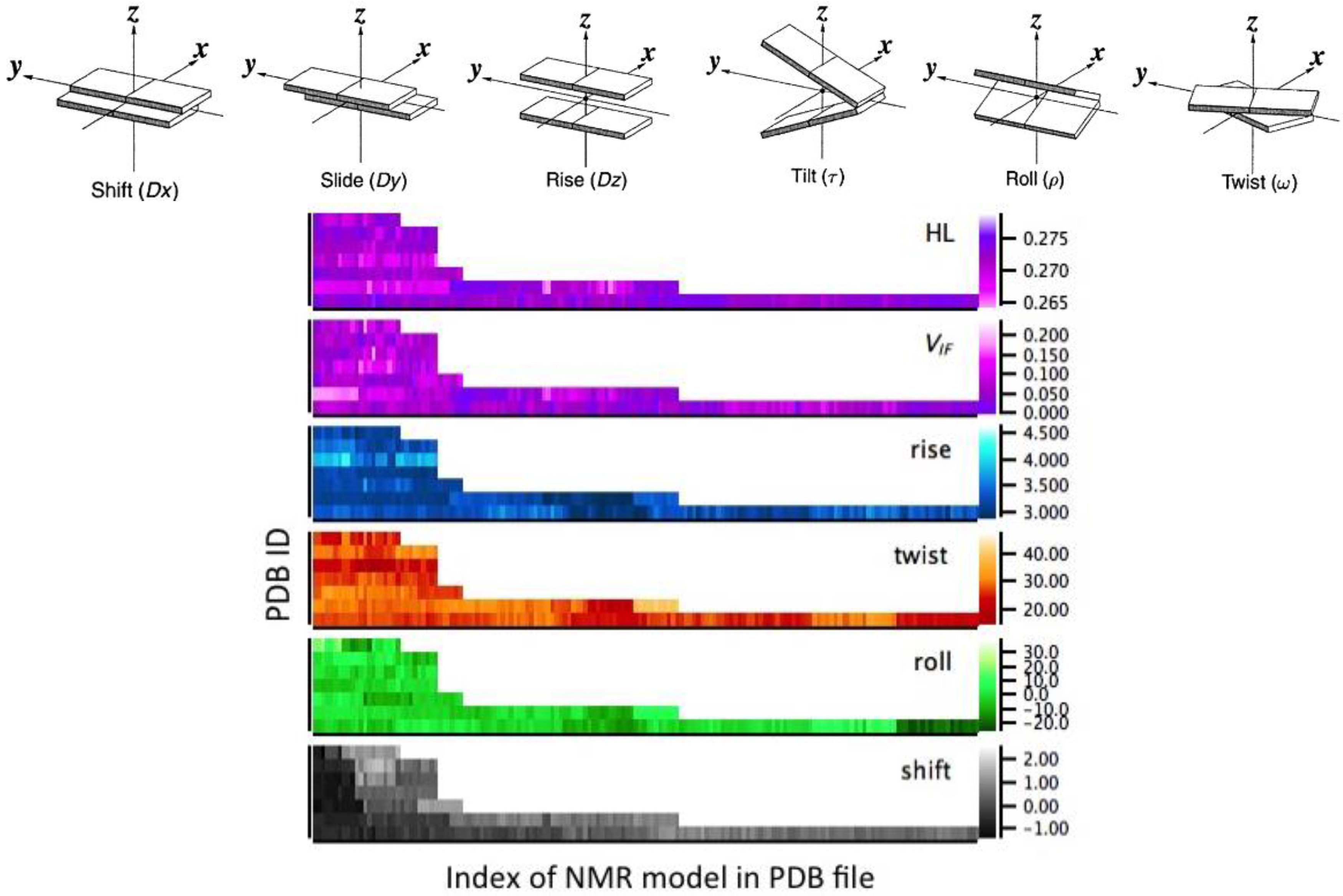
4.1. Structural Analysis
4.2. Computational Approach—Electronic Structure Calculations
4.3. Statistical Analysis—Maximizing the Pearson’s Correlation Coefficient with the Transfer Integral for a Linear Combination of Helix Shape Parameters
- compute the covariance of each inter-base helix parameter xn with VIF and with all the other inter-base helix parameters xm; the former is vector (this vector can also be obtained for the electronic quantity t = HL), the latter is matrix A;
- diagonalize matrix A;
- use the eigenvalues and eigenvectors of A to determine the coefficients that maximize the shape-electronic Pearson’s correlation coefficient;
- calculate the Pearson’s correlation coefficient of this combination, which is an effective helix parameter, with VIF (and HL), reported in Table S1.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GBA | glycosydic bond angle |
| DFT | density functional theory |
| Nr. | number |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest unoccupied molecular orbital |
| HL | HOMO-LUMO gap |
| BHH | Becke half-and-half functional |
| NMR | nuclear magnetic resonance |
| PDB | protein data bank |
References
- Livshits, G.I.; Stern, A.; Rotem, D.; Borovok, N.; Eidelshtein, G.; Migliore, A.; Penzo, E.; Wind, S.J.; Di Felice, R.; Skourtis, S.S.; et al. Long-range charge transport in single G-quadruplex DNA molecules. Nat. Nanotechnol. 2014, 9, 1040–1046. [Google Scholar] [CrossRef] [PubMed]
- Yatsunyk, L.A.; Mendoza, O.; Mergny, J.L. “Nano-oddities”: Unusual Nucleic Acid Assemblies for DNA-Based Nanostructures and Nanodevices. Accounts Chem. Res. 2014, 47, 1836–1844. [Google Scholar] [CrossRef] [PubMed]
- Seeman, N.C. DNA in a material world. Nature 2003, 421, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Maizels, N.; Gray, L.T. The G4 genome. PLoS Genet. 2013, 9, e1003468. [Google Scholar] [CrossRef] [PubMed]
- Biffi, G.; Di Antonio, M.; Tannahill, D.; Balasubramanian, S. Visualization and selective chemical targeting of RNA G-quadruplex structures in the cytoplasm of human cells. Nat. Chem. 2014, 6, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Biffi, G.; Tannahill, D.; McCafferty, J.; Balasubramanian, S. Quantitative visualization of DNA G-quadruplex structures in human cells. Nat. Chem. 2013, 5, 182–186. [Google Scholar] [CrossRef] [PubMed]
- Webba da Silva, M. Geometric formalism for DNA quadruplex folding. Chemistry 2007, 13, 9738–9745. [Google Scholar] [CrossRef] [PubMed]
- Webba da Silva, M.; Trajkovski, M.; Sannohe, Y.; Ma'ani Hessari, N.; Sugiyama, H.; Plavec, J. Design of a G-quadruplex topology through glycosidic bond angles. Angew. Chem. 2009, 48, 9167–9170. [Google Scholar] [CrossRef] [PubMed]
- Karsisiotis, A.I.; Hessari, N.M.; Novellino, E.; Spada, G.P.; Randazzo, A.; Webba da Silva, M. Topological characterization of nucleic acid G-quadruplexes by UV absorption and circular dichroism. Angew. Chem. 2011, 50, 10645–10648. [Google Scholar] [CrossRef] [PubMed]
- Gattuso, H.; Spinello, A.; Terenzi, A.; Assfeld, X.; Barone, G.; Monari, A. Circular Dichroism of DNA G-Quadruplexes: Combining Modeling and Spectroscopy to Unravel Complex Structures. J. Phys. Chem. B 2016, 120, 3113. [Google Scholar] [CrossRef] [PubMed]
- Ambrus, A.; Chen, D.; Dai, J.; Jones, R.A.; Yang, D. Solution structure of the biologically relevant G-quadruplex element in the human c-MYC promoter. Implications for G-quadruplex stabilization. Biochemistry 2005, 44, 2048–2058. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.T.; Kuryavyi, V.; Burge, S.; Neidle, S.; Patel, D.J. Structure of an unprecedented G-quadruplex scaffold in the human c-kit promoter. J. Am. Chem. Soc. 2007, 129, 4386–4392. [Google Scholar] [CrossRef] [PubMed]
- Luu, K.N.; Phan, A.T.; Kuryavyi, V.; Lacroix, L.; Patel, D.J. Structure of the human telomere in K+ solution: An intramolecular (3 + 1) G-quadruplex scaffold. J. Am. Chem. Soc. 2006, 128, 9963–9970. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Punchihewa, C.; Ambrus, A.; Chen, D.; Jones, R.A.; Yang, D. Structure of the intramolecular human telomeric G-quadruplex in potassium solution: A novel adenine triple formation. Nucleic Acids Res. 2007, 35, 2440–2450. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Carver, M.; Punchihewa, C.; Jones, R.A.; Yang, D. Structure of the Hybrid-2 Type Intramolecular Human Telomeric G-Quadruplex in K+ Solution: Insights into Structure Polymorphism of the Human Telomeric Sequence. Nucleic Acids Res. 2007, 35, 4927. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.W.; Lacroix, L.; Yue, D.J.; Lim, J.K.; Lim, J.M.; Phan, A.T. Coexistence of two distinct G-quadruplex conformations in the hTERT promoter. J. Am. Chem. Soc. 2010, 132, 12331–12342. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Patel, D.J. Solution structure of the Tetrahymena telomeric repeat d(T2G4)4 G-tetraplex. Structure 1994, 2, 1141–1156. [Google Scholar] [CrossRef]
- Hu, L.; Lim, K.W.; Bouaziz, S.; Phan, A.T. Giardia telomeric sequence d(TAGGG)4 forms two intramolecular G-quadruplexes in K+ solution: Effect of loop length and sequence on the folding topology. J. Am. Chem. Soc. 2009, 131, 16824–16831. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Patel, D.J. Solution structure of the Oxytricha telomeric repeat d[G4(T4G4)3] G-tetraplex. J. Mol. Biol. 1995, 251, 76–94. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Patel, D.J. Solution structure of the human telomeric repeat d[AG3(T2AG3)3] G-tetraplex. Structure 1993, 1, 263–282. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, J.; Veliath, E.; Jones, R.A.; Yang, D. Structure of a two-G-tetrad intramolecular G-quadruplex formed by a variant human telomeric sequence in K+ solution: Insights into the interconversion of human telomeric G-quadruplex structures. Nucleic Acids Res. 2010, 38, 1009–1021. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.W.; Alberti, P.; Guedin, A.; Lacroix, L.; Riou, J.F.; Royle, N.J.; Mergny, J.L.; Phan, A.T. Sequence variant (CTAGGG)n in the human telomere favors a G-quadruplex structure containing a G.C.G.C tetrad. Nucleic Acids Res. 2009, 37, 6239–6248. [Google Scholar] [CrossRef] [PubMed]
- Schultze, P.; Macaya, R.F.; Feigon, J. Three-dimensional solution structure of the thrombin-binding DNA aptamer d(GGTTGGTGTGGTTGG). J. Mol. Biol. 1994, 235, 1532–1547. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.W.; Amrane, S.; Bouaziz, S.; Xu, W.; Mu, Y.; Patel, D.J.; Luu, K.N.; Phan, A.T. Structure of the human telomere in K+ solution: A stable basket-type G-quadruplex with only two G-tetrad layers. J. Am. Chem. Soc. 2009, 131, 4301–4309. [Google Scholar] [CrossRef] [PubMed]
- Migliore, A.; Corni, S.; Varsano, D.; Klein, M.L.; Di Felice, R. First Principles Effective Electronic Couplings for Hole Transfer in Natural and Size-Expanded DNA. J. Phys. Chem. B 2009, 113, 9402–9415. [Google Scholar] [CrossRef] [PubMed]
- Lech, C.J.; Phan, A.T.; Michel-Beyerle, M.E.; Voityuk, A.A. Electron-Hole Transfer in G-Quadruplexes with Different Tetrad Stacking Geometries: A Combined QM and MD Study. J. Phys. Chem. B 2013, 117, 9851–9856. [Google Scholar] [CrossRef] [PubMed]
- Kubar, T.; Elstner, M. What governs the charge transfer in DNA? The role of DNA conformation and environment. J. Phys. Chem. B 2008, 112, 8788–8798. [Google Scholar] [CrossRef] [PubMed]
- Woiczikowski, P.B.; Kubar, T.; Gutierrez, R.; Cuniberti, G.; Elstner, M. Structural stability versus conformational sampling in biomolecular systems: Why is the charge transfer efficiency in G4-DNA better than in double-stranded DNA? J. Chem. Phys. 2010, 133, 035103. [Google Scholar] [CrossRef] [PubMed]
- Borovok, N.; Iram, N.; Zikich, D.; Ghabboun, J.; Livshits, G.I.; Porath, D.; Kotlyar, A.B. Assembling of G-strands into novel tetra-molecular parallel G4-DNA nanostructures using avidinbiotin recognition. Nucleic Acids Res. 2008, 36, 5050–5060. [Google Scholar] [CrossRef] [PubMed]
- Lavery, R.; Sklenar, H. Defining the Structure of Irregular Nucleic-Acids - Conventions and Principles. J. Biomol. Struct. Dyn. 1989, 6, 655–667. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity and Panmixia. Philos. Trans. R. Soc. London 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Harris, J.; Jones, R.O. Surface-Energy of a Bounded Electron-Gas. J. Phys. F Met. Phys. 1974, 4, 1170–1186. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Lundqvist, B.I. Exchange and Correlation in Atoms, Molecules, and Solids by Spin-Density Functional Formalism. Phys. Rev. B 1976, 13, 4274–4298. [Google Scholar] [CrossRef]
- Langreth, D.C.; Perdew, J.P. Exchange-Correlation Energy of a Metallic Surface—Wave-Vector Analysis. Phys. Rev. B 1977, 15, 2884–2901. [Google Scholar] [CrossRef]
- Harris, J. Adiabatic-Connection Approach to Kohn-Sham Theory. Phys. Rev. A 1984, 29, 1648–1659. [Google Scholar] [CrossRef]
- Migliore, A. Full-electron calculation of effective electronic couplings and excitation energies of charge transfer states: Application to hole transfer in DNA pi-stacks. J. Chem. Phys. 2009, 131, 114113. [Google Scholar] [CrossRef] [PubMed]
- Waller, M.P.; Robertazzi, A.; Platts, J.A.; Hibbs, D.E.; Williams, P.A. Hybrid density functional theory for pi-stacking interactions: Application to benzenes, pyridines, and DNA bases. J. Comput. Chem. 2006, 27, 491–504. [Google Scholar] [CrossRef] [PubMed]
- Miura, M.; Aoki, Y.; Champagne, B. Assessment of time-dependent density functional schemes for computing the oscillator strengths of benzene, phenol, aniline, and fluorobenzene. J. Chem. Phys. 2007, 127, 084103. [Google Scholar] [CrossRef] [PubMed]
- Migliore, A. Nonorthogonality Problem and Effective Electronic Coupling Calculation: Application to Charge Transfer in pi-Stacks Relevant to Biochemistry and Molecular Electronics. J. Chem. Theory Comput. 2011, 7, 1712–1725. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Cammi, R.; Mennucci, B. Medium effects on the properties of chemical systems: An overview of recent formulations in the polarizable continuum model (PCM). Int. J. Quantum. Chem. 1999, 75, 783–803. [Google Scholar] [CrossRef]
- Shapir, E.; Cohen, H.; Calzolari, A.; Cavazzoni, C.; Ryndyk, D.A.; Cuniberti, G.; Kotlyar, A.; Di Felice, R.; Porath, D. Electronic structure of single DNA molecules resolved by transverse scanning tunnelling spectroscopy. Nat. Mater. 2008, 7, 68–74. [Google Scholar] [CrossRef] [PubMed]
- De Pablo, P.J.; Moreno-Herrero, F.; Colchero, J.; Gomez-Herrero, J.; Herrero, P.; Baro, A.M.; Ordejon, P.; Soler, J. M.; Artacho, E. Absence of dc-conductivity in lambda-DNA. Phys. Rev. Lett. 2000, 85, 4992–4995. [Google Scholar] [CrossRef] [PubMed]
- Berlin, Y.A.; Kurnikov, I.V.; Beratan, D.N.; Ratner, M.A.; Burin, A.L. DNA Electron Transfer Processes: Some Theoretical Notions. Top. Curr. Chem. 2004, 237, 1–36. [Google Scholar]
- Tong, G.S.M.; Kurnikov, I.V.; Beratan, D.N. Tunneling Energy Effects on GC Oxidation in DNA. J. Phys. Chem. B 2002, 106, 2381–2392. [Google Scholar] [CrossRef]
- Liang, C.; Newton, M.D. Ab Initio Studies of Electron Transfer: Pathway Analysis of Effective Transfer Integrals. J. Phys. Chem. 1992, 96, 2855–2866. [Google Scholar] [CrossRef]
- Brédas, J.L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-Transfer and Energy-Transfer Processes in p-Conjugated Oligomers and Polymers: A Molecular Picture. Chem. Rev. 2004, 104, 4971–5004. [Google Scholar] [CrossRef] [PubMed]
- Voityuk, A. Electronic Coupling for Chanrge Transfer in Donor-Bridge-Acceptor Systems. Performance of the two-state FCD Model. Phys. Chem. Chem. Phys. 2012, 14, 13789–13793. [Google Scholar] [CrossRef] [PubMed]
- Castet, F.; Aurel, P.; Fritsch, A.; Ducasse, L.; Liotard, D.; Linares, M.; Cornil, J.; Beljonne, D. Electronic Polarization Effects on Charge Carriers in Anthracene: A Valence Bond Study. Phys. Rev. B 2008, 77, 115210. [Google Scholar] [CrossRef]
| Group | PDB Code | Nr. G4 § | P(VIF-HL) † |
|---|---|---|---|
| I | 1XAV | 3 | −0.49 |
| 2O3M | 3 | −0.73 | |
| II | 2GKU | 3 | −0.71 |
| 2HY9 | 3 | −0.87 | |
| 2JPZ | 3 | −0.81 | |
| 2KZD | 3 | −0.82 | |
| 186D | 3 | −0.78 | |
| III | 2KOW | 2 | −0.92 |
| 201D | 4 | −0.60 | |
| 143D | 3 | −0.57 | |
| 2KKA | 2 | −0.41 | |
| 2KM3 | 2 | −0.94 | |
| 148D | 2 | −0.87 | |
| 2KF8 | 2 | −0.94 |
| PDB Code | Nr. Models † | Nr. Tetrads ‡ | Nr. Guanines | Strand Directions | Parent Sequence | |
|---|---|---|---|---|---|---|
| Group I | 1XAV [11] | 20 | 3 | 22 | ++++ | 5’-TGAGGGTGGGTAGGGTGGGTAA-3’ |
| 2O3M [12] | 11 | 3 | 22 | ++++ | 5’-AGGGAGGGCGCTGGGAGGAGGG-3’ | |
| Group II | 2GKU [13] | 12 | 3 | 24 | ++−+ | 5’-TTGGGTTAGGGTTAGGGTTAGGGA-3’ |
| 2HY9 [14] | 10 | 3 | 26 | ++−+ | 5’-AAAGGGTTAGGGTTAGGGTTAGGGAA-3’ | |
| 2JPZ [15] | 10 | 3 | 26 | +−++ | 5’-TTAGGGTTAGGGTTAGGGTTAGGGTT-3’ | |
| 2KZD [16] | 10 | 3 | 20 | +−++ | 5’-AGGGIAGGGGCTGGGAGGGC-3’ | |
| 186D [17] | 7 | 3 | 24 | +−++ | 5’-TTGGGGTTGGGGTTGGGGTTGGGG-3’ | |
| Group III | 2KOW [18] | 10 | 2 | 20 | +−+− | 5’-TAGGGTAGGGTAGGGTAIGG-3’ |
| 201D [19] | 6 | 4 | 28 | +−+− | 5’-GGGGTTTTGGGGTTTTGGGGTTTTGGGG-3’ | |
| 143D [20] | 6 | 3 | 22 | +−+− | 5’-AGGGTTAGGGTTAGGGTTAGGG-3’ | |
| 2KKA [21] | 8 | 2 | 23 | +−+− | 5’-AGGGTTAGGGTTAIGGTTAGGGT-3’ | |
| 2KM3 [22] | 10 | 2 | 22 | +−+− | 5’-AGGGCTAGGGCTAGGGCTAGGG-3’ | |
| 148D [23] | 12 | 2 | 15 | +−+− | 5’-GGTTGGTGTGGTTGG-3’ | |
| 2KF8 [24] | 10 | 2 | 22 | +−+− | 5’-GGGTTAGGGTTAGGGTTAGGGT-3’ |
| PDB Code | Nr. G-G Couples for VIF * Statistics (Figure 1) | Nr. G-G Couples for Conformation Fluctuations and Structure-Electronic Correlations (Figure 2 and Figure 3) | |
|---|---|---|---|
| Group I | 1XAV | 160 | 160 |
| 2O3M | 88 | 88 | |
| total group I | 248 | 248 | |
| Group II | 2GKU | 96 | 36 |
| 2HY9 | 80 | 30 | |
| 2JPZ | 80 | 30 | |
| 2KZD | 80 | 30 | |
| 186D | 56 | 21 | |
| total group II | 392 | 147 | |
| Group III | 2KOW | 40 | 0 |
| 201D | 72 | 0 | |
| 143D | 48 | 0 | |
| 2KKA | 32 | 0 | |
| 2KM3 | 40 | 0 | |
| 148D | 48 | 0 | |
| 2KF8 | 40 | 0 | |
| total group III | 320 | 0 |
| PDB Code | Strand 1 | Strand 2 | Strand 3 | Strand 4 | Strand Directions | |
|---|---|---|---|---|---|---|
| Group I | 1XAV | 4(a) 5(a) 6(a) | 8(a) 9(a) 10(a) | 13(a) 14(a) 15(a) | 17(a) 18(a) 19(a) | ++++ |
| 2O3M | 2(a) 3(a) 4(a) | 6(a) 7(a) 8(a) | 13(a) 14(a) 15(a) | 10(a) 21(a) 22(a) | ++++ | |
| Group II | 2GKU | 3(s) 4(a) 5(a) | 9(s) 10(a) 11(a) | 17(a) 16(s) 15(s) | 21(s) 22(a) 23(a) | ++−+ |
| 2HY9 | 4(s) 5(a) 6(a) | 10(s) 11(a) 12(a) | 18(a) 17(s) 16(s) | 22(s) 23(a) 24(a) | ++−+ | |
| 2JPZ | 4(s) 5(a) 6(a) | 12(a) 11(s) 10(s) | 16(s) 17(a) 18(a) | 22(s) 23(a) 24(a) | +−++ | |
| 2KZD | 2(s) 3(a) 4(a) | 10(a) 9(s) 8(s) | 13(s) 14(a) 15(a) | 17(s) 18(a) 19(a) | +−++ | |
| 186D | 3(s) 4(a) 5(a) | 12(a) 11(s) 10(s) | 16(s) 17(a) 18(a) | 21(s) 22(a) 23(a) | +−++ | |
| Group III | 2KOW | 3(s) 4(a) | 9(a) 8(s) | 14(s) 15(a) | 19(a) 20(s) | +−+− |
| 201D | 1(s) 2(a) 3(s) 4(a) | 12(a) 11(s) 10(a) 9(s) | 17(s) 18(a) 19(s) 20(a) | 28(a) 27(s) 26(a) 25(s) | +−+− | |
| 143D | 2(a) 3(s) 4(a) | 10(s) 9(a) 8(s) | 14(a) 15(s) 16(a) | 22(s) 21(a) 20(s) | +−+− | |
| 2KKA | 2(s) 3(a) | 9(a) 8(s) | 15(s) 16(a) | 21(a) 20(s) | +−+− | |
| 2KM3 | 3(s) 4(a) | 10(a) 9(s) | 15(s) 16(a) | 22(a) 21(s) | +−+− | |
| 148D | 1(s) 2(a) | 6(a) 5(s) | 10(s) 11(a) | 15(a) 14(s) | +−+− | |
| 2KF8 | 1(s) 2(a) | 8(a) 7(s) | 14(s) 15(a) | 20(a) 19(s) | +−+− |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Varsano, D.; Di Felice, R. Effects of G-Quadruplex Topology on Electronic Transfer Integrals. Nanomaterials 2016, 6, 184. https://doi.org/10.3390/nano6100184
Sun W, Varsano D, Di Felice R. Effects of G-Quadruplex Topology on Electronic Transfer Integrals. Nanomaterials. 2016; 6(10):184. https://doi.org/10.3390/nano6100184
Chicago/Turabian StyleSun, Wenming, Daniele Varsano, and Rosa Di Felice. 2016. "Effects of G-Quadruplex Topology on Electronic Transfer Integrals" Nanomaterials 6, no. 10: 184. https://doi.org/10.3390/nano6100184
APA StyleSun, W., Varsano, D., & Di Felice, R. (2016). Effects of G-Quadruplex Topology on Electronic Transfer Integrals. Nanomaterials, 6(10), 184. https://doi.org/10.3390/nano6100184