Thermal Emission Control via Bandgap Engineering in Aperiodically Designed Nanophotonic Devices
Abstract
:1. Introduction
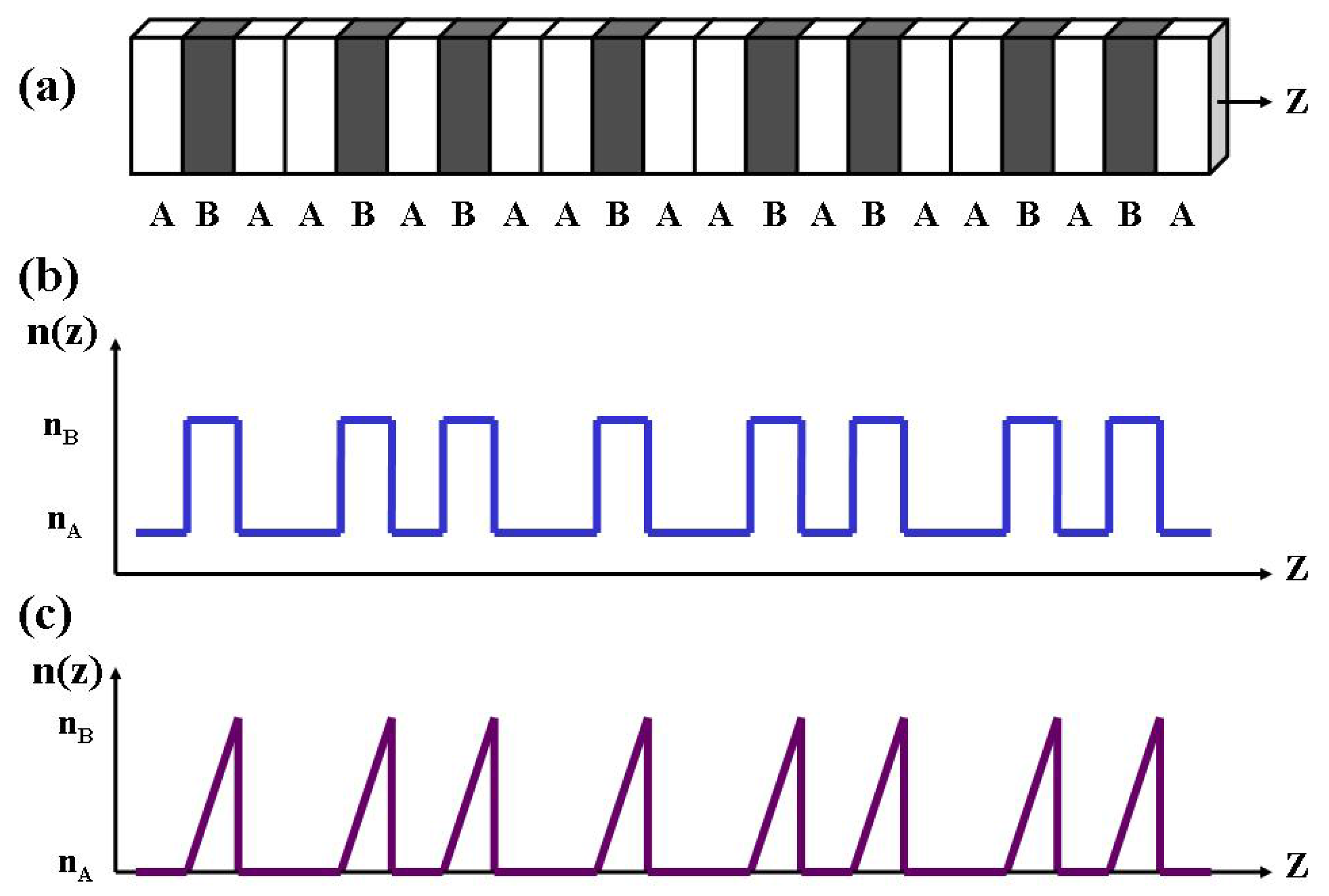
2. Aperiodicity by Design
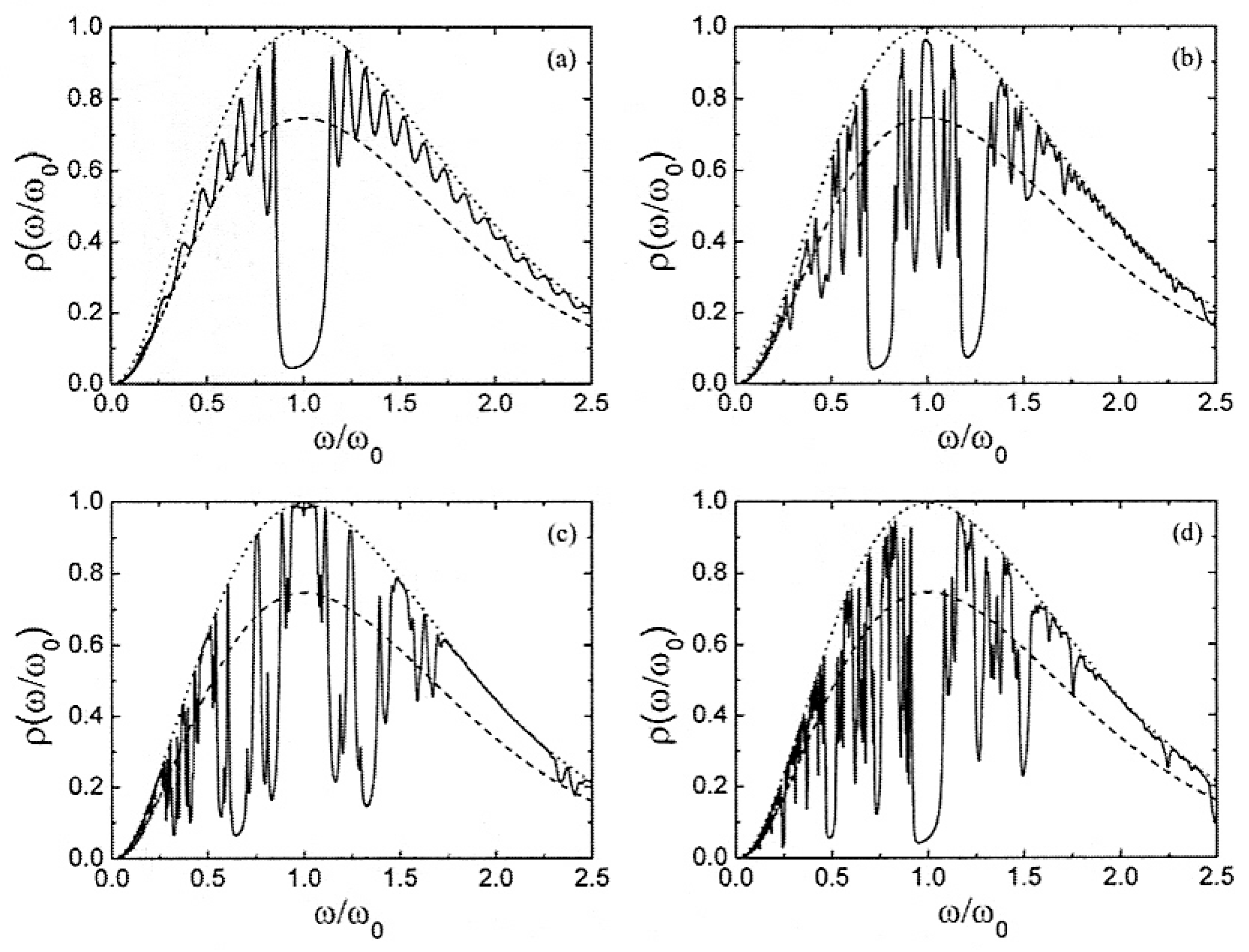
3. Thermal Emission Control
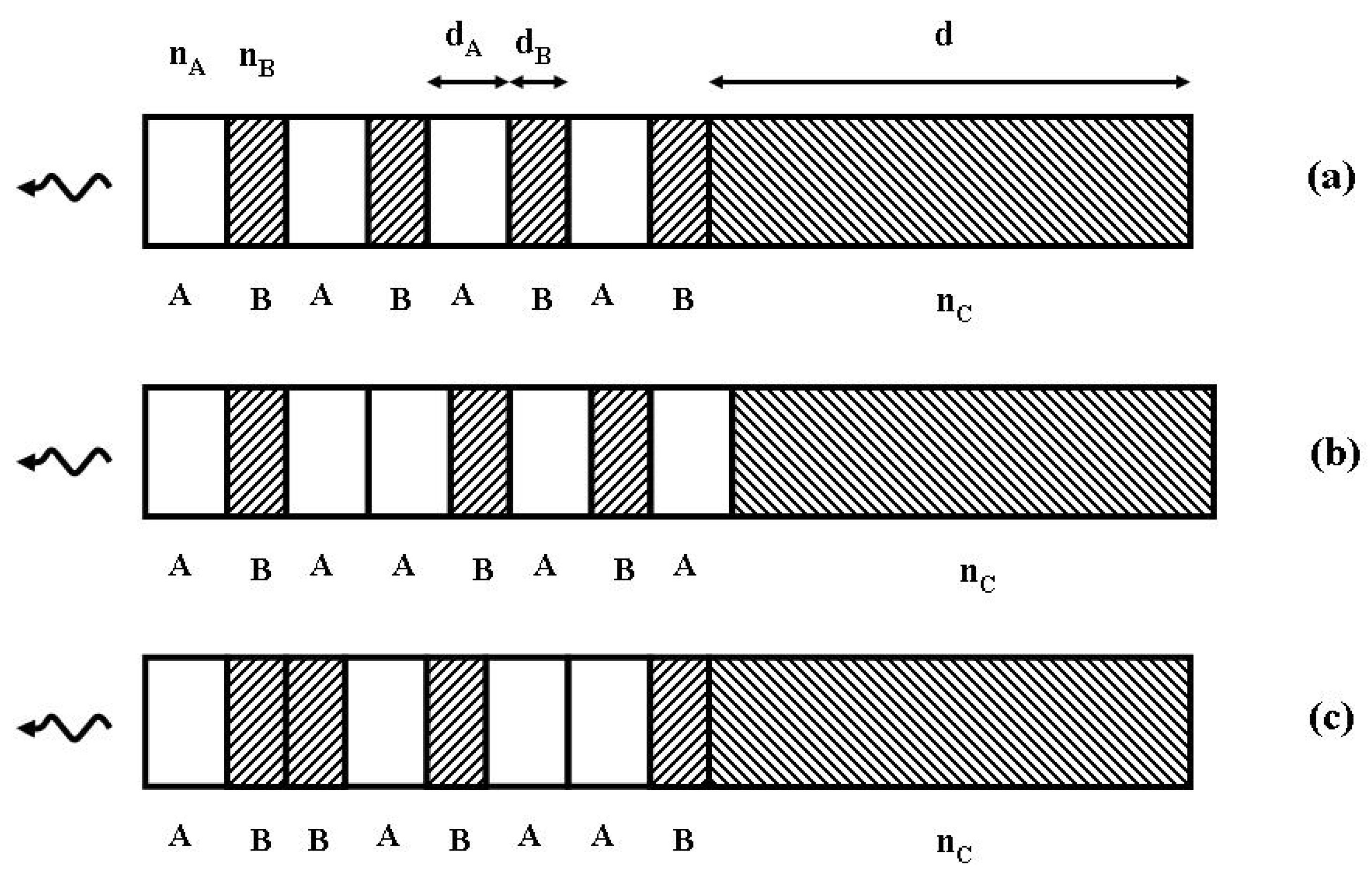
4. Possible Applications
4.1. Daytime Radiative Coolers
4.2. Solar Cells and Solar Thermoelectric Generators
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 415, 540–545. [Google Scholar] [CrossRef]
- Cornelius, C.M.; Dowling, J.P. Modification of Planck blackbody radiation by photonic band-gap structures. Phys. Rev. A 1999, 59, 4736–4746. [Google Scholar] [CrossRef]
- Dal Negro, L.; Lawrence, J.; Trevine, J.; Walsh, G. Aperiodic Order for Nanophotonics. In Optics of Aperiodic Structures: Fundamentals and Device Applications; Dal Negro, L., Ed.; Pan Stanford Publishing: Boca Raton, FL, USA, 2014; pp. 1–55. [Google Scholar]
- Maciá, E. The Importance of being Aperiodic: Optical Devices. In Optics of Aperiodic Structures: Fundamentals and Device Applications; Dal Negro, L., Ed.; Pan Stanford Publishing: Boca Raton, FL, USA, 2014; pp. 57–90. [Google Scholar]
- Maciá, E. Exploiting aperiodic designs in nanophotonic devives. Rep. Prog. Phys. 2012, 75, 036502. [Google Scholar] [CrossRef] [PubMed]
- Dal Negro, L.; Boriskina, S.V. Deterministic aperiodic nanostructures for photonics and plasmonics applications. Laser Photonics Rev. 2012, 6, 178–218. [Google Scholar] [CrossRef]
- Maciá Barber, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; Taylor & Francis CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
- Vishnyakov, E.A.; Kamenets, F.F.; Kondratenko, V.V.; Luginin, M.S.; Panchenko, A.V.; Pershin, Y.P.; Pirozhkov, A.S.; Ragozin, E.N. Aperiodic multilayer structures in soft X-ray radiation optics. Quantum Electron. 2012, 42, 143–152. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, J.; Wang, Z.; Zhang, Z.; Zhang, S.; Wu, W.; Chen, L.; Michette, A.G.; Powell, A.K.; Pfauntsch, S.J.; et al. Broadband Mo/Si multilayer analyzers for the 15–17 nm wavelength range. Thin Solid Films 2006, 515, 2523–2526. [Google Scholar] [CrossRef]
- Champeaux, J.P.; Troussel, P.; Villier, B.; Vidal, V.; Khachroum, T.; Vidal, B.; Krumrey, M. Development and realization of non-periodic W/Si multilayer mirrors for 5–14 keV X-ray plasma diagnostic. Nuclear Instrum. Methods Phys. Res. A 2007, 581, 687–694. [Google Scholar] [CrossRef]
- Gu, X.; Chen, X.; Chen, Y.; Zeng, X.; Xia, Y.; Chan, Y. Narrowband multiple wavelengths filter in aperiodic optical superlattice. Opt. Commun. 2004, 237, 53–58. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems; University Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Jiang, L.; Zheng, G.; Shi, L.; Yuan, J.; Li, X. Broad omnidirectional reflectors design using genetic algorithm. Opt. Commun. 2008, 281, 4882–4888. [Google Scholar] [CrossRef]
- Griniasty, M.; Fishman, S. Localization by pseudorandom potentials in one dimension. Phys. Rev. Lett. 1988, 60, 1334–1338. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, E.M.; de Moura, F.A.B.F.; Lyra, M.L. Suppressed transmission in aperiodically modulated multilayered dielectric structures. Photonic. Nanostruct. 2009, 7, 101–107. [Google Scholar] [CrossRef]
- De Medeiros, F.F.; Albuquerque, E.L.; Vasconcelos, M.S.; Maritz, P.W. Thermal radiation in quasiperiodic photonic crystals with negative refractive index. J. Phys. 2007, 19, 496212. [Google Scholar]
- Maksimovic, M.; Jaksic, Z. Emittance and absortance tailoring by negative refractive index metamaterial-based Cantor multilayers. J. Opt. A 2006, 8, 355–362. [Google Scholar] [CrossRef]
- Gentle, A.R.; Smith, G.B. Radiative heat pumping from the earth using surface phonon resonant nanoparticles. Nano Lett. 2010, 10, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Rephaeli, E.; Raman, A.; Fan, S. Ultrabroadband photonic structures to achive high-performance daytime radiative cooling. Nano Lett. 2013, 13, 1457–1461. [Google Scholar] [PubMed]
- Guo, M.; Xie, K.; Wang, Y.; Zhou, L.; Huang, H. Aperiodic TiO2 nanotube photonic crystal: Full-visible-spectrum solar light harvesting on photonic devices. Sci. Rep. 2014, 4, 6442. [Google Scholar] [CrossRef] [PubMed]
- Alagappan, G.; Wu, P. Geometrically distributed one-dimensional photonic crystals for light-reflection in all angles. Opt. Express 2009, 17, 11550–11557. [Google Scholar] [CrossRef] [PubMed]
- Gaponenko, S.V. Introduction to Nanophotonics; Cambridge University Press: Cambridge, UK, 2010; pp. 258–270. [Google Scholar]
- Zhukovsky, S.V.; Lavrinenko, A.V.; Gaponenko, S.V. Optical Filters Based in Fractal and Aperiodic Multilayers. In Optics of Aperiodic Structures: Fundamentals and Device Applications; Dal Negro, L., Ed.; Pan Stanford Publishing: Boca Raton, FL, USA, 2014; pp. 91–142. [Google Scholar]
- Zhukovsky, S.V.; Lavrinenko, A.V.; Gaponenko, S.V. Spectral scalability as a result of geometrical self-similarity in fractal multilayers. Europhys. Lett. 2004, 66, 455. [Google Scholar] [CrossRef]
- Gaponenko, S.V.; Zhukovsky, S.V.; Lavrinenko, A.V.; Sandomirskii, K.S. Propagation of waves in layered structures viewed as number recognition. Opt. Commun. 2002, 205, 49–57. [Google Scholar] [CrossRef]
- Chigrin, D.N.; Lavrinenko, A.V.; Yarotsky, D.A.; Gaponenko, S.V. Observation of total omnidirectional reflection from a one-dimensional dielectric lattice. Appl. Phys. A 1999, 68, 25–28. [Google Scholar] [CrossRef]
- Lavrinenko, A.V.; Zhukovsky, S.V.; Sandomirski, K.S.; Gaponenko, S.V. Propagation of classical waves in nonperiodic media: Scaling properties of an optical Cantor filter. Phys. Rev. E 2002, 65, 036621. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, P.; Pandey, P.C. Tunable photonic band-gaps in one-dimensional photonic crystals containing linear graded index material. Appl. Phys. B 2014, 117, 947–956. [Google Scholar] [CrossRef]
- Singh, B.K.; Pandey, P.C. Influence of graded index materials on the photonic localization in one-dimensional quasiperiodic (Thue-Morse and Double-Periodic) photonic crystals. Opt. Commun. 2014, 333, 84–91. [Google Scholar] [CrossRef]
- Micco, A.; Ricciardi, A.; Pisco, M.; La Ferrara, V.; Mercaldo, L.V.; Delli Veneri, P.; Cutolo, A.; Cusano, A. Light trapping efficiency of periodic and quasiperiodic back-reflectors for thin film solar cells: A comparative study. J. Appl. Phys. 2013, 114, 063103. [Google Scholar] [CrossRef]
- Chen, G. Theoretical efficiency of solar thermoelectric energy generators. J. Appl. Phys. 2011, 109, 104908. [Google Scholar] [CrossRef]
- De Leob, M.T.; Chong, H.; Kraft, M. Solar thermoelectric generators fabricated on a silicon-on-insulator substrate. J. Micromech. Microeng. 2014, 24, 085011. [Google Scholar] [CrossRef]
- Ariga, K.; Yamauchi, Y.; Rydzek, G.; Ji, Q.; Yonamine, Y.; Wu, K.C.-W.; Hill, J.P. Layer-by-layer nanoarchitectonics: Invention, innovation, and evolution. Chem. Lett. 2014, 43, 36–68. [Google Scholar] [CrossRef]
- Costa, R.R.; Mano, J.F. Polyelectrolyte multilayered assemblies in biomedical technologies. Chem. Soc. Rev. 2014, 43, 3453–3479. [Google Scholar] [CrossRef] [PubMed]
- Joseph, N.; Ahmadiannamini, P.; Hoogenboom, R.; Vankelecom, F.J. Layer-by-layer preparation of polyelectrolyte multilayer membranes for separation. Polym. Chem. 2014, 5, 1817–1831. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciá, E. Thermal Emission Control via Bandgap Engineering in Aperiodically Designed Nanophotonic Devices. Nanomaterials 2015, 5, 814-825. https://doi.org/10.3390/nano5020814
Maciá E. Thermal Emission Control via Bandgap Engineering in Aperiodically Designed Nanophotonic Devices. Nanomaterials. 2015; 5(2):814-825. https://doi.org/10.3390/nano5020814
Chicago/Turabian StyleMaciá, Enrique. 2015. "Thermal Emission Control via Bandgap Engineering in Aperiodically Designed Nanophotonic Devices" Nanomaterials 5, no. 2: 814-825. https://doi.org/10.3390/nano5020814
APA StyleMaciá, E. (2015). Thermal Emission Control via Bandgap Engineering in Aperiodically Designed Nanophotonic Devices. Nanomaterials, 5(2), 814-825. https://doi.org/10.3390/nano5020814




