Comparison of Two Measurement Methods for Scattering and Absorption Coefficients in Boron Carbide Nanodispersions
Abstract
1. Introduction
2. Experimental
3. Results
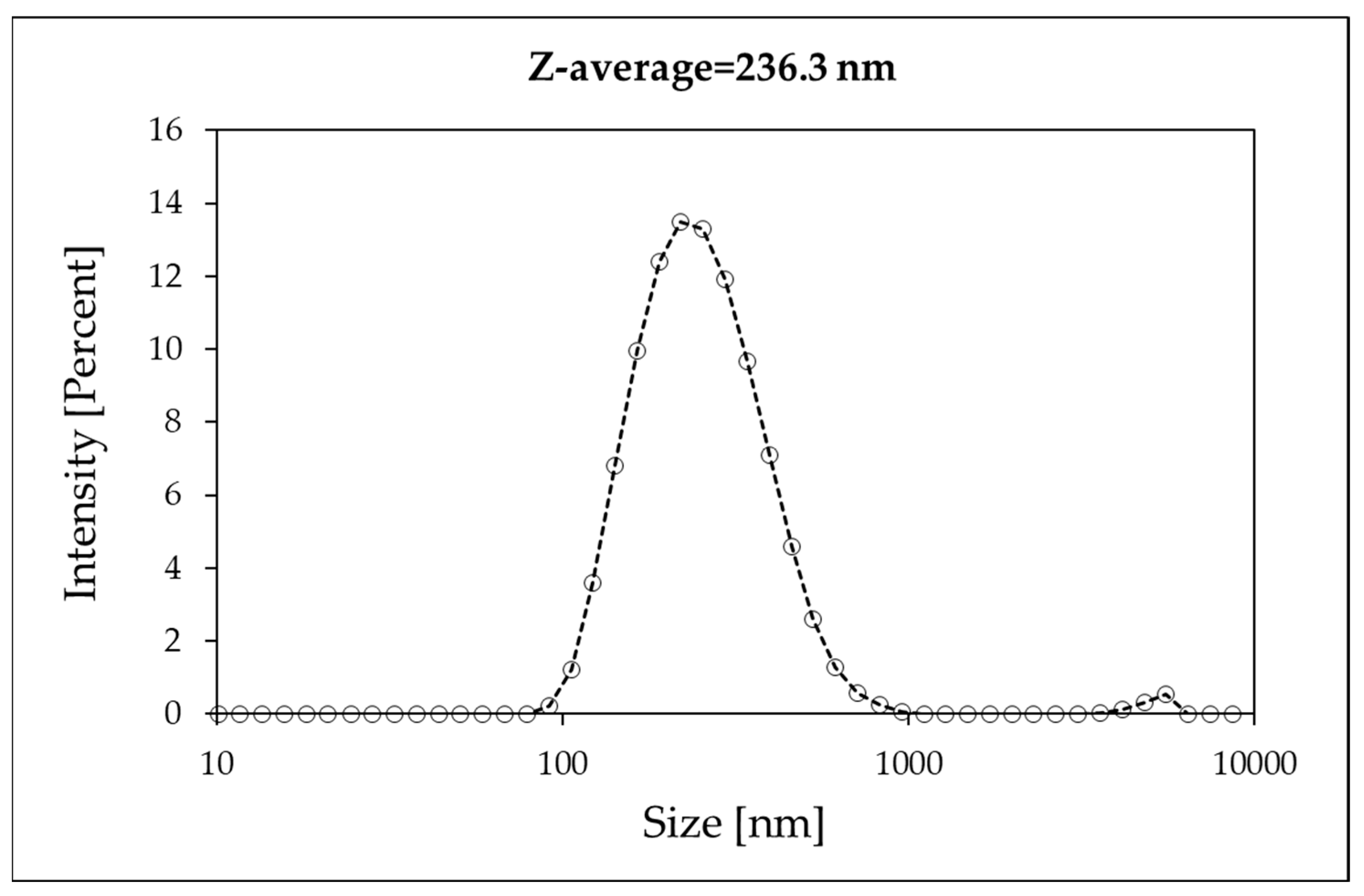
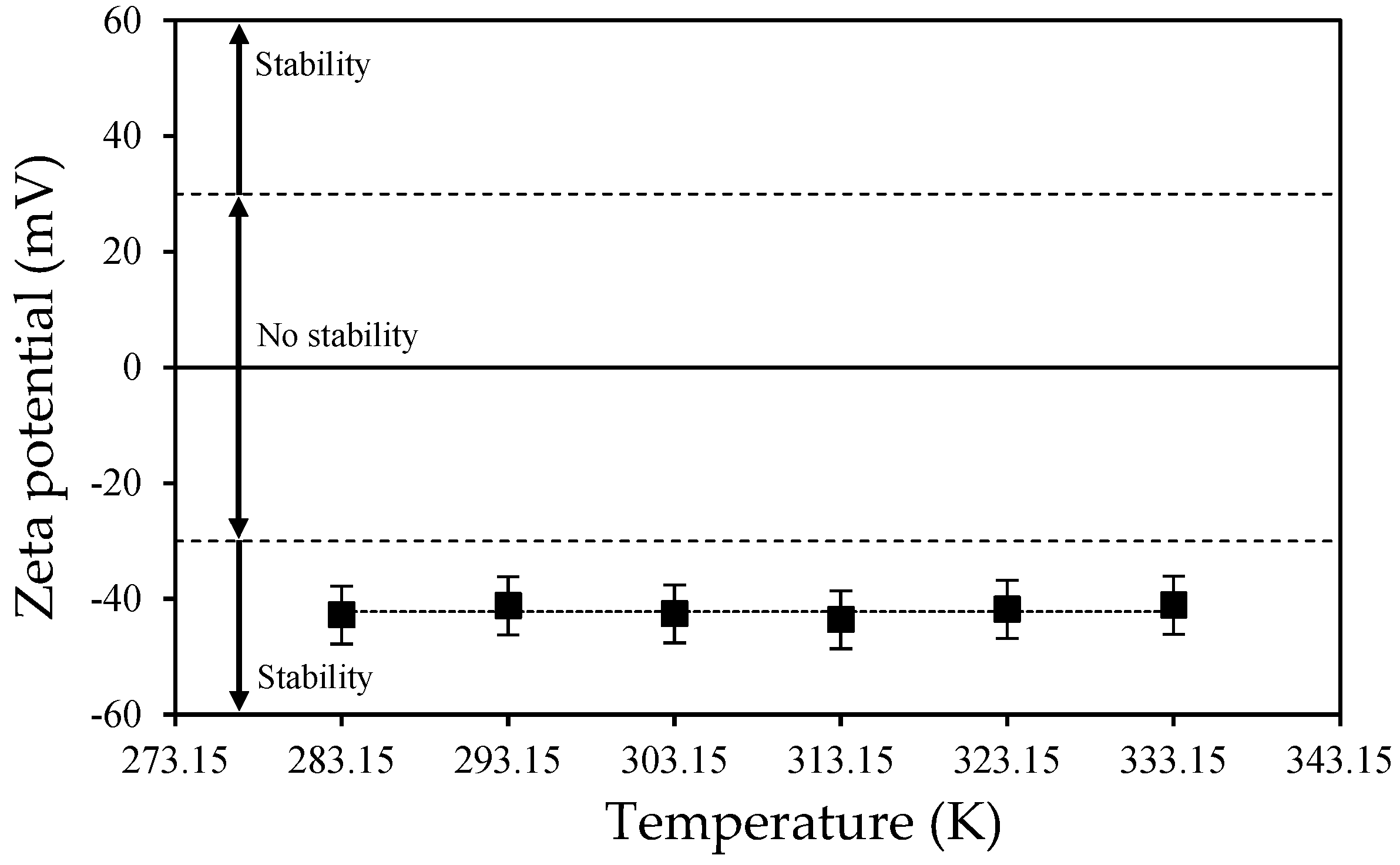
3.1. AFM and DLS Measurements
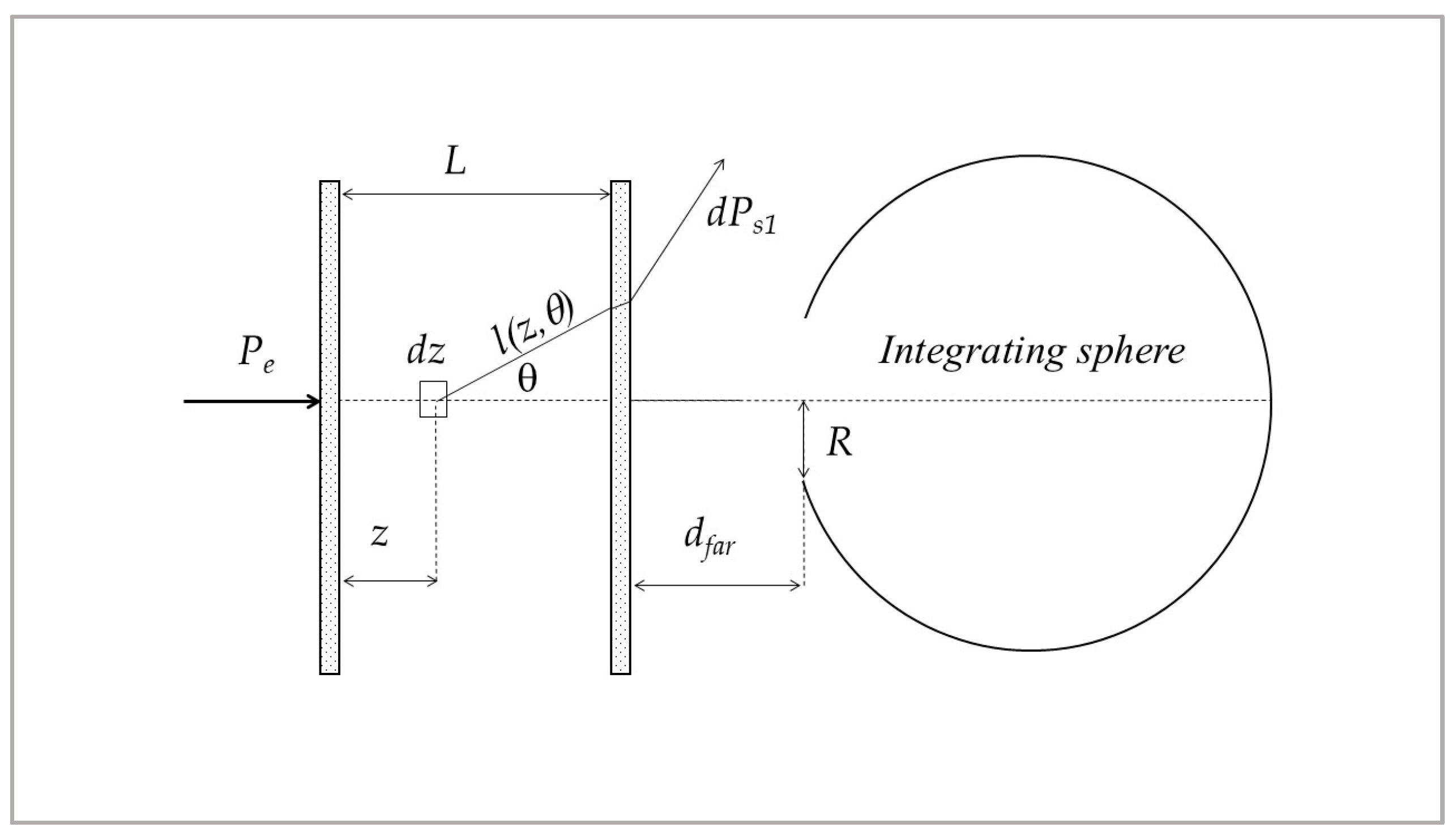
3.2. Monochromatic Measurements
3.3. Spectrophotometric Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S. Renewable energy for sustainable development. Renew. Energy 2022, 199, 1145–1152. [Google Scholar] [CrossRef]
- Hamzat, A.K.; Omisanya, M.I.; Sahin, A.Z.; Oyetunji, O.R.; Olaitan, N.A. Application of nanofluid in solar energy harvesting devices: A comprehensive review. Energy Convers. Manag. 2022, 266, 115790. [Google Scholar] [CrossRef]
- Goel, N.; Taylor, R.A.; Otanicar, T. A review of nanofluid-based direct absorption solar collectors: Design considerations and experiments with hybrid PV/Thermal and direct steam generation collectors. Renew. Energy 2020, 145, 903–913. [Google Scholar] [CrossRef]
- Sainz-Mañas, M.; Bataille, F.; Caliot, C.; Vossier, V.; Flamant, G. Direct absorption nanofluid-based solar collectors for low and medium temperatures. A review. Energy 2022, 260, 124916. [Google Scholar] [CrossRef]
- Sani, E.; Vallejo, J.P.; Cabaleiro, D.; Lugo, L. Functionalized graphene nanoplatelet-nanofluids for solar thermal collectors. Sol. Energy Mater. Sol. Cells 2018, 185, 205–209. [Google Scholar] [CrossRef]
- Bortolato, M.; Dugaria, S.; Agresti, F.; Barison, S.; Fedele, L.; Sani, E.; Del Col, D. Investigation of a single wall carbon nanohorn-based nanofluid in a full-scale direct absorption parabolic trough solar collector. Energy Convers. Manag. 2017, 150, 693–703. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Sani, E.; Żyła, G.; Lugo, L. Tailored silver/graphene nanoplatelet hybrid nanofluids for solar applications. J. Mol. Liq. 2019, 296, 112007. [Google Scholar] [CrossRef]
- Pavía, M.; Alajami, K.; Estellé, P.; Desforges, A.; Vigolo, B. A critical review on thermal conductivity enhancement of graphene-based nanofluids. Adv. Colloid Interface Sci. 2021, 294, 102452. [Google Scholar] [CrossRef]
- Aguilar, T.; Sani, E.; Mercatelli, L.; Carrillo-Berdugo, I.; Torres, E.; Navas, J. Exfoliated graphene oxide-based nanofluids with enhanced thermal and optical properties for solar collectors in concentrating solar power. J. Mol. Liq. 2020, 306, 112862. [Google Scholar] [CrossRef]
- Balaji, T.; Selvam, C.; Mohan Lal, D. A Review on Electronics Cooling using Nanofluids. In IOP Conference Series: Materials Science and Engineering, Proceedings of the International Conference on Advances in Renewable and Sustainable Energy Systems (ICARSES 2020) Chennai, India, 3–5 December 2020; IOP Publishing Ltd.: Bristol, UK, 2021; Volume 1130. [Google Scholar] [CrossRef]
- Balitskii, A.; Kindrachuk, M.; Volchenko, D.; Abramek, K.F.; Balitskii, O.; Skrypnyk, V.; Zhuravlev, D.; Bekish, I.; Ostashuk, M.; Kolesnikov, V. Hydrogen Containing Nanofluids in the Spark Engine’s Cylinder Head Cooling System. Energies 2022, 15, 59. [Google Scholar] [CrossRef]
- Hamze, S.; Cabaleiro, D.; Estellé, P. Graphene-based nanofluids: A comprehensive review about rheological behavior and dynamic viscosity. J. Mol. Liq. 2021, 325, 115207. [Google Scholar] [CrossRef]
- Zhang, T.; Zou, Q.; Cheng, Z.; Chen, Z.; Liu, Y.; Jiang, Z. Effect of particle concentration on the stability of water-based SiO2 nanofluid. Powder Technol. 2021, 379, 457–465. [Google Scholar] [CrossRef]
- Crouch, I.G.; Franks, G.V.; Tallon, C.; Thomas, S.; Naebe, M. Glasses and ceramics. In The Science of Armour Materials; Woodhead Publishing: Cambridgeshire, UK, 2017; pp. 331–393. [Google Scholar]
- Ni, D.; Cheng, Y.; Zhang, J.; Liu, J.X.; Zou, J.; Chen, B.; Wu, H.; Li, H.; Dong, S.; Han, J.; et al. Advances in ultra-high temperature ceramics, composites, and coatings. J. Adv. Ceram. 2022, 11, 1–56. [Google Scholar] [CrossRef]
- Sani, E.; Mercatelli, L.; Meucci, M.; Silvestroni, L.; Balbo, A.; Sciti, D. Process and composition dependence of optical properties of zirconium, hafnium and tantalum borides for solar receiver applications. Sol. Energy Mater. Sol. Cells 2016, 155, 368–377. [Google Scholar] [CrossRef]
- Song, Z.Z.; Wu, Z.Y.; Mo, Z.Y. Transmission Performance of Water-based Nano Fluid Based on Computational Fluid Dynamics. In Advanced Materials Research; Trans Tech Publications Ltd.: Baech, Switzerland, 2015; Volume 1095, pp. 58–62. [Google Scholar]
- Vallejo, J.P.; Żyła, G.; Ansia, L.; Fal, J.; Traciak, J.; Lugo, L. Thermophysical, rheological and electrical properties of mono and hybrid TiB2/B4C nanofluids based on a propylene glycol: Water mixture. Powder Technol. 2022, 395, 391–399. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Ansia, L.; Calvino, U.; Marcos, M.A.; Fernández-Seara, J.; Lugo, L. Convection behaviour of mono and hybrid nanofluids containing B4C and TiB2 nanoparticles. Int. J. Therm. Sci. 2023, 189, 108268. [Google Scholar] [CrossRef]
- Sani, E.; Martina, M.R.; Vallejo, J.P.; Lugo, L. Hybrid B4C/TiCN aqueous nanofluids for solar absorber applications. Sol. Energy Mater. Sol. Cells 2023, 254, 112280. [Google Scholar] [CrossRef]
- Di Ninni, P.; Martelli, F.; Zaccanti, G. The use of India ink in tissue-simulating phantoms. Opt. Express 2010, 18, 26854–26865. [Google Scholar] [CrossRef] [PubMed]
- Mercatelli, L.; Sani, E.; Giannini, A.; Di Ninni, P.; Martelli, F.; Zaccanti, G. Carbon nanohorn-based nanofluids: Characterization of the spectral scattering albedo. Nanoscale Res. Lett. 2012, 7, 96. [Google Scholar] [CrossRef]
- Mehrali, M.; Sadeghinezhad, E.; Latibari, S.T.; Kazi, S.N.; Mehrali, M.; Zubir, M.N.B.M.; Metselaar, H.S.C. Investigation of thermal conductivity and rheological properties of nanofluids containing graphene nanoplatelets. Nanoscale Res. Lett. 2014, 9, 15. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.P.; Mercatelli, L.; Martina, M.R.; Di Rosa, D.; Dell’Oro, A.; Lugo, L.; Sani, E. Comparative study of different functionalized graphene-nanoplatelet aqueous nanofluids for solar energy applications. Renew. Energy 2019, 141, 791–801. [Google Scholar] [CrossRef]
- Ghadimi, A.; Saidur, R.; Metselaar, H.S.C. A review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transf. 2011, 54, 4051–4068. [Google Scholar] [CrossRef]
- Jianguang, J.; Zhaoxu, Z.; Hao, C.; Hongyu, P.; Long, J.; Wen-Hao, S.; Qiang, C.; Yingwen, T.; Jianming, P.; Kai, Y. Full life circle of micro-nano bubbles: Generation, characterization and applications. Chem. Eng. J. 2023, 471, 144621. [Google Scholar] [CrossRef]
- Martelli, F.; Bassani, M.; Alianelli, L.; Zangheri, L.; Zaccanti, G. Accuracy of the diffusion equation to describe photon migration through an infinitemedium: Numerical and experimental investigation. Phys. Med. Biol. 2000, 45, 1359–1373. [Google Scholar] [CrossRef]
- Zaccanti, G.; Del Bianco, S.; Martelli, F. Measurements of optical properties of high density media. Appl. Opt. 2003, 42, 4023–4030. [Google Scholar] [CrossRef]
- Martelli, F.; Zaccanti, G. Calibration of scattering and absorption properties of a liquid diffusive medium at NIR wavelengths. CW method. Opt. Exp. 2007, 15, 486–500. [Google Scholar] [CrossRef]
- Mercatelli, L.; Sani, E.; Zaccanti, G.; Martelli, F.; Di Ninni, P.; Barison, S.; Pagura, C.; Agresti, F.; Jafrancesco, D. Absorption and scattering properties of carbon nanohorn-based nanofluids for direct sunlight absorbers. Nanoscale Res. Lett. 2011, 6, 282. [Google Scholar] [CrossRef]
- Plass, G. Mie Scattering and Absorption Cross Sections for Absorbing Particles. Appl. Opt. 1966, 5, 279–285. [Google Scholar] [CrossRef]
- Lahiri, A. Basic Optics Principles and Concepts; Elsevier: Amsterdam, The Netherlands, 2016; eBook; ISBN 9780128093078. [Google Scholar]

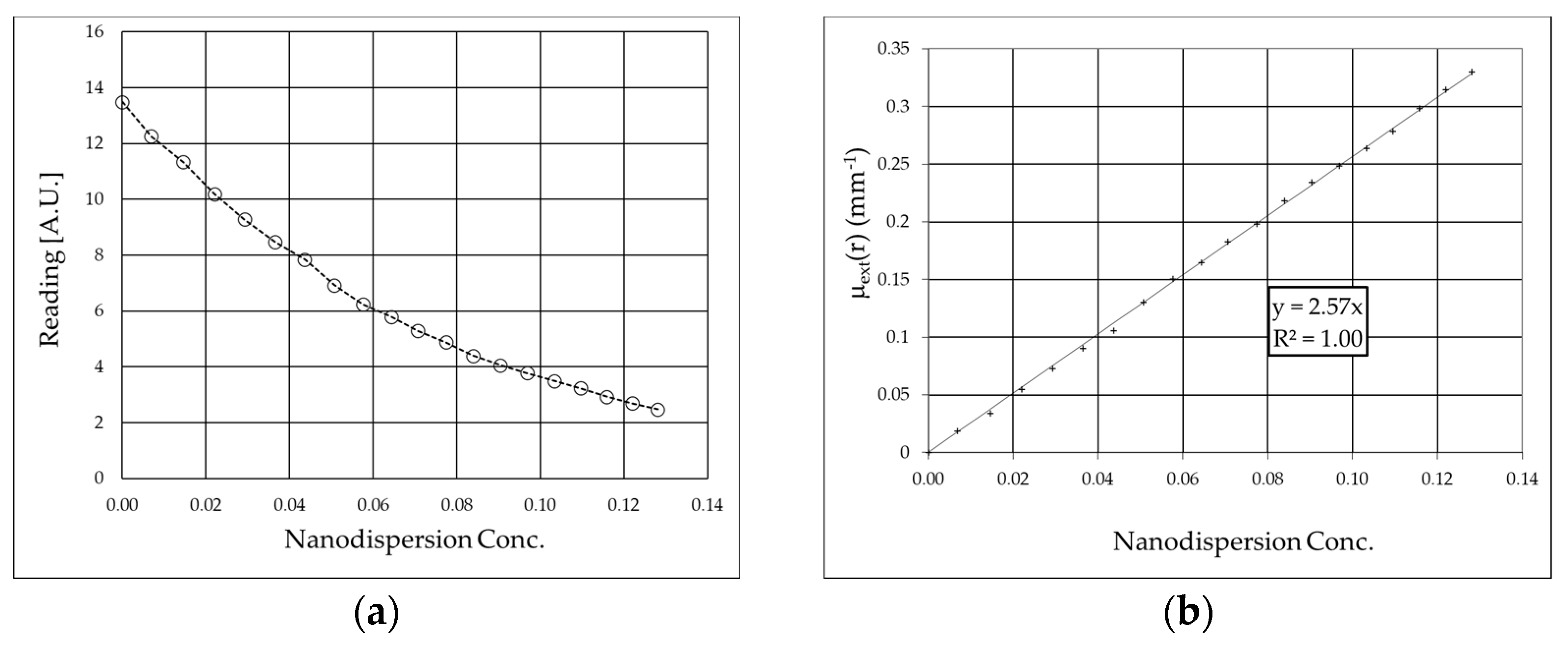
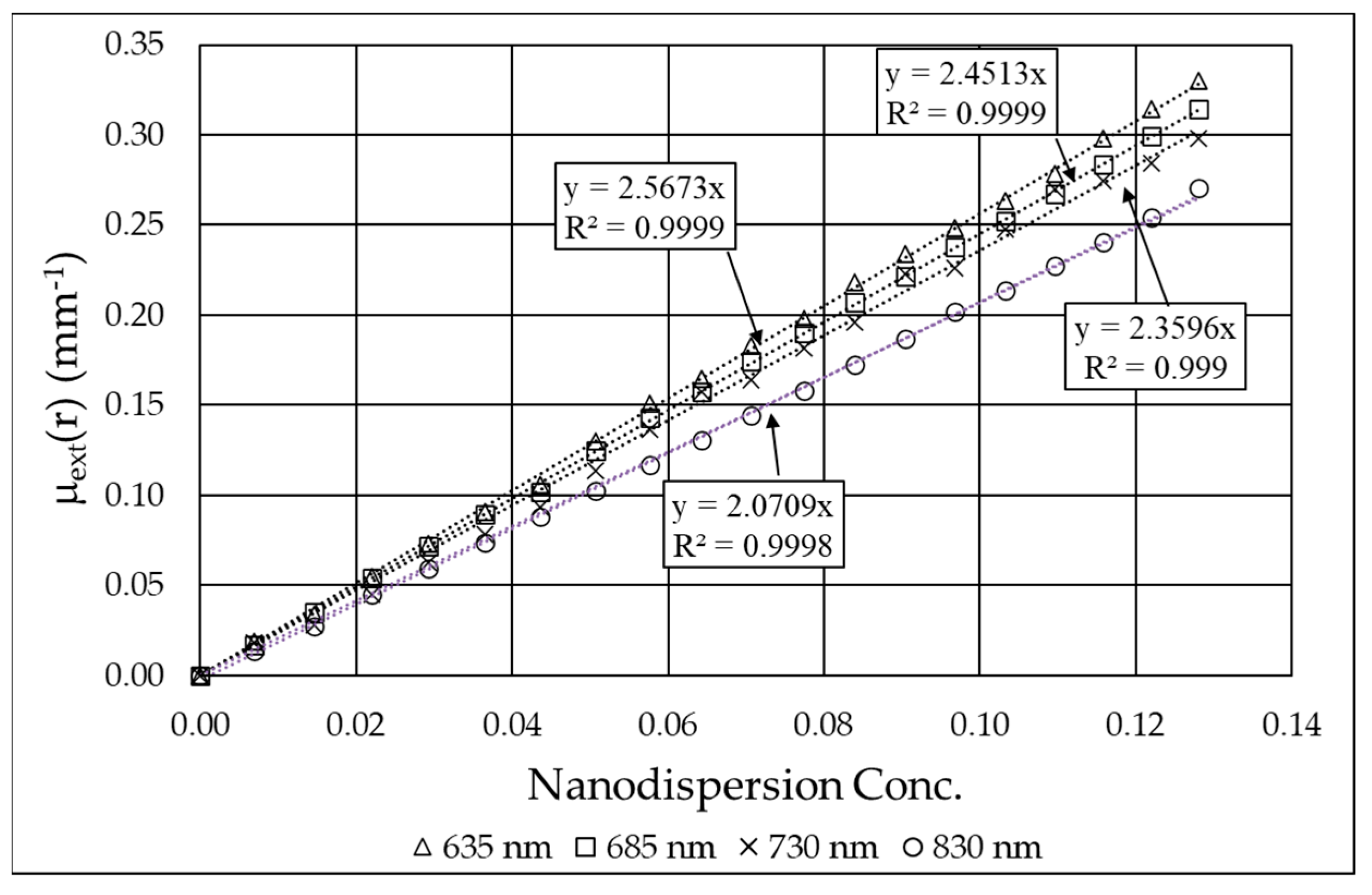
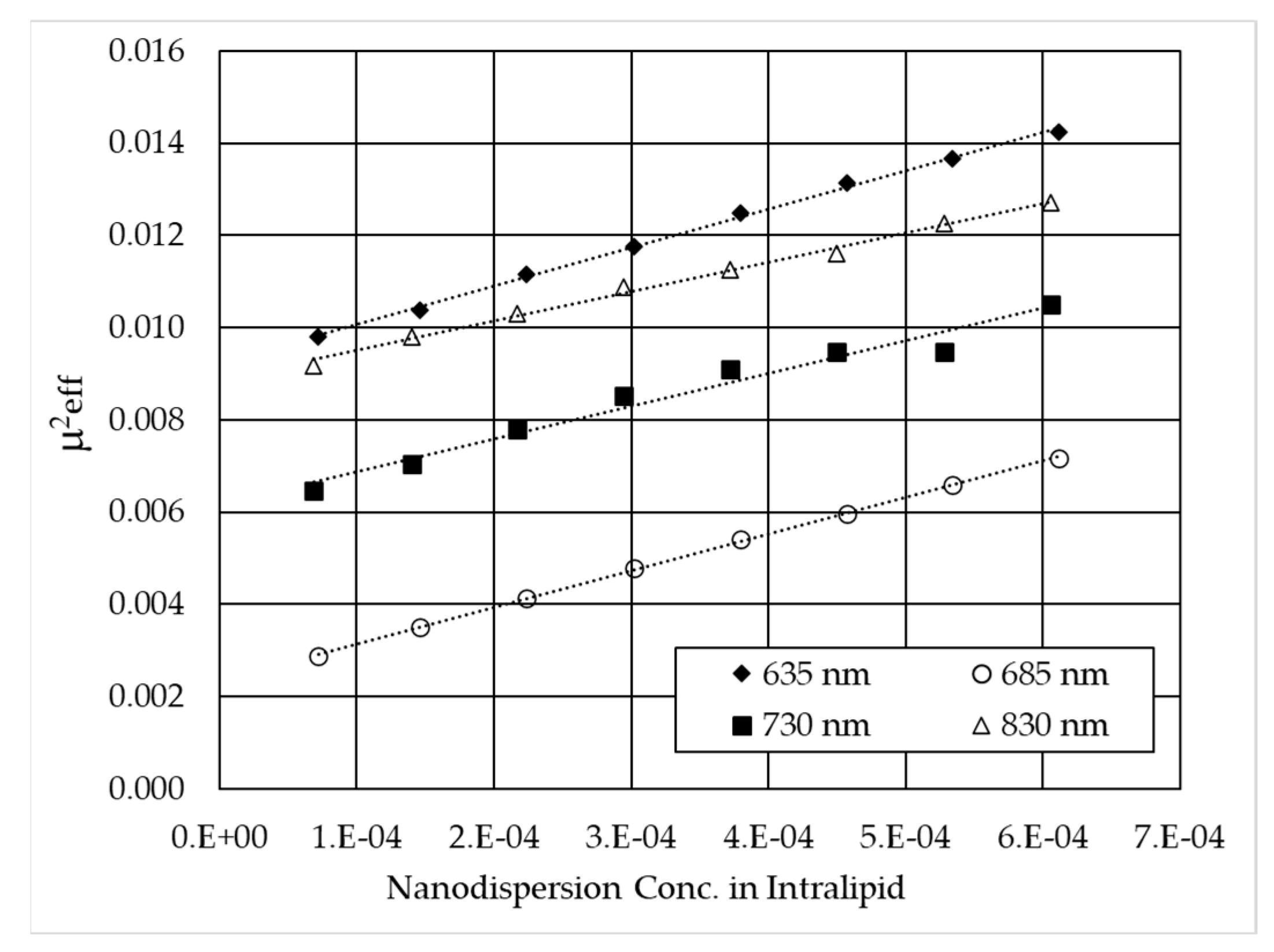
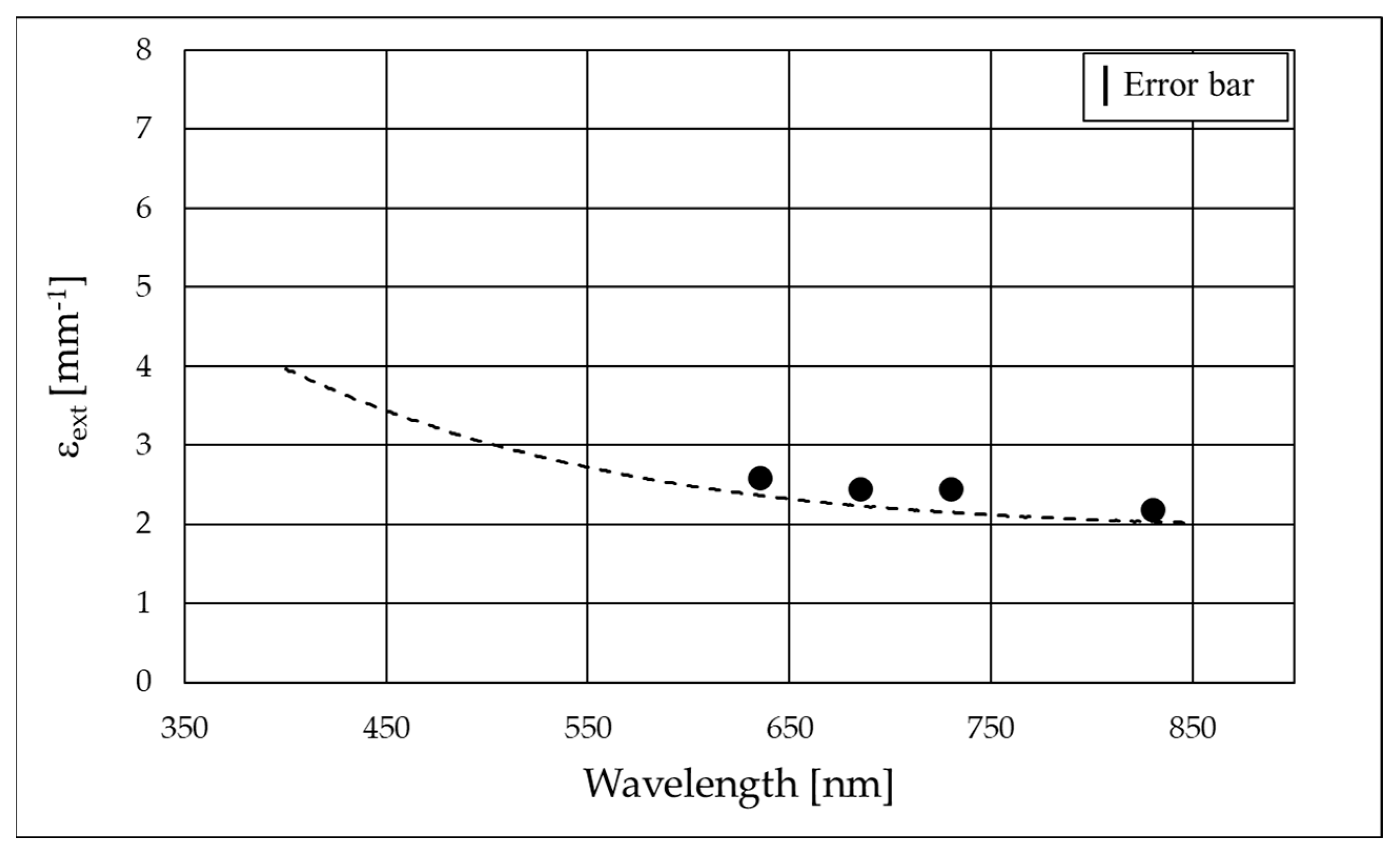
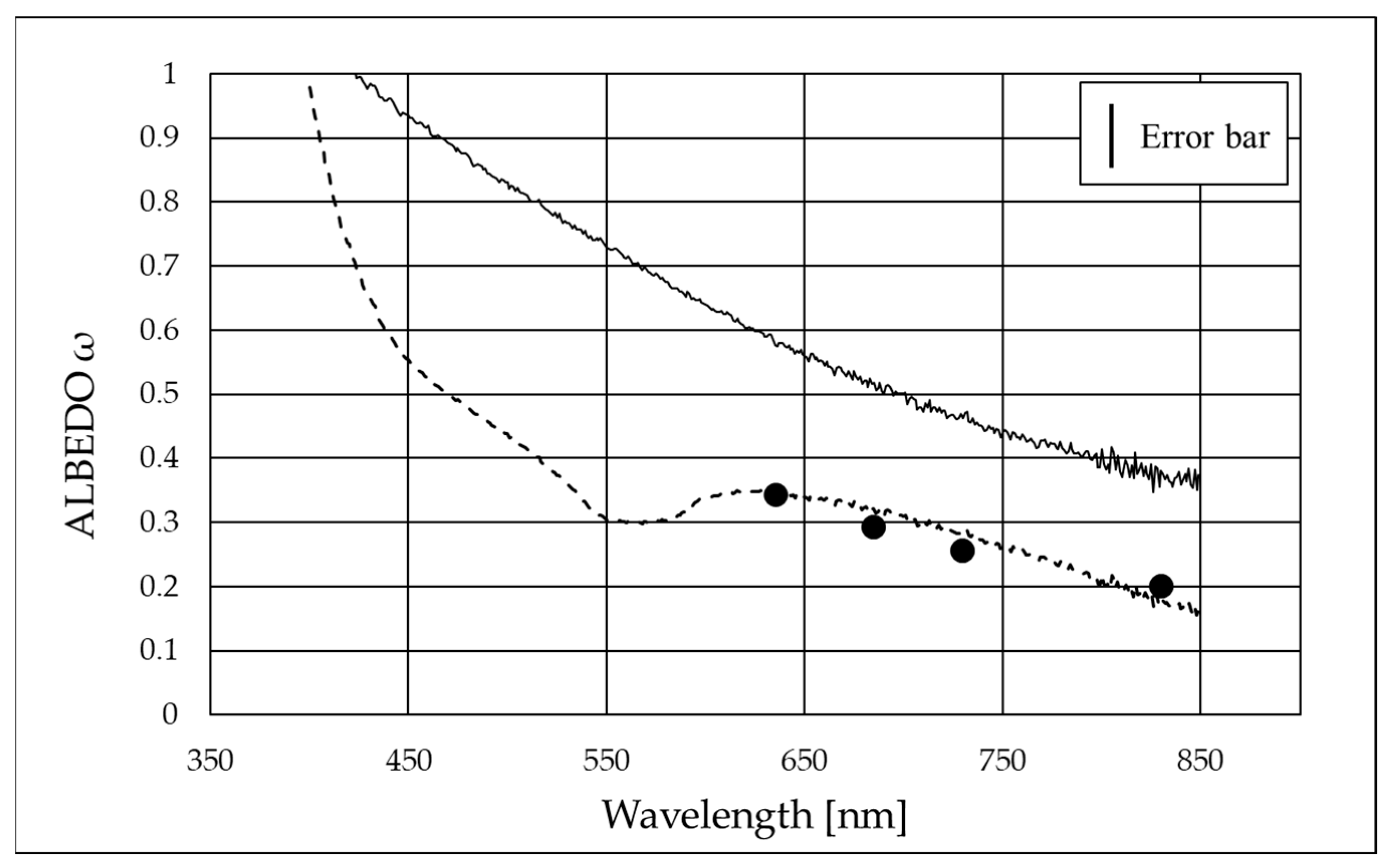
| Laser Wavelength [nm] | Extinction Coefficient of B4C (εextB4C) [mm−1] | Absorption Coefficient of B4C (εaB4C) [mm−1] | Scattering Coefficient of B4C (εsB4C) [mm−1] | Albedo of B4C (ωB4C) |
|---|---|---|---|---|
| 635 | 2.57 ± 0.02 | 1.69 ± 0.12 | 0.9 ± 0.1 | 0.34 ± 0.06 |
| 685 | 2.45 ± 0.02 | 1.73 ± 0.12 | 0.7 ± 0.1 | 0.29 ± 0.06 |
| 730 | 2.36 ± 0.02 | 1.75 ± 0.12 | 0.6 ± 0.1 | 0.26 ± 0.06 |
| 830 | 2.07 ± 0.02 | 1.65 ± 0.12 | 0.4 ± 0.1 | 0.20 ± 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercatelli, L.; Martina, M.R.; Vallejo, J.P.; Lugo, L.; Sani, E. Comparison of Two Measurement Methods for Scattering and Absorption Coefficients in Boron Carbide Nanodispersions. Nanomaterials 2025, 15, 1598. https://doi.org/10.3390/nano15201598
Mercatelli L, Martina MR, Vallejo JP, Lugo L, Sani E. Comparison of Two Measurement Methods for Scattering and Absorption Coefficients in Boron Carbide Nanodispersions. Nanomaterials. 2025; 15(20):1598. https://doi.org/10.3390/nano15201598
Chicago/Turabian StyleMercatelli, Luca, Maria Raffaella Martina, Javier P. Vallejo, Luis Lugo, and Elisa Sani. 2025. "Comparison of Two Measurement Methods for Scattering and Absorption Coefficients in Boron Carbide Nanodispersions" Nanomaterials 15, no. 20: 1598. https://doi.org/10.3390/nano15201598
APA StyleMercatelli, L., Martina, M. R., Vallejo, J. P., Lugo, L., & Sani, E. (2025). Comparison of Two Measurement Methods for Scattering and Absorption Coefficients in Boron Carbide Nanodispersions. Nanomaterials, 15(20), 1598. https://doi.org/10.3390/nano15201598








