Sensitive Detection of Multi-Point Temperature Based on FMCW Interferometry and DSP Algorithm
Abstract
1. Introduction
2. Multi-Point Location and Sensitization Principle
2.1. Location of Sensors
2.2. Modulated Vernier Sensitization Principle
3. Experiments and Discussions
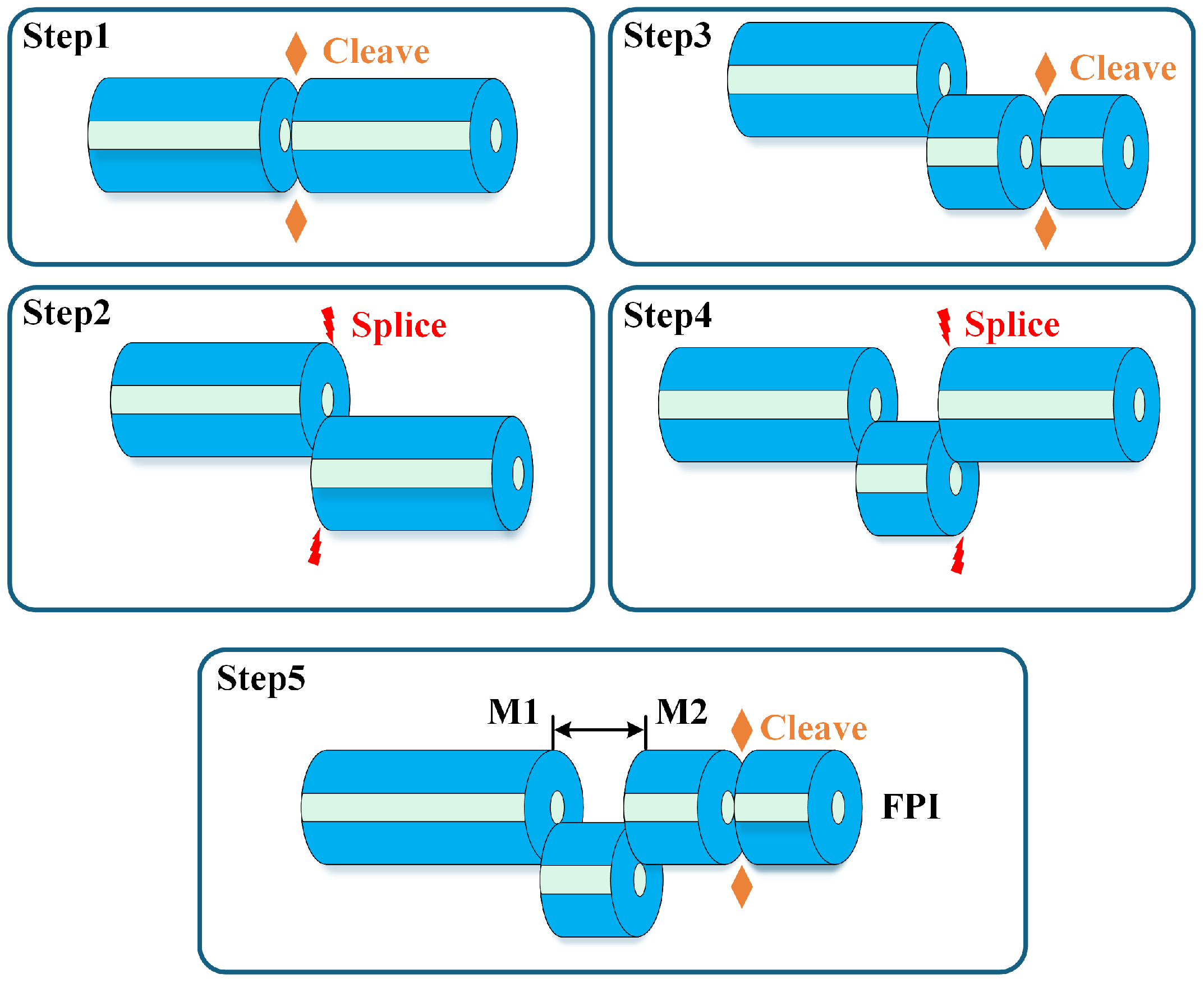
3.1. Fabrication of Sensing Probes
3.2. Experimental Setup and Operation Procedure
- 1.
- The raw signals from the main and additional interferometers are labeled as and , respectively. The instantaneous frequency f is obtained by applying the Hilbert transform and arctangent operation to .
- 2.
- The independent variable t in is replaced by the instantaneous frequency f, resulting in a new measurement signal .
- 3.
- The nonlinear instantaneous frequency f is rearranged into a linearized version . A one-dimensional linear interpolation and resampling of against yields the corrected signal , thereby compensating for the nonlinear frequency sweep of the laser.
- 4.
- A Fast Fourier Transform (FFT) is applied to to obtain the corrected spatial domain information, enabling the localization of the FPI sensor array.
- 5.
- A bandpass filter is applied to the reflection peaks of the fiber micro-cavities, followed by an Inverse FFT (IFFT) to retrieve the wavelength-domain (time-domain) information. Under initial conditions, the envelope of the wavelength-domain signal is extracted to obtain the SIS of the fiber micro-cavity.
- 6.
- The SIS is modulated with the modulation function from Equation (7). An FFT is then applied to the modulated result, and the first peak is filtered and extracted to serve as the ARS for the FPI.
- 7.
- The software-generated ARS is multiplied with the experimentally acquired SIS. Subsequent spectral analysis is performed to select the envelope term, yielding the modulated Vernier envelope interference spectrum.
- 8.
- Finally, the same procedure is iterated for each FPI micro-cavity to achieve quasi-distributed and sensitivity-enhanced seawater temperature detection.
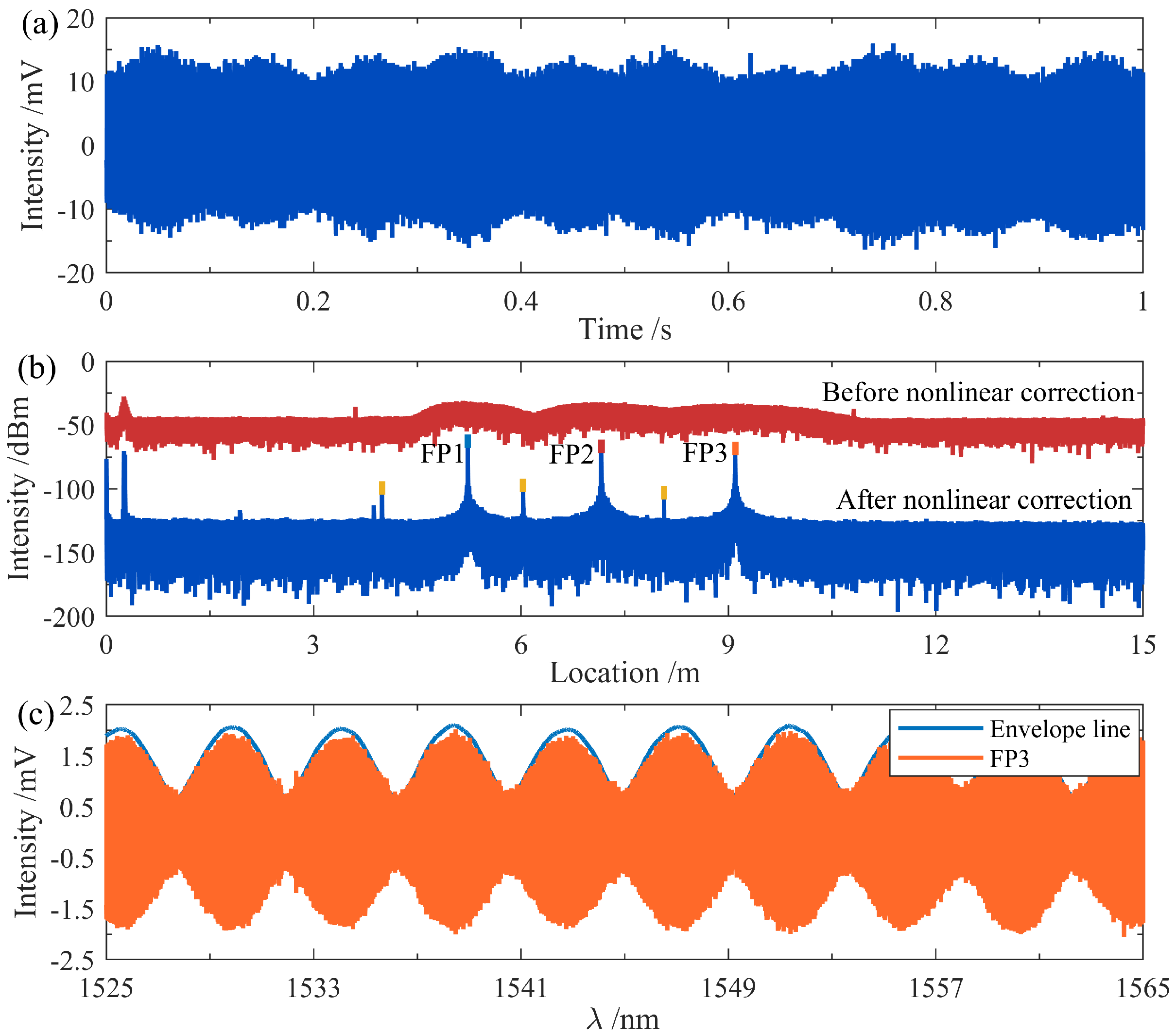
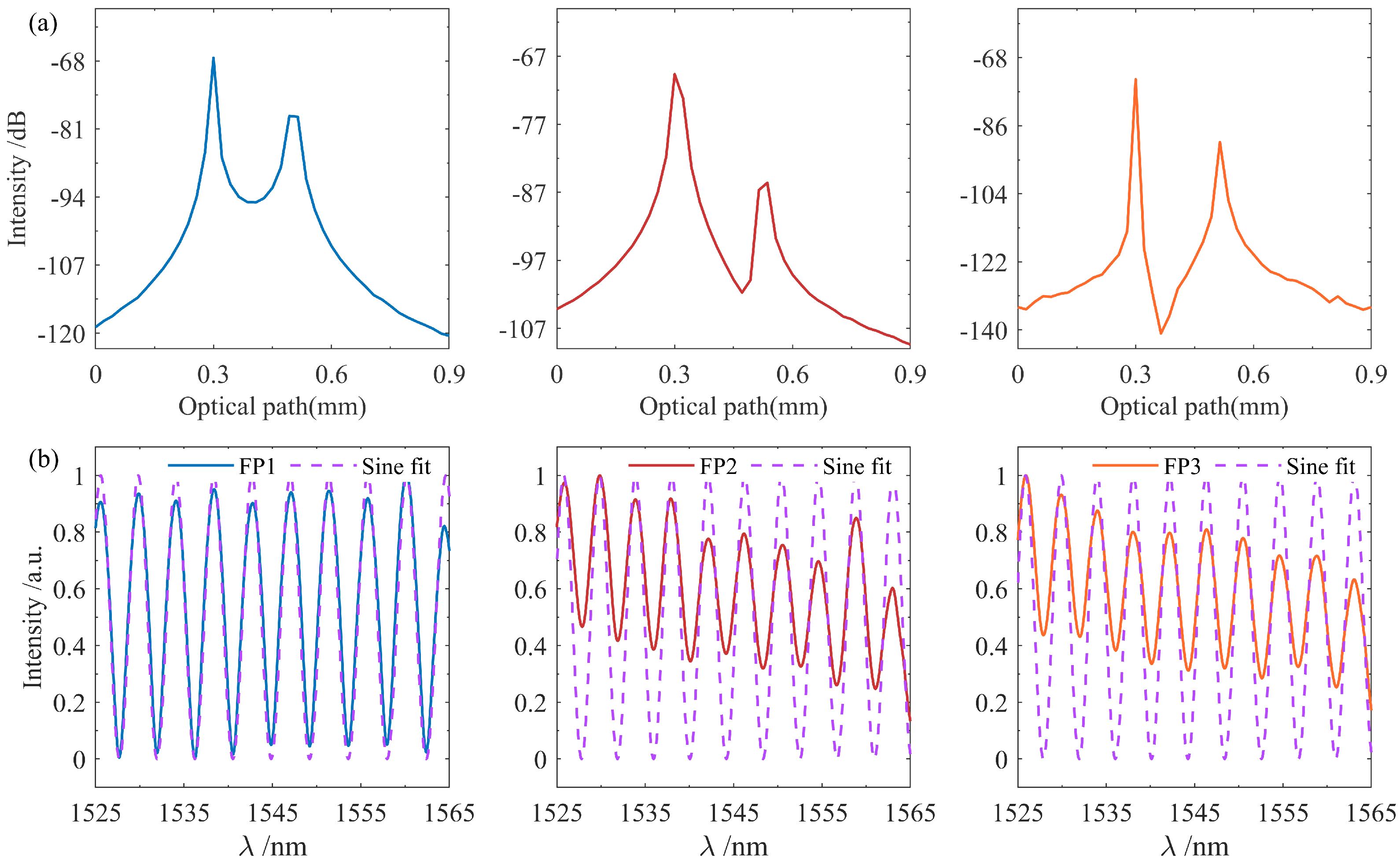
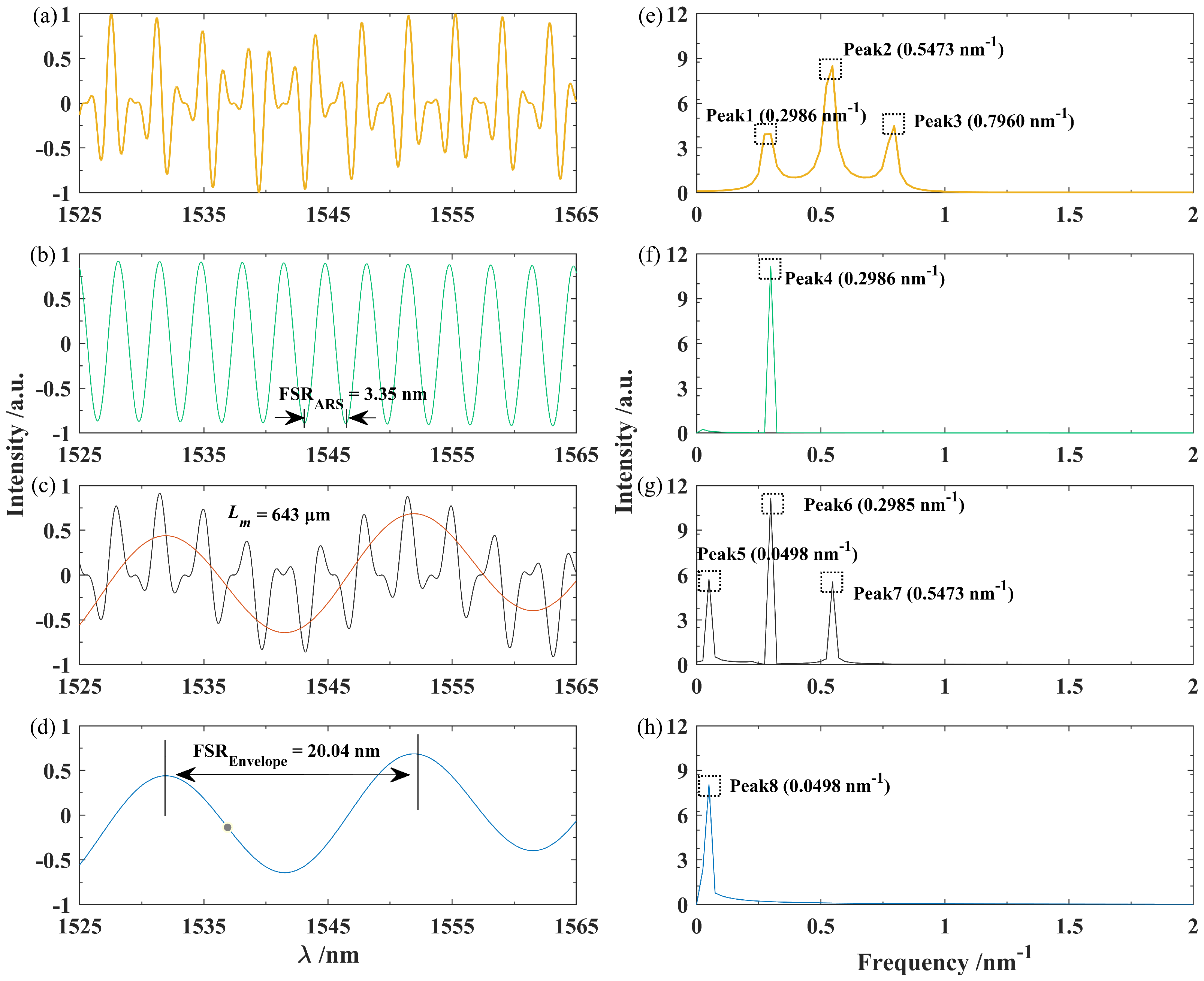
3.3. Demodulation of Sensing Signal
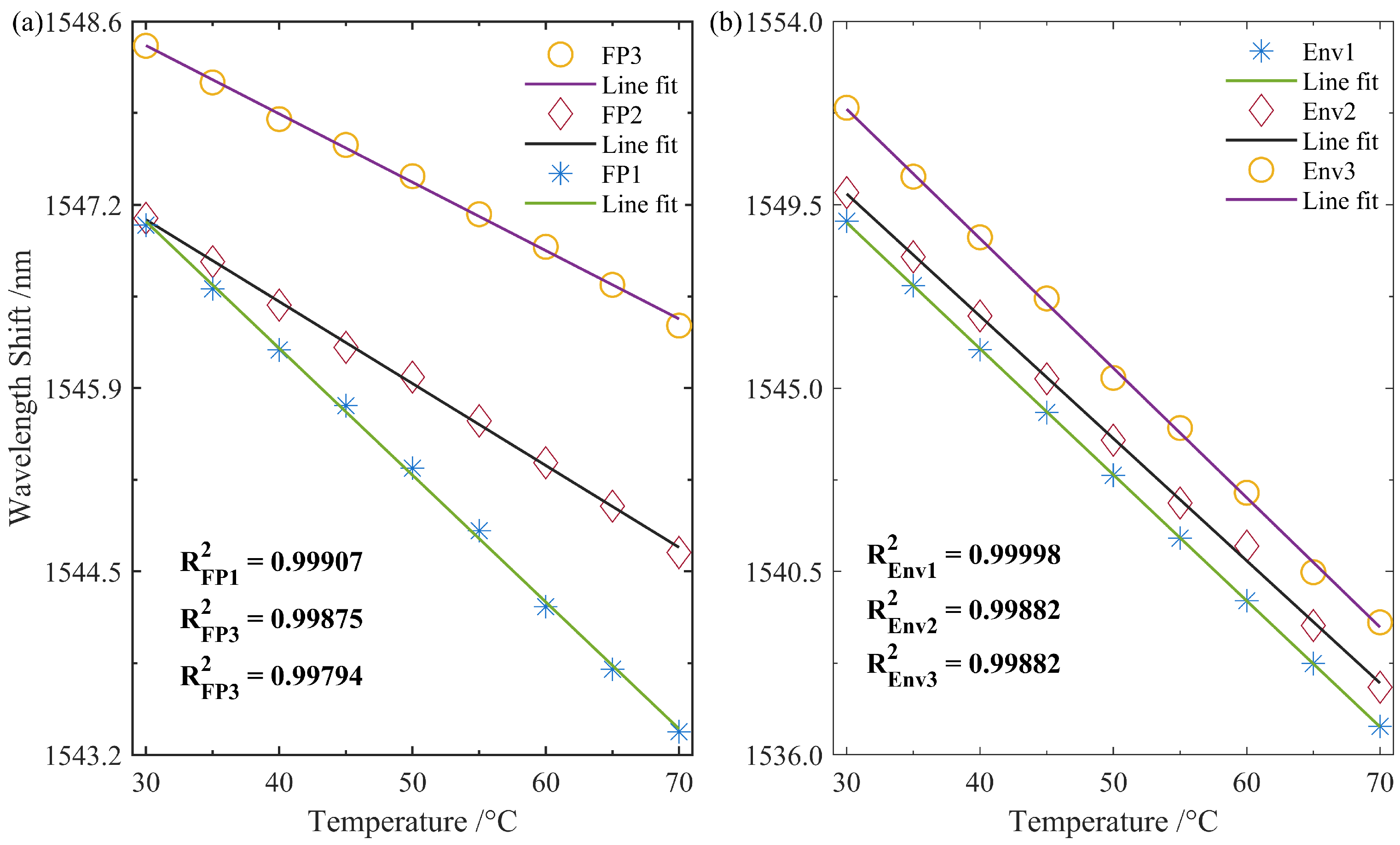
3.4. Sensitization of Temperature Response
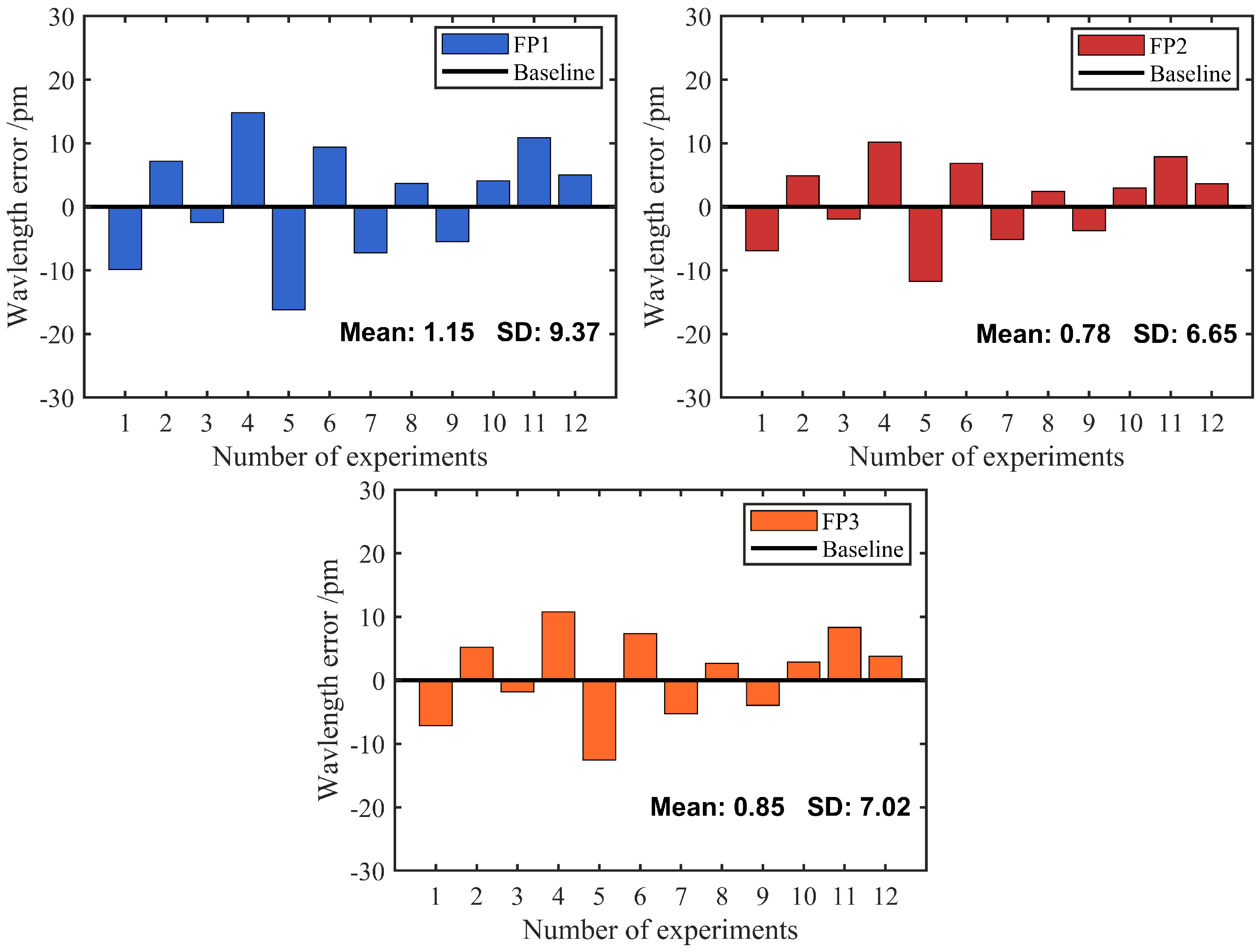
3.5. Stability of System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FMCW | Frequency-modulated continuous wave |
| DSP | Digital signal processing |
| FPI | Fabry–Perot interferometer |
| SIS | Sensing interference spectrum |
| ARS | Artificial reference spectrum |
| EIS | Envelope interference spectrum |
References
- Roemmich, D.; Johnson, G.; Riser, S.; Davis, R.; Gilson, J.; Owens, W.B.; Garzoli, S.; Schmid, C.; Ignaszewski, M. The Argo Program: Observing the Global Oceans with Profiling Floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A Review of Global Ocean Temperature Observations: Implications for Ocean Heat Content Estimates and Climate Change. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Donlon, C.; Robinson, I.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Arino, O.; Gentemann, C.; May, D.; LeBorgne, P.; Piollé, J.; et al. The Global Ocean Data Assimilation Experiment High-Resolution Sea Surface Temperature Pilot Project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1214. [Google Scholar] [CrossRef]
- Xue, D.; Zhang, H.; Wang, S.; Li, H.; Jiang, J.; Jia, D.; Liu, T. High Sensitivity Composite F-P Cavity Fiber Optic Sensor Based on MEMS for Temperature and Salinity Measurement of Seawater. Opt. Express 2023, 31, 33241. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-C.; Zheng, H.-N.; Li, S.-Y.; Wang, Y.; Tong, R.-J. An SPR-MZ Interference-Based Fiber-Optic Sensor for Dual-Parameter Measurement of Seawater Temperature and Salinity. IEEE Sens. J. 2025, 25, 27314–27321. [Google Scholar] [CrossRef]
- Ma, Y.; Han, B.; Liu, R.; Zhao, J.; Zhao, Y. Dual-Channel Mach-Zehnder Interferometer Based on Femtosecond Laser Writing Waveguide for Seawater Temperature and Salinity Sensing. J. Light. Technol. 2024, 42, 6108–6114. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Zhao, Q. High Sensitivity Seawater Temperature Sensor Based on No-Core Optical Fiber. Opt. Fiber Technol. 2020, 54, 102115. [Google Scholar] [CrossRef]
- Liang, H.; Wang, J.; Zhang, L.; Liu, J.; Wang, S. Review of Optical Fiber Sensors for Temperature, Salinity, and Pressure Sensing and Measurement in Seawater. Sensors 2022, 22, 5363. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, Y.; Peng, Y.; Zhao, J.-C. High-Sensitivity Optical Fiber SPR Sensor with Cascaded Biconical Fiber and Hetero-Core Structure for Simultaneous Measurement of Seawater Salinity and Temperature. Opt. Laser Technol. 2024, 170, 110275. [Google Scholar] [CrossRef]
- Zhu, Y.; Sheng, Q.; Han, M. Effect of Laser Polarization on Fiber Bragg Grating Fabry-Perot Interferometer for Ultrasound Detection. IEEE Photonics J. 2020, 12, 1–8. [Google Scholar] [CrossRef]
- Xia, Q.; Zhang, X.; Zhang, K.; Wang, H.; Yuan, L.; Yuan, T. Research on Fiber Bragg Grating Fabry-Perots Bending Sensor Based on Principal Component Analysis. Opt. Express 2025, 33, 8014. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, D.; Xing, M.; Yan, C.; Liu, B. Simultaneous Measurement of Temperature and Pressure Sensing Technology Based on Double Cavity Matching in Batteries. Opt. Fiber Technol. 2024, 87, 103954. [Google Scholar] [CrossRef]
- Zhu, T.; Ke, T.; Rao, Y.; Chiang, K.S. Fabry–Perot Optical Fiber Tip Sensor for High Temperature Measurement. Opt. Commun. 2010, 283, 3683–3685. [Google Scholar] [CrossRef]
- Ding, Z.; Guo, H.; Liu, K.; Hua, P.; Zhang, T.; Li, S.; Liu, J.; Jiang, J.; Liu, T. Advances in Distributed Optical Fiber Sensors Based on Optical Frequency-Domain Reflectometry: A Review. IEEE Sens. J. 2023, 23, 26925–26941. [Google Scholar] [CrossRef]
- Chen, T.; Xu, Z.; Tu, L.; Wang, L.; Tang, M. Improving OFDR Sensing Performance Based on SEFR in Both Reference and Measurement Stages. Opt. Lett. 2024, 49, 7134. [Google Scholar] [CrossRef]
- Liang, C.; Zhou, X.; Wang, Y.; Gao, Y.; Zhang, H.; Jin, B.; Bai, Q. Sensing Distance Enhancement in OFDR Using Multi-Arms Interferometer Phase Noise Compensation Method. J. Light. Technol. 2025, 43, 2371–2378. [Google Scholar] [CrossRef]
- Li, P.; Shang, C.; Tong, Z.; Wang, H. Temperature Sensitivity Enhancement of OFDR Fibers Based on PDMS/Glycerol Films. Opt. Mater. (Amst.) 2025, 163, 116940. [Google Scholar] [CrossRef]
- Kong, D.; Chen, C.; Zhao, X.; Tao, Y.; Wan, J.; Wen, Y.; Zhang, X.; Yuan, S.; Liu, X. Distributed Temperature Sensing on Silicon-on-Insulator Chip by Optical Frequency Domain Reflectometry. Opt. Express 2024, 32, 25519. [Google Scholar] [CrossRef]
- Froggatt, M.E.; Gifford, D.K.; Kreger, S.; Wolfe, M.; Soller, B.J. Characterization of Polarization-Maintaining Fiber Using High-Sensitivity Optical-Frequency-Domain Reflectometry. J. Light. Technol. 2006, 24, 4149–4154. [Google Scholar] [CrossRef]
- Li, J.; Gan, J.; Zhang, Z.; Heng, X.; Yang, C.; Qian, Q.; Xu, S.; Yang, Z. High Spatial Resolution Distributed Fiber Strain Sensor Based on Phase-OFDR. Opt. Express 2017, 25, 27913. [Google Scholar] [CrossRef]
- Xu, J.-J.; Tang, C.-S.; Yang, Y.; Zeng, Z.-J.; Li, L.; Cheng, Q.; Zhang, X.-Y.; Shi, B. Monitoring Soil Cracking Using OFDR-Based Distributed Temperature Sensing Framework. Geoderma 2024, 452, 117090. [Google Scholar] [CrossRef]
- Sun, Z.; Xiao, X.; Zhao, W.; Ai, K.; Lv, Y.; Liu, H.; Sun, Q.; Yan, Z. High-Precision Distributed Temperature Sensor Based on Phase-Shifted FBGs Interrogated by OFDR. J. Light. Technol. 2025, 43, 2357–2362. [Google Scholar] [CrossRef]
- Zhu, Z.; Ba, D.; Liu, L.; Qiu, L.; Yang, S.; Dong, Y. Temperature-Compensated Multi-Point Refractive Index Sensing Based on a Cascaded Fabry-Perot Cavity and FMCW Interferometry. Opt. Express 2021, 29, 19034. [Google Scholar] [CrossRef]
- Zhu, Z.; Ba, D.; Liu, L.; Qiu, L.; Yang, S.; Dong, Y. Multiplexing of Fabry-Pérot Sensor by Frequency Modulated Continuous Wave Interferometry for Quais-Distributed Sensing Application. J. Light. Technol. 2021, 39, 4529–4534. [Google Scholar] [CrossRef]
- Feng, Z.; Tang, Y.; Cheng, Y.; Sima, C.; Yuan, L. High-Spatial-Resolution Quasi-Distributed Fiber Sensing Technique Based on Cascaded FP Cavities and DSP Algorithm. J. Light. Technol. 2024, 42, 2186–2192. [Google Scholar] [CrossRef]
- Shao, L.-Y.; Luo, Y.; Zhang, Z.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Sensitivity-Enhanced Temperature Sensor with Cascaded Fiber Optic Sagnac Interferometers Based on Vernier-Effect. Opt. Commun. 2015, 336, 73–76. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, D.; Xu, K.; Zhang, N.; Liu, S.; Zhao, J.; Luo, Q.; Snyman, L.W.; Swart, J.W. Optoelectronic Properties Analysis of Silicon Light-Emitting Diode Monolithically Integrated in Standard CMOS IC*. Chin. Phys. B 2019, 28, 107801. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Chen, Q.; Li, B.; Li, S. Experimental Study on Dual-Parameter Sensing Based on Cascaded Sagnac Interferometers With Two PANDA Fibers. J. Light. Technol. 2022, 40, 3090–3097. [Google Scholar] [CrossRef]
- Yin, G.; Jiang, R.; Zhu, T. In-Fiber Auxiliary Interferometer to Compensate Laser Nonlinear Tuning in Simplified OFDR. J. Light. Technol. 2022, 40, 837–843. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Mu, X.; Li, Y.; Zhang, Y.; Mo, C.; Xia, H.; Huang, Z. Sensitivity-Enhanced Optical Fiber Sensor Based on the Vernier Effect for Detection of Ammonia in Water. Opt. Express 2024, 32, 36686. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, W.; Li, J.; Lin, C.; Chen, Z.; Zhang, M.; Huang, S.; Lu, D.; Wan, M.; Qiu, X. Signal Processing Assisted Vernier Effect in a Single Interferometer for Sensitivity Magnification. Opt. Express 2021, 29, 11570. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Lyu, R.; Zhao, Y.; Peng, Y.; Lin, Z.; Liu, R. Research on the Distributed Measurement Method of Ocean Optical Fiber Sensor Based on Interferometer. IEEE/CAA J. Autom. Sin. 2023, 49, 1941–1950. [Google Scholar] [CrossRef]
- Ozgur, F.O.; Çimen, D.; Denizli, A.; Bereli, N. Surface Plasmon Resonance Based Sensor for Amaranth Detection With Molecularly Imprinted Nanoparticles. Photonic Sens. 2023, 13, 230201. [Google Scholar] [CrossRef]


| Parameter | FP1 | FP2 | FP3 | Env1 | Env2 | Env3 |
|---|---|---|---|---|---|---|
| Range | – | |||||
| FSR (nm) | 4.34 | 4.18 | 4.12 | 20.10 | 20.00 | 20.04 |
| Modulation length () | 643 | 643 | 643 | / | / | / |
| R2 | 0.99907 | 0.99875 | 0.99794 | 0.99998 | 0.99882 | 0.99882 |
| Sensitivity () | −82.89 | −54.67 | −45.78 | −275.56 | −269.78 | −280.67 |
| Magnification M | 3.32 | 4.93 | 6.13 | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, C.; Yang, Y.; Mu, X.; Li, F.; Li, Y. Sensitive Detection of Multi-Point Temperature Based on FMCW Interferometry and DSP Algorithm. Nanomaterials 2025, 15, 1545. https://doi.org/10.3390/nano15201545
Mo C, Yang Y, Mu X, Li F, Li Y. Sensitive Detection of Multi-Point Temperature Based on FMCW Interferometry and DSP Algorithm. Nanomaterials. 2025; 15(20):1545. https://doi.org/10.3390/nano15201545
Chicago/Turabian StyleMo, Chengyu, Yuqiang Yang, Xiaoguang Mu, Fujiang Li, and Yuting Li. 2025. "Sensitive Detection of Multi-Point Temperature Based on FMCW Interferometry and DSP Algorithm" Nanomaterials 15, no. 20: 1545. https://doi.org/10.3390/nano15201545
APA StyleMo, C., Yang, Y., Mu, X., Li, F., & Li, Y. (2025). Sensitive Detection of Multi-Point Temperature Based on FMCW Interferometry and DSP Algorithm. Nanomaterials, 15(20), 1545. https://doi.org/10.3390/nano15201545






