Understanding the Magnetic Exchange Pathways of Transition-Metal-Doped Monolayer TiS2 Using First-Principles Calculations
Abstract
1. Introduction
2. Methodology
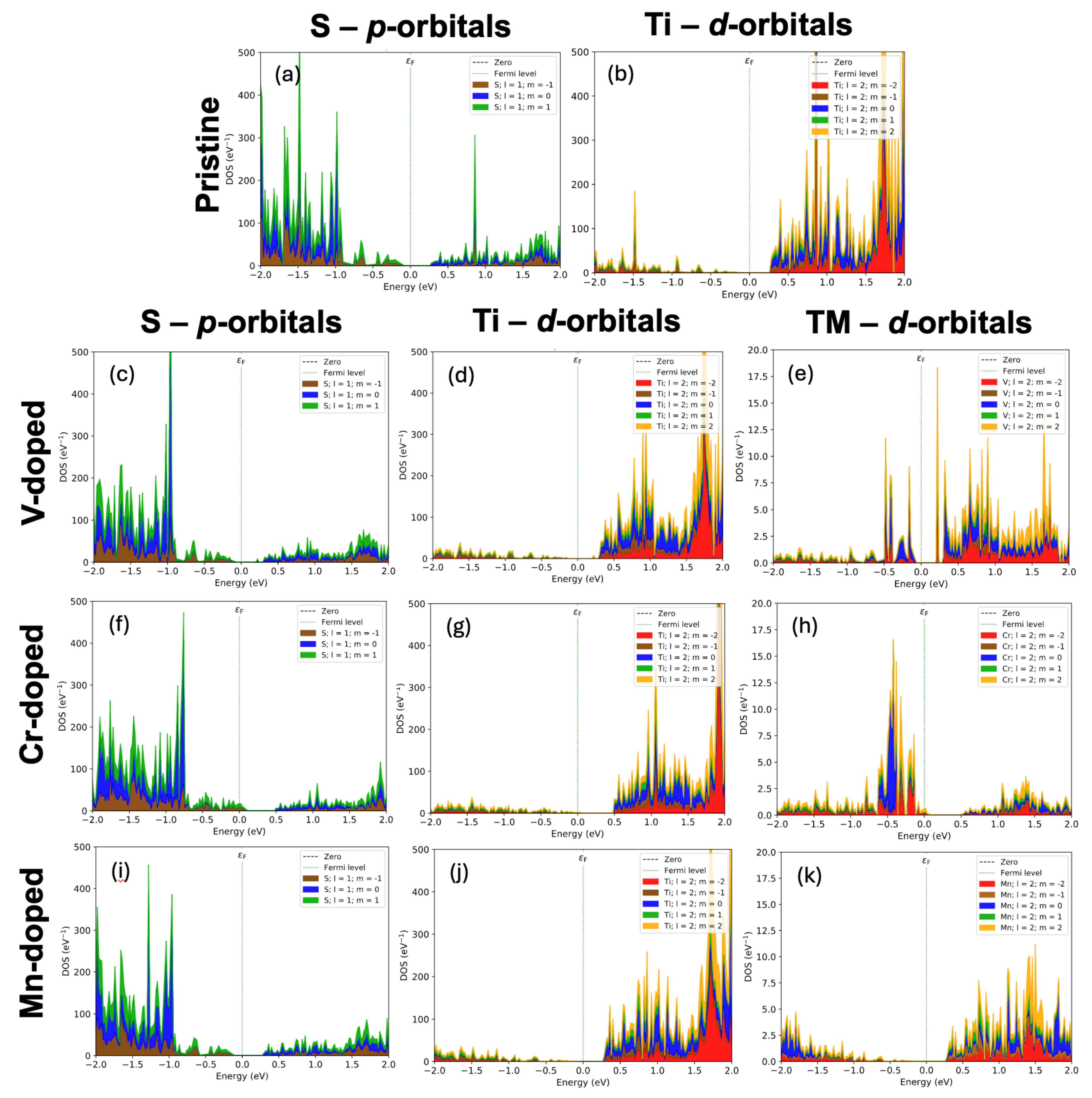
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krause, M.J.; Tolaymat, T. Quantification of energy and carbon costs for mining cryptocurrencies. Nat. Sustain. 2018, 1, 711–718. [Google Scholar] [CrossRef]
- Kristiansen Nøland, J.; Hjelmeland, M.; Korpås, M. Will Energy-Hungry AI Create a Baseload Power Demand Boom? IEEE Access 2024, 12, 110353–110360. [Google Scholar] [CrossRef]
- García-Martín, E.; Rodrigues, C.F.; Riley, G.; Grahn, H. Estimation of energy consumption in machine learning. J. Parallel Distrib. Comput. 2019, 134, 75–88. [Google Scholar] [CrossRef]
- Rimmler, B.H.; Pal, B.; Parkin, S.S.P. Non-collinear antiferromagnetic spintronics. Nat. Rev. Mater. 2025, 10, 109–127. [Google Scholar] [CrossRef]
- Al-Douri, Y.; Ameri, M. Physical studies of spintronics-based Heusler alloys. Crit. Rev. Solid State Mater. Sci. 2025, 50, 189–238. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, S.Y.; Yin, Y.; Zheng, N.; Ali, A.; Younis, M.; Ruan, S.; Zeng, Y.J. Emerging ferromagnetic materials for electrical spin injection: Towards semiconductor spintronics. npj Spintron. 2025, 3, 10. [Google Scholar] [CrossRef]
- Slaughter, J.M.; Dave, R.W.; DeHerrera, M.; Durlam, M.; Engel, B.N.; Janesky, J.; Rizzo, N.D.; Tehrani, S. Fundamentals of MRAM Technology. J. Supercond. 2002, 15, 19–25. [Google Scholar] [CrossRef]
- Huai, Y. Spin-transfer torque MRAM (STT-MRAM): Challenges and prospects. AAPPS Bull. 2008, 18, 33–40. [Google Scholar]
- Bhatti, S.; Sbiaa, R.; Hirohata, A.; Ohno, H.; Fukami, S.; Piramanayagam, S. Spintronics based random access memory: A review. Mater. Today 2017, 20, 530–548. [Google Scholar] [CrossRef]
- Na, T.; Kang, S.H.; Jung, S.O. STT-MRAM sensing: A review. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 12–18. [Google Scholar] [CrossRef]
- Glavin, N.R.; Rao, R.; Varshney, V.; Bianco, E.; Apte, A.; Roy, A.; Ringe, E.; Ajayan, P.M. Emerging applications of elemental 2D materials. Adv. Mater. 2020, 32, 1904302. [Google Scholar] [CrossRef]
- Feng, Y.P.; Shen, L.; Yang, M.; Wang, A.; Zeng, M.; Wu, Q.; Chintalapati, S.; Chang, C.R. Prospects of spintronics based on 2D materials. WIREs Comput. Mol. Sci. 2017, 7, e1313. [Google Scholar] [CrossRef]
- Yu, X.; Xu, L.; Shi, W.; Meng, X.; Huang, X.; Peng, Z.; Tong, L.; Sun, H.; Miao, X.; Ye, L. 2D materials-based flash memory device: Mechanism, structure, application. Mater. Horiz. 2025. Advance Article. [Google Scholar] [CrossRef]
- Aggarwal, S.; Almasi, H.; DeHerrera, M.; Hughes, B.; Ikegawa, S.; Janesky, J.; Lee, H.; Lu, H.; Mancoff, F.; Nagel, K.; et al. Demonstration of a reliable 1 Gb standalone spin-transfer torque MRAM for industrial applications. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2.1.1–2.1.4. [Google Scholar]
- Yakout, S.M. Spintronics: Future Technology for New Data Storage and Communication Devices. J. Supercond. Nov. Magn. 2020, 33, 2557–2580. [Google Scholar] [CrossRef]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
- Bertolazzi, S.; Bondavalli, P.; Roche, S.; San, T.; Choi, S.Y.; Colombo, L.; Bonaccorso, F.; Samorì, P. Nonvolatile memories based on graphene and related 2D materials. Adv. Mater. 2019, 31, 1806663. [Google Scholar] [CrossRef]
- Sethulakshmi, N.; Mishra, A.; Ajayan, P.; Kawazoe, Y.; Roy, A.K.; Singh, A.K.; Tiwary, C.S. Magnetism in two-dimensional materials beyond graphene. Mater. Today 2019, 27, 107–122. [Google Scholar] [CrossRef]
- Min, J.; Kim, J.H.; Kang, J. Chalcogen Vacancy Engineering of Two-Dimensional Transition Metal Dichalcogenides for Electronic Applications. ACS Appl. Nano Mater. 2024, 7, 26377–26396. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, L.; Yu, H.; Liao, Q.; Kang, Z.; Zhang, Z.; Zhang, Y. Single-Atom Vacancy Doping in Two-Dimensional Transition Metal Dichalcogenides. Acc. Mater. Res. 2021, 2, 655–668. [Google Scholar] [CrossRef]
- Hawkins, C.G.; Whittaker-Brooks, L. Controlling Sulfur Vacancies in TiS2-x Cathode Insertion Hosts via the Conversion of TiS3 Nanobelts for Energy-Storage Applications. ACS Appl. Nano Mater. 2018, 1, 851–859. [Google Scholar] [CrossRef]
- Chen, K.; Song, M.; Sun, Y.Y.; Xu, H.; Qi, D.C.; Su, Z.; Gao, X.; Xu, Q.; Hu, J.; Zhu, J.; et al. Defects controlled doping and electrical transport in TiS2 single crystals. Appl. Phys. Lett. 2020, 116, 121901. [Google Scholar] [CrossRef]
- Loh, L.; Zhang, Z.; Bosman, M.; Eda, G. Substitutional doping in 2D transition metal dichalcogenides. Nano Res. 2021, 14, 1668–1681. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, K.; Pan, F.; Zhou, C.; Zhou, F.; Chai, Y. Doping, Contact and Interface Engineering of Two-Dimensional Layered Transition Metal Dichalcogenides Transistors. Adv. Funct. Mater. 2017, 27, 1603484. [Google Scholar] [CrossRef]
- Chen, S.; Yang, L.; Wang, D. Photoelectric Properties of Single Layer TiS2 Modified by Non-Metal Doping. Russ. J. Phys. Chem. A 2022, 96, 3031–3037. [Google Scholar] [CrossRef]
- Chen, H.; Yin, J.; Yang, J.; Zhang, X.; Liu, M.; Jiang, Z.; Wang, J.; Sun, Z.; Guo, T.; Liu, W.; et al. Transition-metal dichalcogenides heterostructure saturable absorbers for ultrafast photonics. Opt. Lett. 2017, 42, 4279–4282. [Google Scholar] [CrossRef]
- Selamneni, V.; Sahatiya, P. Mixed dimensional Transition Metal Dichalcogenides (TMDs) vdW Heterostructure based Photodetectors: A review. Microelectron. Eng. 2023, 269, 111926. [Google Scholar] [CrossRef]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Zhao, B.; Shen, D.; Zhang, Z.; Lu, P.; Hossain, M.; Li, J.; Li, B.; Duan, X. 2D Metallic Transition-Metal Dichalcogenides: Structures, Synthesis, Properties, and Applications. Adv. Funct. Mater. 2021, 31, 2105132. [Google Scholar] [CrossRef]
- Liu, H.; Yang, L.; Zhao, Y.; Sun, S.; Wei, X. Photoelectric and Magnetic Variation of Transition Metal-Doped Monolayer TiS2: A First-Principles Calculation. J. Supercond. Nov. Magn. 2024, 37, 639–655. [Google Scholar] [CrossRef]
- Let, A.L.; Mainwaing, D.; Rix, C.; Murugaraj, P. Synthesis and Optical Properties of TiS2 Nanoclusters. Rev. Roum. Chim. 2007, 52, 235–241. [Google Scholar]
- Zeb, J.; Zhao, X.; Ullah, S.; Menezes, M.G.; Zhang, W. Tunable optoelectronic properties in multilayer 1T-TiS2: The effects of strain and an external electric field. J. Mater. Sci. 2021, 56, 6891–6902. [Google Scholar] [CrossRef]
- El-Kouch, H.; Farh, L.E. Electronic and Optical Properties of TiS2 Determined from Modified Becke–Johnson GGA Potential. Rev. Roum. Chim. 2018, 63, 873–880. [Google Scholar]
- Wang, H.; Qiu, Z.; Xia, W.; Ming, C.; Han, Y.; Cao, L.; Lu, J.; Zhang, P.; Zhang, S.; Xu, H.; et al. Semimetal or Semiconductor: The Nature of High Intrinsic Electrical Conductivity in TiS2. J. Phys. Chem. Lett. 2019, 10, 6996–7001. [Google Scholar] [CrossRef]
- Huang, X.; Tang, J.; Luo, B.; Knibbe, R.; Lin, T.; Hu, H.; Rana, M.; Hu, Y.; Zhu, X.; Gu, Q.; et al. Sandwich-Like Ultrathin TiS2 Nanosheets Confined within N, S Codoped Porous Carbon as an Effective Polysulfide Promoter in Lithium-Sulfur Batteries. Adv. Energy Mater. 2019, 9, 1901872. [Google Scholar] [CrossRef]
- Sun, K.; Fu, M.; Xie, Z.; Su, D.; Zhong, H.; Bai, J.; Dooryhee, E.; Gan, H. Improvement of Li-S battery electrochemical performance with 2D TiS2 additive. Electrochim. Acta 2018, 292, 779–788. [Google Scholar] [CrossRef]
- Huckaba, A.J.; Gharibzadeh, S.; Ralaiarisoa, M.; Roldán-Carmona, C.; Mohammadian, N.; Grancini, G.; Lee, Y.; Amsalem, P.; Plichta, E.J.; Koch, N.; et al. Low-Cost TiS2 as Hole-Transport Material for Perovskite Solar Cells. Small Methods 2017, 1, 1700250. [Google Scholar] [CrossRef]
- Alias, N.; Ali Umar, A.; Malek, N.A.A.; Liu, K.; Li, X.; Abdullah, N.A.; Rosli, M.M.; Abd Rahman, M.Y.; Shi, Z.; Zhang, X.; et al. Photoelectrical Dynamics Uplift in Perovskite Solar Cells by Atoms Thick 2D TiS2 Layer Passivation of TiO2 Nanograss Electron Transport Layer. ACS Appl. Mater. Interfaces 2021, 13, 3051–3061. [Google Scholar] [CrossRef]
- Mahuli, N.; Sarkar, S.K. Atomic layer deposition of titanium sulfide and its application in extremely thin absorber solar cells. J. Vac. Sci. Technol. A 2014, 33, 01A150. [Google Scholar] [CrossRef]
- Toularoud, S.A.; Hadipour, H.; Soleimani, H.R. Engineering the electronic and magnetic properties of monolayer TiS2 through systematic transition-metal doping. Phys. B Condens. Matter 2024, 694, 416413. [Google Scholar] [CrossRef]
- QuantumATK Version R-2020.09, Synopsys QuantumATK, Sunnydale CA, USA, 2020. Available online: https://www.synopsys.com/quantumatk (accessed on 17 September 2025).
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef] [PubMed]
- van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Buchelnikov, V. Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State. Metals 2023, 13, 728. [Google Scholar] [CrossRef]
- Bartók, A.P.; Yates, J.R. Regularized SCAN functional. J. Chem. Phys. 2019, 150, 161101. [Google Scholar] [CrossRef] [PubMed]
- Bihlmayer, G. Density Functional Theory for Magnetism and Magnetic Anisotropy. In Handbook of Materials Modeling: Methods: Theory and Modeling; Andreoni, W., Yip, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–23. [Google Scholar] [CrossRef]
- Kovács, P.; Tran, F.; Blaha, P.; Madsen, G.K.H. Comparative study of the PBE and SCAN functionals: The particular case of alkali metals. J. Chem. Phys. 2019, 150, 164119. [Google Scholar] [CrossRef]
- Blundell, S. Magnetism in Condensed Matter; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Wang, Y.; Puggioni, D.; Rondinelli, J.M. Assessing exchange-correlation functional performance in the chalcogenide lacunar spinels GaM4Q8 (M = Mo, V, Nb, Ta; Q = S, Se). Phys. Rev. B 2019, 100, 115149. [Google Scholar] [CrossRef]
- Baltzer, P.K.; Wojtowicz, P.J.; Robbins, M.; Lopatin, E. Exchange Interactions in Ferromagnetic Chromium Chalcogenide Spinels. Phys. Rev. 1966, 151, 367–377. [Google Scholar] [CrossRef]
- Miessler, G.L.; Fischer, P.J.; Tarr, D.A. Inorganic Chemistry, 5th ed.; Pearson: London, UK, 2013. [Google Scholar]
- Atkins, P.; Overton, T. Shriver and Atkins’ Inorganic Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Cotton, F.A.; Wilkinson, G.; Murillo, C.A.; Bochmann, M. Advanced Inorganic Chemistry, 6th ed.; Wiley-Interscience: New York, NY, USA, 1999. [Google Scholar]
- Ghosh, R. Bose–Stoner Formula in Magnetochemistry. Resonance 2022, 27, 1131–1133. [Google Scholar] [CrossRef]
- Dresselhaus, M.S. Solid State Physics Part III: Magnetic Properties of Solids. Lecture Notes from MIT Course 6.732. 2001. Available online: https://web.mit.edu/6.732/www/6.732-pt3.pdf (accessed on 17 September 2025).




| System | Dopant Separation (Å) | EA-EF (eV) | () | () | MTotal () |
|---|---|---|---|---|---|
| 1V | – | – | 1.091 | – | 1.073 |
| 2V1 | 3.079 | 0.23096 | 1.231 | 1.149 | 2.077 |
| 2V2 | 6.619 | 0.05378 | 1.095 | 1.122 | 2.122 |
| 2V3 | 10.218 | 0.0103 | 1.082 | 1.095 | 2.086 |
| 2V4 | 13.667 | 0 | 1.144 | 1.075 | 2.179 |
| 1Cr | – | – | 2.972 | – | 2.914 |
| 2Cr1 | 3.453 | 0.0260 | 2.939 | 2.94 | 5.502 |
| 2Cr2 | 6.829 | −0.0055 | 2.943 | −2.945 | −0.013 |
| 2Cr3 | 10.258 | −0.00099 | 2.948 | −2.962 | 0 |
| 2Cr4 | 13.65 | 0.00012 | −2.953 | 2.954 | 5.645 |
| 1Mn | – | – | 3.102 | – | 2.995 |
| 2Mn1 | 3.388 | 0.46438 | 3.136 | 3.139 | 5.989 |
| 2Mn2 | 6.779 | −0.0066 | −3.115 | 3.104 | −0.002 |
| 2Mn3 | 10.250 | −0.00028 | −3.120 | 3.109 | −0.003 |
| 2Mn4 | 13.654 | −0.00032 | −3.119 | 3.0108 | −0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keeney, P.J.; Coelho, P.M.; Haraldsen, J.T. Understanding the Magnetic Exchange Pathways of Transition-Metal-Doped Monolayer TiS2 Using First-Principles Calculations. Nanomaterials 2025, 15, 1435. https://doi.org/10.3390/nano15181435
Keeney PJ, Coelho PM, Haraldsen JT. Understanding the Magnetic Exchange Pathways of Transition-Metal-Doped Monolayer TiS2 Using First-Principles Calculations. Nanomaterials. 2025; 15(18):1435. https://doi.org/10.3390/nano15181435
Chicago/Turabian StyleKeeney, P. J., P. M. Coelho, and J. T. Haraldsen. 2025. "Understanding the Magnetic Exchange Pathways of Transition-Metal-Doped Monolayer TiS2 Using First-Principles Calculations" Nanomaterials 15, no. 18: 1435. https://doi.org/10.3390/nano15181435
APA StyleKeeney, P. J., Coelho, P. M., & Haraldsen, J. T. (2025). Understanding the Magnetic Exchange Pathways of Transition-Metal-Doped Monolayer TiS2 Using First-Principles Calculations. Nanomaterials, 15(18), 1435. https://doi.org/10.3390/nano15181435






