Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures
Abstract
1. Introduction
2. Materials and Methods
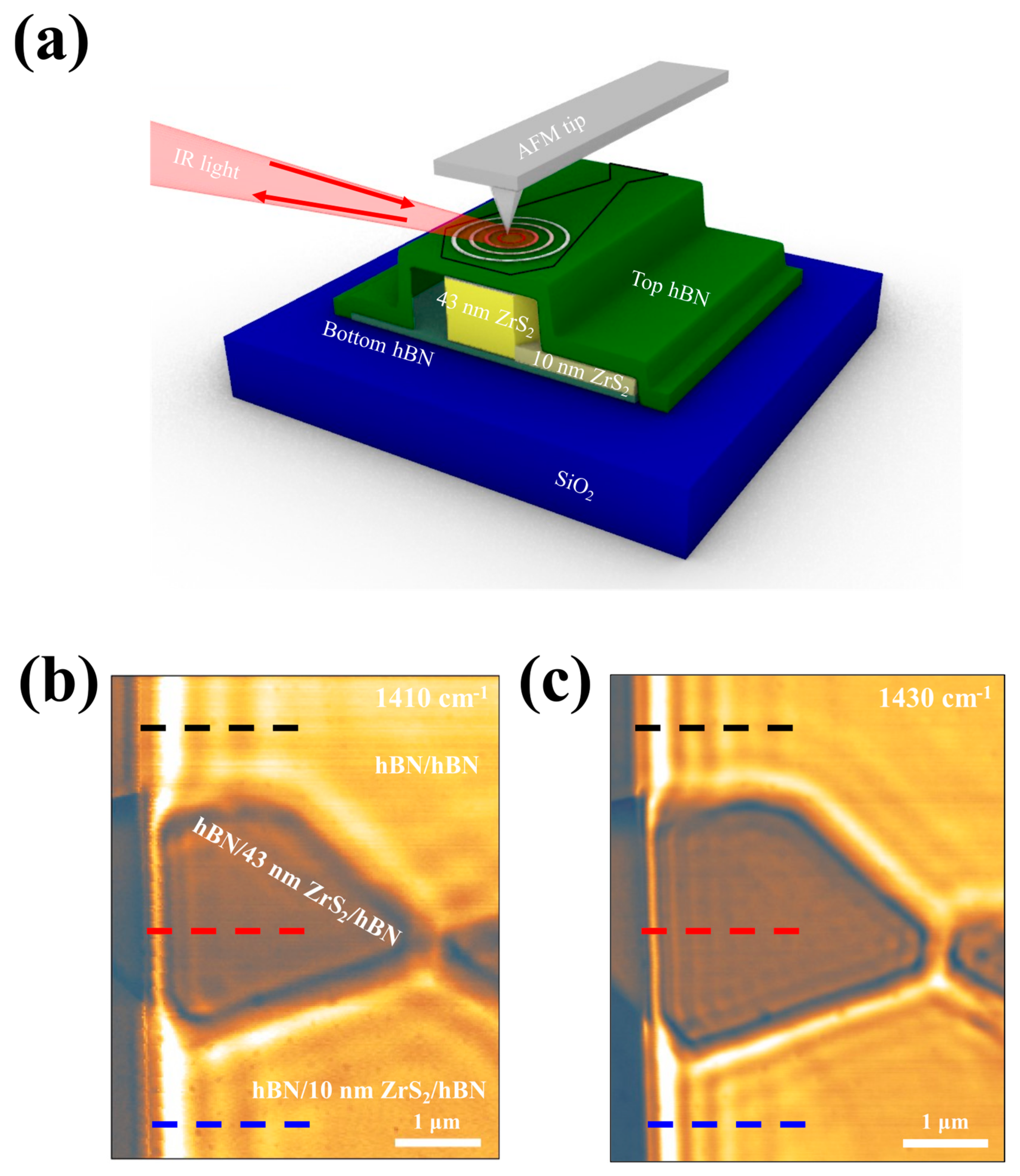
2.1. Sample Preparation
2.2. Fabrication of van der Waals Heterostructures
2.3. Near-Field Infrared Radiation Nano-Imaging
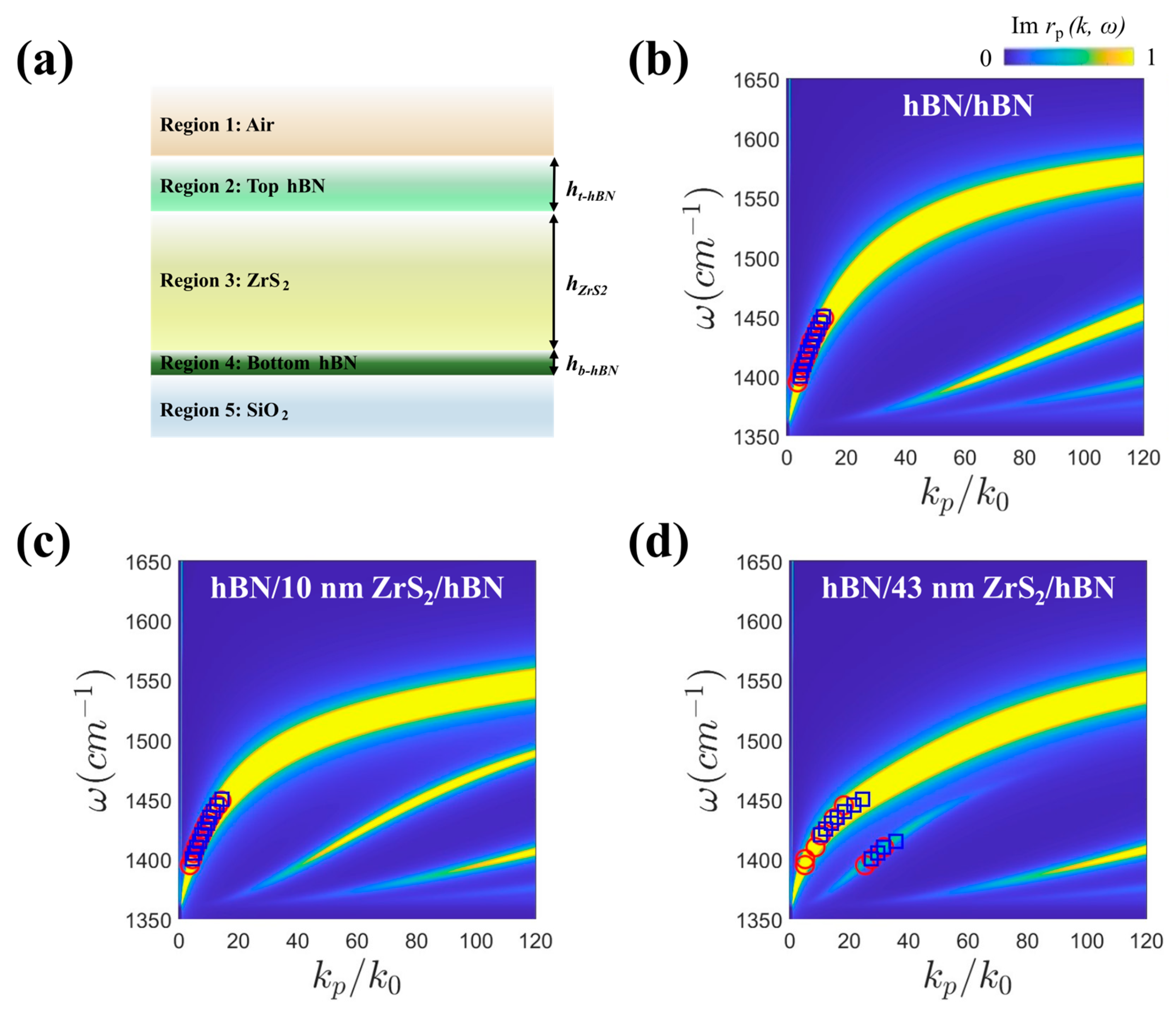
2.4. Full-Wave Electromagnetic Numerical Simulation
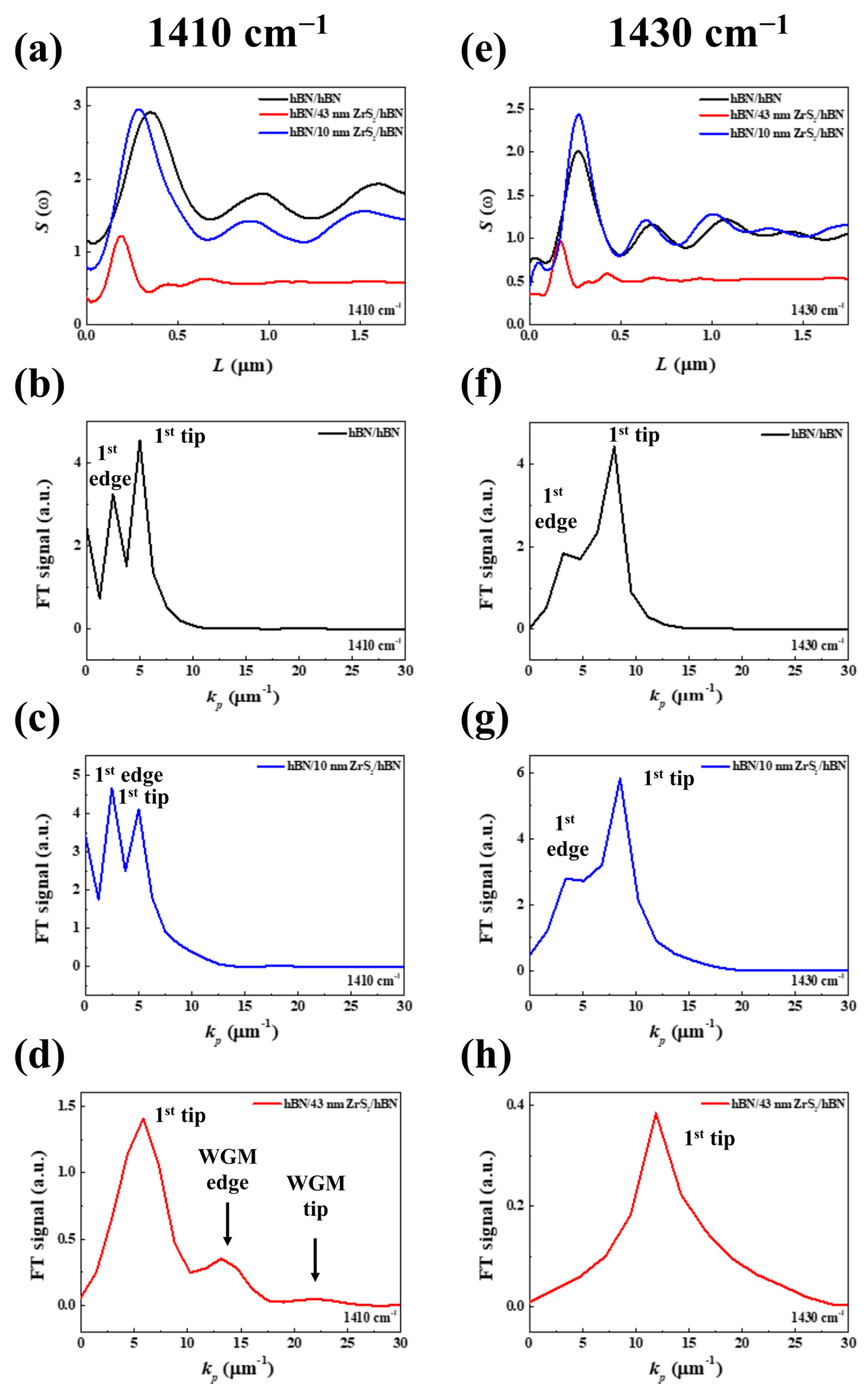
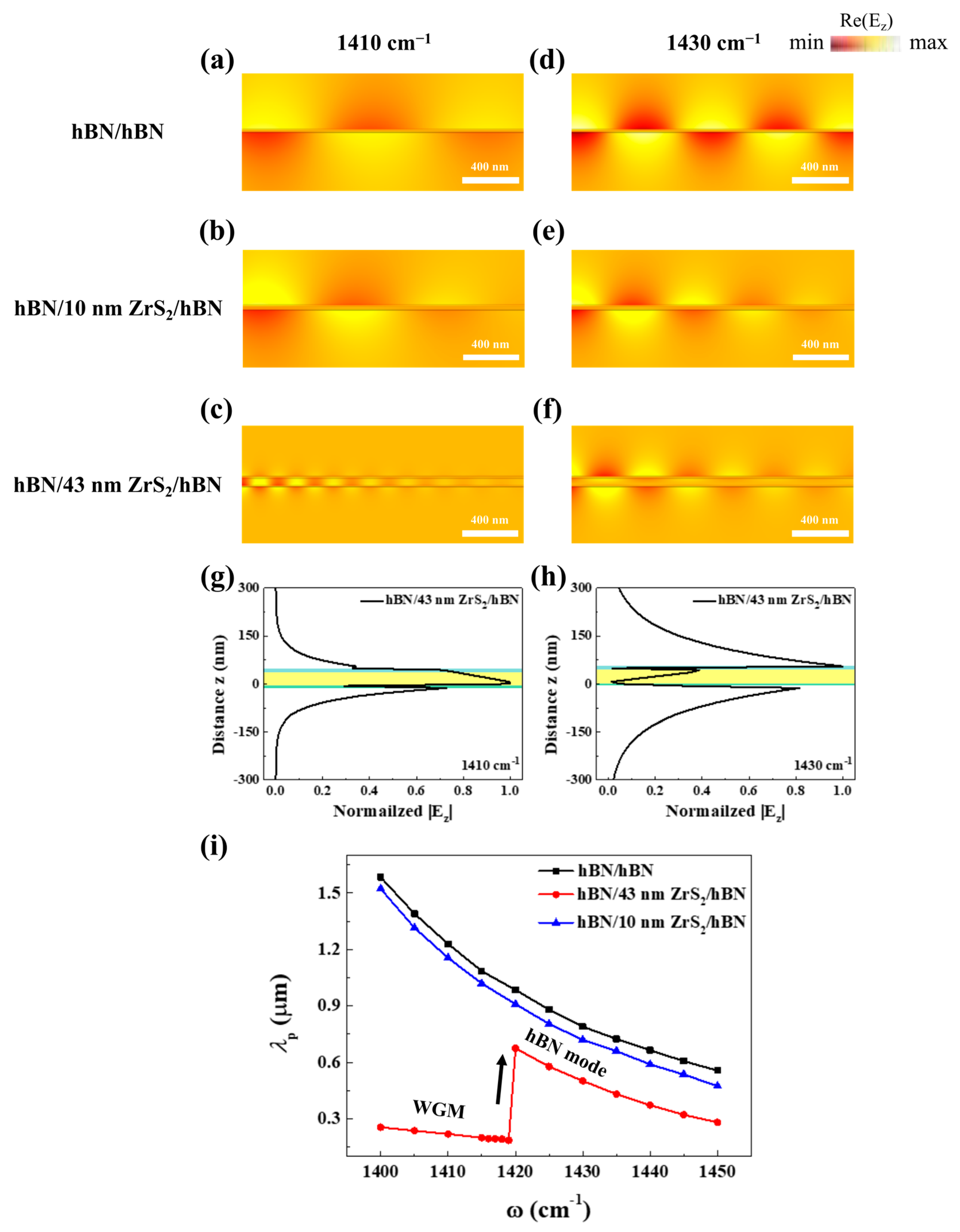
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, S.; Fei, Z.; Ma, Q.; Rodin, A.S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Gannett, W.; Regan, W.; Watanabe, K.; et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 2014, 343, 1125–1129. [Google Scholar] [CrossRef] [PubMed]
- Basov, D.N.; Fogler, M.M.; de Abajo, F.J.G. Polaritons in van der Waals materials. Science 2016, 354, aag1992. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Perez, G.; Foland, T.G.; Errea, I.; Taboada-Gutiérrez, J.; Duan, J.H.; Martín-Sánchez, J.; Tresguerres-Mata, A.I.F.; Matson, J.R.; Bylinkin, A.; He, M.Z.; et al. Infrared Permittivity of the Biaxial van der Waals Semiconductor α-MoO3 from Near- and Far-Field Correlative Studies. Adv. Mater. 2020, 32, 1908176. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.W.; Shen, J.L.; Qiu, C.W.; Alù, A.; Dai, S.Y. Phonon Polaritons and Hyperbolic Response in van der Waals Materials. Adv. Opt. Mater. 2020, 8, 1901393. [Google Scholar] [CrossRef]
- Taboada-Gutiérrez, J.; Alvarez-Pérez, G.; Duan, J.H.; Ma, W.L.; Crowley, K.; Prieto, I.; Bylinkin, A.; Autore, M.; Volkova, H.; Kimura, K.; et al. Broad spectral tuning of ultra-low-loss polaritons in a van der Waals crystal by intercalation. Nat. Mater. 2020, 19, 964–968. [Google Scholar] [CrossRef] [PubMed]
- Juraschek, D.M.; Narang, P. Highly Confined Phonon Polaritons in Monolayers of Perovskite Oxides. Nano Lett. 2021, 21, 5098–5104. [Google Scholar] [CrossRef]
- Mancini, A.; Nan, L.; Wendisch, F.J.; Berte, R.; Ren, H.R.; Cortes, E.; Maier, S.A. Near-Field Retrieval of the Surface Phonon Polariton Dispersion in Free-Standing Silicon Carbide Thin Films. ACS Photonics 2022, 9, 3696–3704. [Google Scholar] [CrossRef]
- Yoxall, E.; Schnell, M.; Nikitin, A.Y.; Txoperena, O.; Woessner, A.; Lundeberg, M.B.; Casanova, F.; Hueso, L.E.; Koppens, F.H.L.; Hillenbrand, R. Direct observation of ultraslow hyperbolic polariton propagation with negative phase velocity. Nat. Photonics 2015, 9, 674–678. [Google Scholar] [CrossRef]
- Chen, M.Y.; Lin, X.; Dinh, T.H.; Zheng, Z.R.; Shen, J.L.; Ma, Q.; Chen, H.S.; Jarillo-Herrero, P.; Dai, S.Y. Configurable phonon polaritons in twisted α-MoO3. Nat. Mater. 2020, 19, 1307–1311. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Chen, N.; Teng, H.C.; Yu, R.W.; Qu, Y.P.; Sun, J.Z.; Xue, M.F.; Hu, D.B.; Wu, B.; Li, C.; et al. Doping-driven topological polaritons in graphene/α-MoO3 heterostructures. Nat. Nanotechnol. 2022, 17, 940–946. [Google Scholar] [CrossRef] [PubMed]
- Ruta, F.L.; Kim, B.S.Y.; Sun, Z.Y.; Rizzo, D.J.; McLeod, A.S.; Rajendran, A.; Liu, S.; Millis, A.J.; Hone, J.C.; Basov, D.N. Surface plasmons induce topological transition in graphene/α-MoO3 heterostructures. Nat. Commun. 2022, 13, 3719. [Google Scholar] [CrossRef] [PubMed]
- Sternbach, A.J.; Moore, S.L.; Rikhter, A.; Zhang, S.; Jing, R.; Shao, Y.; Kim, B.S.Y.; Xu, S.; Liu, S.; Edgar, J.H.; et al. Negative refraction in hyperbolic hetero-bicrystals. Science 2023, 379, 555–557. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Song, R.K.; Xu, J.B.; Ni, X.; Dang, Z.J.; Zhao, Z.C.; Quan, J.M.; Dong, S.Y.; Hu, W.D.; Huang, D.; et al. Gate-Tuning Hybrid Polaritons in Twisted α-MoO3/Graphene Heterostructures. Nano Lett. 2023, 23, 11252–11259. [Google Scholar] [CrossRef]
- Caldwell, J.D.; Kretinin, A.V.; Chen, Y.G.; Giannini, V.; Fogler, M.M.; Francescato, Y.; Ellis, C.T.; Tischler, J.G.; Woods, C.R.; Giles, A.J.; et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 2014, 5, 5221. [Google Scholar] [CrossRef] [PubMed]
- Li, P.N.; Dolado, I.; Alfaro-Mozaz, F.J.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; Nikitin, A.Y.; Vélez, S.; Hillenbrand, R. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 2018, 359, 892–896. [Google Scholar] [CrossRef] [PubMed]
- Li, P.N.; Hu, G.W.; Dolado, I.; Tymchenko, M.; Qiu, C.W.; Alfaro-Mozaz, F.J.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; et al. Collective near-field coupling and nonlocal phenomena in infrared-phononic metasurfaces for nano-light canalization. Nat. Commun. 2020, 11, 3663. [Google Scholar] [CrossRef] [PubMed]
- Follan, T.G.; Fali, A.; White, S.T.; Matson, J.R.; Liu, S.; Aghamiri, N.A.; Edgar, J.H.; Haglund, R.F.; Abate, Y.; Caldwell, J.D. Reconfigurable infrared hyperbolic metasurfaces using phase change materials. Nat. Commun. 2018, 9, 4371. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.Y.; Zhang, J.W.; Ma, Q.; Kittiwatanakul, S.; McLeod, A.; Chen, X.Z.; Corder, S.G.; Watanabe, K.; Taniguchi, T.; Lu, J.W.; et al. Phase-Change Hyperbolic Heterostructures for Nanopolaritonics: A Case Study of hBN/VO2. Adv. Mater. 2019, 31, 1900251. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Yuan, C.; Elias, C.; Wang, J.Y.; Zhang, X.T.; Ye, G.H.; Huang, C.R.; Kuball, M.; Eda, G.; Redwing, J.M.; et al. Hexagonal Boron Nitride Single Crystal Growth from Solution with a Temperature Gradient. Chem. Mater. 2020, 32, 5066–5072. [Google Scholar] [CrossRef]
- Dai, S.Y.; Quan, J.M.; Hu, G.W.; Qiu, C.W.; Tao, T.H.; Li, X.Q.; Alù, A. Hyperbolic Phonon Polaritons in Suspended Hexagonal Boron Nitride. Nano Lett. 2019, 19, 1009–1014. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.Y.; Guo, Y.H.; Si, K.Y.; Ren, Z.Y.; Bai, J.T.; Xu, X.L. Elastic, electronic, and dielectric properties of bulk and monolayer ZrS2, ZrSe2, HfS2, HfSe2 from van der Waals density-functional theory. Phys. Status Solidi B Basic Solid State Phys. 2017, 254, 1700033. [Google Scholar] [CrossRef]
- Dai, S.Y.; Ma, Q.; Yang, Y.F.; Rosenfeld, J.; Goldflam, M.D.; McLeod, A.; Sun, Z.Y.; Andersen, T.I.; Fei, Z.; Liu, M.K.; et al. Efficiency of Launching Highly Confined Polaritons by Infrared Light Incident on a Hyperbolic Material. Nano Lett. 2017, 17, 5285–5290. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.Y.; Tymchenko, M.; Xu, Z.Q.; Tran, T.T.; Yang, Y.F.; Ma, Q.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P.; Aharonovich, I.; et al. Nanostructure Diagnosis with Hyperbolic Phonon Polaritons in Hexagonal Boron Nitride. Nano Lett. 2018, 18, 5205–5210. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhong, Y.; Harris, E.; Li, J.; Zheng, Z.; Chen, H.; Wu, J.S.; Jarillo-Herrero, P.; Ma, Q.; Edgar, J.H.; et al. Van der Waals isotope heterostructures for engineering phonon polariton dispersions. Nat. Commun. 2023, 14, 4782. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Pan, D.; Guo, X.D.; Hu, H.; Dai, Q. Substrate effects on the near-field radiative heat transfer between bi-planar graphene/hBN heterostructures. Int. J. Therm. Sci. 2022, 176, 107493. [Google Scholar] [CrossRef]
- Gjerding, M.N.; Petersen, R.; Pedersen, T.G.; Mortensen, N.A.; Thygesen, K.S. Layered van der Waals crystals with hyperbolic light dispersion. Nat. Commun. 2017, 8, 320. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.P.; Hu, X.; Lo, T.W.; Guo, X.Y.; Fung, K.H.; Zhu, Y.; Lau, S.P. Edge-Orientation Dependent Nanoimaging of Mid-Infrared Waveguide Modes in High-Index PtSe2. Adv. Opt. Mater. 2021, 9, 2100294. [Google Scholar] [CrossRef]
- Guo, Z.W.; Long, Y.; Jiang, H.T.; Ren, J.; Chen, H. Anomalous unidirectional excitation of high-k hyperbolic modes using all-electric metasources. Adv. Photonics 2021, 3, 036001. [Google Scholar] [CrossRef]
- Legrand, F.; Gérardin, B.; Bruno, F.; Laurent, J.; Lemoult, F.; Prada, C.; Aubry, A. Cloaking, trapping and superlensing of lamb waves with negative refraction. Sci. Rep. 2021, 11, 23901. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Long, C.; Li, J.H.; Zhu, H.; Chen, L.; Guan, J.G.; Li, X. Ultra-wideband microwave absorber by connecting multiple absorption bands of two different-sized hyperbolic metamaterial waveguide arrays. Sci. Rep. 2015, 5, 15367. [Google Scholar] [CrossRef] [PubMed]
- Kaina, N.; Lemoult, F.; Fink, M.; Lerosey, G. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature 2015, 525, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Giles, A.J.; Dai, S.Y.; Vurgaftman, I.; Man, T.H.; Liu, S.; Lindsay, L.; Ellis, C.T.; Assefa, N.; Chatzakis, I.; Reinecke, T.L.; et al. Ultralow-loss polaritons in isotopically pure boron nitride. Nat. Mater. 2018, 17, 134–139. [Google Scholar] [CrossRef] [PubMed]
| ω (cm−1) | εhBN,x | εhBN,z | εSiO2 | εZrS2 |
|---|---|---|---|---|
| 1410 | −21.69 + 1.895i | 2.322 + 0.0002i | 1.07 | 2.2 + 0.0001i |
| 1430 | −14.003 + 0.969i | 2.743 + 0.0006i |
| Dimension | Top hBN | ZrS2 | Bottom hBN | SiO2 |
|---|---|---|---|---|
| Width | 10 μm | |||
| Thickness | 11.5 nm | 0/10/43 nm | 6.5 nm | 300 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, B.-I.; Reza, S.; Hardy, C.; Li, J.; Taba, A.; Mahjouri-Samani, M.; Edgar, J.H.; Dai, S. Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures. Nanomaterials 2024, 14, 1344. https://doi.org/10.3390/nano14161344
Noh B-I, Reza S, Hardy C, Li J, Taba A, Mahjouri-Samani M, Edgar JH, Dai S. Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures. Nanomaterials. 2024; 14(16):1344. https://doi.org/10.3390/nano14161344
Chicago/Turabian StyleNoh, Byung-Il, Salvio Reza, Cassie Hardy, Jiahan Li, Adib Taba, Masoud Mahjouri-Samani, James H. Edgar, and Siyuan Dai. 2024. "Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures" Nanomaterials 14, no. 16: 1344. https://doi.org/10.3390/nano14161344
APA StyleNoh, B.-I., Reza, S., Hardy, C., Li, J., Taba, A., Mahjouri-Samani, M., Edgar, J. H., & Dai, S. (2024). Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures. Nanomaterials, 14(16), 1344. https://doi.org/10.3390/nano14161344







