Quantum Transport through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets with Noncollinear Magnetizations
Abstract
1. Introduction
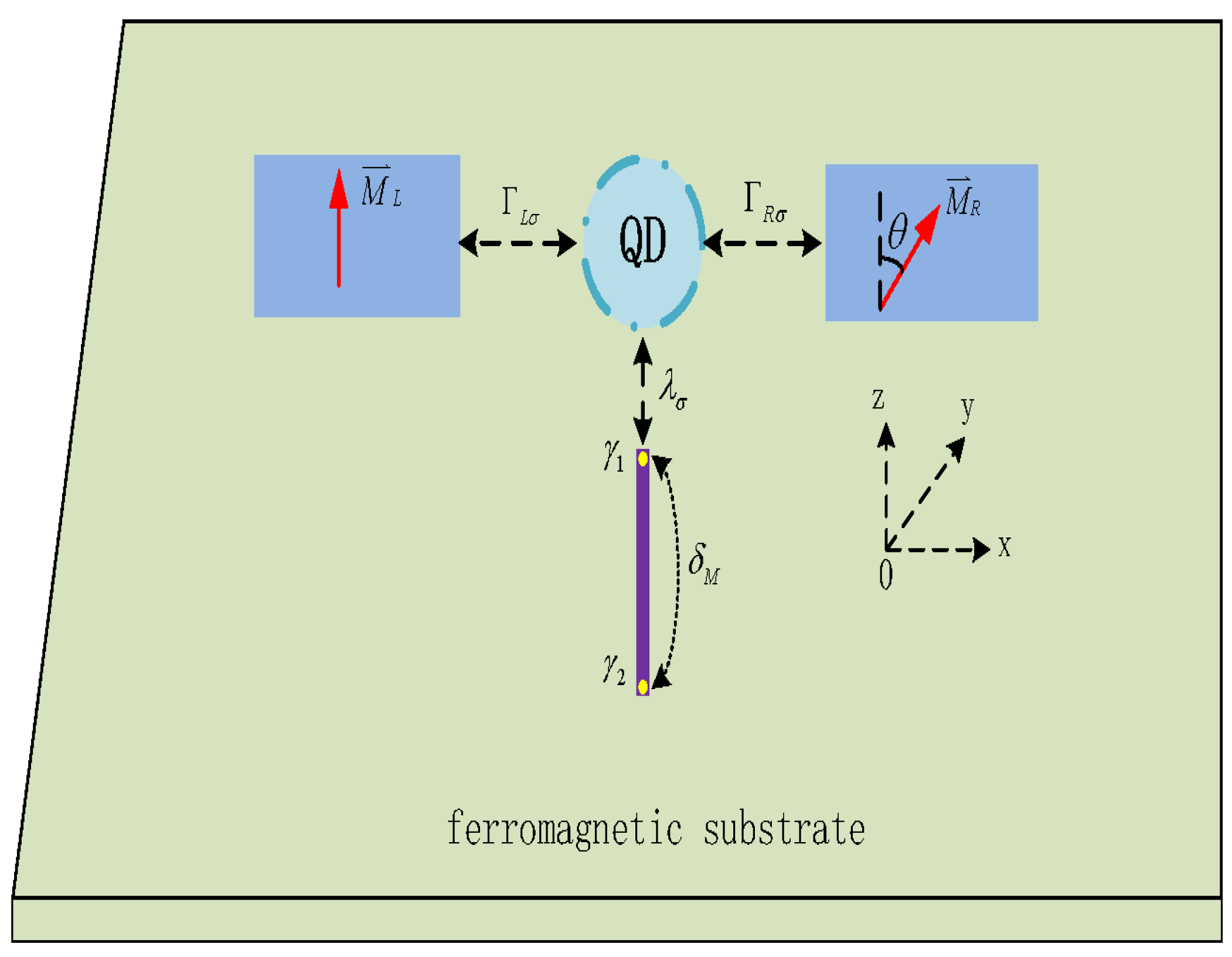
2. Model and Method
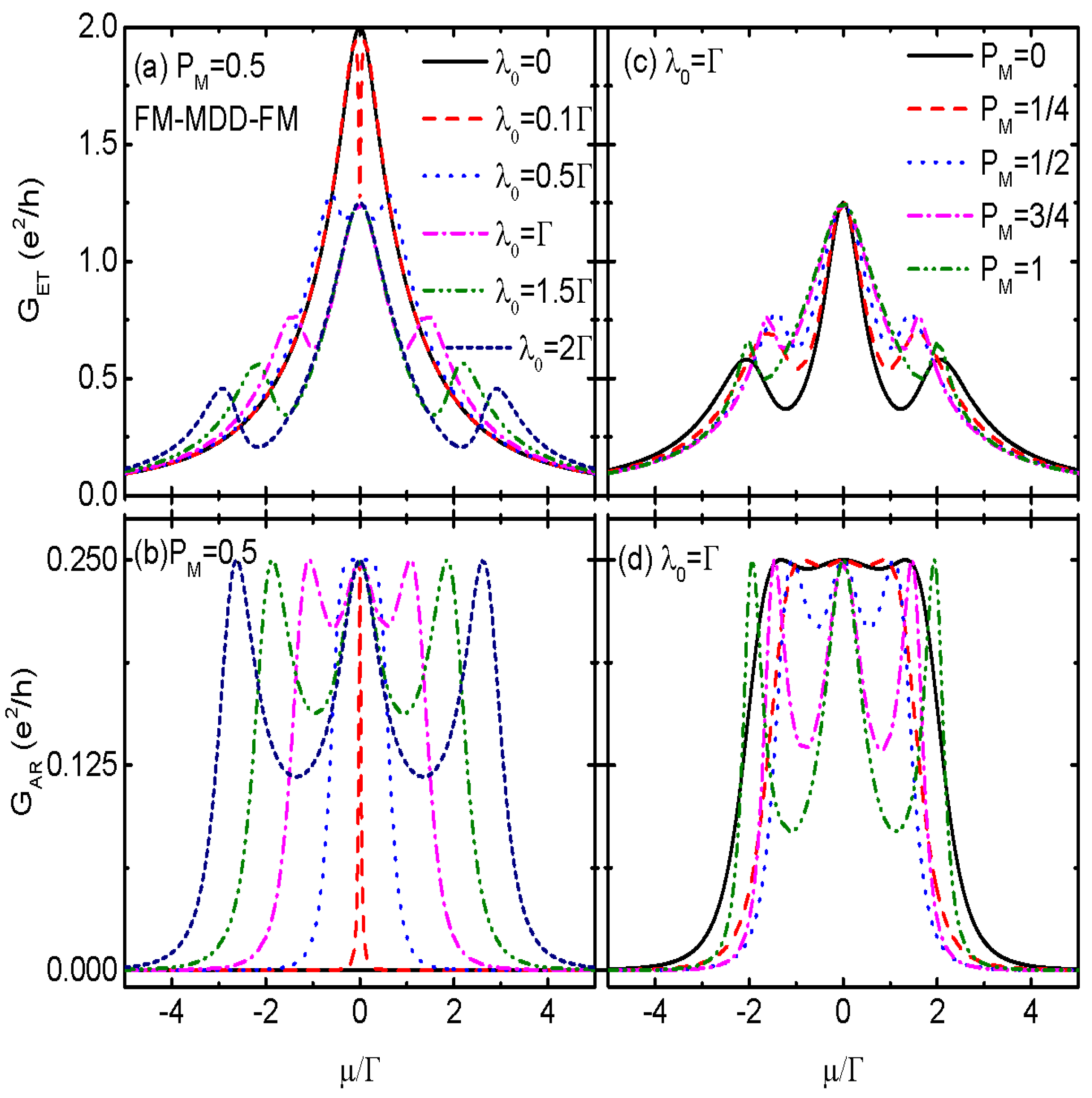
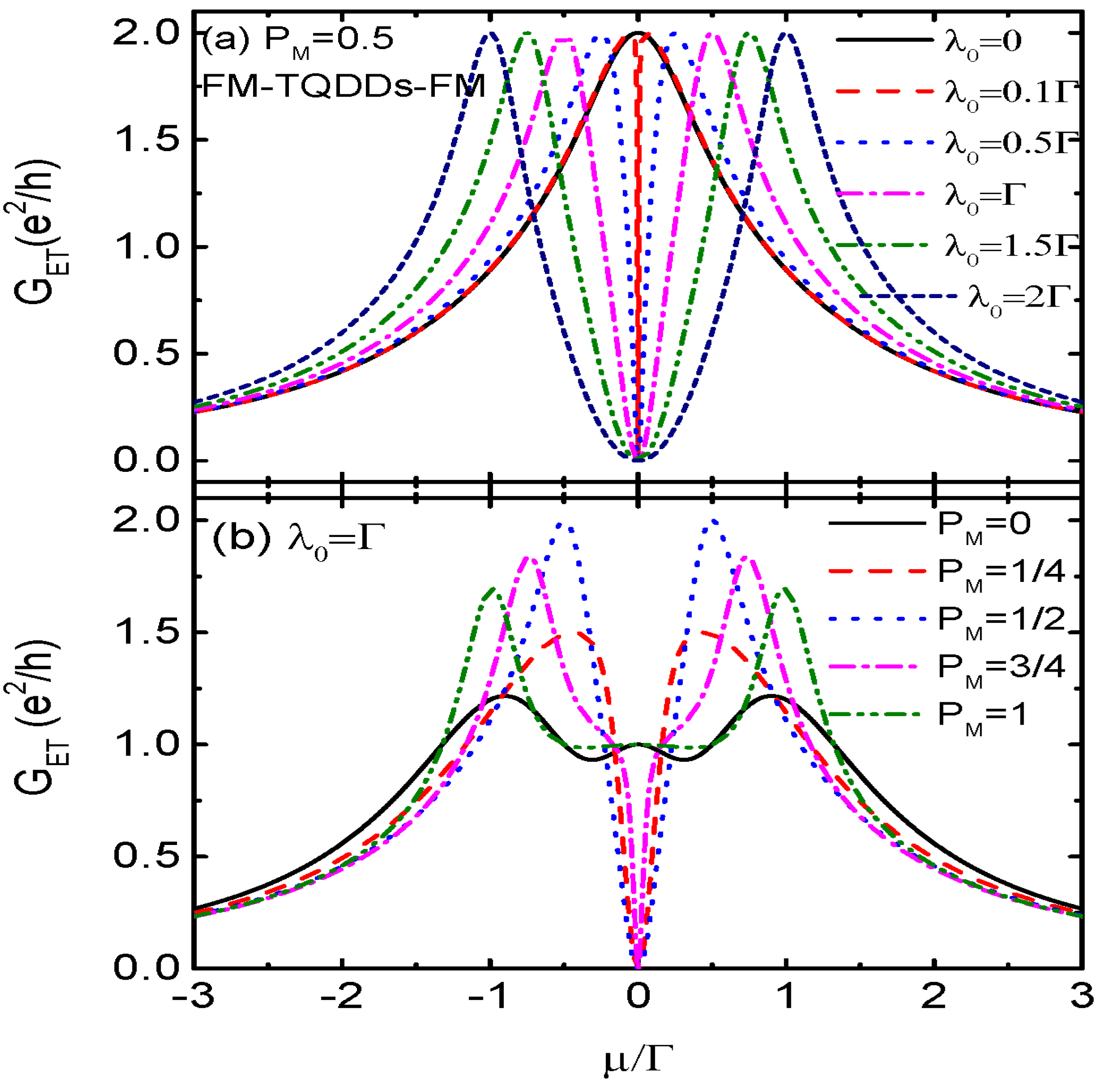
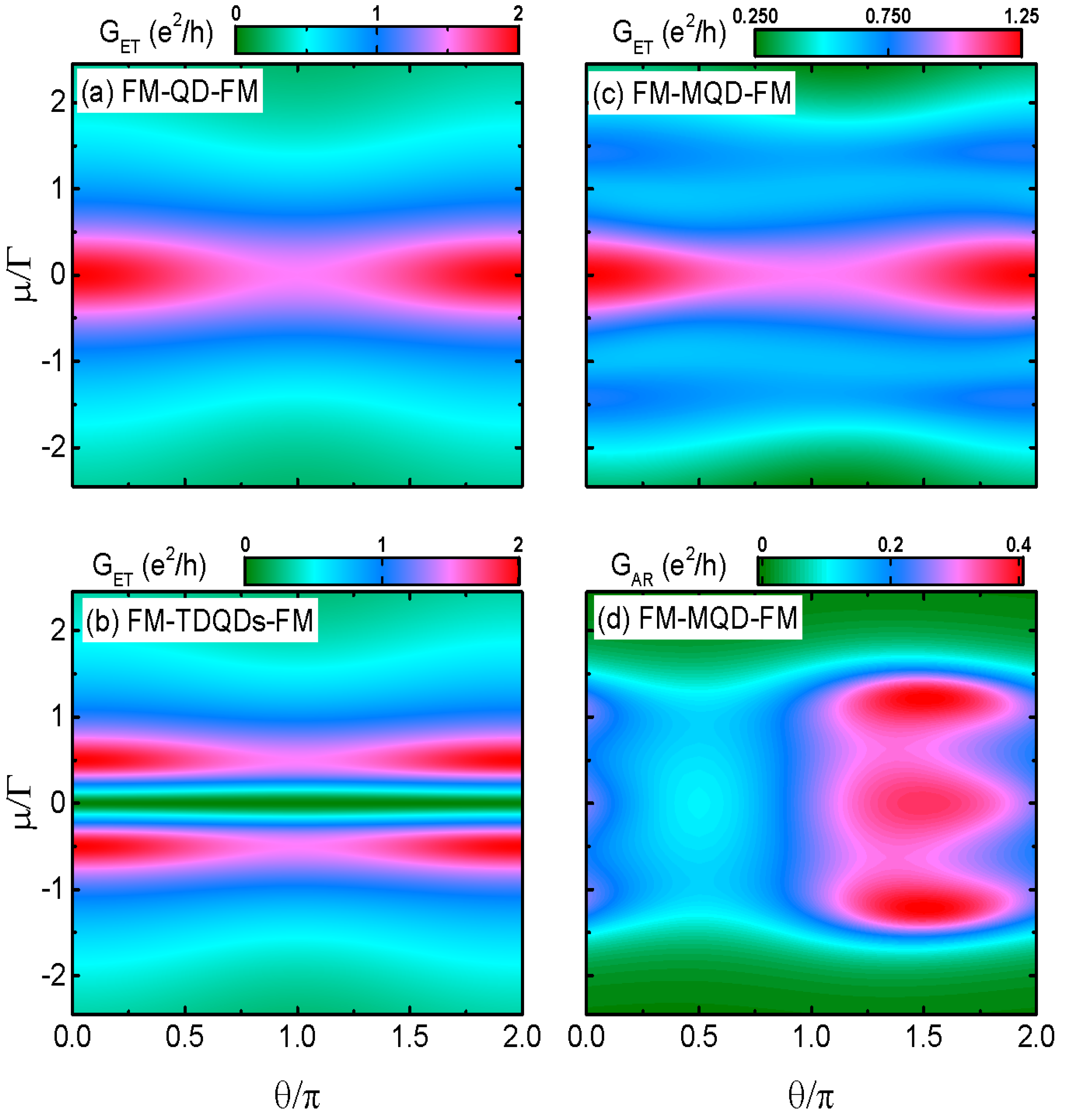
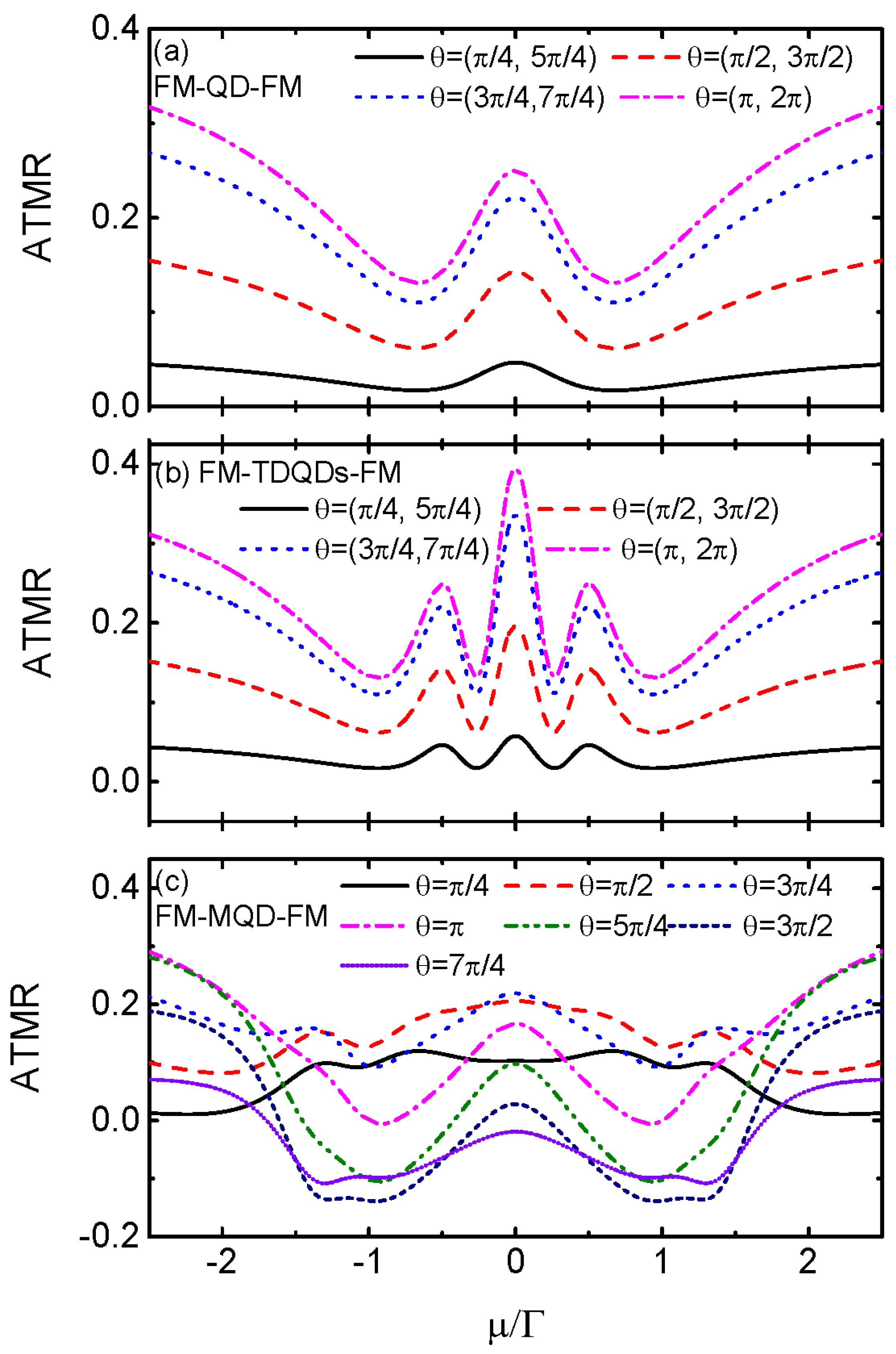
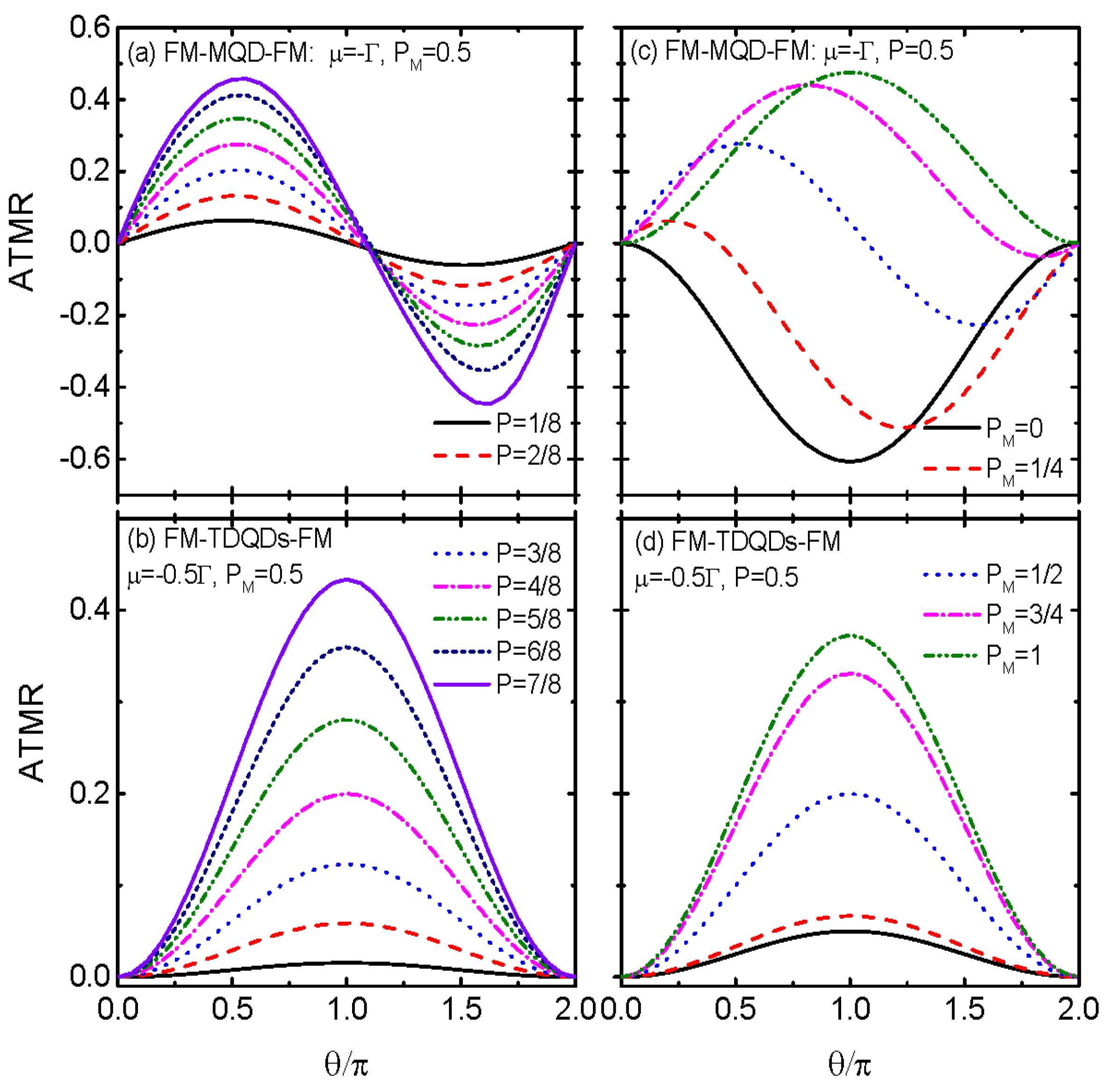
3. Numerical Results
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, Z.; Shi, R.; Yang, Z. ICT Development and Sustainable Energy Consumption: A Perspective of Energy Productivity. Sustainability 2018, 10, 2568. [Google Scholar] [CrossRef]
- Gelenbe, E. Electricity Consumption by ICT: Facts, trends, and measurements. Ubiquity 2023, 2023, 1–15. [Google Scholar] [CrossRef]
- Shi, J.L.; Li, C.; Li, H.J. Energy consumption in China’s ICT sectors: From the embodied energy perspective. Renew. Sustain. Energy Rev. 2022, 160, 112313. [Google Scholar] [CrossRef]
- Brataas, A.; Bauer, G.E.W.; Kelly, P.J. Non-collinear magnetoelectronics. Phys. Rep. 2006, 427, 157. [Google Scholar] [CrossRef]
- Qin, P.X.; Yan, H.; Wang, X.N.; Feng, Z.X.; Guo, H.X.; Zhou, X.R.; Wu, H.J.; Zhang, X.; Leng, Z.G.G.; Chen, H.Y. Noncollinear spintronics and electric-field control: A review. Rare Met. 2020, 39, 95. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Ye, Z.; Sun, Z.; Ye, G.; Sung, S.H.; Ge, H.; Yan, S.; Fu, Y.; Tian, S. Evidence of non-collinear spin texture in magnetic moiré superlattices. Nat. Phys. 2023, 19, 1150. [Google Scholar] [CrossRef]
- Sergueev, N.; Sun, Q.F.; Guo, H.; Wang, B.G.; Wang, J. Spin-polarized transport through a quantum dot: Anderson model with on-site Coulomb repulsion. Phys. Rev. B 2002, 65, 165303. [Google Scholar] [CrossRef]
- Braun, M.; Kong, J.; Martinek, J. Theory of transport through quantum-dot spin valves in the weak-coupling regime. Phys. Rev. B 2004, 70, 195345. [Google Scholar] [CrossRef]
- Yuan, Z.; Hals, K.M.; Liu, Y.; Starikov, A.A. Gilbert Damping in Noncollinear Ferromagnets. Phys. Rev. Lett. 2014, 113, 266603. [Google Scholar] [CrossRef]
- Jiménez-Bustamante, J.; Lindner, A.; Koyun, H.N.; Salikhov, R.; Lenz, K.; Lindner, J.; Gallardo, R.A. Static and dynamic properties of noncollinear magnetized ferromagnetic films. Phys. Rev. B 2024, 109, 094403. [Google Scholar] [CrossRef]
- Lertzman-Lepofsky, G.; Terko, A.; Koraltan, S.; Suess, D.; Girt, E.; Abert, C. Energy landscape of noncollinear exchange coupled magnetic multilayers. Phys. Rev. B 2024, 109, 224421. [Google Scholar] [CrossRef]
- Huang, J.; Liu, C.; Cui, Y.; Ling, Y.; Chen, K.; Zhao, K.; Xiao, X.; Yuan, B.; Paul, A. Non-collinear magnetic configuration mediated exchange coupling at the interface of antiferromagnet and rare-earth nanolayers. Sci. Rep. 2022, 12, 21836. [Google Scholar] [CrossRef]
- Deng, S.; Gomonay, O.; Chen, J.; Fischer, G.; He, L.; Wang, C.; Huang, Q.; Shen, F.; Tan, Z.; Zhou, R. Phase transitions associated with magnetic-field induced topological orbital momenta in a non-collinear antiferromagnet. Nat. Commun. 2024, 15, 822. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Tong, S.; Zheng, W.; Sun, Y.; Lu, J.; Lei, N.; Wei, D.; Zhao, J. Noncollinear spin state and unusual magnetoresistance in ferrimagnet Co-Gd. Phys. Rev. Mater. 2022, 6, 014402. [Google Scholar] [CrossRef]
- Zemen, J. Collinear and noncollinear ferrimagnetic phases in Mn4N investigated by magneto-optical Kerr spectroscopy. J. Appl. Phys. 2023, 134, 203902. [Google Scholar] [CrossRef]
- Yu, S.; Xu, Y.; Dai, Y.; Sun, D.; Huang, B.; Wei, W. Electrical control of noncollinear magnetism in VAl2S4 van der Waals structures. Appl. Phys. Lett. 2024, 124, 212903. [Google Scholar] [CrossRef]
- Wang, W.H.; Pan, C.Y.; Liu, C.M.; Lin, W.C.; Jiang, P.H. Chirality-Induced Noncollinear Magnetization and Asymmetric Domain-Wall Propagation in Hydrogenated CoPd Thin Films. ACS Appl. Mater. Interfaces 2022, 14, 20151. [Google Scholar] [CrossRef]
- Lozada-Cassou, M.; Dong, S.H.; Yu, J. Quantum features of semiconductor quantum dots. Phys. Lett. A 2004, 331, 45. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217. [Google Scholar] [CrossRef]
- Swirkowicz, R.; Wilczynski, M.; Wawrzyniak, M.; Barnas, J. Kondo effect in quantum dots coupled to ferromagnetic leads with noncollinear magnetizations. Phys. Rev. B 2006, 73, 193312. [Google Scholar] [CrossRef]
- Simon, P.; Cornaglia, P.S.; Feinberg, D.; Balseiro, C.A. Kondo effect with noncollinear polarized leads: A numerical renormalization group analysis. Phys. Rev. B 2007, 75, 045310. [Google Scholar] [CrossRef]
- Hornberger, R.; Koller, S.; Begemann, G.; Donarini, A.; Grifoni, M. Transport through a double-quantum-dot system with noncollinearly polarized leads. Phys. Rev. B 2008, 77, 245313. [Google Scholar] [CrossRef]
- Chi, F.; Bai, X.F.; Huang, L.; Zhao, J. Spin-dependent transport in a Rashba ring connected to noncollinear ferromagnetic leads. J. Appl. Phys. 2010, 108, 073702. [Google Scholar] [CrossRef]
- Chen, X.B.; Liu, D.P.; Duan, W.H.; Guo, H. Photon-assisted thermoelectric properties of noncollinear spin valves. Phys. Rev. B 2013, 87, 085427. [Google Scholar] [CrossRef]
- Vettoliere, A.; Satariano, R.; Ferraiuolo, R.; Di Palma, L.; Ahmad, H.G.; Ausanio, G.; Pepe, G.P.; Tafuri, F.; Massarotti, D.; Montemurro, D.; et al. High-Quality Ferromagnetic Josephson Junctions Based on Aluminium Electrodes. Nanomaterials 2022, 12, 4155. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Ciria, M.; Ahmad, M.; Plank, H.; Marcuello, C. A Review of the Current State of Magnetic Force Microscopy to Unravel the Magnetic Properties of Nanomaterials Applied in Biological System and Future Directions for Quantum Technologies. Nanomaterials 2023, 13, 2585. [Google Scholar] [CrossRef] [PubMed]
- Dumitrescu, E.; Roberts, B.; Tewari, S.; Sau, J.D.; Das Sarma, S. Majorana fermions in chiral topological ferromagnetic nanowires. Phys. Rev. B 2015, 91, 094505. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Alicea, J.; Oreg, Y.; Refael, G. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 2011, 7, 412. [Google Scholar] [CrossRef]
- Lian, B.; Sun, X.Q.; Vaezi, A.; Zhang, S.C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl. Acad. Sci. USA 2018, 115, 10938. [Google Scholar] [CrossRef]
- Takei, S.; Fregoso, B.M.; Galitski, V.; Sarma, S.D. Topological superconductivity and Majorana fermions in hybrid structures involving cuprate high-Tc superconductors. Phys. Rev. B 2013, 87, 014504. [Google Scholar] [CrossRef]
- Sau, J.D.; Brydon, P.M.R. Bound States of a Ferromagnetic Wire in a Superconductor. Phys. Rev. Lett. 2015, 115, 127003. [Google Scholar] [CrossRef] [PubMed]
- Schneider, L.; Beck, P.; Posske, T.; Crawford, D.; Mascot, E.; Rachel, S.; Wiesendanger, R.; Wiebe, J. Topological Shiba bands in artificial spin chains on superconductors. Nat. Phys. 2021, 17, 943. [Google Scholar] [CrossRef]
- Livanas, G.; Vanas, N.; Varelogiannis, G. Majorana Zero Modes in Ferromagnetic Wires without Spin-Orbit Coupling. Condens. Matter 2021, 6, 44. [Google Scholar] [CrossRef]
- Livanas, G.; Vanas, N.; Sigrist, M.; Varelogiannis, G. Platform for controllable Majorana zero modes using superconductor/ferromagnet heterostructures. Eur. Phys. J. B 2022, 95, 47. [Google Scholar] [CrossRef]
- Chatterjee, P.; Banik, S.; Bera, S.; Ghosh, A.K.; Pradhan, S.; Saha, A.; Nandy, A.K. Topological superconductivity by engineering noncollinear magnetism in magnet/superconductor heterostructures: A realistic prescription for the two-dimensional Kitaev model. Phys. Rev. B 2024, 109, L121301. [Google Scholar] [CrossRef]
- Lee, E.J.; Jiang, X.; Aguado, R.; Katsaros, G.; Lieber, C.M.; De Franceschi, S. Zero-Bias anomaly in a nanowire quantum dot coupled to superconductors. Phys. Rev. Lett. 2012, 109, 186802. [Google Scholar] [CrossRef] [PubMed]
- Lopez, R.; Lee, M.; Serra, L.; Lim, J. Thermoelectrical detection of majorana states. Phys. Rev. B 2014, 89, 205418. [Google Scholar] [CrossRef]
- Deng, M.T.; Vaitiekenas, S.; Prada, E. Nonlocality of Majorana modes in hybrid nanowires. Phys. Rev. B 2018, 98, 085125. [Google Scholar] [CrossRef]
- Jack, B.; Xie, Y.; Yazdani, A. Detecting and distinguishing Majorana zero modes with the scanning tunnelling microscope. Nat. Rev. Phys. 2021, 3, 541. [Google Scholar] [CrossRef]
- Stefanski, P. Tunneling magnetoresistance anomalies in a Coulomb blockaded quantum dot. Phys. Rev. B 2009, 79, 085312. [Google Scholar] [CrossRef]
- Chi, F.; Zeng, H.; Yuan, X.Q. Flux-dependent tunnel magnetoresistance in parallel-coupled double quantum dots. Superlattices Microstruct. 2009, 46, 523. [Google Scholar] [CrossRef]
- Tang, L.W.; Mao, W.G. Detection of Majorana Bound States by Sign Change of the Tunnel Magnetoresistance in a Quantum Dot Coupled to Ferromagnetic Electrodes. Front. Phys. 2020, 8, 00147. [Google Scholar] [CrossRef]
- Liu, D.E.; Baranger, H.U. Detecting a majorana-fermion zero mode using a quantum dot. Phys. Rev. B 2011, 84, 201308R. [Google Scholar] [CrossRef]
- Gorski, G.; Kucab, K. The Spin-Dependent Coupling in the Hybrid Quantum Dot-Majorana Wire System. Phys. Status Solidi B 2019, 256, 1800492. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X. Tunable Josephson Current through a Semiconductor Quantum Dot Hybridized to Majorana Trijunction. Coatings 2023, 13, 1627. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Yi, Z.; Liu, L.; Chi, F. Thermophase Seebeck Coefficient in Hybridized Superconductor-Quantum-Dot-Superconductor Josephson Junction Side-Coupled to Majorana Nanowire. Nanomaterials 2023, 13, 2489. [Google Scholar] [CrossRef]
- Chi, F.; Jia, Q.S.; Liu, J.; Gao, Q.G.; Yi, Z.C.; Liu, L.M. Electronic Tunnelling in Superconductor/Quantum-Dot Josephson Junction Side-Coupled to Majorana Nanowire. Coatings 2023, 13, 612. [Google Scholar] [CrossRef]
- Chi, F.; Jia, Q.S.; Liu, J.; Gao, Q.G.; Yi, Z.C.; Liu, L.M. Enhancement of the Josephson Current in a Quantum Dot Connected to Majorana Nanowires. Nanomaterials 2023, 13, 1482. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.T.; Li, X.Q.; Sun, Q.F. Majorana dc Josephson current mediated by a quantum dot. J. Phys. Condens. Matter 2017, 29, 195301. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev reflection through a quantum dot coupled with two ferromagnets and a superconductor. Phys. Rev. B 2001, 65, 024516. [Google Scholar] [CrossRef]
- Sun, Q.F.; Wang, J.; Lin, T.H. Photon-assisted Andreev tunneling through a mesoscopic hybrid system. Phys. Rev. B 1999, 59, 13126. [Google Scholar] [CrossRef]
- Sun, Q.F.; Wang, J.; Lin, T.H. Control of the supercurrent in a mesoscopic four-terminal Josephson junction. Phys. Rev. B 2000, 62, 648. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev bound states and the π-junction transition in a superconductor/quantum-dot/superconductor system. J. Phys. Condens. Matter 2001, 13, 8783. [Google Scholar] [CrossRef]
- Mathe, L.; Sticlet, D.; Zarbo, L.P. Quantum transport through a quantum dot side-coupled to a Majorana bound state pair in the presence of electron-phonon interaction. Phys. Rev. B 2022, 105, 155409. [Google Scholar] [CrossRef]
- Cheng, S.G.; Sun, Q.F. Josephson current transport through T-shaped double quantum dots. J. Phys. Condens. Matter 2008, 20, 505202. [Google Scholar] [CrossRef]
- Zhang, H.R.; Sun, L.L.; Liu, J. Josephson dc Current through T-Shaped Double-Quantum-Dots Hybridized to Majorana Nanowires. Coatings 2023, 13, 523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.-M.; Shen, Y.-H.; Chi, F.; Yi, Z.-C.; Liu, L.-M. Quantum Transport through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets with Noncollinear Magnetizations. Nanomaterials 2024, 14, 1210. https://doi.org/10.3390/nano14141210
Gao Y-M, Shen Y-H, Chi F, Yi Z-C, Liu L-M. Quantum Transport through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets with Noncollinear Magnetizations. Nanomaterials. 2024; 14(14):1210. https://doi.org/10.3390/nano14141210
Chicago/Turabian StyleGao, Yu-Mei, Yao-Hong Shen, Feng Chi, Zi-Chuan Yi, and Li-Ming Liu. 2024. "Quantum Transport through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets with Noncollinear Magnetizations" Nanomaterials 14, no. 14: 1210. https://doi.org/10.3390/nano14141210
APA StyleGao, Y.-M., Shen, Y.-H., Chi, F., Yi, Z.-C., & Liu, L.-M. (2024). Quantum Transport through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets with Noncollinear Magnetizations. Nanomaterials, 14(14), 1210. https://doi.org/10.3390/nano14141210






