Structured-Light 3D Imaging Based on Vector Iterative Fourier Transform Algorithm
Abstract
1. Introduction
2. Principles and Methods
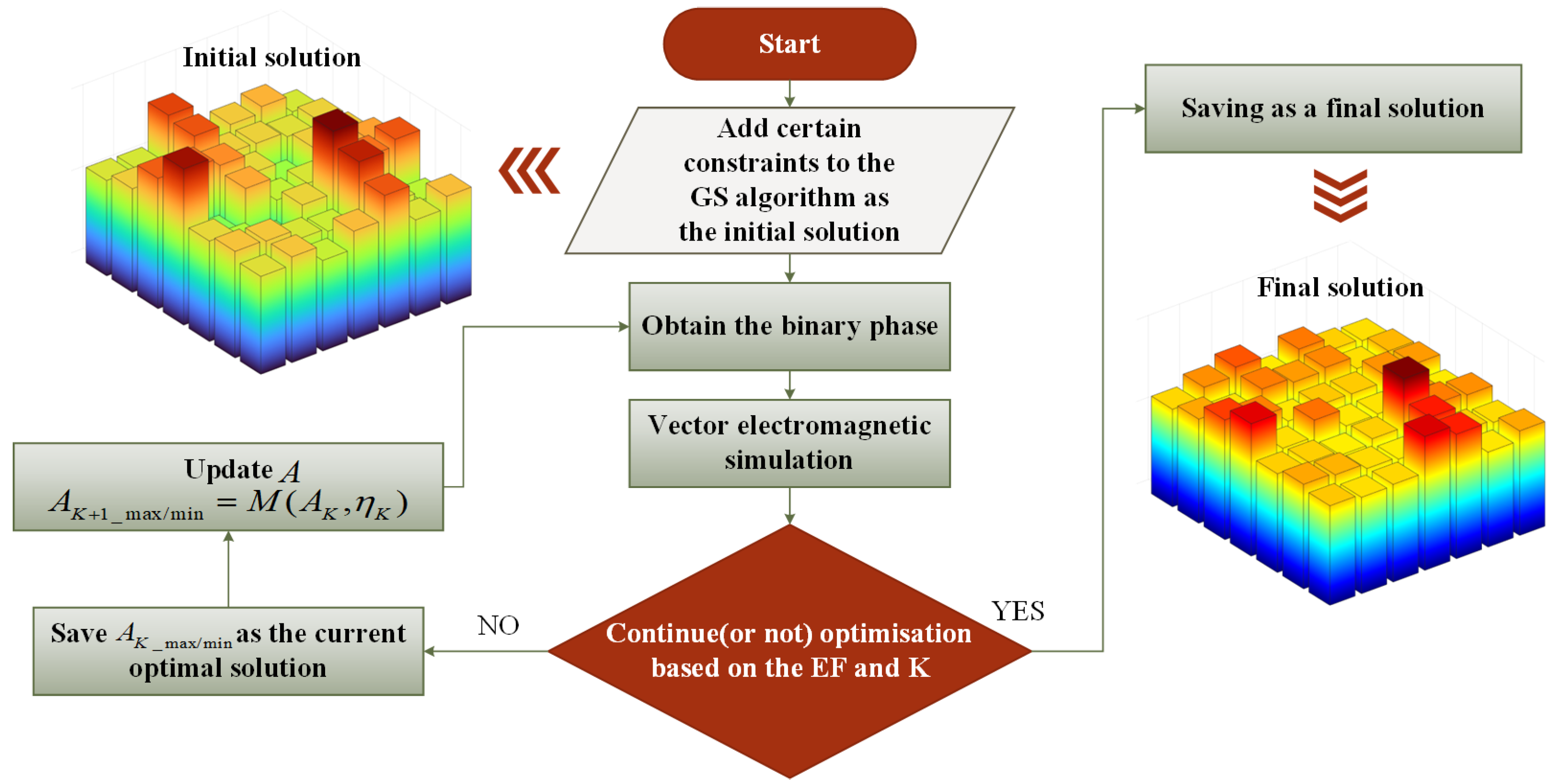
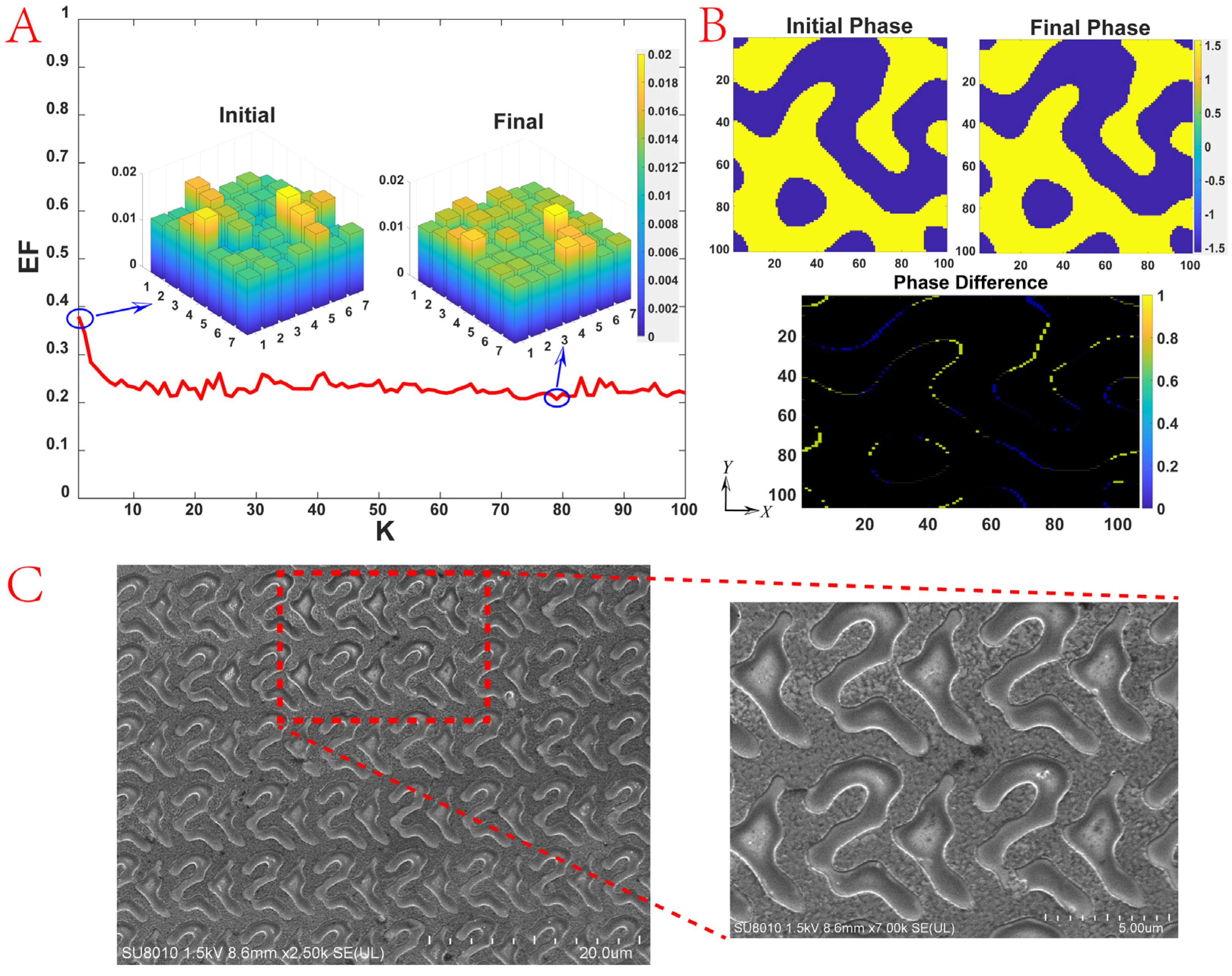
2.1. Design of 7 × 7 DOE with Uniform Energy Distribution
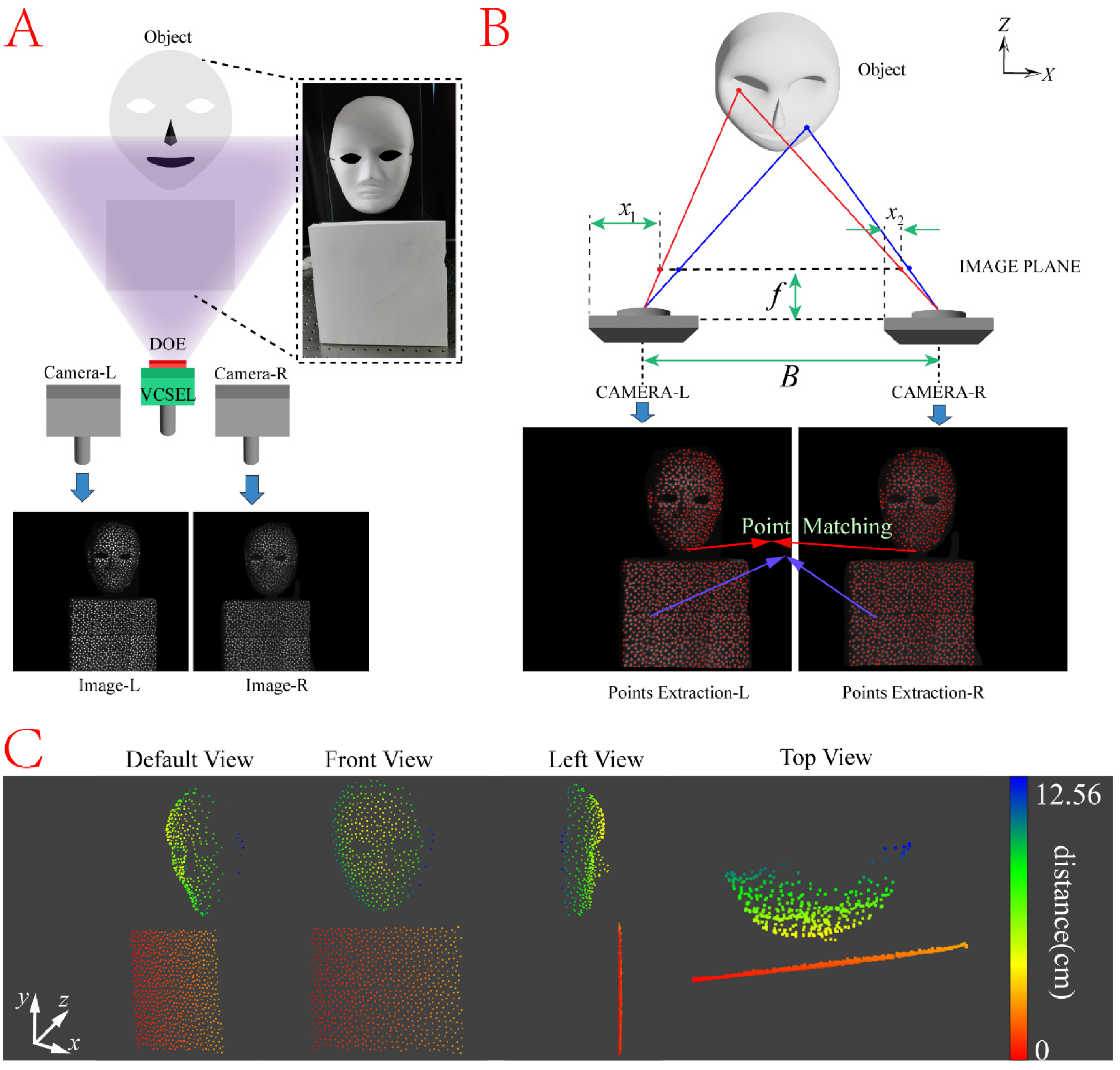
2.2. Point Matching in Structured-Light 3D Imaging and Target Reconstruction
3. Results
3.1. Design of 7 × 7 DOE with Uniform Energy Distribution
3.2. Structured-Light 3D Imaging and Target Reconstruction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, X. Principles of Electromagnetic Waves in Metasurfaces. Sci. China Phys. Mech. Astron. 2015, 58, 594201. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface Holograms for Visible Light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric Gradient Metasurface Optical Elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Tymchenko, M.; Gomez-Diaz, J.S.; Lee, J.; Nookala, N.; Belkin, M.A.; Alù, A. Gradient Nonlinear Pancharatnam-Berry Metasurfaces. Phys. Rev. Lett. 2015, 115, 207403. [Google Scholar] [CrossRef] [PubMed]
- Rubin, N.A.; D’Aversa, G.; Chevalier, P.; Shi, Z.; Chen, W.T.; Capasso, F. Matrix Fourier Optics Enables a Compact Full-Stokes Polarization Camera. Science 2019, 365, eaax1839. [Google Scholar] [CrossRef] [PubMed]
- Rubin, N.A.; Chevalier, P.; Juhl, M.; Tamagnone, M.; Chipman, R.; Capasso, F. Imaging Polarimetry through Metasurface Polarization Gratings. Opt. Express 2022, 30, 9389. [Google Scholar] [CrossRef] [PubMed]
- Teng, J. A Novel Method for Designing Crosstalk-Free Achromatic Full Stokes Imaging Polarimeter. Opto Electron. Adv. 2023, 6, 230113. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, S.; Pu, M.; He, Q.; Jin, J.; Xu, M.; Zhang, Y.; Gao, P.; Luo, X. Spin-Decoupled Metasurface for Simultaneous Detection of Spin and Orbital Angular Momenta via Momentum Transformation. Light Sci. Appl. 2021, 10, 63. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Huang, C.; Pu, M.; Lu, X.; Ma, X.; Guo, Y.; Luo, J.; Luo, X. Transmission–Reflection-Integrated Quadratic Phase Metasurface for Multifunctional Electromagnetic Manipulation in Full Space. Adv. Opt. Mater. 2022, 10, 2102111. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-Optical Controlled-NOT Logic Gate Achieving Directional Asymmetric Transmission Based on Metasurface Doublet. Opto Electron. Adv. 2023, 6, 220073. [Google Scholar] [CrossRef]
- Dănilă, O.; Bărar, A.; Vlădescu, M.; Mănăilă-Maximean, D. An Extended K-Surface Framework for Electromagnetic Fields in Artificial Media. Materials 2021, 14, 7842. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, X.; Liu, S.; Zhang, Y. Highly Efficient Vectorial Field Manipulation Using a Transmitted Tri-Layer Metasurface in the Terahertz Band. Opto Electron. Adv. 2023, 6, 220012. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Q.; Tang, D.; Liu, K.; Zhang, H.; Shi, L.; He, M.; Guo, Y.; Xiao, S. Broadband High-Efficiency Dielectric Metalenses Based on Quasi-Continuous Nanostrips. Opto Electron. Adv. 2024, 7, 230126. [Google Scholar] [CrossRef]
- Danila, O.; Manaila-Maximean, D. Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations. Materials 2021, 14, 2201. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Fan, Y.; Lei, D. Thermally Tunable Binary-Phase VO2 Metasurfaces for Switchable Holography and Digital Encryption. Nanophotonics 2024, 13, 1109–1117. [Google Scholar] [CrossRef]
- He, C.; Zhao, D.; Fan, F.; Zhou, H.; Li, X.; Li, Y.; Li, J.; Dong, F.; Miao, Y.-X.; Wang, Y.; et al. Pluggable Multitask Diffractive Neural Networks Based on Cascaded Metasurfaces. Opto Electron. Adv. 2024, 7, 230005. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, J.; Qiu, T.; Yang, D.; Feng, B.; Chu, Z.; Liu, T.; Han, Y.; Chen, H.; Qu, S.; et al. Direct Field-to-Pattern Monolithic Design of Holographic Metasurface via Residual Encoder-Decoder Convolutional Neural Network. Opto Electron. Adv. 2023, 6, 220148. [Google Scholar] [CrossRef]
- Yuan, G.H.; Zheludev, N.I. Detecting Nanometric Displacements with Optical Ruler Metrology. Science 2019, 364, 771–775. [Google Scholar] [CrossRef] [PubMed]
- Barboza, R.; Babazadeh, A.; Marrucci, L.; Cardano, F.; De Lisio, C.; D’Ambrosio, V. Ultra-Sensitive Measurement of Transverse Displacements with Linear Photonic Gears. Nat. Commun. 2022, 13, 1080. [Google Scholar] [CrossRef]
- Tong, J.; Suo, F.; Ma, J.Y.M.; Tobing, L.; Qian, L.; Hua Zhang, D. Surface Plasmon Enhanced Infrared Photodetection. Opto Electron. Adv. 2019, 2, 18002601–18002610. [Google Scholar] [CrossRef]
- Zhang, F.; Pu, M.; Li, X.; Ma, X.; Guo, Y.; Gao, P.; Yu, H.; Gu, M.; Luo, X. Extreme-Angle Silicon Infrared Optics Enabled by Streamlined Surfaces. Adv. Mater. 2021, 33, 2008157. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary Optics for Achromatic Generation of Perfect Optical Angular Momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef]
- Guo, Y.; Pu, M.; Zhao, Z.; Wang, Y.; Jin, J.; Gao, P.; Li, X.; Ma, X.; Luo, X. Merging Geometric Phase and Plasmon Retardation Phase in Continuously Shaped Metasurfaces for Arbitrary Orbital Angular Momentum Generation. ACS Photonics 2016, 3, 2022–2029. [Google Scholar] [CrossRef]
- Li, J.; Zhang, F.; Pu, M.; Guo, Y.; Li, X.; Ma, X.; Wang, C.; Luo, X. Quasi-Continuous Metasurface Beam Splitters Enabled by Vector Iterative Fourier Transform Algorithm. Materials 2021, 14, 1022. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, C.; Jin, G.; Wang, T. Design of an Omnidirectional Gaze Optical Imaging System with Ultrahigh Resolution. Opt. Rev. 2021, 28, 8–17. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Zhang, W.; Yang, J.K.W. Toward Near-Perfect Diffractive Optical Elements via Nanoscale 3D Printing. ACS Nano 2020, 14, 10452–10461. [Google Scholar] [CrossRef]
- Ho, C.M.B.; Hu, K.; Mishra, A.; Noh, J.; Kim, J.; Lee, S.; Yoon, M.; Yoon, Y.-J. Printing of Woodpile Scaffold Using Fresnel Lens for Tissue Engineering. Int. J. Precis. Eng. Manuf. Green Tech. 2022, 9, 507–522. [Google Scholar] [CrossRef]
- Kim, G.; Kim, Y.; Yun, J.; Moon, S.-W.; Kim, S.; Kim, J.; Park, J.; Badloe, T.; Kim, I.; Rho, J. Metasurface-Driven Full-Space Structured Light for Three-Dimensional Imaging. Nat. Commun. 2022, 13, 5920. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-C.; Chang, C.-H.; Hong, Y.-H.; Kuo, H.-C.; Huang, Y.-W. Metasurface- and PCSEL-Based Structured Light for Monocular Depth Perception and Facial Recognition. Nano Lett. 2024, 24, 1808–1815. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Capasso, F. Tunable Structured Light with Flat Optics. Science 2022, 376, eabi6860. [Google Scholar] [CrossRef]
- Bhattacharya, S. Simplified Mesh Techniques for Design of Beam-Shaping Diffractive Optical Elements. Optik 2008, 119, 321–328. [Google Scholar] [CrossRef]
- Thibault, S.; Arfaoui, A.; Desaulniers, P. Cross-Diffractive Optical Elements for Wide Angle Geometric Camera Calibration. Opt. Lett. 2011, 36, 4770. [Google Scholar] [CrossRef] [PubMed]
- Barlev, O.; Golub, M.A. Multifunctional Binary Diffractive Optical Elements for Structured Light Projectors. Opt. Express 2018, 26, 21092. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, P.; Serio, B.; Raulot, V.; Guilhem, M. Three-Dimensional Shape Measurement Based on Light Patterns Projection Using Diffractive Optical Elements. Proc. SPIE 2010, 7716, 77162I. [Google Scholar] [CrossRef]
- Mellin, S.; Nordin, G. Limits of Scalar Diffraction Theory and an Iterative Angular Spectrum Algorithm for Finite Aperture Diffractive Optical Element Design. Opt. Express 2001, 8, 705. [Google Scholar] [CrossRef] [PubMed]
- Gorthi, S.S.; Rastogi, P. Fringe Projection Techniques: Whither We Are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Sriyotha, P.; Yamazaki, K.; Zhang, X.; Mori, M. An Experimental Study on the Vibration-Free, High-Speed Operation of a Three-Dimensional Coordinate Measuring Machine. J. Manuf. Syst. 2004, 23, 173–181. [Google Scholar] [CrossRef]
- Brown, G.M. Overview of Three-Dimensional Shape Measurement Using Optical Methods. Opt. Eng. 2000, 39, 10. [Google Scholar] [CrossRef]
- Salgado-Remacha, F.J. Laguerre-Gaussian Beams Shaping by Binary Phase Plates as Illumination Sources in Micro-Optics. Appl. Opt. 2014, 53, 6782–6788. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chui, H.; Rangarajan, A. A New Point Matching Algorithm for Non-Rigid Registration. Comput. Vis. Image Underst. 2003, 89, 114–141. [Google Scholar] [CrossRef]
- Tsin, Y.; Kanade, T. A Correlation-Based Approach to Robust Point Set Registration. Comput. Vis. ECCV 2004, 2004, 558–569. [Google Scholar] [CrossRef] [PubMed]
- Myronenko, A.; Song, X. Point Set Registration: Coherent Point Drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B Stat. Methodol. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; ISBN 978-0-19-853849-3. [Google Scholar]
- Pang, H.; Cao, A.; Liu, W.; Shi, L.; Deng, Q. Alternative Design of Dammann Grating for Beam Splitting with Adjustable Zero-Order Light Intensity. IEEE Photonics J. 2019, 11, 1500909. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
| Parameter | Result | |
|---|---|---|
| Camera—Left | Internal Reference Matrix | |
| Distortion Factor | −0.197, 0.183, −0.156, −0.00007, 0.00065 | |
| Camera—Right | Internal Reference Matrix | |
| Distortion Factor | −0.1897, 0.093, 0.1385, −0.00001, −0.0002 | |
| System | Rotation Matrix | |
| Translation Matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Qiao, S.; Luo, Y.; Guo, Y.; Li, X.; Zhang, Q.; Fan, Y.; Zhao, Z.; Luo, X. Structured-Light 3D Imaging Based on Vector Iterative Fourier Transform Algorithm. Nanomaterials 2024, 14, 929. https://doi.org/10.3390/nano14110929
Zhang R, Qiao S, Luo Y, Guo Y, Li X, Zhang Q, Fan Y, Zhao Z, Luo X. Structured-Light 3D Imaging Based on Vector Iterative Fourier Transform Algorithm. Nanomaterials. 2024; 14(11):929. https://doi.org/10.3390/nano14110929
Chicago/Turabian StyleZhang, Runzhe, Siyuan Qiao, Yixiong Luo, Yinghui Guo, Xiaoyin Li, Qi Zhang, Yulong Fan, Zeyu Zhao, and Xiangang Luo. 2024. "Structured-Light 3D Imaging Based on Vector Iterative Fourier Transform Algorithm" Nanomaterials 14, no. 11: 929. https://doi.org/10.3390/nano14110929
APA StyleZhang, R., Qiao, S., Luo, Y., Guo, Y., Li, X., Zhang, Q., Fan, Y., Zhao, Z., & Luo, X. (2024). Structured-Light 3D Imaging Based on Vector Iterative Fourier Transform Algorithm. Nanomaterials, 14(11), 929. https://doi.org/10.3390/nano14110929






