Directly Controlling the Transport Properties of All-Nitride Josephson Junctions by N-Vacancy Defects
Abstract
1. Introduction
2. Materials and Methods
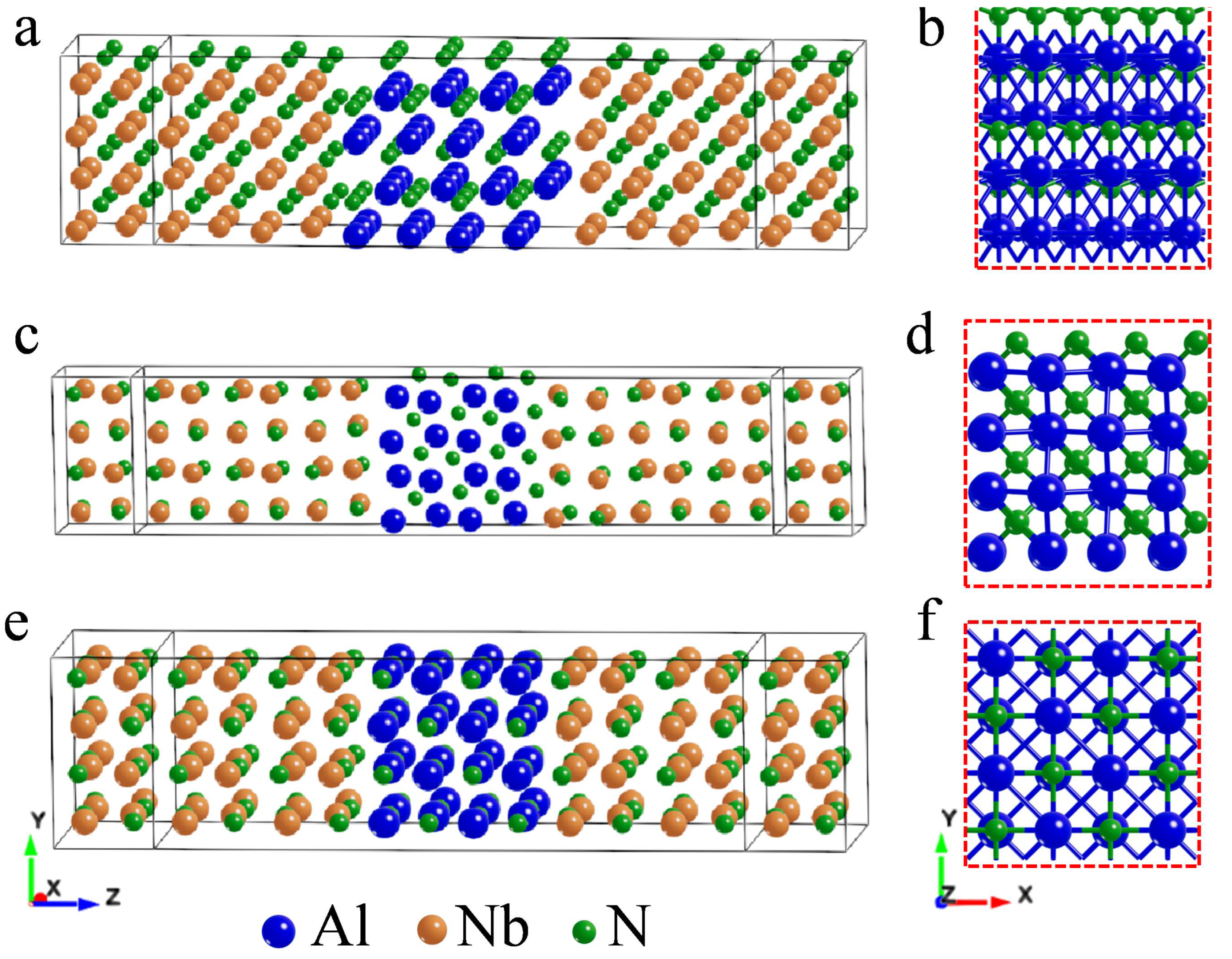
2.1. Designing Defect Models with N Vacancies in the Barrier
2.2. Interface Configuration
2.3. Model Calculation
3. Results and Discussion
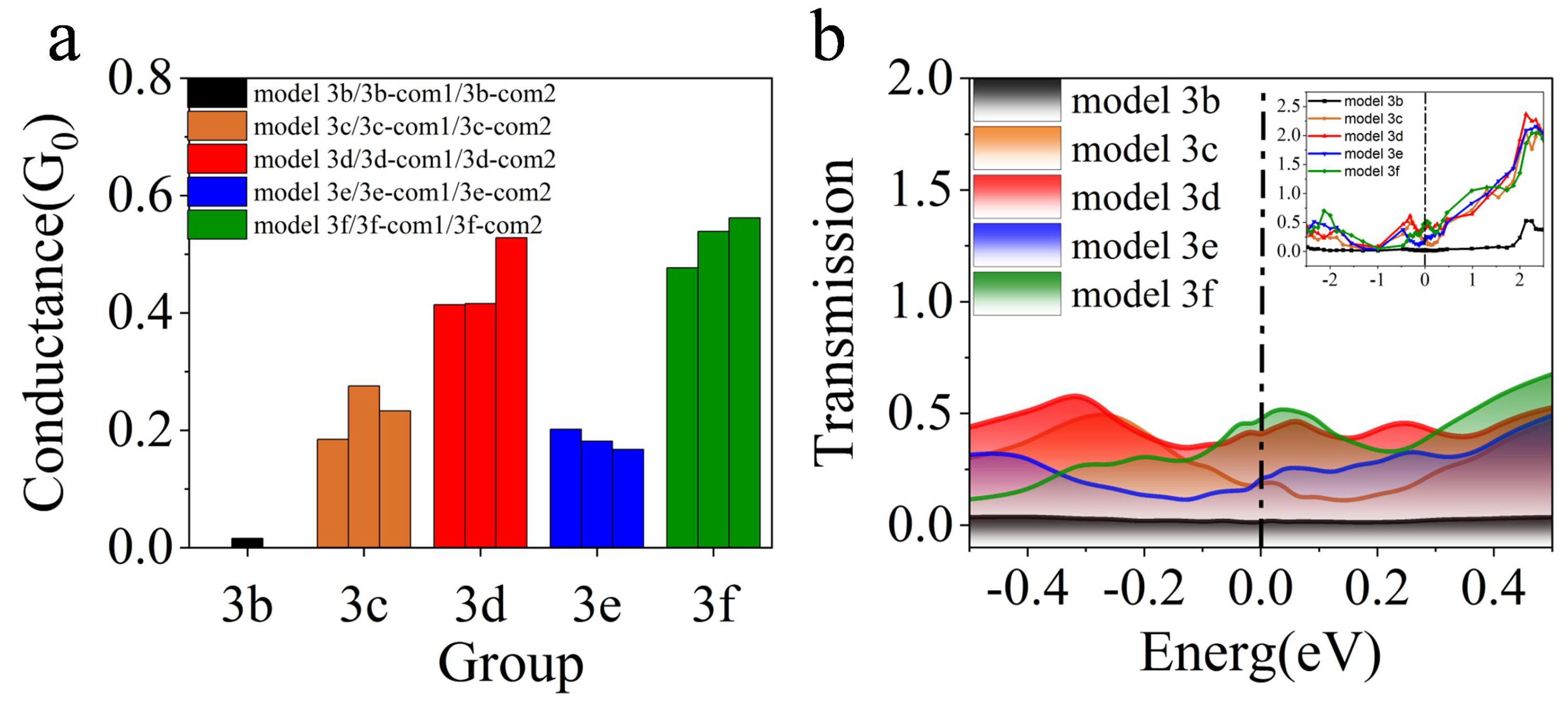
3.1. Electrical Properties of Defect Models
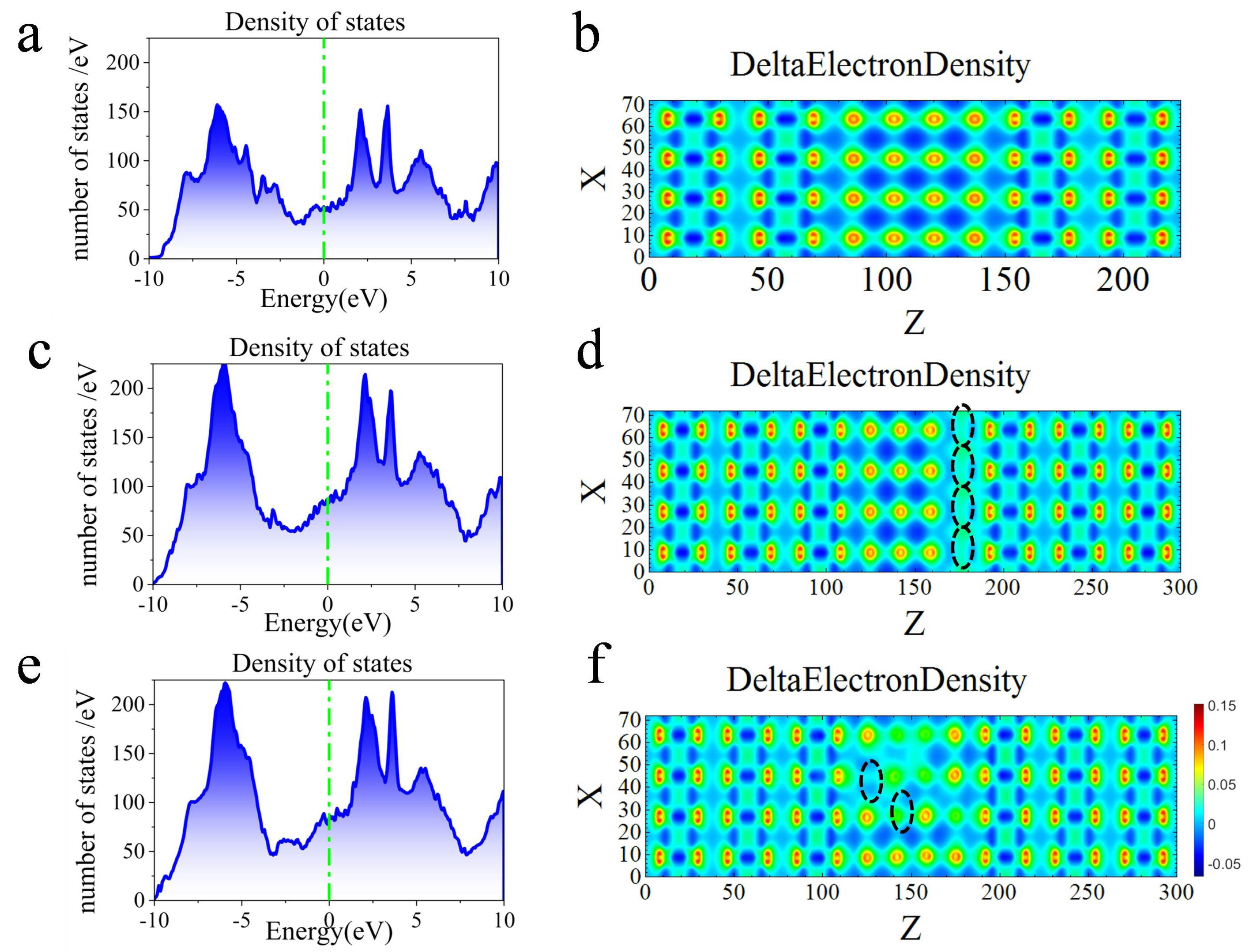
3.2. Electron Density
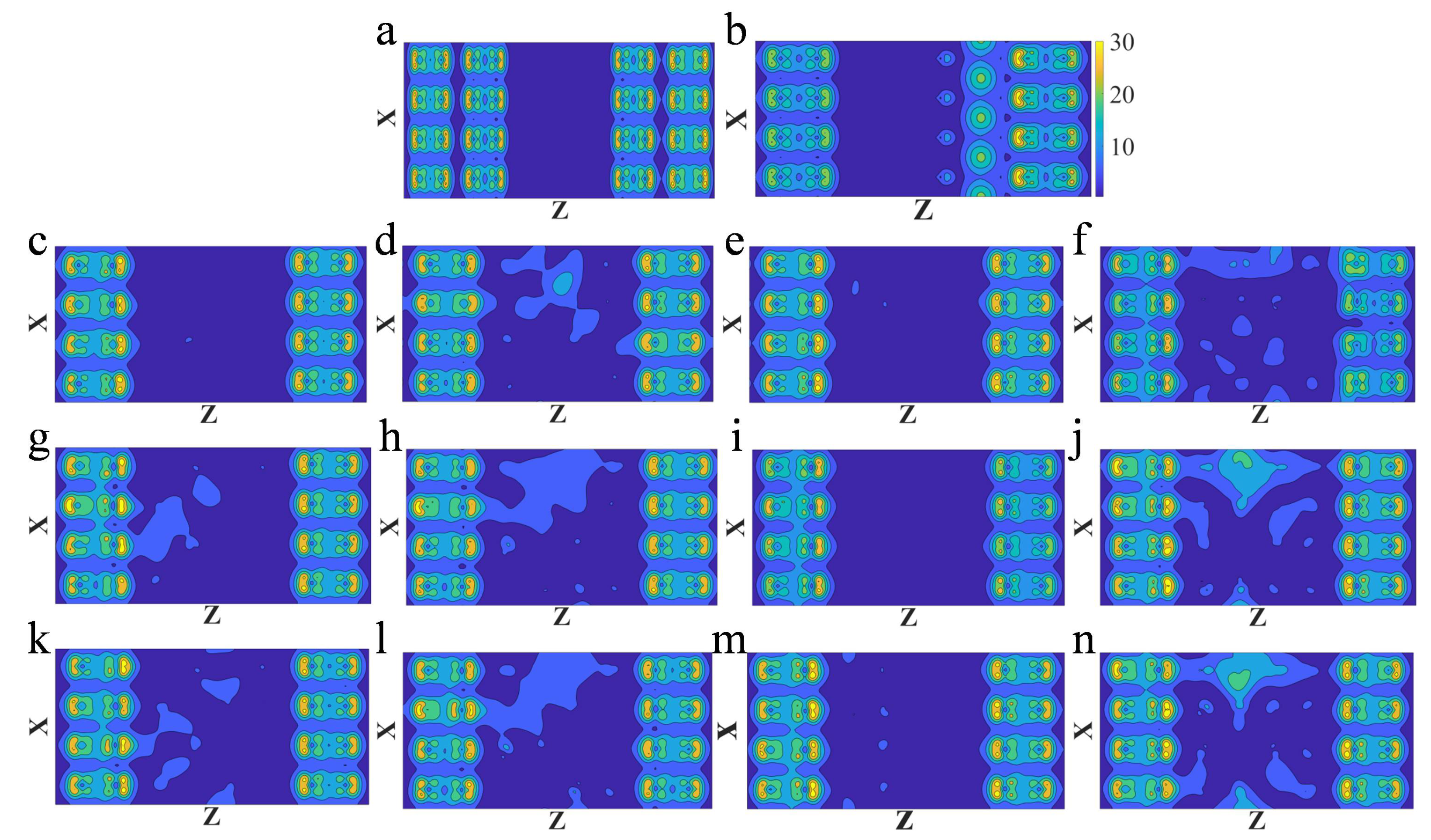
3.3. Analyzing Vacancies Distribution
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. System Models
| Model | Lattice Constant(Å) | Miller Indices | Supercell | Mismatch | Binding Energy (eV) | |||
|---|---|---|---|---|---|---|---|---|
| NbN | AlN | NbN | AlN | NbN | AlN | |||
| model 1 | a = 3.39 | a = 3.13 | 100 | 100 | 2*2*1 | 3*2*2 | 2.3% | 1295.76 |
| model 2 | a = 3.15 | a = 3.11 | 100 | 001 | 1*2*1 | 2*2*2 | 0.6% | 677.80 |
| model 3 | a = 3.15 | a = 2.88 | 100 | 001 | 2*2*1 | 2*2*2 | 0.03% | 1329.80 |
Appendix A.2. Optimizing Models
Appendix A.3. Electrical Properties of Defect-Free Models

References
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Oliver, W.D.; Welander, P.B. Materials in superconducting quantum bits. MRS Bull. 2013, 38, 816–825. [Google Scholar] [CrossRef]
- Nakamura, Y.; Terai, H.; Inomata, K.; Yamamoto, T.; Qiu, W.; Wang, Z. Superconducting qubits consisting of epitaxially grown NbN/AlN/NbN Josephson junctions. Appl. Phys. Lett. 2011, 99, 212502. [Google Scholar] [CrossRef]
- Qiu, W.; Makise, K.; Terai, H.; Wang, Z. Developing superconducting flux qubit by using epitaxial NbN/AlN/NbN junction. Phys. Procedia 2012, 36, 360–364. [Google Scholar] [CrossRef]
- Brown, K.R.; Chiaverini, J.; Sage, J.M.; Häffner, H. Materials challenges for trapped-ion quantum computers. Nat. Rev. Mater. 2021, 6, 892–905. [Google Scholar] [CrossRef]
- Wu, Y.; Ying, L.L.; Li, G.Q.; Zhang, X.; Peng, W.; Ren, J.; Wang, Z. Film stress influence on Nb/Al-AlO x/Nb Josephson junctions. IEEE Trans. Appl. Supercond. 2019, 29, 1102105. [Google Scholar] [CrossRef]
- Place, A.P.M.; Rodgers, L.V.H.; Mundada, P.; Smitham, B.M.; Fitzpatrick, M.; Leng, Z.Q.; Premkumar, A.; Bryon, J.; Vrajitoarea, A.; Sussman, S.; et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 2021, 12, 1779. [Google Scholar] [CrossRef]
- Makise, K.; Sun, R.; Terai, H.; Wang, Z. Fabrication and characterization of epitaxial TiN-based Josephson junctions for superconducting circuit applications. IEEE Trans. Appl. Supercond. 2014, 25, 1100204. [Google Scholar] [CrossRef]
- Kim, S.; Terai, H.; Yamashita, T.; Qiu, W.; Fuse, T.; Yoshihara, F.; Ashhab, S.; Inomata, K.; Semba, K. Enhanced coherence of all-nitride superconducting qubits epitaxially grown on silicon substrate. Commun. Mater. 2021, 2, 98. [Google Scholar] [CrossRef]
- Kjaergaard, M.; Schwartz, M.E.; Braumüller, J.; Krantz, P.; Wang, J.I.-J.; Gustavsson, S.; Oliver, W.D. Superconducting qubits: Current state of play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. [Google Scholar] [CrossRef]
- Wang, Z.; Kawakami, A.; Uzawa, Y.; Komiyama, B. High critical current density NbN/AlN/NbN tunnel junctions fabricated on ambient temperature MgO substrates. Appl. Phys. Lett. 1994, 64, 2034–2036. [Google Scholar] [CrossRef]
- Merker, M.; Bohn, C.; Völlinger, M.; Ilin, K.; Siegel, M. High critical current density NbN/AlN/NbN tunnel junctions fabricated on ambient temperature MgO substrates. IEEE Trans. Appl. Supercond. 2016, 27, 1–5. [Google Scholar] [CrossRef]
- All-Nitride Superconducting Qubit Made on a Silicon Substrate. Available online: https://www.sciencedaily.com/releases/2021/09/210920100915.htm (accessed on 30 October 2021).
- de Espiau, L.R.; Odier, P.; Villégier, J.-C. Microstructure of NbN epitaxial ultrathin films grown on A-, M-, and R-plane sapphire. Appl. Phys. Lett. 2007, 91, 232501. [Google Scholar] [CrossRef]
- Wang, Z.; Terai, H.; Qiu, W.; Makise, K.; Uzawa, Y.; Kimoto, K.; Nakamura, Y. High-quality epitaxial NbN/AlN/NbN tunnel junctions with a wide range of current density. Appl. Phys. Lett. 2013, 102, 142604. [Google Scholar] [CrossRef]
- Wang, Z.; Kawakami, A.; Uzawa, Y.; Komiyama, B. Superconducting properties and crystal structures of single-crystal niobium nitride thin films deposited at ambient substrate temperature. J. Appl. Phys. 1996, 79, 7837–7842. [Google Scholar] [CrossRef]
- Gao, J.R.; Hajenius, M.; Tichelaar, F.D.; Klapwijk, T.M.; Voronov, B.; Grishin, E.; Gol’Tsman, G.; Zorman, C.A.; Mehregany, M. Monocrystalline NbN nanofilms on a 3 C-Si C/Si substrate. Appl. Phys. Lett. 2007, 91, 062504. [Google Scholar] [CrossRef]
- Mino, T.; Hirayama, H.; Takano, T.; Tsubaki, K.; Sugiyama, M. Characteristics of epitaxial lateral overgrowth AlN templates on (111) Si substrates for AlGaN deep-UV LEDs fabricated on different direction stripe patterns. Phys. Status Solid C 2012, 9, 802–805. [Google Scholar] [CrossRef]
- Wang, Z.; Terai, H.; Kawakami, A.; Uzawa, Y. Interface and tunneling barrier heights of NbN/AlN/NbN tunnel junctions. Appl. Phys. Lett. 1999, 75, 701–703. [Google Scholar] [CrossRef]
- Lucci, M.; Thanh, H.N.; Davoli, I. Electron spectroscopy analysis on NbN to grow and characterize NbN/AlN/NbN Josephson junction. Superlattices Microstruct. 2008, 43, 518–523. [Google Scholar] [CrossRef]
- Qiu, W.; Terai, H. Fabrication of deep-sub-micrometer NbN/AlN/NbN epitaxial junctions on a Si-substrate. Appl. Phys. Express 2020, 13, 126501. [Google Scholar]
- Tea, E.; Huang, J.Q.; Li, G.; Hin, C. Atomic bonding and electrical potential at metal/oxide interfaces, a first principle study. J. Chem. Phys. 2017, 146, 124706. [Google Scholar] [CrossRef] [PubMed]
- John, H.D.F.; Miguel, J.; Espitia, R.; Octavio, J.S.P. DFT study of structural and electronic properties of TiN/AlN/TiN interlayer. Int. J. Appl. Eng. Res. 2018, 13, 13734–13736. [Google Scholar]
- Zhang, L.B.; Yan, H.; Zhu, G.; Liu, S.; Gan, Z.Y. Molecular dynamics simulation of aluminum nitride deposition: Temperature and N: Al ratio effects. R. Soc. Open Sci. 2018, 5, 180629. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.P. Research on Resistive Random Memory Based on Aluminum Nitride. Master’s Thesis, Xidian University, Xi’an, China, 2021. [Google Scholar]
- Zhang, D.; Liu, F.M.; Cai, L.G. N vacancy, substitutional O, and Al defects in the bandgap of composition-tunable nonstoichiometric AlN powder. Chin. Phys. B 2014, 23, 67803. [Google Scholar] [CrossRef]
- Makise, K.; Terai, H.; Uzawa, Y. NbN/AlN/NbN/TiN tunnel junctions on Si (100) substrate for superconducting devices. IEEE Trans. Appl. Supercond. 2016, 26, 1100403. [Google Scholar] [CrossRef]
- Sun, R.; Makise, K.; Zhang, L.; Terai, H.; Wang, Z. Epitaxial NbN/AlN/NbN tunnel junctions on Si substrates with TiN buffer layers. AIP Adv. 2016, 6, 065119. [Google Scholar] [CrossRef]
- Qu, Y.P. First Principles of Two-Dimensional Aluminum Nitride Nanosheets. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2019. [Google Scholar]
- Jung, H.; Kim, Y.; Jung, K.; Im, H.; Pashkin, Y.A.; Astafiev, O.; Nakamura, Y.; Lee, H.; Miyamoto, Y.; Tsai, J.S. Potential barrier modification and interface states formation in metal-oxide-metal tunnel junctions. Phys. Rev. B 2009, 80, 125413. [Google Scholar] [CrossRef]
- Zeng, L.J.; Tran, D.T.; Tai, C.W.; Svensson, G.; Olsson, E. Atomic structure and oxygen deficiency of the ultrathin aluminium oxide barrier in Al/AlOx/Al Josephson junctions. Sci. Rep. 2016, 6, 29679. [Google Scholar] [CrossRef]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Impact of oxygen vacancy ordering on the formation of a conductive filament in TiO2 for resistive switching memory. IEEE Electron Device Lett. 2010, 13, 197–199. [Google Scholar]
- Li, L. The Mechanism of Resistive Switching and Catalysis on Defective Titania: First-Principle Analysis. Ph.D. Thesis, Soochow University, Soochow, China, 2016. [Google Scholar]
- Hao, C.L. Preparation and Characteristics of Aluminum Nitride Thin Film. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Cyster, M.J.; Smith, J.S.; Vaitkus, J.A.; Vogt, N.; Russo, S.P.; Cole, J.H. Effect of atomic structure on the electrical response of aluminum oxide tunnel junctions. Phys. Rev. Res. 2020, 2, 013110. [Google Scholar] [CrossRef]
- Liu, L. Theoretical Study of Intrinsic Defects and Oxygen-Vacancy Distribution in In2O3. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. [Google Scholar]
- Janotti, A.; Van de Walle, C.G. Oxygen vacancies in ZnO. Appl. Phys. Lett. 2005, 87, 122102. [Google Scholar] [CrossRef]
- Clark, S.J.; Robertson, J.; Lany, S.; Zunger, A. Intrinsic defects in ZnO calculated by screened exchange and hybrid density functionals. Phys. Rev. B 2010, 81, 115311. [Google Scholar] [CrossRef]
- Zhang, X.P.; Tang, F.W.; Wang, M.; Zhan, W.B.; Hu, H.X.; Li, Y.R.; Friend, R.H.; Song, X.Y. Femtosecond visualization of oxygen vacancies in metal oxides. Sci. Adv. 2020, 6, eaax9427. [Google Scholar] [CrossRef] [PubMed]
- Holec, D.; Franz, R.; Mayrhofer, P.H.; Mitterer, C. Structure and stability of phases within the NbN–AlN system. J. Phys. D Appl. Phys. 2010, 43, 145403. [Google Scholar] [CrossRef]
- Koberidze, M.; Puska, M.J.; Nieminen, R.M. Structural details of Al/Al2O3 junctions and their role in the formation of electron tunnel barriers. Phys. Rev. B 2018, 97, 195406. [Google Scholar] [CrossRef]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]


| Model | The Upper Interface | The Lower Interface | ||
|---|---|---|---|---|
| Al-N(Å) | N-Nb(Å) | Al-N(Å) | N-Nb(Å) | |
| Relaxation before | 2.090 | 2.248 | 2.265 | 2.448 |
| 3 | 1.991 | 2.292 | 1.996 | 2.296 |
| 3b | 1.982 | — * | 1.959 | 2.318 |
| 3c | 1.928 | 2.388 | 1.916 | 2.406 |
| 3c-com1 | 1.939 | 2.355 | 1.916 | 2.411 |
| 3c-com2 | 1.932 | 2.413 | 1.917 | 2.442 |
| 3d | 1.930 | 2.357 | 1.931 | 2.349 |
| 3d-com1 | 1.935 | 2.365 | 1.939 | 2.348 |
| 3d-com2 | 1.946 | 2.382 | 1.943 | 2.394 |
| 3e | 1.914 | 2.378 | 1.904 | 2.398 |
| 3e-com1 | 1.923 | 2.405 | 1.912 | 2.472 |
| 3e-com2 | 1.920 | 2.389 | 1.915 | 2.425 |
| 3f | 1.938 | 2.344 | 1.921 | 2.446 |
| 3f-com1 | 1.919 | 2.417 | 1.927 | 2.400 |
| 3f-com2 | 1.920 | 2.408 | 1.927 | 2.406 |
| Model | Vacancy Distribution | Variance of Vacancy Distribution | Conductance (G0) | Average Growth Rate (%) |
|---|---|---|---|---|
| 3 | — * | — * | 0.0032 | — * |
| 3b | (8, 0, 0, 0) | 12 | 0.0155 | 3.8 |
| 3c | (0, 3, 2, 3) | 1.5 | 0.1845 | 71.2 |
| 3c-com1 | (0, 3, 2, 3) | 1.5 | 0.276 | |
| 3c-com2 | (0, 3, 2, 3) | 1.5 | 0.2328 | |
| 3e | (2, 1, 1, 4) | 1.5 | 0.2018 | 56.3 |
| 3e-com1 | (2, 1, 1, 4) | 1.5 | 0.1813 | |
| 3e-com2 | (2, 1, 1, 4) | 1.5 | 0.1671 | |
| 3d | (1, 2, 3, 2) | 0.5 | 0.4138 | 140.4 |
| 3d-com1 | (1, 2, 3, 2) | 0.5 | 0.4157 | |
| 3d-com2 | (1, 2, 3, 2) | 0.5 | 0.5278 | |
| 3f | (2, 2, 2, 2) | 0 | 0.4767 | 163.3 |
| 3f-com1 | (2, 2, 2, 2) | 0 | 0.5386 | |
| 3f-com2 | (2, 2, 2, 2) | 0 | 0.5621 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, J.; Sun, H.; Hu, Y.; Wang, S.; Han, C.; Shan, Z. Directly Controlling the Transport Properties of All-Nitride Josephson Junctions by N-Vacancy Defects. Nanomaterials 2023, 13, 542. https://doi.org/10.3390/nano13030542
Qiu J, Sun H, Hu Y, Wang S, Han C, Shan Z. Directly Controlling the Transport Properties of All-Nitride Josephson Junctions by N-Vacancy Defects. Nanomaterials. 2023; 13(3):542. https://doi.org/10.3390/nano13030542
Chicago/Turabian StyleQiu, Junling, Huihui Sun, Yibin Hu, Shuya Wang, Chuanbing Han, and Zheng Shan. 2023. "Directly Controlling the Transport Properties of All-Nitride Josephson Junctions by N-Vacancy Defects" Nanomaterials 13, no. 3: 542. https://doi.org/10.3390/nano13030542
APA StyleQiu, J., Sun, H., Hu, Y., Wang, S., Han, C., & Shan, Z. (2023). Directly Controlling the Transport Properties of All-Nitride Josephson Junctions by N-Vacancy Defects. Nanomaterials, 13(3), 542. https://doi.org/10.3390/nano13030542






