Engulfment and Pushing of Cylindrical Liquid Nano-Inclusion by Advancing Crystal/Melt Interface: An Atomistic Simulation Study
Abstract
:1. Introduction
2. Simulation Methodology
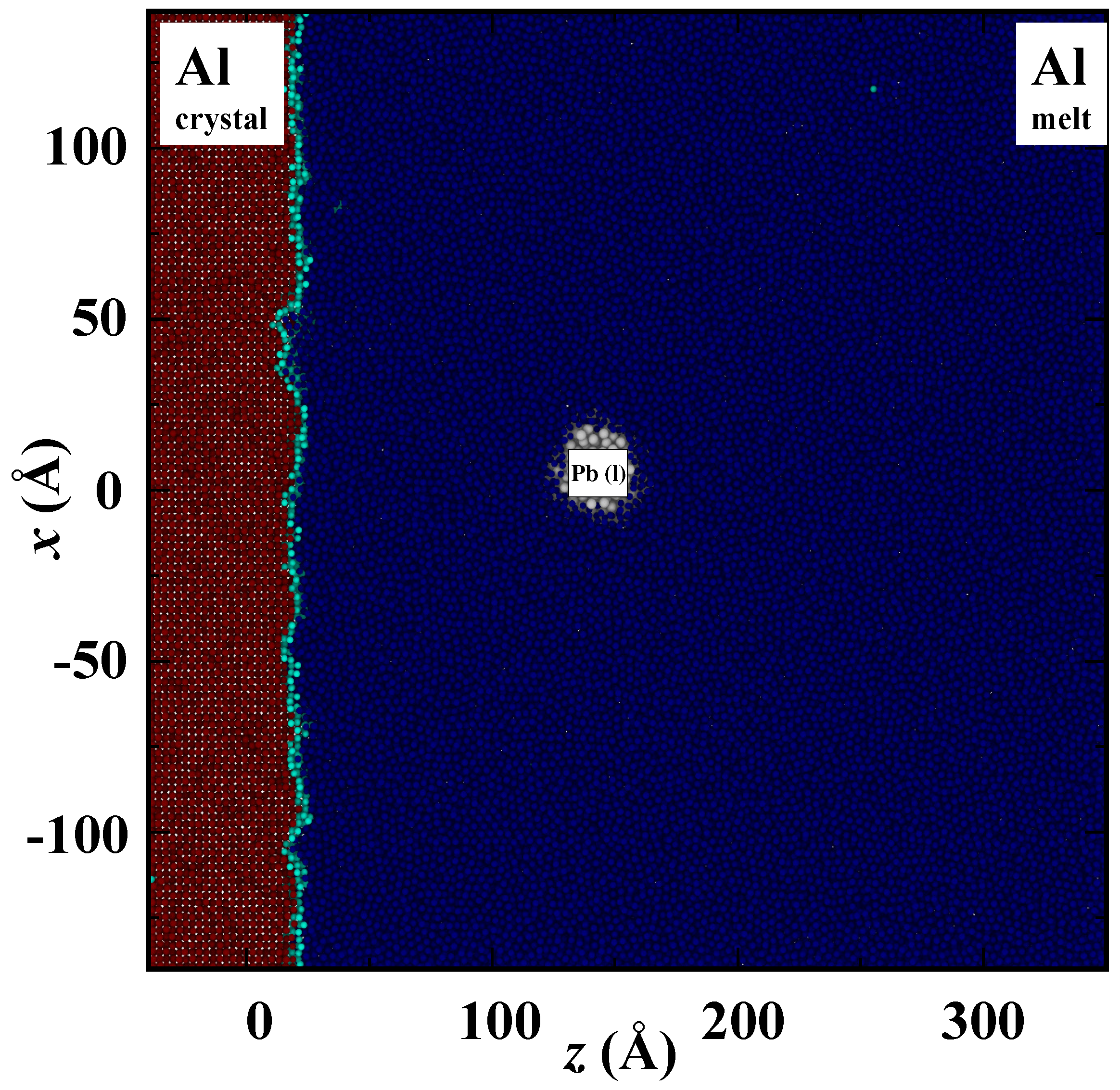
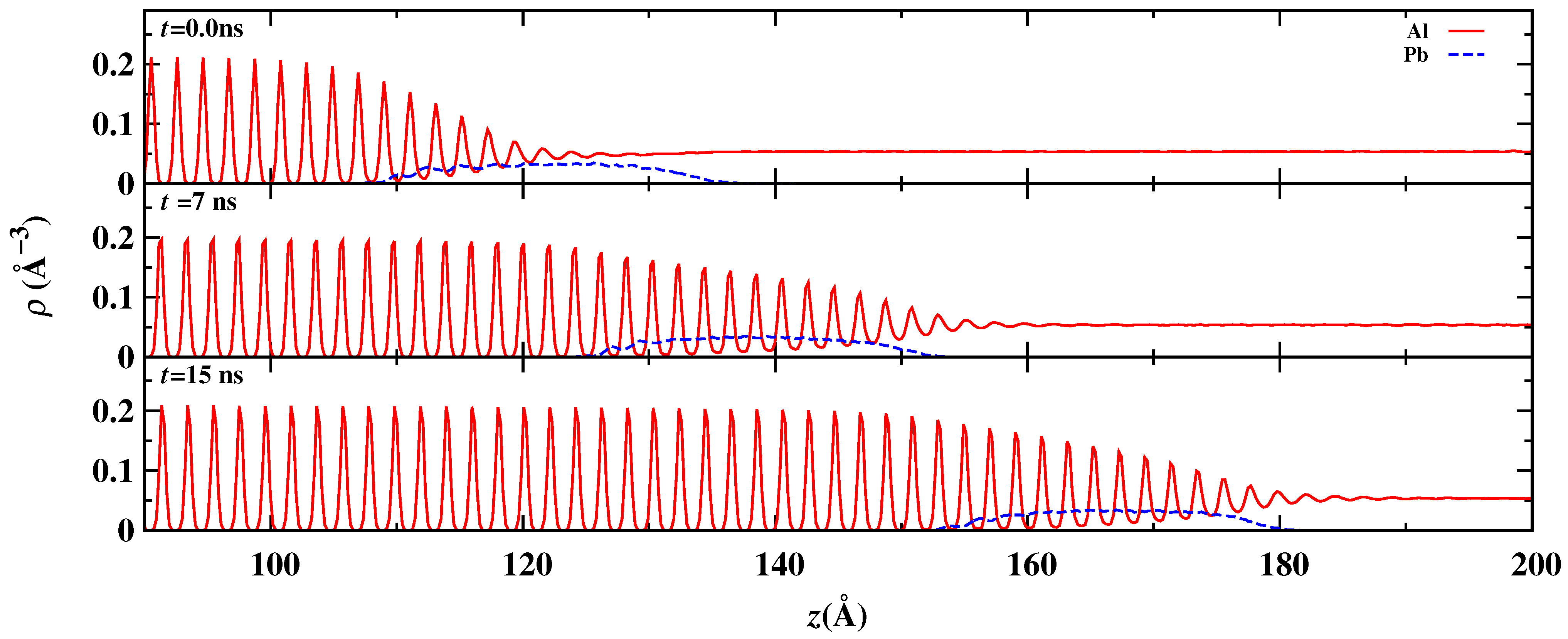
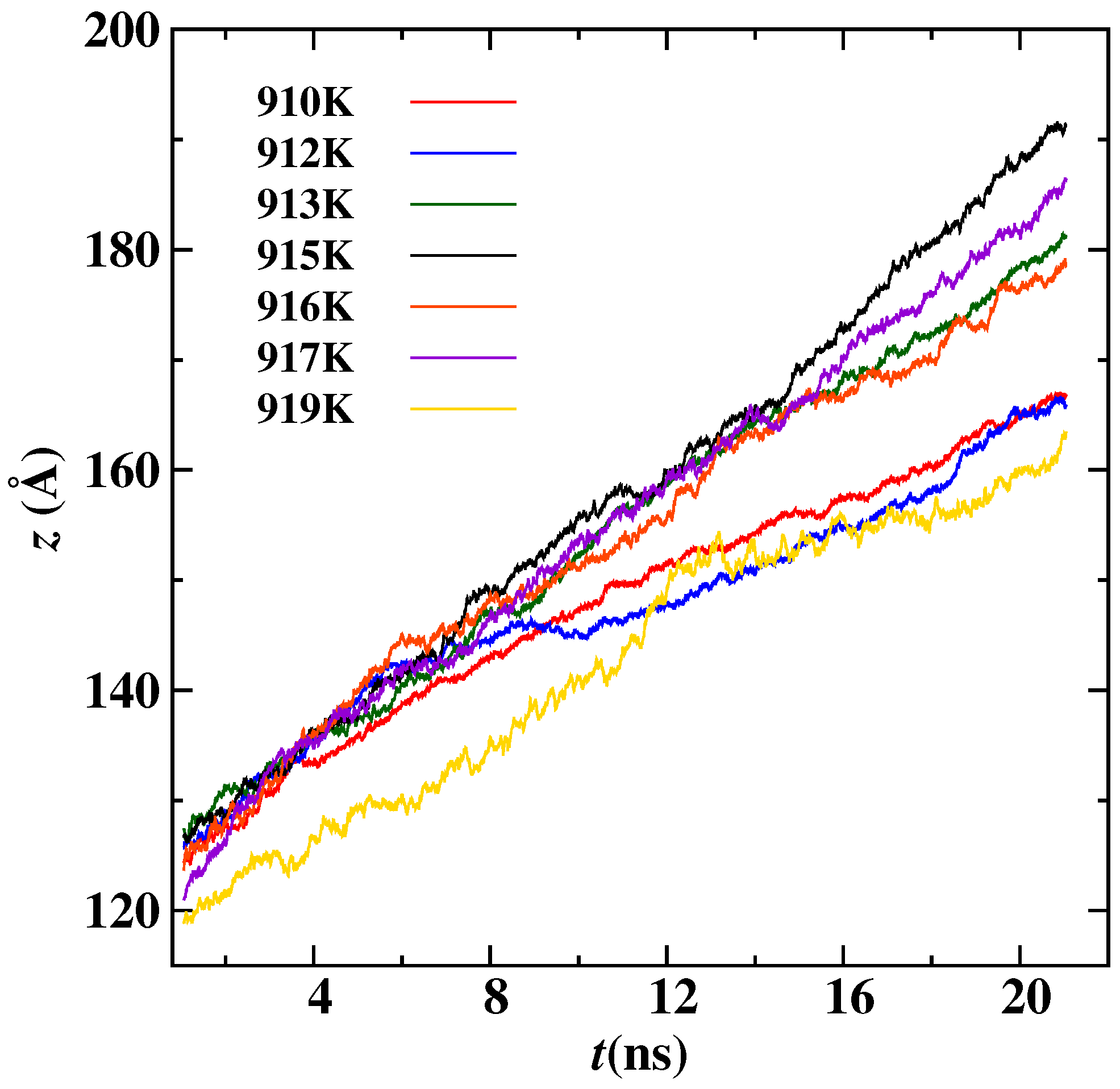
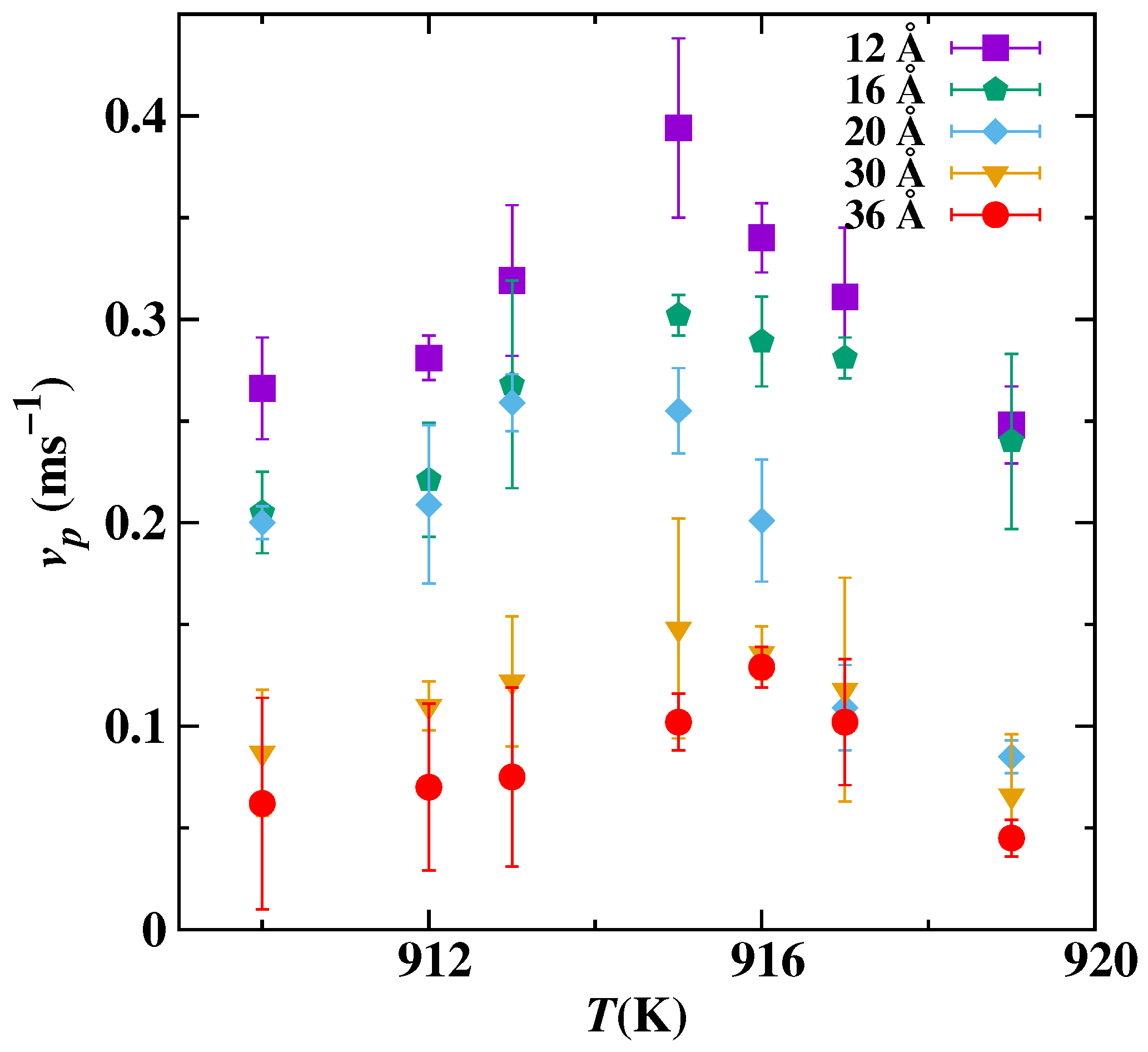
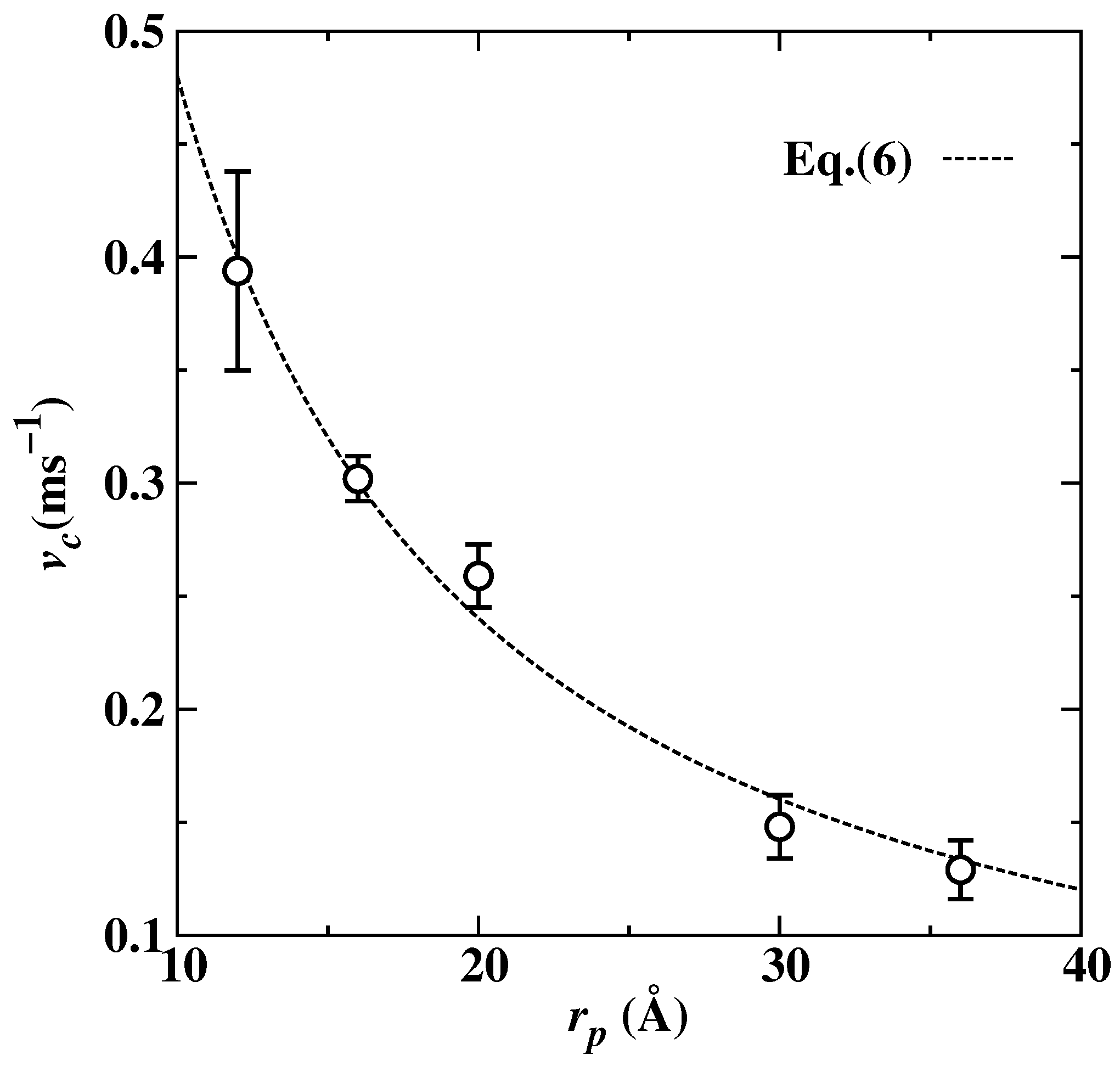
3. Results
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stefanescu, D.; Dhindaw, B.; Kacar, S.; Moitra, A. Behavior of ceramic particles at the solid-liquid metal interface in metal matrix composites. Metall. Trans. A 1988, 19, 2847–2855. [Google Scholar] [CrossRef]
- Zhang, H.; Hussain, I.; Brust, M.; Butler, M.F.; Rannard, S.P.; Cooper, A.I. Aligned two-and three-dimensional structures by directional freezing of polymers and nanoparticles. Nat. Mater. 2005, 4, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Rempel, A.; Worster, M. The interaction between a particle and an advancing solidification front. J. Cryst. Growth 1999, 205, 427–440. [Google Scholar] [CrossRef]
- Rempel, A.; Worster, M. Particle trapping at an advancing solidification front with interfacial-curvature effects. J. Cryst. Growth 2001, 223, 420–432. [Google Scholar] [CrossRef]
- Park, M.S.; Golovin, A.A.; Davis, S.H. The encapsulation of particles and bubbles by an advancing solidification front. J. Fluid Mech. 2006, 560, 415. [Google Scholar] [CrossRef]
- Garvin, J.; Yang, Y.; Udaykumar, H. Multiscale modeling of particle–solidification front dynamics, Part I: Methodology. Int. J. Heat Mass Transf. 2007, 50, 2952–2968. [Google Scholar] [CrossRef]
- Tao, Y.; Sorgenfrei, T.; Jauß, T.; Cröll, A.; Reimann, C.; Friedrich, J.; Derby, J.J. Particle engulfment dynamics under oscillating crystal growth conditions. J. Cryst. Growth 2017, 468, 24–27. [Google Scholar] [CrossRef]
- Tao, Y.; Yeckel, A.; Derby, J.J. Analysis of particle engulfment during the growth of crystalline silicon. J. Cryst. Growth 2016, 452, 1–5. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Tomsia, A.P. Ice-templated porous alumina structures. Acta Mater. 2007, 55, 1965–1974. [Google Scholar] [CrossRef]
- Hashim, J.; Looney, L.; Hashmi, M. Particle distribution in cast metal matrix composites—Part I. J. Mater. Process. Technol. 2002, 123, 251–257. [Google Scholar] [CrossRef]
- Gan, K.; Chen, N.; Wang, Y.; Gu, M. SiC/Cu composites with tungsten coating prepared by powder metallurgy. Mater. Sci. Technol. 2007, 23, 119–122. [Google Scholar] [CrossRef]
- Asthana, R.; Tewari, S. The engulfment of foreign particles by a freezing interface. J. Mater. Sci. 1993, 28, 5414–5425. [Google Scholar] [CrossRef]
- Lloyd, D. The solidification microstructure of particulate reinforced aluminium/SiC composites. Compos. Sci. Technol. 1989, 35, 159–179. [Google Scholar] [CrossRef]
- Liu, L.; Nakano, S.; Kakimoto, K. Carbon concentration and particle precipitation during directional solidification of multicrystalline silicon for solar cells. J. Cryst. Growth 2008, 310, 2192–2197. [Google Scholar] [CrossRef]
- Körber, C. Phenomena at the advancing ice–liquid interface: Solutes, particles and biological cells. Q. Rev. Biophys. 1988, 21, 229–298. [Google Scholar] [CrossRef] [PubMed]
- Bronstein, V.; Itkin, Y.; Ishkov, G. Rejection and capture of cells by ice crystals on freezing aqueous solutions. J. Cryst. Growth 1981, 52, 345–349. [Google Scholar] [CrossRef]
- Shangguan, D.; Ahuja, S.; Stefanescu, D. An analytical model for the interaction between an insoluble particle and an advancing solid/liquid interface. Metall. Trans. A 1992, 23, 669–680. [Google Scholar] [CrossRef]
- Dash, J.; Rempel, A.; Wettlaufer, J. The physics of premelted ice and its geophysical consequences. Rev. Mod. Phys. 2006, 78, 695. [Google Scholar] [CrossRef]
- Rahman, M.S. Handbook of Food Preservation; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Cisse, J.; Bolling, G. The steady-state rejection of insoluble particles by salol grown from the melt. J. Cryst. Growth 1971, 11, 25–28. [Google Scholar] [CrossRef]
- Chen, K.H.; Wilcox, W.R. Anomalous influence of body force on trapping of foreign particles during solidification. J. Cryst. Growth 1977, 40, 214–220. [Google Scholar] [CrossRef]
- Kuo, V.H.; Wilcox, W.R. Particle Chromatography. Sep. Sci. 1973, 8, 375–377. [Google Scholar] [CrossRef]
- Stefanescu, D.; Catalina, A.; Juretzko, F.R.; Sen, S.; Curreri, P. Particle Engulfment and Pushing By Solidifying Interfaces-Recent Theoretical and Experimental Developments; NASA Marshall Space Flight Center: Huntsville, AL, USA, 2003.
- Nota, F.; Savino, R.; Fico, S. The interaction between drops and solidification front in presence of Marangoni effect. Acta Astronaut. 2006, 59, 20–31. [Google Scholar] [CrossRef]
- Omenyi, S. Attraction and Repulsion of Particles by Solidification Fronts. Ph.D. Dissertation, University of Toronto, Toronto, ON, Canada, 1978; p. 23. [Google Scholar]
- Peppin, S.; Elliott, J.; Worster, M.G. Solidification of colloidal suspensions. J. Fluid Mech. 2006, 554, 147. [Google Scholar] [CrossRef]
- Omenyi, S.; Neumann, A. Thermodynamic aspects of particle engulfment by solidifying melts. J. Appl. Phys. 1976, 47, 3956–3962. [Google Scholar] [CrossRef]
- Uhlmann, D.R.; Chalmers, B.; Jackson, K. Interaction between particles and a solid-liquid interface. J. Appl. Phys. 1964, 35, 2986–2993. [Google Scholar] [CrossRef]
- Chernov, A.; Temkin, D.; Mel’Nikova, A. Theory of the capture of solid inclusions during the growth of crystals from the melt. Sov. Phys. Crystallogr. 1976, 21, 369–373. [Google Scholar]
- Temkin, D.; Chernov, A.; Mel’nikova, A. Capture of foreign particles by a crystal growing from a melt containing impurities. Sov. Phys. Crystallogr. 1977, 22, 13–17. [Google Scholar]
- Gilpin, R. Theoretical studies of particle engulfment. J. Colloid Interface Sci. 1980, 74, 44–63. [Google Scholar] [CrossRef]
- Aubourg, P.F. Interaction of Second-Phase Particles with a Crystal Growing from the Melt. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1978. [Google Scholar]
- Landa, A.; Wynblatt, P.; Siegel, D.; Adams, J.; Mryasov, O.; Liu, X.Y. Development of glue-type potentials for the Al–Pb system: Phase diagram calculation. Acta Mater. 2000, 48, 1753–1761. [Google Scholar] [CrossRef]
- Lim, H.; Ong, C.; Ercolessi, F. Stability of face-centered cubic and icosahedral lead clusters. Surf. Sci. 1992, 269, 1109–1115. [Google Scholar] [CrossRef]
- Shi, Z.; Wynblatt, P.; Srinivasan, S. Melting behavior of nanosized lead particles embedded in an aluminum matrix. Acta Mater. 2004, 52, 2305–2316. [Google Scholar] [CrossRef]
- Landa, A.; Wynblatt, P.; Johnson, E.; Dahmen, U. Computer simulation of Pb/Al interfaces. Acta Mater. 2000, 48, 2557–2563. [Google Scholar] [CrossRef]
- Yang, Y.; Olmsted, D.L.; Asta, M.; Laird, B.B. Atomistic characterization of the chemically heterogeneous Al–Pb solid–liquid interface. Acta Mater. 2012, 60, 4960–4971. [Google Scholar] [CrossRef]
- Dad, M.U.; Perveen, A.; Liang, H.; Yang, Y. Interface migration in aluminum bicrystals via premelting. Surfaces Interfaces 2021, 26, 101344. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: Amsterdam, The Netherlands, 2001; Volume 1. [Google Scholar]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. EPL (Europhys. Lett.) 1994, 26, 583. [Google Scholar] [CrossRef]
- Yang, Y.; Asta, M.; Laird, B.B. Solid-liquid interfacial premelting. Phys. Rev. Lett. 2013, 110, 096102. [Google Scholar] [CrossRef] [PubMed]
- Webb, E.; Hoyt, J.J.; Grest, G.S.; Heine, D.R. Atomistic simulations of reactive wetting in metallic systems. J. Mater. Sci. 2005, 40, 2281–2286. [Google Scholar] [CrossRef]
- Webb, E.B.; Grest, G.S.; Heine, D.R.; Hoyt, J. Dissolutive wetting of Ag on Cu: A molecular dynamics simulation study. Acta Mater. 2005, 53, 3163–3177. [Google Scholar] [CrossRef]
- Webb, E.B.; Grest, G.S.; Heine, D.R. Precursor Film Controlled Wetting of Pb on Cu. Phys. Rev. Lett. 2003, 91, 236102. [Google Scholar] [CrossRef]
- Heine, D.R.; Grest, G.S.; Webb, E.B. Spreading dynamics of polymer nanodroplets in cylindrical geometries. Phys. Rev. E 2004, 70, 011606. [Google Scholar] [CrossRef] [PubMed]
- Heine, D.R.; Grest, G.S.; Webb, E.B. Surface Wetting of Liquid Nanodroplets: Droplet-Size Effects. Phys. Rev. Lett. 2005, 95, 107801. [Google Scholar] [CrossRef] [PubMed]
- Radetic, T.; Johnson, E.; Olmsted, D.; Yang, Y.; Laird, B.; Asta, M.; Dahmen, U. Step-controlled Brownian motion of nanosized liquid Pb inclusions in a solid Al matrix. Acta Mater. 2017, 141, 427–433. [Google Scholar] [CrossRef]
- Yang, Y.; Laird, B.B. Droplet spreading on a surface exhibiting solid-liquid interfacial premelting. Acta Mater. 2018, 143, 319–328. [Google Scholar] [CrossRef]
- Ma, X.M.; Liang, H.T.; Lu, W.L.; Zhang, X.; Yu, Z.Y.; Yang, Y. Atomistic characterization of the dispersed liquid droplet in immiscible Al–Pb alloy. J. Mater. Res. Technol. 2021, 15, 2993–3004. [Google Scholar] [CrossRef]
- Morris, J.R. Complete mapping of the anisotropic free energy of the crystal-melt interface in Al. Phys. Rev. B 2002, 66, 144104. [Google Scholar] [CrossRef]
- Yang, Y.; Humadi, H.; Buta, D.; Laird, B.B.; Sun, D.; Hoyt, J.J.; Asta, M. Atomistic simulations of nonequilibrium crystal-growth kinetics from alloy melts. Phys. Rev. Lett. 2011, 107, 025505. [Google Scholar] [CrossRef]
- Hadji, L.; Davis, A. The influence of insoluble spherical particles on the stability of a planar solidifying interface. J. Cryst. Growth 1998, 191, 889–896. [Google Scholar] [CrossRef]
- Stefanescu, D.M.; Juretzko, F.; Catalina, A.; Dhindaw, B.; Sen, S.; Curreri, P.A. Particle engulfment and pushing by solidifying interfaces: Part II. Microgravity experiments and theoretical analysis. Metall. Mater. Trans. A 1998, 29, 1697–1706. [Google Scholar] [CrossRef]
- Kim, J.; Rohatgi, P. An analytical solution of the critical interface velocity for the encapturing of insoluble particles by a moving solid/liquid interface. Metall. Mater. Trans. A 1998, 29, 351–358. [Google Scholar] [CrossRef]
- Azouni, M.; Casses, P. Thermophysical properties effects on segregation during solidification. Adv. Colloid Interface Sci. 1998, 75, 83–106. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Solidification of metal matrix composites. In Science and Engineering of Casting Solidification; Springer: Berlin/Heidelberg, Germany, 2015; pp. 305–341. [Google Scholar]
- Shibata, H.; Yin, H.; Yoshinaga, S.; Emi, T.; Suzuki, M. In-Situ observation of engulfment and pushing of nonmetallic inclusions in steel melt by advancing melt/solid interface. ISIJ Int. 1998, 38, 149–156. [Google Scholar] [CrossRef]
- Juretzko, F.R.; Stefanescu, D.M.; Dhindaw, B.K.; Sen, S.; Curreri, P.A. Particle engulfment and pushing by solidifying interfaces: Part 1. Ground experiments. Metall. Mater. Trans. A 1998, 29, 1691–1696. [Google Scholar] [CrossRef]
- Hwang, H.; Weitz, D.A.; Spaepen, F. Direct observation of crystallization and melting with colloids. Proc. Natl. Acad. Sci. USA 2019, 116, 1180–1184. [Google Scholar] [CrossRef]
| Å | ||
|---|---|---|
| 12 | 158,100 | 445 |
| 16 | 157,704 | 687 |
| 20 | 156,778 | 1218 |
| 30 | 154,135 | 2730 |
| 36 | 151,629 | 5918 |
| Matrix/Particle System | n | |
|---|---|---|
| Biphenyl/acetal | 0.90 | 1132 [27] |
| Biphenyl/nylon | 0.64 | 199 [27] |
| Naphthalene/acetal | 0.30 | 195 [27] |
| Naphthalene/nylon | 0.46 | 142 [27] |
| Succinonitrile/polystyrene | 1.0 | 12.1 [57] |
| Steel/silica–alumina (liquid) | 1.0 | 24 [58] |
| Aluminum/zirconia | 1.0 | 250 [59] |
| Aluminum/lead (liquid) | 1.0 | 347.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perveen, A.; Liang, H.; Alexandrov, D.V.; Umar Dad, M.; Yang, Y. Engulfment and Pushing of Cylindrical Liquid Nano-Inclusion by Advancing Crystal/Melt Interface: An Atomistic Simulation Study. Nanomaterials 2023, 13, 3164. https://doi.org/10.3390/nano13243164
Perveen A, Liang H, Alexandrov DV, Umar Dad M, Yang Y. Engulfment and Pushing of Cylindrical Liquid Nano-Inclusion by Advancing Crystal/Melt Interface: An Atomistic Simulation Study. Nanomaterials. 2023; 13(24):3164. https://doi.org/10.3390/nano13243164
Chicago/Turabian StylePerveen, Atia, Hongtao Liang, Dmitri V. Alexandrov, Muhammad Umar Dad, and Yang Yang. 2023. "Engulfment and Pushing of Cylindrical Liquid Nano-Inclusion by Advancing Crystal/Melt Interface: An Atomistic Simulation Study" Nanomaterials 13, no. 24: 3164. https://doi.org/10.3390/nano13243164
APA StylePerveen, A., Liang, H., Alexandrov, D. V., Umar Dad, M., & Yang, Y. (2023). Engulfment and Pushing of Cylindrical Liquid Nano-Inclusion by Advancing Crystal/Melt Interface: An Atomistic Simulation Study. Nanomaterials, 13(24), 3164. https://doi.org/10.3390/nano13243164







