Plasmon Hybridizations in Compound Nanorod–Nanohole Arrays
Abstract
1. Introduction
2. Materials and Methods
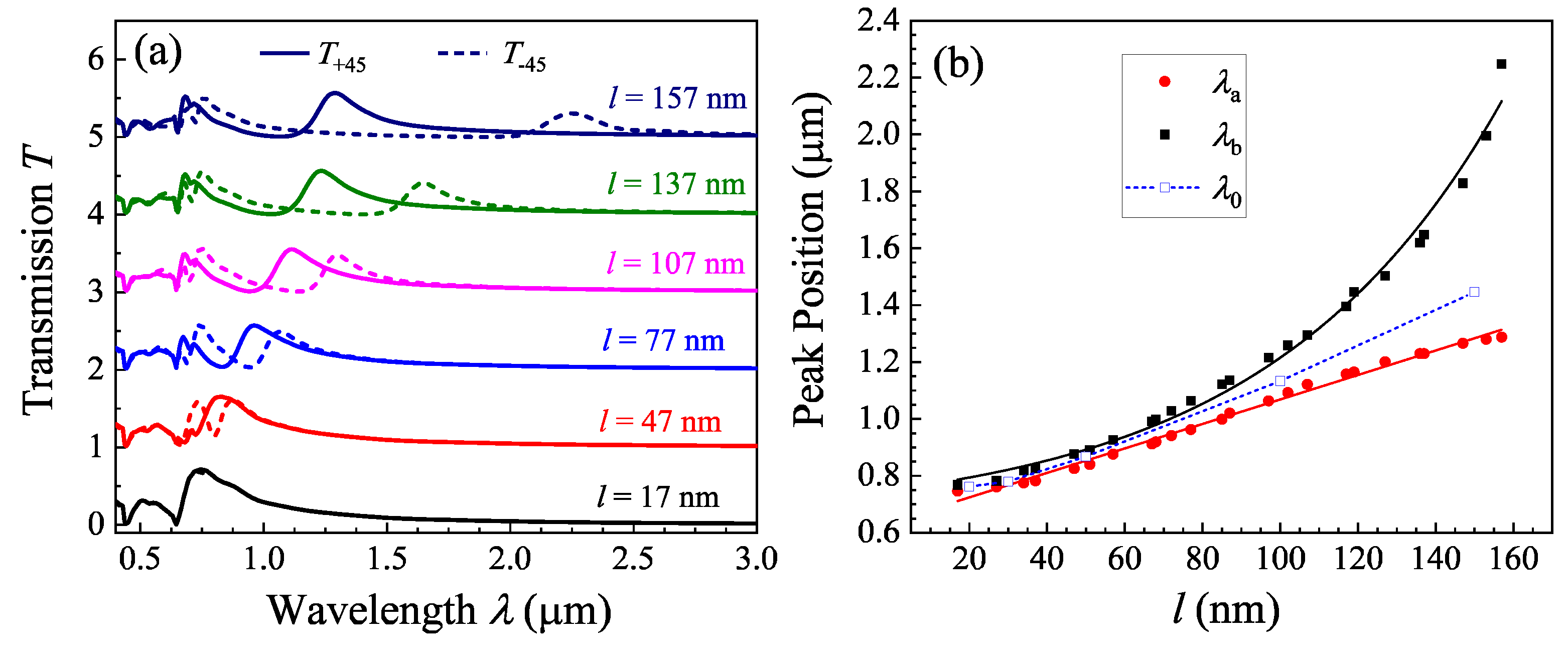
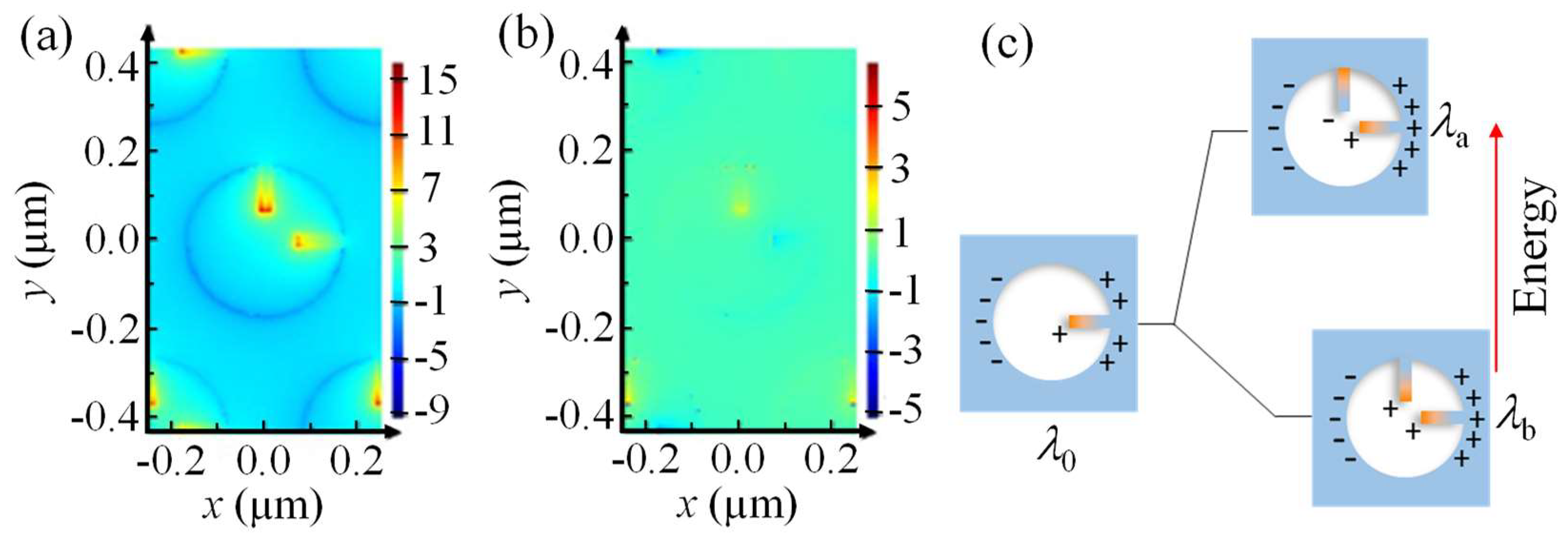
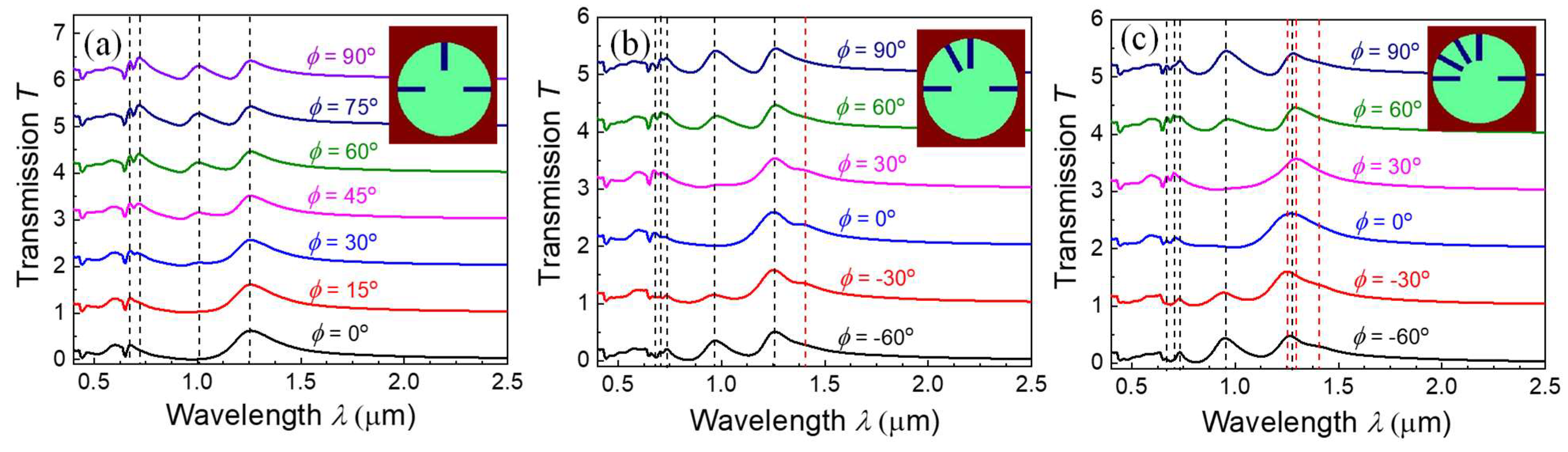
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Gordon, R.; Brolo, A.G.; Sinton, D.; Kavanagh, K.L. Resonant optical transmission through hole-arrays in metal films: Physics and applications. Laser Photonics Rev. 2010, 4, 311–335. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Grupp, D.E.; Lezec, H.J.; Thio, T.; Ebbesen, T.W. Beyond the Bethe Limit: Tunable Enhanced Light Transmission Through a Single Sub-Wavelength Aperture. Adv. Mater. 1999, 11, 860–862. [Google Scholar] [CrossRef]
- Thio, T.; Pellerin, K.M.; Linke, R.A.; Lezec, H.J.; Ebbesen, T.W. Enhanced light transmission through a single subwavelength aperture. Opt. Lett. 2001, 26, 1972–1974. [Google Scholar] [CrossRef]
- Lezec, H.J.; Degiron, A.; Devaux, E.; Linke, R.A.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Ebbesen, T.W. Beaming Light from a Subwavelength Aperture. Science 2002, 297, 820–822. [Google Scholar] [CrossRef]
- Baida, F.I.; Van Labeke, D. Light transmission by subwavelength annular aperture arrays in metallic films. Opt. Commun. 2002, 209, 17–22. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, S.; Minhas, B.; Malloy, K.J.; Brueck, S.R.J. Enhanced Infrared Transmission through Subwavelength Coaxial Metallic Arrays. Phys. Rev. Lett. 2005, 94, 033902. [Google Scholar] [CrossRef]
- Lockyear, M.J.; Hibbins, A.P.; Sambles, J.R.; Lawrence, C.R. Microwave Transmission through a Single Subwavelength Annular Aperture in a Metal Plate. Phys. Rev. Lett. 2005, 94, 193902. [Google Scholar] [CrossRef]
- Salvi, J.; Roussey, M.; Baida, F.I.; Bernal, M.P.; Mussot, A.; Sylvestre, T.; Maillotte, H.; Van Labeke, D.; Perentes, A.; Utke, I.; et al. Annular aperture arrays: Study in the visible region of the electromagnetic spectrum. Opt. Lett. 2005, 30, 1611–1613. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Yang, Y.; Zhang, Y.; Jia, P.; Ebendorff-Heidepriem, H.; Ruan, Y.; Yang, D. Enhancement of extraordinary optical transmission and sensing performance through coupling between metal nanohole and nanoparticle arrays. J. Phys. D Appl. Phys. 2019, 52, 275201. [Google Scholar] [CrossRef]
- Ni, H.; Wang, M.; Shen, T.; Zhou, J. Self-Assembled Large-Area Annular Cavity Arrays with Tunable Cylindrical Surface Plasmons for Sensing. ACS Nano 2015, 9, 1913–1925. [Google Scholar] [CrossRef]
- Weiler, M.; Quint, S.B.; Klenk, S.; Pacholski, C. Bottom-up fabrication of nanohole arrays loaded with gold nanoparticles: Extraordinary plasmonic sensors. Chem. Commun. 2014, 50, 15419–15422. [Google Scholar] [CrossRef] [PubMed]
- Yoo, D.; Mohr, D.A.; Vidal-Codina, F.; John-Herpin, A.; Jo, M.; Kim, S.; Matson, J.; Caldwell, J.D.; Jeon, H.; Nguyen, N.-C.; et al. High-Contrast Infrared Absorption Spectroscopy via Mass-Produced Coaxial Zero-Mode Resonators with Sub-10 nm Gaps. Nano Lett. 2018, 18, 1930–1936. [Google Scholar] [CrossRef] [PubMed]
- Cai, H.; Meng, Q.; Zhao, H.; Li, M.; Dai, Y.; Lin, Y.; Ding, H.; Pan, N.; Tian, Y.; Luo, Y.; et al. High-Throughput Fabrication of Ultradense Annular Nanogap Arrays for Plasmon-Enhanced Spectroscopy. ACS Appl. Mater. Interfaces 2018, 10, 20189–20195. [Google Scholar] [CrossRef]
- Zhu, A.; Qian, Q.; Yan, Y.; Hu, J.; Zhao, X.; Wang, C. Ultrathin plasmonic quarter waveplate using broken rectangular annular metasurface. Opt. Laser Technol. 2017, 92, 120–125. [Google Scholar] [CrossRef]
- Wang, Y.; Luong, H.; Zhang, Z.; Zhao, Y. Coupling between plasmonic nanohole array and nanorod array: The emerging of a new extraordinary optical transmission mode and epsilon-near-zero property. J. Phys. D Appl. Phys. 2020, 53, 275202. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Zhao, Y. The effect of nanorod position on the plasmonic properties of the complex nanorod in nanohole arrays. J. Phys. D Appl. Phys. 2021, 54, 155201. [Google Scholar] [CrossRef]
- Wang, Y.; Ao, S.; Yang, F.; Zhang, Z.; Zhao, Y. Coupling between Surface Plasmon Modes of Single-Layer Complex Silver Nanohole Arrays and Enhancing Index Sensing. ACS Appl. Nano Mater. 2022, 5, 9761–9770. [Google Scholar] [CrossRef]
- Wang, Y.; Chong, H.B.; Zhang, Z.; Zhao, Y. Large-Area Fabrication of Complex Nanohole Arrays with Highly Tunable Plasmonic Properties. ACS Appl. Mater. Interfaces 2020, 12, 37435–37443. [Google Scholar] [CrossRef]
- Wang, Y.; Choi, I.; Zhang, K.; Yang, Y.; Ao, S.; Xue, X.; Fu, W.; Zhang, Z.; Zhao, Y. Highly Conductive Nanograting–Nanohole Structures with Tunable and Dual-Band Spectral Transparency. ACS Appl. Electron. Mater. 2021, 3, 3489–3500. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A Hybridization Model for the Plasmon Response of Complex Nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Yanik, A.A.; Adato, R.; Erramilli, S.; Altug, H. Hybridized nanocavities as single-polarized plasmonic antennas. Opt. Express 2009, 17, 20900–20910. [Google Scholar] [CrossRef]
- Larson, S.; Luong, H.; Song, C.; Zhao, Y. Dipole Radiation-Induced Extraordinary Optical Transmission for Silver Nanorod-Covered Silver Nanohole Arrays. J. Phys. Chem. C 2019, 123, 5634–5641. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Li, Y. Plasmonic Optics: Theory and Applications; SPIE Press: Bellingham, WA, USA, 2017. [Google Scholar]
- Li, Z.-B.; Zhou, W.-Y.; Kong, X.-T.; Tian, J.-G. Polarization dependence and independence of near-field enhancement through a subwavelength circle hole. Opt. Express 2010, 18, 5854–5860. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.T.; Mock, J.J.; Hucknall, A.; Wolter, S.D.; Jokerst, N.M.; Smith, D.R.; Chilkoti, A. Plasmon ruler with angstrom length resolution. ACS Nano 2012, 6, 9237–9246. [Google Scholar] [CrossRef]
- Yoon, J.H.; Yoon, S. Probing interfacial interactions using core-satellite plasmon rulers. Langmuir 2013, 29, 14772–14778. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.M.; Wilding, D.; Speed, J.D.; Russell, A.E.; Bartlett, P.N.; Baumberg, J.J. Dressing plasmons in particle-in-cavity architectures. Nano Lett. 2011, 11, 1221–1226. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razavi, S.; Zhao, Y. Plasmon Hybridizations in Compound Nanorod–Nanohole Arrays. Nanomaterials 2023, 13, 2135. https://doi.org/10.3390/nano13142135
Razavi S, Zhao Y. Plasmon Hybridizations in Compound Nanorod–Nanohole Arrays. Nanomaterials. 2023; 13(14):2135. https://doi.org/10.3390/nano13142135
Chicago/Turabian StyleRazavi, Shahab, and Yiping Zhao. 2023. "Plasmon Hybridizations in Compound Nanorod–Nanohole Arrays" Nanomaterials 13, no. 14: 2135. https://doi.org/10.3390/nano13142135
APA StyleRazavi, S., & Zhao, Y. (2023). Plasmon Hybridizations in Compound Nanorod–Nanohole Arrays. Nanomaterials, 13(14), 2135. https://doi.org/10.3390/nano13142135






