1. Introduction
Magnetic skyrmions [
1,
2] are topologically nontrivial spin textures with smooth rotation from magnetization, which are commonly embedded into homogeneously magnetized “parental” states and are stabilized by a specific Dzyaloshinskii–Moriya interaction (DMI) [
3,
4,
5]. DMI performs the function of protecting skyrmions from radial instability and overcoming the constraints of the Hobart–Derrick theorem [
6,
7]. Phenomenologically, DMI is expressed by the energy terms linear in the first derivatives ofmagnetization
with respect to spatial coordinates, which are so-called Lifshitz invariants (LI):
For cubic helimagnets belonging to 23 (T) symmetry classes (as MnSi [
8], FeGe [
9], and other B20 compounds), which are the subject of the present paper, the Dzyaloshinskii–Moriya interaction reduces to a particularly simple form:
and underlies the Bloch-like fashion of the magnetization rotation with the helicity value,
[
1].
The characteristic length scale of isolated skyrmions (IS) [
10,
11] is specified by the competition between ferromagnetic exchange and DM interactions [
3,
4,
5] and ranges from nanometers to microns [
12]. In a cubic helimagnet FeGe, the periodicity length
of the helix in zero field was found to be 70 nm (or 149 unit cells) [
13]. Cubic B20 alloys Fe
Co
Si have an even larger period (with a maximal value of 230 nm for
x = 0.3) [
14,
15]. Topologically, skyrmions are elements of the second homotopy group [
16]
and are characterized by integer-valued topological invariants, the skyrmion numbers
Q [
2,
16], which also indicate that skyrmions cannot be continuously unwound into a homogeneous state without introducing point defects [
17].
.
During the first years of skyrmionics [
8,
18] an intensive search for chiral skyrmions was undertaken in bulk samples of cubic helimagnets such as FeGe [
9,
13,
18]. Experimental results clearly indicated a complex multidimensional character of chiral modulated states in small regions of the phase diagrams near the ordering temperatures (so-called precursor states [
18,
19]). Subsequently, chiral skyrmions (isolated and bound into hexagonal lattices) have been microscopically observed in thin layers of cubic helimagnets (Fe,Co)Si [
15] and FeGe [
20] in a broad range of temperatures and magnetic fields far below the precursor regions.
The enhanced stability skyrmions’ gain in thin layers of chiral magnets rests on additional surface twists [
21,
22] of the magnetization near the confining surfaces. Indeed, in bulk helimagnets, only the Lifshitz invariants
in (
1) induce the magnetization rotation in the transverse plane
. In magnetic nanolayers, on the contrary, the Lifshitz invariants
with the magnetization derivative along
z play a decisive role. This is the same energy term that also stipulates the magnetization rotation within the conical phase with the wave vector
along
z. For skyrmions, as a result,
leads to the gradual variation in the skyrmion helicity (
) towards upper and lower surfaces [
21,
22]. This effect accumulates additional negative energy as compared with the cones and leads to the SkL stability [
22,
23]. Such an effect of confinement is mostly manifested when the size of the system is comparable with the characteristic length corresponding to the order parameters of the chiral medium. In particular, the SkL pocket at the phase diagram (film thickness,
T—an applied magnetic field,
H) extends up to the confinement ratio
, where
is a spiral pitch [
22,
23].
In modern skyrmionics, skyrmions are considered as promising objects for the next-generation memory and logic devices. Indeed, they are often hailed as being “topologically protected” [
24], they have a nanometer size [
12] and can be manipulated by electric currents [
25,
26,
27]. In particular, in the skyrmion racetrack [
28,
29], information flow is encoded in isolated skyrmions moving within a narrow strip. At the same time, there is an obvious obstacle in the way of the practical use of skyrmion-based devices—the skyrmion Hall effect (SHE), which leads to the curved trajectory of moving skyrmions due to the transverse skyrmion deflection [
30,
31]. In turn, this imposes the problem of skyrmion confinement within the nanostrip, which is usually achieved by the edge states of the magnetization rotating towards the free boundaries. The main strategy to overcome this obstacle is to consider localized skyrmion particles with zero topological charge, which would be able to cancel the Magnus force. Among such skyrmion varieties are skyrmionium [
32] (also called target-skyrmion [
33]), antiferromagnetic skyrmion [
34], and/or states of coupled merons with the opposite topological charges [
35].
In the present paper, we introduce an alternative mechanism to harness the skyrmion Hall effect. We consider ordinary isolated skyrmions with the unit topological charge. However, we place them into wedge-shaped samples of cubic helimagnets with gradually increasing thickness. Then, the suppression of the SHE and the control over the skyrmion trajectory is based on the balance of the Magnus force, which pushes skyrmions towards the increasing thickness of the wedge (and thus leads to their energy increase) and the restoring force, which tries to return the skyrmion into a position with the minimal eigen-energy near the thinner wedge boundary. We show that this unique equilibrium, which results in straight skyrmion trajectories parallel to the wedge boundaries, is achieved in a wide range of current densities, but ceases to exist at some critical current value. For this, skyrmions are uncontrollably deflected in the transverse direction, irrespective of their increasing eigen-energy.
We also focus on the internal properties of such skyrmion states, which exhibit drastic variation, e.g., of their helicity and characteristic sizes, depending on the film thickness. We complement the phase diagram of states in thin layers of chiral magnets and point to the parameter region, where the mentioned dynamic mechanism could be utilized. In particular, we show that the phase transition between the helical state with the wave vector perpendicular to the field and the conical state with the wave vector along the field may become of the second-order with a smooth transformation between the two spiral states. Moreover, detailed numerical analysis of the current-induced skyrmion dynamics makes it possible to underlie two distinct regimes with different spacings between skyrmion tracks/trajectories for the same increment of the current density. We argue that augmented internal properties of isolated skyrmions in wedge geometries make them effective candidates to be employed in the nanoelectronic devices of the next generation in which nanopatterning is boiled down to a minimum.
2. Phenomenological Model and Equations
In the present paper, we use the simplest model for magnetic states in confined noncentrosymmetric ferromagnets based on the following energy density functional [
4,
5,
36]:
where
and
D are coefficients of exchange and Dzyaloshinskii–Moriya interactions;
is a magnetic field, which is applied along the
z-axis; and
are the Cartesian components of the spatial variable. In this form, functional (
3) includes only basic interactions essential for stabilizing different modulated and localized states.
As a primary numerical tool to minimize the functional (
3), we use the MuMax3 software package (version 3.10), which calculates magnetization dynamics by solving the Landau–Lifshitz equation using the finite-difference discretization technique (see for details Ref. [
37]). MuMax3 is a reliable GPU-accelerated software for addressing samples with complex geometries, including notches [
38]. For this, we introduce non-dimensional units for the reduced magnetic field,
, and spatial coordinates,
. In particular, the thickness is expressed as
. Here,
is the characteristic length unit of the modulated states. The value
for
is the
helix period for bulk helimagnets.
. Different micromagnetic structures are described via the magnetization vector
with a fixed length normalized to unity.
In the subsequent simulations on the current-induced skyrmion dynamics (
Section 4.3), however, we use the material parameters for FeGe: DMI,
mJ/m
; the saturation magnetization,
kA/m; and the exchange stiffness,
J/m [
18]. At the same time, we omit the contribution of the cubic anisotropy, which may have some impact on the obtained solutions. In particular, it is known that due to the cubic anisotropy, the propagation directions of the spirals point to <100> crystallographic axes just below the Curie temperature and change to <111> when decreasing the temperature below 220 K [
13]. Moreover, the symmetry analysis of the P213 structure of FeGe made by Bak and Jensen [
36] and by Nakanishi [
39] justified that the expansion of the free energy in a slow-varying spin density
, besides gradient terms of Equation (
3), must be supplemented by the gradient term of the exchange anisotropy. This energy term will be, however, also omitted in the present paper, although it is known to induce spiral flips into positions oblique with respect to the field direction [
40].
We investigate functional (
3) in thin films with the constant thickness
T and in wedges with varying thickness
T. The free boundary conditions are used on these confining upper and lower surfaces. Both geometries are infinite along
y directions (which is the direction of skyrmion motion and current flow) and are confined by the vertical lateral boundaries with free conditions (which confine skyrmions within the racetracks). The tilt angle
characterizes the wedge slope (
in thin films). For simplicity [and following previous publications [
22,
23,
41] we neglect the demagnetizing effects, although we realize that at small film thicknesses they might play an important role. The effect of magnetostatic interactions will be considered elsewhere as soon as the phase diagram of states in thin-film samples, which is the subject of many publications, is completed without them. Moreover, since the information on the parameter range at which skyrmions in wedges could be utilized is extracted from the corresponding phase diagram for thin films, one needs the same phase diagram for thin films, taking into account the demagnetizing fields. At the moment, we assume that the DM interactions suppress demagnetization effects and are the main driving force leading to the magnetization rotation and to the equilibrium periodicity.
At this point, we also introduce a conical phase—a spiral solution of functional (
3) with the propagation direction along the magnetic field in which the magnetization rotation retains a single-harmonic character. The order parameter can be presented as
, and the equilibrium parameters are expressed in analytical form [
36] as
For both bulk and thin-film helimagnets, the saturation field of the conical state in units of
equals
when
. At this field, the conical phase transforms into the saturated state with
.
3. The Simplified Phase Diagram of States in Thin-Layered Systems
In the previous studies [
22,
23], it was found that the hexagonal skyrmion lattice (hSkL) occupies a vast area at the phase diagram (
)–(h); at lower fields, it borders the helical state, and at higher fields, it borders the conical (for larger
) or the homogeneous state (for smaller
). In theory, such an hSkL represents an ideal state, the energy density (
3) of which is just minimized with respect to the hexagonal cell size and computed for different values of
and
h. In experiment, however (see, e.g., Ref. [
22] for details), the SkL nucleates at the thin boundary of a wedge-shaped sample and thus creates an energetically costly domain boundary with respect to the conical state. In general, due to the attracting skyrmion interaction, ISs form clusters being surrounded by the conical phase (see, e.g., Refs. [
42,
43]). This results in a much smaller critical film thickness
for SkL/cluster stability presumably comparable with the parameter region, in which the energy of an IS becomes negative with respect to the conical state. Taking into account these experimental scenarios, we first look for the mentioned region of ISs with the negative eigen-energy and omit the region of hSkL stability. Thus, the following states will be included into the phase diagram: helicoids, cones, the homogeneous state and ISs (
Figure 1a).
3.1. Helicoid–Cone Phase Transition
The helicoid (also called a chiral soliton lattice, CSL [
44]) occupies the blue-shaded area of the phase diagram (
Figure 1a). The wave vector of CSL lies within the plane
(for definiteness, along
x-axis) (
Figure 1b). For low field values, such spirals have lower energy compared to the conical state, which is readily explained by the additional surface twists for any thickness of the film (mechanism described in the introduction). This effect accumulates additional negative energy as opposed to the cones [
21,
22], which are not decorated by the surface twists [
21,
22]. Cones in this geometry (schematically shown in
Figure 1c) are oriented along the field and stabilize in the green-shaded region of the phase diagram (
Figure 1a). Since usually the film thickness is a non-integer multiple of the helical wavelength, the magnetization of the cones has an uncompensated value of the in-plane component
even in a zero magnetic field. Along the line
A–
b (
Figure 1a), the CSL transforms into the conical state by the first-order phase transition, which must be accompanied by the coexisting domains of both phases, which are readily resolved experimentally by Lorentz transmission electron microscopy investigations in thin layers of cubic helimagnets, e.g., in FeGe (see Figure 4 in Ref. [
22]). At the line
A–
c the CSL period tends towards infinity, as observed experimentally in the helimagnet Cr
NbS
[
44]. To the left of the point
A at the line
A–
a, however, the CSL-cone transition becomes of second-order, i.e., both processes occur simultaneously. Indeed, for such small thicknesses, the angle spanned by the magnetization in the conical phase becomes less than
(first panel in
Figure 1c). As a result, the domains of the conical phase nucleate and broaden directly within the helical state; in this case, the rotating magnetization of the conical phase reproduces the surface twists of the helicoid, as schematically depicted in
Figure 1b.
3.2. Overlap of Surface Twists in Isolated Skyrmions within Thin-Film Helimagnets
In the red-shaded region, the energy of an IS becomes negative with respect to the surrounding state—with respect to the homogeneous state above the line of the cone saturation,
(
4), and with respect to the conical state below the line
B–
f. Interestingly, the line
B–
d coincides with the expansion process of hSkL, whereas in point
B, both processes diverge; at line
B–
e, which is just an auxiliary line, the hSkL period tends to infinity, and the lattice expands into the homogeneous state (for bulk samples, the field value corresponds to 0.4, as defined in Refs. [
10,
11]). In the same way, as discussed above for the helical state, one may speculate about the conical phase penetrating the inter-skyrmion space during this realistic scenario.
Remarkably, the whole phase diagram of states constructed in Refs. [
22,
23], which includes hSkL, can be easily reproduced by the following simplified procedure: one extracts the total energy of the surface twists from an hSkL solution with some large film thickness
(e.g.,
). Then, this energy, which is assumed to be constant for varying film thicknesses, can be added to the solutions for the hSkL in bulk samples without any surface twists. The method, however, ceases to “work” in thin samples. In this case, as shown in
Figure 2a for isolated skyrmions, the surface twists start to overlap with the decreasing thickness
. As a result, the total eigen-energy of ISs exhibits minimum at some critical thickness
(
Figure 2c). Such a phenomenon prompts the placing of ISs in wedge-shaped geometries, where ISs may find an equilibrium “pit stop” position within the energy minimum (
Section 4). At the phase diagram (
Figure 1a), the points corresponding to the energy minimum of ISs for different field values are located along the line
C–
D. We, however, terminate this line in the stability region of the conical phase at the point
D, since in this case, ISs undergo instability towards tilted spiral states, which stabilize in the form of a thin “belt” around the line
a–
A–
b (on the properties of tilted spiral states, see for details, e.g., Ref. [
41]).
3.3. The Properties of ISs in Ultrathin Films
Before we switch to wedge-shaped samples of chiral magnets, which are the main subject of the present paper, we systematize the properties of ISs in thin films with decreasing thickness.
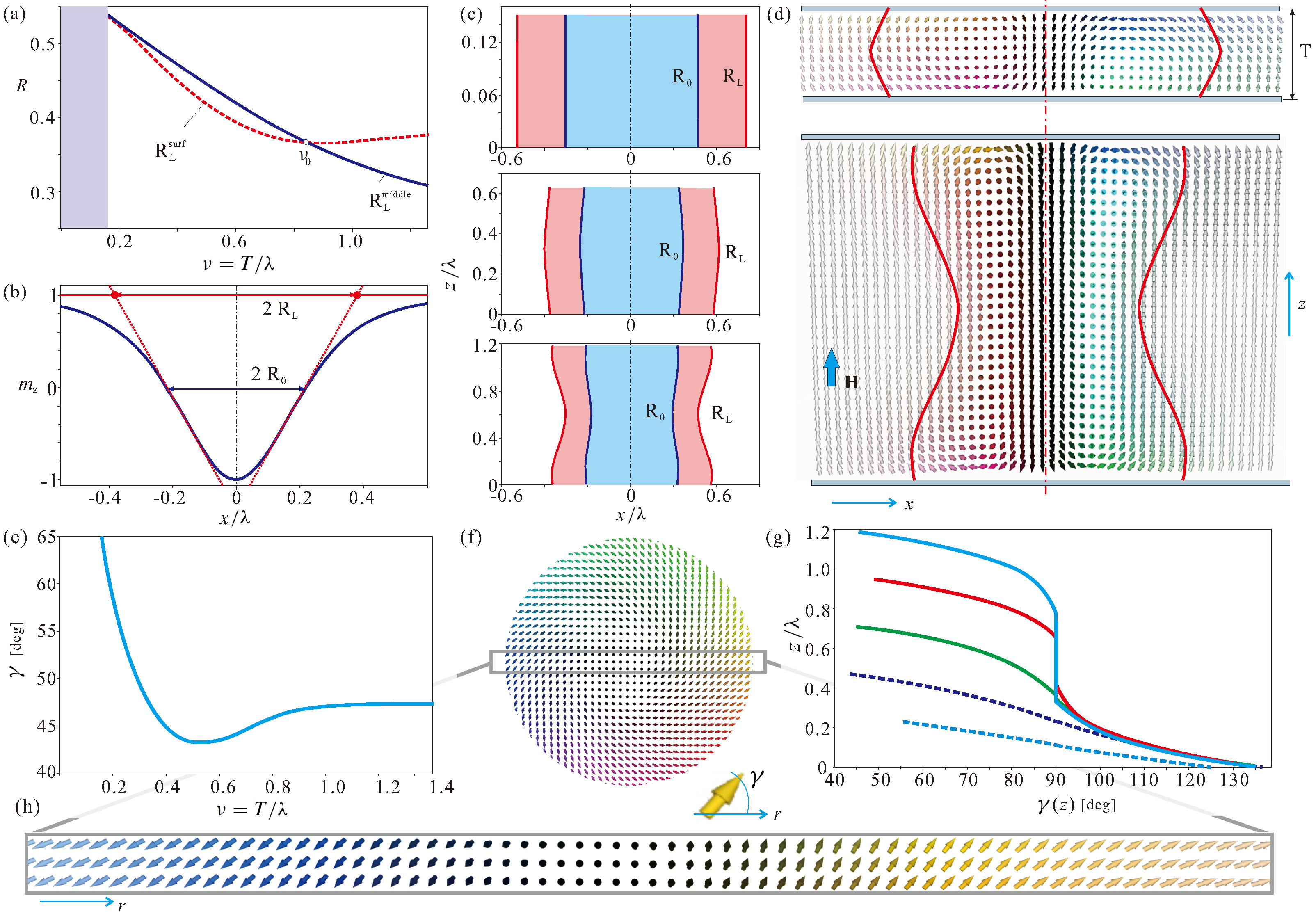
First, we highlight the shape transformation of ISs (
Figure 3a–d). We define the thickness-dependent size of ISs,
, according to the commonly used Lilley’s definition [
45] as a distance between the points at which the tangents at the inflection points of the skyrmion profiles intersect the lines
(
Figure 3b). Additionally, we define the skyrmion size
at the levels with
. Both characteristic radii are shown across the layer interface by blue and red solid lines in
Figure 3c. It is seen that ISs, being essentially cylindrical objects for small values of
(first panel in
Figure 3c), take a convex shape (second panel in
Figure 3c), which subsequently turns into a concave one (last panel in
Figure 3c,d). The critical thickness value, corresponding to this process,
(
Figure 3a), is directly related to the described overlap of surface twists. In
Figure 3a, the skyrmion radii are determined at the confining surfaces,
(red dotted line), and in the middle of the layer,
(blue solid line).
Second, we notice that the helicity is also subject to thickness change (
Figure 3e–h). As shown in
Figure 3f,h, the helicity value varies in dependence on the radial coordinate
r across the IS center. To be consistent in the following speculations, we define IS helicity at the point with the largest in-plane magnetization component, i.e., at the point with
. In
Figure 3g, we plot this helicity value dependent on the
z coordinate for samples with different film thicknesses. As shown by the helicity profiles, the magnetization continuously rotates from the upper to the lower surface (dotted profiles in
Figure 3g). For larger film thicknesses, the helicity equals
in the middle of the layer (solid lines in
Figure 3g), which is the case also for bulk samples. The helicity at the surface, as shown in
Figure 3e, may reach very distinct values for thin samples,
, whereas in thicker films, the helicity saturates at the value
consistent with previous studies [
22].
4. Static and Dynamic Properties of ISs in Wedge-Shaped Geometries
In the present section, we focus on the modification of skyrmion properties in wedge-shaped samples as compared with their thin-film counterparts. We consider axisymmetric skyrmions within the homogeneous state corresponding to the red-shaded region of the phase diagram (
Figure 1a) above the field
. Partly, this is justified by the feasibility of skyrmion nucleation; since the eigen-energy of ISs is negative in this region, the system facilitates their formation from the sharp end of the wedge specifically with additional notches [
46] (see
Supplementary Video S1). In some sense, such a mechanism of skyrmion nucleation is reminiscent of that in stripes of frustrated magnets described in Ref. [
47]. The edge states formed at the lateral boundaries of racetracks in Ref. [
47] were found to be topologically non-trivial; under an applied electric current, they emitted and absorbed skyrmions and antiskyrmions. A similar mechanism of skyrmion nucleation in wedge-shaped samples was recently modeled and observed in Ref. [
48] as also applied to a frustrated magnet Fe
Sn
. Instead of a spin-polarized current, however, the authors of Ref. [
48] induced a reversible transformation from magnetic stripes to skyrmions, and vice versa, by a switching of the in-plane magnetic field. The process of skyrmion nucleation in wedge-shaped helimagnets will be considered in detail elsewhere.
In the following simulations, we also avoid the parameter region in which ISs are surrounded by the conical state below the line
(
Figure 1a). In Ref. [
41], the nascent conical state was shown to shape the skyrmion internal structure in such a way that ISs developed anisotropic inter-skyrmion and edge-skyrmion attraction. Such non-axisymmetric ISs are expected to demonstrate complex dynamic behavior (will also be considered elsewhere).
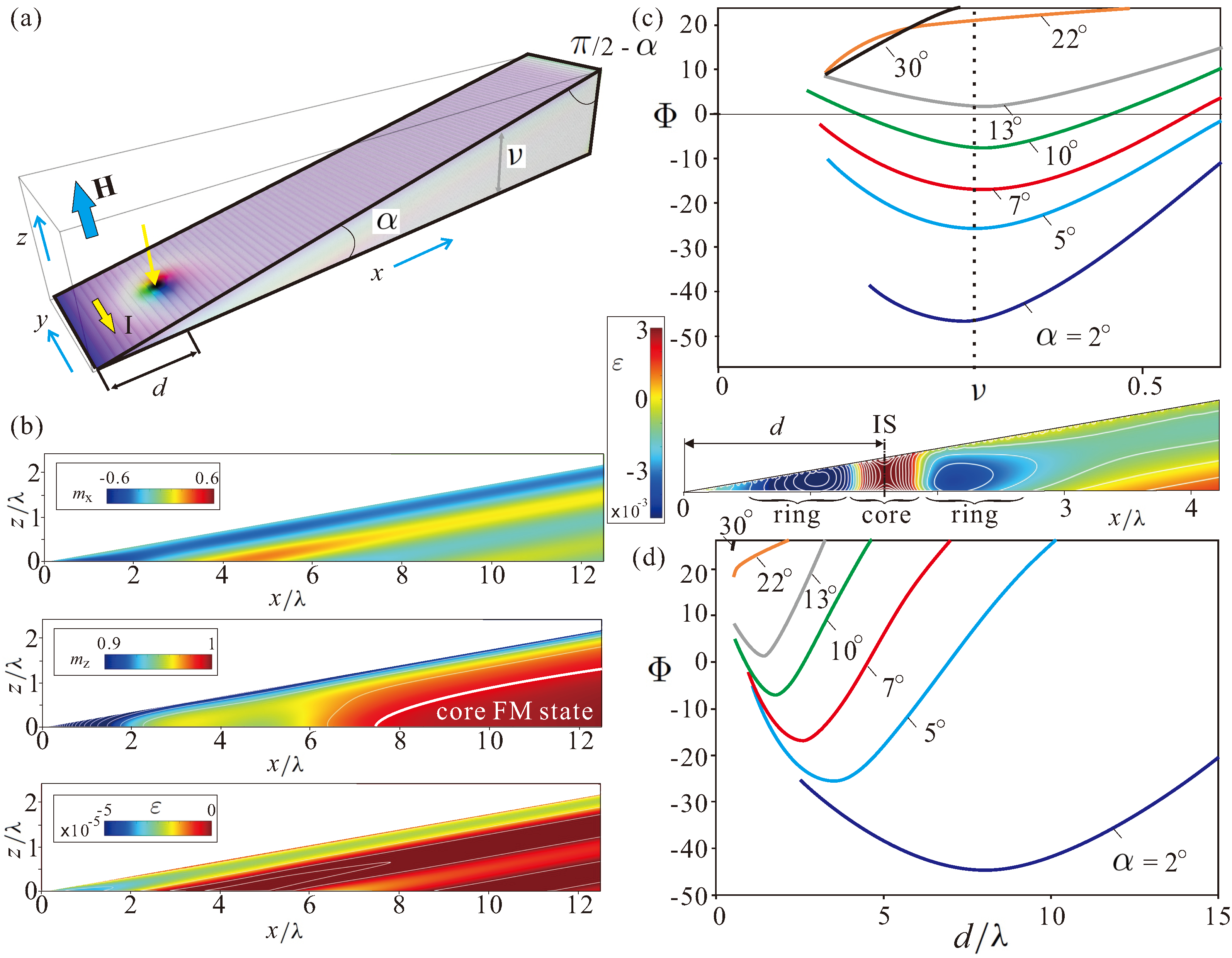
The schematics of the problem are shown in
Figure 4a. The position of the skyrmion center with respect to the sharp boundary of the wedge is characterized by the distance
d. The current is applied along the
y direction to ensure that ISs move along the thickness gradient due to the non-adiabatic spin-transfer torque, i.e., ISs “climb” the wedge “hill”. The Landau–Lifshitz–Gilbert equation is thus supplemented by the Zhang-Li spin-transfer torque (see formula (26) in Ref. [
37]). Current spin polarization rate,
; the Gilbert damping,
; nonadiabaticity of spin-transfer torque,
. An applied magnetic field
corresponds to the nondimensional value
. For dimensional simulations, we use the grid with the cell size 2 nm.
4.1. Internal Structure of Edge States in Wedge Geometries
In thin-film magnetic nanostructures, the practical use of skyrmions hinges on their repulsion from lateral edges, which would keep moving skyrmions within the racetracks [
49]. In chiral magnets, such a repulsion is naturally provided by the DMI, which tilts the magnetization vector away from the magnetic field direction at the edges of a magnet, giving rise to the so-called edge states [
50,
51]. The interaction potential between edge states and ISs is “flat”, and according to the model in Ref. [
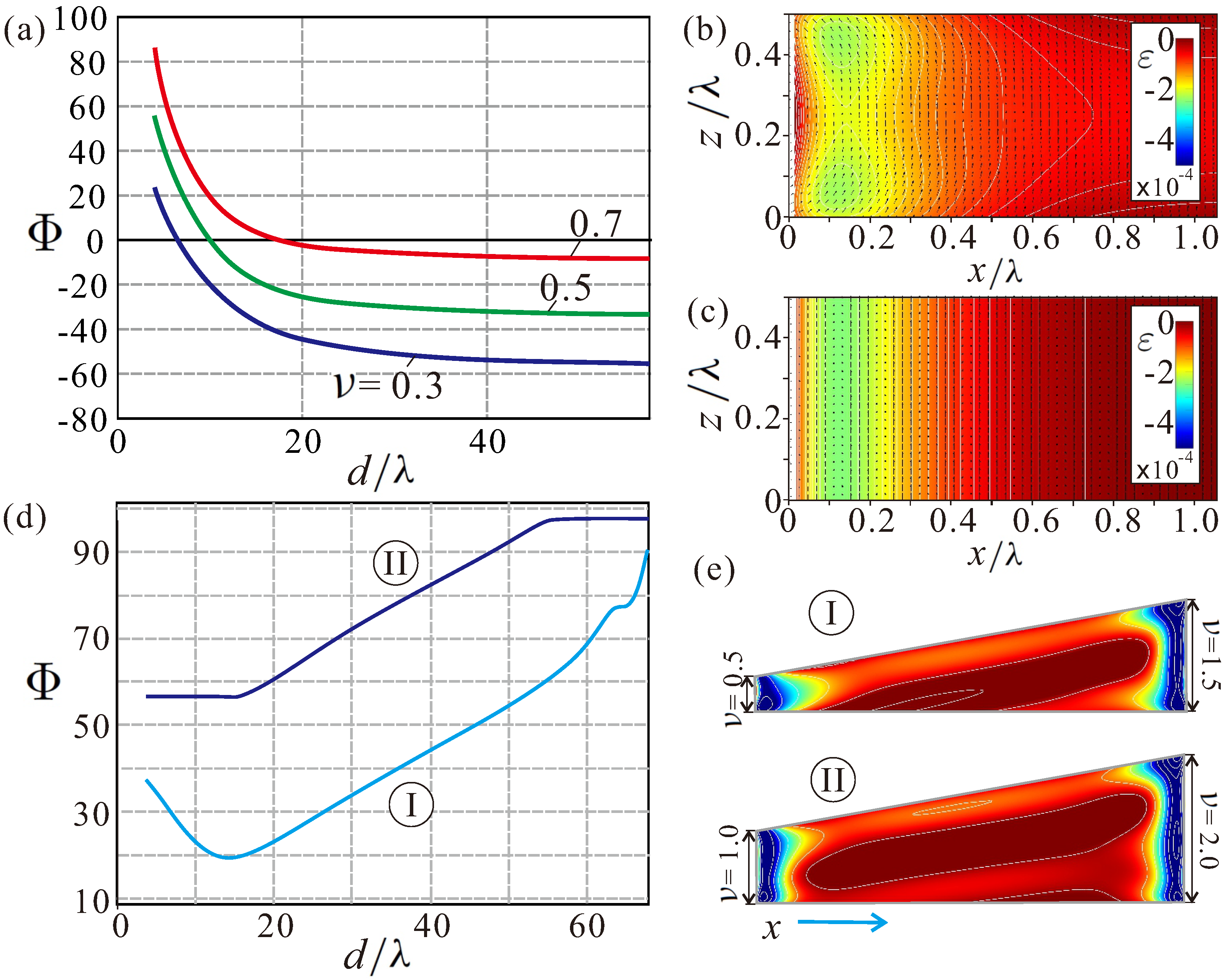
52], it decays exponentially with the skyrmion–edge separation distance, i.e., for zero current, the skyrmions are slowly pushed away from the edges. In Figure 6a, we plot interaction potentials
for thin films with different thicknesses
.
were calculated by imposing the constraint
at the skyrmion center and minimizing the energy with respect to spins at all other sites. Then,
represents an energy difference of states with and without ISs, i.e., the skyrmion eigen-energy.
In wedge-shaped nanostructures (
Figure 4a), however, the internal structure of edge modulations becomes more involved.
Figure 4b shows
and
components of the magnetization (first two panels) as well as the energy density (third panel). We zoom the color plots within a particular range to reflect all the subtleties of the magnetization distribution. For example, the
component is highlighted in the range
. We notice that the main magnetic inhomogeneity is localized near the sharp boundary of the wedge. Just like in the case of thin films, the energy of these edge states is negative as compared with the homogeneous state. The homogeneous state on its own accepts the value
only deep inside the wedge (second panel in
Figure 4b), and the magnetization contorts towards the upper confining surface. From the behavior of the
magnetization component (first panel in
Figure 4b), we can deduce that the magnetization twists towards the surface, which leads to the layer of the negative energy density also immediately under the confining surface (third panel in
Figure 4b). Interestingly, such layers with a negative energy density are also spotted across the whole wedge, indicating small perturbations of the homogeneous state.
4.2. Skyrmion “Pit Stops”
In
Figure 4c,d, we plot the eigen-energy of ISs,
, depending on the distance
d from the sharp wedge boundary. The energy density distribution in this case is shown in the inset. The skyrmion core with a positive energy density (over the homogeneous state) is found to be embraced by a distorted ring with a negative energy density. Towards the sharp edge, this ring leans upon the negative energy of edge states; in the opposite direction, the ring weakens and merges with the homogeneous state. We notice that the edge–IS interaction potentials in this case exhibit the minima (
Figure 4c) at about the same thickness, irrespective of the wedge angle
, which roughly corresponds to the critical thickness calculated in
Figure 2c for thin-film geometries. The minima originate from the balance between the increasing eigen-energy of ISs while moving into the region with high
and the edge-skyrmion repulsion. For smaller wedge angles (dark-blue line in
Figure 4c,d), the edge states almost do not influence the magnetization distribution within ISs, and the IS energy is essentially the same as for the thin-film geometries in
Figure 2c. For larger elevation angles, however, the equilibrium skyrmion position is found within the edge states, which results in an increase in their energy. Notice that the equilibrium skyrmion position
d in
Figure 2d moves closer to the sharp edge until the minimum disappears for larger angles
. According to our simulations, there are two critical wedge angles: (i) in the angle range
, the energy of an IS remains negative with respect to the surrounding homogeneous state (i.e., we separately calculated the magnetization distribution and its total energy within a wedge without ISs); however, for
it becomes positive; (ii) for
, the energy minimum shallows, which means that ISs existing within the nanostructure would inevitably “slide” towards the wedge boundary and annihilate (
Supplementary Video S2). We dubbed this energy minimum a skyrmion “pit stop” position. Indeed, every time the current would switch off, ISs return to this equilibrium (
Supplementary Video S3).
4.3. Current-Driven Dynamics of ISs in Wedge-Shaped Geometries
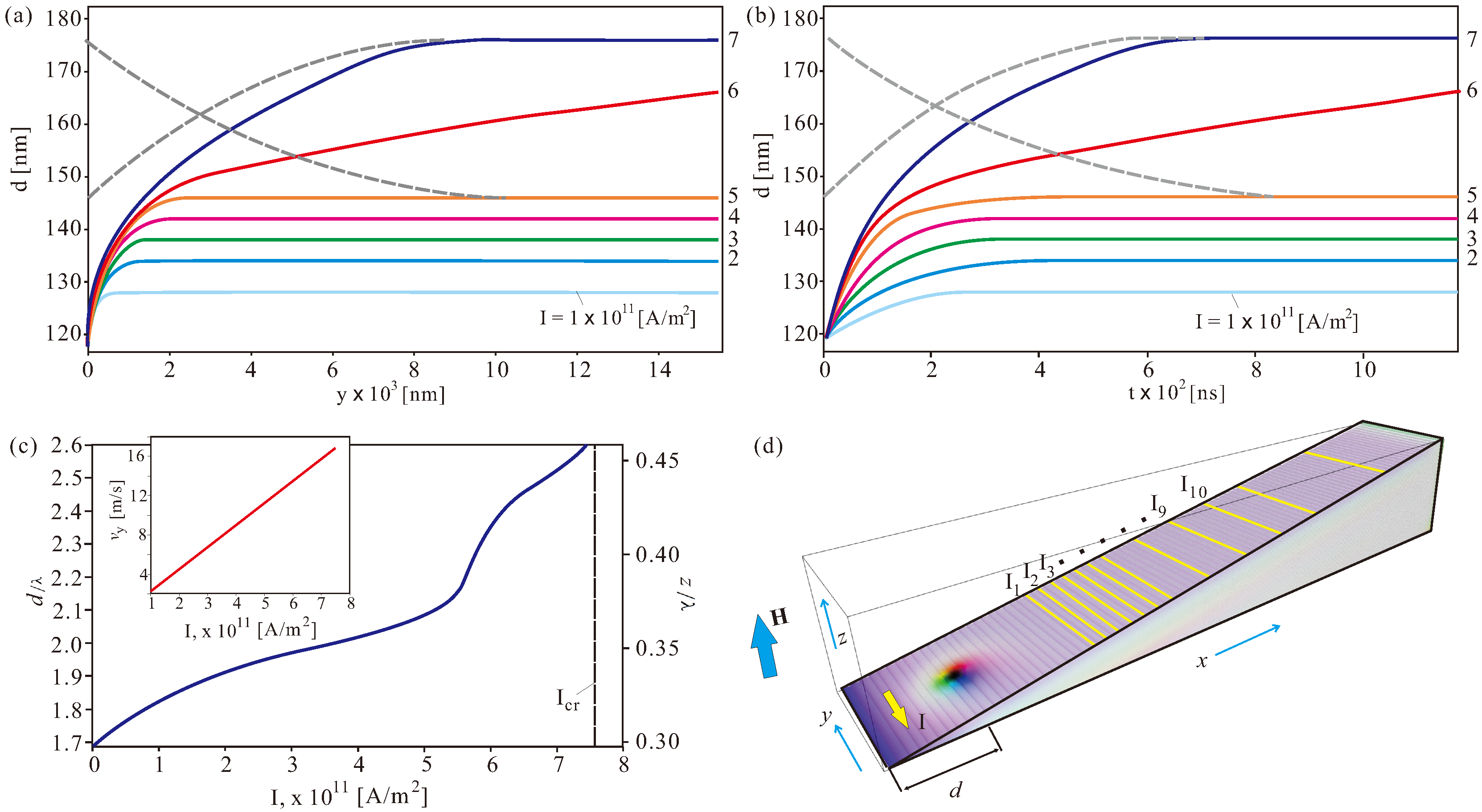
Figure 5a shows the offset skyrmion position
d as calculated with respect to the sharp edge during the current-driven ascent of the wedge. The wedge angle is
, and the current increment is
A/m
. For each current value, ISs are found to reach a straight trajectory parallel to the
y axis (see also schematics in
Figure 5d). It takes around 300 ns to reach an appropriate track, as can be drawn from the time-dependent characteristics
in
Figure 5b. Even for relatively small current values (e.g., for
A/m
), an IS leaves its “pit stop” position corresponding to the energy minimum (as described in
Figure 4d) and elevates until the appropriate thickness is reached to ensure a balance between the restoring force (proportional to the volume change of ISs) and the Magnus force (proportional to the volume of the magnetization inhomogeneity). In some current range (i.e., from
A/m
to
A/m
), the correlation between the current magnitude and the distance
d becomes nearly linear, i.e., equal increments of the spin-polarized current result in the equidistant skyrmion tracks. This effect is related to the curvature of the skyrmion potentials in
Figure 4d, giving rise to the restoring forces. At larger current magnitudes, however, this behavior becomes essentially non-linear. Small changes in the current lead to larger skyrmion elevations until, at the critical current
A/m
, the restoring force cannot balance the skyrmion Hall effect, which pushes ISs uphill until they reach the upper wedge boundary and probably even penetrate through the edge states and annihilate. One cannot engage the Thiele equation [
53] to address the considered breakdown of the balanced skyrmion propagation along the straight tracks. Indeed, a core assumption of the Thiele equation is the unchangeability of the internal structure of ISs. That is why the Thiele equation is usually applied to two-dimensional ISs, with the repulsive interaction between them. But once the skyrmions become essentially three-dimensional and modulate their shape and volume while moving (as systematized in
Figure 2), Thiele equation becomes invalid [
54].
Remarkably, one can get enhanced control not only over the skyrmion ascent for increasing electric currents, but also over their descent; one can return skyrmions to lower elevations/tracks by decreasing the current density. Grey dashed lines in
Figure 5a,b demonstrate the feasibility of such a process; first, we displaced an IS from the track with
A/m
to the track with
A/m
and then sent it back by dropping the current to its initial value.
4.4. Comment on the Skyrmion “Pit Stops” in Truncated Wedges
The internal structure of edge states near the thicker wedge boundary with the angle
(
Figure 4a) is almost the same as the magnetization distribution in thin-film geometries (
Figure 6b. Indeed, the wedge slope (e.g.,
in
Figure 4 and
Figure 5) deviates only by a small amount from
in thin films. Then, these edge states underlie repulsive potentials [
55,
56] as already mentioned in
Section 4.1 (
Figure 6a). However, the film thickness decreasing towards the sharp end of the wedge (related to the decrease of the IS eigen-energy) would lead even to the stronger skyrmion-edge repulsion, i.e., the “flat” interaction potentials for thin layers (
Figure 6a) would accept a negative slope downwards. Thus, those isolated skyrmions, which reached the upper lateral boundary of the wedge for
, will necessarily slide into their “pit stop” positions near the sharp end after the current is switched off.
We also notice the magnetic deformation of the edge states in thin films (
Figure 6b) as compared with the “infinite” samples (
Figure 6c) having only vertical free boundaries and flat edge states, depending only on one spatial coordinate [
51]. In thin films, the magnetic inhomogeneity bears a two-dimensional character with condensed energy “lumps” near the horizontal surfaces (
Figure 6b). The skyrmion dynamics in thin films with
are demonstrated in the supplement (see
Supplementary Videos S4 and S5). As expected, skyrmions can move along the edge [
55,
56] until the repulsive force from the edge states is unable to balance the SHE. Then, skyrmions collapse at the racetrack boundary.
Our findings in the truncated wedge-like samples also indicate that the edge states formed around the obtuse angles (
Figure 6c) are not very effective in maintaining skyrmions within the racetracks. If, for the wedges with a smaller thickness at the lower end (
), the ISs still develop an energy minimum; for larger thicknesses (
), this minimum flattens and practically disappears (
Figure 6d). One may conclude that such truncated geometries are less efficient, as opposed to the mentioned wedges with the sharp ends. Surprisingly, skyrmions in such truncated wedge-shaped nanostructures were shown to persist even for much higher wedge angles in Ref. [
54]. The reason presumably lies in the considered skyrmion lattice state, which had a negative energy density on its own and would not annihilate.