The Role of Polymer Chain Stiffness and Guest Nanoparticle Loading in Improving the Glass Transition Temperature of Polymer Nanocomposites
Abstract
1. Introduction
2. Model and Simulation Method
3. Results and Discussion
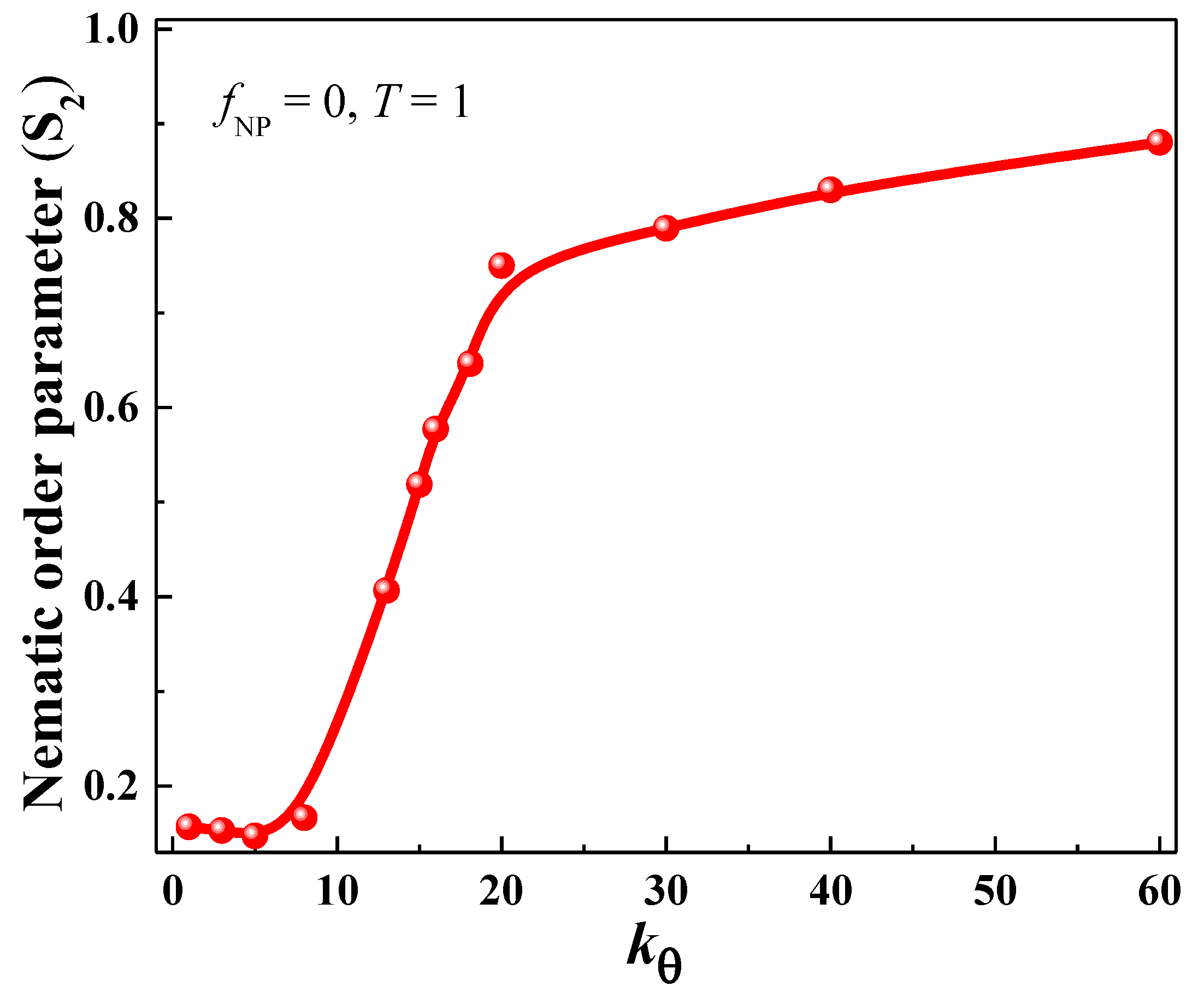
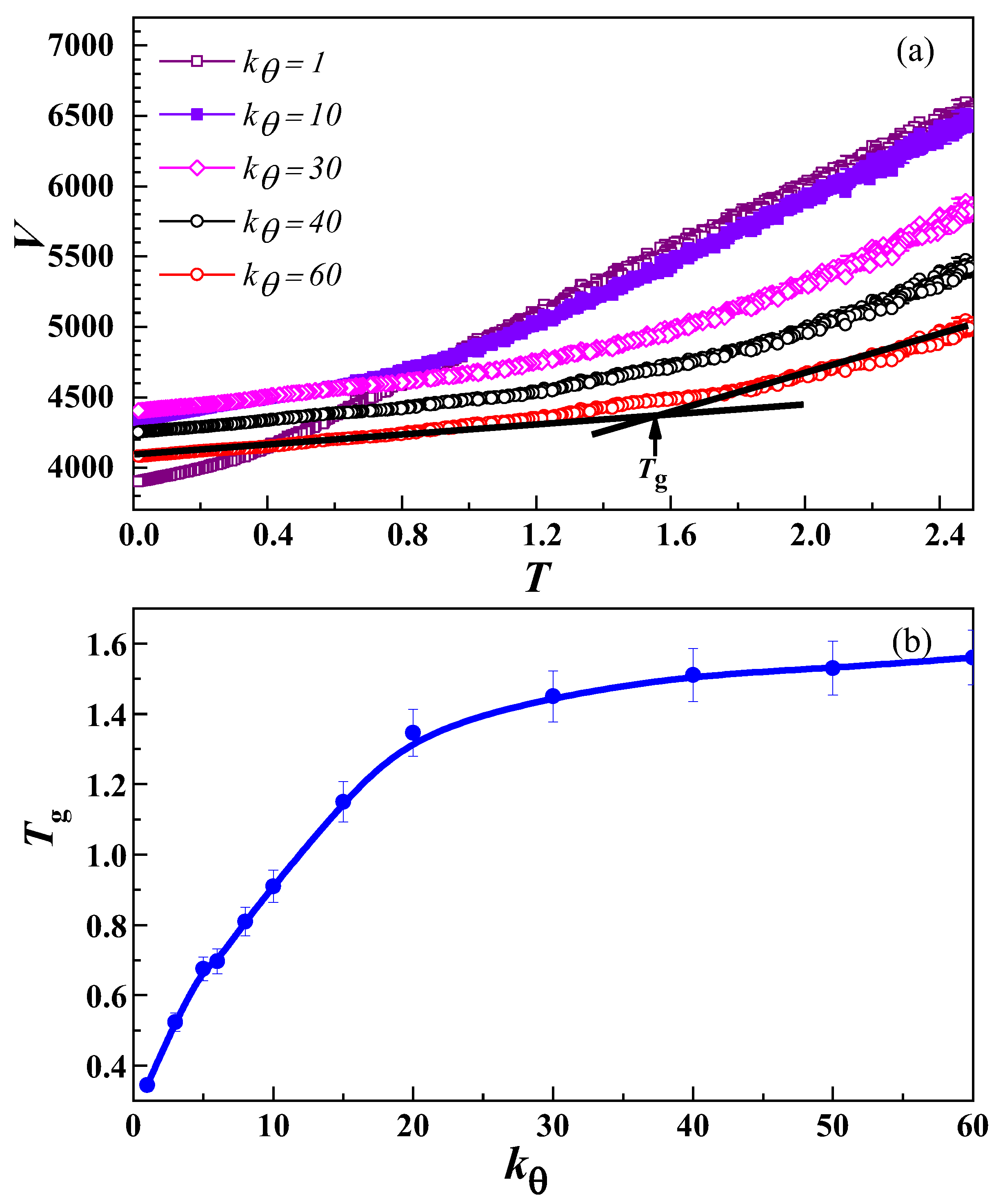
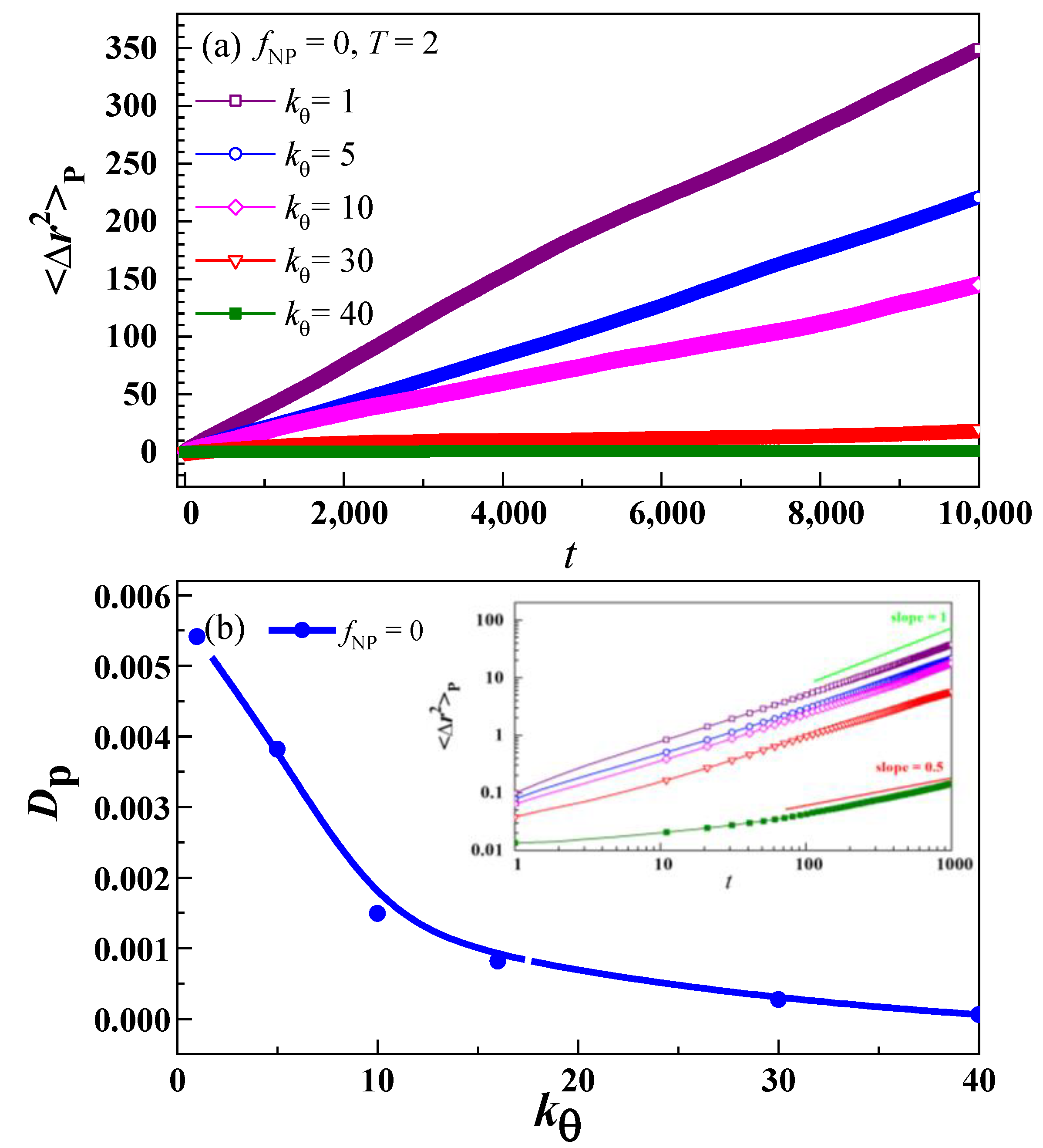
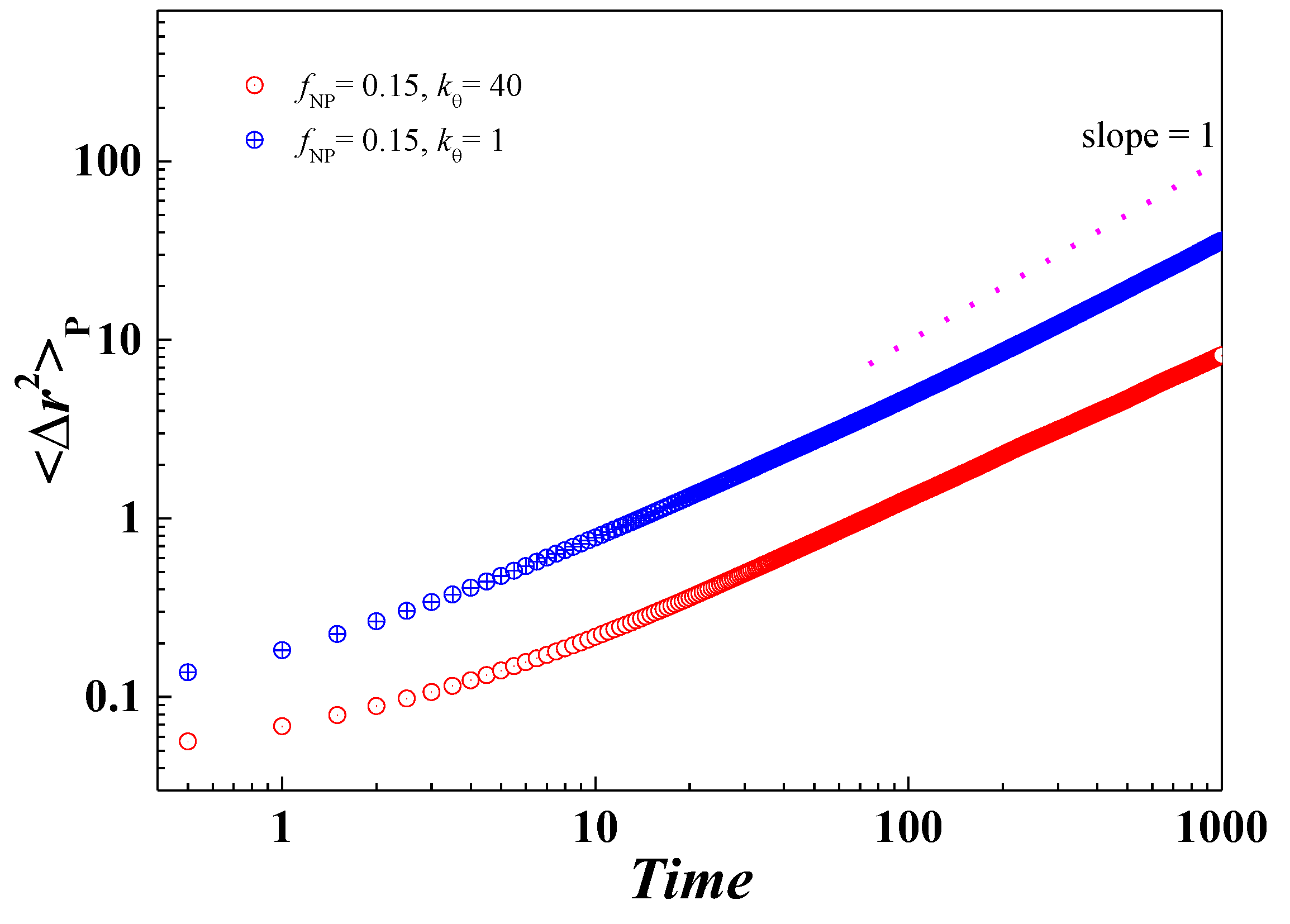
3.1. Glass Transition and Diffusion in Bulk Polymer System
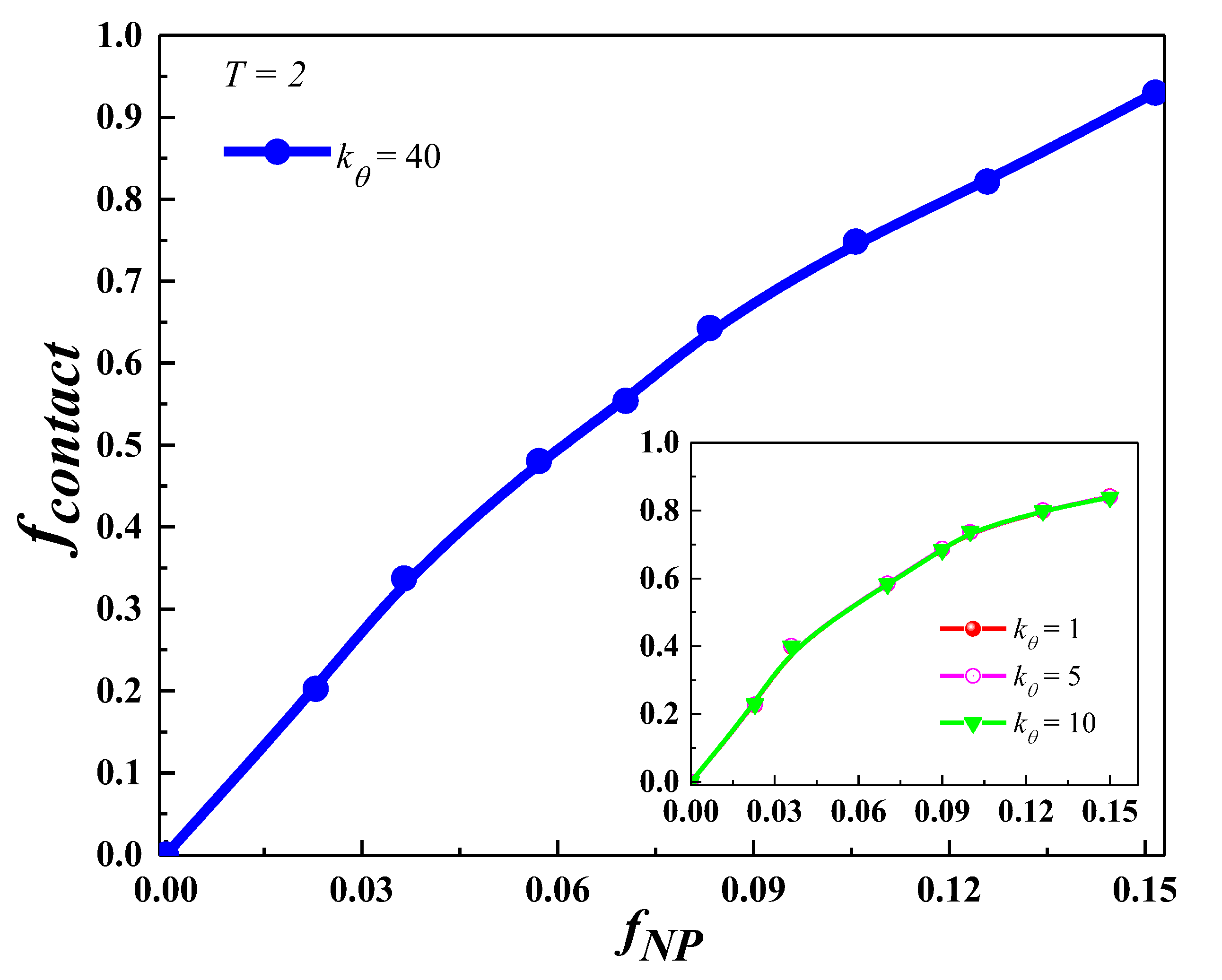
3.2. Glass Transition in Polymer Nanocomposites
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podsiadlo, P.; Kaushik, A.K.; Arruda, E.M.; Waas, A.M.; Shim, B.S.; Xu, J.; Nandivada, H.; Pumplin, B.G.; Lahann, J.; Ramamoorthy, A. Ultrastrong and stiff layered polymer nanocomposites. Science 2007, 318, 80–83. [Google Scholar] [CrossRef]
- Yu, B.; Liang, H.; Rumyantsev, A.M.; de Pablo, J.J. Isotropic-to-Nematic Transition in Salt-Free Polyelectrolyte Coacervates from Coarse-Grained Simulations. Macromolecules 2022, 55, 9627–9639. [Google Scholar] [CrossRef]
- Tsehay, D.A.; Luo, M. Static and dynamic properties of a semiflexible polymer in a crowded environment with randomly distributed immobile nanoparticles. Phys. Chem. Chem. Phys. 2018, 20, 9582–9590. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers. J. Chem. Phys. 2015, 143, 144901. [Google Scholar] [CrossRef] [PubMed]
- Cha, C.; Kohman, R.H.; Kong, H. Biodegradable polymer crosslinker: Independent control of stiffness, toughness, and hydrogel degradation rate. Adv. Funct. Mater. 2009, 19, 3056–3062. [Google Scholar] [CrossRef]
- Semenov, A.N.; Khokhlov, A.R. Statistical physics of liquid-crystalline polymers. Sov. Phys. Uspekhi 1988, 31, 988. [Google Scholar] [CrossRef]
- Chen, Z.Y. Nematic ordering in semiflexible polymer chains. Macromolecules 1993, 26, 3419–3423. [Google Scholar] [CrossRef]
- Dijkstra, M.; Frenkel, D. Simulation study of the isotropic-to-nematic transitions of semiflexible polymers. Phys. Rev. E 1995, 51, 5891. [Google Scholar] [CrossRef]
- Lai, J.C.; Mei, J.F.; Jia, X.Y.; Li, C.H.; You, X.Z.; Bao, Z. A stiff and healable polymer based on dynamic-covalent boroxine bonds. Adv. Mater. 2016, 28, 8277–8282. [Google Scholar] [CrossRef] [PubMed]
- Escobedo, F.A.; de Pablo, J.J. Monte Carlo simulation of athermal mesogenic chains: Pure systems, mixtures, and constrained environments. J. Chem. Phys. 1997, 106, 9858–9868. [Google Scholar] [CrossRef]
- Weber, H.; Paul, W.; Binder, K. Monte Carlo simulation of a lyotropic first-order isotropic-nematic phase transition in a lattice polymer model. Phys. Rev. E 1999, 59, 2168. [Google Scholar] [CrossRef]
- Egorov, S.A.; Milchev, A.; Virnau, P.; Binder, K. A new insight into the isotropic–nematic phase transition in lyotropic solutions of semiflexible polymers: Density-functional theory tested by molecular dynamics. Soft Matter 2016, 12, 4944–4959. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A.; Nikoubashman, A.; Binder, K. The smectic phase in semiflexible polymer materials: A large scale molecular dynamics study. Comput. Mater. Sci. 2019, 166, 230–239. [Google Scholar] [CrossRef]
- Biswas, S.; Fukushima, H.; Drzal, L.T. Mechanical and electrical property enhancement in exfoliated graphene nanoplatelet/liquid crystalline polymer nanocomposites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 371–375. [Google Scholar] [CrossRef]
- Shakya, A.; King, J.T. DNA local-flexibility-dependent assembly of phase-separated liquid droplets. Biophys. J. 2018, 115, 1840–1847. [Google Scholar] [CrossRef]
- Lueckheide, M.; Vieregg, J.R.; Bologna, A.J.; Leon, L.; Tirrell, M.V. Structure–property relationships of oligonucleotide polyelectrolyte complex micelles. Nano Lett. 2018, 18, 7111–7117. [Google Scholar] [CrossRef]
- Bunn, C. The melting points of chain polymers. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 799–819. [Google Scholar] [CrossRef]
- Dudowicz, J.; Freed, K.F.; Douglas, J.F. The glass transition temperature of polymer melts. J. Phys. Chem. B 2005, 109, 21285–21292. [Google Scholar] [CrossRef]
- Winkler, R.G.; Reineker, P.; Harnau, L. Models and equilibrium properties of stiff molecular chains. J. Chem. Phys. 1994, 101, 8119–8129. [Google Scholar] [CrossRef]
- Barkema, G.T.; Panja, D.; Van Leeuwen, J. Semiflexible polymer dynamics with a bead-spring model. J. Stat. Mech. Theory Exp. 2014, 2014, P11008. [Google Scholar] [CrossRef]
- Aharoni, S.M. Increased glass transition temperature in motionally constrained semicrystalline polymers. Polym. Adv. Technol. 1998, 9, 169–201. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D. Structural changes in metallic glass-forming liquids on cooling and subsequent vitrification in relationship with their properties. Materials 2022, 15, 7285. [Google Scholar] [CrossRef] [PubMed]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. On Structural Rearrangements during the Vitrification of Molten Copper. Materials 2022, 15, 1313. [Google Scholar] [CrossRef]
- Laudat, J.; Laudat, F. Indications of glass transition in DNA. EPL Europhys. Lett. 1992, 20, 663. [Google Scholar] [CrossRef]
- Ringe, D.; Petsko, G.A. The ‘glass transition’in protein dynamics: What it is, why it occurs, and how to exploit it. Biophys. Chem. 2003, 105, 667–680. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Yang, H.; Yu, H.; Shi, Q.; Wang, X.; Chen, J. Excluded volume effect on confined polymer translocation through a short nanochannel. J. Chem. Phys. 2006, 124, 174906. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Kremer, K. Static and dynamic properties of large polymer melts in equilibrium. J. Chem. Phys. 2016, 144, 154907. [Google Scholar] [CrossRef]
- Guigas, G.; Weiss, M. Sampling the cell with anomalous diffusion—The discovery of slowness. Biophys. J. 2008, 94, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.; Elsner, M.; Kartberg, F.; Nilsson, T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004, 87, 3518–3524. [Google Scholar] [CrossRef]
- Banks, D.S.; Fradin, C. Anomalous diffusion of proteins due to molecular crowding. Biophys. J. 2005, 89, 2960–2971. [Google Scholar] [CrossRef]
- Saxton, M.J. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys. J. 2007, 92, 1178–1191. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Tejedor, V.; Burov, S.; Barkai, E.; Selhuber-Unkel, C.; Berg-Sørensen, K.; Oddershede, L.; Metzler, R. In vivo anomalous diffusion and weak ergodicity breaking of lipid granules. Phys. Rev. Lett. 2011, 106, 048103. [Google Scholar] [CrossRef]
- Barkai, E.; Garini, Y.; Metzler, R. Strange kinetics of single molecules in living cells. Phys. Today 2012, 65, 29. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Goychuk, I.; Pöschel, T. Fingerprints of viscoelastic subdiffusion in random environments: Revisiting some experimental data and their interpretations. Phys. Rev. E 2021, 104, 034125. [Google Scholar] [CrossRef]
- Baez, W.D.; Wiese, K.J.; Bundschuh, R. Behavior of random RNA secondary structures near the glass transition. Phys. Rev. E 2019, 99, 022415. [Google Scholar] [CrossRef] [PubMed]
- Hui, S.; Tang, L.-H. Ground state and glass transition of the RNA secondary structure. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 53, 77–84. [Google Scholar] [CrossRef]
- Frank, A.T.; Zhang, Q.; Al-Hashimi, H.M.; Andricioaei, I. Slowdown of interhelical motions induces a glass transition in RNA. Biophys. J. 2015, 108, 2876–2885. [Google Scholar] [CrossRef]
- Doster, W. The protein-solvent glass transition. Biochim. Biophys. Acta (BBA)-Proteins Proteom. 2010, 1804, 3–14. [Google Scholar] [CrossRef]
- Norberg, J.; Nilsson, L. Glass transition in DNA from molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 1996, 93, 10173–10176. [Google Scholar] [CrossRef] [PubMed]
- Tsereteli, G.; Belopolskaya, T.; Grunina, N.; Vaveliouk, O. Calorimetric study of the glass transition process in humid proteins and DNA. J. Therm. Anal. Calorim. 2000, 62, 89–99. [Google Scholar] [CrossRef]
- Kumar, P.; Yan, Z.; Xu, L.; Mazza, M.G.; Buldyrev, S.; Chen, S.-H.; Sastry, S.; Stanley, H. Glass transition in biomolecules and the liquid-liquid critical point of water. Phys. Rev. Lett. 2006, 97, 177802. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Uhl, F.M.; Morgan, A.B.; Wilkie, C.A. Studies on the mechanism by which the formation of nanocomposites enhances thermal stability. Chem. Mater. 2001, 13, 4649–4654. [Google Scholar] [CrossRef]
- Lee, J.Y.; Buxton, G.A.; Balazs, A.C. Using nanoparticles to create self-healing composites. J. Chem. Phys. 2004, 121, 5531–5540. [Google Scholar] [CrossRef]
- Bockstaller, M.R.; Mickiewicz, R.A.; Thomas, E.L. Block copolymer nanocomposites: Perspectives for tailored functional materials. Adv. Mater. 2005, 17, 1331–1349. [Google Scholar] [CrossRef]
- Rittigstein, P.; Torkelson, J.M. Polymer–nanoparticle interfacial interactions in polymer nanocomposites: Confinement effects on glass transition temperature and suppression of physical aging. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2935–2943. [Google Scholar] [CrossRef]
- White, S.I.; Mutiso, R.M.; Vora, P.M.; Jahnke, D.; Hsu, S.; Kikkawa, J.M.; Li, J.; Fischer, J.E.; Winey, K.I. Electrical percolation behavior in silver nanowire–polystyrene composites: Simulation and experiment. Adv. Funct. Mater. 2010, 20, 2709–2716. [Google Scholar] [CrossRef]
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, phase behavior, and properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef]
- Suzuki, N.; Zakaria, M.B.; Chiang, Y.-D.; Wu, K.C.-W.; Yamauchi, Y. Thermally stable polymer composites with improved transparency by using colloidal mesoporous silica nanoparticles as inorganic fillers. Phys. Chem. Chem. Phys. 2012, 14, 7427–7432. [Google Scholar] [CrossRef]
- Qi, X.; Tan, C.; Wei, J.; Zhang, H. Synthesis of graphene–conjugated polymer nanocomposites for electronic device applications. Nanoscale 2013, 5, 1440–1451. [Google Scholar] [CrossRef] [PubMed]
- Burgos-Marmol, J.J.; Patti, A. Unveiling the impact of nanoparticle size dispersity on the behavior of polymer nanocomposites. Polymer 2017, 113, 92–104. [Google Scholar] [CrossRef]
- Al-Shamari, A.; Abdelghany, A.; Alnattar, H.; Oraby, A. Structural and optical properties of PEO/CMC polymer blend modified with gold nanoparticles synthesized by laser ablation in water. J. Mater. Res. Technol. 2021, 12, 1597–1605. [Google Scholar] [CrossRef]
- Ming, Y.; Zhou, Z.; Hao, T.; Nie, Y. Polymer Nanocomposites: Role of modified filler content and interfacial interaction on crystallization. Eur. Polym. J. 2022, 162, 110894. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Wang, W.-H.; Zhang, Z.; Xu, L.; Li, P. Study of the glass transition temperature and the mechanical properties of PET/modified silica nanocomposite by molecular dynamics simulation. Eur. Polym. J. 2016, 75, 36–45. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, W.; Si, M.; Gelfer, M.; Hsiao, B.; Rafailovich, M.; Sokolov, J.; Zaitsev, V.; Schwarz, S. Dynamics of polymers in organosilicate nanocomposites. Macromolecules 2003, 36, 823–829. [Google Scholar] [CrossRef]
- Desai, T.; Keblinski, P.; Kumar, S.K. Molecular dynamics simulations of polymer transport in nanocomposites. J. Chem. Phys. 2005, 122, 134910. [Google Scholar] [CrossRef]
- Lin, C.-C.; Gam, S.; Meth, J.S.; Clarke, N.; Winey, K.I.; Composto, R.J. Do attractive polymer–nanoparticle interactions retard polymer diffusion in nanocomposites? Macromolecules 2013, 46, 4502–4509. [Google Scholar] [CrossRef]
- Tung, W.-S.; Bird, V.; Composto, R.J.; Clarke, N.; Winey, K.I. Polymer chain conformations in CNT/PS nanocomposites from small angle neutron scattering. Macromolecules 2013, 46, 5345–5354. [Google Scholar] [CrossRef]
- Li, C.-Y.; Luo, M.-B.; Huang, J.-H.; Li, H. Equilibrium and dynamical properties of polymer chains in random medium filled with randomly distributed nano-sized fillers. Phys. Chem. Chem. Phys. 2015, 17, 31877–31886. [Google Scholar] [CrossRef]
- Huang, X.-W.; Peng, Y.; Huang, J.-H.; Luo, M.-B. A study on the diffusivity of polymers in crowded environments with periodically distributed nanoparticles. Phys. Chem. Chem. Phys. 2017, 19, 29975–29983. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Zhang, H.; Huang, X.-W.; Huang, J.-H.; Luo, M.-B. Monte Carlo simulation on the dynamics of a semi-flexible polymer in the presence of nanoparticles. Phys. Chem. Chem. Phys. 2018, 20, 26333–26343. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wei, W.; Jin, X.; Xiong, H. Chain Dimension and Dynamics of Polymers in Well-Defined Non-sticky Nanocomposites of Molecular Nanoparticle Polyhedral Oligomeric Silsesquioxane/Poly (butylene oxide). Macromolecules 2020, 53, 5627–5637. [Google Scholar] [CrossRef]
- Khan, R.A.A.; Qi, H.-K.; Huang, J.-H.; Luo, M.-B. A simulation study on the effect of nanoparticle size on the glass transition temperature of polymer nanocomposites. Soft Matter 2021, 17, 8095–8104. [Google Scholar] [CrossRef]
- Khan, R.A.A.; Zulfqar, A.; Mateen, M.; Hussain, M.; Rasool, R.T.; Ashraf, G.A.; Xianlong, G. Improvement of the glass transition temperature in novel molybdenum carbide doped polyaniline nanocomposites. Ceram. Int. 2023; in press. [Google Scholar] [CrossRef]
- Iyer, P.; Coleman, M.R. Thermal and mechanical properties of blended polyimide and amine-functionalized poly (orthosiloxane) composites. J. Appl. Polym. Sci. 2008, 108, 2691–2699. [Google Scholar] [CrossRef]
- Ndoro, T.V.; Böhm, M.C.; Müller-Plathe, F. Interface and interphase dynamics of polystyrene chains near grafted and ungrafted silica nanoparticles. Macromolecules 2012, 45, 171–179. [Google Scholar] [CrossRef]
- Bulacu, M.; van der Giessen, E. Molecular-dynamics simulation study of the glass transition in amorphous polymers with controlled chain stiffness. Phys. Rev. E 2007, 76, 011807. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Bulacu, M.; van der Giessen, E. Effect of bending and torsion rigidity on self-diffusion in polymer melts: A molecular-dynamics study. J. Chem. Phys. 2005, 123, 114901. [Google Scholar] [CrossRef]
- Gersappe, D. Molecular mechanisms of failure in polymer nanocomposites. Phys. Rev. Lett. 2002, 89, 058301. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Cheng, S.; Xie, S.-J.; Carrillo, J.-M.Y.; Carroll, B.; Martin, H.; Cao, P.-F.; Dadmun, M.D.; Sumpter, B.G.; Novikov, V.N.; Schweizer, K.S. Big effect of small nanoparticles: A shift in paradigm for polymer nanocomposites. ACS Nano 2017, 11, 752–759. [Google Scholar] [CrossRef] [PubMed]
- Sorichetti, V.; Hugouvieux, V.; Kob, W. Structure and dynamics of a polymer–nanoparticle composite: Effect of nanoparticle size and volume fraction. Macromolecules 2018, 51, 5375–5391. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Qin, J.; Gu, Y. Molecular dynamics simulation on glass transition temperature of isomeric polyimide. Express Polym. Lett. 2009, 3, 665–675. [Google Scholar] [CrossRef]
- Burgos-Mármol, J.J.; Álvarez-Machancoses, O.S.; Patti, A. Modeling the effect of polymer chain stiffness on the behavior of polymer nanocomposites. J. Phys. Chem. B 2017, 121, 6245–6256. [Google Scholar] [CrossRef]
- Martínez-Fernández, D.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Local and Global Order in Dense Packings of Semi-flexible Polymers of Hard Spheres. Polymers 2023, 15, 551. [Google Scholar] [CrossRef]
- Milchev, A.; Egorov, S.A.; Midya, J.; Binder, K.; Nikoubashman, A. Blends of Semiflexible Polymers: Interplay of Nematic Order and Phase Separation. Polymers 2021, 13, 2270. [Google Scholar] [CrossRef]
- Eslami, H.; Muller-Plathe, F. How thick is the interphase in an ultrathin polymer film? Coarse-grained molecular dynamics simulations of polyamide-6, 6 on graphene. J. Phys. Chem. C 2013, 117, 5249–5257. [Google Scholar] [CrossRef]
- Eslami, H.; Rahimi, M.; Müller-Plathe, F. Molecular dynamics simulation of a silica nanoparticle in oligomeric poly (methyl methacrylate): A model system for studying the interphase thickness in a polymer–nanocomposite via different properties. Macromolecules 2013, 46, 8680–8692. [Google Scholar] [CrossRef]
- Khan, R.A.A.; Chen, X.; Qi, H.-K.; Huang, J.-H.; Luo, M.-B. A novel shift in the glass transition temperature of polymer nanocomposites: A molecular dynamics simulation study. Phys. Chem. Chem. Phys. 2021, 23, 12216–12225. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, R.A.A.; Luo, M.; Alsaad, A.M.; Qattan, I.A.; Abedrabbo, S.; Hua, D.; Zulfqar, A. The Role of Polymer Chain Stiffness and Guest Nanoparticle Loading in Improving the Glass Transition Temperature of Polymer Nanocomposites. Nanomaterials 2023, 13, 1896. https://doi.org/10.3390/nano13131896
Khan RAA, Luo M, Alsaad AM, Qattan IA, Abedrabbo S, Hua D, Zulfqar A. The Role of Polymer Chain Stiffness and Guest Nanoparticle Loading in Improving the Glass Transition Temperature of Polymer Nanocomposites. Nanomaterials. 2023; 13(13):1896. https://doi.org/10.3390/nano13131896
Chicago/Turabian StyleKhan, Raja Azhar Ashraaf, Mengbo Luo, Ahmad M. Alsaad, Issam A. Qattan, Sufian Abedrabbo, Daoyang Hua, and Afsheen Zulfqar. 2023. "The Role of Polymer Chain Stiffness and Guest Nanoparticle Loading in Improving the Glass Transition Temperature of Polymer Nanocomposites" Nanomaterials 13, no. 13: 1896. https://doi.org/10.3390/nano13131896
APA StyleKhan, R. A. A., Luo, M., Alsaad, A. M., Qattan, I. A., Abedrabbo, S., Hua, D., & Zulfqar, A. (2023). The Role of Polymer Chain Stiffness and Guest Nanoparticle Loading in Improving the Glass Transition Temperature of Polymer Nanocomposites. Nanomaterials, 13(13), 1896. https://doi.org/10.3390/nano13131896







