Broadband Tamm Plasmons in Chirped Photonic Crystals for Light-Induced Water Splitting
Abstract
:1. Introduction
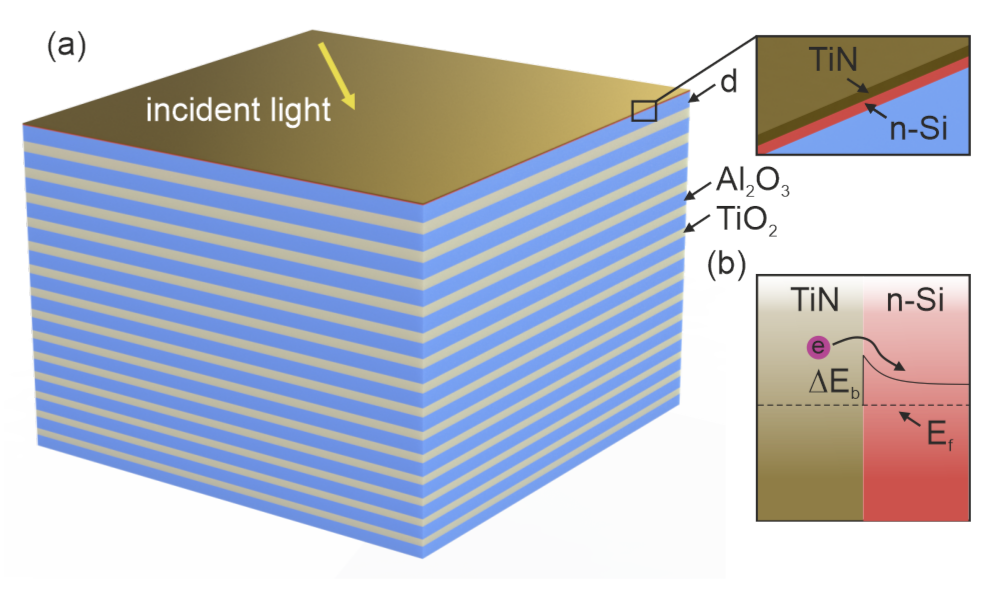
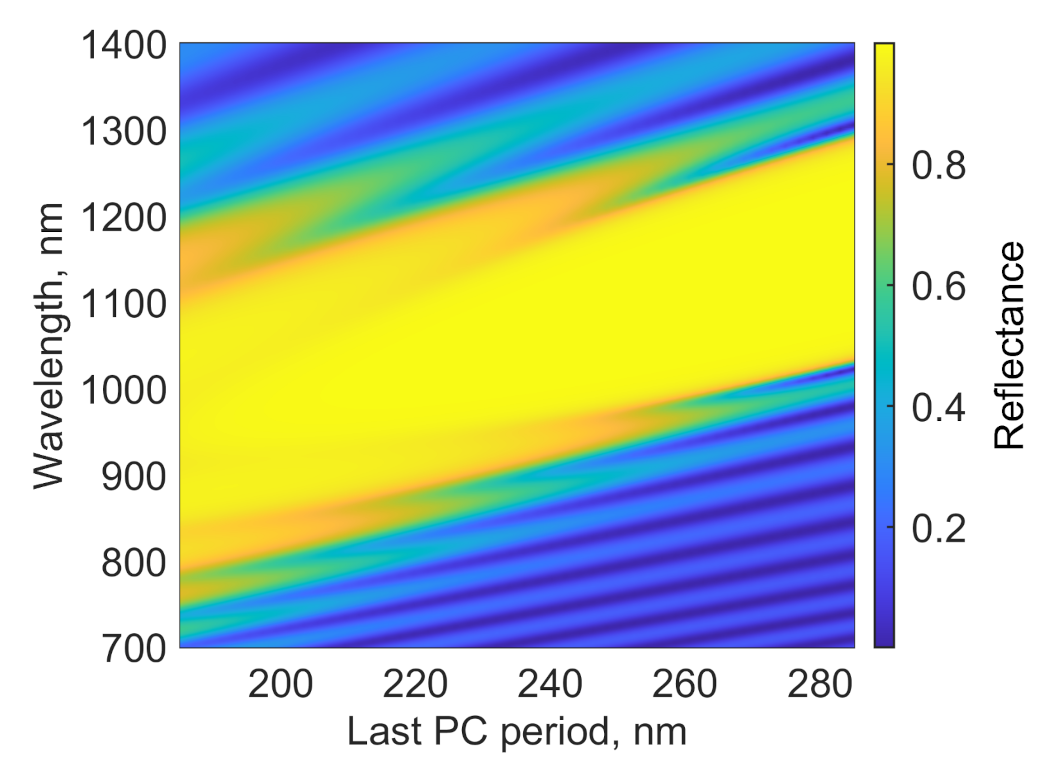
2. Design of the Structure
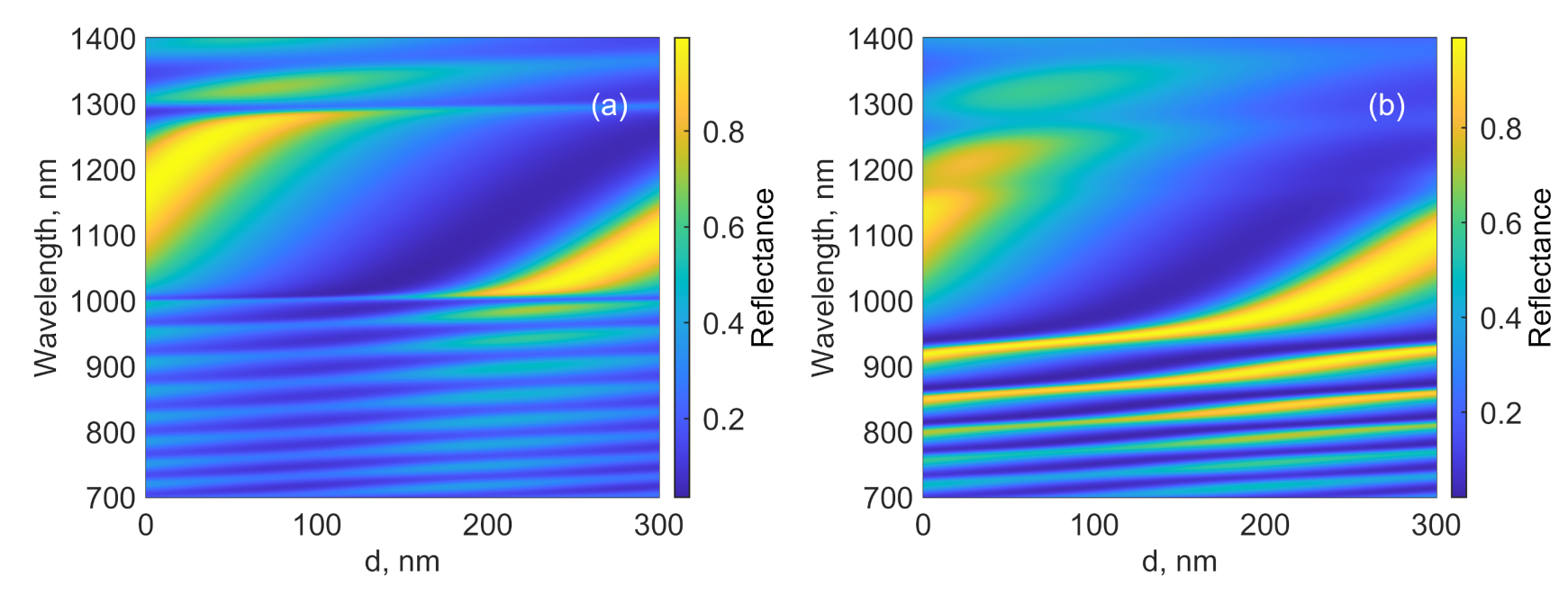
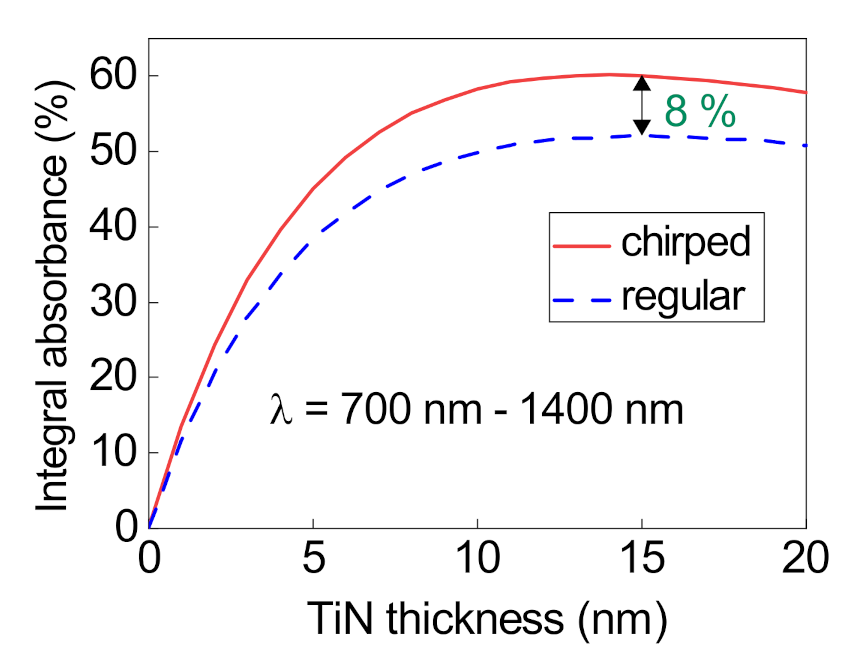
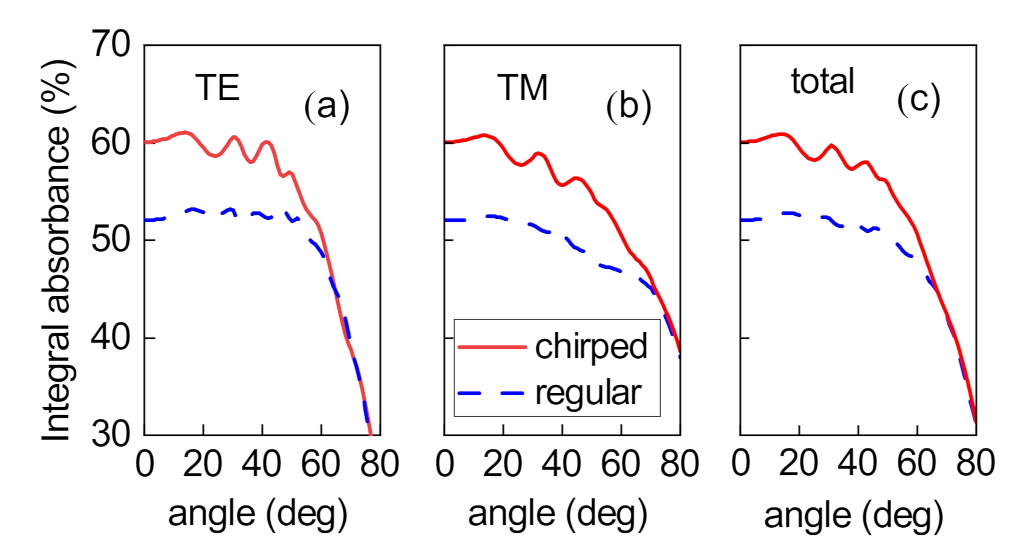
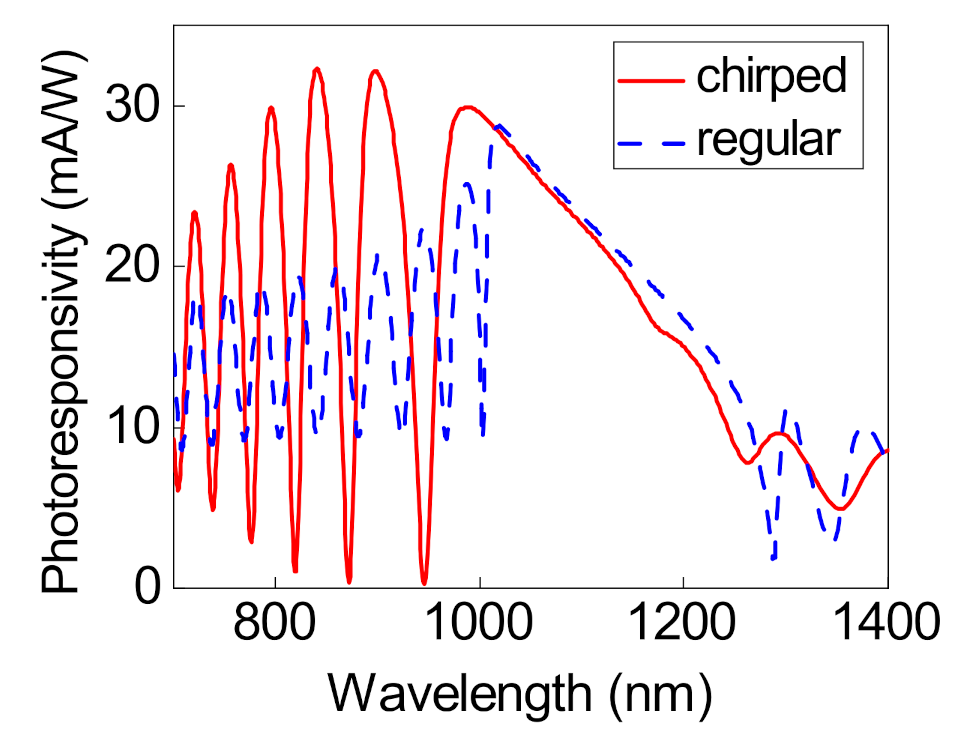
3. Absorption Properties of the Structure
- 1.
- Plasmons nonradiatively decay into hot electrons;
- 2.
- Hot electrons are transferred to the metal–semiconductor interface prior to thermalization;
- 3.
- Hot electrons are injected into the conduction band of the semiconductor through internal photoemission.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fujishima, A.; Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37. [Google Scholar] [CrossRef] [PubMed]
- Hamdani, I.R.; Bhaskarwar, A.N. Recent progress in material selection and device designs for photoelectrochemical water-splitting. Renew. Sustain. Energy Rev. 2021, 138, 110503. [Google Scholar] [CrossRef]
- Lan, Y.; Lu, Y.; Ren, Z. Mini review on photocatalysis of titanium dioxide nanoparticles and their solar applications. Nano Energy 2013, 2, 1031. [Google Scholar] [CrossRef]
- Atwater, H.; Polman, A. Plasmonics for improved photovoltaic devices. Nature Mater. 2010, 9, 205. [Google Scholar] [CrossRef]
- Milichko, V.A.; Shalin, A.S.; Mukhin, I.S.; Kovrov, A.E.; Krasilin, A.A.; Vinogradov, A.V.; Belov, P.A.; Simovski, C.R. Solar photovoltaics: Current state and trends. Phys. Uspekhi 2016, 59, 727. [Google Scholar] [CrossRef]
- Guo, L.-J.; Luo, J.-W.; He, T.; Wei, S.-H.; Li, S.-S. Photocorrosion-limited maximum efficiency of solar photoelectrochemical water splitting. Phys. Rev. Appl. 2018, 10, 064059. [Google Scholar] [CrossRef] [Green Version]
- Dorfi, A.E.; West, A.C.; Esposito, D.V. Quantifying losses in photoelectrode performance due to single hydrogen bubbles. J. Phys. Chem. C 2017, 121, 26587. [Google Scholar] [CrossRef]
- Mascaretti, L.; Dutta, A.; Kment, Š.; Shalaev, V.M.; Boltasseva, A.; Zboril, R.; Naldoni, A. 2019 Plasmon-enhanced photoelectrochemical water splitting for efficient renewable energy storage. Adv. Mater. 2019, 31, 1805513. [Google Scholar] [CrossRef]
- Xiang, C.; Weber, A.Z.; Ardo, S.; Berger, A.; Chen, Y.; Coridan, R.; Fountaine, K.T.; Haussener, S.; Hu, S.; Liu, R.; et al. Modeling, simulation, and implementation of solar-driven water-splitting devices. Angew. Chem. Int. Ed. 2016, 55, 12974. [Google Scholar] [CrossRef] [Green Version]
- Dutta, A.; Naldoni, A.; Malara, F.; Govorov, A.O.; Shalaev, V.M.; Boltasseva, A. Gap-plasmon enhanced water splitting with ultrathin hematite films: The role of plasmonic-based light trapping and hot electrons. Faraday Disk 2019, 214, 283. [Google Scholar] [CrossRef]
- Kim, J.K.; Shi, X.; Jeong, M.J.; Park, J.; Han, H.S.; Kim, S.H.; Guo, Y.; Heinz, T.F.; Fan, S.; Lee, C.-L.; et al. Enhancing Mo: BiVO4 solar water splitting with patterned Au nanospheres by plasmon-induced energy transfer. Adv. Energy Mater. 2018, 8, 1701765. [Google Scholar] [CrossRef]
- Naldoni, A.; Guler, U.; Wang, Z.; Marelli, M.; Malara, F.; Meng, X.; Besteiro, L.V.; Govorov, A.O.; Kildishev, A.V.; Boltasseva, A.; et al. Broadband hot-electron collection for solar water splitting with plasmonic titanium nitride. Adv. Opt. Mater. 2017, 5, 1601031. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.M.; Lee, B.W.; Jung, M.S.; Han, H.S.; Kim, S.H.; Chen, K.; Kim, D.H.; Heinz, T.F.; Fan, S.; Lee, J.; et al. Retarded Charge–Carrier Recombination in Photoelectrochemical Cells from Plasmon-Induced Resonance Energy Transfer. Adv. Energy Mater. 2020, 10, 2000570. [Google Scholar] [CrossRef]
- Guselnikova, O.; Trelin, A.; Miliutina, E.; Elashnikov, R.; Sajdl, P.; Postnikov, P.; Kolska, Z.; Svorcik, V.; Lyutakov, O. Plasmon-induced water splitting—Through flexible hybrid 2D architecture up to hydrogen from seawater under NIR Light. ACS Appl. Mater. Int. 2020, 12, 28110. [Google Scholar] [CrossRef]
- Voronin, A.S.; Nemtsev, I.V.; Molokeev, M.S.; Simunin, M.M.; Kozlova, E.A.; Markovskaya, D.V.; Lebedev, D.V.; Lopatin, D.S.; Khartov, S.V. Laser-Induced Chemical Liquid-Phase Deposition Plasmonic Gold Nanoparticles on Porous TiO2 Film with Great Photoelectrochemical Performance. Appl. Sci. 2022, 12, 30. [Google Scholar] [CrossRef]
- Zheng, Z.; Zheng, Y.; Luo, Y.; Yi, Z.; Zhang, J.; Liu, Z.; Yang, W.; Yu, Y.; Wuf, X.; Wug, P. A switchable terahertz device combining ultra-wideband absorption and ultra-wideband complete reflection. Phys. Chem. Chem. Phys. 2022, 24, 2527. [Google Scholar] [CrossRef]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Liu, H.; Qiao, T.; Hou, G.; Liu, H.; Xu, J.; Zhu, J.; Zhou, L. Tamm plasmon enabled narrowband thermal emitter for solar thermophotovoltaics. Sol. Energy Mater. Sol. Cells 2022, 238, 111589. [Google Scholar] [CrossRef]
- Xu, W.-H.; Chou, Y.-H.; Yang, Z.-Y.; Liu, Y.-Y.; Yu, M.-W.; Huang, C.-H.; Chang, C.-T.; Huang, C.-Y.; Lu, T.-C.; Lin, T.R.; et al. Tamm Plasmon-Polariton Ultraviolet Lasers. Adv. Photonics Res. 2021, 3, 21001200. [Google Scholar] [CrossRef]
- Leuthold, J.; Dorodnyy, A. On-demand emission from Tamm plasmons. Nat. Mater. 2021, 20, 1595–1596. [Google Scholar] [CrossRef]
- Xue, C.H.; Wu, F.; Jiang, H.T.; Li, Y.; Zhang, Y.W.; Chen, H. Wide-angle Spectrally Selective Perfect Absorber by Utilizing Dispersionless Tamm Plasmon Polaritons. Sci. Rep. 2016, 6, 39418. [Google Scholar] [CrossRef] [Green Version]
- Vyunishev, A.M.; Bikbaev, R.G.; Svyakhovskiy, S.E.; Timofeev, I.V.; Pankin, P.S.; Evlashin, S.A.; Vetrov, S.Y.; Myslivets, S.A.; Arkhipkin, V.G. Broadband Tamm plasmon polariton. JOSA B 2019, 36, 2299. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Y.; Wang, W.; Li, Y.; Gao, R.; Yu, P.; Xu, H.; Wang, Z. Broadband Tamm plasmon-enhanced planar hot-electron photodetector. Nanoscale 2020, 12, 23945. [Google Scholar] [CrossRef]
- Maigyte, L.; Staliunas, K. Spatial filtering with photonic crystals. Appl. Phys. Rev. 2015, 2, 011102. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in Stratified and Anisotropic Media: 4 × 4-Matrix Formulation. J. Opt. Soc. Am. 1972, 62, 502. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Gosciniak, J.; Atar, F.B.; Corbett, B.; Rasras, R. CMOS-compatible titanium nitride for on-chip plasmonic Schottky photodetectors. ACS Omega 2019, 4, 17223. [Google Scholar] [CrossRef]
- Zhang, X.L.; Song, J.F.; Li, X.B.; Feng, J.; Sun, H.B. Optical Tamm states enhanced broad-band absorption of organic solar cells. Appl. Phys. Lett. 2012, 101, 243901. [Google Scholar] [CrossRef] [Green Version]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V.; Shabanov, V.F. Photosensitivity and reflectivity of the active layer in a Tamm-plasmon-polariton-based organic solar cell. Appl. Opt. 2021, 60, 3338. [Google Scholar] [CrossRef] [PubMed]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V.; Shabanov, V.F. Tamm Plasmon Polaritons for Light Trapping in Organic Solar Cells. Dokl. Phys. 2020, 65, 161–163. [Google Scholar] [CrossRef]
- Zhou, F.; Qin, F.; Yi, Z.; Yao, W.; Liu, Z.; Wud, X.; Wu, P. Ultra-wideband and wide-angle perfect solar energy absorber based on Ti nanorings surface plasmon resonance. Phys. Chem. Chem. Phys. 2021, 23, 17041. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.M.; Lee, J.; Kim, Y.S.; Song, J.; Oh, J.; Lee, S.M.; Jeong, M.; Kim, Y.; Kwak, J.H.; Cho, S.; et al. High-performance and stable photoelectrochemical water splitting cell with organic-photoactive-layer-based photoanode. Nat. Commun. 2020, 11, 5509. [Google Scholar] [CrossRef] [PubMed]
- Gong, T.; Munday, J.N. Angle-independent hot carrier generation and collection using transparent conducting oxides. Nano Lett. 2015, 15, 147. [Google Scholar] [CrossRef] [PubMed]
- Blandre, E.; Jalas, D.; Petrov, A.Y.; Eich, M. Limit of efficiency of generation of hot electrons in metals and their injection inside a semiconductor using a semiclassical approach. ACS Photonics 2018, 5, 3613. [Google Scholar] [CrossRef]
- Spicer, W.E. Photoemissive, photoconductive, and optical absorption studies of alkali-antimony compounds. Phys. Rev. 1958, 112, 114. [Google Scholar] [CrossRef]
- Spicer, W.E. Negative affinity 3–5 photocathodes: Their physics and technology. Appl. Phys. 1977, 12, 115. [Google Scholar] [CrossRef]
- Fowler, R.H. The analysis of photoelectric sensitivity curves for clean metals at various temperatures. Phys. Rev. 1931, 38, 45. [Google Scholar] [CrossRef]
- Li, W.; Valentine, J. Metamaterial perfect absorber based hot electron photodetection. Nano Lett. 2014, 14, 3510. [Google Scholar] [CrossRef]
- Shao, W.; Liu, T. Planar narrowband Tamm plasmon-based hot-electron photodetectors with double distributed Bragg reflectors. Nano Express 2021, 2, 040009. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, K.; Giannini, V.; Li, X. Planar Hot-Electron Photodetection with Tamm Plasmons. ACS Nano 2017, 11, 1719–1727. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.; Xiao, Z.; Xu, H.; Deng, H.; Li, H.; Chen, W.; Liu, Z.; Long, Y. Ultranarrow-bandwidth planar hot electron photodetector based on coupled dual Tamm plasmons. Opt. Express 2020, 28, 31330. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyatnov, M.V.; Bikbaev, R.G.; Timofeev, I.V.; Ryzhkov, I.I.; Vetrov, S.Y.; Shabanov, V.F. Broadband Tamm Plasmons in Chirped Photonic Crystals for Light-Induced Water Splitting. Nanomaterials 2022, 12, 928. https://doi.org/10.3390/nano12060928
Pyatnov MV, Bikbaev RG, Timofeev IV, Ryzhkov II, Vetrov SY, Shabanov VF. Broadband Tamm Plasmons in Chirped Photonic Crystals for Light-Induced Water Splitting. Nanomaterials. 2022; 12(6):928. https://doi.org/10.3390/nano12060928
Chicago/Turabian StylePyatnov, Maxim V., Rashid G. Bikbaev, Ivan V. Timofeev, Ilya I. Ryzhkov, Stepan Ya. Vetrov, and Vasily F. Shabanov. 2022. "Broadband Tamm Plasmons in Chirped Photonic Crystals for Light-Induced Water Splitting" Nanomaterials 12, no. 6: 928. https://doi.org/10.3390/nano12060928
APA StylePyatnov, M. V., Bikbaev, R. G., Timofeev, I. V., Ryzhkov, I. I., Vetrov, S. Y., & Shabanov, V. F. (2022). Broadband Tamm Plasmons in Chirped Photonic Crystals for Light-Induced Water Splitting. Nanomaterials, 12(6), 928. https://doi.org/10.3390/nano12060928








