Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk
Abstract
:1. Introduction
2. Materials and Methods
3. Numerical Procedure of the Multiple Solutions
Verification of the Scheme
4. Analysis of Results and Discussions
4.1. Analysis of the Constructed Tables
4.2. For the Example of Non-Rotating Disk Parameter αA = 0.0
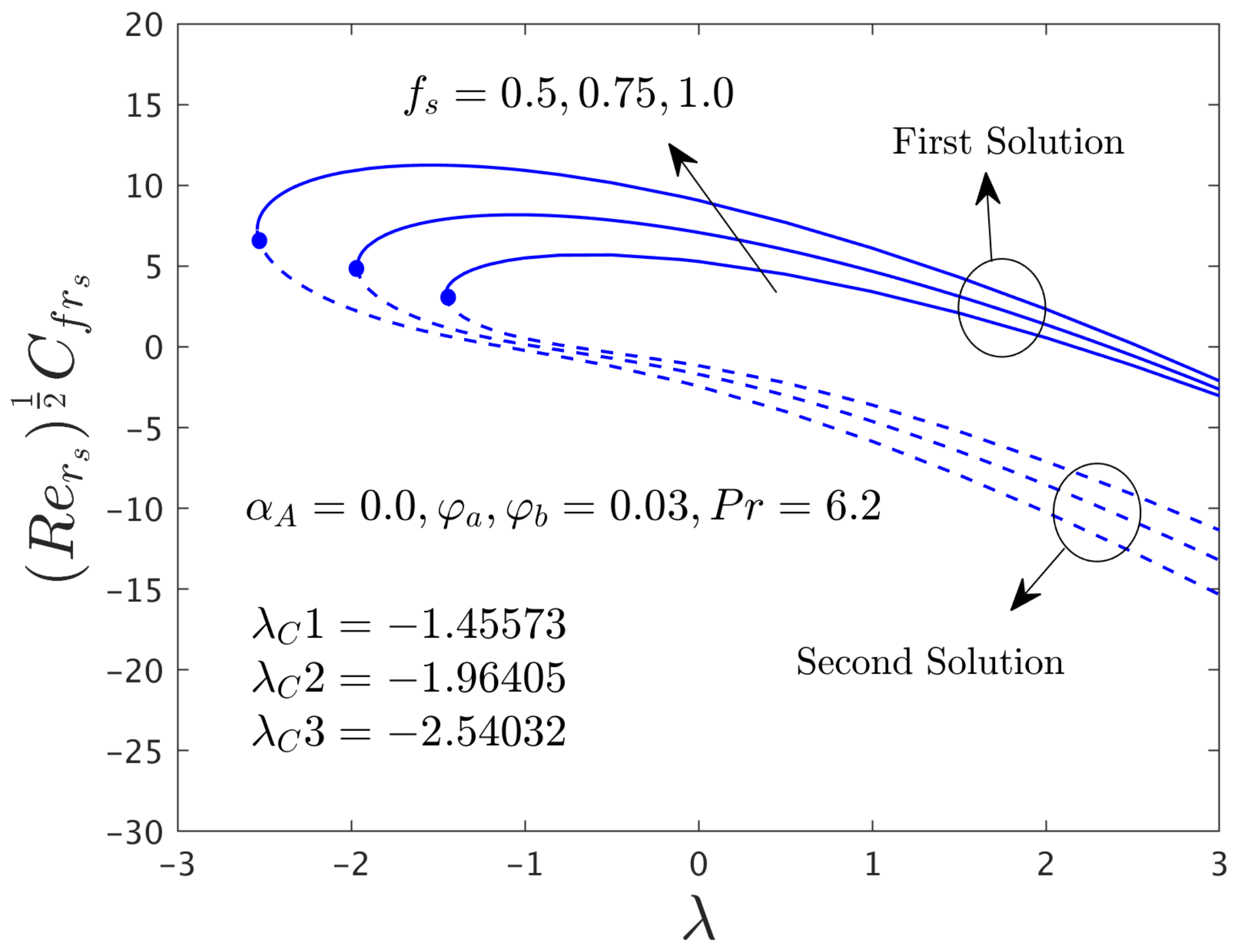
4.2.1. Consequence of the Mass Flux Parameter (fs)
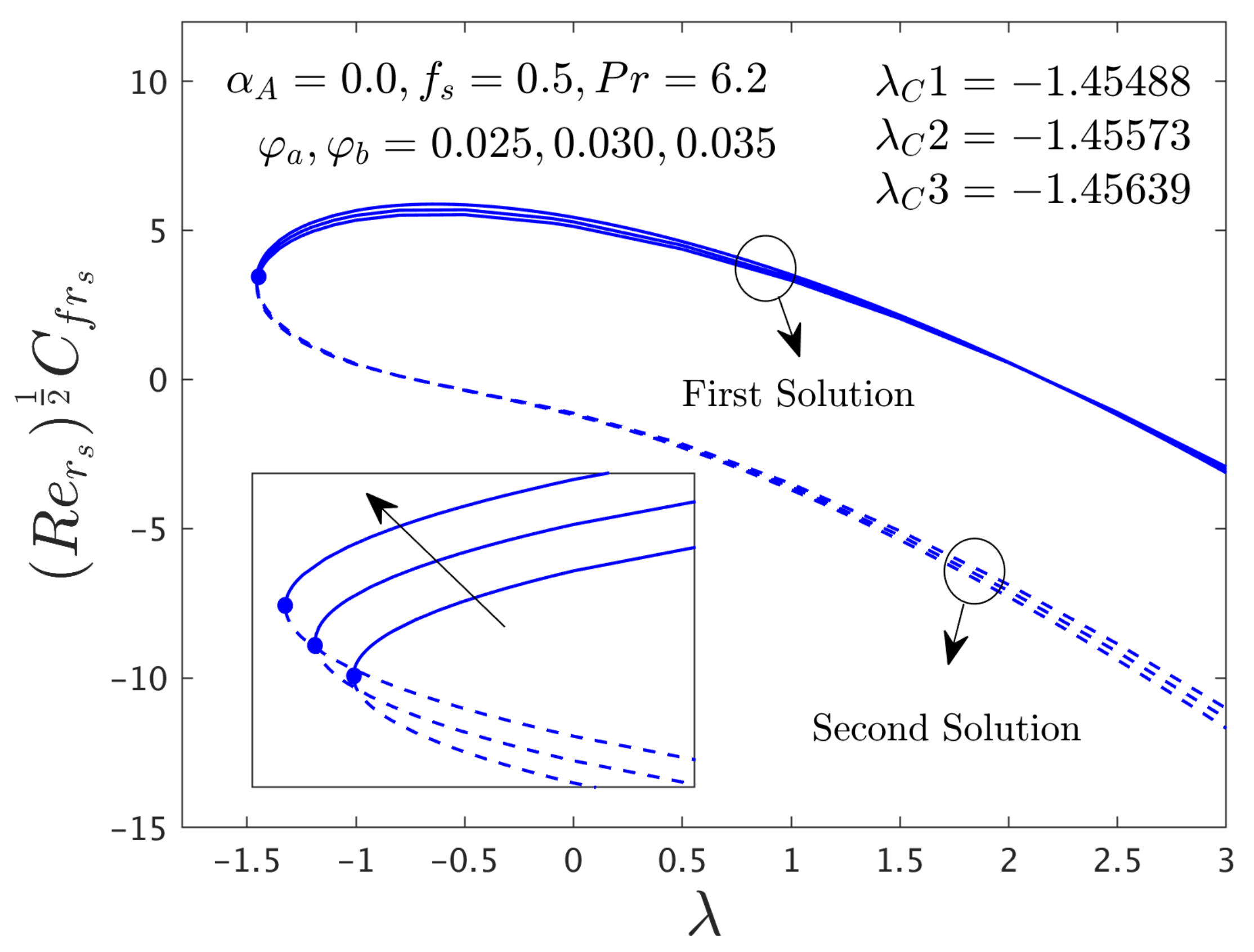
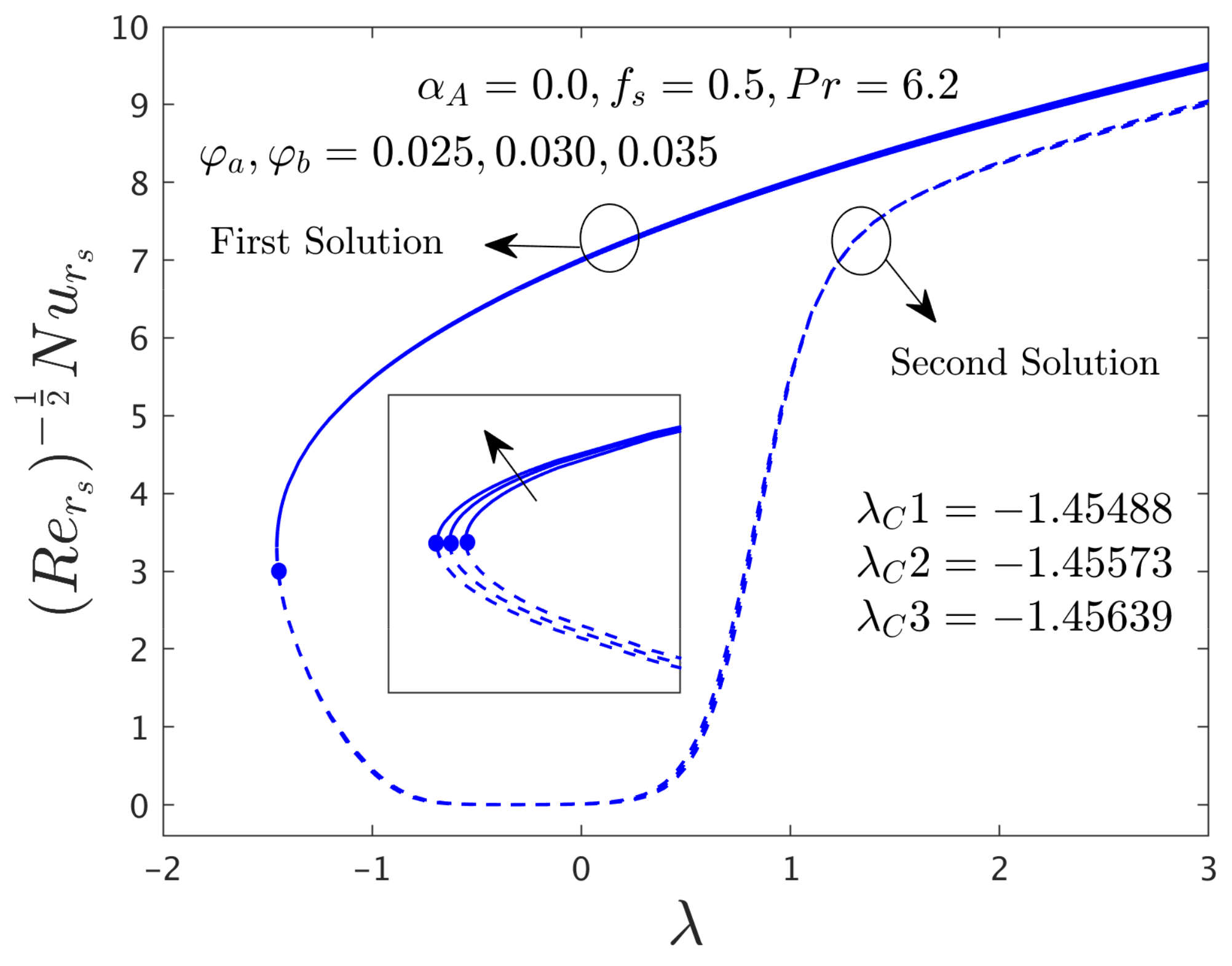
4.2.2. Consequence of Hybrid (GO-MoS2/Water) Nanoparticle (ϕ)
4.3. For the Example of Rotating Disk Parameter, αA ≠ 0.0
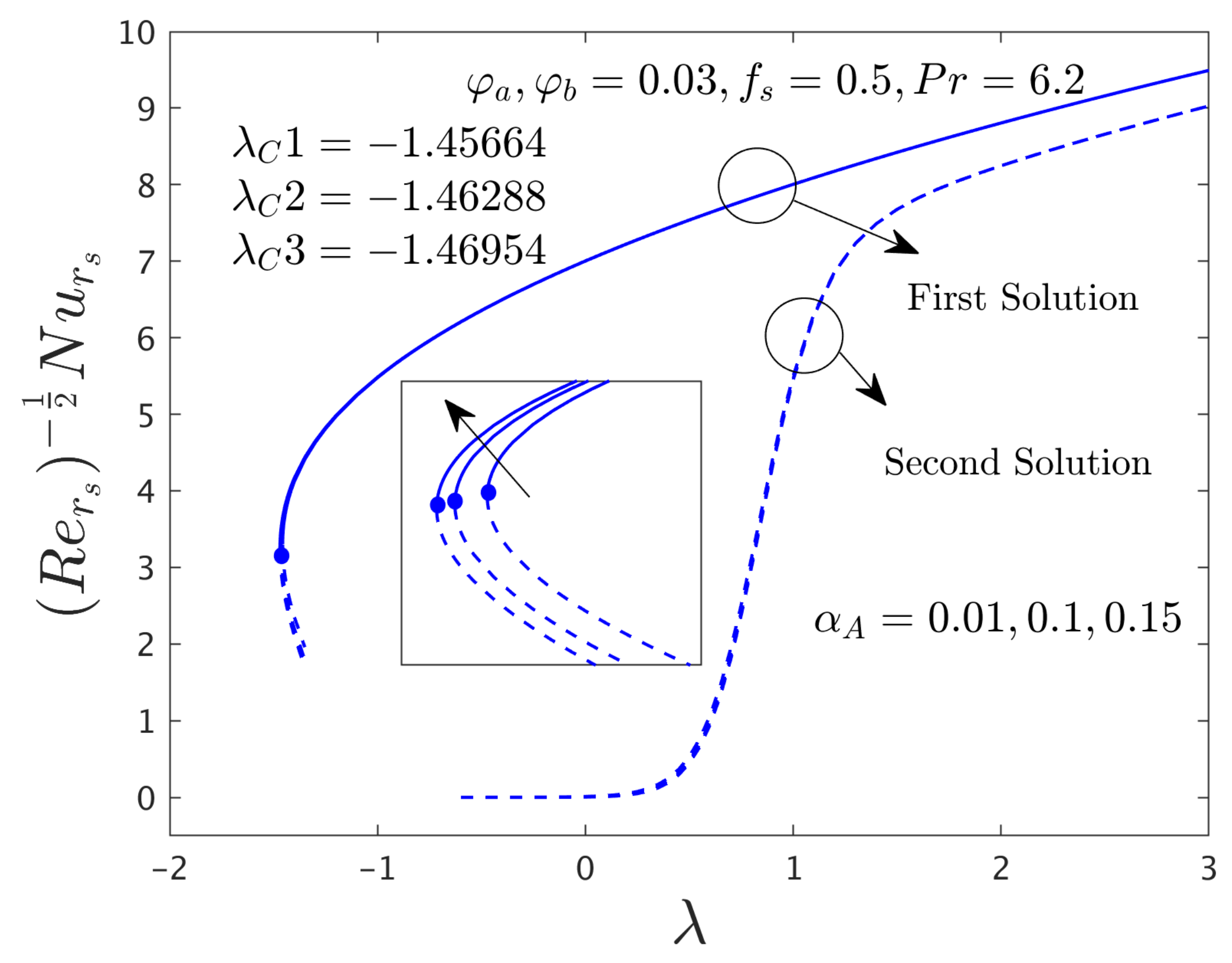
4.3.1. Consequence of the Rotating Disk Parameter (αA)
4.3.2. Consequence of the Mass Flux Parameter (fs)
4.3.3. Consequence of Hybrid (GO-MoS2/Water) Nanoparticle (ϕ)
5. Conclusions
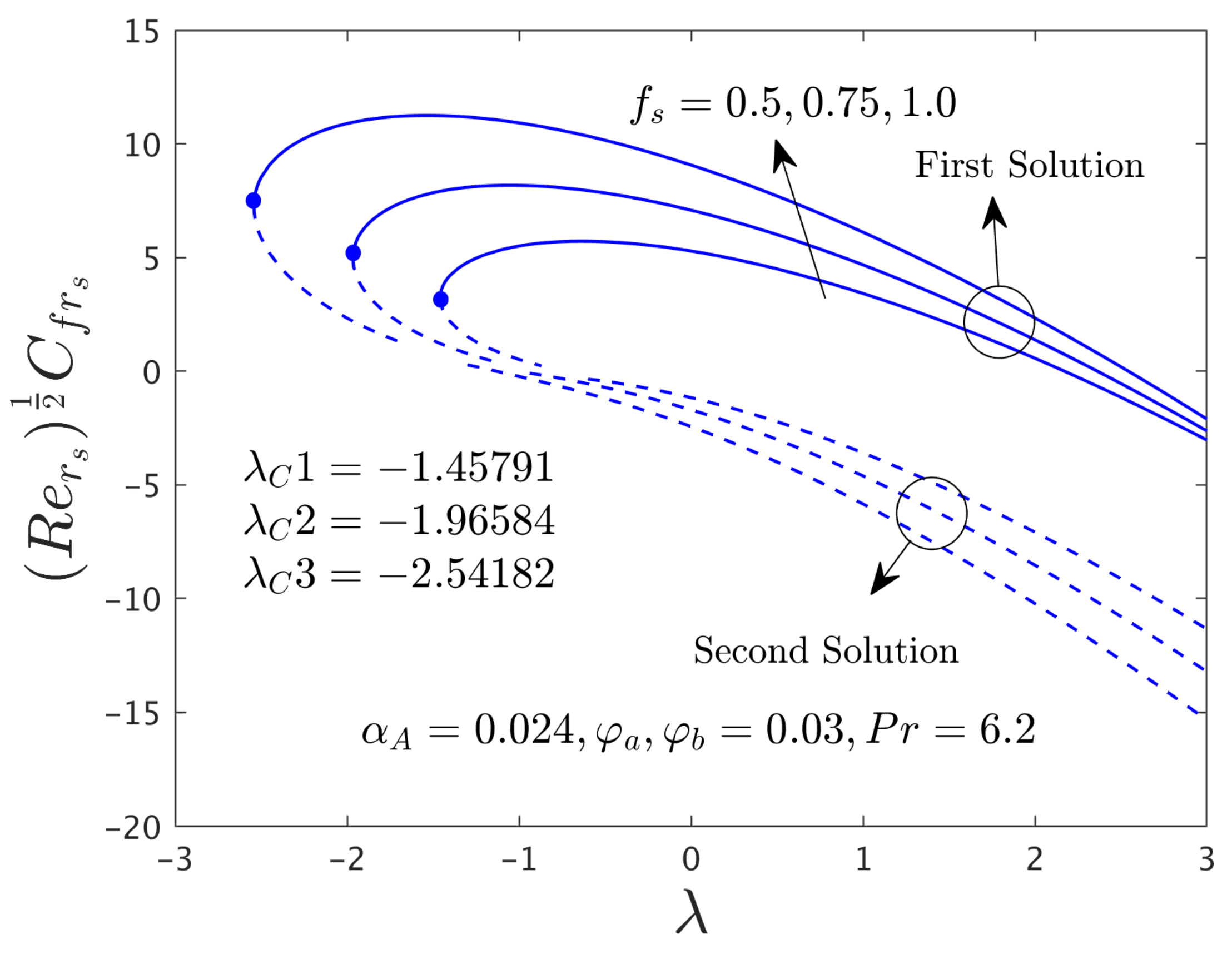
- The shear stress in the radial direction upsurges for the first solution but reduces for the second solution with higher values of S when αA = 0, Pr = 6.2, ϕa = 0.03 and ϕb = 0.03 while the significantly rises.
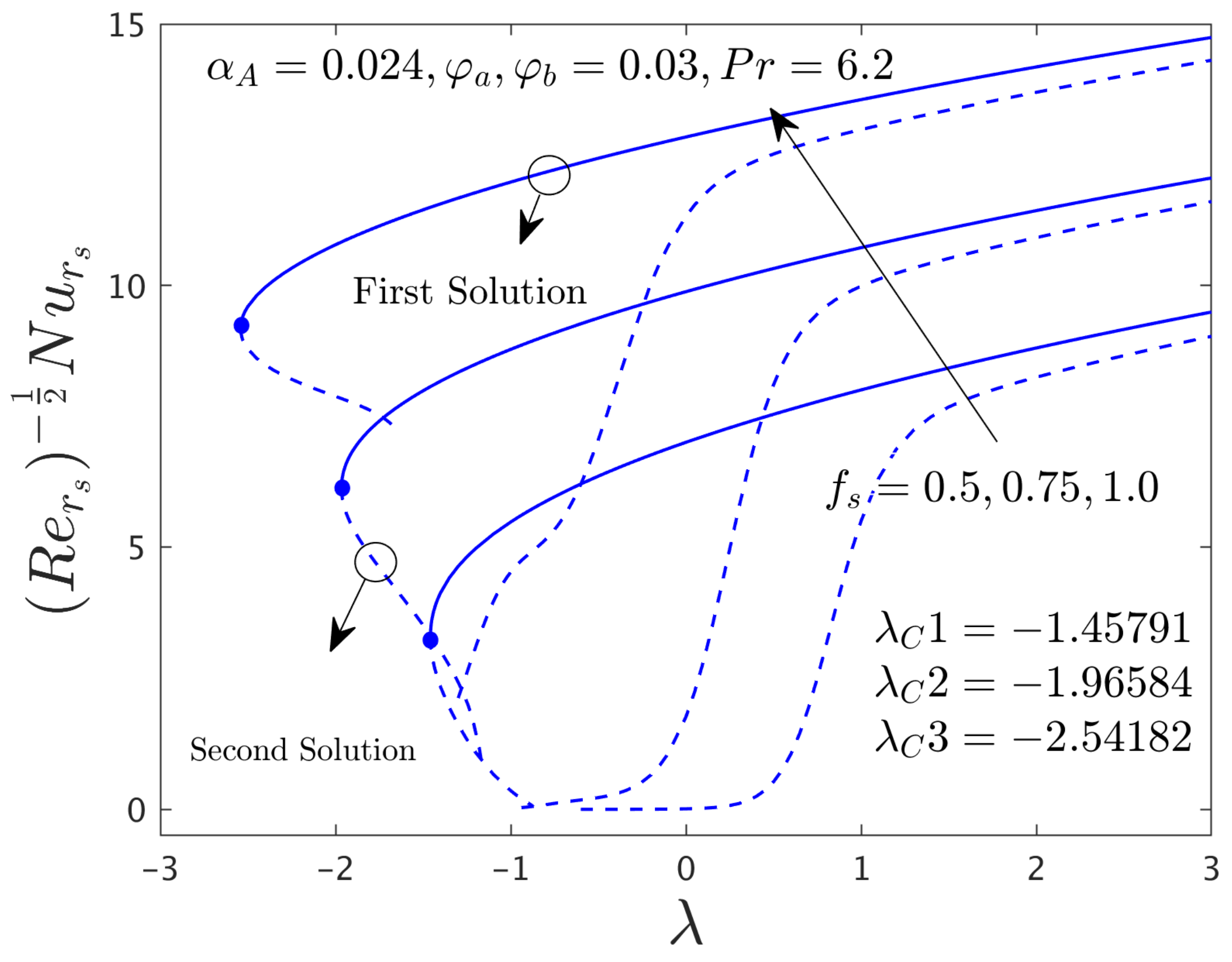
- The influence of hybrid nanoparticles on heat transfer rate suggests an improvement for FB outcome but decays for the SB outcome when αA = 0, Pr = 6.2 and fs = 0.5 while the SFC in the direction of radial enriches for two solution branches.
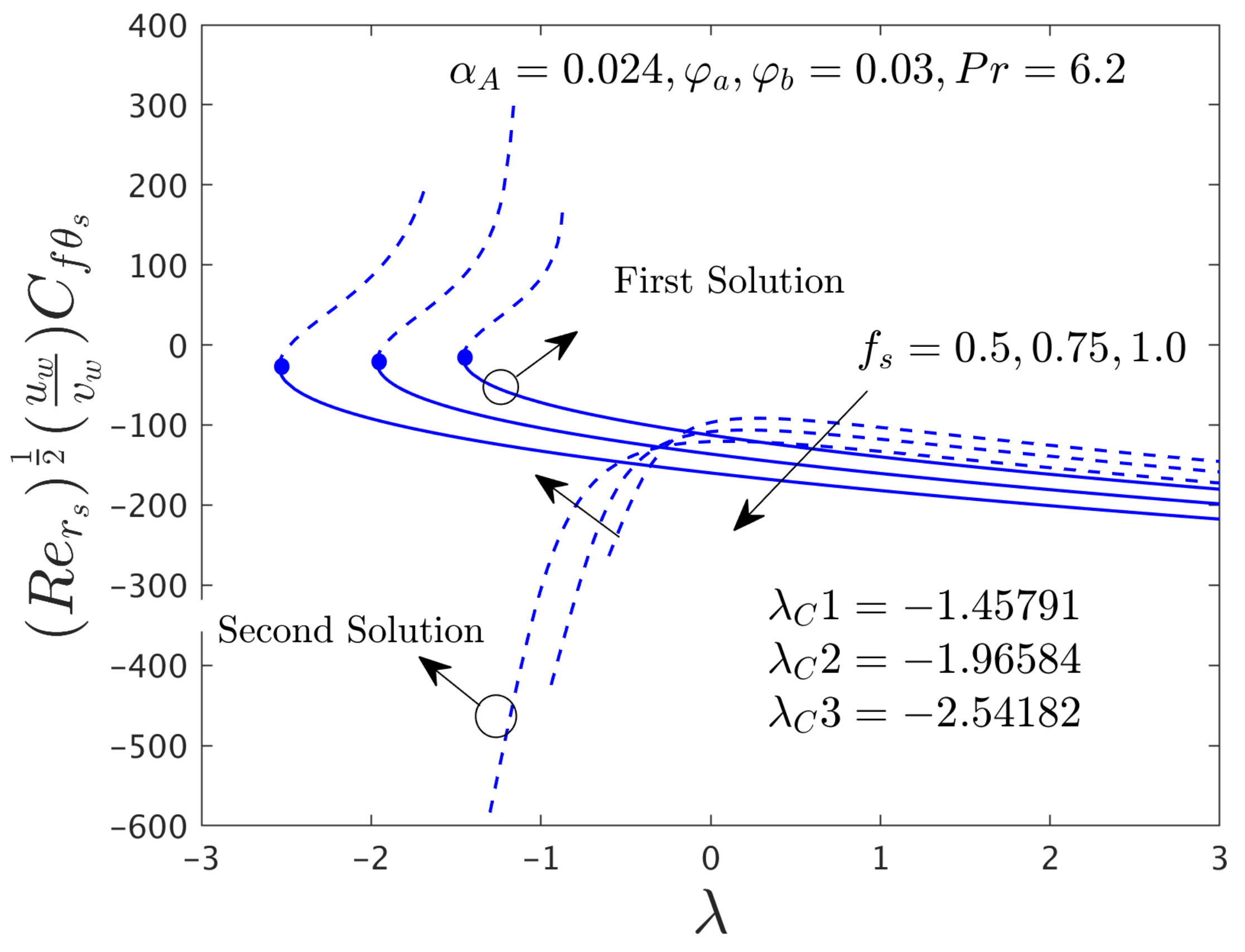
- The rate of heat transfer and the augments for the first solution and declines for the second solution with higher values of αA while the shear stress in the azimuthal direction improves for two dissimilar branch outcomes.
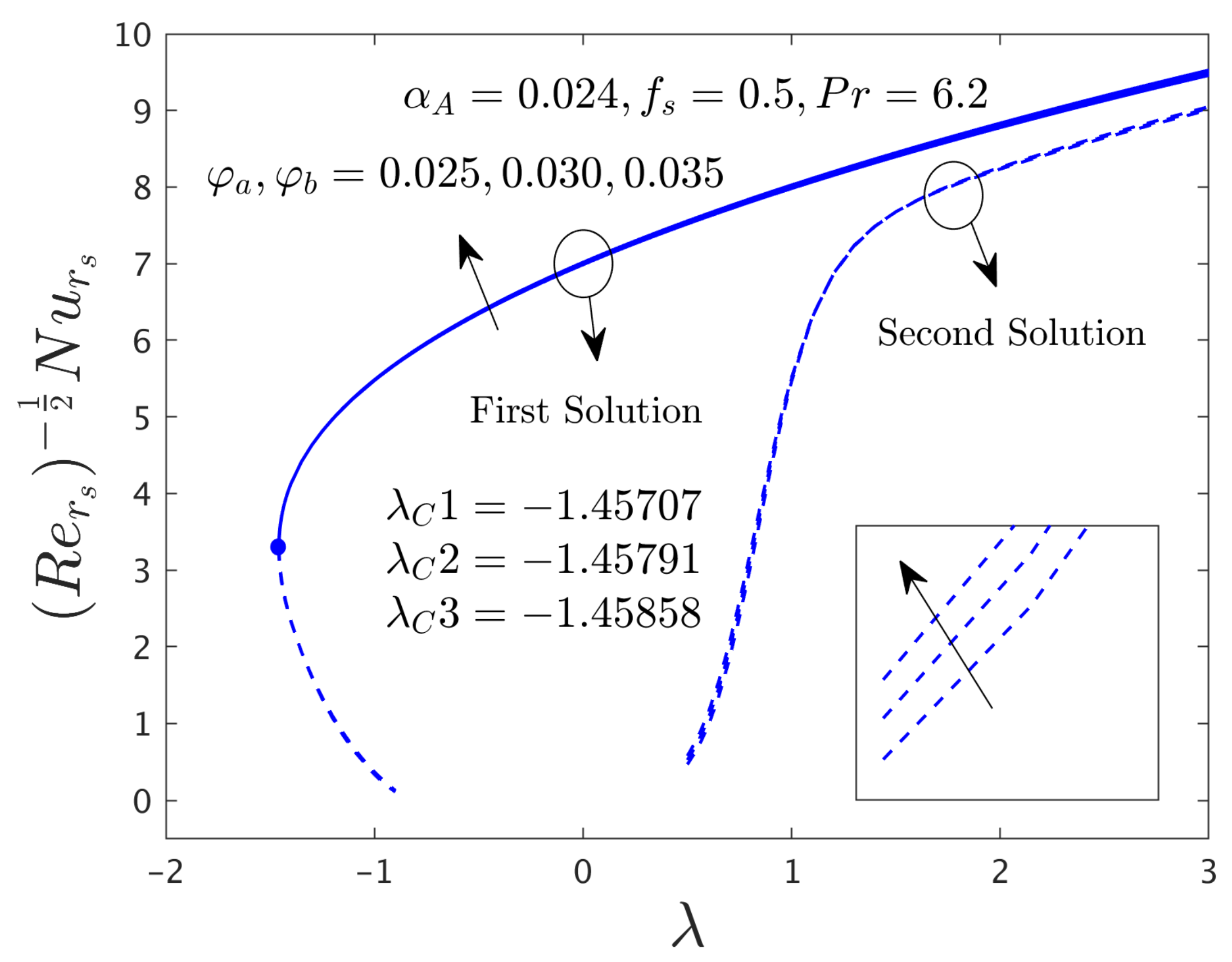
- The multiple branch outcomes exist for both cases of stretching (λ > 0) and shrinking (λ < 0), whereas, a solution is unique for (λ = λC) and no solution found for λ < λC. Also, the full line and broken line are generated for the SBS when αA = 0 and αA = 0.024, respectively, versus the stretching/shrinking parameter λ owing to the selected comprised dimensionless parameters.
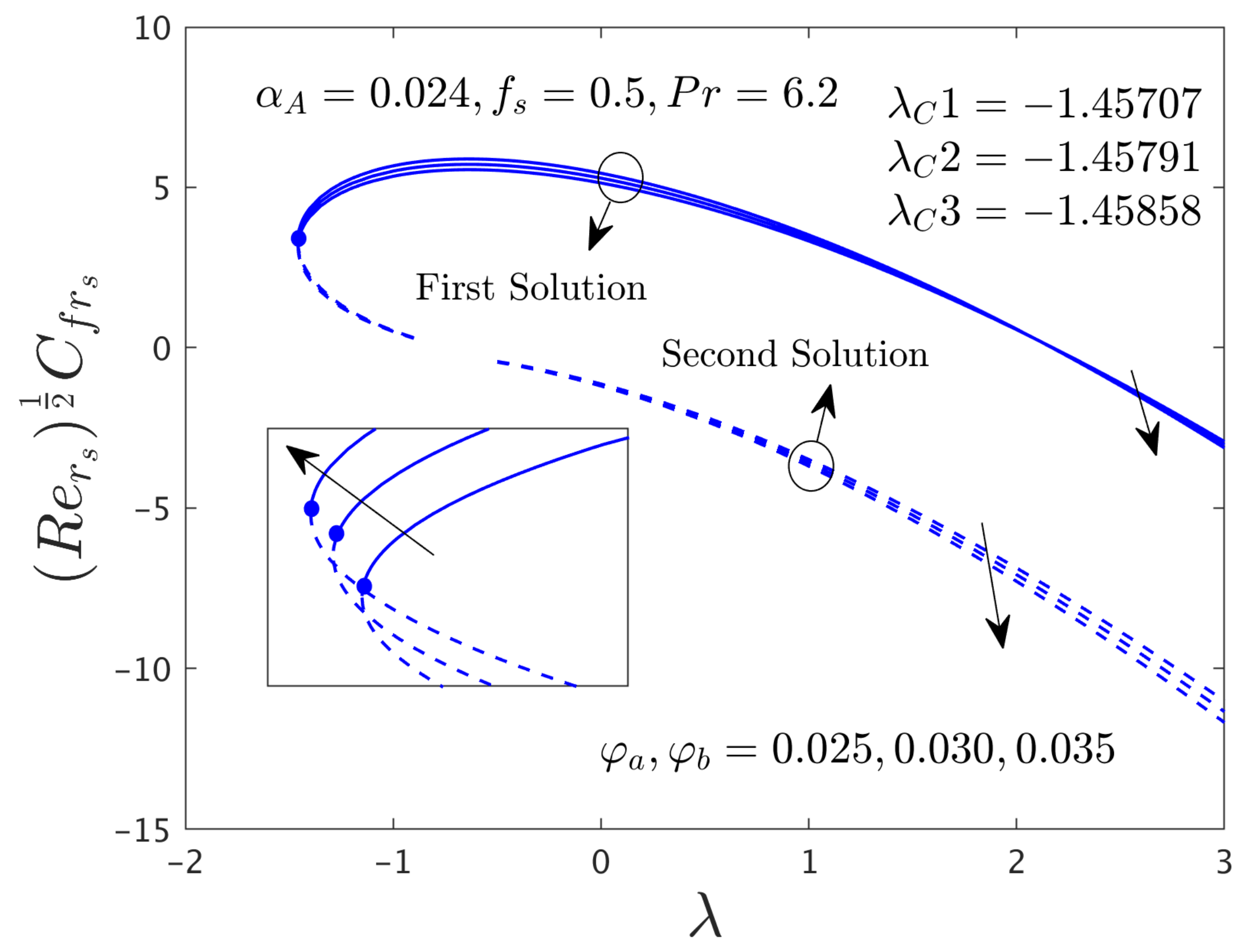
- For the variation of the selected influential parameters such as mass flux parameter S and hybrid nanoparticles ϕa and ϕb, the magnitude or absolute of the bifurcation values are sophisticated for the case of αA = 0.024 as compared to the case of αA = 0.0.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| F(ξ), G(ξ) | Dimensionless velocity stream function |
| cp | Specific heat at constant pressure (J/kg K) |
| Local Reynolds number | |
| Local Nusselt number | |
| Ps | Pressure (kg/m s2) |
| Skin friction coefficient along the azimuthal direction | |
| (us, vs, ws) | Velocity components (m/s) |
| (uE, vE, wE) | Free-stream velocities (m/s) |
| wa | Constant mass flux velocity (m/s) |
| Pr | Prandtl number |
| Ts | Temperature of the fluid (K) |
| fs | Mass suction parameter |
| uw | Surface velocity of the disk (m/s) |
| Skin friction coefficient along the radial direction | |
| Tw | Constant surface temperature (K) |
| (rs, θs, zs) | Cylindrical coordinate system (m) |
| a | Constant parameter having units (m s)−1 |
| T∞ | Constant ambient temperature (K) |
| vw | Rotating velocity of the disk (m/s) |
| k | Thermal conductivity (W/(m K)) |
| S(ξ) | Dimensionless tempetature |
| Greek symbols | |
| α | Thermal diffusivity (m2/s) |
| α | ARotating disk parameter |
| λ | Stretching/Shrinking parameter |
| μ | Absolute viscosity (N s/m2) |
| νf | Kinematic viscosity (m2/s) |
| ξ | Pseudo-similarity variable |
| ρ | Density (kg/m3) |
| ϕ | Solid volume fraction of nanoparticles |
| ψ | Stream function |
| ω | sConstant angular velocity (s−1) |
| Acronyms | |
| GO | Graphene oxide |
| PDEs | Partial differential equations |
| SFCs | Skin friction coefficients |
| FS | First solution |
| H2O | Water |
| bvp4cBoundary value problem of the fourth-order | |
| SS | Second solution |
| MoS2 | Molybdenum disulfide |
| FBS | First branch solution |
| BCs | Boundary conditions |
| SBS | Second branch solution |
| ICs | Initial conditions |
| Subscripts | |
| w | Wall boundary condition |
| hnf | Hybrid nanofluid |
| f | Working base fluid |
| a, b | Hybrid nanoparticles (GO and MoS2) |
| ∞ | Far-field condition |
| Superscript | |
| ′ | Differentiation with respect to ξ |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Bovand, M.; Rashidi, S.; Ahmadi, G.; Esfahani, J.A. Effects of trap and reflect particle boundary conditions on particle transport and convective heat transfer for duct flow—A two-way coupling of Eulerian-Lagrangian model. Appl. Therm. Eng. 2016, 108, 368–377. [Google Scholar] [CrossRef]
- Guthrie, D.G.; Torabi, M.; Karimi, N. Combined heat and mass transfer analyses in catalytic microreactors partially filled with porous material—The influences of nanofluid and different porous-fluid interface models. Int. J. Therm. Sci. 2019, 140, 96–113. [Google Scholar] [CrossRef] [Green Version]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Thaker, R.; Patel, J.R. A review on application of nanofluids in solar energy. Am. J. Nano Res. Appl. 2015, 2, 53–61. [Google Scholar]
- Bachok, N.; Ishak, A.; Nazar, R.; Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Phys. B Condens. Matter 2010, 405, 4914–4918. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non-newtonian nanofluids flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Three-dimensional flow of nanofluid over a non-linearly stretching sheet: An application to solar energy. Int. J. Heat Mass Transf. 2015, 86, 158–164. [Google Scholar] [CrossRef]
- Li, Y.-X.; Alqsair, U.F.; Ramesh, K.; Khan, S.U.; Khan, M.I. Nonlinear Heat Source/Sink and Activation Energy Assessment in Double Diffusion Flow of Micropolar (Non-Newtonian) Nanofluid with Convective Conditions. Arab. J. Sci. Eng. 2021, 47, 859–866. [Google Scholar] [CrossRef]
- Kotresh, M.J.; Ramesh, G.K.; Shashikala, V.K.R.; Prasannakumara, B.C. Assessment of Arrhenius activation energy in stretched flow of nanofluid over a rotating disc. Heat Transf. 2021, 50, 2807–2828. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.; Shahid, A.; Ellahi, R.; Bég, O.A.; Sait, S.M. Nonlinear nanofluid fluid flow under the consequences of Lorentz forces and Arrhenius kinetics through a permeable surface: A robust spectral approach. J. Taiwan Inst. Chem. Eng. 2021, 124, 98–105. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Abu Bakar, S.; Animasaun, I.; Yook, S.-J. Insights into the dynamics of blood conveying gold nanoparticles on a curved surface when suction, thermal radiation, and Lorentz force are significant: The case of Non-Newtonian Williamson fluid. Math. Comput. Simul. 2022, 193, 250–268. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Arain, M.B.; Zeeshan, A.; Ellahi, R.; Doranehgard, M.H. Swimming of Gyrotactic Microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage 2022, 45, 103511. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Jamil, M.M.; Japar, W.M.A.A.; Adamu, I.M. A review on preparation methods, stability and applications of hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 80, 1112–1122. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Yousefi, M.; Dinarvand, S.; Yazdi, M.E.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Kumar, K.A.; Sandeep, N.; Sugunamma, V.; Animasaun, I.L. Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid. J. Therm. Anal. Cal. 2020, 139, 2145–2153. [Google Scholar] [CrossRef]
- Khan, U.; Ishak, A.; Zaib, A. Hybrid nanofluid flow containing single-wall and multi-wall CNTs induced by a slender stretchable sheet. Chin. J. Phys. 2021, 74, 350–364. [Google Scholar] [CrossRef]
- Kolsi, L.; Abbasi, A.; Alqsair, U.F.; Farooq, W.; Omri, M.; Khan, S.U. Thermal enhancement of ethylene glycol base material with hybrid nanofluid for oblique stagnation point slip flow. Case Stud. Therm. Eng. 2021, 28, 101468. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.M.; Michaelides, E.E.; Marin, M.; Ellahi, R. Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 2021, 1–13. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Pop, I.; Abu Bakar, S.; Ishak, A. Stagnation point flow of a micropolar fluid filled with hybrid nanoparticles by considering various base fluids and nanoparticle shape factors. Int. J. Numer. Methods Heat Fluid Flow 2021. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformingen Flussigkeitsstrom eingetauchten graden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Homann, F. Der Einfluss grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel. J. Appl. Math. Mech. (ZAMP) 1936, 16, 153–164. [Google Scholar] [CrossRef]
- Hannah, D.M. Forced flow against a rotating disk. Rep. Mem. Aerosp. Res. Coun. Lond. 1947, 2772. Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/3325 (accessed on 31 January 2022).
- Agrawal, H.L. A new exact solution of the equations of viscous motion with axial symmetry. Q. J. Mech. Appl. Math. 1957, 10, 42–44. [Google Scholar] [CrossRef]
- Weidman, P. Axisymmetric rotational stagnation-point flow impinging on a rotating disk. Z. Angew. Math. Phys. 2015, 66, 3425–3431. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Three dimensional MHD stagnation flow due to a stretchable rotating disk. Int. J. Heat Mass Transf. 2012, 55, 6959–6965. [Google Scholar] [CrossRef]
- Weidman, P. Axisymmetric rotational stagnation point flow impinging on a flat liquid surface. Eur. J. Mech. B Fluids 2016, 56, 188–191. [Google Scholar] [CrossRef]
- Weidman, P. Axisymmetric rotational stagnation point flow impinging on a radially stretching sheet. Int. J. Non-Linear Mech. 2016, 82, 1–5. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Merkin, J.H.; Pop, I. Axisymmetric rotational stagnation-point flow impinging on a permeable stretching/shrinking rotating disk. Eur. J. Mech. B Fluids 2018, 72, 275–292. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E.; Akbar, T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 2017, 114, 1054–1066. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Radiative and magnetohydrodynamic micropolar hybrid nanofluid flow over a shrinking sheet with Joule heating and viscous dissipation effects. Neural Comput. Appl. 2021, 34, 3783–3794. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Khan, U.; Waini, I.; Ishak, A.; Pop, I. Unsteady hybrid nanofluid flow over a radially permeable shrinking/stretching surface. J. Mol. Liq. 2021, 331, 115752. [Google Scholar] [CrossRef]
- Ridha, A. Aiding flows non-unique similarity solutions of mixed-convection boundary-layer equations. Z. Angew. Math. Phys. 1996, 47, 341–352. [Google Scholar] [CrossRef]





| Properties | Pr | |||
|---|---|---|---|---|
| water | 997.1 | 4179 | 0.613 | 6.2 |
| GO | 1800 | 717 | 5000 | - |
| MoS2 | 5060 | 397.21 | 904.4 | - |
| αA | Present Results |
|---|---|
| 0 | 2.0000000 |
| 25 | 6.8191539 |
| 100 | 17.055614 |
| 225 | 30.488228 |
| 400 | 46.443400 |
| 625 | 64.560920 |
| 900 | 84.604186 |
| ϕa, ϕb | fs | αA | ||||
|---|---|---|---|---|---|---|
| First Solution | Second Solution | First Solution | Second Solution | |||
| 0.030 | 0.5 | 0.025 | 5.48360000 | −0.30821143 | −77.457484 | −321.05271 |
| 0.034 | - | - | 5.58925670 | −0.31700310 | −78.899781 | −327.49352 |
| 0.038 | - | - | 5.69667990 | −0.32631734 | −80.359778 | −334.07201 |
| 0.030 | 0.5 | - | 5.48360000 | −0.30821143 | −77.457484 | −321.05271 |
| - | 0.6 | - | 6.35703390 | −0.28259111 | −87.837482 | −313.34468 |
| - | 0.7 | - | 7.24986100 | −0.31207114 | −97.893453 | −289.31890 |
| 0.030 | 0.5 | 0.05 | 5.49047030 | −0.40387954 | −38.740770 | −122.06876 |
| - | - | 0.10 | 5.50419650 | −0.56038023 | −19.382388 | −47.018143 |
| - | - | 0.15 | 5.51790350 | −0.70282081 | −12.929571 | −27.155183 |
| ϕa, ϕb | fs | αA | ||
|---|---|---|---|---|
| First Solution | Second Solution | |||
| 0.030 | 0.5 | 0.025 | 5.81200290 | 0.00001712 |
| 0.034 | - | - | 5.81058090 | 0.00002175 |
| 0.038 | - | - | 5.80924700 | 0.00002739 |
| 0.030 | 0.5 | - | 5.81200290 | 0.00001712 |
| - | 0.6 | - | 7.02627280 | 0.00079153 |
| - | 0.7 | - | 8.23881650 | 0.01663883 |
| 0.030 | 0.5 | 0.05 | 5.81281430 | 0.00000319 |
| - | - | 0.10 | 5.81443370 | 0.00000021 |
| - | - | 0.15 | 5.81604840 | 0.00000002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, U.; Zaib, A.; Ishak, A.; Waini, I.; Abdel-Aty, A.-H.; Sheremet, M.A.; Yahia, I.S.; Zahran, H.Y.; Galal, A.M. Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk. Nanomaterials 2022, 12, 787. https://doi.org/10.3390/nano12050787
Khan U, Zaib A, Ishak A, Waini I, Abdel-Aty A-H, Sheremet MA, Yahia IS, Zahran HY, Galal AM. Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk. Nanomaterials. 2022; 12(5):787. https://doi.org/10.3390/nano12050787
Chicago/Turabian StyleKhan, Umair, Aurang Zaib, Anuar Ishak, Iskandar Waini, Abdel-Haleem Abdel-Aty, Mikhail A. Sheremet, Ibrahim S. Yahia, Heba Y. Zahran, and Ahmed M. Galal. 2022. "Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk" Nanomaterials 12, no. 5: 787. https://doi.org/10.3390/nano12050787
APA StyleKhan, U., Zaib, A., Ishak, A., Waini, I., Abdel-Aty, A.-H., Sheremet, M. A., Yahia, I. S., Zahran, H. Y., & Galal, A. M. (2022). Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk. Nanomaterials, 12(5), 787. https://doi.org/10.3390/nano12050787











