Understanding the Role of Soft X-ray in Charging Solid-Film and Cellular Electrets
Abstract
1. Introduction
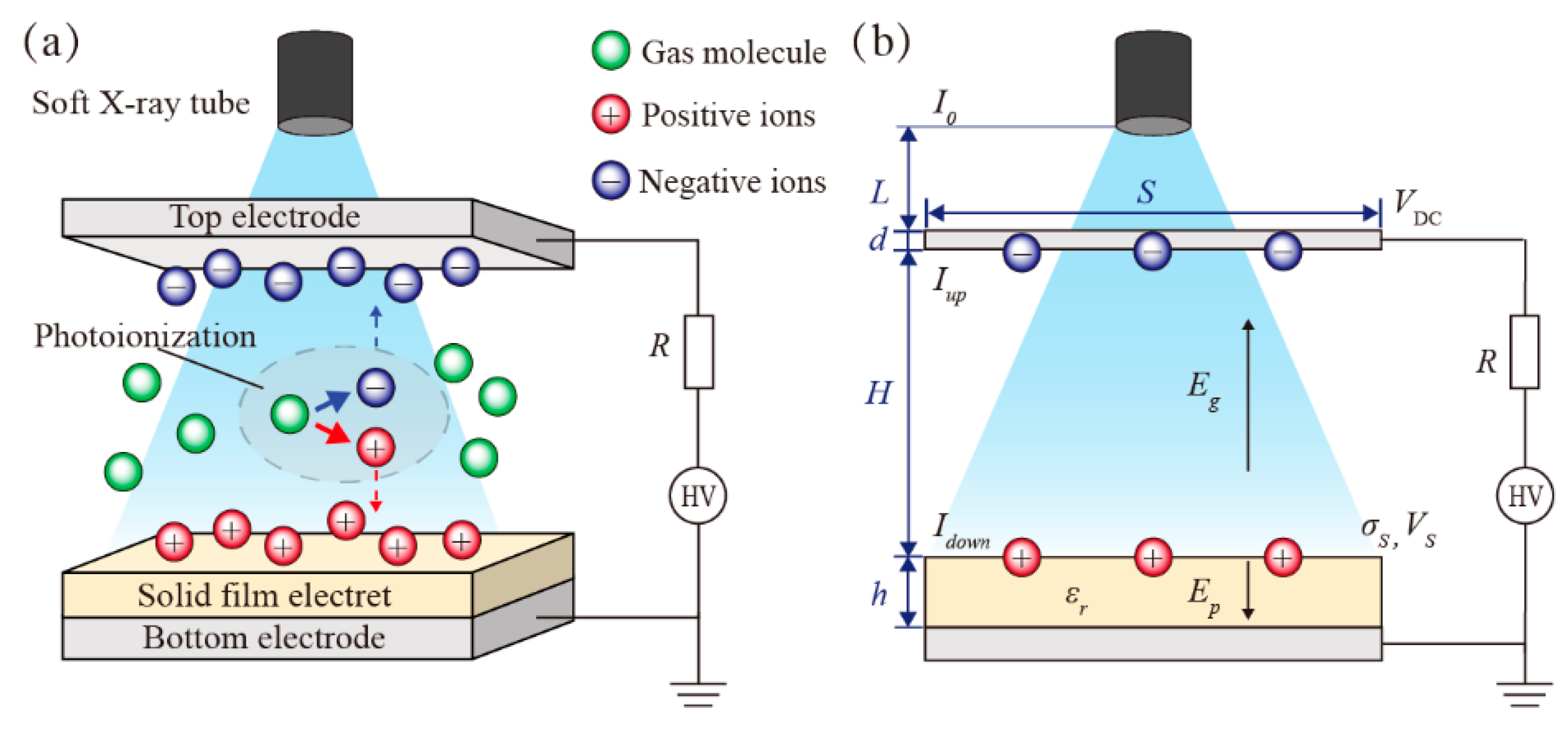
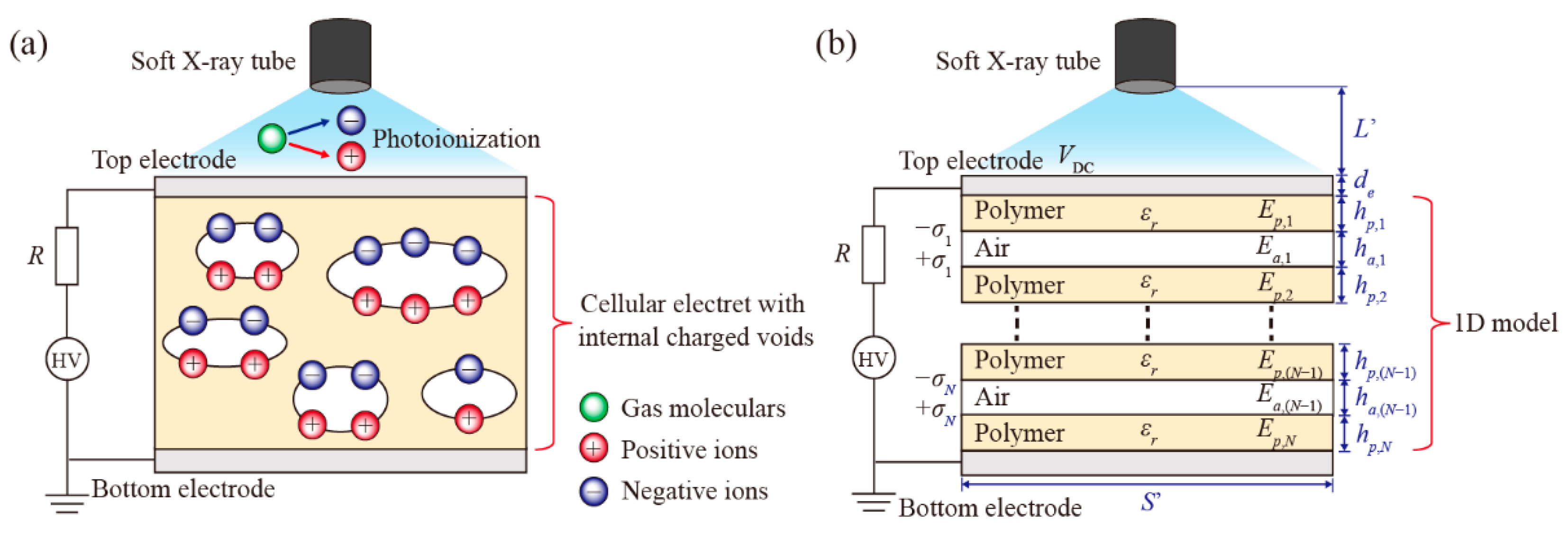
2. Theoretical Modeling of Soft X-ray Charging Method
2.1. Charging Solid-Film Electrets
2.2. Charging Cellular Electrets
3. Materials and Methods
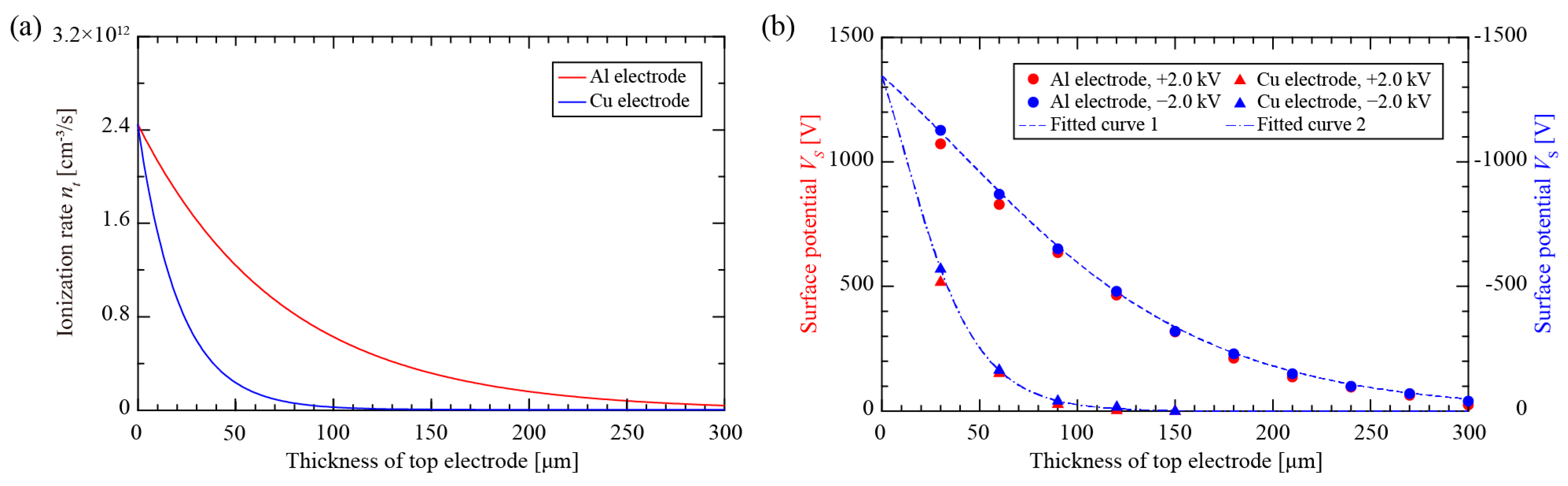
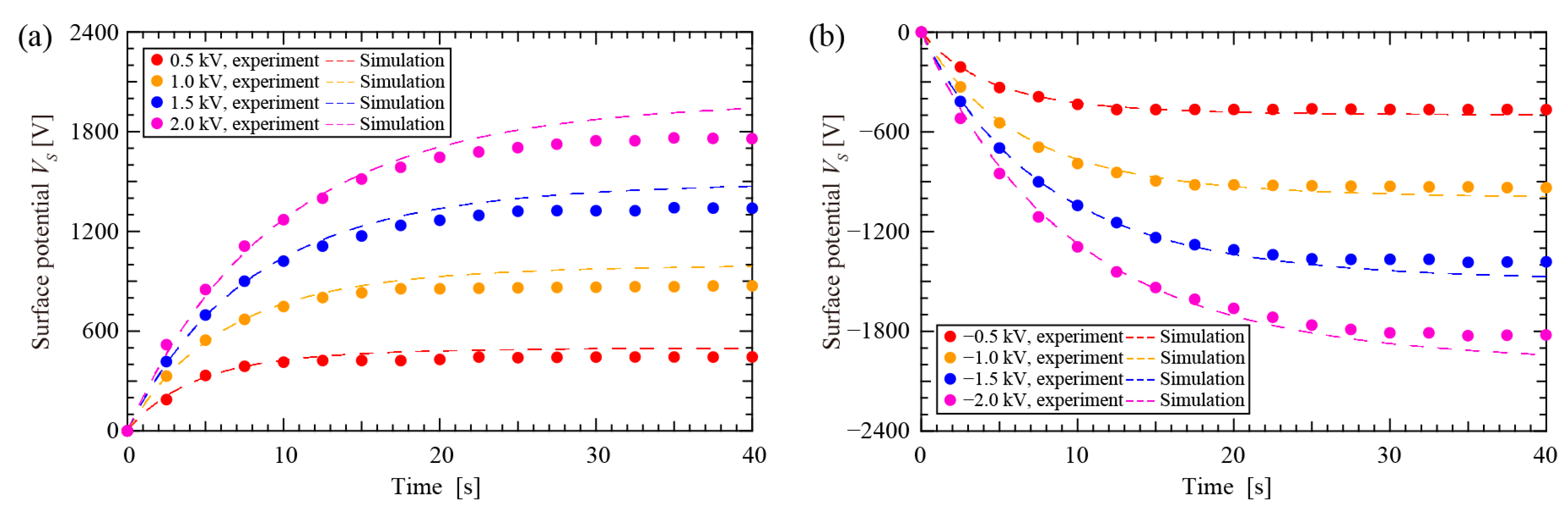
4. Results and Discussion
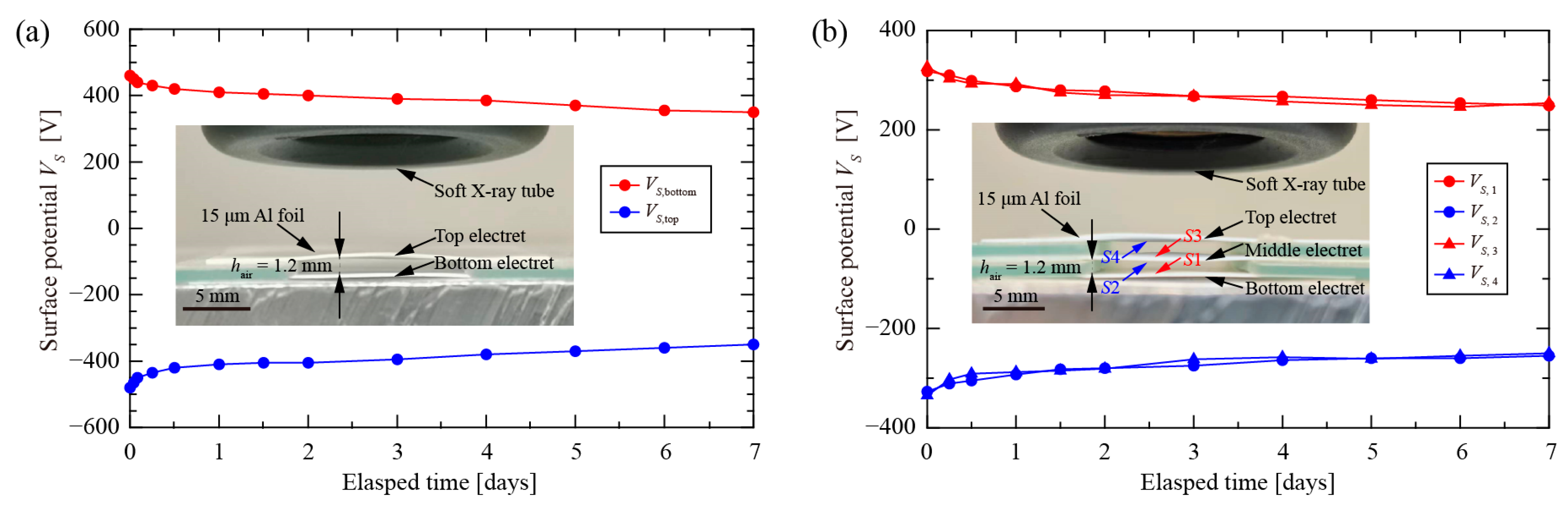
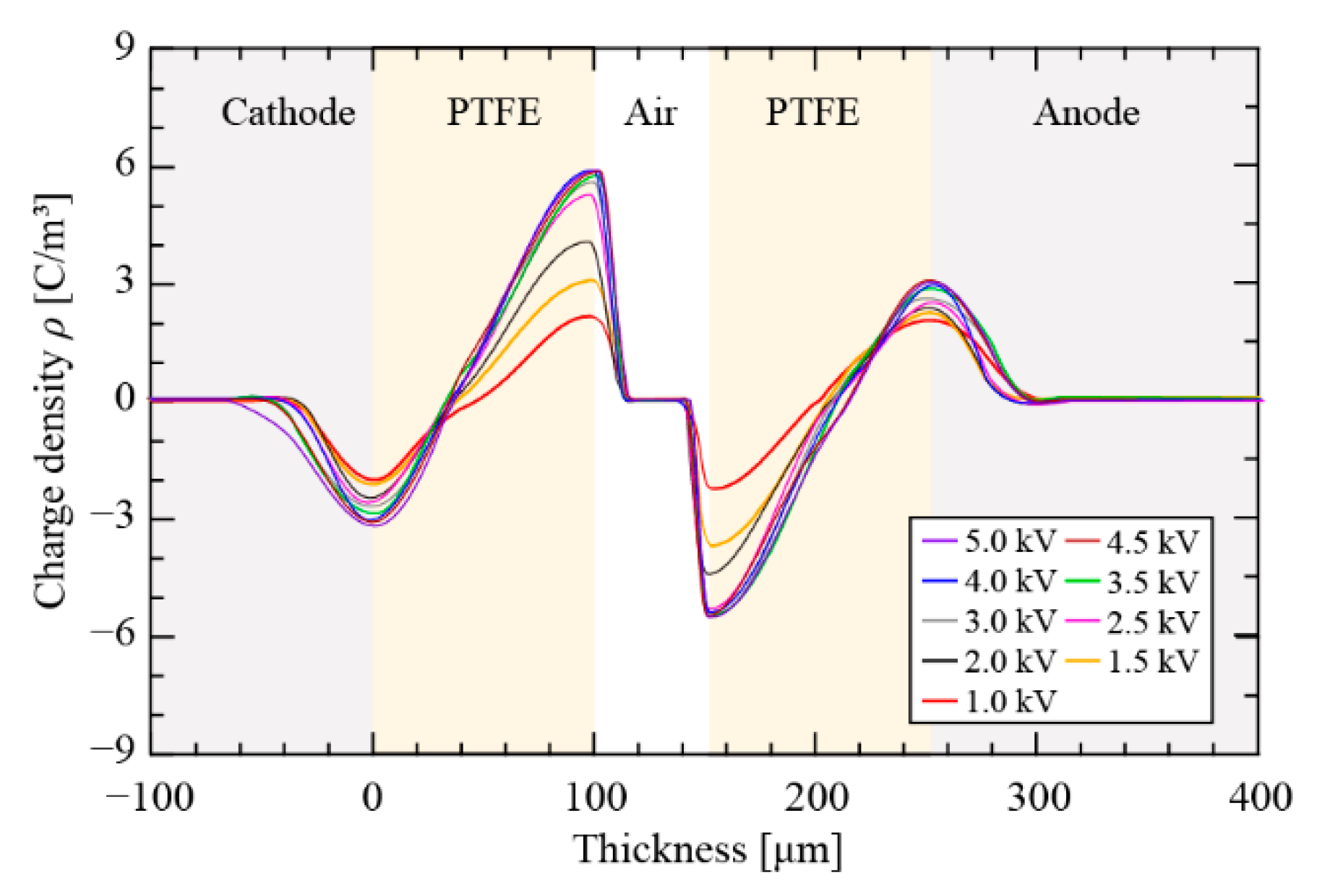
4.1. Solid-Film PTFE Electret
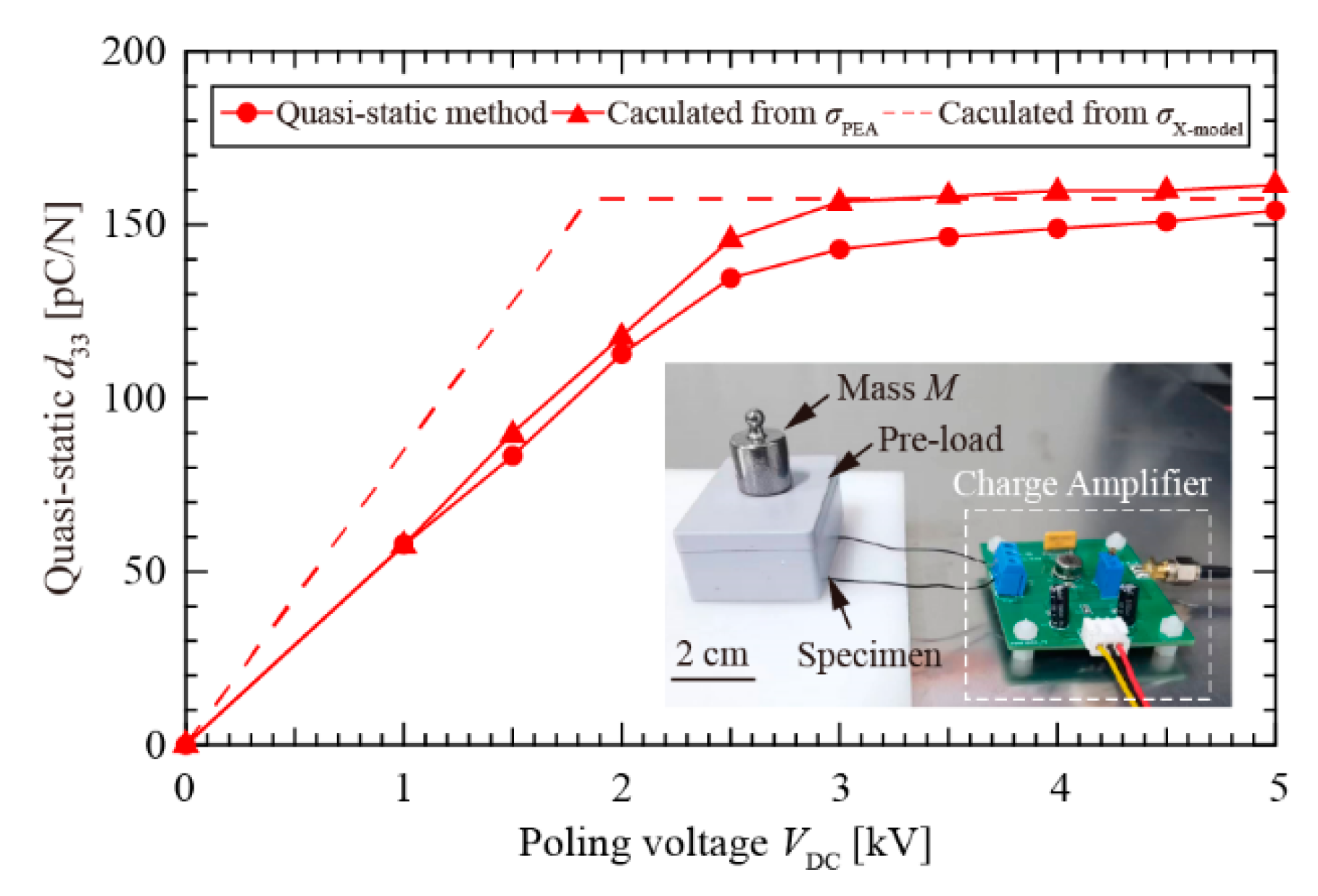
4.2. Cellular PTFE Electret
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Wang, Y.; Xu, M.; Shi, Y.; Wang, H.; Yang, X.; Ying, H.; Zhang, Q. Polymer electrets and their applications. J. Appl. Polym. Sci. 2021, 138, 50406. [Google Scholar] [CrossRef]
- Sessler, G.M. Electrets, 2nd ed.; Springer: Berlin, Germany, 1987. [Google Scholar]
- Hillenbrand, J.; Sessler, G.M. Piezoelectricity in cellular electret films. IEEE Trans. Dielect. Electr. Insul. 2000, 7, 537–542. [Google Scholar] [CrossRef]
- Qiu, X.; Bian, Y.; Liu, J.; Xiang, Y.; Ding, T.; Zhu, W.; Xuan, F.Z. Ferroelectrets: Recent developments. IET Nanodielectr. 2022, 1–12. [Google Scholar] [CrossRef]
- Tao, K.; Chen, Z.; Yi, H.; Zhang, R.; Shen, Q.; Wu, J.; Tang, L.; Fan, K.; Fu, Y.; Miao, J.; et al. Hierarchical honeycomb-structured electret/triboelectric nanogenerator for biomechanical and morphing wing energy harvesting. Nano-Micro Lett. 2021, 13, 123. [Google Scholar] [CrossRef] [PubMed]
- Hillenbrand, J.; Motz, T.; Sessler, G.M. High sensitivity electret accelerometer with integrated FET. IEEE Sens. J. 2014, 14, 1770–1777. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, Z.; Fu, D.; Ren, W. Velocity-amplified monostable dual-charged electret dome energy harvester using low-speed finger tapping. Appl. Phys. Lett. 2020, 116, 063905. [Google Scholar] [CrossRef]
- Ma, X.; Yang, X.; von Seggern, H.; Dai, Y.; He, P.; Sessler, G.M.; Zhang, X. Tuneable resonance frequency vibrational energy harvester with electret-embedded variable capacitor. IET Nanodielectr. 2021, 4, 53–62. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, Z.; Han, Y. High-performance gap-closing vibrational energy harvesting using electret-polarized dielectric oscillators. Appl. Phys. Lett. 2018, 112, 032901. [Google Scholar] [CrossRef]
- Sano, C.; Ataka, M.; Hashiguchi, G.; Toshiyoshi, H. An electret-augmented low-voltage MEMS electrostatic out-of-plane actuator for acoustic transducer applications. Micromachines 2020, 11, 267. [Google Scholar] [CrossRef]
- Kim, S.; Suzuki, K.; Sugie, A.; Yoshida, H.; Yoshida, M.; Suzuki, Y. Effect of end group of amorphous perfluoro-polymer electrets on electron trapping. Sci. Technol. Adv. Mater. 2018, 19, 486–494. [Google Scholar] [CrossRef] [PubMed]
- Zhukov, S.; Ma, X.; Seggern, H.V.; Sessler, G.M.; Dali, O.B.; Kupnik, M.; Zhang, X. Biodegradable cellular polylactic acid ferroelectrets with strong longitudinal and transverse piezoelectricity. Appl. Phys. Lett. 2020, 117, 112901. [Google Scholar] [CrossRef]
- Hagiwara, K.; Goto, M.; Iguchi, Y.; Tajima, T.; Yasuno, Y.; Kodama, H.; Kidokoro, K.; Suzuki, Y. Electret charging method based on soft X-ray photoionization for MEMS transducers. IEEE Trans. Dielect. Electr. Insul. 2012, 19, 1291–1298. [Google Scholar] [CrossRef]
- Feng, Y.; Hagiwara, K.; Iguchi, Y.; Suzuki, Y. Trench-filled cellular parylene electret for piezoelectric transducer. Appl. Phys. Lett. 2012, 100, 262901. [Google Scholar] [CrossRef]
- Kierzewski, I.; Bedair, S.S.; Hanrahan, B.; Tsang, H.; Hu, L.; Lazarus, N. Adding an electroactive response to 3D printed materials: Printing a piezoelectret. Addit. Manuf. 2020, 31, 100963. [Google Scholar] [CrossRef]
- Gulyakova, A.A.; Galikhanov, M.F.; Ma, X.; Zhang, X.; Fang, P. The Peculiarities of Electret Effect in Corona Electrets Based on Nonpolar and Polar Polymers with Dispersed Montmorillonite. IEEE Trans. Dielect. Electr. Insul. 2022, 29, 840–844. [Google Scholar] [CrossRef]
- Moreno, R.A.; Gross, B. Measurement of potential buildup and decay, surface charge density, and charging currents of corona-charged polymer foil electrets. J. Appl. Phys. 1976, 47, 3397–3402. [Google Scholar] [CrossRef]
- Hagiwara, K.; Goto, M.; Iguchi, Y.; Yasuno, Y.; Kodama, H.; Kidokoro, K.; Tajima, T. Soft X-ray charging method for a silicon electret condenser microphone. Appl. Phys. Express 2010, 3, 091502. [Google Scholar] [CrossRef]
- Lu, J.; Suzuki, Y. Push-button kinetic energy harvester with soft-x-ray-charged folded multilayer piezoelectret. J. Phys. Conf. Ser. 2019, 1407, 012021. [Google Scholar] [CrossRef]
- Wu, M.L.; Wang, D.; Wan, L.J. Directed block copolymer self-assembly implemented via surface-embedded electrets. Nat. Commun. 2016, 7, 10752. [Google Scholar] [CrossRef]
- Bonacci, F.; Di Michele, A.; Caponi, S.; Cottone, F.; Mattarelli, M. High charge density silica micro-electrets fabricated by electron beam. Smart Mater. Struct. 2018, 27, 075052. [Google Scholar] [CrossRef]
- Qiu, X.; Gerhard, R.; Mellinger, A. Turning polymer foams or polymer-film systems into ferroelectrets: Dielectric barrier discharges in voids. IEEE Trans. Dielect. Electr. Insul. 2011, 18, 34–42. [Google Scholar] [CrossRef]
- Zhukov, S.; Eder-Goy, D.; Biethan, C.; Fedosov, S.; Xu, B.X.; von Seggern, H. Tubular fluoropolymer arrays with high piezoelectric response. Smart Mater. Struct. 2017, 27, 015010. [Google Scholar] [CrossRef]
- Attwood, D. Soft X-rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ooka, M.; Sasaoka, H.; Nishimura, K. An X-ray generator using nano-diamond field emission devices. J. Jpn. Soc. Abras. Technol. 2007, 51, 725–728. [Google Scholar] [CrossRef]
- Jackson, D.F.; Hawkes, D.J. X-ray attenuation coefficients of elements and mixtures. Phys. Rep. 1981, 70, 169–233. [Google Scholar] [CrossRef]
- Kang, W.S.; Park, J.M.; Kim, Y.; Hong, S.H. Numerical study on influences of barrier arrangements on dielectric barrier discharge characteristics. IEEE Trans. Plasma Sci. 2003, 31, 504–510. [Google Scholar] [CrossRef]
- Wintle, H.J. Surface-charge decay in insulators with nonconstant mobility and with deep trapping. J. Appl. Phys. 1972, 43, 2927–2930. [Google Scholar] [CrossRef]
- Imburgia, A.; Miceli, R.; Sanseverino, E.R.; Romano, P.; Viola, F. Review of space charge measurement systems: Acoustic, thermal and optical methods. IEEE Trans. Dielect. Electr. Insul. 2016, 23, 3126–3142. [Google Scholar] [CrossRef]
- Umran, H.M.; Wang, F.; He, Y. Ageing: Causes and effects on the reliability of polypropylene film used for HVDC capacitor. IEEE Access 2020, 8, 40413–40430. [Google Scholar] [CrossRef]
- Zhai, J.; Li, W.; Zha, J.; Cheng, Q.; Bian, X.; Dang, Z. Space charge suppression of polyethylene induced by blending with ethylene-butyl acrylate copolymer. CSEE J. Power Energy Syst. 2019, 6, 152–159. [Google Scholar] [CrossRef]
- Li, Z.; Su, J.; Du, B.; Hou, Z.; Han, C. Inhibition Effect of Graphene on Space Charge Injection and Accumulation in Low-Density Polyethylene. Nanomaterials 2018, 8, 956. [Google Scholar] [CrossRef]
- Imburgia, A.; Romano, P.; Rizzo, G.; Viola, F.; Ala, G.; Chen, G. Reliability of PEA Measurement in Presence of an Air Void Defect. Energies 2020, 13, 5652. [Google Scholar] [CrossRef]
- Komeijani, A.; Bagheri, H.; Shekarchi, B. Surface potential uniformity and sensitivity of large-area PTFE electret discs of different thicknesses produced by a modified corona poling rotating system for dosimetry applications. J. Adv. Dielectr. 2019, 9, 1950050. [Google Scholar] [CrossRef]
- Jiang, P.; Zhao, X.; Li, Y.; Liao, Y.; Hua, T.; Yin, X.; Yu, J.; Ding, B. Moisture and oily molecules stable nanofibrous electret membranes for effectively capturing PM2. 5. Compos. Commun. 2017, 6, 34–40. [Google Scholar] [CrossRef]
- Vu-Cong, T.; Jean-Mistral, C.; Sylvestre, A. Electrets substituting external bias voltage in dielectric elastomer generators: Application to human motion. Smart Mater. Struct. 2013, 22, 025012. [Google Scholar] [CrossRef]
- Diniş, C.M.; Popa, G.N. Experimental analysis of direct current corona discharge. IOP Conf. Ser. Mater. Sci. Eng. 2017, 163, 012035. [Google Scholar] [CrossRef]
- Vu, T.T.N.; Teyssedre, G.; Le Roy, S.; Laurent, C. Maxwell–Wagner effect in multi-layered dielectrics: Interfacial charge measurement and modelling. Technologies 2017, 5, 27. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Rao, Z.; Song, K.-Y.; Tang, X.; Zhou, Z.; Xiong, Y. Understanding the Role of Soft X-ray in Charging Solid-Film and Cellular Electrets. Nanomaterials 2022, 12, 4143. https://doi.org/10.3390/nano12234143
Feng Y, Rao Z, Song K-Y, Tang X, Zhou Z, Xiong Y. Understanding the Role of Soft X-ray in Charging Solid-Film and Cellular Electrets. Nanomaterials. 2022; 12(23):4143. https://doi.org/10.3390/nano12234143
Chicago/Turabian StyleFeng, Yue, Zehong Rao, Ki-Young Song, Xusong Tang, Zilong Zhou, and Ying Xiong. 2022. "Understanding the Role of Soft X-ray in Charging Solid-Film and Cellular Electrets" Nanomaterials 12, no. 23: 4143. https://doi.org/10.3390/nano12234143
APA StyleFeng, Y., Rao, Z., Song, K.-Y., Tang, X., Zhou, Z., & Xiong, Y. (2022). Understanding the Role of Soft X-ray in Charging Solid-Film and Cellular Electrets. Nanomaterials, 12(23), 4143. https://doi.org/10.3390/nano12234143





