Study on Tensile Properties of Fly Ash, Sugarcane Fiber and Carbon Nanotube-Reinforced Polymer Matrix Composite Using Objective Evolutionary Algorithm
Abstract
1. Introduction
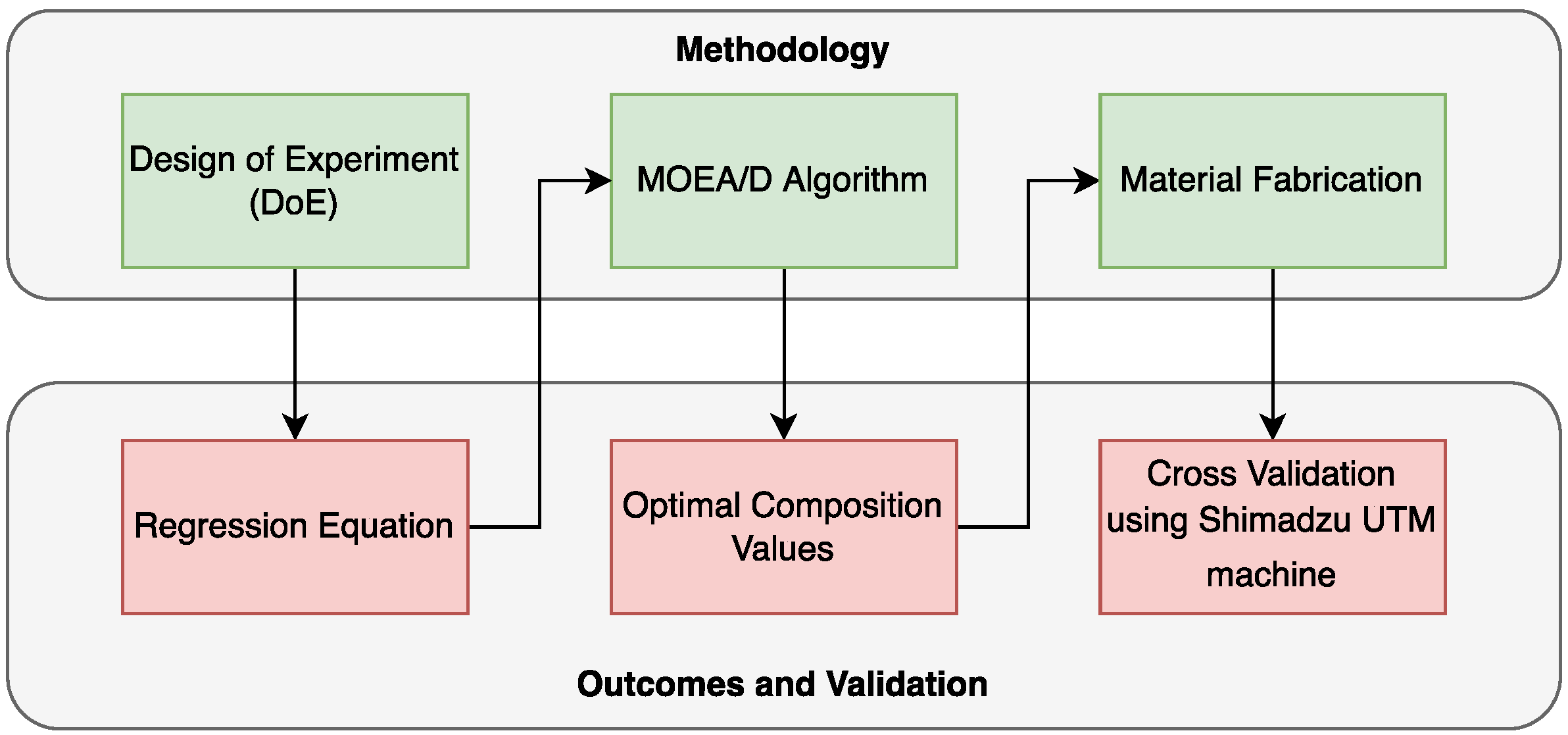
2. Methodology
2.1. Materials and Methods
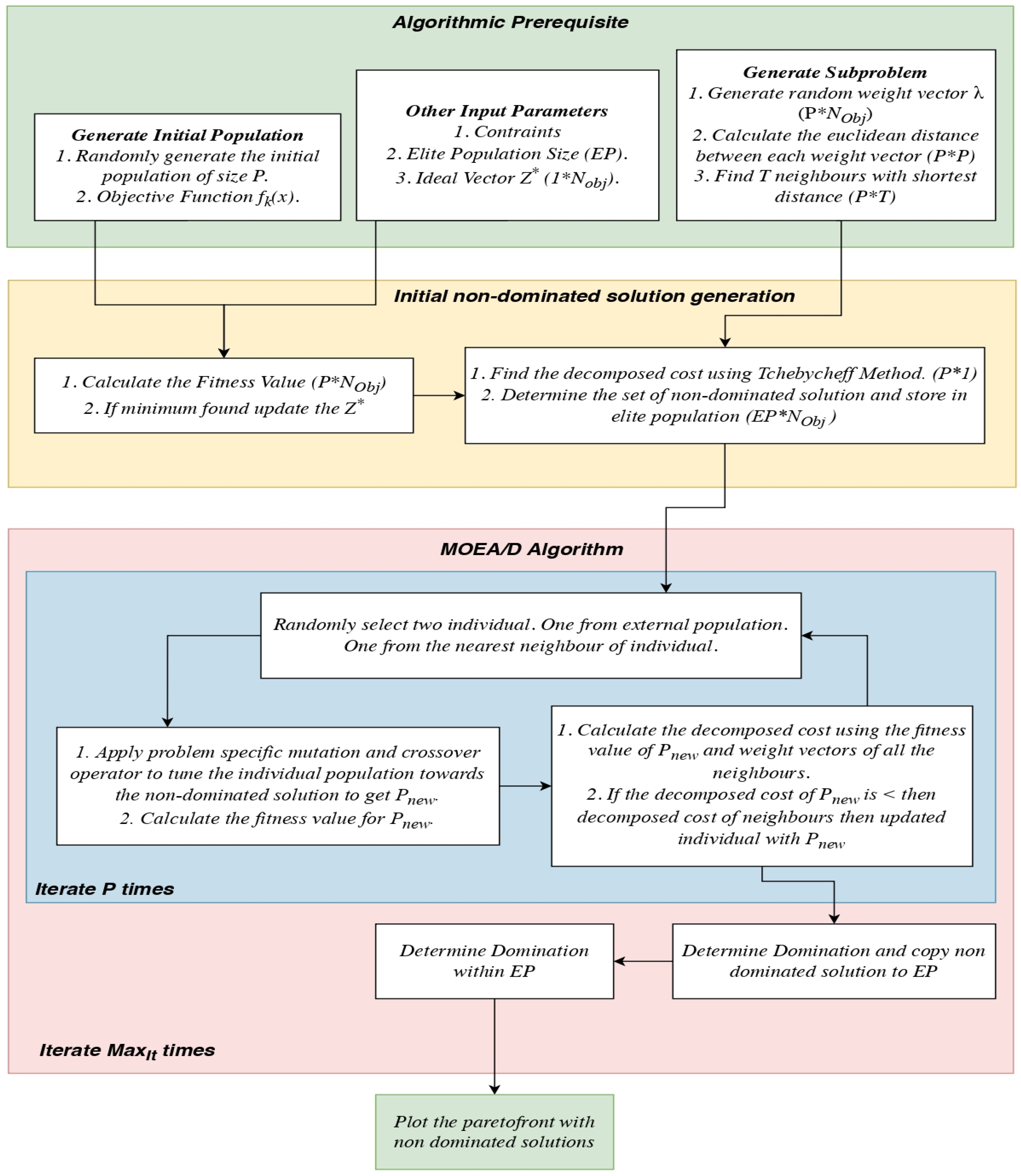
2.2. Development of MOEA/D
3. Results and Discussions
3.1. Tensile Test
3.2. Results of Modelling
3.3. Confirmatory Test
4. Conclusions
- It is evident that fly ash has many environmental disposal issues. Additionally, biodegradable composites can be constructed with the use of SCF and recyclable material such as CNTs.
- A mixture of 0.5 wt.% of fly ash, 2 wt.% of SCF, and 0.5 wt.% of CNTs exhibited better maximum yield strength, Young’s modulus, and UTS values compared with the optimized values obtained via the RSM.
- Increasing the wt.% of CNTs improved the ultimate tensile strength, but it did not influence the composite material’s yield strength and Young’s modulus.
- As the content of fly ash reduced, the YS and YM were increased and the UTS was somewhat degraded; however, making reusable, biodegradable, and recyclable composites necessitates using waste fly ash.
- The MOEA/D is an efficient and effective algorithm that can be used to solve multi-response optimization problems including the one considered in the present study, as it suggests a set of alternate optimal solutions in a short period.
- In this way, the described design parameter combinations are expected to not only ensure the meeting of product quality specifications but also to enhance stability outcomes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| UTS | Ultimate Tensile Strength |
| CNT | Carbon Nanotube |
| YS | Yield Strength |
| YM | Young’s Modulus |
| MOEA/D | Multi-Objective Evolutionary Algorithm with Decomposition |
| DOE | Design of Experiment |
| ANOVA | Analysis Of Variance |
| RSM | Response Surface Methodology |
| SCF | Sugarcane Fiber |
| EP | External Population |
| CCD | Central Composite Design |
| MWCNT | Multi-Wall Carbon Nanotube |
| PF | Pareto Front |
| UTM | Universal Tensile Machine |
References
- Hale, D.K. The physical properties of composite materials. J. Mater. Sci. 1976, 11, 2105–2141. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor and Francis: Abingdon, UK, 2015; pp. 1–538. [Google Scholar]
- Naslain, R.R.; Pomeroy, M.R. Ceramic Matrix Composites: Matrices and Processing. Ref. Modul. Mater. Sci. Mater. Eng. 2016, 1–7. [Google Scholar] [CrossRef]
- Taylor, D. On the application of the Theory of Critical Distances for prediction of fracture in fibre composites. Frat. Ed Integrità Strutt. 2009, 11, 3–9. [Google Scholar] [CrossRef]
- Soepangkat, B.O.P.; Norcahyo, R.; Khoirul Effendi, M.; Pramujati, B. Multi-response optimization of carbon fiber reinforced polymer (CFRP) drilling using back propagation neural network-particle swarm optimization (BPNN-PSO). Eng. Sci. Technol. Int. J. 2020, 23, 700–713. [Google Scholar] [CrossRef]
- Javier, S.C. A procedure to design optimum composite plates using implicit decision trees. Struct. Multidiscip. Optim. 2017, 56, 1169–1183. [Google Scholar] [CrossRef]
- Mahrach, M.; Miranda, G.; Coromoto, L.; Segredo, E. Comparison between Single and Multi-Objective Evolutionary Algorithms to Solve the Knapsack Problem and the Travelling Salesman Problem. Mathematics 2020, 8, 2018. [Google Scholar] [CrossRef]
- Coello, C.A.C. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Genetic Algorithms and Evolutionary Computation; Springer: New York, NY, USA, 2007. [Google Scholar]
- Darwish, A. Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications. Future Comput. Inform. J. 2018, 3, 231–246. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, C.; Wan, B.; Song, W.W. A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization. Entropy 2021, 23, 874. [Google Scholar] [CrossRef]
- Segura, C.; Coello, C.A.C.; Miranda, G.; León, C. Using Multi-objective evolutionary algorithms for single-objective constrained and unconstrained optimization. Ann. Oper. Res. 2016, 240, 217–250. [Google Scholar] [CrossRef]
- Naik, G.N.; Gopalakrishnan, S.; Ganguli, R. Design optimization of composites using genetic algorithms and failure mechanism-based failure criterion. Compos. Struct. 2008, 83, 354–367. [Google Scholar] [CrossRef]
- Gillet, A.; Francescato, P.; Saffre, P. Single-and multiobjective optimization of composite structures: The influence of design variables. J. Compos. Mater. 2010, 44, 457–480. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. An evolutionary algorithm for multiobjective optimization: The strength pareto approach. TIK-Rep. 1998, 1-43, 1–43. [Google Scholar]
- Almeida, F.S.; Awruch, A.M. Design optimization of composite laminated structures using genetic algorithms and finite element analysis. Compos. Struct. 2009, 88, 443–454. [Google Scholar] [CrossRef]
- Irisarri, F.X.; Laurin, F.; Leroy, F.H.; Maire, J.F. Computational strategy for multiobjective optimization of composite stiffened panels. Compos. Struct. 2011, 93, 1158–1167. [Google Scholar] [CrossRef]
- Spears, W.M.; Anand, V. A study of crossover operators in genetic programming. In International Symposium on Methodologies for Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 1991; pp. 409–418. [Google Scholar]
- Sheyka, M.P.; Altunc, A.B.; Taha, M.R. Multiobjective genetic topological optimization for design of blast resistant composites. Appl. Compos. Mater. 2012, 19, 785–798. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H. MOGA: Multiobjective genetic algorithms. IEEE Int. Conf. Evol. Comput. 1995, 1, 289–294. [Google Scholar]
- Murata, T.; Takada, K. Performance Evaluation of a Distributed Genetic Algorithm with Cellular Structures on Function Optimization Problems. Int. J. Knowl.-Based Intell. Eng. Syst. 2004, 3213, 1128–1135. [Google Scholar]
- Alvarez-Benitez, J.E.; Everson, R.M.; Fieldsend, J.E. A MOPSO algorithm based exclusively on Pareto dominance concepts. In International Conference on Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 459–473. [Google Scholar]
- Lee, D.S.; Morillo, C.; Bugeda, G.; Oller, S.; Onate, E. Multilayered composite structure design optimisation using distributed/parallel multi-objective evolutionary algorithms. Compos. Struct. 2012, 94, 1087–1096. [Google Scholar] [CrossRef]
- Duy, K.; Tam, T.T.; Thoi, N.T. Multi-Objective Optimization of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Plates Using Deep Feedforward Neural Networks-NSGAII Algorithm. Int. J. Comput. Methods 2022, 19, 2150065. [Google Scholar]
- Toupe, J.L.; Chimeni, D.Y.; Trokourey, A.; Rodrigue, D. Optimizing the Performance of Natural Fiber Reinforced Plastics Composites: Influence of Combined Optimization Paths on Microstructure and Mechanical Properties. Polym. Polym. Compos. 2015, 23, 535–544. [Google Scholar] [CrossRef]
- Badallo, P.; Trias, D.; Marin, L.; Mayugo, J.A. A comparative study of genetic algorithms for the multiobjective optimization of composite stringers under compression loads. Compos. Part B Eng. 2013, 47, 130–136. [Google Scholar] [CrossRef]
- Deb, K. An Efficient Constraint Handling Method for Genetic Algorithm. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Munck, M.D.; De Sutter, S.; Verbruggen, S.; Tysmans, T.; Coelho, R.F. Multi objective weight and cost optimization of hybrid composite-concrete beams. Compos. Struct. 2015, 134, 369–377. [Google Scholar] [CrossRef]
- Hwang, S.F.; Hsu, Y.C.; Chen, Y. A genetic algorithm for the optimization of fiber angles in composite laminates. J. Mech. Sci. Technol. 2014, 28, 3163–3169. [Google Scholar] [CrossRef]
- Gopalan, V.; Kumar Sharma, S.; Jangid, A.K.; Vignesh, P.; Nilesh, S.N.N.; Pandivelan, C. Investigations on Tensile and Flexural Characteristics of Flyash and Banana Fiber-Reinforced Epoxy Matrix Composites. Eng. Trans. 2020, 68, 89–101. [Google Scholar]
- Gopalan, V.; Vyas, R.; Goswami, I.; Shah, A.; Pragasam, V. Tensile Behaviour of Sugarcane Fibre/Fly Ash/Carbon Nano Tubes Reinforced Epoxy Composites. U.P.B. Sci. Bull. Ser. 2021, 83, 181–192. [Google Scholar]
- Sim, J.; Kang, Y.; Kim, B.J.; Park, Y.H.; Lee, Y.C. Preparation of Fly Ash/Epoxy composites and its effects on mechanical properties. Polymers 2020, 12, 79. [Google Scholar] [CrossRef]
- Khonder, O.A.; Ishaiku, U.S.; Nakai, A.; Hamada, H. Fabrication Mechanical Properties of Unidirectional Jute/PP Composites Using Jute Yarns by Film Stacking Method. J. Environ. Polym. Degrad. 2005, 13, 115–126. [Google Scholar] [CrossRef]
- Takemura, K.; Minekage, Y. Effect of molding condition on tensile properties of hemp fiber reinforced composite. Adv. Compos. Mater. 2007, 16, 385–394. [Google Scholar] [CrossRef]
- Golewski, G.L.; Szostak, B. Application of the C-S-H Phase Nucleating Agents to Improve the Performance of Sustainable Concrete Composites Containing Fly Ash for Use in the Precast Concrete Industry. Materials 2021, 14, 6514. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Ahmad, W.; Amin, M.N.; Nazar, S. Nano-Silica-Modified Concrete: A Bibliographic Analysis and Comprehensive Review of Material Properties. Nanomaterials 2022, 12, 1989. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Wei, S.; Zheng, Y.; Wang, F.; Hu, S. Effect of Single and Synergistic Reinforcement of PVA Fiber and Nano-SiO2 on Workability and Compressive Strength of Geopolymer Composites. Polymers 2022, 14, 3765. [Google Scholar] [CrossRef] [PubMed]
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber–reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019, 105, 2289–2308. [Google Scholar] [CrossRef]
- Wicks, S.S.; de Villoria, R.G.; Wardle, B.L. Interlaminar and intralaminar reinforcement of composite laminates with aligned carbon nanotubes. Compos. Sci. Technol. 2010, 70, 20–28. [Google Scholar] [CrossRef]

| Parameters | Levels | ||||
|---|---|---|---|---|---|
| −2 | −1 | 0 | 1 | 2 | |
| Wt.% of fly ash | 0 | 0.5 | 1 | 1.5 | 2 |
| Wt.% of sugarcane | 0 | 0.5 | 1 | 1.5 | 2 |
| Wt.% of CNTs | 0 | 0.25 | 0.5 | 0.75 | 1 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | UTS | Young’s Modulus |
|---|---|---|---|---|---|
| 0.0000 | 2.0000 | 0.3854 | 8.5817 | 11.1184 | 1457.8263 |
| 0.0000 | 2.0000 | 0.4394 | 8.5145 | 12.4660 | 1444.6030 |
| 0.0000 | 2.0000 | 0.4586 | 8.4877 | 12.9753 | 1439.2135 |
| 0.0000 | 2.0000 | 0.4586 | 8.4877 | 12.9753 | 1439.2135 |
| 0.0000 | 2.0000 | 0.4626 | 8.4820 | 13.0832 | 1438.0467 |
| 0.0000 | 2.0000 | 0.4647 | 8.4789 | 13.1393 | 1437.4367 |
| 0.0000 | 2.0000 | 0.4768 | 8.4611 | 13.4691 | 1433.8081 |
| 0.0002 | 2.0000 | 0.4889 | 8.4417 | 13.8056 | 1429.8687 |
| 0.0000 | 2.0000 | 0.5164 | 8.3986 | 14.5919 | 1420.9335 |
| 0.0000 | 2.0000 | 0.5672 | 8.3095 | 16.1206 | 1402.2802 |
| 0.0001 | 2.0000 | 0.5728 | 8.2983 | 16.2963 | 1399.9466 |
| 0.0002 | 2.0000 | 0.5738 | 8.2959 | 16.3245 | 1399.4750 |
| 0.0000 | 2.0000 | 0.6491 | 8.1441 | 18.8052 | 1367.0065 |
| 0.0000 | 2.0000 | 0.6501 | 8.1419 | 18.8396 | 1366.5375 |
| 0.0002 | 2.0000 | 0.6555 | 8.1290 | 19.0212 | 1363.8128 |
| 0.0002 | 2.0000 | 0.6734 | 8.0893 | 19.6476 | 1355.2231 |
| 0.0000 | 2.0000 | 0.6815 | 8.0715 | 19.9389 | 1351.3340 |
| 0.0000 | 2.0000 | 0.7704 | 7.8509 | 23.2671 | 1303.1678 |
| 0.0000 | 2.0000 | 0.7733 | 7.8429 | 23.3808 | 1301.4316 |
| 0.0000 | 2.0000 | 0.7865 | 7.8075 | 23.9046 | 1293.6286 |
| 0.0000 | 2.0000 | 0.8227 | 7.7065 | 25.3722 | 1271.3319 |
| 0.0000 | 2.0000 | 0.8366 | 7.6664 | 25.9492 | 1262.4478 |
| 0.0000 | 2.0000 | 0.8713 | 7.5629 | 27.4220 | 1239.4876 |
| 0.0000 | 2.0000 | 1.0301 | 7.0278 | 34.7887 | 1119.6232 |
| 0.0000 | 2.0000 | 1.1885 | 6.3955 | 43.1286 | 976.3933 |
| 0.0241 | 2.0000 | 1.6714 | 3.7524 | 73.8677 | 376.8456 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | UTS | Young’s Modulus |
|---|---|---|---|---|---|
| 0.2093 | 2.0000 | 0.5780 | 7.2319 | 14.6589 | 1224.2724 |
| 0.2000 | 2.0000 | 0.6566 | 7.1290 | 16.9695 | 1199.8914 |
| 0.2010 | 2.0000 | 0.7181 | 6.9935 | 18.8788 | 1170.5120 |
| 0.2000 | 2.0000 | 0.7197 | 6.9944 | 18.9424 | 1170.4461 |
| 0.2016 | 2.0000 | 0.7205 | 6.9853 | 18.9512 | 1168.8706 |
| 0.2000 | 2.0000 | 0.7317 | 6.9670 | 19.3357 | 1164.4170 |
| 0.2021 | 2.0000 | 0.7390 | 6.9405 | 19.5532 | 1159.1280 |
| 0.2026 | 2.0000 | 0.7397 | 6.9366 | 19.5702 | 1158.4023 |
| 0.2019 | 2.0000 | 0.7440 | 6.9297 | 19.7214 | 1156.6933 |
| 0.2005 | 2.0000 | 0.7549 | 6.9101 | 20.1045 | 1152.0019 |
| 0.2000 | 2.0000 | 0.8001 | 6.7999 | 21.6878 | 1127.4320 |
| 0.2000 | 2.0000 | 0.8243 | 6.7365 | 22.5624 | 1113.3198 |
| 0.2016 | 2.0000 | 0.8404 | 6.6860 | 23.1372 | 1102.4820 |
| 0.2000 | 2.0000 | 0.9602 | 6.3370 | 27.9146 | 1023.6403 |
| 0.2000 | 2.0000 | 0.9771 | 6.2821 | 28.6331 | 1011.2377 |
| 0.2000 | 2.0000 | 1.0785 | 5.9301 | 33.1704 | 931.3588 |
| 0.2000 | 2.0000 | 1.0893 | 5.8902 | 33.6772 | 922.2885 |
| 0.2000 | 2.0000 | 1.2829 | 5.0970 | 43.5611 | 740.7246 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | UTS | Young’s Modulus |
|---|---|---|---|---|---|
| 0.5273 | 2.0000 | 1.5353 | 2.8402 | 49.2434 | 298.4288 |
| 0.5003 | 2.0000 | 1.0391 | 4.9895 | 26.1341 | 791.7830 |
| 0.5002 | 2.0000 | 0.9459 | 5.2731 | 22.7455 | 856.7120 |
| 0.5000 | 2.0000 | 0.9306 | 5.3169 | 22.2262 | 866.6686 |
| 0.5000 | 2.0000 | 0.9201 | 5.3459 | 21.8733 | 873.2882 |
| 0.5000 | 2.0000 | 0.8442 | 5.5434 | 19.4455 | 918.1744 |
| 0.5000 | 1.9998 | 0.8327 | 5.5702 | 19.0966 | 924.3141 |
| 0.5000 | 1.9963 | 0.7745 | 5.6816 | 17.4055 | 950.6806 |
| 0.5000 | 1.9983 | 0.7461 | 5.7549 | 16.6386 | 966.4199 |
| 0.5000 | 2.0000 | 0.7364 | 5.7849 | 16.3898 | 972.5752 |
| 0.5000 | 2.0000 | 0.7362 | 5.7855 | 16.3829 | 972.6952 |
| 0.5000 | 2.0000 | 0.7362 | 5.7855 | 16.3829 | 972.6952 |
| 0.5000 | 2.0000 | 0.7327 | 5.7926 | 16.2907 | 974.2889 |
| 0.5000 | 2.0000 | 0.6919 | 5.8714 | 15.2614 | 991.8523 |
| 0.5000 | 2.0000 | 0.6786 | 5.8957 | 14.9396 | 997.2479 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | Young’s Modulus | UTS * |
|---|---|---|---|---|---|
| 0.0000 | 2.0000 | 0.1598 | 8.7384 | 1483.2924 | 6.7355 |
| 0.0000 | 2.0000 | 0.3464 | 8.6231 | 1465.6664 | 10.2167 |
| 0.0000 | 2.0000 | 0.1535 | 8.7399 | 1483.3125 | 6.6427 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | Young’s Modulus | UTS * |
|---|---|---|---|---|---|
| 0.3998 | 2.0000 | 0.6095 | 6.3738 | 1081.4500 | 14.0438 |
| 0.2000 | 2.0000 | 0.3984 | 7.5167 | 1281.1804 | 10.5416 |
| 0.3296 | 2.0000 | 0.4227 | 6.2962 | 1076.4423 | 10.2521 |
| Fly Ash | Sugarcane Fiber | CNT | Yield Strength | Young’s Modulus | UTS * |
|---|---|---|---|---|---|
| 0.5000 | 2.0000 | 0.5000 | 6.1543 | 1053.4000 | 11.3038 |
| 2.0000 | 1.6414 | 0.6483 | 4.1821 | 733.3386 | 10.1031 |
| 1.9946 | 1.9946 | 0.7960 | 5.3122 | 930.3963 | 11.0937 |
| 0.6780 | 1.9180 | 0.9287 | 4.3665 | 712.0578 | 19.6167 |
| 2.0000 | 1.9803 | 0.6774 | 5.3314 | 941.1743 | 12.0220 |
| 2.0000 | 2.0000 | 0.5781 | 5.4256 | 961.7629 | 13.4703 |
| 2.0000 | 2.0000 | 0.6012 | 5.4264 | 961.2842 | 13.1353 |
| 0.7813 | 1.9717 | 0.8859 | 4.5504 | 753.1745 | 17.4100 |
| Optimization Using (MOEA/D) Algorithm | Optimization Using RSM | ||
|---|---|---|---|
| Fly Ash % (wt.) | Yield Strength (MPa) | Fly Ash % (wt.) | Yield Strength (MPa) |
| 0.2 | 7.5167 | 0.5 | 5.53 |
| Sugarcane fiber % (wt.) | Ultimate tensile stress (MPa) | Sugarcane fiber % (wt.) | Ultimate tensile stress (MPa) |
| 2 | 10.5416 | 0.5 | 19.62 |
| CNT % (wt.) | Young’s modulus (MPa) | CNT % (wt.) | Young’s modulus (MPa) |
| 0.3984 | 1281.1804 | 0.5 | 914.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkatachalam, G.; Gopu, A.; Velu, P.S.; Venkataraman, N.; Salunke, D.R.; Mukkamala, R.R. Study on Tensile Properties of Fly Ash, Sugarcane Fiber and Carbon Nanotube-Reinforced Polymer Matrix Composite Using Objective Evolutionary Algorithm. Nanomaterials 2022, 12, 4112. https://doi.org/10.3390/nano12234112
Venkatachalam G, Gopu A, Velu PS, Venkataraman N, Salunke DR, Mukkamala RR. Study on Tensile Properties of Fly Ash, Sugarcane Fiber and Carbon Nanotube-Reinforced Polymer Matrix Composite Using Objective Evolutionary Algorithm. Nanomaterials. 2022; 12(23):4112. https://doi.org/10.3390/nano12234112
Chicago/Turabian StyleVenkatachalam, Gopalan, Arunkumar Gopu, Pitchumani Shenbaga Velu, Neelanarayanan Venkataraman, Dinesh Ramesh Salunke, and Raghava Rao Mukkamala. 2022. "Study on Tensile Properties of Fly Ash, Sugarcane Fiber and Carbon Nanotube-Reinforced Polymer Matrix Composite Using Objective Evolutionary Algorithm" Nanomaterials 12, no. 23: 4112. https://doi.org/10.3390/nano12234112
APA StyleVenkatachalam, G., Gopu, A., Velu, P. S., Venkataraman, N., Salunke, D. R., & Mukkamala, R. R. (2022). Study on Tensile Properties of Fly Ash, Sugarcane Fiber and Carbon Nanotube-Reinforced Polymer Matrix Composite Using Objective Evolutionary Algorithm. Nanomaterials, 12(23), 4112. https://doi.org/10.3390/nano12234112







